An Asymmetric Model Position Dependent Mass: Quantum Mechanical Study
Abstract
1. Introduction
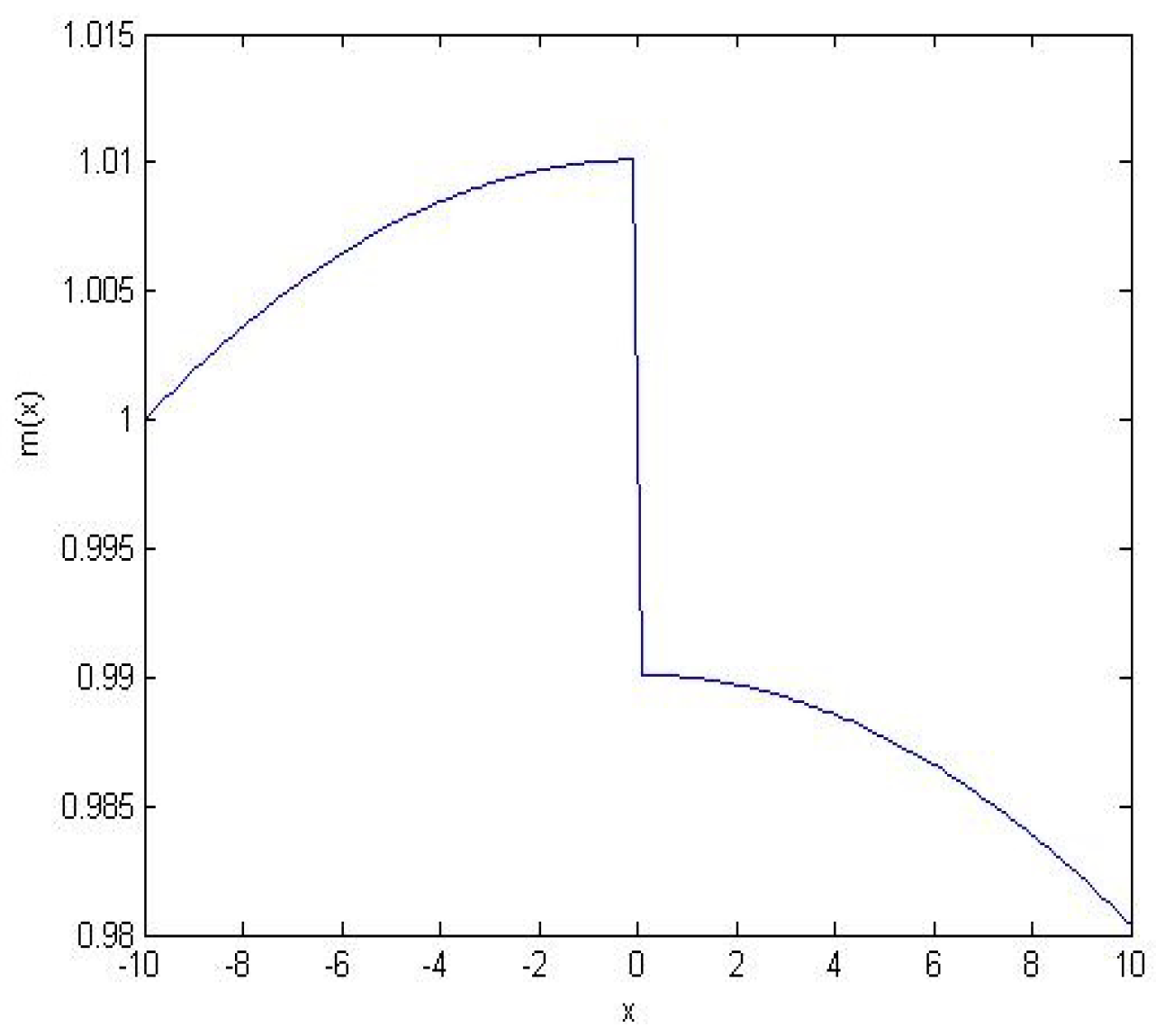
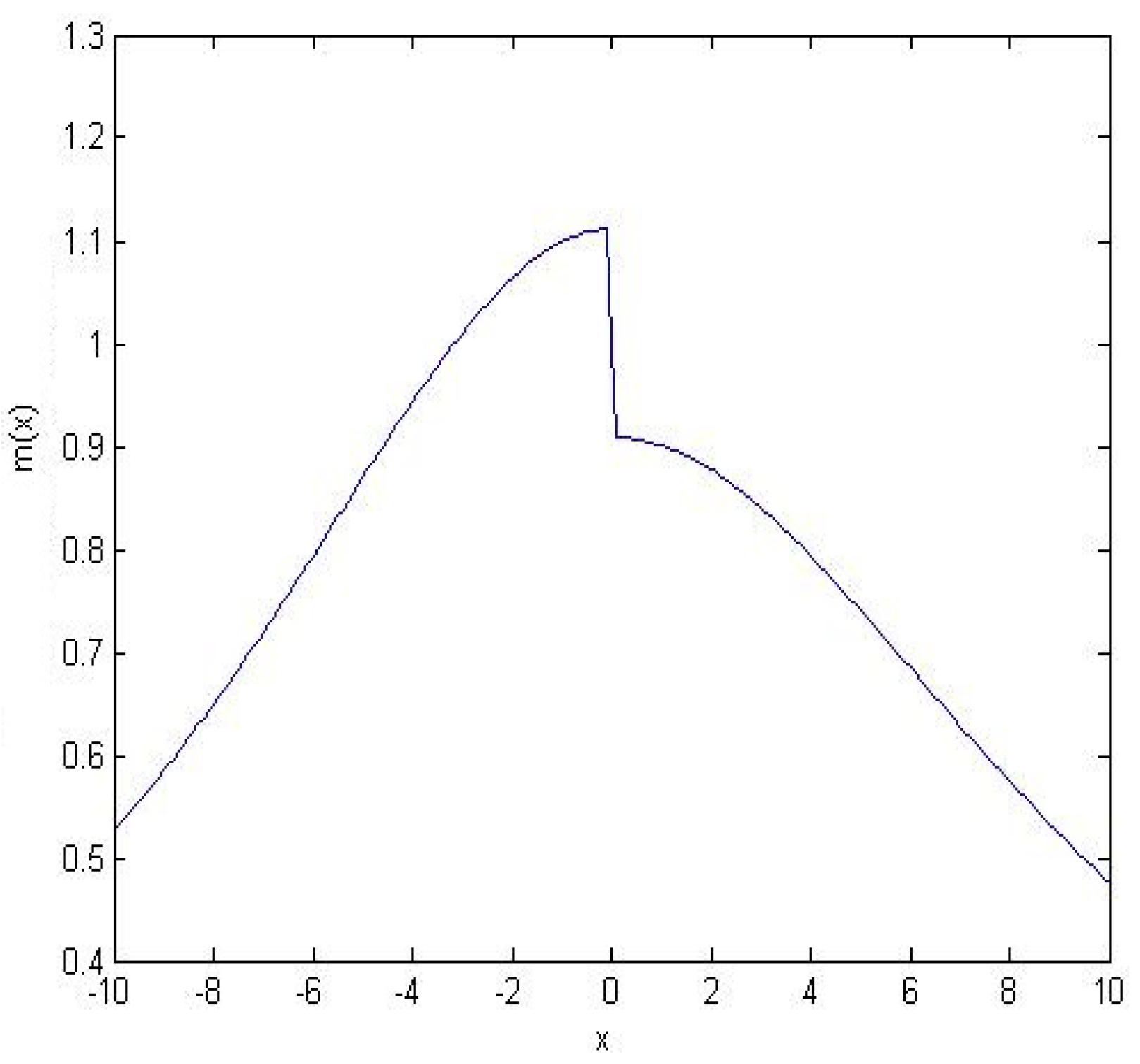
2. Characteristic Features of New Asymmetric PDM
3. Quantum Mechanical Study on the New PDM Systems
4. Effect of Potential
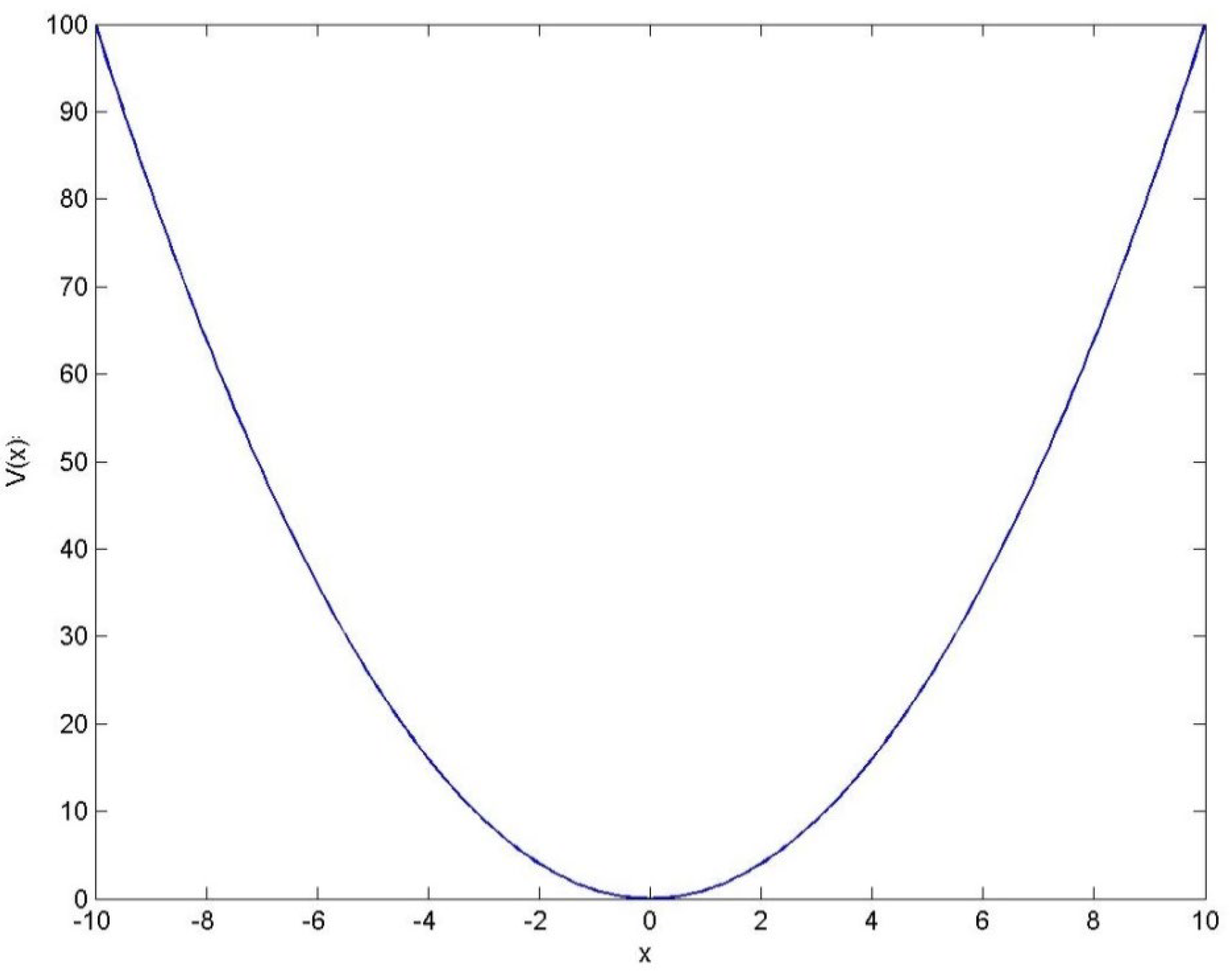
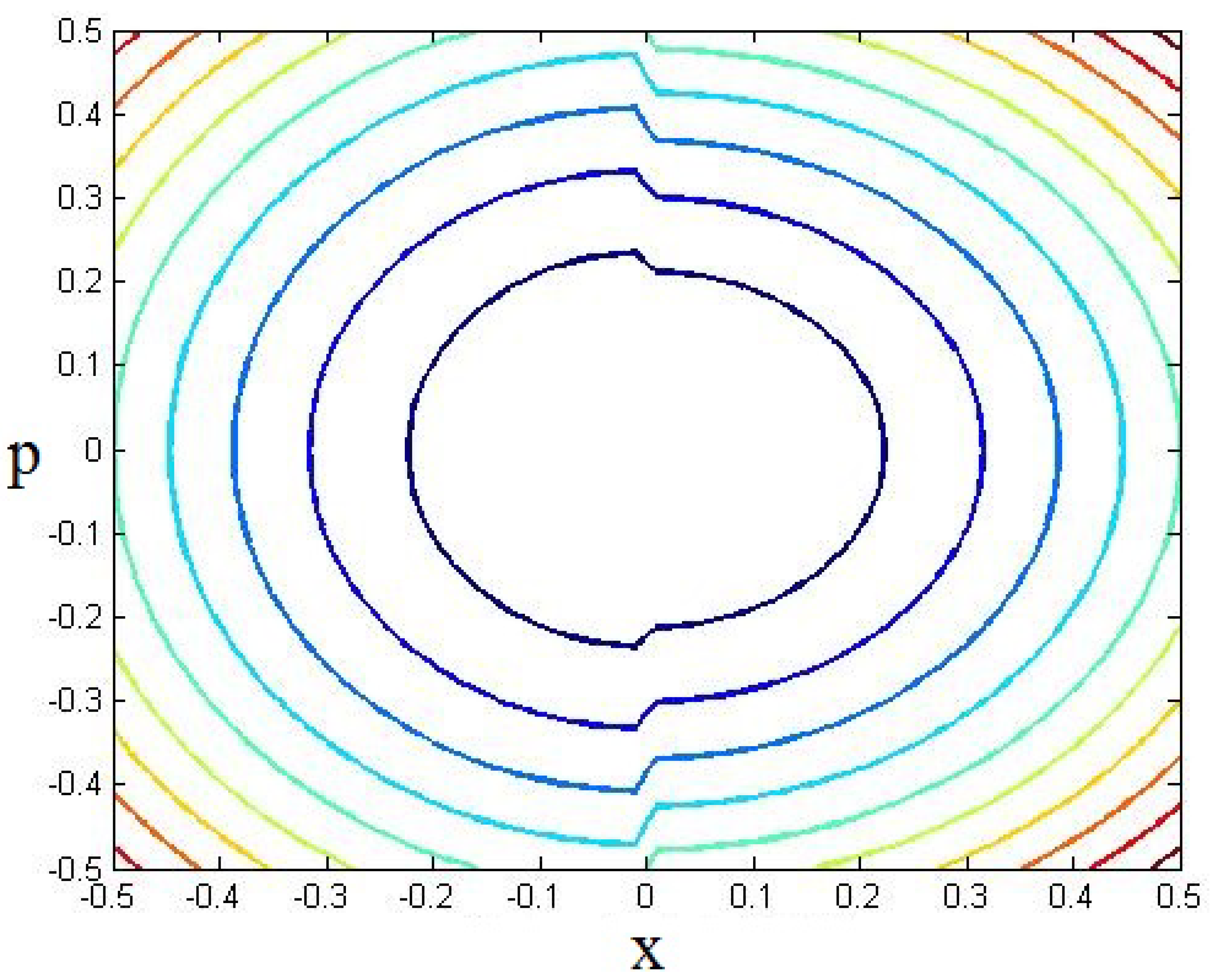
4.1. Single Well Potential
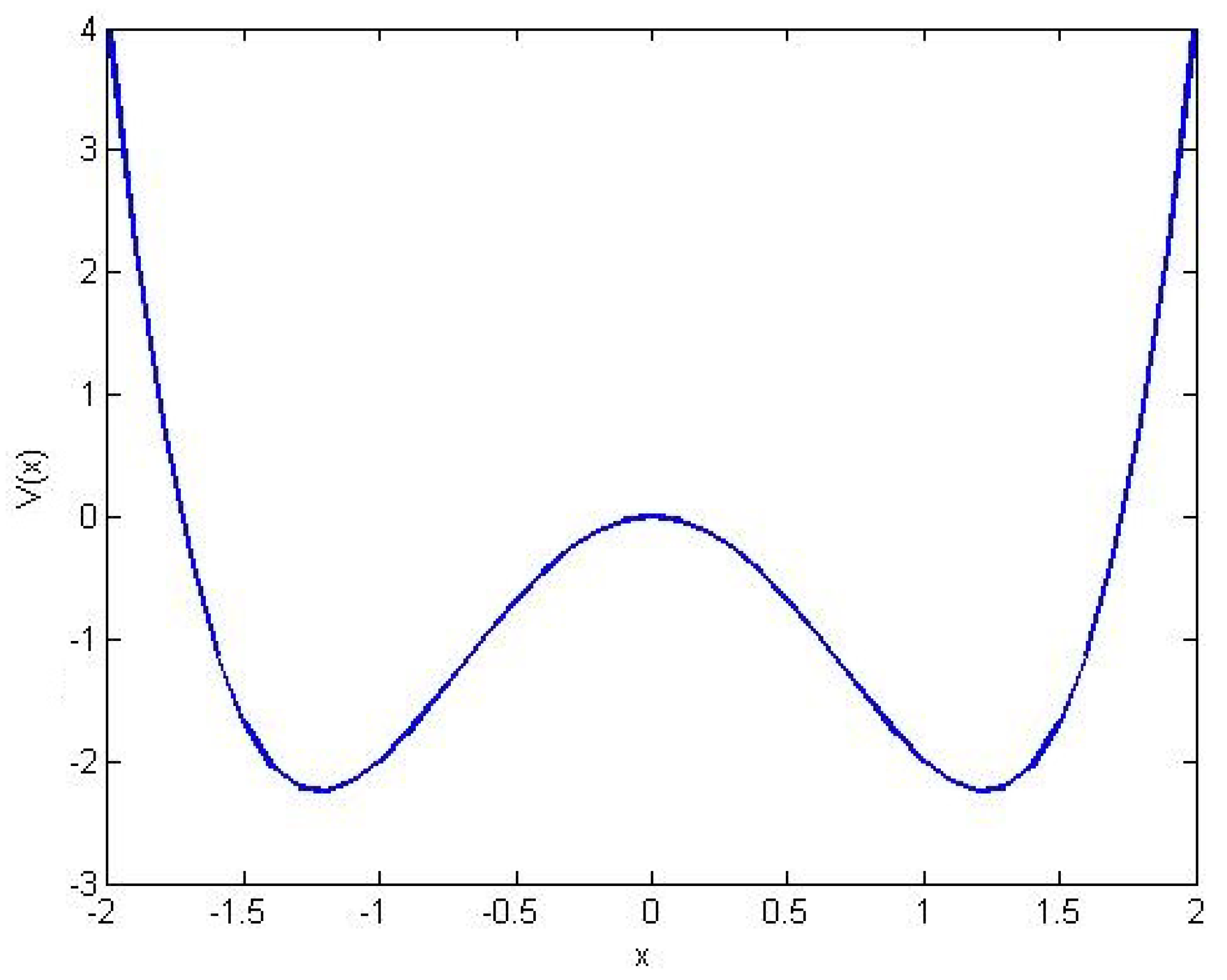
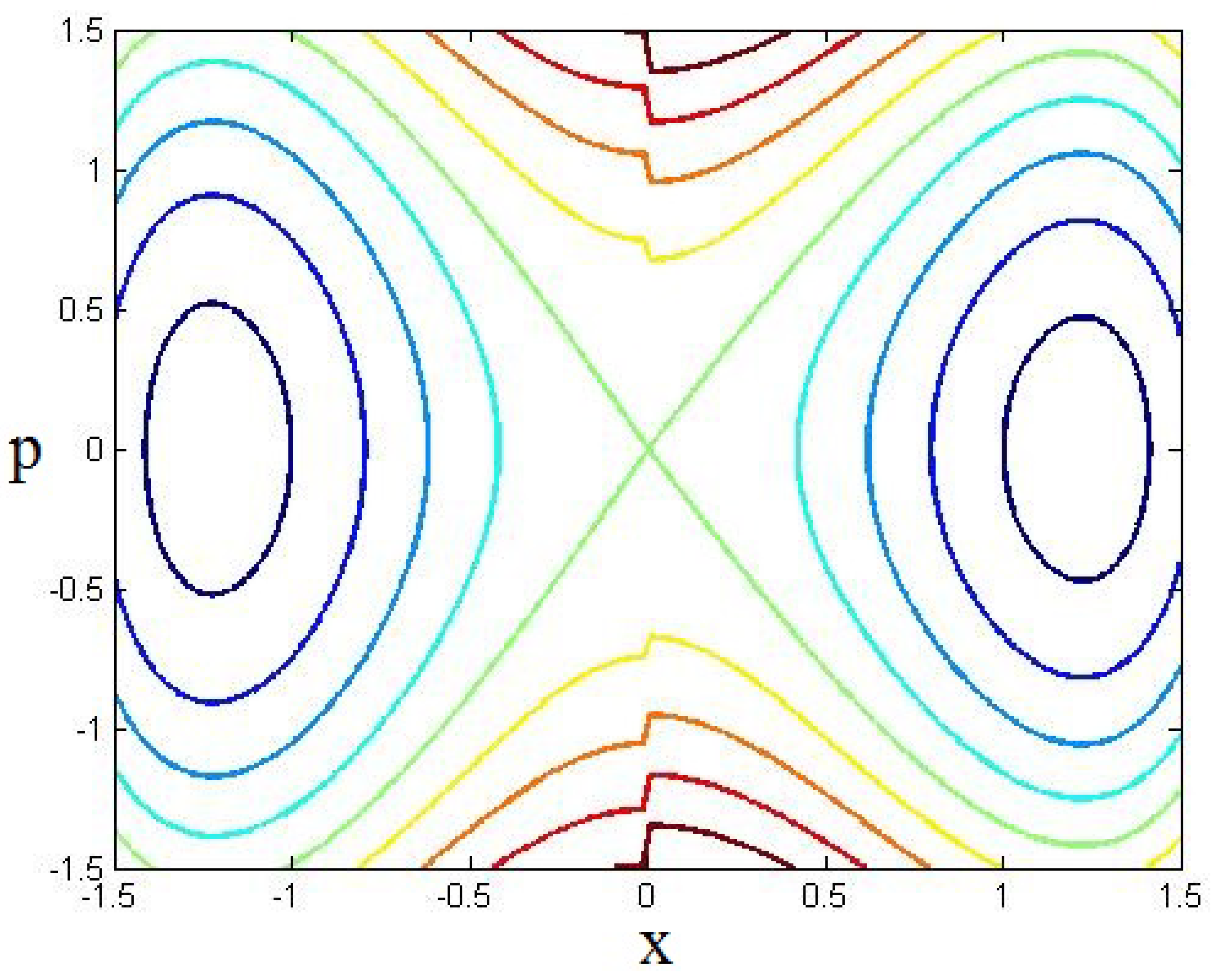
4.2. Double Well Potential
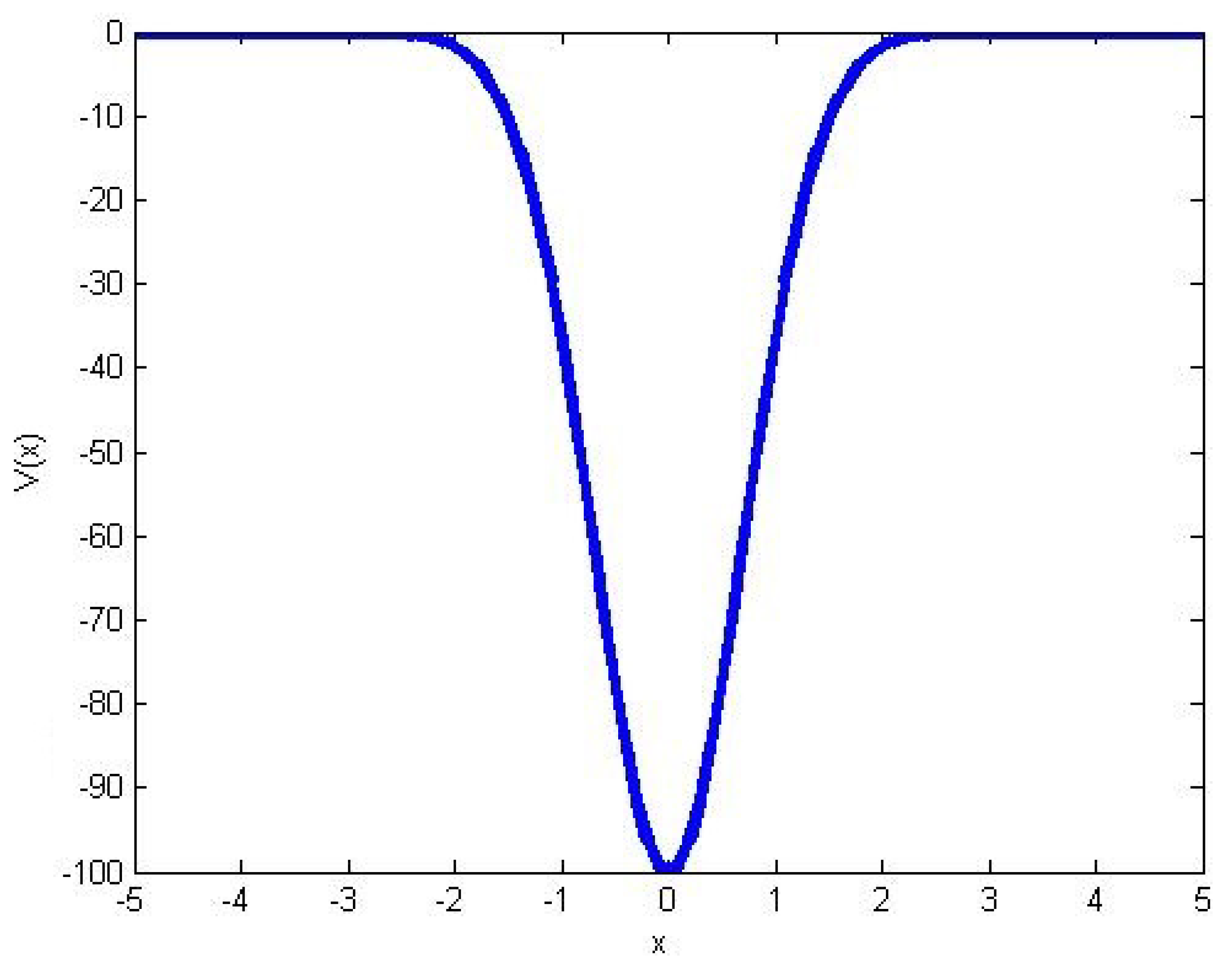
4.3. Gaussian Single Well Potential
4.4. Rath Triangular Potential
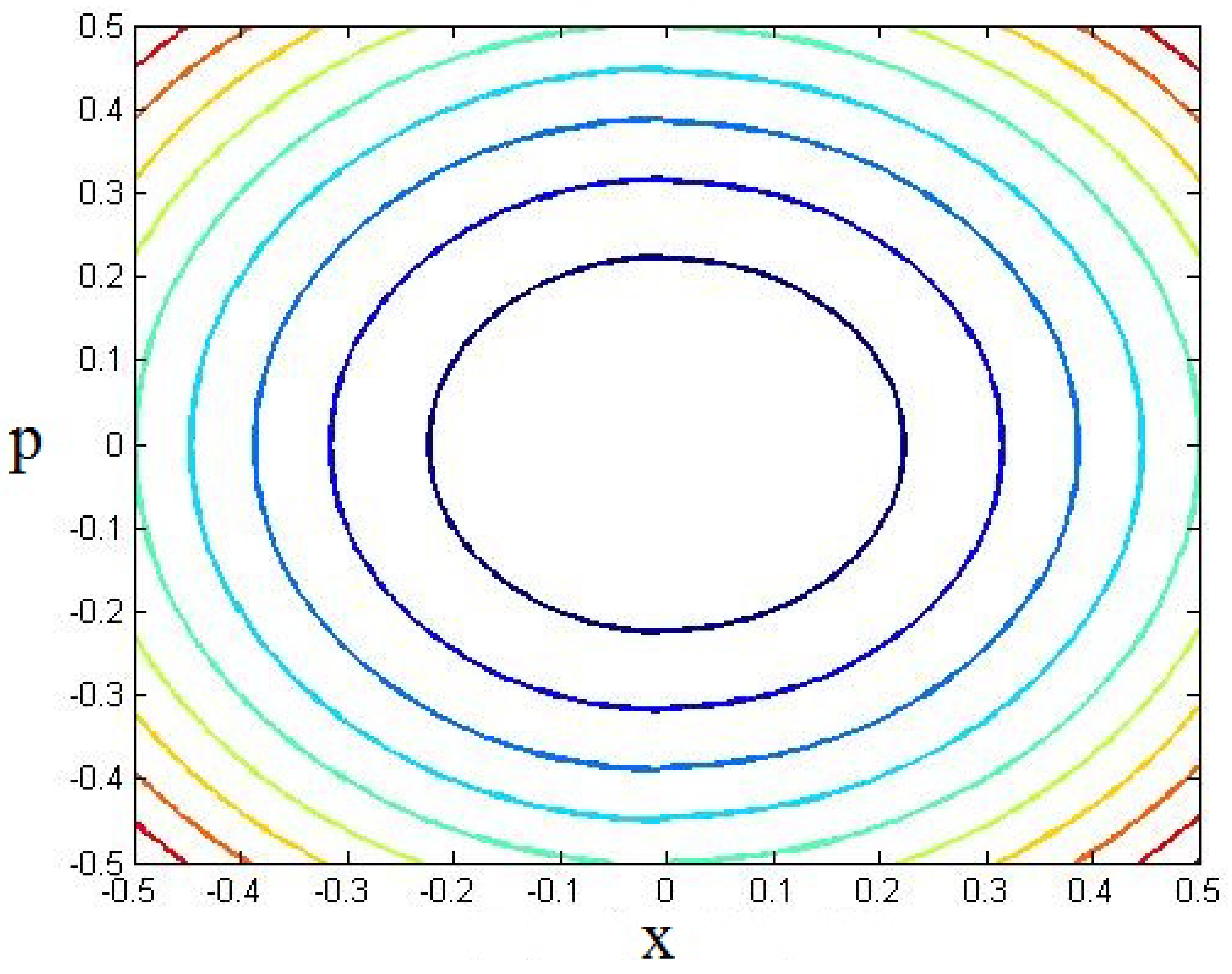
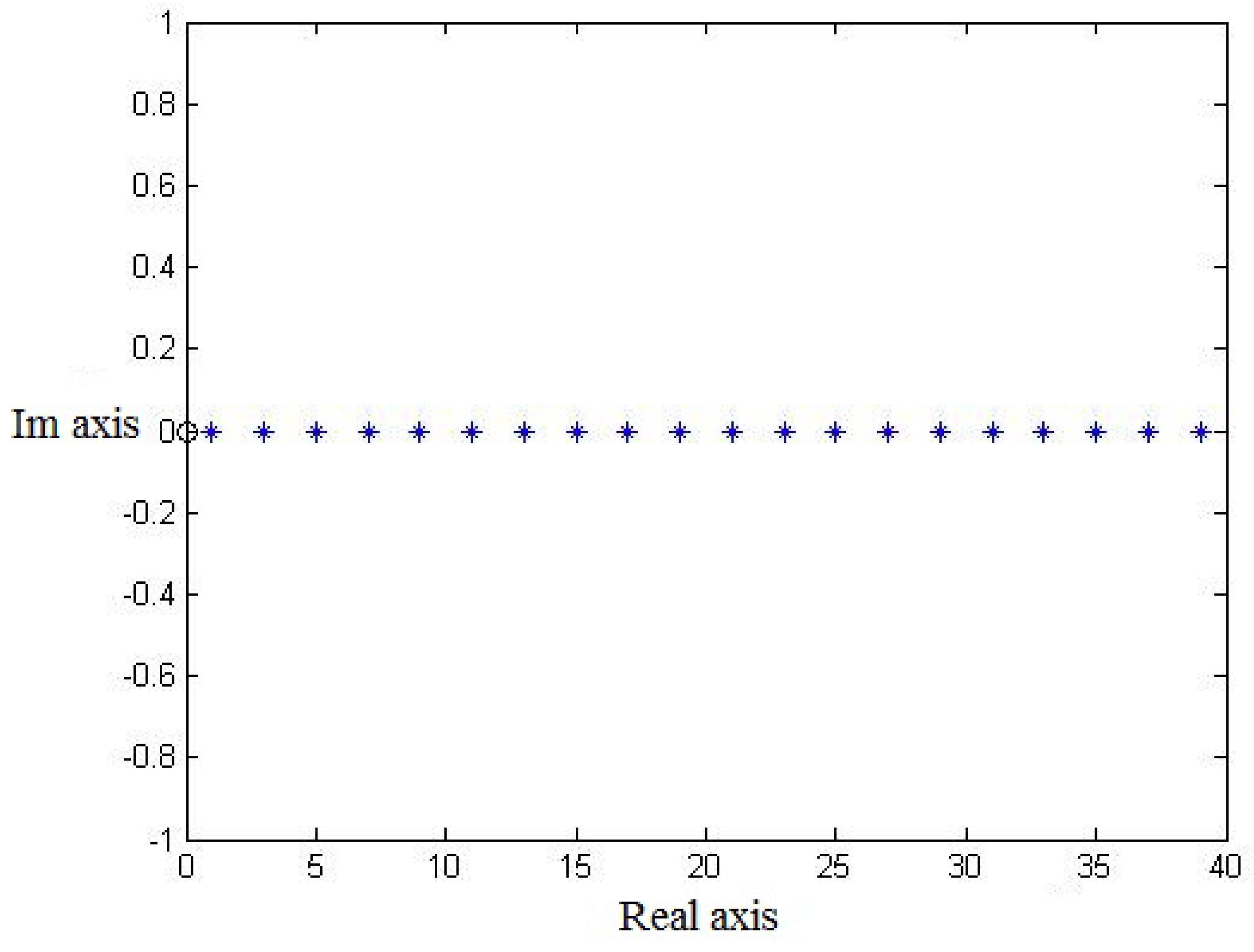
5. Validity of Uncertainty Relation
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Asad, J.; Mallick, P.; Samei, M.E.; Rath, B.; Mohapatra, P.; Shanak, H.; Jarrar, R. Asymmetric variation of a finite mass harmonic like oscillator. Results Phys. 2020, 19, 103335. [Google Scholar] [CrossRef]
- Rath, B.; Mallick, P.; Mohapatra, P.; Asad, J.; Shanak, H.; Jarrar, R. Position-dependent finite symmetric mass harmonic like oscillator: Classical and quantum mechanical study. Open Phys. 2021, 19, 266–276. [Google Scholar] [CrossRef]
- Dong, S.-H.; Huang, W.-H.; Sedaghatnia, P.; Hassanabadi, H. Exact solutions of an exponential type position dependent mass problem. Results Phys. 2022, 34, 105294. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. A generalized self-consistent approach to study position-dependent mass in semiconductors organic heterostructures and crystalline impure materials. Phys. E 2020, 134, 114295. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. A new approach to Schrodinger equation with position-dependent mass and its implications in quantum dots and semiconductors. J. Phys. Chem. Sol. 2020, 140, 109384. [Google Scholar] [CrossRef]
- Peter, A.J. The effect of position dependent effective mass of hydrogrnic impurities in parabolic GaAs/GaAlAs quantum dots in a strong magnetic field. Int. J. Mod. Phys. B 2009, 23, 5109. [Google Scholar] [CrossRef]
- Sinha, A. Scattering states of a particle, with position-dependent mass, in a double heterojunction. Eur. Phys. Lett. 2011, 96, 20008. [Google Scholar] [CrossRef]
- Costa Filho, R.N.; Almeida, M.P.; Farias, G.A.; Andrade, J.S., Jr. Displacement operator for quantum systems with position-dependent mass. Phys. Rev. A 2011, 84, 050102. [Google Scholar] [CrossRef]
- Ullah, K.; Ullah, H. Enhanced optomechanically induced transparency and slow/fast light in a position-dependent mass optomechanics. Eur. Phys. J. D 2020, 74, 197. [Google Scholar] [CrossRef]
- Da Costa, B.G.; Gomez, I.S.; Rath, B. Exact solution and coherent states of an asymmetric oscillator with position-dependent mass. J. Math. Phys. 2023, 64, 012102. [Google Scholar] [CrossRef]
- Biswas, K.; Saha, J.P.; Patra, P. On the position-dependent effective mass Hamiltonian. Eur. Phys. J. Plus 2020, 135, 457. [Google Scholar] [CrossRef]
- Cruz y Cruz, S.; Rosas-Ortiz, O. Position-dependent mass oscillators and coherent states. J. Phys. A Math. Theor. 2009, 42, 185205. [Google Scholar] [CrossRef]
- Sari, H.; Kasapoglu, E.; Sakiroglu, S.; Sökmen, I.; Duque, C.A. Effect of position-dependent effective mass on donor impurity- and exciton-related electronic and optical properties of 2D Gaussian quantum dots. Eur. Phys. J. Plus 2022, 137, 341. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Dynamics of position-dependent mass particle in crystal lattices microstructures. Phys. E 2021, 127, 114525. [Google Scholar] [CrossRef]
- Silva, J.E.G.; Furtado, J.; Ramos, A.C.A. Position-dependent mass effects on a bilayer graphene catenoid bridge. Eur. J. Phys. B 2021, 94, 127. [Google Scholar] [CrossRef]
- Roy-Layinde, T.O.; Omoteso, K.A.; Oyero, B.A.; Laoye, J.A.; Vincent, U.E. Vibrational resonance of ammonia molecule with doubly singular position-dependent mass. Eur. J. Phys. B 2022, 95, 80. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Quantum dynamics in low-dimensional systems with position-dependent mass and product-like fractal geometry. Phys. E 2021, 134, 114827. [Google Scholar] [CrossRef]
- Ghosh, A.P.; Mandal, A.; Sarkar, S.; Ghosh, M. Influence of position-dependent effective mass on the nonlinear optical properties of impurity doped quantum dots in presence of Gaussian white noise. Opt. Commun. 2016, 367, 325–334. [Google Scholar] [CrossRef]
- Alpdogan, S.; Havare, A. Dirac Particle for the Position Dependent Mass in the Generalized Asymmetric Woods-Saxon Potential. Adv. High Energy Phys. 2014, 2014, 973847. [Google Scholar] [CrossRef]
- Aydogdu, O.; Arda, A.; Sever, R. Effective-mass Dirac equation for Woods-Saxon potential: Scattering, bound states, and resonances. J. Math. Phys. 2012, 53, 042106. [Google Scholar] [CrossRef]
- Rajashabala, S.; Navaneethakrishnan, K. Effects of dielectric screening and position dependent effective mass on donor binding energies and on diamagnetic susceptibility in a quantum well. Superlattices Microstruct. 2008, 43, 247–261. [Google Scholar] [CrossRef]
- Amir, N.; Iqbal, S. Coherent states for nonlinear harmonic oscillator and some of its properties. J. Math. Phys. 2015, 56, 062108. [Google Scholar] [CrossRef]
- Dos Santos, M.A.; Gomez, I.S.; da Costa, B.G.; Mustafa, O. Probability density correlation for PDM-Hamiltonians and superstatistical PDM-partition functions. Eur. Phys. J. Plus 2021, 136, 96. [Google Scholar] [CrossRef]
- Chen, Y.; Yan, J.; Mihalache, D. Stable flat-top solitons and peakons in the 𝓟𝓣-symmetric δ-signum potentials and nonlinear media. Chaos 2019, 29, 083108. [Google Scholar] [CrossRef]
- Marques, F.; Negrini, O.; da Silva, A.J. A new simple class of superpotentials in SUSY quantum mechanics. J. Phys. A Math. Theor. 2012, 45, 115307. [Google Scholar] [CrossRef]
- Rath, B.; Mallick, P.; Akande, J.; Mohapatra, P.P.; Adja, D.K.K.; Koudahoun, L.H.; Kpomahou, Y.J.F.; Monsia, M.D.; Sahoo, R.R. A General type of Liénard Second Order Differential Equation: Classical and Quantum Mechanical Study. Proc. Indian Natl. Sci. Acad. 2017, 83, 935–940. [Google Scholar]
- Von Roos, O. Position-dependent effective masses in semiconductor theory. Phys. Rev. B 1983, 27, 7547. [Google Scholar] [CrossRef]
- Von Roos, O.; Mavromatis, H. Position-dependent effective masses in semiconductor theory. II. Phys. Rev. B 1985, 31, 2294. [Google Scholar] [CrossRef]
- Rath, B.; Mavromatis, H.A. Energy-level calculation through modified Hill determinant approach: For general oscillator. Indian J. Phys. 1999, 73B, 641. [Google Scholar]
- Killingbeck, J.P.; Scott, T.; Rath, B. A matrix method for power series potentials. J. Phys. A Math. Gen. 2000, 33, 6999. [Google Scholar] [CrossRef]
- Jones, H.F. Comment on Solvable model of bound states in the continuum (BIC) in on dimension (2019, 94, 105214). Phys. Scr. 2021, 96, 087001. [Google Scholar] [CrossRef]
- Zettili, N. Quantum Mechanics: Concepts and Applications, 2nd ed.; John Wiley: New York, NY, USA, 2001; p. 37. [Google Scholar]
- Da Costa, B.G.; Da Silva, G.A.C.; Gomez, I.S. Supersymmetric quantum mechanics and coherent states for a deformed oscillator with position-dependent effective mass. J. Math. Phys. 2021, 62, 092101. [Google Scholar] [CrossRef]
- Asad, J.; Mallick, P.; Samei, M.E.; Rath, B.; Mohapatra, P.; Shanak, H.; Jarrar, R. Reply to Comment on “Asymmetric Variation of a Finite Mass Harmonic Like Oscillator”. Results Phys. 2022, 32, 105148. [Google Scholar] [CrossRef]
- Mathews, P.M.; Lakshmanan, M. On a unique nonlinear oscillator. Q. Appl. Math. 1974, 32, 215–218. [Google Scholar] [CrossRef]
- Ahmed, Z.; Kumar, S.; Ghosh, D.; Goswami, T. Solvable model of bound states in the continuum (BIC) in one dimension. Phys. Scr. 2019, 94, 105214. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rath, B.; Mallick, P.; Asad, J.; Wannan, R.; Jarrar, R.; Shanak, H. An Asymmetric Model Position Dependent Mass: Quantum Mechanical Study. Axioms 2023, 12, 318. https://doi.org/10.3390/axioms12040318
Rath B, Mallick P, Asad J, Wannan R, Jarrar R, Shanak H. An Asymmetric Model Position Dependent Mass: Quantum Mechanical Study. Axioms. 2023; 12(4):318. https://doi.org/10.3390/axioms12040318
Chicago/Turabian StyleRath, Biswanath, Pravanjan Mallick, Jihad Asad, Rania Wannan, Rabab Jarrar, and Hussein Shanak. 2023. "An Asymmetric Model Position Dependent Mass: Quantum Mechanical Study" Axioms 12, no. 4: 318. https://doi.org/10.3390/axioms12040318
APA StyleRath, B., Mallick, P., Asad, J., Wannan, R., Jarrar, R., & Shanak, H. (2023). An Asymmetric Model Position Dependent Mass: Quantum Mechanical Study. Axioms, 12(4), 318. https://doi.org/10.3390/axioms12040318






