An Accelerated Double-Integral ZNN with Resisting Linear Noise for Dynamic Sylvester Equation Solving and Its Application to the Control of the SFM Chaotic System
Abstract
1. Introduction
- Based on the novel ZNN design formula, an innovative ADIZNN is constructed for settling the dynamic Sylvester equation under the linear noise.
- The ADIZNN model has a novel double integral structure and activation function, which guarantees accelerated convergence and enhanced anti-noise capacity.
- Theoretical analyses and simulation results are provided to ensure that the ADIZNN model can handle the DSE with excellent convergence and robustness.
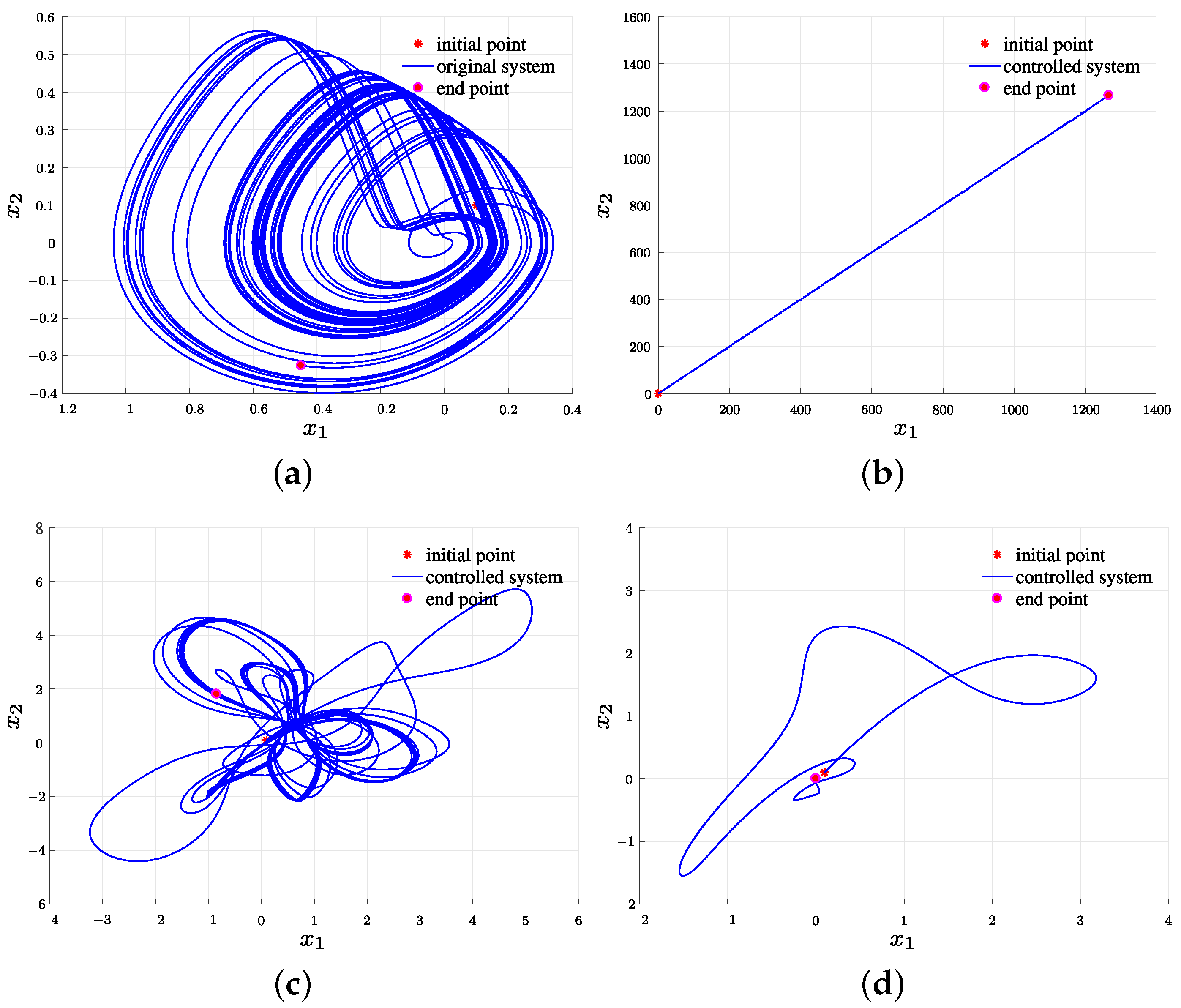
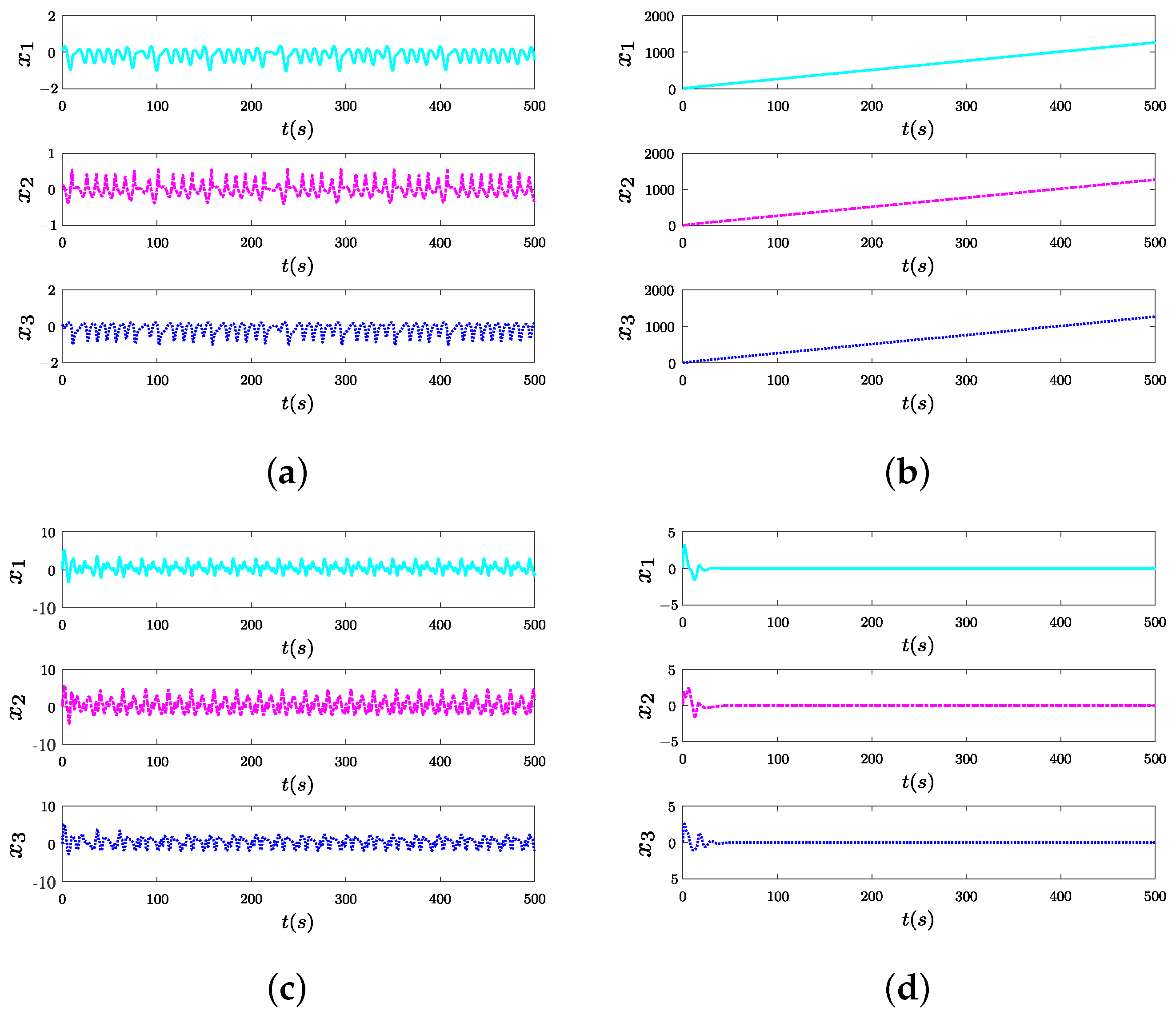
- Chaos control schemes of the TFM chaotic system are established to display that the controller based on the ADIZNN has superior performance than that based on the OZNN and IEZNN.
2. DSE Description and Models Design
2.1. Description of DSE
2.2. Relevant Models Design
2.3. ADIZNN Model Design
- The and sign(ı) of FTAF (14) are to suppress noise;
- Based on the novel ZNN design formula, an innovative ADIZNN is constructed for settling the DSE under the linear noise.
- The novel double integral structure and activation function, which guarantees accelerated convergence and enhanced anti-noise capacity.
3. Theoretical Analyses
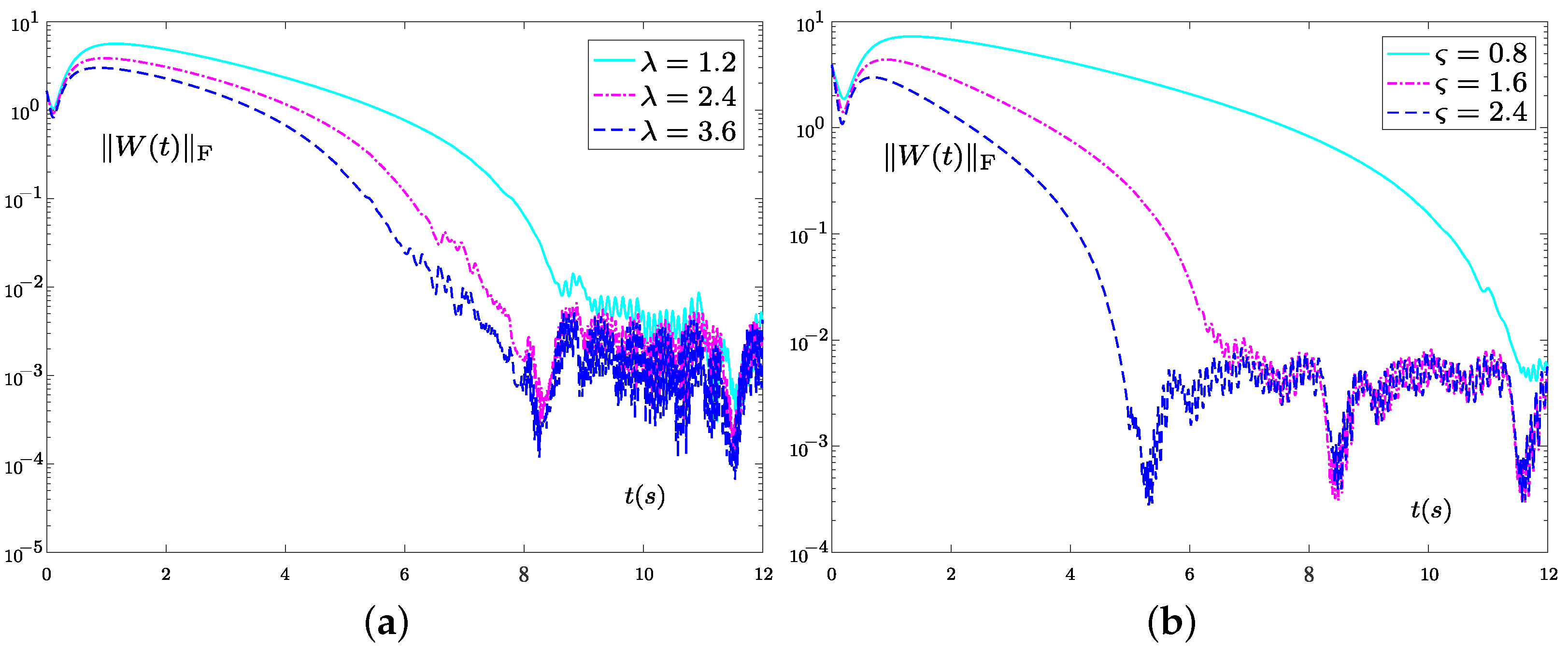
3.1. Convergence
3.2. Robustness
4. Examples Verification
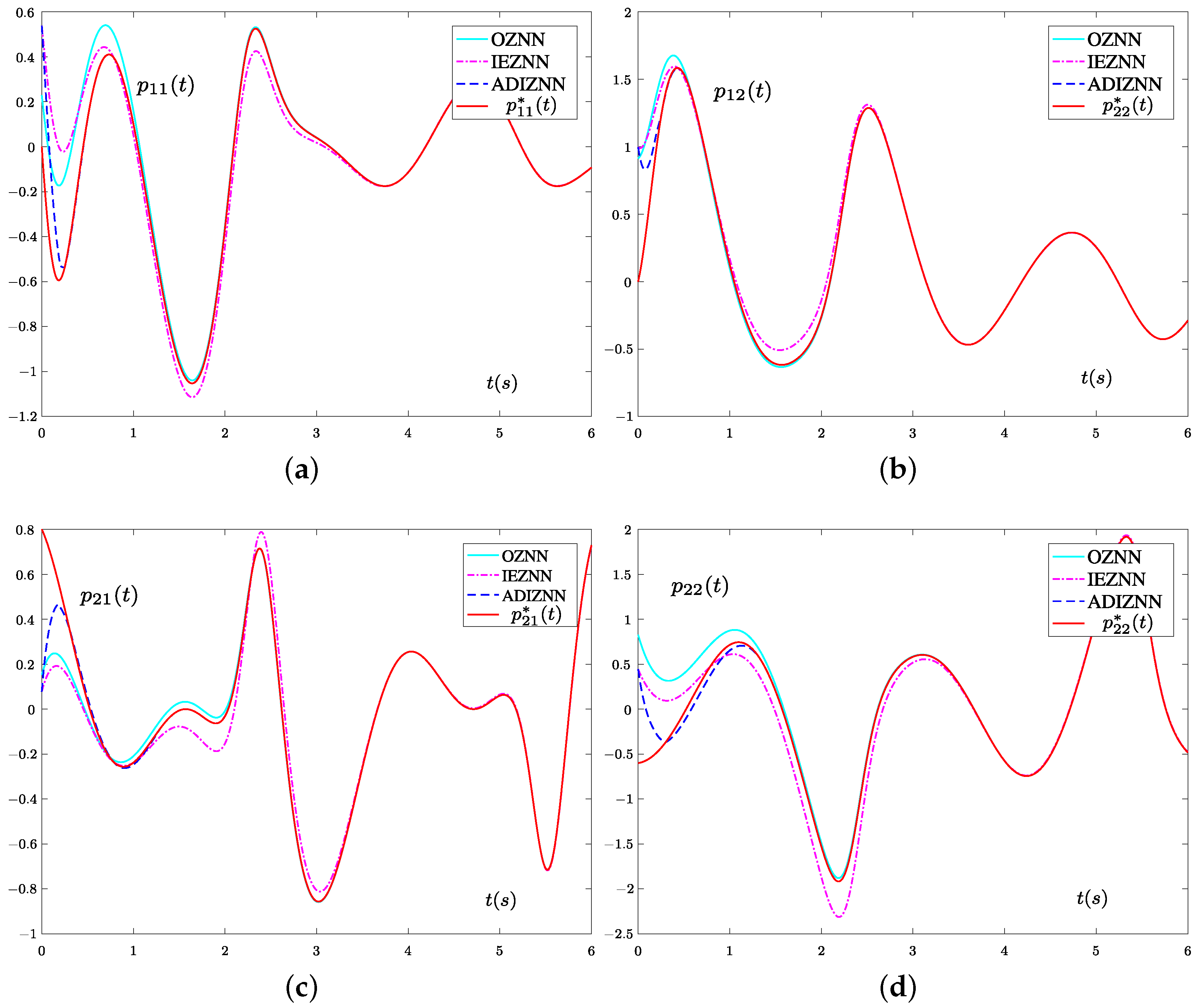
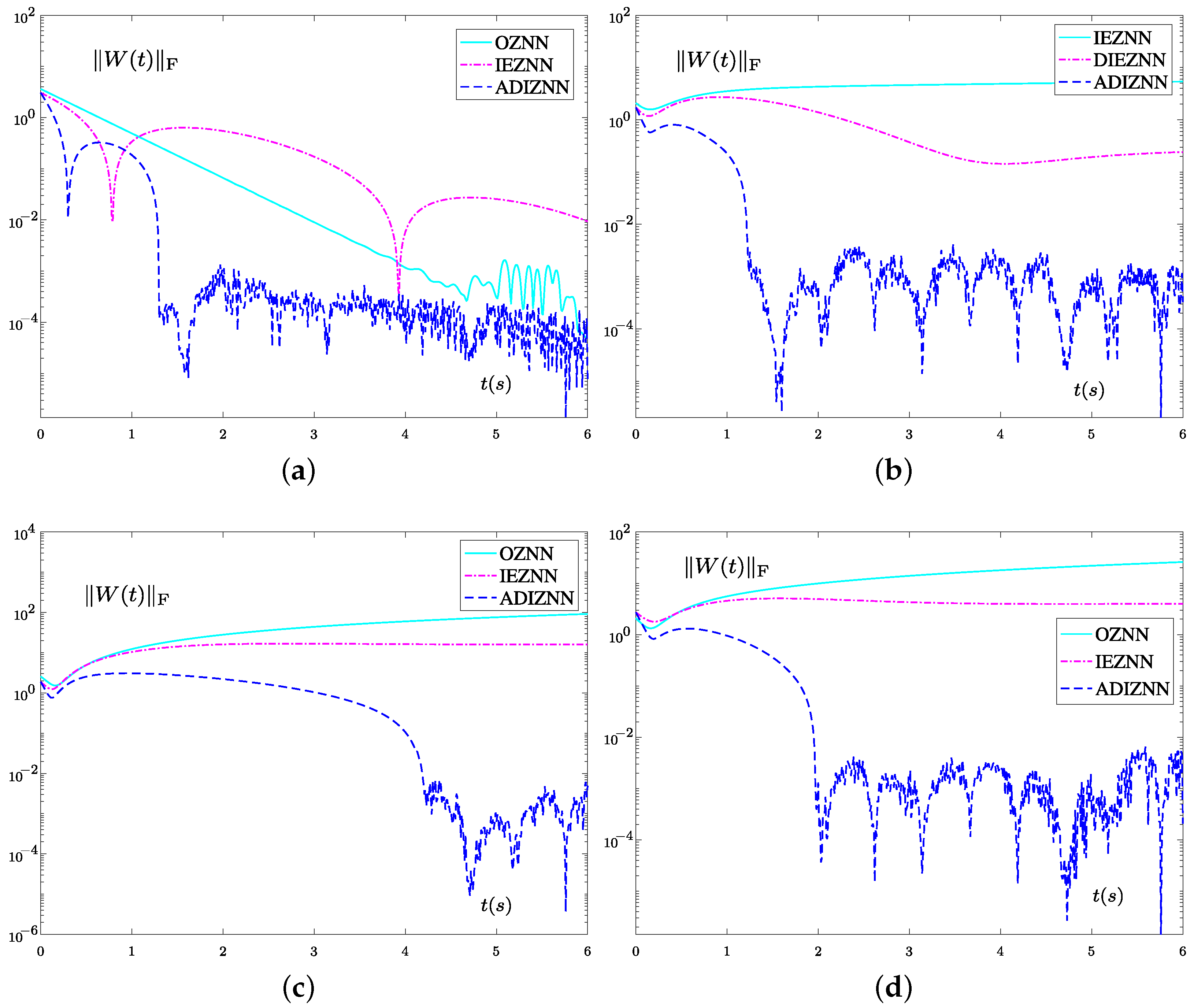
4.1. Experiment 1
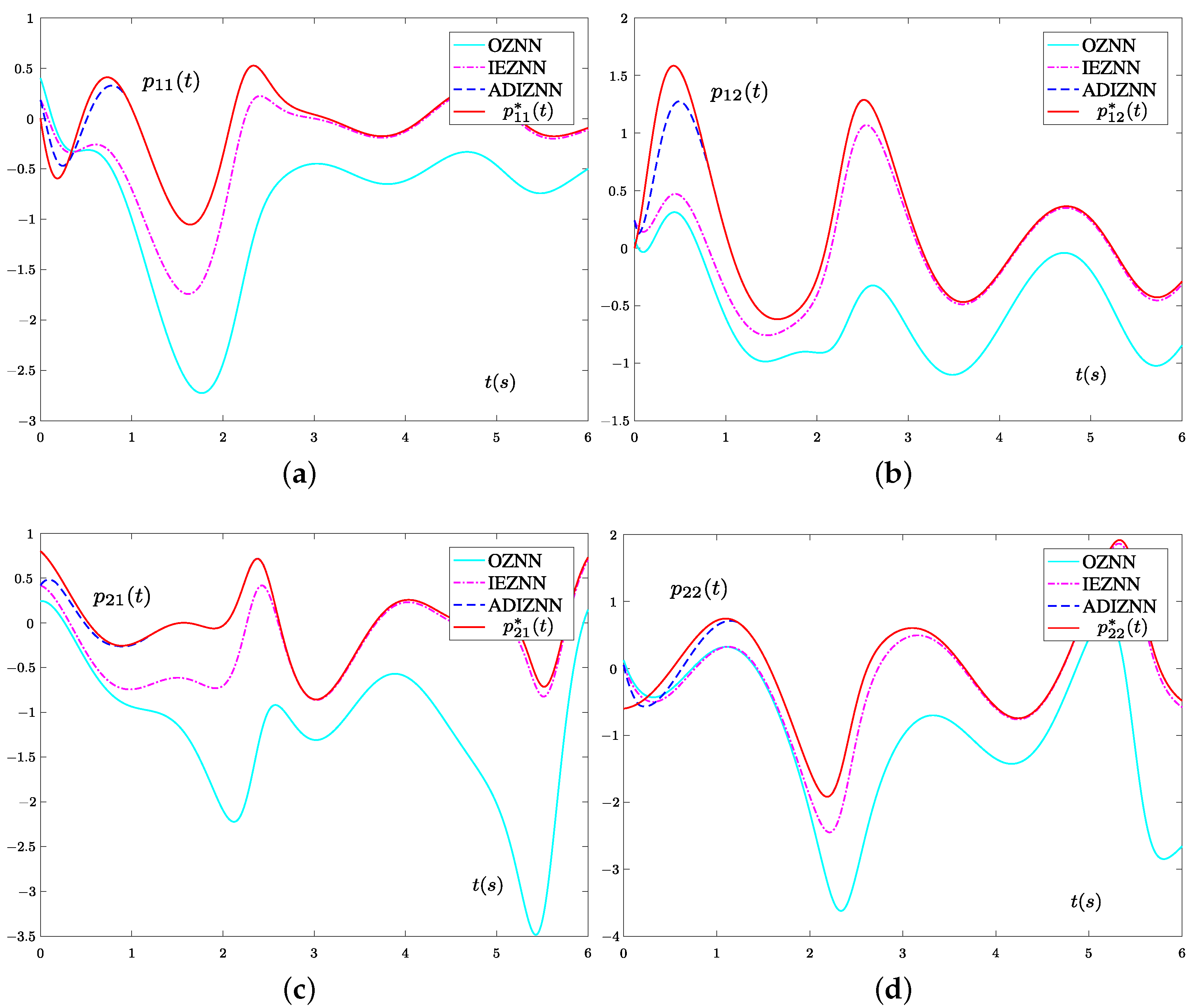
4.2. Experiment 2
5. Application to the Control of the Sine Function Memristor Chaotic System
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DSE | Dynamic Sylvester equation |
| ZNN | Zeroing neural network |
| OZNN | Original zeroing neural network |
| ADIZNN | Accelerated double integral ZNN |
| SFM | Sine function memristor |
| RNNs | recurrent neural networks |
| GNN | Gradient neural network |
| IEZNN | integral enhanced ZNN model |
| FTAF | fixed-time activation function |
References
- Wei, Q.; Dobigeon, N.; Tourneret, J.Y.; Bioucas-Dias, J.; Godsill, S. R-FUSE: Robust fast fusion of multiband images based on solving a Sylvester equation. IEEE Signal Process. Lett. 2016, 23, 1632–1636. [Google Scholar] [CrossRef]
- Huo, L.; Yang, S.; Jiao, L.; Wang, S.; Shi, J. Local graph regularized coding for salient object detection. Infrared Phys. Technol. 2016, 77, 124–131. [Google Scholar] [CrossRef]
- Shaker, H.R.; Tahavori, M. Control configuration selection for bilinear systems via generalised Hankel interaction index array. Int. J. Control 2015, 88, 30–37. [Google Scholar] [CrossRef]
- Dolgov, S.; Pearson, J.W.; Savostyanov, D.V.; Stoll, M. Fast tensor product solvers for optimization problems with fractional differential equations as constraints. Appl. Math. Comput. 2016, 273, 604–623. [Google Scholar] [CrossRef]
- Jin, L.; Yan, J.; Du, X.; Xiao, X.; Fu, D. RNN for solving time-variant generalized Sylvester equation with applications to robots and acoustic source localization. IEEE Trans. Ind. Inform. 2020, 16, 6359–6369. [Google Scholar] [CrossRef]
- Katsikis, V.N.; Mourtas, S.D.; Stanimirović, P.S.; Zhang, Y. Solving complex-valued time-varying linear matrix equations via QR decomposition with applications to robotic motion tracking and on angle-of-arrival localization. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 3415–3424. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Han, L.; Xiao, X.; Liao, B.; Peng, C. A gradient-based neural network accelerated for vision-based control of an RCM-constrained surgical endoscope robot. Neural Comput. Appl. 2022, 34, 1329–1343. [Google Scholar] [CrossRef]
- Li, Z.; Liao, B.; Xu, F.; Guo, D. A new repetitive motion planning scheme with noise suppression capability for redundant robot manipulators. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 5244–5254. [Google Scholar] [CrossRef]
- Liao, B.; Han, L.; Cao, X.; Li, S.; Li, J. Double integral-enhanced Zeroing neural network with linear noise rejection for time-varying matrix inverse. CAAI Trans. Intell. Technol. 2023, 1–14. [Google Scholar] [CrossRef]
- Yan, X.; Liu, M.; Jin, L.; Li, S.; Hu, B.; Zhang, X.; Huang, Z. New zeroing neural network models for solving nonstationary Sylvester equation with verifications on mobile manipulators. IEEE Trans. Ind. Inform. 2019, 15, 5011–5022. [Google Scholar] [CrossRef]
- Song, C.; Feng, J.; Wang, X.; Zhao, J. Finite iterative method for solving coupled Sylvester-transpose matrix equations. J. Appl. Math. Comput. 2014, 46, 351–372. [Google Scholar] [CrossRef]
- Ali Beik, F.P.; Movahed, F.S.; Ahmadi-Asl, S. On the Krylov subspace methods based on tensor format for positive definite Sylvester tensor equations. Numer. Linear Algebra Appl. 2016, 23, 444–466. [Google Scholar] [CrossRef]
- Wu, H.C.; Chen, T.C.T.; Chiu, M.C. Constructing a precise fuzzy feedforward neural network using an independent fuzzification approach. Axioms 2021, 10, 282. [Google Scholar] [CrossRef]
- Tuyen, D.N.; Tuan, T.M.; Le, X.H.; Tung, N.T.; Chau, T.K.; Van Hai, P.; Gerogiannis, V.C.; Son, L.H. RainPredRNN: A new approach for precipitation nowcasting with weather radar echo images based on deep learning. Axioms 2022, 11, 107. [Google Scholar] [CrossRef]
- Su, L.; Zhou, L. Exponential synchronization of memristor-based recurrent neural networks with multi-proportional delays. Neural Comput. Appl. 2019, 31, 7907–7920. [Google Scholar] [CrossRef]
- Khan, A.H.; Li, S.; Luo, X. Obstacle avoidance and tracking control of redundant robotic manipulator: An RNN-based metaheuristic approach. IEEE Trans. Ind. Inform. 2019, 16, 4670–4680. [Google Scholar] [CrossRef]
- Jin, L.; Li, S.; Hu, B. RNN models for dynamic matrix inversion: A control-theoretical perspective. IEEE Trans. Ind. Inform. 2017, 14, 189–199. [Google Scholar] [CrossRef]
- He, X.; Liu, Q.; Yang, Y. MV-GNN: Multi-view graph neural network for compression artifacts reduction. IEEE Trans. Image Process. 2020, 29, 6829–6840. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, D.; Wang, J. A recurrent neural network for solving Sylvester equation with time-varying coefficients. IEEE Trans. Neural Netw. 2002, 13, 1053–1063. [Google Scholar] [CrossRef]
- Zhang, Z.; Zheng, L.; Weng, J.; Mao, Y.; Lu, W.; Xiao, L. A new varying-parameter recurrent neural-network for online solution of time-varying Sylvester equation. IEEE Trans. Cybern. 2018, 48, 3135–3148. [Google Scholar] [CrossRef] [PubMed]
- Xiao, L.; Zhang, Z.; Zhang, Z.; Li, W.; Li, S. Design, verification and robotic application of a novel recurrent neural network for computing dynamic Sylvester equation. Neural Netw. 2018, 105, 185–196. [Google Scholar] [CrossRef]
- Qiu, B.; Zhang, Y.; Yang, Z. New discrete-time ZNN models for least-squares solution of dynamic linear equation system with time-varying rank-deficient coefficient. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5767–5776. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Liao, B.; Xiao, L.; Han, L.; Xiao, X. Double accelerated convergence ZNN with noise-suppression for handling dynamic matrix inversion. Mathematics 2021, 10, 50. [Google Scholar] [CrossRef]
- Xiao, L.; He, Y.; Li, Y.; Dai, J. Design and analysis of two nonlinear ZNN models for matrix LR and QR factorization with application to 3D moving target location. IEEE Trans. Ind. Inform. 2022, 1–11. [Google Scholar] [CrossRef]
- Katsikis, V.N.; Mourtas, S.D.; Stanimirović, P.S.; Zhang, Y. Continuous-time varying complex QR decomposition via zeroing neural dynamics. Neural Process Lett. 2021, 53, 3573–3590. [Google Scholar] [CrossRef]
- Xiao, L.; He, Y. A noise-suppression ZNN model with new variable parameter for dynamic Sylvester equation. IEEE Trans. Ind. Inform. 2021, 17, 7513–7522. [Google Scholar] [CrossRef]
- Tang, G.; Li, X.; Xu, Z.; Li, S.; Zhou, X. An integration-enhanced noise-resistant RNN model with superior performance illustrated via time-varying sylvester equation solving. In Proceedings of the IEEE 2020 Chinese Control And Decision Conference (CCDC), Hefei, China, 22–24 August 2020; pp. 1906–1911. [Google Scholar]
- Gong, J.; Jin, J. A faster and better robustness zeroing neural network for solving dynamic Sylvester equation. Neural Process Lett. 2021, 53, 3591–3606. [Google Scholar] [CrossRef]
- Han, L.; Liao, B.; He, Y.; Xiao, X. Dual noise-suppressed ZNN with predefined-time convergence and its application in matrix inversion. In Proceedings of the IEEE 2021 11th International Conference on Intelligent Control and Information Processing (ICICIP), Denver, CO, USA, 28–30 September 2021; pp. 410–415. [Google Scholar]
- Xiao, L.; He, Y.; Dai, J.; Liu, X.; Liao, B.; Tan, H. A variable-parameter noise-tolerant zeroing neural network for time-variant matrix inversion with guaranteed robustness. IEEE Trans. Neural Netw. Learn. Syst. 2020, 33, 1535–1545. [Google Scholar] [CrossRef]
- Guo, D.; Li, S.; Stanimirović, P.S. Analysis and application of modified ZNN design with robustness against harmonic noise. IEEE Trans. Ind. Inform. 2019, 16, 4627–4638. [Google Scholar] [CrossRef]
- Jin, L.; Zhang, Y.; Li, S. Integration-enhanced Zhang neural network for real-time-varying matrix inversion in the presence of various kinds of noises. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 2615–2627. [Google Scholar] [CrossRef]
- Dzieciol, H.; Sillekens, E.; Lavery, D. Extending phase noise tolerance in UDWDM access networks. In Proceedings of the 2020 IEEE Photonics Society Summer Topicals Meeting Series (SUM), Virtual, 13–15 July 2020; pp. 1–2. [Google Scholar]
- Xiang, Q.; Liao, B.; Xiao, L.; Jin, L. A noise-tolerant Z-type neural network for time-dependent pseudoinverse matrices. Optik 2018, 165, 16–28. [Google Scholar] [CrossRef]
- Johnson, M.A.; Moradi, M.H. PID Control; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Liao, B.; Han, L.; He, Y.; Cao, X.; Li, J. Prescribed-time convergent adaptive ZNN for time-varying matrix inversion under harmonic noise. Electronics 2022, 11, 1636. [Google Scholar] [CrossRef]
- Jin, J.; Qiu, L. A robust fast convergence zeroing neural network and its applications to dynamic Sylvester equation solving and robot trajectory tracking. J. Frankl. Inst. 2022, 359, 3183–3209. [Google Scholar] [CrossRef]
- Zhang, Y.; Yi, C.; Guo, D.; Zheng, J. Comparison on Zhang neural dynamics and gradient-based neural dynamics for online solution of nonlinear time-varying equation. Neural Comput. Appl. 2011, 20, 1–7. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, L.; Ke, Z. Superior performance of using hyperbolic sine activation functions in ZNN illustrated via time-varying matrix square roots finding. Comput. Sci. Inf. Syst. 2012, 9, 1603–1625. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, Y. Superior robustness of power-sum activation functions in Zhang neural networks for time-varying quadratic programs perturbed with large implementation errors. Neural Comput. Appl. 2013, 22, 175–185. [Google Scholar] [CrossRef]
- Zhang, Y.; Ding, Y.; Qiu, B.; Zhang, Y.; Li, X. Signum-function array activated ZNN with easier circuit implementation and finite-time convergence for linear systems solving. Inf. Process. Lett. 2017, 124, 30–34. [Google Scholar] [CrossRef]
- Benner, P. Factorized solution of Sylvester equations with applications in control. Sign (H) 2004, 1, 2. [Google Scholar]
- Castelan, E.B.; da Silva, V.G. On the solution of a Sylvester equation appearing in descriptor systems control theory. Syst. Control Lett. 2005, 54, 109–117. [Google Scholar] [CrossRef]
- Wei, Q.; Dobigeon, N.; Tourneret, J.Y. Fast fusion of multi-band images based on solving a Sylvester equation. IEEE Trans. Image Process. 2015, 24, 4109–4121. [Google Scholar] [CrossRef]
- Diao, H.; Shi, X.; Wei, Y. Effective condition numbers and small sample statistical condition estimation for the generalized Sylvester equation. Sci. China Math. 2013, 56, 967–982. [Google Scholar] [CrossRef]
- Zhang, R.; Xi, X.; Tian, H.; Wang, Z. Dynamical analysis and finite-time synchronization for a chaotic system with hidden attractor and surface equilibrium. Axioms 2022, 11, 579. [Google Scholar] [CrossRef]
- Rasouli, M.; Zare, A.; Hallaji, M.; Alizadehsani, R. The synchronization of a class of time-delayed chaotic systems using sliding mode control based on a fractional-order nonlinear PID sliding surface and its application in secure communication. Axioms 2022, 11, 738. [Google Scholar] [CrossRef]
- He, W.; Luo, T.; Tang, Y.; Du, W.; Tian, Y.C.; Qian, F. Secure communication based on quantized synchronization of chaotic neural networks under an event-triggered strategy. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 3334–3345. [Google Scholar] [CrossRef] [PubMed]
- Xiao, L.; He, Y.; Liao, B. A parameter-changing zeroing neural network for solving linear equations with superior fixed-time convergence. Expert Syst. Appl. 2022, 208, 118086. [Google Scholar] [CrossRef]
- Su, H.; Luo, R.; Huang, M.; Fu, J. Robust fixed time control of a class of chaotic systems with bounded uncertainties and disturbances. Int. J. Control Autom. Syst. 2022, 20, 813–822. [Google Scholar] [CrossRef]
- Singer, J.; Wang, Y.; Bau, H.H. Controlling a chaotic system. Phys. Rev. Lett. 1991, 66, 1123. [Google Scholar] [CrossRef]
- Sun, J.; Zhao, X.; Fang, J.; Wang, Y. Autonomous memristor chaotic systems of infinite chaotic attractors and circuitry realization. Nonlinear Dyn. 2018, 94, 2879–2887. [Google Scholar] [CrossRef]
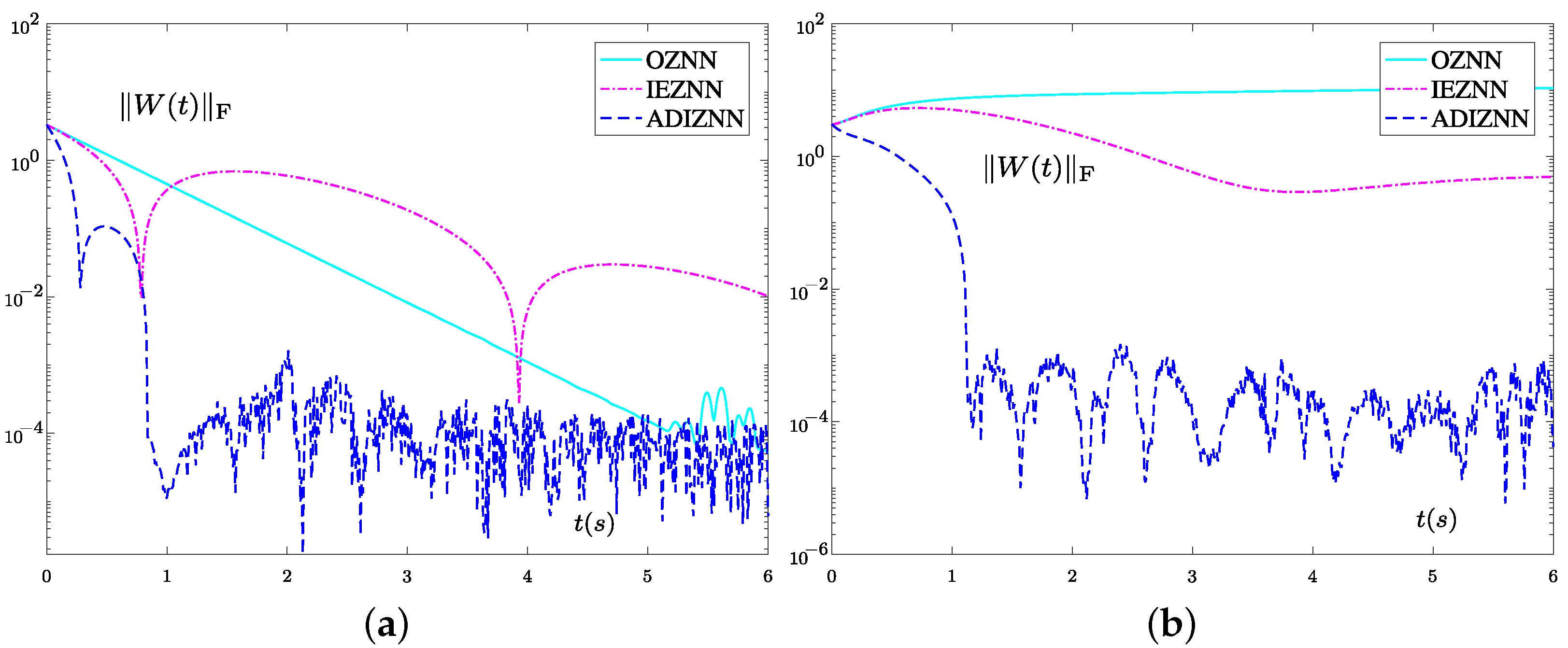
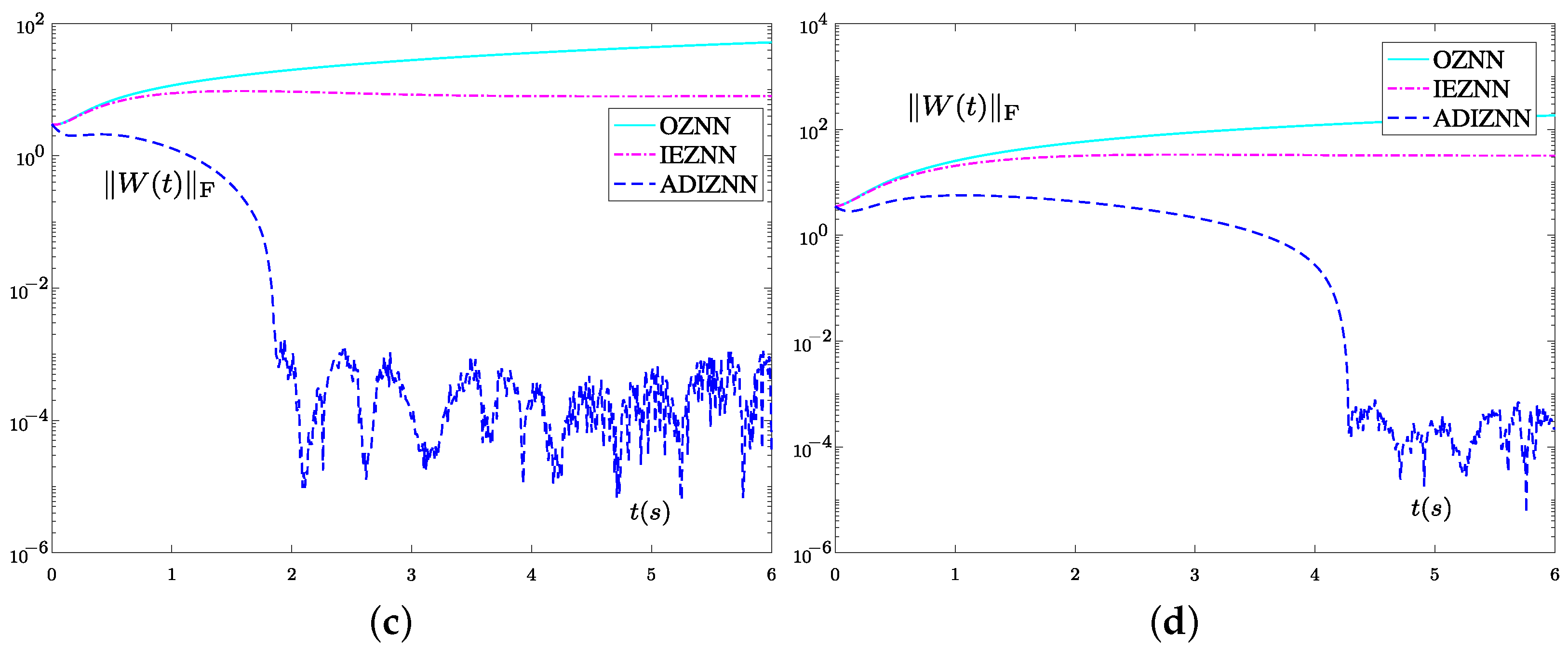
| Noise | OZNN Model (9) | IEZNN Model (12) | ADIZNN Model (19) |
|---|---|---|---|
| convergent | convergent | convergent | |
| diverging | diverging | convergent | |
| diverging | diverging | convergent | |
| diverging | diverging | convergent |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, L.; He, Y.; Liao, B.; Hua, C. An Accelerated Double-Integral ZNN with Resisting Linear Noise for Dynamic Sylvester Equation Solving and Its Application to the Control of the SFM Chaotic System. Axioms 2023, 12, 287. https://doi.org/10.3390/axioms12030287
Han L, He Y, Liao B, Hua C. An Accelerated Double-Integral ZNN with Resisting Linear Noise for Dynamic Sylvester Equation Solving and Its Application to the Control of the SFM Chaotic System. Axioms. 2023; 12(3):287. https://doi.org/10.3390/axioms12030287
Chicago/Turabian StyleHan, Luyang, Yongjun He, Bolin Liao, and Cheng Hua. 2023. "An Accelerated Double-Integral ZNN with Resisting Linear Noise for Dynamic Sylvester Equation Solving and Its Application to the Control of the SFM Chaotic System" Axioms 12, no. 3: 287. https://doi.org/10.3390/axioms12030287
APA StyleHan, L., He, Y., Liao, B., & Hua, C. (2023). An Accelerated Double-Integral ZNN with Resisting Linear Noise for Dynamic Sylvester Equation Solving and Its Application to the Control of the SFM Chaotic System. Axioms, 12(3), 287. https://doi.org/10.3390/axioms12030287






