A Space-Time Legendre-Petrov-Galerkin Method for Third-Order Differential Equations
Abstract
1. Introduction
2. Space-Time Legendre-Petrov-Galerkin Scheme
3. Error Estimate
4. Implementation
5. Numerical Experiments
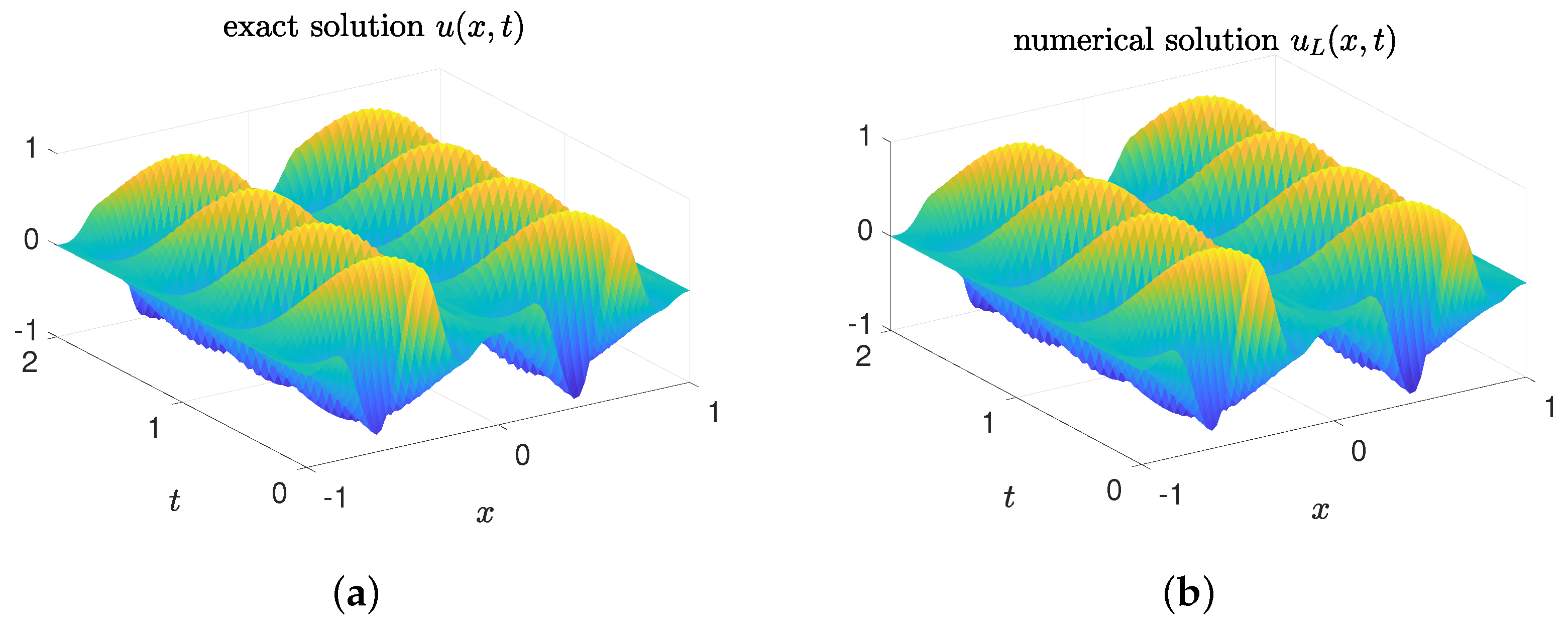
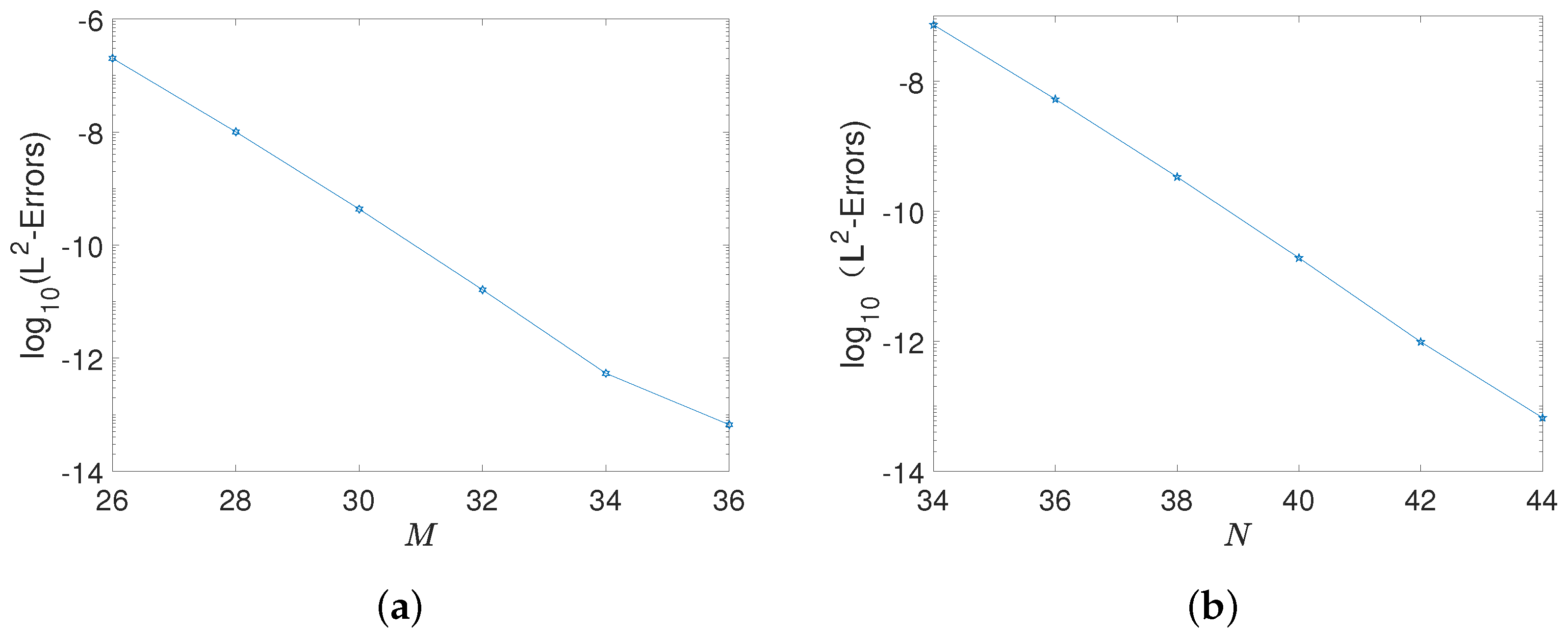
5.1. Example 1
5.2. Example 2
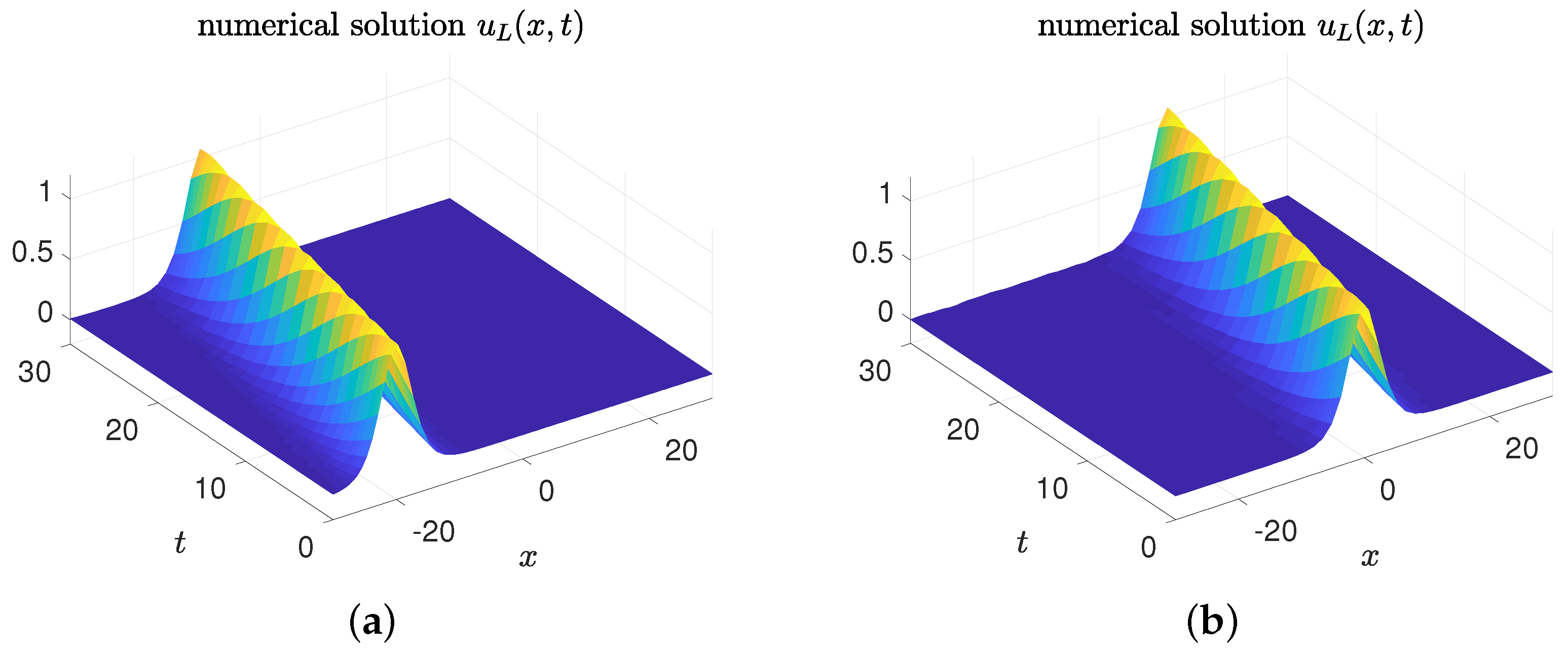
5.3. Example 3
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boyd, J.P. Chebyshev and Fourier Spectral Methods; Courier Corporation: Mineola, NY, USA, 2001; ISBN 0-486-41183-4. [Google Scholar]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Methods: Fundamentals in Single Domains; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007; ISBN 978-3-540-30725-9. [Google Scholar]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Methods: Evolution to Complex Geometries and Applications to Fluid Dynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007; ISBN 978-3-540-30727-3. [Google Scholar]
- Guo, B. Spectral Methods and Their Applications; World Scientific: Singapore, 1998; ISBN 9-810-23333-7. [Google Scholar]
- Shen, J.; Tang, T.; Wang, L.L. Spectral Methods: Algorithms, Analysis and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; ISBN 978-3-540-71040-0. [Google Scholar]
- Bernardi, C.; Maday, Y. Spectral methods. Handb. Numer. Anal. 1997, 5, 209–485. [Google Scholar] [CrossRef]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Methods in Fluid Dynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; ISBN 978-3-540-52205-8. [Google Scholar]
- Tal-Ezer, H. Spectral methods in time for hyperbolic equations. SIAM J. Numer. Anal. 1986, 23, 11–26. [Google Scholar] [CrossRef]
- Fakhar-Izadi, F.; Dehghan, M. Space-time spectral method for a weakly singular parabolic partial integro-differential equation on irregular domains. Comput. Math. Appl. 2014, 67, 1884–1904. [Google Scholar] [CrossRef]
- Shan, Y.; Liu, W.; Wu, B. Space-time Legendre-Gauss-Lobatto collocation method for two-dimensional generalized Sine-Gordon equation. Appl. Numer. Math. 2017, 12, 92–107. [Google Scholar] [CrossRef]
- Tang, S.; Li, H.; Yin, B. A space-time spectral method for multi-dimensional Sobolev equations. J. Math. Anal. Appl. 2021, 499, 124937. [Google Scholar] [CrossRef]
- Shen, J.; Wang, L. Fourierization of the Legendre-Galerkin method and a new space-time spectral method. Appl. Numer. Math. 2007, 57, 710–720. [Google Scholar] [CrossRef]
- Zhang, C.; Yao, H.; Li, H. New space-time spectral and structured spectral element methods for high order problems. J. Comput. Appl. Math. 2019, 351, 153–166. [Google Scholar] [CrossRef]
- Pei, C.; Mark, S.; Hussaini, M.Y. New multi-implicit space-time spectral element methods for advection-diffusion-reaction problems. J. Sci. Comput. 2019, 78, 653–686. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Zaky, M.A. An improved collocation method for multi-dimensional space-time variable-order fractional Schrödinger equations. Appl. Numer. Math. 2017, 111, 197–218. [Google Scholar] [CrossRef]
- Zheng, M.; Liu, F.; Anh, V.; Turner, I. A high-order spectral method for the multi-term time-fractional diffusion equations. Appl. Math. Model. 2016, 40, 4970–4985. [Google Scholar] [CrossRef]
- Ma, H.; Sun, W. A Legendre-Petrov-Galerkin and Chebyshev collocation method for third-order differential equations. SIAM J. Numer. Anal. 2000, 38, 1425–1438. [Google Scholar] [CrossRef]
- Ma, H.; Guo, B. The Fourier pseudo-spectral method with a restrain operator for the Korteweg-de Vries equation. J. Comput. Phys. 1986, 65, 120–137. [Google Scholar]
- Djidjeli, K.; Price, W.G.; Twizell, E.H.; Wang, Y. Numerical methods for the solution of the third and fifth-order dispersive Korteweg-de Vries equations. J. Comput. Appl. Math. 1995, 58, 307–336. [Google Scholar] [CrossRef]
- Carey, G.F.; Shen, Y. Approximations of the KdV equation by least squares finite elements. Comput. Methods Appl. Mech. Eng. 1991, 93, 1–11. [Google Scholar] [CrossRef]
- Chan, T.F.; Kerkhoven, T. Fourier methods with extended stability intervals for the Korteweg-de Vries equation. SIAM J. Numer. Anal. 1985, 22, 441–454. [Google Scholar] [CrossRef]
- Kovalyov, M. On the structure of the two-soliton interaction for the Korteweg-de Vries equation. J. Differ. Equ. 1999, 152, 431–438. [Google Scholar] [CrossRef]
- van Groesen, E. Andonowati, Variational derivation of KdV-type models for surface water waves. Phys. Lett. A 2007, 366, 195–201. [Google Scholar] [CrossRef]
- Shen, J. A new dual-Petrov-Galerkin method for third and higher odd-order differential equations: Application to the KDV equation. SIAM J. Numer. Anal. 2003, 41, 1595–1619. [Google Scholar] [CrossRef]
- Huang, W.; Sloan, D.M. The pseudo-spectral method for third-order differential equations. SIAM J. Numer. Anal. 1992, 29, 1626–1647. [Google Scholar] [CrossRef]
- Pavoni, D. Single and multidomain Chebyshev collocation methods for the Korteweg-de Vries equation. Calcolo 1988, 25, 311–346. [Google Scholar] [CrossRef]
- Li, J.; Ma, H.; Sun, W. Error analysis for solving the Korteweg-de Vries equation by a Legendre pseudo-spectral method. Numer. Methods Partial Differ. Equations Int. J. 2000, 16, 513–534. [Google Scholar] [CrossRef]
- Qin, Y.; Ma, H. Legendre-tau-Galerkin and spectral collocation method for nonlinear evolution equations. Appl. Numer. Math. 2020, 153, 52–65. [Google Scholar] [CrossRef]
- Laub, A.J. Matrix Analysis for Scientists and Engineers; SIAM: Davis, CA, USA, 2005; ISBN 978-0-898715-76-7. [Google Scholar]
- Ma, H.; Sun, W. Optimal error estimates of the Legendre-Petrov-Galerkin method for the Korteweg-de Vries equation. SIAM J. Numer. Anal. 2001, 39, 1380–1394. [Google Scholar] [CrossRef]
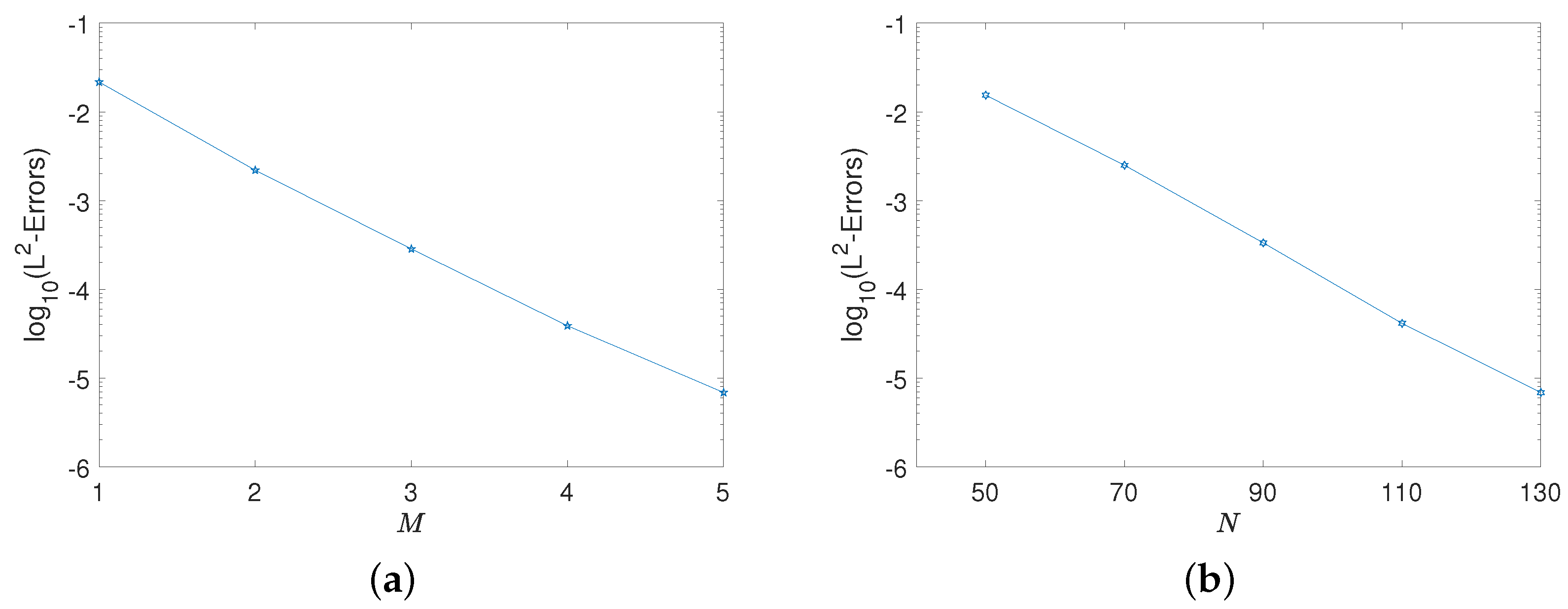
| Scheme (7) with | Scheme (2.2) with = in [17] | ||
|---|---|---|---|
| - | - | ||
| 32 | 16 | ||
| 39 | 32 | ||
| 44 | 64 | ||
| Scheme (7) with M = 3 | Scheme (2.3) with = 1e-06 in [27] | ||
|---|---|---|---|
| - | N | - | |
| 40 | 10 | ||
| 60 | 20 | ||
| 80 | 40 | ||
| 100 | 80 | ||
| 120 | 160 | ||
| Scheme (7) with N = 140 | Scheme (2.3) with N = 160 in [27] | ||
|---|---|---|---|
| - | - | ||
| 2 | |||
| 3 | |||
| 4 | |||
| Temporal Errors with | Spatial Errors with | ||
|---|---|---|---|
| - | - | ||
| 1 | 14 | ||
| 2 | 24 | ||
| 3 | 34 | ||
| 4 | 44 | ||
| 5 | 54 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, S.; Li, H. A Space-Time Legendre-Petrov-Galerkin Method for Third-Order Differential Equations. Axioms 2023, 12, 281. https://doi.org/10.3390/axioms12030281
Tang S, Li H. A Space-Time Legendre-Petrov-Galerkin Method for Third-Order Differential Equations. Axioms. 2023; 12(3):281. https://doi.org/10.3390/axioms12030281
Chicago/Turabian StyleTang, Siqin, and Hong Li. 2023. "A Space-Time Legendre-Petrov-Galerkin Method for Third-Order Differential Equations" Axioms 12, no. 3: 281. https://doi.org/10.3390/axioms12030281
APA StyleTang, S., & Li, H. (2023). A Space-Time Legendre-Petrov-Galerkin Method for Third-Order Differential Equations. Axioms, 12(3), 281. https://doi.org/10.3390/axioms12030281







