Applying the Fuzzy BWM to Determine the Cryptocurrency Trading System under Uncertain Decision Process

Abstract

The crypto and digital assets ecosystems have attracted investment, regulators, and speculators to their environment. As the blockchain-based framework can reduce transaction costs, generate distributed trust, and enable decentralized platforms, it has become a potential new base for decentralized business models. Previous studies have highlighted the advantages and drawbacks of each platform, such as interest rates, cost concerns, transparency issues, hacking issues, and hazards. Consequently, it is challenging for investors to evaluate the cryptocurrency trading system which determines the optimum exchanges and crucial aspects. Therefore, in order to rank the optimal digital token trading system, this paper develops an evaluation architecture to determine the various token trading systems. The developed architecture integrates fuzzy theory and the best-worst method (BWM) into the decision-making process to assess decision behaviors regarding preference for digital token trading systems in investors in Taiwan. First, this work establishes the views and parameters by modifying the Delphi method based on a literature review and survey. Second, the fuzzy-BWM is applied to obtain the fuzzy weights of the views and parameters. Then, defuzzification and BWM are used to rank the optimal alternatives of the digital token trading systems for investors. The results indicate that the optimal digital token trading system is the decentralized platform, and the critical parameters are gas fees, interest rates, and the mechanism of savings under fuzzy uncertain scenarios. This means that when considering the uncertain and ambiguous characteristics of the expert decision process in digital token trading systems, the evaluation is decentralized and the gas fees are the most important parameter in the digital token investment platform. Academically, the fuzzy BWM-based decision-making architecture can provide corporations and investors with valuable guidance to rank the optimal digital token trading systems based on fuzzy uncertain scenarios. Commercially, the proposed architecture could provide corporations and investors with a useful model to measure the optimal digital token trading system.

1. Introduction

The crypto and digital assets ecosystems have attracted investment, regulators, and speculators to their environment. Chen and Bellavitis (2020) indicated that the blockchain-based framework can reduce transaction costs, generate distributed trust [1], and enable decentralized platforms, thus becoming a potential new base for decentralized business models. This means that they were interested in developing a new economic system and business models for trade and investment. From a financial point of view, the blockchain was initially developed as the technology behind cryptocurrencies such as Bitcoin. Tapscott and Tapscott (2017) stated that the worldwide distributed ledger runs on millions of devices and can record everything with value [2]. Zhang et al. (2020) suggested that the blockchain system can securely store transactions, such as digital cryptocurrencies, data/information regarding debt, copyrights, shares, and digital assets [3]. The CoinMarketCap website shows the rising market of the cryptocurrency field, where its total market capital in August of 2020 [4] was over 366 billion USD, and the ten main market shares and relevant cryptocurrency criteria were detailed in

Table 1. The top 10 on market capitals of cryptocurrencies in 2020.

Rank	Name	Market Cap	Price	Volume	Circulating Supply
1	Bitcoin	$219,679,310,494	11,889.05	27,330,559,813	18,477,450 BTC
2	Ethereum	$53,740,791,220	477.99	19,321,812,596	112,431,030 ETH
3	XRP	$13,468,921,708	0.30	1,858,933,164	44,994,863,318 XRP
4	Tether	$13,459,127,857	1.00	50,455,204,000	13,430,692,319 USDT
5	Chainlink	$5,630,358,881	16.09	1,483,004,097	350,000,000 LINK
6	Bitcoin Cash	$5,362,817,506	289.78	1,825,084,351	18,506,269 BCH
7	Litecoin	$4,108,015,224	62.85	2,726,870,502	65,364,257 LTC
8	Bitcoin SV	$3,731,654,286	201.66	913,662,559	18,504,883 BSV
9	Binance Coin	$3,658,101,413	25.33	549,692,320	144,406,560 BNB
10	Crypto.com Coin	$3,578,866,307	0.18	82,320,135	19,733,333,333 CRO

Source: CoinMarketCap [4].

. The Libra association (2019) expressed that numerous companies have invested in digital tokens and accept them as major commercial instruments [5].

Chen and Bellavitis (2020) proposed that merchants can considerably reduce their costs and increase their profitability due to the low transaction fees of cryptocurrency [1]. For investors, initial coin offerings (ICOs) have emerged as an innovative funding mechanism for the early stage ventures of investors which allows startups and innovators to raise billions of dollars from global investors [6]. This indicates that different digital asset exchanges are available worldwide and can be accessed. The operational features of digital asset investment platforms (exchanges) are disassembled into three styles: (1) decentralized exchanges [7,8,9,10,11,12,13,14], (2) centralized exchanges [7,8,9,10,12], and (3) margin lending exchanges [7,8].

Ivaniuk (2020) indicated that the purpose of decentralized trading systems is to provide direct person-to-person trades for individuals without the need for a middleman, meaning that it is entirely administered and maintained by software [7]. Popular decentralized trading systems such as Compound and Dharma have some distinctions between them. Dharma has a set interest rate, while Compound has a fluctuating interest rate. The deposit restriction is a time deposit for Dharma and current in Compound, meaning that the Compound platform has a mechanism for compounding interest, whereas Dharma does not. Thus, the accompanying currencies on the two platforms are also different. According to the DeFi Market Cap website, the market for decentralized tokens is growing, with an overall market capitalization total of more than 170 billion USD [15].

Table 2. The top 10 on market capitals of decentralized trading systems in 2020.

Rank	Name	Market Cap	Price	Circulating Supply
1	UMA Voting Token v1	$1,463,396,629	$26.86	54,475,686
				UMA
2	Compound Dai	$1,016,510,374	$0.02	48,829,509,452
				cDAI
3	Yearn.finance	$1,014,590,443	$33,860.99	29,963
				YFI
4	EthLend Token	$941,993,746	$0.75	1,256,361,932
				LEND
5	Synthetix Network Token	$871,275,367	$7.45	116,890,573
				SNX
6	Compound	$773,709,650	$240.09	3,222,544
				COMP
7	Curve Y Pool	$686,504,604	$1.05	655,355,323
				yCrv
8	Maker	$643,939,815	$713.89	902,021
				MKR
9	Ampleforth	$505,359,342	$2.40	210,465,977
				AMPL
10	Compound Ether	$472,244,935	$9.55	49,443,723
				cETH

Source: DeFi Market Cap [15].

displays the top ten market capitalizations on decentralized exchanges, as well as their respective token requirements. Investors may benefit from decentralization trading platforms in several ways, including transparency, anonymity, peer-to-peer cryptocurrency networks, no inflation, and open-source cryptocurrency mining. Meanwhile, the downsides include the potential for money laundering, terrorist activities, illegal activity financing, and the lack of a central issuer, meaning that there is no legal formal body to guarantee in the event of bankruptcy [1,16,17]. Previous studies of the decentralized applications ecosystem focused on analyzing possible problems and providing solutions for the decentralized applications ecosystem [1,18], blockchain technology applications [19,20,21,22], the examination of business models, and their implementation on the decentralized trading platform [1,14,23,24,25].

Centralized exchanges, which are online marketplaces for purchasing and selling bitcoins, are one of the most crucial means of trading for most cryptocurrency investors. In order to ease trade, the centralized trading system contains middlemen, such as businesses, that function as proxies [26]. This concept relates to the employment of an intermediary or third party to facilitate transactions, wherein buyers and sellers alike entrust their possessions to middlemen that perform fiat-to-cryptocurrency and crypto-to-crypto exchanges through the centralized exchange ecosystem [27]. According to Arslanian and Fischer (2019), a user may deposit fiat money into their e-wallet (e.g., USD, EUR, and JPY) and convert it to the selected crypto-asset via a fiat-to-cryptocurrency converter [27]. The crypto-to-crypto exchange does not include fiat currencies and solely allows the exchange of one crypto-asset for another. The members of the centralized trading ecosystem, such as NEXO and Celsius, also have certain differences between them. Celsius has a fluctuating interest rate, whereas NEXO has a fixed interest rate. The interest is paid daily in NEXO, whereas in Celsius, the interest is paid weekly. According to the CoinGecko website, there are more than 70 million USD market capitals in the NEXO system [28], while the Celsius network has over 174 million USD in market capitalization [29]. As a result, the centralized trading ecosystem is an essential vehicle for digital currency transactions. Shapiro (2018) demonstrated that the centralized approach benefits both market participants and regulators, as traders and investors need not be concerned with execution details or counterparty default risk [30]. This means that they can obtain the benefits from liquidity, as provided by market makers on the centralized trading exchange, and custodians can be relied on by regulators for rule enforcement, accountability, and information reporting [30]. Nevertheless, centralized trading exchanges have several drawbacks, such as costs [30], hacking activities and financial mismanagement by custodians, that lead to insolvency, employee operational failures, and sudden account freezes [12]. Furthermore, because centralized financial organizations must safeguard their centralized ledgers by limiting access, centralized finance cannot have complete transparency [1]. Prior research on centralized finance mostly emphasized price discovery [31,32], examination of risk exposure [33,34], and the volatility of digital tokens [35,36,37].

In light of the literature on the most recent token trading ecosystem, the hybrid trading system, we can conclude the following. The EtherDelta system is more akin to a hybrid architecture [13]. The benefits of the centralization and decentralization ecosystem are combined in the hybrid trading ecosystem. While all transactions were always carried out through calling operations in smart contracts, hybrid systems address the problem of trade discovery by keeping a centralized order management database. Nevertheless, the high price of gas fees and confirmation of transactions delay brought on by such frequent on-chain transactions is not resolved by hybrid exchanges. This would be particularly pertinent for cryptocurrency dealers who trade frequently, since more cryptocurrency transactions cause higher gas prices and longer transaction confirmation times. Therefore, hybrid trading systems do not address the possible transaction congestion issue created by too many simultaneous transactions [13].

With the emergence of blockchain technology in cryptocurrency, an increasing number of investors are paying attention to crypto concerns, such as Bitcoin, Ethereum, and Ripple. According to the above literature review, this study summarized three different types of exchanges in the digital token trading ecosystem: a centralized system, a decentralized system, and a hybrid system. Based on the foregoing arguments, several studies have highlighted the advantages and drawbacks of each platform, such as interest rates, cost concerns, transparency issues, hacking issues, and hazards. Consequently, evaluating a cryptocurrency trading system for investors is challenging, as is determining the optimum exchanges and crucial aspects. Moreover, numerous traders in digital assets do not evaluate the cryptocurrency trading system before adding cryptocurrencies to their portfolios, which entails significant financial risks. Previous works on cryptocurrencies focused on price forecasting [21,22,23,24,25,26,27,28,29,30,31,38], examination of risk exposure [33,34], the volatility of digital tokens [35,36,37,39], and risk problems in tokens [40,41,42]. Even though there is an increasing amount of material available regarding the cryptocurrency field, solutions to the issue of the optimal cryptocurrency trading platform and important assessment criteria for token traders have not been found. To date, no research has produced a comprehensive framework for investors during decision-making processes when evaluating the optimal cryptocurrency trading platform, the critical critera, or the digital asset traders in Taiwan. This means that they frequently lack objective scientific decision-making procedures when assessing the ideal cryptocurrency trading platform; thus, the risks of using an inappropriate token exchange are quite significant. Therefore, the goal of this investigation is to establish an evaluation framework based on a scientific decision-making process for obtaining the optimal cryptocurrency trading platform and critical criterion.

In order to establish a framework and obtain the optimal solution, the multi-criteria decision-making (MCDM) process was adopted to evaluate the optimal cryptocurrency trading platform and critical criterion [43,44,45,46,47]. The literature has demonstrated that the analytic hierarchy process (AHP) approach can solve optimization problems [48,49,50]. While AHP is quite popular in various industries, it requires the use of a pairwise comparison matrix, which requires additional indications, meaning the evaluation process would be more complicated. Therefore, Rezaei (2015) and Rezaei (2016) presented a novel MCDM methodology, known as the best-worst method (BWM) [51,52], which may simplify the complicated process of the AHP method and provide the ideal alternative and criterion weights through MCDM planning. Furthermore, one of the benefits of the BWM method is that it is a powerful way to identify the parameter weights of MCDM problems [53,54,55,56]. Omrani et al. (2020) integrated data envelopment analysis (DEA) with a BWM model to analyze the efficiency of road safety [57], while Malek and Desai (2019) proposed a BWM model to evaluate sustainable manufacturing hurdles [58]. Kheybari et al. (2019) implemented the BWM process to evaluate a bioethanol factory site [55]. However, despite its advantages, the BWM model cannot fully address the inherent uncertainties and imprecisions associated with translating decision makers’ impressions into accurate figures [59]. According to Ayhan (2013) and Khan et al. (2019), unclear and ambiguous specialist judgments lead to greater complexities, which implies that numerical prediction is much more difficult for humans than qualitative prediction [60,61]. Thus, Güngör et al. (2009) proposed that fuzzy features could aid in translating human qualitative expressions into meaningful numerical forecasts [62]. Akram and Niaz (2022) determined an attribute group decision-making method that combines compromise solutions (COCOSO) with criteria importance through inter-criteria correlation (CRITIC) into Fermatean fuzzy numbers, which can solve uncertain issues in valve selections [63]. Mahmood and Ali (2022) indicated that decision-making involves erratic conditions and uncertainties [64]. They developed the complex single-valued neutrosophic with a prioritized Muirhead mean (PMM) (CSVNPMM) operator and a CSVN prioritized dual Muirhead mean (PDMM) operator based on a fuzzy environment to deal with MADM problems. Therefore, to reduce the uncertainties and imprecisions in this paper, this study integrated a fuzzy model and the BWM process to provide an assessment architecture for prioritizing, in which expert comparison judgments were represented by fuzzy triangular numbers. The evaluation architecture in this study is a fuzzy variation of BWM, and its usefulness is demonstrated by numerical examples. Based on previous reports and interviews with financial specialists, including investors and financial academics, this study employed the modified Delphi technique and fuzzy-BWM to establish an assessment architecture capable of determining the optimal cryptocurrency trading system and critical parameters in Taiwan for investors.

Consequently, this work integrated the fuzzy concept with the BWM process to calculate the weights of the perspectives and elements in the digital asset market for investors or businesses, and then assigned an appropriate relative weight to each view and parameter within the fuzzy-BWM architecture in order to obtain suitable alternatives. Regarding academic works, the fuzzy-BWM decision-making architecture may provide significant recommendations to investors or companies to determine the optimal cryptocurrency trading system for their investment projects in cryptocurrency areas. Regarding commercial works, the proposed architecture can provide administrators with a valuable instrument to determine the optimal cryptocurrency trading system and critical parameters for investors or corporations in Taiwan.

This work is constructed in three sections. Section 1 explains the evaluation architecture, including the modified Delphi method, BWM, and fuzzy-BWM. Section 2 presents the findings of the empirical investigation. Finally, Section 3 offers our remarks and conclusions.

2. Evaluation Architecture

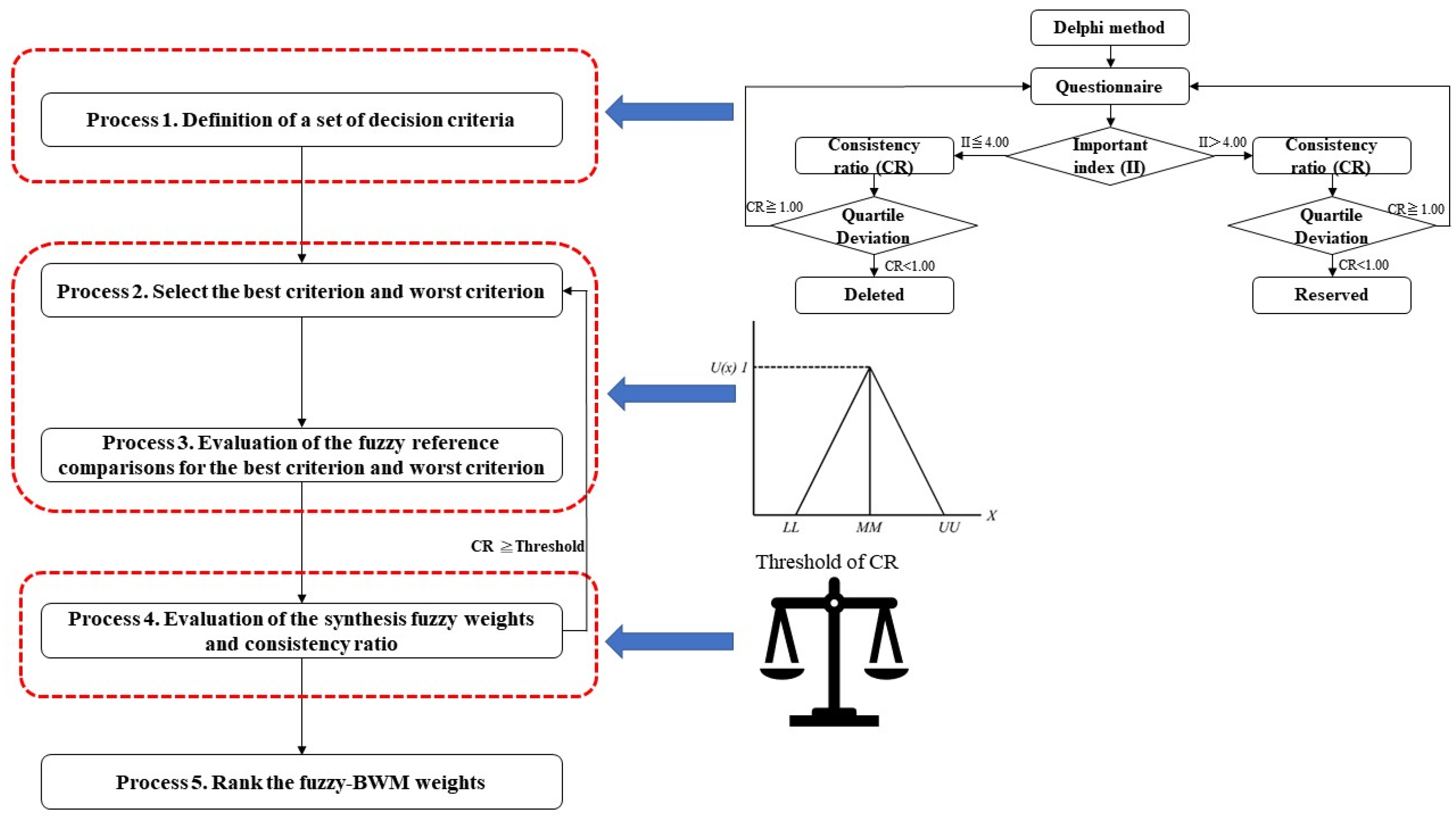
Expert opinions were produced using the modified Delphi technique, which highlights the procedure determinants, examines the weighted parameters, and ranks opinions using the fuzzy-BWM framework. The modified Delphi technique, fuzzy ideas, and BWM assessment processes are as follows (see Figure 1).

2.1. Modified Delphi Method

According to Wu et al. (2007), the Delphi technique proceeds as follows [65]: (I) determine the anonymous professionals; (II) present the questionnaire survey with the first round; (III) present the questionnaire survey with the second round; (IV) present the questionnaire survey after the third round; and (V) collect suggestions from professionals to reach an agreement. Steps (III) and (IV) are typically performed when a specific issue is resolved [66]. All the survey’s common perspectives were determined according to the literature review and expert interviews. The modified Delphi approach was used to replace the regularly utilized open-style inquiry in step (II) [66]. Additionally, Hasson and Keeney (2011) recommended the number of professional practitioners to be between five and nine [67].

2.2. Best-Worst Method (BWM)

Rezaei (2015) and Rezaei (2016) presented the BWM, which has five phases for evaluating weights in a decision issue [51,52]. The BWM method has been effectively used in various research topics, such as measuring an optimal location [55], quantifying the hurdles to sustainable manufacturing [58], and evaluating logistics performance indicators [54]. The BWM’s five phases are presented as follows [51,52]:

• Phase 1. Definition of a set of decision parameters

In the first phase, the decision variables $\left\{C_1,C_2,C_3,\dots C_n\right\}$ must be determined to arrive at a conclusion, and the parameters that should be utilized to assess the alternatives are evaluated. The modified Delphi approach was used in this study to obtain the assessment parameters for rating the optimal cryptocurrency trading system for Taiwanese traders, and can be presented at distinct levels.

• Phase 2. Best parameter and worst parameter

The second phase selects the best parameter (the most important parameter) and the worst parameter according to the experts, but does not evaluate the values of the parameters and alternatives.

• Phase 3. Confirmation of the preference in best-to-others (BO)

In Phase 3, participants ranked their preferences on a scale of 1 to 9, with 1 representing equal importance and 9 indicating that the best parameter is more essential than the remaining parameters. The resulting BO vector is as follows.

$$A_b=\left(a_{b1},a_{b2},\mathrm{\dots }{a}_{bn}\right)$$

(1)

where $a_{bj}$ represents that the preference of b over j and $a_{bb}=1$.

• Phase 4. Confirmation of the preference in others-to-worst (OW)

In Phase 4, participants chose a number between 1 to 9 that denotes their preference for all other factors over the criterion chosen as the least important, with 1 representing equal importance and 9 denoting that the parameter in the issue is significantly more essential than the least important parameter. The resulting OW vector is as follows.

$$A_w={(a_{1w},a_{2w},\mathrm{\dots }{a}_{nw})}^T$$

(2)

where $a_{jw}$ denotes that the preference of j over w and $a_{ww}=1$.

• Phase 5. Determine the synthesis weights

In phase 5, the synthesis values $\left(w_1^{*},w_2^{*},w_3^{*},\dots ,w_n^{*}\right)$ were determined. The synthesized value for such linear system is one that minimizes the largest absolute difference for the set ($\left|\frac{W_b}{W_j}-a_{bj}\right|, \left|\frac{W_j}{W_w}-a_{jw}\right|$). The sum of all the weights should equal one, and no value may be negative, thus prompting the subjects to decide on the best answer.

$$min ma{x}_j \left\{\left|\frac{W_{b }}{W_j}-a_{bj}\right|,\left|\frac{W_b}{W_j}-a_{bj}\right|\right\}$$

(3)

Subject to

$$\begin{gathered} {\displaystyle \sum }_j{w}_j=1 \\ {w}_j\ge 0, \mathrm{for} \mathrm{all} j. \end{gathered}$$

This problem is solvable by converting it to a linear programming problem (4).

$$\mathit{min} {\zeta }^L$$

(4)

Subject to

$$\begin{gathered} \left|w_b-a_{bj}{w}_j\right|\le {\zeta }^L, \mathrm{for} \mathrm{all} j \\ \left|w_j-a_{jw}{w}_w\right|\le {\zeta }^L, \mathrm{for} \mathrm{all} j \\ {\displaystyle \sum }_j{w}_j=1 \\ {w}_j\ge 0, \mathrm{for} \mathrm{all} j \end{gathered}$$

Through the outcome of this linear programming issue (4), the optimal weight and ${\zeta }^L$ are obtained. The consistency rate of the comparison system is denoted by ${\zeta }^L$, and a consistency rate value close to 0 indicates that the participants’ pairwise comparisons are consistent.

We use the following formula to ensure the consistency ratio of the comparisons:

$$\mathrm{Consistency} \mathrm{Ratio}=\frac{{\zeta }^L}{Consistency index}$$

(5)

Table 3. The consistency index (CI).

${\mathit{a}}_{\mathit{b}\mathit{w}}$	1	2	3	4	5	6	7	8	9
CI (max $\zeta$)	0.00	0.44	1.00	1.63	2.30	3.00	3.73	4.47	5.23

Source: Rezaei [51].

shows the consistency index.

2.3. Fuzzy-BWM

The BWM model, as proposed by Rezaei in 2015 [51], can improve the complexity problem of an AHP model based on a multi-objective programming concept to analyze the optimal solution and critical factors. While BWM can improve decision-making efficiency, it is unable to effectively address the inherent uncertainties and imprecisions involved with translating decision makers’ views into exact numbers [59]. In order to describe the uncertainties generated by imprecise and confusing human cognitive processes, Zadeh (1965) created the fuzzy set theory [68]. Negoita (1985) and Zimmermann (1985) proposed that the theory’s fundamental concept of fuzzy logic in each parameter includes a membership degree in a fuzzy system, meaning it has the advantage of quantitatively capturing uncertainty and ambiguity. Therefore, this study integrated the fuzzy theory in the BWM model to solve the uncertainty field [69,70].

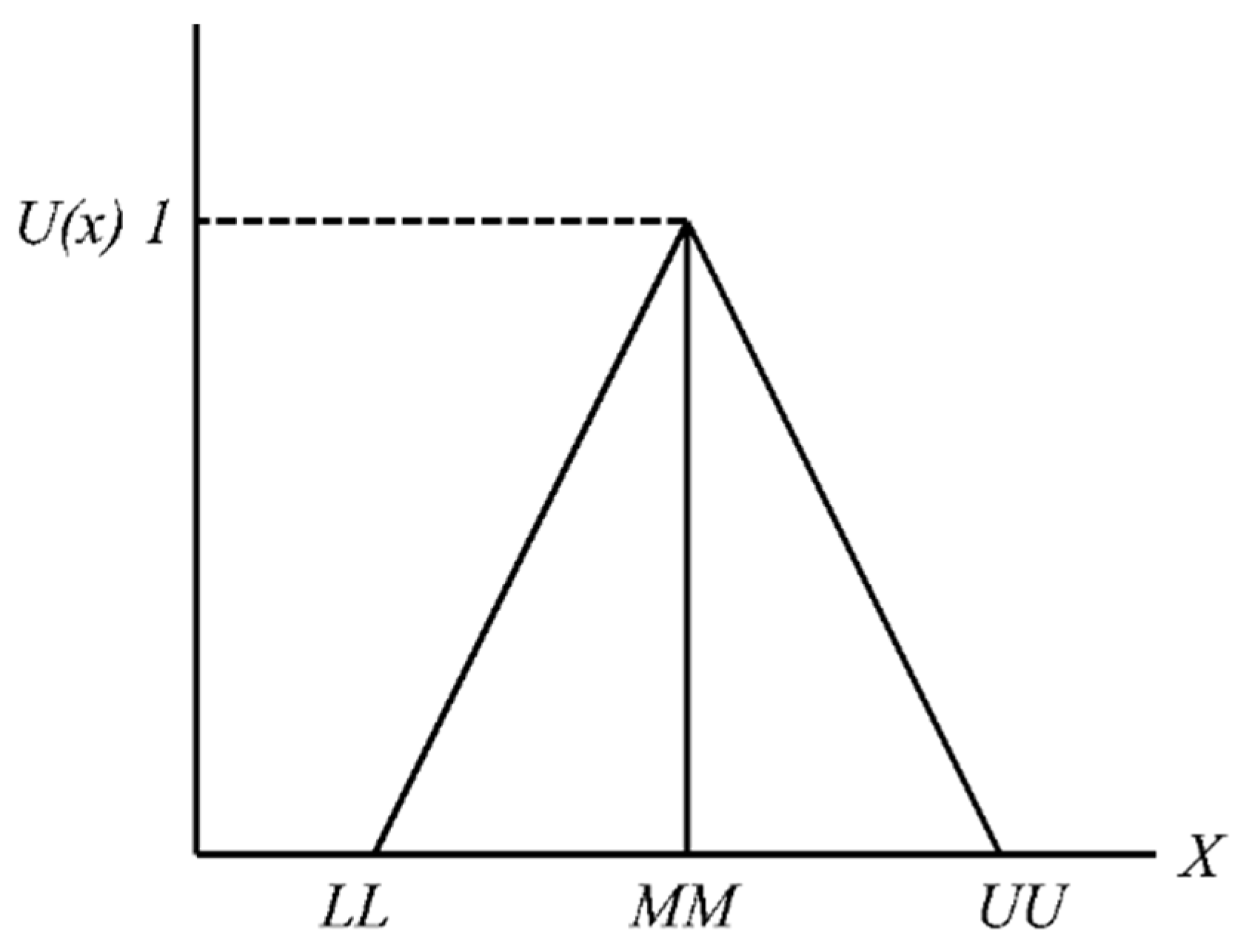
This study adopted triangular fuzzy numbers (TFNs) to indicate preferences for one criterion over another. Figure 2 depicts the structure of TFNs, while Table 4 depicts the membership function. The fuzzy-BWM assessment phases are as follows.

• Phase 1. Definition of a set of decision parameters

In the first phase, the decision parameters $\left\{C_1,C_2,C_3,\dots C_n\right\}$ must be determined in order to arrive at a conclusion, and the parameters that assess the alternatives are evaluated.

• Phase 2. Confirm the best parameter and worst parameter

The second phase confirms the best parameter (the critical important parameter) and worst parameter according to experts, where C_B is the definition of the best parameter and C_W is the worst parameter.

• Phase 3. Evaluating fuzzy reference comparisons for the best and worst parameters

Table 4 illustrates the linguistic scale of the fuzzy system, which makes it possible to confirm the fuzzy preferences of the best parameter over all other parameters. The final fuzzy best-to-others (FBO) vector obtained is:

$${\tilde{A}}_B=\left({\tilde{\alpha }}_{B1},{\tilde{\alpha }}_{B2,}\mathrm{\dots },{\tilde{\alpha }}_{Bn}\right)$$

${\tilde{A}}_B$ indicates the FBO vector; ${\tilde{\alpha }}_{Bj}$ indicates the best parameter in fuzzy C_B over parameter j, j = 1, 2,…, n. Therefore, the fuzzy preference of ${\tilde{\alpha }}_{BB}$ is (1, 1, 1).

Table 4 presents the fuzzy inference scale, where all parameters above the worst parameter of fuzzy preferences were examined. The resulting fuzzy others-to-worst (FOW) vector is:

$${\tilde{A}}_W=\left({\tilde{\alpha }}_{1W},{\tilde{\alpha }}_{2W,}\mathrm{\dots },{\tilde{\alpha }}_{nW}\right)$$

${\tilde{A}}_W$ indicates the FOW vector; ${\tilde{\alpha }}_{iW}$ indicates parameter i in the fuzzy preference over the worst parameter C_W, i = 1, 2,…, n. Therefore, the fuzzy preference of ${\tilde{\alpha }}_{WW}$ is (1, 1, 1).

• Phase 4. Evaluation of the synthesis fuzzy weights and consistency ratio

This process was applied to evaluate the synthesis fuzzy weights, where Equation (6) was applied to obtain the fuzzy weights.

$$min ma{x}_j \left\{\left|\frac{{\tilde{W}}_B}{{\tilde{W}}_j}-{\tilde{\alpha }}_{Bj}\right|,\left|\frac{{\tilde{W}}_j}{{\tilde{W}}_w}-{\tilde{a}}_{jw}\right|\right\}$$

(6)

Subject to

$$\begin{gathered} {\displaystyle \sum }_{j=1}^{n}R\left({\tilde{w}}_j\right)=1 \\ l{l}_j^w\le m{m}_j^w\le u{u}_{,}^w \\ l{l}_j^w\ge 0 \\ j=1,2,\mathrm{\dots },n \end{gathered}$$

where ${\tilde{W}}_B=\left(l{l}_B^w,m{m}_B^w,u{u}_B^w\right)$, ${\tilde{W}}_j=(l{l}_j^w,m{m}_j^w,u{u}_j^w$), ${\tilde{W}}_w=(l{l}_w^w,m{m}_w^w,u{u}_w^w$), ${\tilde{\alpha }}_{Bj}=\left(l{l}_{Bj},m{m}_{Bj},u{u}_{Bj}\right)$, ${\tilde{\alpha }}_{jw}=\left(l{l}_{jw},m{m}_{jw},u{u}_{jw}\right)$.

Equation (6) can transfer to the following nonlinearly optimization model.

$$min \xi$$

(7)

Subject to

$$\begin{gathered} \left|\frac{{\tilde{W}}_B}{{\tilde{W}}_j}-{\tilde{a}}_{Bj}\right|\le \xi \\ \left|\frac{{\tilde{W}}_j}{{\tilde{W}}_w}-{\tilde{a}}_{jw}\right|\le \xi \\ {{\displaystyle \sum }}_{j=1}^{n}R(\widetilde{w_j)}=1 \\ l{l}_j^w\le m{m}_j^w\le u{u}_{,}^w \\ l{l}_j^w\ge 0 \\ j=1,2,\mathrm{\dots },n \end{gathered}$$

where $\xi =\left(l{l}^{\xi },m{m}^{\xi },u{u}^{\xi }\right)$; suppose ${\xi }^{*}=\left(k^{*},k^{*},k^{*}\right), k^{*}\le l{l}^{\xi }$, then Equation (7) can transfer as:

$$\mathit{min} {\xi }^{*}$$

(8)

Subject to

$$\begin{gathered} \left|\frac{l{l}_B^{w}m{m}_B^{w}u{u}_B^w}{l{l}_W^{w}m{m}_W^{w}u{u}_W^w}-\left(l{l}_{Bj},m{m}_{Bj},u{u}_{Bj}\right)\right|\le \left(k^{*},k^{*},k^{*}\right) \\ \left|\frac{l{l}_j^{w}m{m}_j^{w}u{u}_j^w}{l{l}_W^{w}m{m}_W^{w}u{u}_W^w}-\left(l{l}_{jW},m{m}_{jW},u_{ujW}\right)\right|\le \left(k^{*},k^{*},k^{*}\right) \\ {\displaystyle \sum }_{j=1}^{n}R\left({\tilde{w}}_j\right)=1 \\ l{l}_j^w\le m{m}_j^w\le u{u}_{,}^w \\ l{l}_j^w\ge 0 \\ j=1,2,\mathrm{\dots },n \end{gathered}$$

This work employed the defuzzification process of Chen and Hsieh (2000), meaning the graded mean integration representation (GMIR) model, to identify the fuzzy synthesis results of TFN and obtain the crisp weight [71].

$$R_{(\widetilde{a_i)}}=\frac{l{l}_i+4m{m}_i+u{u}_i}{6}$$

(9)

$R_{(\widetilde{a_i)}}$ represents the ranking of TFN. The crisp weights of the fuzzy preference results were obtained through Equation (9).

Table 4. Transformation rules of linguistic scale.

Linguistic Terms	Membership Function
Equally importance (EI)	(1, 1, 1)
Weakly important (WI)	(2/3, 1, 3/2)
Fairly Important (FI)	(3/2, 2, 5/2)
Very important (VI)	(5/2, 3, 7/2)
Absolutely important (AI)	(7/2, 4, 9/2)

Source: Guo and Zhao [72].

Table 4. Transformation rules of linguistic scale.

Linguistic Terms	Membership Function
Equally importance (EI)	(1, 1, 1)
Weakly important (WI)	(2/3, 1, 3/2)
Fairly Important (FI)	(3/2, 2, 5/2)
Very important (VI)	(5/2, 3, 7/2)
Absolutely important (AI)	(7/2, 4, 9/2)

Source: Guo and Zhao [72].

Finally, as the sum of the defuzzification weights of each criterion is not equal to 1, the defuzzification weights must be normalized to a new weight (NW).

The formula of NW is:

$$N{W}_i=\frac{R_{(\widetilde{a_i)}}}{{{\displaystyle \sum }}_{i=1}^n{R}_{(\widetilde{\alpha )}}}$$

(10)

where NWi is the weight of fuzzy-BWM in each criterion.

The consistency ratio (C.R.) for fuzzy-BWM is a significant measure for determining the degree of consistency in pairwise comparisons (see Equation (5)). Guo and Zhao (2017) presented the fuzzy-BWM’s consistency index (CI), as shown in

Table 5. Consistency index for fuzzy-BWM.

Linguistic Terms	Equally Importance (EI)	Weakly Important (WI)	Fairly Important (FI)	Very Important (VI)	Absolutely Important (AI)
${\tilde{\alpha }}_{BW}$ Consistency index	(1, 1, 1) 3.00	(2/3, 1, 3/2) 3.80	(3/2, 2, 5/2) 5.29	(5/2, 3, 7/2) 6.69	(7/2, 4, 9/2) 8.04

Source: Guo & Zhao [72] and Liang et al., [73].

[72]. This study integrated the C.R. ratio in [72,73] to examine the obtained C.R.

• Phase 5. Rank the fuzzy-BWM weights

A selection of solutions can be shown in a preference list in the descending order of NWi.

3. Case Study

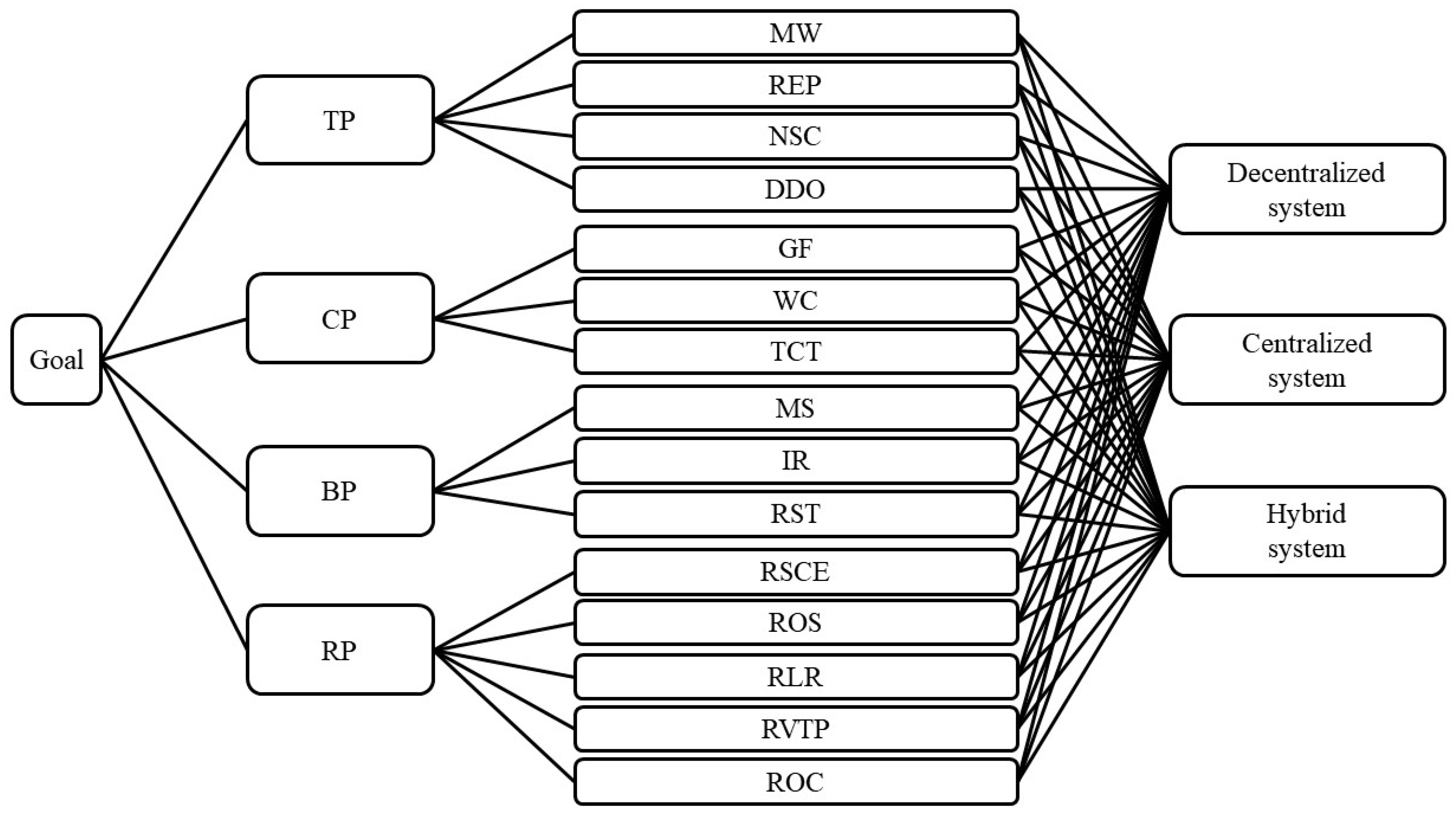
This study developed parameters for evaluating the optimal cryptocurrency trading systems and crucial parameters for investors in Taiwan, and then determined a suitable relative weight for each criterion according to the fuzzy-BWM architecture. By doing so, the optimal cryptocurrency trading systems were ranked and the research architecture was constructed, as shown in Figure 3. Based on the fuzzy-BWM algorithm, the modified Delphi technique was applied to create an assessment architecture for analyzing the ideal cryptocurrency trading systems and criteria in Taiwan. The following are the phases of the proposed model:

• Phase 1. Definition of a set of decision parameters

When constructing a research model, a broad agreement in line with the literature review should be obtained among specialists [74,75]. Hasson and Keeney (2011) recommended the number of practitioners to be between five and nine [67]. This phase was intended to collect the parameters through a literature review, and the seven specialists enrolled in this study included two investors of digital tokens in the commercial field, three scholars in the financial technology field, and two government experts. The goal of this study is to obtain the optimal cryptocurrency trading system and essential parameters for Taiwan, followed by four assessment views that include the cost perspective (CP), benefit perspective (BP), technology perspective (TP), and risk perspective (RP). Meanwhile, the 15 parameters in this study are gas fees (GF), withdrawal costs (WC), time costs of transaction (TCT), mechanism of savings (MS), interest rate (IR), returns of stablecoins (RST), mechanism of withdrawal (MW), regulated exchanges and providers (REP), the number of support coins (NSC), degree of difficulty in operation (DDO), risk of smart contract execution (RSCE), risk of operational security (ROS), risk of legal and regulatory issues (RLR), risk of volatility in token price (RVTP), and risk of collapse (ROC). The final cryptocurrency trading system is illustrated in Figure 3, and the data sources are shown as follows.

The assessment factors and parameters were implemented to determine the optimal cryptocurrency trading system and essential parameters in Taiwan as follows.

• CP:

  1.1

  GF [1,76,77]: the maker and taker’s commissions on the cryptocurrency trading system.

  1.2

  WC [78]: the trading system’s withdrawal costs for digital tokens.

  1.3

  TCT [76,79]: the trading system’s deposit/withdrawal speed and efficiency for digital tokens.

• BP:

  2.1

  MS: various saving mechanisms, including current deposit and timed deposit, within the cryptocurrency trading system.

  2.2

  IR: the various levels of interest rates, such as fixed and variable rates, within the cryptocurrency trading system.

  2.3

  RST [80]: the internal rate of return of a pegged token within a system for digital token trading.

• TP:

  3.1

  MW: the many withdrawal mechanisms in cryptocurrency trading systems, such as slowly, promptly, and immediately, by trader payback.

  3.2

  REP [81]: the many types of regulated trading systems and service providers in cryptocurrency trading systems, such as smart contracts, Bitgo, and Gemini.

  3.3

  NSC [80]: each cryptocurrency trading system has a distinct scale of tokens.

  3.4

  DDO [76,82]: the user experience and user interface of many trading systems, such as operation speed and transaction process complexity.

• RP:

  4.1

  RSCE [83]: the security concerns associated with smart contracts, including code flaws and hacking.

  4.2

  ROS [83,84]: The admin keys enable a specific set of people to update contracts and undertake emergency actions. If keyholders do not create or preserve their keys securely, malevolent third parties may gain access to them.

  4.3

  RLR [76,85]: the uncertainty of regulations in the digital assets market.

  4.4

  RVTP [76,84]: the level of volatility in token prices within the trading systems.

  4.5

  ROC [76]: the threat that the trading system for digital currencies may collapse due to a low transaction volume, liquidity issues, and exit fraud.

• Cryptocurrency trading system:

  5.1

  Decentralization of the trading system [7,8,9,10,11,12,14]: This trading system was designed to provide direct person-to-person trades for individuals without the need for a middleman, and it is administered and maintained entirely by smart contracts, which reduces the possibility of exit fraud. However, the fundamentals are fraught with ambiguity.

  5.2

  Centralization of the trading system [7,8,9,10,12]: This trading system denotes the employment of a middleman or third party to facilitate transactions, meaning both buyers and sellers alike entrust their possessions to this middleman. While the volume and liquidity of transactions are steady, the hazards of security and fraud concerns are greater for investors.

  5.3

  Hybrid trading system [7,8,12]: The hybrid trading system integrates the benefits of decentralized and centralized ecosystems. However, hybrid trading systems do not address the issues of high gas fees or transaction confirmation delays, as caused by frequent on-chain transactions.

• Phase 2. Confirm the best parameter and worst parameter

This phase confirms the best and worst parameters via seven experts. These experts include two investors of digital tokens in the commercial field, three scholars in the financial technology field, and two government experts. The best and worst parameters could be different according to the perceptions of experts.

Table 6. The best and worst parameters.

Specialties	Views		Parameters
			TP		CP		BP		RP
	Worst	Best	Worst	Best	Worst	Best	Worst	Best	Worst	Best
A	TP	BP	REP	NSC	GF	TCT	ROS	IR	RLR	ROC
B	TP	RP	NSC	DDO	GF	TCT	ROS	IR	RLR	ROC
C	CP	RP	MW	REP	WC	TCT	ROS	IR	RSCE	ROC
D	TP	BP	MW	NSC	TCT	GF	MS	ROS	ROC	RLR
E	TP	CP	REP	MW	WC	GF	MS	ROS	RVTP	ROS
F	CP	BP	REP	MW	WC	GF	MS	IR	RLR	ROC
G	TP	BP	REP	DDO	WC	GF	MS	IR	RLR	ROC

Source: expert results of this study.

shows the best and worst parameters based on the opinions of each expert.

• Phase 3. Evaluating fuzzy reference comparisons for the best and worst parameters

In line with the linguistic scale of the fuzzy system, as shown in Table 4, it is feasible to validate the best parameter’s fuzzy preferences over all other parameters. Then, the fuzzy best-to-others (FBO) and fuzzy others-to-worst (FOW) values were computed.

Table 7. The FBO vectors.

Specialties	Fuzzy Preferences of the Best Parameter over All the Views
	TP	CP	BP	RP
A	(7/2, 4, 9/2)	(2/3, 1, 3/2)	(3/2, 2, 5/2)	(1, 1, 1)
B	(1, 1, 1)	(5/2, 3, 7/2)	(3/2, 2, 5/2)	(1, 1, 1)
C	(7/2, 4, 9/2)	(3/2, 2, 5/2)	(1, 1, 1)	(3/2, 2, 5/2)
D	(7/2, 4, 9/2)	(3/2, 2, 5/2)	(1, 1, 1)	(2/3, 1, 3/2)
E	(7/2, 4, 9/2)	(1, 1, 1)	(3/2, 2, 5/2)	(2/3, 1, 3/2)
F	(3/2, 2, 5/2)	(7/2, 4, 9/2)	(1, 1, 1)	(3/2, 2, 5/2)
G	(5/2, 3, 7/2)	(2/3, 1, 3/2)	(1, 1, 1)	(3/2, 2, 5/2)

Source: expert results of this study.

displays the FBO and FOW results, meaning that it is possible to obtain the outcomes of fuzzy preferences of all parameters over the worst parameter. The FOW vectors were then validated, and

Table 8. The FOW vectors.

Specialties	Fuzzy Preferences of All Views over the Worst Parameter
	TP	CP	BP	RP
A	(1, 1, 1)	(5/2, 3, 7/2)	(2/3, 1, 3/2)	(7/2, 4, 9/2)
B	(7/2, 4, 9/2)	(1, 1, 1)	(3/2, 2, 5/2)	(5/2, 3, 7/2)
C	(1, 1, 1)	(3/2, 2, 5/2)	(5/2, 3, 7/2)	(2/3, 1, 3/2)
D	(1, 1, 1)	(3/2, 2, 5/2)	(7/2, 4, 9/2)	(2/3, 1, 3/2)
E	(1, 1, 1)	(7/2, 4, 9/2)	(2/3, 1, 3/2)	(3/2, 2, 5/2)
F	(3/2, 2, 5/2)	(1, 1, 1)	(7/2, 4, 9/2)	(3/2, 2, 5/2)
G	(1, 1, 1)	(5/2, 3, 7/2)	(7/2, 4, 9/2)	(3/2, 2, 5/2)

Source: expert results of this study.

displays the FOW results.

• Phase 4. Evaluation of the synthesis fuzzy weights and consistency ratio

This phase evaluates the synthesis fuzzy weights based on the TFNs. Equation (5) was employed to obtain the fuzzy weights, and the results are as follows. To reduce the complexity of the case study, Expert 1 was taken as an example to illustrate this phase, where Equation (11) is the fuzzified results of Expert 1′s opinion.

$$\mathit{min}{k}^{*}$$

(11)

$$s.t. \left\{\begin{array}{c}-k\ast u{u}_3\le l{l}_4-3.5\ast u{u}_3\le k\ast u{u}_3\\ -k\ast m{m}_3\le m{m}_4-4\ast m{m}_3\le k\ast m{m}_3\\ -k\ast l{l}_3\le u{u}_4-4.5\ast l{l}_3\le k\ast l{l}_3\\ -k\ast u{u}_1\le l{l}_4-0.67\ast u{u}_3\le k\ast u{u}_1\\ -k\ast m{m}_1\le m{m}_4-1\ast m{m}_3\le k\ast m{m}_1\\ -k\ast l{l}_1\le u{u}_4-1.5\ast l{l}_3\le k\ast l{l}_1\\ -k\ast u{u}_2\le l{l}_4-1.5\ast u{u}_3\le k\ast u{u}_2\\ -k\ast m{m}_2\le m{m}_4-2\ast m{m}_3\le k\ast m{m}_2\\ -k\ast l{l}_2\le u{u}_4-2.5\ast l{l}_3\le k\ast l{l}_2\\ -k\ast u{u}_3\le l{l}_1-2.5\ast u{u}_3\le k\ast u{u}_3\\ -k\ast m{m}_3\le m{m}_1-3\ast m{m}_3\le k\ast m{m}_3\\ -k\ast l{l}_3\le u{u}_1-3.5\ast l{l}_3\le k\ast l{l}_3\\ -k\ast u{u}_3\le l{l}_2-2.5\ast u{u}_3\le k\ast u{u}_3\\ -k\ast m{m}_3\le m{m}_2-3\ast m{m}_3\le k\ast m{m}_3\\ -k\ast l{l}_3\le u{u}_2-3.5\ast l{l}_3\le k\ast l{l}_3\\ \frac{1}{6}\ast l{l}_1+\frac{1}{6}\ast 4\ast m{m}_1\frac{1}{6}\ast u{u}_1+\frac{1}{6}\ast l{l}_2+\frac{1}{6}\ast 4\ast m{m}_2\frac{1}{6}\ast u{u}_2+\\ \frac{1}{6}\ast l{l}_3+\frac{1}{6}\ast 4\ast m{m}_3\frac{1}{6}\ast u{u}_3+\frac{1}{6}\ast l{l}_4+\frac{1}{6}\ast 4\ast m{m}_4\frac{1}{6}\ast u{u}_4=1\\ l{l}_1\le m{m}_1\le u{u}_1;l{l}_2\le m{m}_2\le u{u}_2;l{l}_3\le m{m}_3\le u{u}_3;l{l}_4\le m{m}_4\le u{u}_4\\ l{l}_1\ge 0;l{l}_2\ge 0;l{l}_3\ge 0;l{l}_4\ge 0;k\ge 0\end{array}\right.$$

This study integrated the C.R. ratios of Guo and Zhao (2017), and Liang et al. (2020) to examine the C.R. of this case study (see Table 5 and

Table 9. The threshold of C.R. in BWM.

	No. Parameter	3	4	5	6	7	8	9
Scales
3		0.168	0.168	0.168	0.168	0.168	0.168	0.168
4		0.112	0.153	0.190	0.221	0.253	0.258	0.268
5		0.135	0.199	0.231	0.255	0.272	0.284	0.296
6		0.133	0.199	0.264	0.304	0.314	0.322	0.326
7		0.129	0.246	0.282	0.303	0.314	0.325	0.340
8		0.131	0.252	0.296	0.315	0.341	0.362	0.366
9		0.136	0.268	0.306	0.334	0.352	0.362	0.366

Source: Guo & Zhao [72] and Liang et al., [73].

) [72,73]. The fuzzy weights of all experts’ opinions in views, parameters, and C.R. are shown in

Table 10. The fuzzy weights of views, parameters, and C.R.

Views	ll	mm	uu	C.R.	Parameters	ll	mm	uu	C.R.
TP	0.06	0.071	0.08	0.059	MW	0.24	0.257	0.279	0.056
					REP	0.098	0.106	0.117
					NSC	0.159	0.174	0.204
					DDO	0.181	0.207	0.241
CP	0.208	0.221	0.231		GF	0.343	0.349	0.408	0.07
					WC	0.18	0.194	0.226
					TCT	0.21	0.25	0.262
BP	0.195	0.204	0.222		MS	0.087	0.102	0.126	0.053
					IR	0.24	0.25	0.265
					RST	0.27	0.276	0.289
RP	0.141	0.175	0.186		RSCE	0.142	0.146	0.151	0.084
					ROS	0.147	0.165	0.173
					RLR	0.088	0.094	0.12
					RVTP	0.11	0.14	0.154
					ROC	0.157	0.164	0.172

Source: expert results of this study.

. The fuzzy weights of the cryptocurrency trading systems and C.R. are shown in

Table 11. The fuzzy weights of cryptocurrency trading systems and C.R.

Views	Systems	ll	mm	uu	C.R.
MW	Decentralized	0.291	0.316	0.378	0.069
	Centralized	0.163	0.166	0.174
	Hybrid	0.178	0.204	0.258
REP	Decentralized	0.301	0.313	0.327	0.082
	Centralized	0.163	0.163	0.163
	Hybrid	0.149	0.229	0.261
NSC	Decentralized	0.327	0.344	0.408	0.051
	Centralized	0.119	0.119	0.13
	Hybrid	0.233	0.262	0.28
DDO	Decentralized	0.322	0.339	0.377	0.061
	Centralized	0.146	0.156	0.178
	Hybrid	0.17	0.213	0.246
GF	Decentralized	0.269	0.31	0.379	0.053
	Centralized	0.127	0.136	0.153
	Hybrid	0.259	0.273	0.298
WC	Decentralized	0.305	0.344	0.425	0.047
	Centralized	0.148	0.157	0.17
	Hybrid	0.173	0.2	0.237
TCT	Decentralized	0.292	0.304	0.316	0.081
	Centralized	0.177	0.183	0.188
	Hybrid	0.135	0.203	0.251
MS	Decentralized	0.285	0.315	0.379	0.067
	Centralized	0.164	0.173	0.186
	Hybrid	0.17	0.201	0.237
IR	Decentralized	0.278	0.325	0.437	0.063
	Centralized	0.138	0.147	0.159
	Hybrid	0.208	0.237	0.252
RST	Decentralized	0.287	0.322	0.406	0.053
	Centralized	0.14	0.149	0.164
	Hybrid	0.22	0.238	0.243
RSCE	Decentralized	0.307	0.318	0.327	0.081
	Centralized	0.171	0.171	0.171
	Hybrid	0.147	0.201	0.257
ROS	Decentralized	0.285	0.347	0.454	0.058
	Centralized	0.134	0.134	0.136
	Hybrid	0.206	0.234	0.254
RLR	Decentralized	0.31	0.317	0.339	0.079
	Centralized	0.31	0.317	0.339
	Hybrid	0.16	0.231	0.25
RVTP	Decentralized	0.279	0.309	0.385	0.047
	Centralized	0.146	0.149	0.162
	Hybrid	0.183	0.253	0.272
ROC	Decentralized	0.281	0.314	0.366	0.065
	Centralized	0.154	0.16	0.166
	Hybrid	0.185	0.232	0.258

Source: expert results of this study.

.

The graded mean integration representation (GMIR) model was implemented in this study to defuzzify the synthesized fuzzy weights of TFN in order to acquire the crisp weights. Finally, as the sum of the defuzzification weights of each criterion was not equal to 1, the defuzzification weights were normalized to new weights (Equations (8) and (9)).

Table 12. The results of defuzzification, normalization and synthesis weights in views and parameters.

Views	DF	NF	PA	DF	NF	SW
TP	0.072	0.108	MW	0.258	0.344	0.037
			REP	0.107	0.143	0.015
			NSC	0.177	0.235	0.025
			DDO	0.209	0.278	0.03
CP	0.22	0.329	GF	0.358	0.447	0.147
			WC	0.198	0.247	0.081
			TCT	0.246	0.307	0.101
BP	0.205	0.307	MS	0.104	0.165	0.051
			IR	0.251	0.397	0.122
			RST	0.277	0.438	0.135
RP	0.171	0.256	RSCE	0.146	0.206	0.053
			ROS	0.164	0.231	0.059
			RLR	0.098	0.137	0.035
			RVTP	0.138	0.194	0.05
			ROC	0.164	0.231	0.059

Note: defuzzification (DF), normalization (NF), synthesis weight (SW), parameters (PA).

shows the results of defuzzification, normalization, and synthesis weights in views and parameters (each view to each parameter), while

Table 13. The results of defuzzification, normalization and synthesis weights in cryptocurrency trading systems.

Views	Systems	DF	NF	SW
MW	Decentralized	0.322	0.449	0.017
	Centralized	0.167	0.234	0.009
	Hybrid	0.208	0.317	0.012
REP	Decentralized	0.313	0.492	0.008
	Centralized	0.163	0.186	0.003
	Hybrid	0.221	0.322	0.005
NSC	Decentralized	0.352	0.443	0.011
	Centralized	0.121	0.266	0.007
	Hybrid	0.26	0.291	0.007
DDO	Decentralized	0.342	0.461	0.014
	Centralized	0.158	0.209	0.006
	Hybrid	0.212	0.329	0.010
GF	Decentralized	0.315	0.433	0.064
	Centralized	0.138	0.189	0.028
	Hybrid	0.275	0.378	0.056
WC	Decentralized	0.351	0.46	0.037
	Centralized	0.158	0.25	0.020
	Hybrid	0.202	0.29	0.024
TCT	Decentralized	0.304	0.462	0.047
	Centralized	0.183	0.239	0.024
	Hybrid	0.200	0.299	0.030
MS	Decentralized	0.321	0.46	0.023
	Centralized	0.174	0.248	0.013
	Hybrid	0.202	0.292	0.015
IR	Decentralized	0.336	0.494	0.060
	Centralized	0.148	0.222	0.027
	Hybrid	0.235	0.284	0.035
RST	Decentralized	0.33	0.468	0.063
	Centralized	0.150	0.205	0.028
	Hybrid	0.236	0.327	0.044
RSCE	Decentralized	0.317	0.48	0.025
	Centralized	0.171	0.165	0.009
	Hybrid	0.202	0.355	0.019
ROS	Decentralized	0.355	0.371	0.022
	Centralized	0.134	0.371	0.022
	Hybrid	0.233	0.258	0.015
RLR	Decentralized	0.32	0.481	0.017
	Centralized	0.32	0.222	0.008
	Hybrid	0.222	0.297	0.01
RVTP	Decentralized	0.317	0.445	0.022
	Centralized	0.151	0.212	0.011
	Hybrid	0.244	0.343	0.017
ROC	Decentralized	0.317	0.45	0.027
	Centralized	0.160	0.227	0.013
	Hybrid	0.228	0.323	0.019

Note: defuzzification (DF), normalization (NF), synthesis weight (SW).

shows the results of defuzzification, normalization and synthesis weights in three cryptocurrency trading systems (each parameter to alternatives).

• Phase 5. Rank the fuzzy-BWM weights

The new weights were evaluated with fuzzy-BWM in order to determine the optimal cryptocurrency trading system, as based on Table 12 and Table 13. The NWs of each view, parameter, and system are the SW results from Table 12 and Table 13, and the comprehensive results and ranking of the systems, views, and parameters are shown in

Table 14. The synthesis results of fuzzy-BWM weights.

Views	NW	Rank	PA	NW	Rank	Systems	NW	Rank
TP	0.108	4	MW	0.037	11	Decentralized	0.03	1
			REP	0.015	15	Centralized	0.015	3
			NSC	0.025	14	Hybrid	0.021	2
			DDO	0.03	13
CP	0.329	1	GF	0.147	1
			WC	0.081	5
			TCT	0.101	4
BP	0.307	2	MS	0.051	9
			IR	0.122	3
			RST	0.135	2
RP	0.256	3	RSCE	0.053	8
			ROS	0.059	6
			RLR	0.035	12
			RVTP	0.05	10
			ROC	0.059	7

Note: new weight (NW), parameters (PA).

.

Table 14 shows the fuzzy-BWM synthesis results regarding the determination of the optimal cryptocurrency trading system for investors in Taiwan’s crypto-token fields: decentralized (0.030), centralized (0.015), and hybrid (0.021). Therefore, the sequential weights of the three cryptocurrency trading systems are decentralized > hybrid > centralized. The sequential weights of the four perspectives are costs (0.329) > benefit (0.307) > risks (0.256) > technologies (0.108), and the sequential weights of the 15 parameters are gas fees (0.147) > returns of stablecoins (0.135) > interest rate (0.122) > time costs of transaction (0.101).

Thus, the optimum cryptocurrency trading system was decentralized, which implies that when businesses or investors in Taiwan wanted to include the commodity of crypto-tokens into their portfolio, the decentralized trading system would be the focus of their investment strategy based on the fuzzy concept. Additionally, the critical views for determining the optimal cryptocurrency trading system in Taiwan were CP and GF, and some critical parameters were ROS, IR, and TCT. This result indicates that when investors utilized crypto-tokens in their financial plan, GF, ROS, IR, and TCT were the important factors to consider. As digital tokens are a virtual commodity for businesses and investors, the cost of gas fees and returns (interest rates) are very important to their financial portfolio. Moreover, investors must also be concerned with the transaction time and operational risks, meaning the transaction times of some trading systems are longer and lack security; thus, hacks may occur in the token field. Even though digital assets become more popular, high returns imply high risks. Overall, investors in Taiwan should concentrate on the costs field and GF when they implement cryptocurrency in an investment project.

4. Conclusions

Blockchain technology can decrease the costs of transactions, build distributed trust and empower decentralized networks, which can create a new basis for decentralized business models. Crypto-tokens have been implemented by numerous corporations and investors for their financial portfolios. The cryptocurrency trading system comprises three types: decentralized, centralized, and hybrid; the benefits and drawbacks of these systems differ for different firms and investors. However, as investors and corporations in Taiwan lack the ability to assess the optimal alternatives for a crypto trading system based on the decision support concept, the evaluation and selection of the optimal cryptocurrency trading system is a complex problem for corporations and investors in Taiwan.

Hence, this study integrated the fuzzy theory and BWM to construct an evaluation architecture for prioritization, where TFNs were used to illustrate expert comparison assessments. As the evaluation architecture, the fuzzy modification of BWM could be used, and its usefulness was demonstrated with numerical examples. According to previous research and surveying specialists in economic and financial fields, such as investors and financial scholars, this study applied the modified Delphi method and fuzzy-BWM to develop an evaluation architecture that can evaluate the optimal cryptocurrency trading system and critical parameters for investors in Taiwan. The results show that the optimal cryptocurrency trading system was decentralized and the critical criterion was GF, which can facilitate investors and corporations to assess the suitable systems and key factors in crypto investment projects. The presented model and the corresponding findings can provide academic and commercial support for firms and investors in Taiwan. In the academic field, the fuzzy-BWM decision-making architecture can provide investors and corporations with valuable guidance for measuring the optimal cryptocurrency trading system for investment projects in crypto-token fields in Taiwan. In the commercial field, the proposed architecture can provide administrators with a valuable method to assess the optimal cryptocurrency trading system for investors and corporations in Taiwan. In addition, as the model integrates fuzzy-BWM, it can address other areas of uncertain decision problems, such as performance evaluation, location selection issues, strategic planning, optimal alternative evaluations, and determining the key factors.

This study has three limitations as follows:

• In order to reduce the complexity of the evaluation process, we implemented triangular fuzzy numbers in the BWM algorithm. Future studies can apply and compare the results of trapezoidal fuzzy numbers and Gaussian fuzzy numbers in this field.
• This study did not consider the α-cut or λ in triangular fuzzy numbers. We suggest that future studies implement these two concepts in fuzzy numbers to obtain a degree of fuzzy sensitivity.
• The BWM algorithm cannot deal with the internal and external dependent relationships of perspectives and parameters. Future studies can also utilize the network concept to solve these relationships, for example, through the analytic network process.