Identification of Chaotic Dynamics in Jerky-Based Systems by Recurrent Wavelet First-Order Neural Networks with a Morlet Wavelet Activation Function
Abstract
1. Introduction
2. Chaotic Dynamical Systems
2.1. Simple Memristive Jerk System
2.2. Unstable Dissipative System of Type I (UDSI)
- 1.
- The linear part of the systems must be dissipative, satisfying , where , are the eigenvalues of . Consider that an eigenvalue must be negative real, and two must be complex and conjugated with the positive real part , resulting in an unstable equilibrium focus-saddle point . This equilibrium presents an stable manifold with a fast eigendirection and an unstable manifold with a slow spiral eigendirection.
- 2.
- The affine vector must be considered as a discrete function that changes domains depending on where the trajectory is located. Thus, .
3. Materials and Methods
3.1. Recurrent Wavelet First-Order Neural Network
3.2. Filtered Error Algorithm
- 1.
- , ∈ (i.e., and are uniformly bounded);
- 2.
4. Neural Identification Results
4.1. Analysis of Identification via the Euclidean Distance between Trajectories
4.2. Neural Identification for MSCS
4.3. Neural Identification for UDSI
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Identification Error Boundedness
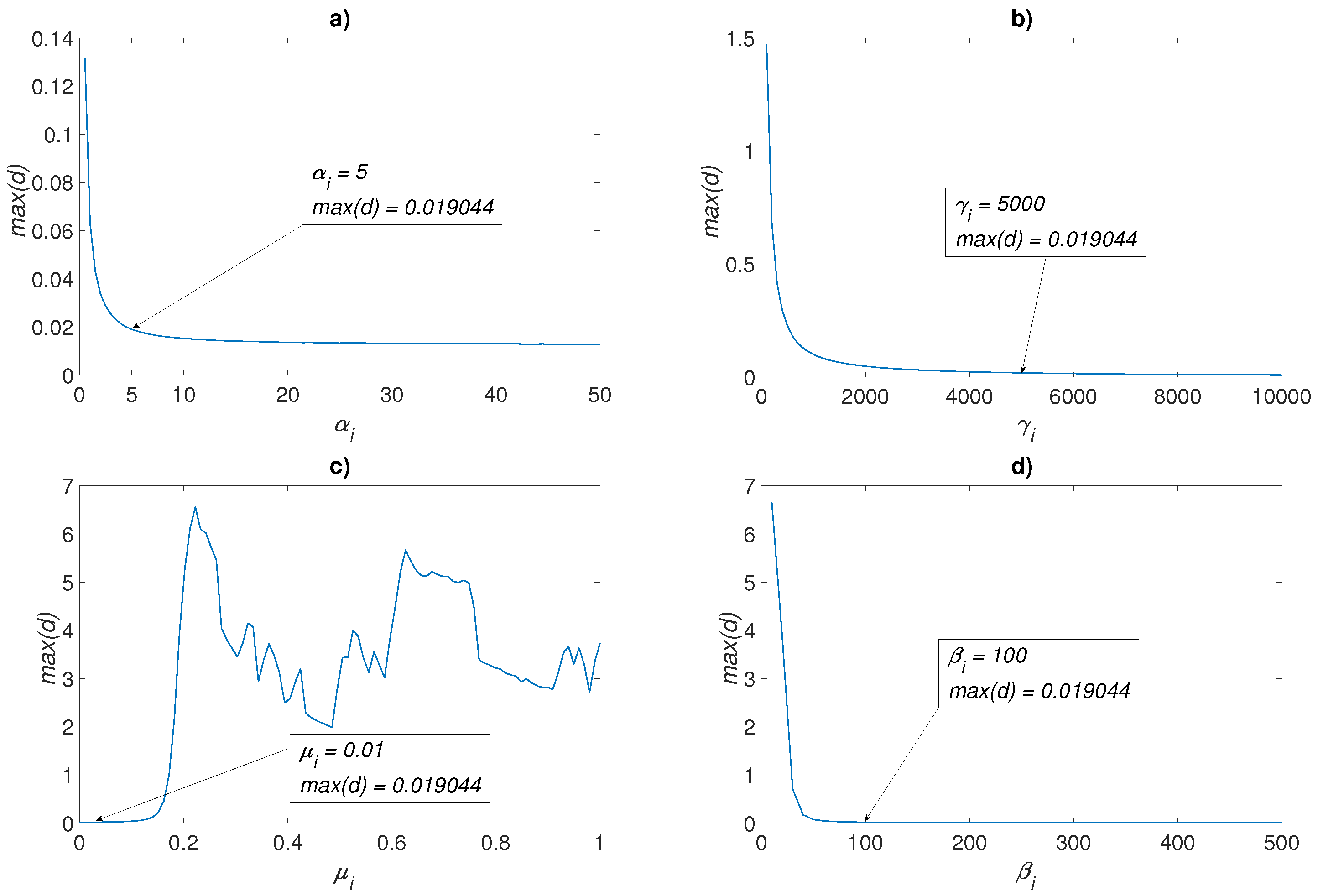
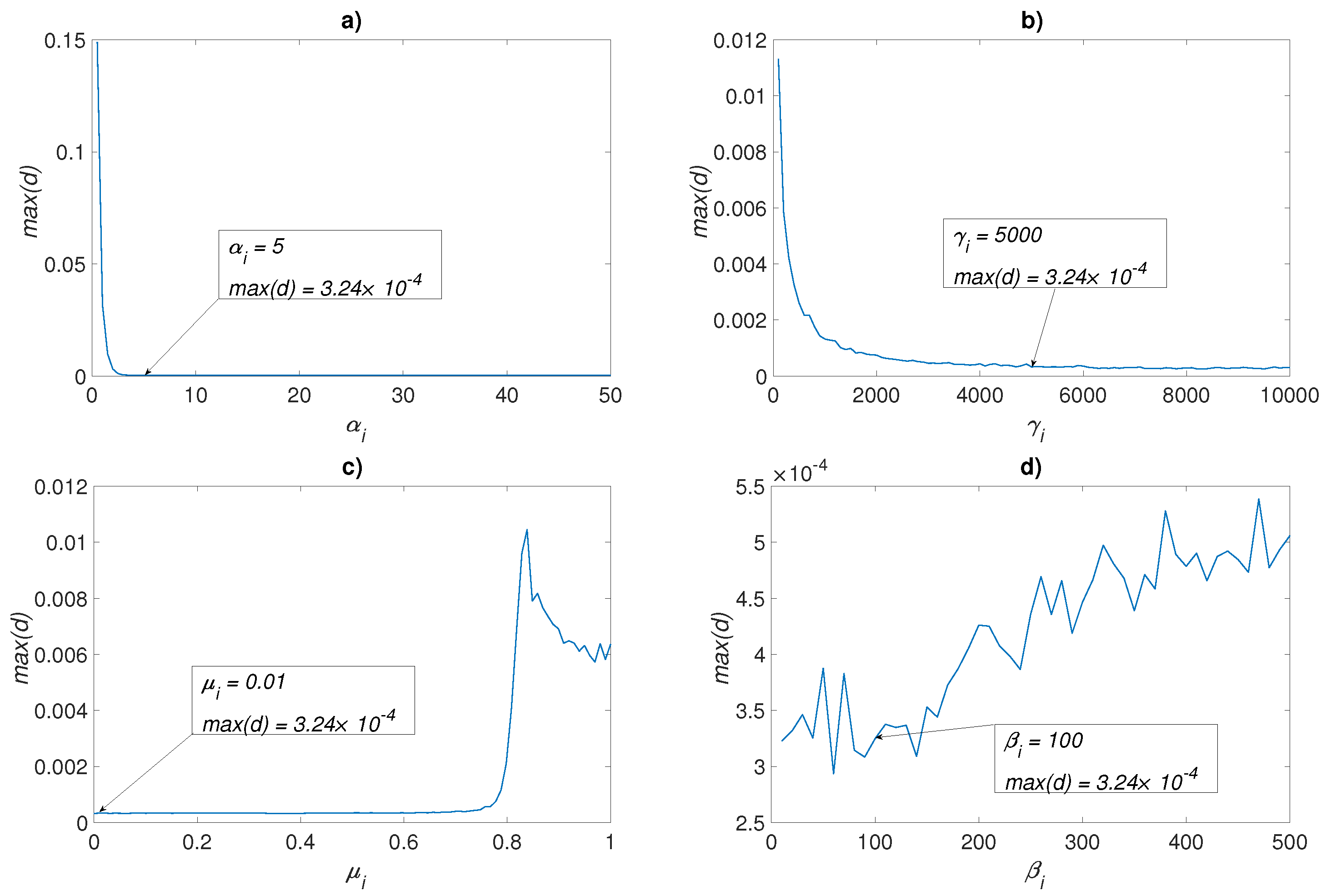
Appendix B. Network Parameter Adjustment
References
- Chaintron, L.P.; Diez, A. Propagation of chaos: A review of models, methods and applications. arXiv 2021, arXiv:2106.14812. [Google Scholar] [CrossRef]
- Cetina-Denis, J.J.; López-Gutiérrez, R.M.; Cruz-Hernández, C.; Arellano-Delgado, A. Design of a Chaotic Trajectory Generator Algorithm for Mobile Robots. Appl. Sci. 2022, 12, 2587. [Google Scholar] [CrossRef]
- Wang, X.; Liu, P. A new full chaos coupled mapping lattice and its application in privacy image encryption. IEEE Trans. Circuits Syst. Regul. Pap. 2021, 69, 1291–1301. [Google Scholar] [CrossRef]
- El-Latif, A.A.A.; Abd-El-Atty, B.; Belazi, A.; Iliyasu, A.M. Efficient Chaos-Based Substitution-Box and Its Application to Image Encryption. Electronics 2021, 10, 1392. [Google Scholar] [CrossRef]
- Fan, J.; Xu, W.; Huang, Y.; Dinesh Jackson, S.R. Application of Chaos Cuckoo Search Algorithm in computer vision technology. Soft Comput. 2021, 25, 12373–12387. [Google Scholar] [CrossRef]
- Basha, J.; Bacanin, N.; Vukobrat, N.; Zivkovic, M.; Venkatachalam, K.; Hubálovský, S.; Trojovský, P. Chaotic Harris Hawks Optimization with Quasi-Reflection-Based Learning: An Application to Enhance CNN Design. Sensors 2021, 21, 6654. [Google Scholar] [CrossRef] [PubMed]
- Escalante-González, R.D.J.; Campos-Cantón, E.; Nicol, M. Generation of multi-scroll attractors without equilibria via piecewise linear systems. Chaos Interdiscip. J. Nonlinear Sci. 2017, 27, 053109. [Google Scholar] [CrossRef] [PubMed]
- Ontanón-García, L.J.; Campos-Cantón, E. Widening of the basins of attraction of a multistable switching dynamical system with the location of symmetric equilibria. Nonlinear Anal. Hybrid Syst. 2017, 26, 38–47. [Google Scholar] [CrossRef]
- García-Grimaldo, C.; Campos, E. Chaotic features of a class of discrete maps without fixed points. Int. J. Bifurc. Chaos 2021, 31, 2150200. [Google Scholar] [CrossRef]
- Echenausía-Monroy, J.L.; Jafari, S.; Huerta-Cuellar, G.; Gilardi-Velázquez, H.E. Predicting the Emergence of Multistability in a Monoparametric PWL System. Int. J. Bifurc. Chaos 2022, 32, 2250206. [Google Scholar] [CrossRef]
- Park, J.H. Synchronization of a class of chaotic dynamic systems with controller gain variations. Chaos Solitons Fract. 2006, 27, 1279–1284. [Google Scholar] [CrossRef]
- Park, J.H.; Ji, D.H.; Won, S.C.; Lee, S.M. H1 synchronization of time-delayed chaotic systems. Appl. Math. Comput. 2008, 204, 170–177. [Google Scholar]
- Kwon, O.M.; Park, J.H.; Lee, S.M. Secure communication based on chaotic synchronization via interval time-varying delay feedback control. Nonlinear Dyn. 2011, 63, 239–252. [Google Scholar] [CrossRef]
- Ontanón-García, L.J.; Jiménez-López, E.; Campos-Cantón, E.; Basin, M. A family of hyperchaotic multi-scroll attractors in Rn. Appl. Math. Comput. 2014, 233, 522–533. [Google Scholar] [CrossRef]
- Chunbiao, L.; Sprott, J.C.; Thio, W.J.C.; Zhenyu, G. A simple memristive jerk system. IET Circuits Devices Syst. 2021, 15, 388–392. [Google Scholar]
- Ontanon-Garcia, L.J.; Lozoya-Ponce, R.E. Analog electronic implementation of unstable dissipative systems of type I with multi-scrolls displaced along space. Int. J. Bifurc. Chaos 2017, 27, 1750093. [Google Scholar] [CrossRef]
- Brugnago, E.L.; Hild, T.A.; Weingärtner, D.; Beims, M.W. Classification strategies in machine learning techniques predicting regime changes and durations in the Lorenz system. Chaos 2020, 30, 053101. [Google Scholar] [CrossRef]
- Subramanian, M.; Tipireddy, R.; Chatterjee, S. Lorenz System State Stability Identification using Neural Networks. arXiv 2021, arXiv:2106.08489. [Google Scholar]
- Alexandridis, A.K.; Zapranis, A.D. Wavelet Neural Networks with Applications in Financial Engineering, Chaos, and Classification; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Magallón, D.A.; Castañeda, C.E.; Jurado, F.; Morfin, O.A. Design of a Neural Super-Twisting Controller to Emulate a Flywheel Energy Storage System. Energies 2021, 14, 6416. [Google Scholar] [CrossRef]
- Quade, M.; Abel, M.; Nathan Kutz, J.; Brunton, S.L. Sparse identification of nonlinear dynamics for rapid model recovery. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 063116. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Magallón, D.A.; Jaimes-Reátegui, R.; García-López, J.H.; Huerta-Cuellar, G.; López-Mancilla, D.; Pisarchik, A.N. Control of Multistability in an Erbium-Doped Fiber Laser by an Artificial Neural Network: A Numerical Approach. Mathematics 2022, 17, 3140. [Google Scholar] [CrossRef]
- Kosmatopoulos, E.B.; Polycarpou, M.M.; Christodoulou, M.A.; Ioannou, P.A. High-order neural network structures for identification of dynamical systems. IEEE Trans. Neural Netw. 1995, 6, 422–431. [Google Scholar] [CrossRef] [PubMed]
- Vázquez, L.A.; Jurado, F.; Alanís, A.Y. Decentralized identification and control in real-time of a robot manipulator via recurrent wavelet first-order neural network. Math. Probl. Eng. 2015, 2015, 451049. [Google Scholar] [CrossRef]
- Hale, J.K. Ordinary Differential Equations; Wiley-InterScience: Maitland, FL, USA, 1969. [Google Scholar]
- Rovithakis, G.A.; Christodoulou, M.A. Adaptive Control with Recurrent High-Order Neural Networks: Theory and Industrial Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magallón-García, D.A.; Ontanon-Garcia, L.J.; García-López, J.H.; Huerta-Cuéllar, G.; Soubervielle-Montalvo, C. Identification of Chaotic Dynamics in Jerky-Based Systems by Recurrent Wavelet First-Order Neural Networks with a Morlet Wavelet Activation Function. Axioms 2023, 12, 200. https://doi.org/10.3390/axioms12020200
Magallón-García DA, Ontanon-Garcia LJ, García-López JH, Huerta-Cuéllar G, Soubervielle-Montalvo C. Identification of Chaotic Dynamics in Jerky-Based Systems by Recurrent Wavelet First-Order Neural Networks with a Morlet Wavelet Activation Function. Axioms. 2023; 12(2):200. https://doi.org/10.3390/axioms12020200
Chicago/Turabian StyleMagallón-García, Daniel Alejandro, Luis Javier Ontanon-Garcia, Juan Hugo García-López, Guillermo Huerta-Cuéllar, and Carlos Soubervielle-Montalvo. 2023. "Identification of Chaotic Dynamics in Jerky-Based Systems by Recurrent Wavelet First-Order Neural Networks with a Morlet Wavelet Activation Function" Axioms 12, no. 2: 200. https://doi.org/10.3390/axioms12020200
APA StyleMagallón-García, D. A., Ontanon-Garcia, L. J., García-López, J. H., Huerta-Cuéllar, G., & Soubervielle-Montalvo, C. (2023). Identification of Chaotic Dynamics in Jerky-Based Systems by Recurrent Wavelet First-Order Neural Networks with a Morlet Wavelet Activation Function. Axioms, 12(2), 200. https://doi.org/10.3390/axioms12020200








