Dynamical Properties of Discrete-Time HTLV-I and HIV-1 within-Host Coinfection Model

Abstract

Infection with human immunodeficiency virus type 1 (HIV-1) or human T-lymphotropic virus type I (HTLV-I) or both can lead to mortality. CD4⁺T cells are the target for both HTLV-I and HIV-1. In addition, HIV-1 can infect macrophages. CD4⁺T cells and macrophages play important roles in the immune system response. This article develops and analyzes a discrete-time HTLV-I and HIV-1 co-infection model. The model depicts the within-host interaction of six compartments: uninfected CD4⁺T cells, HIV-1-infected CD4⁺T cells, uninfected macrophages, HIV-1-infected macrophages, free HIV-1 particles and HTLV-I-infected CD4⁺T cells. The discrete-time model is obtained by discretizing the continuous-time model via the nonstandard finite difference (NSFD) approach. We show that NSFD preserves the positivity and boundedness of the model’s solutions. We deduce four threshold parameters that control the existence and stability of the four equilibria of the model. The Lyapunov method is used to examine the global stability of all equilibria. The analytical findings are supported via numerical simulation. The model can be useful when one seeks to design optimal treatment schedules using optimal control theory.

1. Introduction

Mathematical models of within-host viral infection have enhanced our understanding of the dynamical interactions between viruses, target cells and immune cells. The analytical and numerical investigations of these models can be used to (i) estimate the key biological parameters, such as the half-lives of the virus and infected cell, and the daily viral production; (ii) estimate different antiviral drug efficacies; (iii) evaluate the intensity of the immune system responses; (iv) predict disease progression over long terms [1]. Many scientists and researchers were interested in formulating and studying mathematical models of the within-host dynamics of different viruses that attack humans, such as human immunodeficiency virus type 1 (HIV-1) [2,3,4,5,6,7,8,9,10,11,12,13,14], human T-lymphotropic virus type I (HTLV-I) [15,16,17,18,19,20], hepatitis B virus (HBV) [21], hepatitis C virus (HCV), [22], influenza [23], dengue virus [24], Chikungunya virus [25], ebola virus [26] and recently severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) [27,28,29].

HIV-1 is a retrovirus that attacks the fundamental component of the immune system, CD$4^{+}$T cells. Infection with this virus causes a breakdown in the immune system, exposing the human body to opportunistic diseases. The disease caused by HIV-1 is the acquired immunodeficiency syndrome (AIDS). The two main immune responses against the viral infection are cytotoxic T lymphocyte (CTL) immune response and antibody immune response. CTLs attack and kill the viral infected cells. Antibodies produced by B cells are responsible for neutralizing viruses. The basic HIV-1 dynamics model presented in [2] includes three compartments: uninfected CD4${}^{+}$T cells (x), HIV-1-infected CD4${}^{+}$T cells (y) and free HIV-1 particles (v) as:

$$\begin{array}{cc}\hfill \frac{dx}{dt}& =\stackrel{{\mathrm{CD}4}^{+}\mathrm{T}\mathrm{cells}\mathrm{production}}{\overbrace{\xi }}-\stackrel{\mathrm{death}}{\overbrace{\gamma x}}-\stackrel{\mathrm{HIV}-1\mathrm{infectious}\mathrm{transmission}}{\overbrace{\omega xv}},\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill \frac{dy}{dt}& =\stackrel{\mathrm{HIV}-1\mathrm{infectious}\mathrm{transmission}}{\overbrace{\omega xv}}-\stackrel{\mathrm{death}}{\overbrace{\alpha y}},\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill \frac{dv}{dt}& =\stackrel{\mathrm{generation}\mathrm{of}\mathrm{HIV}-1}{\overbrace{\beta \alpha y}}-\stackrel{\mathrm{death}}{\overbrace{\theta v}}.\hfill \end{array}$$

(3)

Many mathematical models were formulated as an extension of the basic HIV-1 model (1)–(3) to take into account many biological factors such as time delay [5,6], drug therapies [6,7], CTL immunity [2], antibody immunity [8], reaction-diffusion [9], stochastic effects [10] and latent HIV-1 reservoirs [4].

It was found in [4] that HIV-1 can infect macrophages in addition to CD4${}^{+}$T cells. Mathematical HIV-1 models that include macrophages as a second target for HIV-1 are more reasonable and accurate. The HIV-1 infection model with two categories of target cells was presented in [7,11] as:

$$\begin{array}{cc}\hfill \frac{dx}{dt}& =\stackrel{{\mathrm{CD}4}^{+}\mathrm{T}\mathrm{cells}\mathrm{production}}{\overbrace{{\xi }_1}}-\stackrel{\mathrm{death}}{\overbrace{{\gamma }_{1}x}}-\stackrel{\mathrm{HIV}-1\mathrm{infectious}\mathrm{transmission}}{\overbrace{{\omega }_{1}xv}},\hfill \\ \hfill \frac{dy}{dt}& =\stackrel{\mathrm{HIV}-1\mathrm{infectious}\mathrm{transmission}}{\overbrace{{\omega }_{1}xv}}-\stackrel{\mathrm{death}}{\overbrace{{\alpha }_{1}y}},\hfill \\ \hfill \frac{dw}{dt}& =\stackrel{\mathrm{macrophages}\mathrm{production}}{\overbrace{{\xi }_2}}-\stackrel{\mathrm{death}}{\overbrace{{\gamma }_{2}w}}-\stackrel{\mathrm{HIV}-1\mathrm{infectious}\mathrm{transmission}}{\overbrace{{\omega }_{2}wv}},\hfill \\ \hfill \frac{dz}{dt}& =\stackrel{\mathrm{HIV}-1\mathrm{infectious}\mathrm{transmission}}{\overbrace{{\omega }_{2}wv}}-\stackrel{\mathrm{death}}{\overbrace{{\alpha }_{2}z}},\hfill \\ \hfill \frac{dv}{dt}& =\stackrel{\mathrm{generation}\mathrm{of}\mathrm{HIV}-1}{\overbrace{{\beta }_1{\alpha }_{1}y+{\beta }_2{\alpha }_{2}z}}-\stackrel{\mathrm{death}}{\overbrace{\theta v}},\hfill \end{array}$$

where w and z are the concentrations of uninfected macrophages and HIV-1-infected macrophages, respectively. This model was extended in several directions by including optimal treatment schedules [12,13], CTL immunity [14], antibody immunity [30], time delay [30], latent infection [3] and stochastic effects [14].

HTLV-I is a retrovirus that infects the CD$4^{+}$T cells. HTLV-I-associated myelopathy/tropical spastic paraparesis (HAM/TSP) and adult T-cell leukemia (ATL) diseases are the cause of HTLV-I infection. A mathematical HTLV-I infection model without considering the CTL is given as [16]:

$$\begin{array}{cc}\hfill \frac{dx}{dt}& =\stackrel{{\mathrm{CD}4}^{+}\mathrm{T}\mathrm{cells}\mathrm{production}}{\overbrace{{\xi }_1}}-\stackrel{\mathrm{death}}{\overbrace{{\gamma }_{1}x}}-\stackrel{\mathrm{HTLV}-\mathrm{I}\mathrm{infectious}\mathrm{transmission}}{\overbrace{{\omega }_{3}xu}},\hfill \\ \hfill \frac{du}{dt}& =\stackrel{\mathrm{HTLV}-\mathrm{I}\mathrm{infectious}\mathrm{transmission}}{\overbrace{{\omega }_{3}xu}}-\stackrel{\mathrm{death}}{\overbrace{\delta u}},\hfill \end{array}$$

where u represents the concentration of HTLV-I-infected CD4${}^{+}$T cells.

HTLV-I infection models with CTL immune response were addressed in [15,16,17,18]. HTLV-I infection models have been incorporated with intracellular delay in [19,20], and with immune response delay in [18,19]. Reaction–diffusion HTLV-I infection models were investigated in [17].

Both HTLV-I and HIV-1 can be transmitted from an infected individual to healthy individuals through blood transfusions, sexual relationships, organ transplantation and infected sharp objects. HTLV-I and HIV-1 co-infection models were developed and analyzed in [31,32]. In these papers, the presence of macrophages in the HIV-1 dynamics as a second target was not considered. This shortcoming was addressed by modeling the HTLV-I and HIV-1 co-infection as follows [33]:

$$\begin{array}{cc}\hfill \frac{dx}{dt}& =\stackrel{{\mathrm{CD}4}^{+}\mathrm{T}\mathrm{cells}\mathrm{production}}{\overbrace{{\xi }_1}}-\stackrel{\mathrm{death}}{\overbrace{{\gamma }_{1}x}}-\stackrel{\mathrm{HIV}-1\mathrm{infectious}\mathrm{transmission}}{\overbrace{{\omega }_{1}xv}}-\stackrel{\mathrm{HTLV}-\mathrm{I}\mathrm{infectious}\mathrm{transmission}}{\overbrace{{\omega }_{3}xu}},\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill \frac{dy}{dt}& =\stackrel{\mathrm{HIV}-1\mathrm{infectious}\mathrm{transmission}}{\overbrace{{\omega }_{1}xv}}-\stackrel{\mathrm{death}}{\overbrace{{\alpha }_{1}y}},\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill \frac{dw}{dt}& =\stackrel{\mathrm{macrophages}\mathrm{production}}{\overbrace{{\xi }_2}}-\stackrel{\mathrm{death}}{\overbrace{{\gamma }_{2}w}}-\stackrel{\mathrm{HIV}-1\mathrm{infectious}\mathrm{transmission}}{\overbrace{{\omega }_{2}wv}},\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill \frac{dz}{dt}& =\stackrel{\mathrm{HIV}-1\mathrm{infectious}\mathrm{transmission}}{\overbrace{{\omega }_{2}wv}}-\stackrel{\mathrm{death}}{\overbrace{{\alpha }_{2}z}},\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill \frac{dv}{dt}& =\stackrel{\mathrm{generation}\mathrm{of}\mathrm{HIV}-1}{\overbrace{{\beta }_1{\alpha }_{1}y+{\beta }_2{\alpha }_{2}z}}-\stackrel{\mathrm{death}}{\overbrace{\theta v}},\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill \frac{du}{dt}& =\stackrel{\mathrm{HTLV}-\mathrm{I}\mathrm{infectious}\mathrm{transmission}}{\overbrace{{\omega }_{3}xu}}-\stackrel{\mathrm{death}}{\overbrace{\delta u}}.\hfill \end{array}$$

(9)

The analytical solutions for the above-mentioned continuous-time models are unknown due to their nonlinearity. Therefore, numerical discretization is usually used to solve such models. In addition, the real measurements from viral infected individuals are usually taken at discrete-time instants. For these reasons, studying the resulting discrete-time models is important. One important question arises: how can we choose a suitable discretization scheme such that the basic and global properties of solutions of the corresponding continuous-time models can be efficiently maintained? Standard numerical methods for solving nonlinear differential equations such as Euler, Runge–Kutta and others suffer from numerical instability and bias when large step sizes are used in the numerical simulation [34]. In this case, these methods can give non-physical solutions and can produce “false” or “spurious” fixed points, which are not fixed points of the original continuous-time model [35,36]. Based on carefully designed rules, Mickens [37,38] introduced a non-standard finite difference (NSFD) scheme, which has been successfully used in the study of different biological models in epidemiology [35,36,39] and virology [40,41,42]. These models are described by different types of differential equations: ordinary differential equations (ODEs), partial differential equations (PDEs) and fractional differential equations (FDEs). The main advantage of the NSFD method is that the essential qualitative features of the mathematical model such as equilibria, positivity (or nonnegativity), boundedness and global behaviors of solutions are preserved independently of the selected step-size [40]. The NSFD method was applied to discretize continuous-time HIV-1 infection models within a host in [43,44,45,46,47]. In [44], a discrete-time HIV-1 model with the cure rate and Beddington–DeAngelis incidence was studied. Local stability of equilibria was established. Elaiw and Alshaikh [47] studied the global stability of two discrete-time HIV-1 models by including three types of HIV-1-infected cells: latently, long-lived chronically and short-lived. Liu and Zhu [45] developed an HIV-1 infection model with CTL immunity, time delay and diffusion. The system was given by PDEs, and it was discretized via the NSFD method. The global stability of the model’s equilibria was proven via the Lyapunov method.

We noted that the discrete-time version of the within-host HTLV-I single-infection model and the HTLV-I/HIV-1 co-infection model were not studied before. The aim of the present article is to discretize the HIV-1 and HTLV-I co-infection model (4)–(9) using the NSFD method. We first establish the positivity and ultimate boundedness of the discrete-time model’s solutions and then calculate all equilibria and deduce their existence conditions. We examine the global stability of the four equilibria using the Lyapunov approach. We present some numerical simulations to clarify the theoretical results.

2. Discrete-Time HTLV-I and HIV-1 Co-Infection Model

Applying the NSFD approach to system (4)–(9), we get

$$\begin{array}{cc}\hfill \frac{x_{n+1}-x_n}{\Omega \left(h\right)}& ={\xi }_1-{\gamma }_1{x}_{n+1}-{\omega }_1{x}_{n+1}{v}_n-{\omega }_3{x}_{n+1}{u}_n,\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill \frac{y_{n+1}-y_n}{\Omega \left(h\right)}& ={\omega }_1{x}_{n+1}{v}_n-{\alpha }_1{y}_{n+1},\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill \frac{w_{n+1}-w_n}{\Omega \left(h\right)}& ={\xi }_2-{\gamma }_2{w}_{n+1}-{\omega }_2{w}_{n+1}{v}_n,\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill \frac{z_{n+1}-z_n}{\Omega \left(h\right)}& ={\omega }_2{w}_{n+1}{v}_n-{\alpha }_2{z}_{n+1},\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill \frac{v_{n+1}-v_n}{\Omega \left(h\right)}& ={\beta }_1{\alpha }_1{y}_{n+1}+{\beta }_2{\alpha }_2{z}_{n+1}-\theta v_{n+1},\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill \frac{u_{n+1}-u_n}{\Omega \left(h\right)}& ={\omega }_3{x}_{n+1}{u}_n-\delta u_{n+1},\hfill \end{array}$$

(15)

where $h>0$ is the time step and $(x_{n,},y_n,w_n,z_n,v_n,u_n)$ are the approximations of the solution $(x\left(t_n\right),y\left(t_n\right),w\left(t_n\right),z\left(t_n\right),v\left(t_n\right),u\left(t_n\right))$ of the system (4)–(9) at the discrete time point $t_n=nh,$ $n\in N=\{0,1,2,\dots \}$. The denominator function $\Omega \left(h\right)$ is selected such that $\Omega \left(h\right)=h+O\left(h^2\right)$. We consider the following form of $\Omega \left(h\right)$ [48]:

$$\Omega \left(h\right)=\frac{1-e^{-{\gamma }_{1}h}}{{\gamma }_1}.$$

(16)

The initial conditions of system (10)–(15) are

$$(x_0,y_0,w_0,z_0,v_0,u_0)\in {\mathbb{R}}_{+}^6=\{(x,y,w,z,v,u)\mid x>0,y>0,w>0,z>0,v>0,u>0\}.$$

(17)

The discrete-time HTLV-I and HIV-1 co-infection model (10)–(15) may be useful to develop several viral co-infection models such as SARS-CoV-2 and co-infection with other respiratory viruses.

3. Preliminaries

Let $\sigma =min\{{\gamma }_1,{\alpha }_1,\delta ,{\gamma }_2,{\alpha }_2\}$ and ${\xi }_{12}={\xi }_1+{\xi }_2$ and define the sets

$$\begin{array}{cc}\hfill \Gamma & =\left\{(x,y,w,z,u,v)\in {\mathbb{R}}_{+}^6:x\le \frac{{\xi }_1}{{\gamma }_1},w\le \frac{{\xi }_2}{{\gamma }_2},x+y+w+z+u\le \frac{{\xi }_{12}}{\sigma },v\le \frac{({\beta }_1{\alpha }_1+{\beta }_2{\alpha }_2){\xi }_{12}}{\theta \sigma }\right\},\hfill \\ \hfill {\rm Y}& =\left\{(x,0,w,0,0,0)\in {\mathbb{R}}_{+}^6:x\ge 0,w\ge 0\right\}.\hfill \end{array}$$

Lemma 1.

Any solution ($x,y,w,z,v,u$) of models (10)–(15) with initial conditions (17) is positive and ultimately bounded.

Proof. 

Equations (10)–(15) imply that

$$\begin{array}{cc}\hfill x_{n+1}& =\frac{\Omega \left(h\right){\xi }_1+x_n}{1+\Omega \left(h\right)({\gamma }_1+{\omega }_1{v}_n+{\omega }_3{u}_n)},\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill y_{n+1}& =\frac{\Omega \left(h\right){\omega }_1{x}_{n+1}{v}_n+y_n}{1+\Omega \left(h\right){\alpha }_1},\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill w_{n+1}& =\frac{\Omega \left(h\right){\xi }_2+w_n}{1+\Omega \left(h\right)({\gamma }_2+{\omega }_2{v}_n)},\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill z_{n+1}& =\frac{\Omega \left(h\right){\omega }_2{w}_{n+1}{v}_n+z_n}{1+\Omega \left(h\right){\alpha }_2},\hfill \\ \hfill v_{n+1}& =\frac{\Omega \left(h\right)({\beta }_1{\alpha }_1{y}_{n+1}+{\beta }_2{\alpha }_2{z}_{n+1})+v_n}{1+\Omega \left(h\right)\theta },\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill u_{n+1}& =\frac{u_n+\Omega \left(h\right){\omega }_3{x}_{n+1}{u}_n}{1+\Omega \left(h\right)\delta }.\hfill \end{array}$$

(22)

Since all parameters of models (4)–(9) are positive and the initial values are also positive, then by induction we obtain $x_n>0,y_n>0,w_n>0,z_n>0,v_n>0$ and $u_n>0$ for all $n\in N$.

From Equations (10) and (12), we have

$$\begin{array}{cc}\hfill \frac{x_{n+1}-x_n}{\Omega \left(h\right)}& \le {\xi }_1-{\gamma }_1{x}_{n+1}⟹x_{n+1}\le \frac{x_n}{1+{\gamma }_1\Omega \left(h\right)}+\frac{{\xi }_1\Omega \left(h\right)}{1+{\gamma }_1\Omega \left(h\right)}\hfill \\ \hfill \frac{w_{n+1}-w_n}{\Omega \left(h\right)}& \le {\xi }_2-{\gamma }_2{w}_{n+1}⟹w_{n+1}\le \frac{w_n}{1+{\gamma }_2\Omega \left(h\right)}+\frac{{\xi }_2\Omega \left(h\right)}{1+{\gamma }_2\Omega \left(h\right)}.\hfill \end{array}$$

By Lemma 2.2 in [49] we get

$$\begin{array}{cc}\hfill x_n& \le {\left(\frac{1}{1+\Omega \left(h\right){\gamma }_1}\right)}^n{x}_0+\frac{{\xi }_1}{{\gamma }_1}\left[1-{\left(\frac{1}{1+\Omega \left(h\right){\gamma }_1}\right)}^n\right],\hfill \\ \hfill w_n& \le {\left(\frac{1}{1+\Omega \left(h\right){\gamma }_2}\right)}^n{w}_0+\frac{{\xi }_2}{{\gamma }_2}\left[1-{\left(\frac{1}{1+\Omega \left(h\right){\gamma }_2}\right)}^n\right].\hfill \end{array}$$

Consequently,$\underset{n\to \infty }{lim\; sup}{x}_n\le \frac{{\xi }_1}{{\gamma }_1}$ and $\underset{n\to \infty }{lim\; sup}{w}_n\le \frac{{\xi }_2}{{\gamma }_2}$. We define the following sequence $M_n$:

$$M_n=x_n+y_n+w_n+z_n+u_n.$$

Hence

$$\begin{array}{cc}\hfill M_{n+1}-M_n& =(x_{n+1}-x_n)+(y_{n+1}-y_n)+(w_{n+1}-w_n)+(z_{n+1}-z_n)+(u_{n+1}-u_n)\hfill \\ \hfill & =\Omega \left(h\right)\left[{\xi }_1-{\gamma }_1{x}_{n+1}-{\omega }_1{x}_{n+1}{v}_n-{\omega }_3{x}_{n+1}{u}_n+{\omega }_1{x}_{n+1}{v}_n+{\alpha }_1{y}_{n+1}+{\xi }_2\right.\hfill \\ \hfill & \left.-{\gamma }_2{w}_{n+1}-{\omega }_2{w}_{n+1}{v}_n+{\omega }_2{w}_{n+1}{v}_n-{\alpha }_2{z}_{n+1}+{\omega }_3{x}_{n+1}{u}_n-\delta u_{n+1}\right]\hfill \\ \hfill & =\Omega \left(h\right)\left[{\xi }_1-{\gamma }_1{x}_{n+1}-{\alpha }_1{y}_{n+1}+{\xi }_2-{\gamma }_2{w}_{n+1}-{\alpha }_2{z}_{n+1}-\delta u_{n+1}\right]\hfill \\ \hfill & \le \Omega \left(h\right){\xi }_{12}-\Omega \left(h\right)\sigma [x_{n+1}+y_{n+1}+w_{n+1}+z_{n+1}+u_{n+1}]\hfill \\ \hfill & =\Omega \left(h\right){\xi }_{12}-\Omega \left(h\right)\sigma M_{n+1},\hfill \end{array}$$

and

$$M_{n+1}\le \frac{M_n}{1+\Omega \left(h\right)\sigma }+\frac{\Omega \left(h\right){\xi }_{12}}{1+\Omega \left(h\right)\sigma }.$$

It follows that

$$M_n\le {\left(\frac{1}{1+\Omega \left(h\right)\sigma }\right)}^n{M}_0+\frac{{\xi }_{12}}{\sigma }\left[1-{\left(\frac{1}{1+\Omega \left(h\right)\sigma }\right)}^n\right].$$

Consequently,$\underset{n\to \infty }{lim\; sup}{M}_n\le \frac{{\xi }_{12}}{\sigma }$. We have

$$\begin{array}{cc}\hfill v_{n+1}-v_n& =\Omega \left(h\right)\left[{\beta }_1{\alpha }_1{y}_{n+1}+{\beta }_2{\alpha }_2{z}_{n+1}-\theta v_{n+1}\right]\hfill \\ \hfill & \le \Omega \left(h\right)\left[{\beta }_1{\alpha }_1\frac{{\xi }_{12}}{\sigma }+{\beta }_2{\alpha }_2\frac{{\xi }_{12}}{\sigma }-\theta v_{n+1}\right].\hfill \end{array}$$

Hence,

$$v_{n+1}\le \frac{v_n}{1+\Omega \left(h\right)\theta }+\frac{\Omega \left(h\right)({\beta }_1{\alpha }_1+{\beta }_2{\alpha }_2){\xi }_{12}}{(1+\Omega (h\left)\theta \right)\sigma }.$$

By induction, we get

$$v_n\le {\left(\frac{1}{1+\Omega \left(h\right)\theta }\right)}^n{v}_0+\frac{({\beta }_1{\alpha }_1+{\beta }_2{\alpha }_2){\xi }_{12}}{\theta \sigma }\left[1-{\left(\frac{1}{1+\Omega \left(h\right)\theta }\right)}^n\right].$$

Consequently,$\underset{n\to \infty }{lim\; sup}{v}_n\le \frac{({\beta }_1{\alpha }_1+{\beta }_2{\alpha }_2){\xi }_{12}}{\theta \sigma }$. Therefore ($x_n,y_n,w_n,z_n,v_n,u_n)$ converge to $\Gamma$ as $n\to \infty .$ □

4. Equilibria

Here, we calculate the model’s equilibria and deduce their existence conditions.

Lemma 2.

Models (10)–(15) have four equilibria determined by four threshold parameters $R_j>0,$ $j=0,1,2,3$:

(1) Infection-free equilibrium $E{Q}_0=(x^0,0,w^0,0,0,0),$ which always exists.

(2) Chronic HIV-1 single-infection equilibrium $E{Q}_1=(\widehat{x},\widehat{y},\widehat{w},\widehat{z},\widehat{v},0)$ exists when $R_0=R_{01}+R_{02}>1.$

(3) Chronic HTLV-I single-infection equilibrium $E{Q}_2=(\tilde{x},0,\tilde{w},0,0,\tilde{u})$ exists when $R_1>1$.

(4) Chronic HTLV-I/HIV-1 co-infection equilibrium $E{Q}_3=(\overline{x},\overline{y},\overline{w},\overline{z},\overline{v},\overline{u})$ exists when $\frac{R_1}{R_{01}}>1,$ $R_2>1$ and $R_3>1.$

Proof. 

Any equilibrium $EQ=(x,y,w,z,v,u)$ satisfies

$$\begin{array}{cc}\hfill 0& ={\xi }_1-{\gamma }_{1}x-{\omega }_{1}xv-{\omega }_{3}xu,\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill 0& ={\omega }_{1}xv-{\alpha }_{1}y,\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill 0& ={\xi }_2-{\gamma }_{2}w-{\omega }_{2}wv,\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill 0& ={\omega }_{2}wv-{\alpha }_{2}z,\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill 0& ={\beta }_1{\alpha }_{1}y+{\beta }_2{\alpha }_{2}w-\theta v,\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill 0& ={\omega }_{3}xu-\delta u.\hfill \end{array}$$

(28)

From Equation (28), we get two options: $u=0$ and $x=\frac{\delta }{{\omega }_3}$. First, we consider $u=0$; then, from Equations (24) and (26), we get

$$y=\frac{{\omega }_{1}xv}{{\alpha }_1}\mathrm{and}z=\frac{{\omega }_{2}wv}{{\alpha }_2}.$$

(29)

Now, substituting in Equation (27), we get

$$({\beta }_1{\omega }_{1}x+{\beta }_2{\omega }_{2}w-\theta )v=0.$$

(30)

There are two solutions to Equation (30): $v=0$ and ${\beta }_1{\alpha }_{1}x+{\beta }_2{\alpha }_{2}w-\theta$. When $v=0,$ we get $y=0$ and $z=0$, which gives infection-free equilibrium $E{Q}_0=(x^0,0,w^0,0,0,0),$ where

$$x^0=\frac{{\xi }_1}{{\gamma }_1}\mathrm{and}{w}^0=\frac{{\xi }_2}{{\gamma }_2}.$$

When $v\ne 0$ and ${\beta }_1{\omega }_{1}x+{\beta }_2{\omega }_{2}w-\theta =0,$ then from Equations (23) and (25), we get

$$\frac{{\beta }_1{\omega }_1{\xi }_1}{{\gamma }_1+{\omega }_{1}v}+\frac{{\beta }_2{\omega }_2{\xi }_2}{{\gamma }_2+{\omega }_{2}v}-\theta =0.$$

We define a function H as

$$H\left(v\right)=\frac{{\beta }_1{\omega }_1{\xi }_1}{{\gamma }_1+{\omega }_{1}v}+\frac{{\beta }_2{\omega }_2{\xi }_2}{{\gamma }_2+{\omega }_{2}v}-\theta =0.$$

Then,

$$H\left(0\right)=\frac{{\beta }_1{\omega }_1{\xi }_1}{{\gamma }_1}+\frac{{\beta }_2{\omega }_2{\xi }_2}{{\gamma }_2}-\theta =\theta \left(\frac{{\beta }_1{\omega }_1{\xi }_1}{{\gamma }_1\theta }+\frac{{\beta }_2{\omega }_2{\xi }_2}{{\gamma }_2\theta }-1\right)=\theta (R_0-1),$$

where

$$R_0=R_{01}+R_{02},R_{01}=\frac{{\beta }_1{\omega }_1{\xi }_1}{{\gamma }_1\theta }\mathrm{and}{R}_{02}=\frac{{\beta }_2{\omega }_2{\xi }_2}{{\gamma }_2\theta }.$$

Thus $H\left(0\right)>0,$ when $R_0>1$. The parameter $R_0$ represents the basic HIV-1 single-infection reproductive number.

$$\underset{v\to \infty }{lim}H\left(v\right)=-\theta .$$

Further,

$$H^{\prime }\left(v\right)=-\left(\frac{{\beta }_1{\xi }_1{\omega }_1^2}{{({\gamma }_1+{\omega }_{1}v)}^2}+\frac{{\beta }_2{\xi }_2{\omega }_2^2}{{({\gamma }_2+{\omega }_{2}v)}^2}\right)<0.$$

Hence, H is a strictly decreasing function of v, and thus there exists a unique $\widehat{v}\in (0,\infty )$ such that $H\left(\widehat{v}\right)=0$. It follows that

$$\widehat{x}=\frac{{\xi }_1}{{\gamma }_1+{\omega }_1\widehat{v}}>0\mathrm{and}\widehat{w}=\frac{{\xi }_2}{{\gamma }_2+{\omega }_2\widehat{v}}>0.$$

Then, Equation (29) gives

$$\widehat{y}=\frac{{\omega }_1\widehat{x}\widehat{v}}{{\alpha }_1}>0\mathrm{and}\widehat{z}=\frac{{\omega }_2\widehat{w}\widehat{v}}{{\alpha }_2}>0.$$

Here,$\widehat{v}$ satisfies the following quadratic equation:

$$A{\widehat{v}}^2+B\widehat{v}+C=0,$$

(31)

with

$$A=\theta {\omega }_1{\omega }_2,$$

$$B=\theta {\gamma }_1{\omega }_2+\theta {\gamma }_2{\omega }_1-{\omega }_1{\omega }_2({\beta }_1{\xi }_1+{\beta }_2{\xi }_2),$$

$$\begin{array}{cc}\hfill C& =\theta {\gamma }_1{\gamma }_2-{\beta }_1{\gamma }_2{\omega }_1{\xi }_1-{\beta }_2{\gamma }_1{\omega }_2{\xi }_2\hfill \\ \hfill & =\theta {\gamma }_1{\gamma }_2\left(1-\frac{{\beta }_1{\omega }_1{\xi }_1}{{\gamma }_1\theta }-\frac{{\beta }_2{\omega }_2{\xi }_2}{{\gamma }_2\theta }\right)\hfill \\ \hfill & =-\theta {\gamma }_1{\gamma }_2(R_0-1).\hfill \end{array}$$

Obviously, $C<0$ when $R_0>1$. Equation (31) has a positive root as

$$\widehat{v}=\frac{-B+\sqrt{B^2-4AC}}{2A}>0.$$

Hence, the chronic HIV-1 single-infection equilibrium $E{Q}_1=(\widehat{x},\widehat{y},\widehat{w},\widehat{z},\widehat{v},0)$ exists when $R_0>1$.

Now consider $\tilde{x}=\frac{\delta }{{\omega }_3}$ and $u\ne 0$. Solving Equations (23)–(27), we obtain two equilibria: the chronic HTLV-I single-infection equilibrium $E{Q}_2=(\tilde{x},0.\tilde{w},0,0,\tilde{u})$, where

$$\tilde{x}=\frac{\delta }{{\omega }_3},\tilde{w}=\frac{{\xi }_2}{{\gamma }_2}=w^0,\tilde{u}=\frac{{\gamma }_1}{{\omega }_3}(R_1-1),$$

where

$$R_1=\frac{{\omega }_3{\xi }_1}{{\gamma }_2\delta }.$$

(32)

Parameter $R_1$ is the basic HTLV-I single-infection reproductive number. Consequently, $E{Q}_2$ exists when $R_1>1$. The other equilibrium is the chronic HTLV-I/HIV-1 co-infection equilibrium $E{Q}_3=(\overline{x},\overline{y},\overline{w},\overline{z},\overline{v},\overline{u}),$ where

$$\begin{array}{cc}\hfill \overline{x}& =\frac{\delta }{{\omega }_3}=\tilde{x},\overline{y}=\frac{{\gamma }_2{\omega }_1\delta }{{\alpha }_1{\omega }_2{\omega }_3}(R_2-1),\overline{v}=\frac{{\gamma }_2}{{\omega }_2}(R_2-1),\overline{w}=\frac{w^0}{R_2},\hfill \\ \hfill \overline{z}& =\frac{w^0}{R_2}(R_2-1)=\frac{{\xi }_2}{{\alpha }_2{R}_{02}}\left(R_{02}+\frac{R_{01}}{R_1}-1\right),\overline{u}=\frac{{\gamma }_2{\omega }_1}{{\omega }_2{\omega }_3}(R_2-1)(R_3-1),\hfill \end{array}$$

and

$$R_2=\frac{{\xi }_2{\beta }_2{\omega }_2{\omega }_3}{{\gamma }_2{\beta }_1{\omega }_1\delta \left(\frac{R_1}{R_{01}}-1\right)},R_3=\frac{{\gamma }_1{\omega }_2}{{\gamma }_2{\omega }_1}\left(\frac{R_1-1}{R_2-1}\right).$$

We can see that, $E{Q}_3$ exists when $\frac{R_1}{R_{01}}>1,$ $R_2>1$ and $R_3>1$. □

5. Global Stability

In this section, we demonstrate the global asymptotic stability of all equilibria by establishing appropriate Lyapunov functions. Define a function $G\left(x\right)\ge 0$ as $G\left(x\right)=x-1-lnx$. We have

$$lnx\le x-1.$$

(33)

Theorem 1.

If $R_0\le 1$ and $R_1\le 1$, then $E{Q}_0=(x^0,0,w^0,0,0,0)$ is globally asymptotically stable (GAS) in Γ.

Proof. 

Define a discrete Lyapunov function ${\Lambda }_n(x_n,y_n,w_n,z_n,v_n,u_n)$ as

$$\begin{array}{cc}\hfill {\Lambda }_n& =\frac{1}{\Omega \left(h\right)}\left(x^{0}G\left(\frac{x_n}{x^0}\right)+y_n+\frac{{\beta }_2{w}^0}{{\beta }_1}G\left(\frac{w_n}{w^0}\right)+\frac{{\beta }_2}{{\beta }_1}{z}_n\right.\hfill \\ \hfill & \left.+\frac{1}{{\beta }_1}(1+\Omega \left(h\right)\theta )v_n+(1+\Omega \left(h\right)\delta )u_n\right).\hfill \end{array}$$

Clearly, ${\Lambda }_n>0$ for all $x_n>0,y_n>0,w_n>0,z_n>0,v_n>0,u_n>0$. In addition, ${\Lambda }_n(x^0,0,w^0,0,0,0)=0$. Evaluating the difference $\Delta {\Lambda }_n={\Lambda }_{n+1}-{\Lambda }_n$ as

$$\begin{array}{cc}\hfill \Delta {\Lambda }_n& ={\Lambda }_{n+1}-{\Lambda }_n=\frac{1}{\Omega \left(h\right)}\left(x^{0}G\left(\frac{x_{n+1}}{x^0}\right)+y_{n+1}+\frac{{\beta }_2{w}^0}{{\beta }_1}G\left(\frac{w_{n+1}}{w^0}\right)+\frac{{\beta }_2}{{\beta }_1}{z}_{n+1}\right.\hfill \\ \hfill & +\frac{1}{{\beta }_1}(1+\Omega \left(h\right)\theta )v_{n+1}+(1+\Omega \left(h\right)\delta )u_{n+1}-x^{0}G\left(\frac{x_n}{x^0}\right)-y_n-\frac{{\beta }_2{w}^0}{{\beta }_1}G\left(\frac{w_n}{w^0}\right)\hfill \\ \hfill & \left.-\frac{{\beta }_2}{{\beta }_1}{z}_n-\frac{1}{{\beta }_1}(1+\Omega \left(h\right)\theta )v_n-(1+\Omega \left(h\right)\delta )u_n\right)\hfill \\ \hfill & =\frac{1}{\Omega \left(h\right)}\left(x^0\left(\frac{x_{n+1}-x_n}{x^0}+ln\left(\frac{x_n}{x_{n+1}}\right)\right)+\left(y_{n+1}-y_n\right)+\frac{{\beta }_2{w}^0}{{\beta }_1}\left(\frac{w_{n+1}-w_n}{w^0}+ln\left(\frac{w_n}{w_{n+1}}\right)\right)\right.\hfill \\ \hfill & \left.+\frac{{\beta }_2}{{\beta }_1}\left(z_{n+1}-z_n\right)+\frac{1}{{\beta }_1}(1+\Omega \left(h\right)\theta )\left(v_{n+1}-v_n\right)+(1+\Omega \left(h\right)\delta )\left(u_{n+1}-u_n\right)\right).\hfill \end{array}$$

Using inequality (33), we obtain

$$\begin{array}{cc}\hfill \Delta {\Lambda }_n& \le \frac{1}{\Omega \left(h\right)}\left(x_{n+1}-x_n+x^0\left(\frac{x_n}{x_{n+1}}-1\right)\right)+\left(y_{n+1}-y_n\right)+\frac{{\beta }_2}{{\beta }_1}\left(w_{n+1}-w_n+w^0\left(\frac{w_n}{w_{n+1}}-1\right)\right)\hfill \\ \hfill & \left.+\frac{{\beta }_2}{{\beta }_1}\left(z_{n+1}-z_n\right)+\frac{1}{{\beta }_1}(1+\Omega \left(h\right)\theta )\left(v_{n+1}-v_n\right)+(1+\Omega \left(h\right)\delta )\left(u_{n+1}-u_n\right)\right)\hfill \\ \hfill & =\frac{1}{\Omega \left(h\right)}\left(\left(1-\frac{x^0}{x_{n+1}}\right)\left(x_{n+1}-x_n\right)+\left(y_{n+1}-y_n\right)+\frac{{\beta }_2}{{\beta }_1}\left(1-\frac{w^0}{w_{n+1}}\right)\left(w_{n+1}-w_n\right)\right.\hfill \\ \hfill & \left.+\frac{{\beta }_2}{{\beta }_1}\left(z_{n+1}-z_n\right)+\frac{1}{{\beta }_1}(1+\Omega \left(h\right)\theta )\left(v_{n+1}-v_n\right)+(1+\Omega \left(h\right)\delta )\left(u_{n+1}-u_n\right)\right).\hfill \end{array}$$

From Equations (10)–(15), we have

$$\begin{array}{cc}\hfill \Delta {\Lambda }_n& \le \left(1-\frac{x^0}{x_{n+1}}\right)\left({\xi }_1-{\gamma }_1{x}_{n+1}-{\omega }_1{x}_{n+1}{v}_n-{\omega }_3{x}_{n+1}{u}_n\right)+\left({\omega }_1{x}_{n+1}{v}_n-{\alpha }_1{y}_{n+1}\right)\hfill \\ \hfill & +\frac{{\beta }_2}{{\beta }_1}\left(1-\frac{w^0}{w_{n+1}}\right)\left({\xi }_2-{\gamma }_2{w}_{n+1}-{\omega }_2{w}_{n+1}{v}_n\right)+\frac{{\beta }_2}{{\beta }_1}\left({\omega }_2{w}_{n+1}{v}_n-{\alpha }_2{z}_{n+1}\right)\hfill \\ \hfill & +\frac{1}{{\beta }_1}\left({\beta }_1{\alpha }_1{y}_{n+1}+{\beta }_2{\alpha }_2{z}_{n+1}-\theta v_{n+1}\right)+\frac{\theta }{{\beta }_1}\left(v_{n+1}-v_n\right)+\left({\omega }_3{x}_{n+1}{u}_n-\delta u_{n+1}\right)\hfill \\ \hfill & +\delta \left(u_{n+1}-u_n\right)\hfill \\ \hfill & =\left(1-\frac{x^0}{x_{n+1}}\right)\left({\xi }_1-{\gamma }_1{x}_{n+1}\right)+\frac{{\beta }_2}{{\beta }_1}\left(1-\frac{w^0}{w_{n+1}}\right)({\xi }_2-{\gamma }_2{w}_{n+1})\hfill \\ \hfill & +\left(\frac{{\beta }_2}{{\beta }_1}{\omega }_2{w}^0+{\omega }_1{x}^0-\frac{\theta }{{\beta }_1}\right)v_n+({\omega }_3{x}^0-\delta )u_n.\hfill \end{array}$$

We have

$${\xi }_1={\gamma }_1{x}^0,{\xi }_2={\gamma }_2{w}^0,$$

then, we obtain

$$\begin{array}{cc}\hfill \Delta {\Lambda }_n& \le \left(1-\frac{x^0}{x_{n+1}}\right)({\gamma }_1{x}^0-{\gamma }_1{x}_{n+1})+\frac{{\beta }_2}{{\beta }_1}\left(1-\frac{w^0}{w_{n+1}}\right)({\gamma }_2{w}^0-{\gamma }_2{w}_{n+1})\hfill \\ \hfill & +\left(\frac{{\beta }_2}{{\beta }_1}{\omega }_2{w}^0+{\omega }_1{x}^0-\frac{\theta }{{\beta }_1}\right)v_n+({\omega }_3{x}^0-\delta )u_n\hfill \\ \hfill & =-{\gamma }_1\frac{{\left(x_{n+1}-x^0\right)}^2}{x_{n+1}}-\frac{{\gamma }_2{\beta }_2}{{\beta }_1}\frac{{(w_{n+1}-w^0)}^2}{w_{n+1}}\hfill \\ \hfill & +\frac{\theta }{{\beta }_1}\left(\frac{{\omega }_1{\beta }_1{\xi }_1}{\theta {\gamma }_1}+\frac{{\omega }_2{\beta }_2{\xi }_2}{\theta {\gamma }_2}-1\right)v_n+\delta \left(\frac{{\omega }_3{\xi }_1}{\delta {\gamma }_1}-1\right)u_n\hfill \\ \hfill & =-{\gamma }_1\frac{{\left(x_{n+1}-x^0\right)}^2}{x_{n+1}}-\frac{{\gamma }_2{\beta }_2}{{\beta }_1}\frac{{(w_{n+1}-w^0)}^2}{w_{n+1}}+\frac{\theta }{{\beta }_1}(R_0-1)v_n+\delta (R_1-1)u_n.\hfill \end{array}$$

Since $R_0\le 1$ and $R_1\le 1,$ then ${\Lambda }_n$ is monotonically decreasing. Clearly, ${\Lambda }_n\ge 0,$ and hence there is a limit ${lim}_{n\to \infty }{\Lambda }_n\ge 0$, and thus ${lim}_{n\to \infty }\Delta {\Lambda }_n=0,$ which gives ${lim}_{n\to \infty }{x}_n=x^0,$ ${lim}_{n\to \infty }{w}_n=w^0,$ ${lim}_{n\to \infty }(R_0-1)v_n=0$ and ${lim}_{n\to \infty }(R_1-1)u_n=0.$ We consider four cases:

(i) $R_0=1$ and $R_1=1,$ and then from Equation (12),

$$0={\xi }_2-{\gamma }_2{w}^0-{\omega }_2{w}^0\underset{n\to \infty }{lim}{v}_n\Rightarrow \underset{n\to \infty }{lim}{v}_n=0.$$

(34)

In addition, from Equations (10) and (14),

$$\begin{array}{cc}\hfill 0& ={\xi }_1-{\gamma }_1{x}^0-{\omega }_1{x}^0\underset{n\to \infty }{lim}{v}_n-{\omega }_3{x}^0\underset{n\to \infty }{lim}{u}_n\Rightarrow \underset{n\to \infty }{lim}{u}_n=0,\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill 0& ={\beta }_1{\alpha }_1\underset{n\to \infty }{lim}{y}_{n+1}+{\beta }_2{\alpha }_2\underset{n\to \infty }{lim}{z}_{n+1}-\theta \underset{n\to \infty }{lim}{v}_{n+1}\Rightarrow \underset{n\to \infty }{lim}{y}_n=\underset{n\to \infty }{lim}{z}_n=0\hfill \end{array}$$

(36)

(ii) $R_0=1$, $R_1<1$ and ${lim}_{n\to \infty }{u}_n=0$. Equations (34) and (36) yield ${lim}_{n\to \infty }{v}_n={lim}_{n\to \infty }{y}_n={lim}_{n\to \infty }{z}_n=0.$

(iii) $R_0<1$, $R_1=1$ and ${lim}_{n\to \infty }{v}_n=0.$ Equations (35) and (36) give ${lim}_{n\to \infty }{u}_n={lim}_{n\to \infty }{y}_n={lim}_{n\to \infty }{z}_n=0$.

(iv) $R_0<1$, $R_1<1$ and ${lim}_{n\to \infty }{v}_n={lim}_{n\to \infty }{u}_n=0$. From Equation (36), we get ${lim}_{n\to \infty }{y}_n={lim}_{n\to \infty }{z}_n=0.$

Consequently, if $R_0\le 1$ and $R_1\le 1$, then ${lim}_{n\to \infty }{x}_n=x^0$, ${lim}_{n\to \infty }{w}_n=w^0$ and ${lim}_{n\to \infty }{y}_n={lim}_{n\to \infty }{z}_n={lim}_{n\to \infty }{v}_n={lim}_{n\to \infty }{u}_n=0$. This shows that $E{Q}_0$ is GAS. □

The result of Theorem 1 shows that if there exist control parameters (e.g., drug therapies) that make $R_0\le 1$ and $R_1\le 1$, then both HTLV-I and HIV-1 will be removed from the body regardless of the initial states.

Theorem 2.

If $R_0>1$ and $R_1\le 1,$ then $E{Q}_1$ GAS in $\Gamma \backslash {\rm Y}$.

Proof. 

Define

$$\begin{array}{cc}\hfill {\Theta }_n& =\frac{1}{\Omega \left(h\right)}\left[\widehat{x}G\left(\frac{x_n}{\widehat{x}}\right)+\widehat{y}G\left(\frac{y_n}{\widehat{y}}\right)+\frac{{\beta }_2\widehat{w}}{{\beta }_1}G\left(\frac{w_n}{\widehat{w}}\right)+\frac{{\beta }_2\widehat{z}}{{\beta }_1}G\left(\frac{z_n}{\widehat{z}}\right)\right.\hfill \\ \hfill & \left.+\frac{\widehat{v}}{{\beta }_1}(1+\Omega \left(h\right)\theta )G\left(\frac{v_n}{\widehat{v}}\right)+(1+\Omega \left(h\right)\delta )u_n\right].\hfill \end{array}$$

Clearly ${\Theta }_n>0$ for all $x_n>0,$ $y_n>0,$ $w_n>0,$ $z_n>0,$ $v_n>0$ and $u_n>0$. In addition ${\Theta }_n(\widehat{x},\widehat{y},\widehat{w},\widehat{z},\widehat{v},0)=0$. Computing the difference $\Delta {\Theta }_n={\Theta }_{n+1}-{\Theta }_n$ as:

$$\begin{array}{cc}\hfill \Delta {\Theta }_n& =\frac{1}{\Omega \left(h\right)}\left[\widehat{x}G\left(\frac{x_{n+1}}{\widehat{x}}\right)+\widehat{y}G\left(\frac{y_{n+1}}{\widehat{y}}\right)+\frac{{\beta }_2\widehat{w}}{{\beta }_1}G\left(\frac{w_{n+1}}{\widehat{w}}\right)+\frac{{\beta }_2\widehat{z}}{{\beta }_1}G\left(\frac{z_{n+1}}{\widehat{z}}\right)\right.\hfill \\ \hfill & +\frac{\widehat{v}}{{\beta }_1}(1+\Omega \left(h\right)\theta )G\left(\frac{v_{n+1}}{\widehat{v}}\right)+(1+\Omega \left(h\right)\delta )u_{n+1}-\widehat{x}G\left(\frac{x_n}{\widehat{x}}\right)-\widehat{y}G\left(\frac{y_n}{\widehat{y}}\right)\hfill \\ \hfill & \left.-\frac{{\beta }_2\widehat{w}}{{\beta }_1}G\left(\frac{w_n}{\widehat{w}}\right)-\frac{{\beta }_2\widehat{z}}{{\beta }_1}G\left(\frac{z_n}{\widehat{z}}\right)-\frac{\widehat{v}}{{\beta }_1}(1+\Omega \left(h\right)\theta )G\left(\frac{v_n}{\widehat{v}}\right)-(1+\Omega \left(h\right)\delta )u_n\right]\hfill \\ \hfill & =\frac{1}{\Omega \left(h\right)}\left[\widehat{x}\left(\frac{x_{n+1}}{\widehat{x}}-\frac{x_n}{\widehat{x}}+ln\left(\frac{x_n}{x_{n+1}}\right)\right)+\widehat{y}\left(\frac{y_{n+1}}{\widehat{y}}-\frac{y_n}{\widehat{y}}+ln\left(\frac{y_n}{y_{n+1}}\right)\right)\right.\hfill \\ \hfill & +\frac{{\beta }_2}{{\beta }_1}\widehat{w}\left(\frac{w_{n+1}}{\widehat{w}}-\frac{w_n}{\widehat{w}}+ln\left(\frac{w_n}{w_{n+1}}\right)\right)+\frac{{\beta }_2}{{\beta }_1}\widehat{z}\left(\frac{z_{n+1}}{\widehat{z}}-\frac{z_n}{\widehat{z}}+ln\left(\frac{z_n}{z_{n+1}}\right)\right)\hfill \\ \hfill & \left.+\frac{1}{{\beta }_1}(1+\Omega \left(h\right)\theta )\widehat{v}\left(\frac{v_{n+1}}{\widehat{v}}-\frac{v_n}{\widehat{v}}+ln\left(\frac{v_n}{v_{n+1}}\right)\right)+(1+\Omega \left(h\right)\delta )\left(u_{n+1}-u_n\right)\right].\hfill \end{array}$$

Using inequality (33), we have

$$\begin{array}{cc}\hfill \Delta {\Theta }_n& \le \frac{1}{\Omega \left(h\right)}\left[x_{n+1}-x_n+\widehat{x}\left(\frac{x_n}{x_{n+1}}-1\right)+y_{n+1}-y_n+\widehat{y}\left(\frac{y_n}{y_{n+1}}-1\right)\right.\hfill \\ \hfill & +\frac{{\beta }_2}{{\beta }_1}\left(w_{n+1}-w_n+\widehat{w}\left(\frac{w_n}{w_{n+1}}-1\right)\right)+\frac{{\beta }_2}{{\beta }_1}\left(z_{n+1}-z_n+\widehat{z}\left(\frac{z_n}{z_{n+1}}-1\right)\right)\hfill \\ \hfill & \left.+\frac{1}{{\beta }_1}\left(v_{n+1}-v_n+\widehat{v}\left(\frac{v_n}{v_{n+1}}-1\right)\right)+(1+\Omega \left(h\right)\delta )\left(u_{n+1}-u_n\right)\right]\hfill \\ \hfill & +\frac{\theta }{{\beta }_1}\left(v_{n+1}-v_n+\widehat{v}ln\left(\frac{v_n}{v_{n+1}}\right)\right)\hfill \\ \hfill & =\frac{1}{\Omega \left(h\right)}\left[\left(1-\frac{\widehat{x}}{x_{n+1}}\right)\left(x_{n+1}-x_n\right)+\left(1-\frac{\widehat{y}}{y_{n+1}}\right)\left(y_{n+1}-y_n\right)+\frac{{\beta }_2}{{\beta }_1}\left(1-\frac{\widehat{w}}{w_{n+1}}\right)\left(w_{n+1}-w_n\right)\right.\hfill \\ \hfill & \left.+\frac{{\beta }_2}{{\beta }_1}\left(1-\frac{\widehat{z}}{z_{n+1}}\right)\left(z_{n+1}-z_n\right)+\frac{1}{{\beta }_1}\left(1-\frac{\widehat{v}}{v_{n+1}}\right)\left(v_{n+1}-v_n\right)+(1+\Omega \left(h\right)\delta )\left(u_{n+1}-u_n\right)\right]\hfill \\ \hfill & +\frac{\theta v_{n+1}}{{\beta }_1}-\frac{\theta }{{\beta }_1}{v}_n+\frac{\theta \widehat{v}}{{\beta }_1}ln\left(\frac{v_n}{v_{n+1}}\right).\hfill \end{array}$$

From Equations (10)–(15), we have

$$\begin{array}{cc}\hfill \Delta {\Theta }_n& \le \left(1-\frac{\widehat{x}}{x_{n+1}}\right)({\xi }_1-{\gamma }_1{x}_{n+1}-{\omega }_1{x}_{n+1}{v}_n-{\omega }_3{x}_{n+1}{u}_n)+\left(1-\frac{\widehat{y}}{y_{n+1}}\right)({\omega }_1{x}_{n+1}{v}_n-{\alpha }_1{y}_{n+1})\hfill \\ \hfill & +\frac{{\beta }_2}{{\beta }_1}\left(1-\frac{\widehat{w}}{w_{n+1}}\right)({\xi }_2-{\gamma }_2{w}_{n+1}-{\omega }_2{w}_{n+1}{v}_n)+\frac{{\beta }_2}{{\beta }_1}\left(1-\frac{\widehat{z}}{z_{n+1}}\right)({\omega }_2{w}_{n+1}{v}_n-{\alpha }_2{z}_{n+1})\hfill \\ \hfill & +\frac{1}{{\beta }_1}\left(1-\frac{\widehat{v}}{v_{n+1}}\right)({\beta }_1{\alpha }_1{y}_{n+1}+{\beta }_2{\alpha }_2{z}_{n+1}-\theta v_{n+1})+\frac{\theta v_{n+1}}{{\beta }_1}-\frac{\theta v_n}{{\beta }_1}+\frac{\theta }{{\beta }_1}\widehat{v}ln\left(\frac{v_n}{v_{n+1}}\right)\hfill \\ \hfill & +({\omega }_3{x}_{n+1}{u}_n-\delta u_{n+1})+\delta (u_{n+1}-u_n)\hfill \\ \hfill & =\left(1-\frac{\widehat{x}}{x_{n+1}}\right)({\xi }_1-{\gamma }_1{x}_{n+1})+{\omega }_1\widehat{x}{v}_n+{\omega }_3\widehat{x}{u}_n-{\omega }_1\frac{x_{n+1}{v}_n\widehat{y}}{y_{n+1}}+{\alpha }_1\widehat{y}\hfill \\ \hfill & +\frac{{\beta }_2}{{\beta }_1}\left(1-\frac{\widehat{w}}{w_{n+1}}\right)({\xi }_2-{\gamma }_2{w}_{n+1})+\frac{{\beta }_2{\omega }_2}{{\beta }_1}{v}_n\widehat{w}-\frac{{\beta }_2{\omega }_2}{{\beta }_1}\frac{w_{n+1}{v}_n\widehat{z}}{z_{n+1}}+\frac{{\beta }_2{\alpha }_2\widehat{z}}{{\beta }_1}\hfill \\ \hfill & -{\alpha }_1\frac{y_{n+1}\widehat{v}}{v_{n+1}}-\frac{{\beta }_2{\alpha }_2}{{\beta }_1}\frac{z_{n+1}\widehat{v}}{v_{n+1}}-\frac{\theta v_{n+1}}{{\beta }_1}+\frac{\theta \widehat{v}}{{\beta }_1}+\frac{\theta v_{n+1}}{{\beta }_1}-\frac{\theta v_n}{{\beta }_1}+\frac{\theta \widehat{v}}{{\beta }_1}ln\left(\frac{v_n}{v_{n+1}}\right)-\delta u_n\hfill \\ \hfill & =\left(1-\frac{\widehat{x}}{x_{n+1}}\right)({\xi }_1-{\gamma }_1{x}_{n+1})+{\omega }_3\widehat{x}\widehat{u}\frac{u_n}{\widehat{u}}-{\omega }_1\widehat{x}\widehat{v}\frac{\widehat{y}{x}_{n+1}{v}_n}{y_{n+1}\widehat{x}\widehat{v}}+{\alpha }_1\widehat{y}\hfill \\ \hfill & +\frac{{\beta }_2}{{\beta }_1}\left(1-\frac{\widehat{w}}{w_{n+1}}\right)({\xi }_2-{\gamma }_2{w}_{n+1})-\frac{{\beta }_2}{{\beta }_1}{\omega }_2\widehat{w}\widehat{v}\frac{\widehat{z}{w}_{n+1}{v}_n}{z_{n+1}\widehat{w}\widehat{v}}+\frac{{\beta }_2}{{\beta }_1}{\alpha }_2\widehat{z}-{\alpha }_1\widehat{y}\frac{\widehat{v}{y}_{n+1}}{v_{n+1}\widehat{y}}\hfill \\ \hfill & -\frac{{\beta }_2}{{\beta }_1}{\alpha }_2\widehat{z}\frac{\widehat{v}{z}_{n+1}}{v_{n+1}\widehat{z}}+\frac{\theta \widehat{v}}{{\beta }_1}+\frac{\theta \widehat{v}}{{\beta }_1}ln\left(\frac{v_n}{v_{n+1}}\right)-\delta \widehat{u}\frac{u_n}{\widehat{u}}+\left({\omega }_1\widehat{x}+\frac{{\beta }_2{\omega }_2\widehat{w}}{{\beta }_1}-\frac{\theta }{{\beta }_1}\right)v_n.\hfill \end{array}$$

Utilizing the following conditions for $E{Q}_1$:

$$\begin{array}{cc}\hfill {\omega }_1\widehat{x}\widehat{v}& ={\alpha }_1\widehat{y},{\xi }_1={\gamma }_1\widehat{x}+{\alpha }_1\widehat{y},\hfill \\ \hfill {\omega }_2\widehat{w}\widehat{v}& ={\alpha }_2\widehat{z},{\xi }_2={\gamma }_2\widehat{w}+{\alpha }_2\widehat{z},\hfill \\ \hfill \theta \widehat{v}& ={\beta }_1{\alpha }_1\widehat{y}+{\beta }_2{\alpha }_2\widehat{z},\hfill \end{array}$$

we get

$$\left({\omega }_1\widehat{x}+\frac{{\beta }_2{\omega }_2\widehat{w}}{{\beta }_1}-\frac{\theta }{{\beta }_1}\right)v_n=\frac{{\omega }_1{\beta }_1\widehat{x}+{\beta }_2{\omega }_2\widehat{w}-\theta }{{\beta }_1}{v}_n=0$$

and

$$\begin{array}{cc}\hfill \Delta {\Theta }_n& \le \left(1-\frac{\widehat{x}}{x_{n+1}}\right)({\gamma }_1\widehat{x}+{\alpha }_1\widehat{y}-{\gamma }_1{x}_{n+1})+{\omega }_3\widehat{x}{u}_n-{\alpha }_1\widehat{y}\frac{x_{n+1}{v}_n\widehat{y}}{\widehat{x}\widehat{v}{y}_{n+1}}+{\alpha }_1\widehat{y}\hfill \\ \hfill & +\frac{{\beta }_2}{{\beta }_1}\left(1-\frac{\widehat{w}}{w_{n+1}}\right)({\gamma }_2\widehat{w}+{\alpha }_2\widehat{z}-{\gamma }_2{w}_{n+1})-\frac{{\beta }_2}{{\beta }_1}{\alpha }_2\widehat{z}\frac{w_{n+1}{v}_n\widehat{z}}{\widehat{w}\widehat{v}{z}_{n+1}}+\frac{{\beta }_2{\alpha }_2}{{\beta }_1}\widehat{z}\hfill \\ \hfill & -{\alpha }_1\widehat{y}\frac{y_{n+1}\widehat{v}}{v_{n+1}\widehat{y}}-\frac{{\beta }_2{\alpha }_2}{{\beta }_1}\widehat{z}\frac{z_{n+1}\widehat{v}}{v_{n+1}\widehat{z}}+{\alpha }_1\widehat{y}+\frac{{\beta }_2{\alpha }_2}{{\beta }_1}\widehat{z}+{\alpha }_1\widehat{y}ln\left(\frac{v_n}{v_{n+1}}\right)\hfill \\ \hfill & +\frac{{\beta }_2{\alpha }_2}{{\beta }_1}\widehat{z}ln\left(\frac{v_n}{v_{n+1}}\right)-\delta u_n\hfill \\ \hfill & =\left(1-\frac{\widehat{x}}{x_{n+1}}\right)({\gamma }_1\widehat{x}-{\gamma }_1{x}_{n+1})+{\alpha }_1\widehat{y}-{\alpha }_1\frac{\widehat{x}\widehat{y}}{x_{n+1}}+{\omega }_3\frac{u_n\widehat{x}\widehat{u}}{\widehat{u}}-{\alpha }_1\frac{\widehat{y}{x}_{n+1}{v}_n\widehat{y}}{y_{n+1}\widehat{x}\widehat{v}}+{\alpha }_1\widehat{y}\hfill \\ \hfill & +\frac{{\beta }_2}{{\beta }_1}\left(1-\frac{\widehat{w}}{w_{n+1}}\right)({\gamma }_2\widehat{w}-{\gamma }_2{w}_{n+1})+\frac{{\beta }_2{\alpha }_2}{{\beta }_1}\widehat{z}-\frac{{\beta }_2{\alpha }_2}{{\beta }_1}\frac{\widehat{w}\widehat{z}}{w_{n+1}}-\frac{{\beta }_2{\alpha }_2}{{\beta }_1}\widehat{z}\frac{w_{n+1}{v}_n\widehat{z}}{z_{n+1}\widehat{w}\widehat{v}}+\frac{{\beta }_2{\alpha }_2}{{\beta }_1}\widehat{z}\hfill \\ \hfill & -{\alpha }_1\frac{\widehat{v}{y}_{n+1}\widehat{y}}{v_{n+1}\widehat{y}}-\frac{{\beta }_2{\alpha }_2}{{\beta }_1}\frac{\widehat{v}{z}_{n+1}\widehat{z}}{v_{n+1}\widehat{z}}+{\alpha }_1\widehat{y}+\frac{{\beta }_2{\alpha }_2}{{\beta }_1}\widehat{z}+{\alpha }_1\widehat{y}ln\left(\frac{v_n}{v_{n+1}}\right)\hfill \\ \hfill & +\frac{{\beta }_2{\alpha }_2}{{\beta }_1}\widehat{z}ln\left(\frac{v_n}{v_{n+1}}\right)-\delta u_n\hfill \\ \hfill & =-{\gamma }_1\frac{{(x_{n+1}-\widehat{x})}^2}{x_{n+1}}-\frac{{\beta }_2{\gamma }_2}{{\beta }_1}\frac{{(w_{n+1}-\widehat{w})}^2}{w_{n+1}}+{\alpha }_1\widehat{y}\left[3-\frac{\widehat{x}}{x_{n+1}}-\frac{\widehat{y}{x}_{n+1}{v}_n}{y_{n+1}\widehat{x}\widehat{v}}-\frac{\widehat{v}{y}_{n+1}}{v_{n+1}\widehat{y}}+ln\left(\frac{v_n}{v_{n+1}}\right)\right]\hfill \\ \hfill & +\frac{{\beta }_2{\alpha }_2}{{\beta }_1}\widehat{z}\left[3-\frac{\widehat{w}}{w_{n+1}}-\frac{\widehat{z}{w}_{n+1}{v}_n}{z_{n+1}\widehat{w}\widehat{v}}-\frac{\widehat{v}{z}_{n+1}}{v_{n+1}\widehat{z}}\right]+ln\left(\frac{v_n}{v_{n+1}}\right)+\left({\omega }_3\widehat{x}-\delta \right)u_n.\hfill \end{array}$$

Using the following equalities:

$$\begin{array}{cc}\hfill ln\left(\frac{v_n}{v_{n+1}}\right)& =ln\left(\frac{\widehat{x}}{x_{n+1}}\right)+ln\left(\frac{\widehat{y}{x}_{n+1}{v}_n}{\widehat{x}{y}_{n+1}\widehat{v}}\right)+ln\left(\frac{\widehat{v}{y}_{n+1}}{v_{n+1}\widehat{y}}\right),\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill ln\left(\frac{v_n}{v_{n+1}}\right)& =ln\left(\frac{\widehat{w}}{w_{n+1}}\right)+ln\left(\frac{\widehat{z}{w}_{n+1}{v}_n}{z_{n+1}\widehat{w}\widehat{v}}\right)+ln\left(\frac{\widehat{v}{z}_{n+1}}{v_{n+1}\widehat{z}}\right).\hfill \end{array}$$

(38)

We get

$$\begin{array}{cc}\hfill \Delta {\Theta }_n& \le -{\gamma }_1\frac{{(x_{n+1}-\widehat{x})}^2}{x_{n+1}}-\frac{{\beta }_2{\gamma }_2}{{\beta }_1}\frac{{(w_{n+1}-\widehat{w})}^2}{w_{n+1}}-{\alpha }_1\widehat{y}\left[G\left(\frac{\widehat{x}}{x_{n+1}}\right)+G\left(\frac{\widehat{y}{x}_{n+1}{v}_n}{y_{n+1}\widehat{x}\widehat{v}}\right)+G\left(\frac{\widehat{v}{y}_{n+1}}{v_{n+1}\widehat{y}}\right)\right]\hfill \\ \hfill & -\frac{{\beta }_2{\alpha }_2}{{\beta }_1}\widehat{z}\left[G\left(\frac{\widehat{w}}{w_{n+1}}\right)+G\left(\frac{\widehat{z}{w}_{n+1}{v}_n}{z_{n+1}\widehat{w}\widehat{v}}\right)+G\left(\frac{\widehat{v}{z}_{n+1}}{v_{n+1}\widehat{z}}\right)\right]+\left(\frac{{\omega }_3{\xi }_1}{{\gamma }_1+{\omega }_1\widehat{v}}-\delta \right)u_n.\hfill \end{array}$$

Since $R_0>1$, then $\widehat{v}>0$. Therefore, we obtain

$$\begin{array}{cc}\hfill \Delta {\Theta }_n& \le -\frac{{\gamma }_1{(x_{n+1}-\widehat{x})}^2}{x_{n+1}}-\frac{{\beta }_2{\gamma }_2}{{\beta }_1}\frac{{(w_{n+1}-\widehat{w})}^2}{w_{n+1}}-{\alpha }_1\widehat{y}\left[G\left(\frac{\widehat{x}}{x_{n+1}}\right)+G\left(\frac{\widehat{y}{x}_{n+1}{v}_n}{y_{n+1}\widehat{x}\widehat{v}}\right)+G\left(\frac{\widehat{v}{y}_{n+1}}{v_{n+1}\widehat{y}}\right)\right]\hfill \\ \hfill & -\frac{{\beta }_2{\alpha }_2}{{\beta }_1}\widehat{z}\left[G\left(\frac{\widehat{w}}{w_{n+1}}\right)+G\left(\frac{\widehat{z}{w}_{n+1}{v}_n}{z_{n+1}\widehat{w}\widehat{v}}\right)+G\left(\frac{\widehat{v}{z}_{n+1}}{v_{n+1}\widehat{z}}\right)\right]+\left(\frac{{\omega }_3{\xi }_1}{{\gamma }_1}-\delta \right)u_n\hfill \\ \hfill & =-{\gamma }_1\frac{{(x_{n+1}-\widehat{x})}^2}{x_{n+1}}-\frac{{\beta }_2{\gamma }_2}{{\beta }_1}\frac{{(w_{n+1}-\widehat{w})}^2}{w_{n+1}}-{\alpha }_1\widehat{y}\left[G\left(\frac{\widehat{x}}{x_{n+1}}\right)+G\left(\frac{\widehat{y}{x}_{n+1}{v}_n}{y_{n+1}\widehat{x}\widehat{v}}\right)+G\left(\frac{\widehat{v}{y}_{n+1}}{v_{n+1}\widehat{y}}\right)\right]\hfill \\ \hfill & -\frac{{\beta }_2}{{\beta }_1}{\alpha }_2\widehat{z}\left[G\left(\frac{\widehat{w}}{w_{n+1}}\right)+G\left(\frac{\widehat{z}{w}_{n+1}{v}_n}{z_{n+1}\widehat{w}\widehat{v}}\right)+G\left(\frac{\widehat{v}{z}_{n+1}}{v_{n+1}\widehat{z}}\right)\right]+\delta \left(R_1-1\right)u_n.\hfill \end{array}$$

Since $R_0>1$ and if $R_1\le 1$, then ${\Theta }_n$ is monotonically decreasing. We have ${\Theta }_n\ge 0,$ and then there is a limit ${lim}_{n\to \infty }{\Theta }_n\ge 0$ and hence ${lim}_{n\to \infty }\Delta {\Theta }_n=0,$ which gives ${lim}_{n\to \infty }{x}_n=\widehat{x}$, ${lim}_{n\to \infty }{y}_n=\widehat{y}$, ${lim}_{n\to \infty }{w}_n=\widehat{w}$, ${lim}_{n\to \infty }{v}_n=\widehat{v}$, ${lim}_{n\to \infty }{z}_n=\widehat{z}$ and ${lim}_{n\to \infty }\left(R_1-1\right)u_n=0$. Now, we address two cases:

(i) $R_1=1,$ and then from Equation (10), we obtain

$$0={\xi }_1-{\gamma }_1\widehat{x}-{\omega }_1\widehat{x}\widehat{v}-{\omega }_3\widehat{x}\underset{n\to \infty }{lim}{u}_n\Rightarrow \underset{n\to \infty }{lim}{u}_n=0.$$

(ii) $R_1<1$ and then ${lim}_{n\to \infty }{u}_n=0.$

Hence, $E{Q}_1$ is GAS. □

Theorem 2 suggests that if the model’s parameters are adjusted such that $R_0>1$ and $R_1\le 1$, then the HTLV-I will be extinct and the patient will have chronic HIV-1 single-infection.

Theorem 3.

if $R_1>1$ and $R_{02}+\frac{R_{01}}{R_1}\le 1$, then $E{Q}_2(\tilde{x},0,\tilde{w},0,0,\tilde{u})$ is GAS in $\Gamma \backslash {\rm Y}$.

Proof. 

Consider a function ${\Phi }_n$ as:

$${\Phi }_n=\frac{1}{\Omega \left(h\right)}\left[\tilde{x}G\left(\frac{x_n}{\tilde{x}}\right)+y_n+\frac{{\beta }_2\tilde{w}}{{\beta }_1}G\left(\frac{w_n}{\tilde{w}}\right)+\frac{{\beta }_2}{{\beta }_1}{z}_n+\frac{1}{{\beta }_1}(1+\theta \Omega \left(h\right))v_n+\tilde{u}(1+\delta \Omega \left(h\right))G\left(\frac{u_n}{\tilde{u}}\right)\right].$$

Computing the difference $\Delta {\Phi }_n={\Phi }_{n+1}-{\Phi }_n$ as:

$$\begin{array}{cc}\hfill \Delta {\Phi }_n& =\frac{1}{\Omega \left(h\right)}\left[\tilde{x}G\left(\frac{x_{n+1}}{\tilde{x}}\right)+y_{n+1}+\frac{{\beta }_2\tilde{w}}{{\beta }_1}G\left(\frac{w_{n+1}}{\tilde{w}}\right)+\frac{{\beta }_2}{{\beta }_1}{z}_{n+1}+\frac{1}{{\beta }_1}(1+\theta \Omega \left(h\right))v_{n+1}\right.\hfill \\ \hfill & +\tilde{u}(1+\delta \Omega \left(h\right))G\left(\frac{u_{n+1}}{\tilde{u}}\right)-\tilde{x}G\left(\frac{x_n}{\tilde{x}}\right)-y_n-\frac{{\beta }_2\tilde{w}}{{\beta }_1}G\left(\frac{w_n}{\tilde{w}}\right)-\frac{{\beta }_2}{{\beta }_1}{z}_n-\frac{1}{{\beta }_1}(1+\theta \Omega \left(h\right))v_n\hfill \\ \hfill & \left.-\tilde{u}(1+\delta \Omega \left(h\right))G\left(\frac{u_n}{\tilde{u}}\right)\right]\hfill \\ \hfill & =\frac{1}{\Omega \left(h\right)}\left[\tilde{x}\left(\frac{x_{n+1}}{\tilde{x}}-\frac{x_n}{\tilde{x}}+ln\left(\frac{x_n}{x_{n+1}}\right)\right)+y_{n+1}-y_n+\frac{{\beta }_2\tilde{w}}{{\beta }_1}\left(\frac{w_{n+1}}{\tilde{w}}-\frac{w_n}{\tilde{w}}+ln\left(\frac{w_n}{w_{n+1}}\right)\right)\right.\hfill \\ \hfill & \left.+\frac{{\beta }_2}{{\beta }_1}\left(z_{n+1}-z_n\right)+\frac{1}{{\beta }_1}(1+\theta \Omega \left(h\right))\left(v_{n+1}-v_n\right)+\tilde{u}\left(\frac{u_{n+1}}{\tilde{u}}-\frac{u_n}{\tilde{u}}+ln\left(\frac{u_n}{u_{n+1}}\right)\right)\right]\hfill \\ \hfill & +\delta \tilde{u}\left(G\left(\frac{u_{n+1}}{\tilde{u}}\right)-G\left(\frac{u_n}{\tilde{u}}\right)\right).\hfill \end{array}$$

Using inequality (33) we get

$$\begin{array}{cc}\hfill \Delta {\Phi }_n& \le \frac{1}{\Omega \left(h\right)}\left[\tilde{x}\left(\frac{x_{n+1}-x_n}{\tilde{x}}+\frac{x_n}{x_{n+1}}-1\right)+y_{n+1}-y_n+\frac{{\beta }_2\tilde{w}}{{\beta }_1}\left(\frac{w_{n+1}-w_n}{\tilde{w}}+\frac{w_n}{w_{n+1}}-1\right)\right.\hfill \\ \hfill & \left.+\frac{{\beta }_2}{{\beta }_1}\left(z_{n+1}-z_n\right)+\frac{1}{{\beta }_1}(1+\theta \Omega \left(h\right))\left(v_{n+1}-v_n\right)+\tilde{u}\left(\frac{u_{n+1}-u_n}{\tilde{u}}+\frac{u_n}{u_{n+1}}-1\right)\right]\hfill \\ \hfill & +\delta \tilde{u}\left(G\left(\frac{u_{n+1}}{\tilde{u}}\right)-G\left(\frac{u_n}{\tilde{u}}\right)\right)\hfill \\ \hfill & =\frac{1}{\Omega \left(h\right)}\left[\left(1-\frac{\tilde{x}}{x_{n+1}}\right)(x_{n+1}-x_n)+y_{n+1}-y_n+\frac{{\beta }_2}{{\beta }_1}\left(1-\frac{\tilde{w}}{w_{n+1}}\right)(w_{n+1}-w_n)\right.\hfill \\ \hfill & \left.+\frac{{\beta }_2}{{\beta }_1}\left(z_{n+1}-z_n\right)+\frac{1}{{\beta }_1}(1+\theta \Omega \left(h\right))\left(v_{n+1}-v_n\right)+\left(1-\frac{\tilde{u}}{u_{n+1}}\right)(u_{n+1}-u_n)\right]\hfill \\ \hfill & +\delta \tilde{u}\left(\frac{u_{n+1}}{\tilde{u}}-\frac{u_n}{\tilde{u}}+ln\left(\frac{u_n}{u_{n+1}}\right)\right).\hfill \end{array}$$

From Equations (10)–(15) we have

$$\begin{array}{cc}\hfill \Delta {\Phi }_n& \le \left(1-\frac{\tilde{x}}{x_{n+1}}\right)({\xi }_1-{\gamma }_1{x}_{n+1}-{\omega }_1{x}_{n+1}{v}_n-{\omega }_3{x}_{n+1}{u}_n)+{\omega }_1{x}_{n+1}{v}_n-{\alpha }_1{y}_{n+1}\hfill \\ \hfill & +\frac{{\beta }_2}{{\beta }_1}\left(1-\frac{\tilde{w}}{w_{n+1}}\right)({\xi }_2-{\gamma }_2{w}_{n+1}-{\omega }_2{w}_{n+1}{v}_n)+\frac{{\beta }_2}{{\beta }_1}\left({\omega }_2{w}_{n+1}{v}_n-{\alpha }_2{z}_{n+1}\right)\hfill \\ \hfill & +\frac{1}{{\beta }_1}\left({\beta }_1{\alpha }_1{y}_{n+1}+{\beta }_2{\alpha }_2{z}_{n+1}-\theta v_{n+1}\right)+\frac{\theta }{{\beta }_1}\left(v_{n+1}-v_n\right)\hfill \\ \hfill & +\left(1-\frac{\tilde{u}}{u_{n+1}}\right)\left({\omega }_3{x}_{n+1}{u}_n-\delta u_{n+1}\right)+\delta \tilde{u}\left(\frac{u_{n+1}}{\tilde{u}}-\frac{u_n}{\tilde{u}}+ln\left(\frac{u_n}{u_{n+1}}\right)\right)\hfill \\ \hfill & =\left(1-\frac{\tilde{x}}{x_{n+1}}\right)({\xi }_1-{\gamma }_1{x}_{n+1})+\frac{{\beta }_2}{{\beta }_1}\left(1-\frac{\tilde{w}}{w_{n+1}}\right)({\xi }_2-{\gamma }_2{w}_{n+1})+{\omega }_1\tilde{x}{v}_n\hfill \\ \hfill & +{\omega }_3\tilde{x}{u}_n+\frac{{\beta }_2}{{\beta }_1}{\omega }_2\tilde{w}{v}_n-\frac{\theta }{{\beta }_1}{v}_n-{\omega }_3{x}_{n+1}{u}_n\frac{\tilde{u}}{u_{n+1}}+\delta \tilde{u}-\delta u_n+\delta \tilde{u}ln\left(\frac{u_n}{u_{n+1}}\right)\hfill \\ \hfill & =\left(1-\frac{\tilde{x}}{x_{n+1}}\right)({\xi }_1-{\gamma }_1{x}_{n+1})+\frac{{\beta }_2}{{\beta }_1}\left(1-\frac{\tilde{w}}{w_{n+1}}\right)({\xi }_2-{\gamma }_2{w}_{n+1})\hfill \\ \hfill & +\left({\omega }_1\tilde{x}+\frac{{\beta }_2}{{\beta }_1}{\omega }_2\tilde{w}-\frac{\theta }{{\beta }_1}\right)v_n+{\omega }_3\tilde{x}\tilde{u}\frac{u_n}{\tilde{u}}-{\omega }_3\tilde{x}\tilde{u}\frac{x_{n+1}{u}_n}{\tilde{x}{u}_{n+1}}+\delta \tilde{u}-\delta \tilde{u}\frac{u_n}{\tilde{u}}\hfill \\ \hfill & +\delta \tilde{u}ln\left(\frac{u_n}{u_{n+1}}\right).\hfill \end{array}$$

Using the equilibria conditions of $E{Q}_2$

$${\xi }_1={\gamma }_1\tilde{x}+{\omega }_3\tilde{x}\tilde{u},{\xi }_2={\gamma }_2\tilde{w},\delta ={\omega }_3\tilde{x}.$$

We get

$$\begin{array}{cc}\hfill \Delta {\Phi }_n& \le \left(1-\frac{\tilde{x}}{x_{n+1}}\right)({\gamma }_1\tilde{x}-{\gamma }_1{x}_{n+1})+\frac{{\beta }_2}{{\beta }_1}\left(1-\frac{\tilde{w}}{w_{n+1}}\right)({\gamma }_2\tilde{w}-{\gamma }_2{w}_{n+1})\hfill \\ \hfill & +\left({\omega }_1\tilde{x}+\frac{{\beta }_2}{{\beta }_1}{\omega }_2\tilde{w}-\frac{\theta }{{\beta }_1}\right)v_n+\delta \tilde{u}-\delta \tilde{u}\frac{\tilde{x}}{x_{n+1}}-\delta \tilde{u}\frac{x_{n+1}{u}_n}{\tilde{x}{u}_{n+1}}+\delta \tilde{u}+\delta \tilde{u}ln\left(\frac{u_n}{u_{n+1}}\right)\hfill \\ \hfill & =-\frac{{\gamma }_1}{x_{n+1}}{(x_{n+1}-\tilde{x})}^2-\frac{{\beta }_2{\gamma }_2}{{\beta }_1{w}_{n+1}}{(w_{n+1}-\tilde{w})}^2+\left({\omega }_1\tilde{x}+\frac{{\beta }_2}{{\beta }_1}{\omega }_2\tilde{w}-\frac{\theta }{{\beta }_1}\right)v_n\hfill \\ \hfill & +\delta \tilde{u}\left(2-\frac{\tilde{x}}{x_{n+1}}-\frac{x_{n+1}{u}_n}{\tilde{x}{u}_{n+1}}+ln\left(\frac{u_n}{u_{n+1}}\right)\right).\hfill \end{array}$$

(39)

We have

$$\begin{array}{cc}\hfill {\omega }_1\tilde{x}+\frac{{\beta }_2}{{\beta }_1}{\omega }_2\tilde{w}-\frac{\theta }{{\beta }_1}& =\frac{{\omega }_1\delta }{{\omega }_3}+\frac{{\beta }_2{\omega }_2{\xi }_2}{{\beta }_1{\gamma }_2}-\frac{\theta }{{\beta }_1}\hfill \\ \hfill & =\frac{\theta }{{\beta }_1}\left(\frac{{\omega }_1{\beta }_1\delta }{\theta {\omega }_3}+\frac{{\beta }_2{\omega }_2{\xi }_2}{\theta {\gamma }_2}-1\right)\hfill \\ \hfill & =\frac{\theta }{{\beta }_1}\left(R_{02}+\frac{R_{01}}{R_1}-1\right);\hfill \end{array}$$

then, using the following equality,

$$ln\left(\frac{u_n}{u_{n+1}}\right)=ln\left(\frac{\tilde{x}}{x_{n+1}}\right)+ln\left(\frac{x_{n+1}{u}_n}{\tilde{x}{u}_{n+1}}\right),$$

(40)

Equation (39) becomes

$$\begin{array}{cc}\hfill \Delta {\Phi }_n& \le -{\gamma }_1\frac{{(x_{n+1}-\tilde{x})}^2}{x_{n+1}}-\frac{{\beta }_2{\gamma }_2}{{\beta }_1}\frac{{(w_{n+1}-\tilde{w})}^2}{w_{n+1}}+\frac{\theta }{{\beta }_1}\left(R_{02}+\frac{R_{01}}{R_1}-1\right)v_n\hfill \\ \hfill & -\delta \tilde{u}\left(G\left(\frac{\tilde{x}}{x_{n+1}}\right)+G\left(\frac{x_{n+1}{u}_n}{\tilde{x}{u}_{n+1}}\right)\right).\hfill \end{array}$$

Since, $R_{02}+\frac{R_{01}}{R_1}\le 1,$ then $\Delta {\Phi }_n\le 0$, for all $n\ge 0$. Hence, the sequence ${\Phi }_n$ is monotonically decreasing. Since ${\Phi }_n\ge 0,$ then ${lim}_{n\to \infty }{\Phi }_n\ge 0$ and thus, ${lim}_{n\to \infty }\Delta {\Phi }_n=0$. Thus, ${lim}_{n\to \infty }{x}_n=\tilde{x},$ ${lim}_{n\to \infty }{w}_n=\tilde{w},$ ${lim}_{n\to \infty }{u}_n=\tilde{u}$ and ${lim}_{n\to \infty }\left(R_{02}+\frac{R_{01}}{R_1}-1\right)v_n=0.$ We have two cases:

(i) $R_{02}+\frac{R_{01}}{R_1}=1,$ and from Equation (10)

$$0={\xi }_1-{\gamma }_1\tilde{x}-{\omega }_1\tilde{x}\underset{n\to \infty }{lim}{v}_n-{\omega }_3\tilde{x}\tilde{u}⟹\underset{n\to \infty }{lim}{v}_n=0.$$

(41)

Moreover, from Equation (14),

$$0={\beta }_1{\alpha }_1\underset{n\to \infty }{lim}{y}_{n+1}+{\beta }_2{\alpha }_2\underset{n\to \infty }{lim}{z}_{n+1}=0⟹\underset{n\to \infty }{lim}{y}_n=0\mathrm{and}\underset{n\to \infty }{lim}{z}_n=0.$$

(42)

(ii) $R_{02}+\frac{R_{01}}{R_1}<1$ and ${lim}_{n\to \infty }{v}_n=0$. Equation (42) implies that ${lim}_{n\to \infty }{y}_n={lim}_{n\to \infty }{z}_n=0$. This proves that $E{Q}_2$ is GAS. □

Theorem 3 suggests that if the model’s parameters are controlled such that $R_1>1$ and $R_{02}+\frac{R_{01}}{R_1}\le 1$, then the HIV-1 will be extinct and the patient will have chronic HTLV-I single-infection.

Theorem 4.

If $\frac{R_1}{R_{01}}>1$, $R_2>1$ and $R_3>1,$ then $E{Q}_3$ is GAS in the interior of Γ.

Proof. 

Consider

$$\begin{array}{cc}\hfill {\Psi }_n& =\frac{1}{\Omega \left(h\right)}\left[\overline{x}G\left(\frac{x_n}{\overline{x}}\right)+\overline{y}G\left(\frac{y_n}{\overline{y}}\right)+\frac{{\beta }_2\overline{w}}{{\beta }_1}G\left(\frac{w_n}{\overline{w}}\right)+\frac{{\beta }_2\overline{z}}{{\beta }_1}G\left(\frac{z_n}{\overline{z}}\right)\right.\hfill \\ \hfill & \left.+\frac{\overline{v}}{{\beta }_1}(1+\Omega \left(h\right)\theta )G\left(\frac{v_n}{\overline{v}}\right)+\overline{u}(1+\Omega \left(h\right)\delta )G\left(\frac{u_n}{\overline{u}}\right)\right].\hfill \end{array}$$

Computing the difference $\Delta {\Psi }_n={\Psi }_{n+1}-{\Psi }_n$ as

$$\begin{array}{cc}\hfill \Delta {\Psi }_n& =\frac{1}{\Omega \left(h\right)}\left[\overline{x}G\left(\frac{x_{n+1}}{\overline{x}}\right)+\overline{y}G\left(\frac{y_{n+1}}{\overline{y}}\right)+\frac{{\beta }_2\overline{w}}{{\beta }_1}G\left(\frac{w_{n+1}}{\overline{w}}\right)+\frac{{\beta }_2\overline{z}}{{\beta }_1}G\left(\frac{z_{n+1}}{\overline{z}}\right)\right.\hfill \\ \hfill & +\frac{\overline{v}}{{\beta }_1}(1+\Omega \left(h\right)\theta )G\left(\frac{v_{n+1}}{\overline{v}}\right)+\overline{u}(1+\Omega \left(h\right)\delta )G\left(\frac{u_{n+1}}{\overline{u}}\right)-\overline{x}G\left(\frac{x_n}{\overline{x}}\right)-\overline{y}G\left(\frac{y_n}{\overline{y}}\right)\hfill \\ \hfill & \left.-\frac{{\beta }_2\overline{w}}{{\beta }_1}G\left(\frac{w_n}{\overline{w}}\right)-\frac{{\beta }_2\overline{z}}{{\beta }_1}G\left(\frac{z_n}{\overline{z}}\right)-\frac{\overline{v}}{{\beta }_1}(1+\Omega \left(h\right)\theta )G\left(\frac{v_n}{\overline{v}}\right)-\overline{u}(1+\Omega \left(h\right)\delta )G\left(\frac{u_n}{\overline{u}}\right)\right]\hfill \\ \hfill & =\frac{1}{\Omega \left(h\right)}\left[\overline{x}\left(\frac{x_{n+1}}{\overline{x}}-\frac{x_n}{\overline{x}}+ln\left(\frac{x_n}{x_{n+1}}\right)\right)+\overline{y}\left(\frac{y_{n+1}}{\overline{y}}-\frac{y_n}{\overline{y}}+ln\left(\frac{y_n}{y_{n+1}}\right)\right)\right.\hfill \\ \hfill & +\frac{{\beta }_2\overline{w}}{{\beta }_1}\left(\frac{w_{n+1}}{\overline{w}}-\frac{w_n}{\overline{w}}+ln\left(\frac{w_n}{w_{n+1}}\right)\right)+\frac{{\beta }_2\overline{z}}{{\beta }_1}\left(\frac{z_{n+1}}{\overline{z}}-\frac{z_n}{\overline{z}}+ln\left(\frac{z_n}{z_{n+1}}\right)\right)\hfill \\ \hfill & \left.+\frac{\overline{v}}{{\beta }_1}\left(\frac{v_{n+1}}{\overline{v}}-\frac{v_n}{\overline{v}}+ln\left(\frac{v_n}{v_{n+1}}\right)\right)+\overline{u}\left(\frac{u_{n+1}}{\overline{u}}-\frac{u_n}{\overline{u}}+ln\left(\frac{u_n}{u_{n+1}}\right)\right)\right]\hfill \\ \hfill & +\frac{\theta \overline{v}}{{\beta }_1}\left(G\left(\frac{v_{n+1}}{\overline{v}}\right)-G\left(\frac{v_n}{\overline{v}}\right)\right)+\delta \overline{u}\left(G\left(\frac{u_{n+1}}{\overline{u}}\right)-G\left(\frac{u_n}{\overline{u}}\right)\right).\hfill \end{array}$$

Using inequality (33), we get

$$\begin{array}{cc}\hfill \Delta {\Psi }_n& \le \frac{1}{\Omega \left(h\right)}\left[\overline{x}\left(\frac{x_{n+1}-x_n}{\overline{x}}+\frac{x_n}{x_{n+1}}-1\right)+\overline{y}\left(\frac{y_{n+1}-y_n}{\overline{y}}+\frac{y_n}{y_{n+1}}-1\right)\right.\hfill \\ \hfill & +\frac{{\beta }_2\overline{w}}{{\beta }_1}\left(\frac{w_{n+1}-w_n}{\overline{w}}+\frac{w_n}{w_{n+1}}-1\right)+\frac{{\beta }_2\overline{z}}{{\beta }_1}\left(\frac{z_{n+1}-z_n}{\overline{z}}+\frac{z_n}{z_{n+1}}-1\right)\hfill \\ \hfill & \left.+\frac{\overline{v}}{{\beta }_1}\left(\frac{v_{n+1}-v_n}{\overline{v}}+\frac{v_n}{v_{n+1}}-1\right)+\overline{u}\left(\frac{u_{n+1}-u_n}{\overline{u}}+\frac{u_n}{u_{n+1}}-1\right)\right]\hfill \\ \hfill & +\frac{\theta \overline{v}}{{\beta }_1}\left(G\left(\frac{v_{n+1}}{\overline{v}}\right)-G\left(\frac{v_n}{\overline{v}}\right)\right)+\delta \overline{u}\left(G\left(\frac{u_{n+1}}{\overline{u}}\right)-G\left(\frac{u_n}{\overline{u}}\right)\right)\hfill \\ \hfill & =\frac{1}{\Omega \left(h\right)}\left[\left(1-\frac{\overline{x}}{x_{n+1}}\right)\left(x_{n+1}-x_n\right)+\left(1-\frac{\overline{y}}{y_{n+1}}\right)\left(y_{n+1}-y_n\right)\right.\hfill \\ \hfill & +\frac{{\beta }_2}{{\beta }_1}\left(1-\frac{\overline{w}}{w_{n+1}}\right)\left(w_{n+1}-w_n\right)+\frac{{\beta }_2}{{\beta }_1}\left(1-\frac{\overline{z}}{z_{n+1}}\right)\left(z_{n+1}-z_n\right)\hfill \\ \hfill & \left.+\frac{1}{{\beta }_1}\left(1-\frac{\overline{v}}{v_{n+1}}\right)\left(v_{n+1}-v_n\right)+\left(1-\frac{\overline{u}}{u_{n+1}}\right)\left(u_{n+1}-u_n\right)\right]\hfill \\ \hfill & +\frac{\theta \overline{v}}{{\beta }_1}\left(\frac{v_{n+1}}{\overline{v}}-\frac{v_n}{\overline{v}}+ln\left(\frac{v_n}{v_{n+1}}\right)\right)+\delta \overline{u}\left(\frac{u_{n+1}}{\overline{u}}-\frac{u_n}{\overline{u}}+ln\left(\frac{u_n}{u_{n+1}}\right)\right).\hfill \end{array}$$

From Equations (10)–(15), we have

$$\begin{array}{cc}\hfill \Delta {\Psi }_n& \le \left(1-\frac{\overline{x}}{x_{n+1}}\right)\left({\xi }_1-{\gamma }_1{x}_{n+1}-{\omega }_1{x}_{n+1}{v}_n-{\omega }_3{x}_{n+1}{u}_n\right)+\left(1-\frac{\overline{y}}{y_{n+1}}\right)\left({\omega }_1{x}_{n+1}{v}_n-{\alpha }_1{y}_{n+1}\right)\hfill \\ \hfill & +\frac{{\beta }_2}{{\beta }_1}\left(1-\frac{\overline{w}}{w_{n+1}}\right)\left({\xi }_2-{\gamma }_2{w}_{n+1}-{\omega }_2{w}_{n+1}{v}_n\right)+\frac{{\beta }_2}{{\beta }_1}\left(1-\frac{\overline{z}}{z_{n+1}}\right)\left({\omega }_2{w}_{n+1}{v}_n-{\alpha }_2{z}_{n+1}\right)\hfill \\ \hfill & +\frac{1}{{\beta }_1}\left(1-\frac{\overline{v}}{v_{n+1}}\right)\left({\beta }_1{\alpha }_1{y}_{n+1}+{\beta }_2{\alpha }_2{z}_{n+1}-\theta v_{n+1}\right)+\left(1-\frac{\overline{u}}{u_{n+1}}\right)\left({\omega }_3{x}_{n+1}{u}_n-\delta u_{n+1}\right)\hfill \\ \hfill & +\frac{\theta \overline{v}}{{\beta }_1}\left(\frac{v_{n+1}}{\overline{v}}-\frac{v_n}{\overline{v}}+ln\left(\frac{v_n}{v_{n+1}}\right)\right)+\delta \overline{u}\left(\frac{u_{n+1}}{\overline{u}}-\frac{u_n}{\overline{u}}+ln\left(\frac{u_n}{u_{n+1}}\right)\right)\hfill \\ \hfill & =\left(1-\frac{\overline{x}}{x_{n+1}}\right)({\xi }_1-{\gamma }_1{x}_{n+1})+{\omega }_1\overline{x}{v}_n+{\omega }_3\overline{x}{u}_n-{\omega }_1\frac{x_{n+1}{v}_n\overline{y}}{y_{n+1}}+{\alpha }_1\overline{y}\hfill \\ \hfill & +\frac{{\beta }_2}{{\beta }_1}\left(1-\frac{\overline{w}}{w_{n+1}}\right)({\xi }_2-{\gamma }_2{w}_{n+1})+\frac{{\beta }_2}{{\beta }_1}{\omega }_2\overline{w}{v}_n-\frac{{\beta }_2}{{\beta }_1}{\omega }_2\frac{w_{n+1}{v}_n\overline{z}}{z_{n+1}}+\frac{{\beta }_2{\alpha }_2}{{\beta }_1}\overline{z}\hfill \\ \hfill & -{\alpha }_1\frac{y_{n+1}\overline{v}}{v_{n+1}}-\frac{{\beta }_2{\alpha }_2}{{\beta }_1}\frac{z_{n+1}\overline{v}}{v_{n+1}}+\frac{\theta }{{\beta }_1}\overline{v}-\frac{\theta }{{\beta }_1}{v}_n+\frac{\theta }{{\beta }_1}\overline{v}ln\left(\frac{v_n}{v_{n+1}}\right)-{\omega }_3\frac{x_{n+1}{u}_n\overline{u}}{u_{n+1}}\hfill \\ \hfill & +\delta \overline{u}-\delta u_n+\delta \overline{u}ln\left(\frac{u_n}{u_{n+1}}\right)\hfill \\ \hfill & =\left(1-\frac{\overline{x}}{x_{n+1}}\right)({\xi }_1-{\gamma }_1{x}_{n+1})+{\omega }_1\overline{x}\overline{v}\frac{v_n}{\overline{v}}+{\omega }_3\overline{x}\overline{u}\frac{u_n}{\overline{u}}-{\omega }_1\overline{x}\overline{v}\frac{\overline{y}{x}_{n+1}{v}_n}{y_{n+1}\overline{x}\overline{v}}+{\alpha }_1\overline{y}\hfill \\ \hfill & +\frac{{\beta }_2}{{\beta }_1}\left(1-\frac{\overline{w}}{w_{n+1}}\right)({\xi }_2-{\gamma }_2{w}_{n+1})+\frac{{\beta }_2}{{\beta }_1}{\omega }_2\overline{w}\overline{v}\frac{v_n}{\overline{v}}-\frac{{\beta }_2}{{\beta }_1}{\omega }_2\overline{w}\overline{v}\frac{\overline{z}{w}_{n+1}{v}_n}{z_{n+1}\overline{w}\overline{v}}+\frac{{\beta }_2}{{\beta }_1}{\alpha }_2\overline{z}\hfill \\ \hfill & -{\alpha }_1\overline{y}\frac{\overline{v}{y}_{n+1}}{v_{n+1}\overline{y}}-\frac{{\beta }_2{\alpha }_2}{{\beta }_1}\overline{z}\frac{\overline{v}{z}_{n+1}}{v_{n+1}\overline{z}}+\frac{\theta }{{\beta }_1}\overline{v}-\frac{\theta }{{\beta }_1}\overline{v}\frac{v_n}{\overline{v}}+\frac{\theta }{{\beta }_1}\overline{v}ln\left(\frac{v_n}{v_{n+1}}\right)-{\omega }_3\overline{x}\frac{\overline{u}{x}_{n+1}{u}_n}{\overline{x}{u}_{n+1}}\hfill \\ \hfill & +\delta \overline{u}-\delta \overline{u}\frac{u_n}{\overline{u}}+\delta \overline{u}ln\left(\frac{u_n}{u_{n+1}}\right).\hfill \end{array}$$

Using the equilibrium conditions for $E{Q}_3$,

$$\begin{array}{cc}\hfill {\omega }_3\overline{x}& =\delta ,{\alpha }_1\overline{y}={\omega }_1\overline{x}\overline{v},\hfill \\ \hfill {\omega }_2\overline{w}\overline{v}& ={\alpha }_2\overline{z},\theta \overline{v}={\beta }_1{\alpha }_1\overline{y}+{\beta }_2{\alpha }_2\overline{z},\hfill \\ \hfill {\xi }_1& ={\gamma }_1\overline{x}+{\alpha }_1\overline{y}+\delta \overline{u},{\xi }_2={\gamma }_2\overline{w}+{\alpha }_2\overline{z}.\hfill \end{array}$$

We get

$$\begin{array}{cc}\hfill \Delta {\Psi }_n& =\left(1-\frac{\overline{x}}{x_{n+1}}\right)({\gamma }_1\overline{x}+{\alpha }_1\overline{y}+\delta \overline{u}-{\gamma }_1{x}_{n+1})+{\alpha }_1\overline{y}\frac{v_n}{\overline{v}}-{\alpha }_1\overline{y}\frac{\overline{y}{x}_{n+1}{v}_n}{\overline{x}{y}_{n+1}\overline{v}}+{\alpha }_1\overline{y}\hfill \\ \hfill & +\frac{{\beta }_2}{{\beta }_1}\left(1-\frac{\overline{w}}{w_{n+1}}\right)({\gamma }_2\overline{w}+{\alpha }_2\overline{z}-{\gamma }_2{w}_{n+1})+\frac{{\beta }_2}{{\beta }_1}{\alpha }_2\overline{z}\frac{v_n}{\overline{v}}-\frac{{\beta }_2}{{\beta }_1}{\alpha }_2\overline{z}\frac{\overline{z}{w}_{n+1}{v}_n}{z_{n+1}\overline{w}\overline{v}}+\frac{{\beta }_2}{{\beta }_1}{\alpha }_2\overline{z}\hfill \\ \hfill & -{\alpha }_1\overline{y}\frac{\overline{v}{y}_{n+1}}{v_{n+1}\overline{y}}-\frac{{\beta }_2}{{\beta }_1}{\alpha }_2\overline{z}\frac{\overline{v}{z}_{n+1}}{v_{n+1}\overline{z}}+{\alpha }_1\overline{y}+\frac{{\beta }_2}{{\beta }_1}{\alpha }_2\overline{z}-{\alpha }_1\overline{y}\frac{v_n}{\overline{v}}-\frac{{\beta }_2}{{\beta }_1}{\alpha }_2\overline{z}\frac{v_n}{\overline{v}}+{\alpha }_1\overline{y}ln\left(\frac{v_n}{v_{n+1}}\right)\hfill \\ \hfill & +\frac{{\beta }_2}{{\beta }_1}{\alpha }_2\overline{z}ln\left(\frac{v_n}{v_{n+1}}\right)-\delta \overline{u}\frac{x_{n+1}{u}_n}{\overline{x}{u}_{n+1}}+\delta \overline{u}+\delta \overline{u}ln\left(\frac{u_n}{u_{n+1}}\right)\hfill \\ \hfill & =\left(1-\frac{\overline{x}}{x_{n+1}}\right)({\gamma }_1\overline{x}-{\gamma }_1{x}_{n+1})+{\alpha }_1\overline{y}+\delta \overline{u}-{\alpha }_1\overline{y}\frac{\overline{x}}{x_{n+1}}-\delta \overline{u}\frac{\overline{x}}{x_{n+1}}-{\alpha }_1\overline{y}\frac{\overline{y}{x}_{n+1}{v}_n}{\overline{x}{y}_{n+1}\overline{v}}\hfill \\ \hfill & +{\alpha }_1\overline{y}+\frac{{\beta }_2}{{\beta }_1}\left(1-\frac{\overline{w}}{w_{n+1}}\right)({\gamma }_2\overline{w}-{\gamma }_2{w}_{n+1})+\frac{{\beta }_2}{{\beta }_1}{\alpha }_2\overline{z}-\frac{{\beta }_2}{{\beta }_1}{\alpha }_2\overline{z}\frac{\overline{w}}{w_{n+1}}\hfill \\ \hfill & -\frac{{\beta }_2}{{\beta }_1}{\alpha }_2\overline{z}\frac{\overline{z}{w}_{n+1}{v}_n}{z_{n+1}\overline{w}\overline{v}}+\frac{{\beta }_2}{{\beta }_1}{\alpha }_2\overline{z}-{\alpha }_1\overline{y}\frac{\overline{v}{y}_{n+1}}{v_{n+1}\overline{y}}-\frac{{\beta }_2}{{\beta }_1}{\alpha }_2\overline{z}\frac{\overline{v}{z}_{n+1}}{v_{n+1}\overline{z}}+{\alpha }_1\overline{y}+\frac{{\beta }_2}{{\beta }_1}{\alpha }_2\overline{z}\hfill \\ \hfill & +{\alpha }_1\overline{y}ln\left(\frac{v_n}{v_{n+1}}\right)+\frac{{\beta }_2}{{\beta }_1}{\alpha }_2\overline{z}ln\left(\frac{v_n}{v_{n+1}}\right)-\delta \overline{u}\frac{x_{n+1}{u}_n}{\overline{x}{u}_{n+1}}+\delta \overline{u}+\delta \overline{u}ln\left(\frac{u_n}{u_{n+1}}\right)\hfill \\ \hfill & =-{\gamma }_1\frac{{(x_{n+1}-\overline{x})}^2}{x_{n+1}}-\frac{{\beta }_2{\gamma }_2}{{\beta }_1}\frac{{(w_{n+1}-\overline{w})}^2}{w_{n+1}}+{\alpha }_1\overline{y}\left[3-\frac{\overline{x}}{x_{n+1}}-\frac{\overline{y}{x}_{n+1}{v}_n}{\overline{x}{y}_{n+1}\overline{v}}-\frac{\overline{v}{y}_{n+1}}{v_{n+1}\overline{y}}+ln\left(\frac{v_n}{v_{n+1}}\right)\right]\hfill \\ \hfill & +\frac{{\beta }_2}{{\beta }_1}{\alpha }_2\overline{z}\left[3-\frac{\overline{w}}{w_{n+1}}-\frac{\overline{z}{w}_{n+1}{v}_n}{z_{n+1}\overline{w}\overline{v}}-\frac{\overline{v}{z}_{n+1}}{v_{n+1}\overline{z}}+ln\left(\frac{v_n}{v_{n+1}}\right)\right]\hfill \\ \hfill & +\delta \overline{u}\left[2-\frac{\overline{x}}{x_{n+1}}-\frac{x_{n+1}{u}_n}{\overline{x}{u}_{n+1}}+ln\left(\frac{u_n}{u_{n+1}}\right)\right].\hfill \end{array}$$

Using equalities similar to Equations (37), (38) and (40), we get

$$\begin{array}{cc}\hfill \Delta {\Psi }_n& \le -{\gamma }_1\frac{{(x_{n+1}-\overline{x})}^2}{x_{n+1}}-\frac{{\gamma }_2{\beta }_2}{{\beta }_1}\frac{{(w_{n+1}-\overline{w})}^2}{w_{n+1}}-{\alpha }_1\overline{y}\left[G\left(\frac{\overline{x}}{x_{n+1}}\right)+G\left(\frac{\overline{y}{x}_{n+1}{v}_n}{\overline{x}{y}_{n+1}\overline{v}}\right)+G\left(\frac{\overline{v}{y}_{n+1}}{v_{n+1}\overline{y}}\right)\right]\hfill \\ \hfill & -\frac{{\beta }_2}{{\beta }_1}{\alpha }_2\overline{z}\left[G\left(\frac{\overline{w}}{w_{n+1}}\right)+G\left(\frac{\overline{v}{z}_{n+1}}{v_{n+1}\overline{z}}\right)+G\left(\frac{\overline{z}{w}_{n+1}{v}_n}{z_{n+1}\overline{w}\overline{v}}\right)\right]-\delta \overline{u}\left[G\left(\frac{\overline{x}}{x_{n+1}}\right)+G\left(\frac{x_{n+1}{u}_n}{\overline{x}{u}_{n+1}}\right)\right].\hfill \end{array}$$

We note that $\Delta {\Psi }_n\le 0.$ Hence, the sequence ${\Psi }_n$ is monotonically decreasing. Since ${\Psi }_n\ge 0,$ then ${lim}_{n\to \infty }{\Psi }_n\ge 0$ and thus, ${lim}_{n\to \infty }\Delta {\Psi }_n=0.$ Thus, ${lim}_{n\to \infty }{x}_n=\overline{x}$, ${lim}_{n\to \infty }{w}_n=\overline{w},$ ${lim}_{n\to \infty }{y}_n=\overline{y},$ ${lim}_{n\to \infty }{v}_n=\overline{v},$ ${lim}_{n\to \infty }{z}_n=\overline{z}$ and ${lim}_{n\to \infty }{u}_n=\overline{u}.$ Hence, $E{Q}_3$ is GAS. □

Theorem 4 suggests that if $\frac{R_1}{R_{01}}>1$, $R_2>1$ and $R_3>1$, then the HTLV-I and HIV-1 co-infection will be established regardless of the initial states.

6. Numerical Simulations

To perform numerical simulations for the discrete-time model (10)–(15), we use the data given in Table 1:

Table 1. Model parameters.

Parameter	Value	Source	Parameter	Value	Source	Parameter	Value	Source
${\xi }_1$	10	[18,50]	${\gamma }_1$	$0.01$	[11,51]	$\theta$	2	[32]
${\xi }_2$	$0.03198$	[12,13]	${\gamma }_2$	$0.01$	[12,13]	$\delta$	$0.2$	[17,32]
${\alpha }_1$	$0.5$	[6,7]	${\beta }_1$	6	[52]	h	$0.1$	[46]
${\alpha }_2$	$0.1$	[32,52]	${\beta }_2$	6	[52]	${\omega }_1$, ${\omega }_2$, ${\omega }_3$	Varied	Assumed

We mention that most of these values are taken from previous studies for HIV-1 single-infection and HTLV-I single-infection models, while other values ${\omega }_1,$ ${\omega }_2$ and ${\omega }_3$ are simply assumed to carry out the numerical simulations. Getting real data from HTLV-I and HIV-1 co-infection patients is not easy and needs more experimental works. Therefore, estimating the parameters of the HTLV-I and HIV-1 co-infection model is still open for future work.

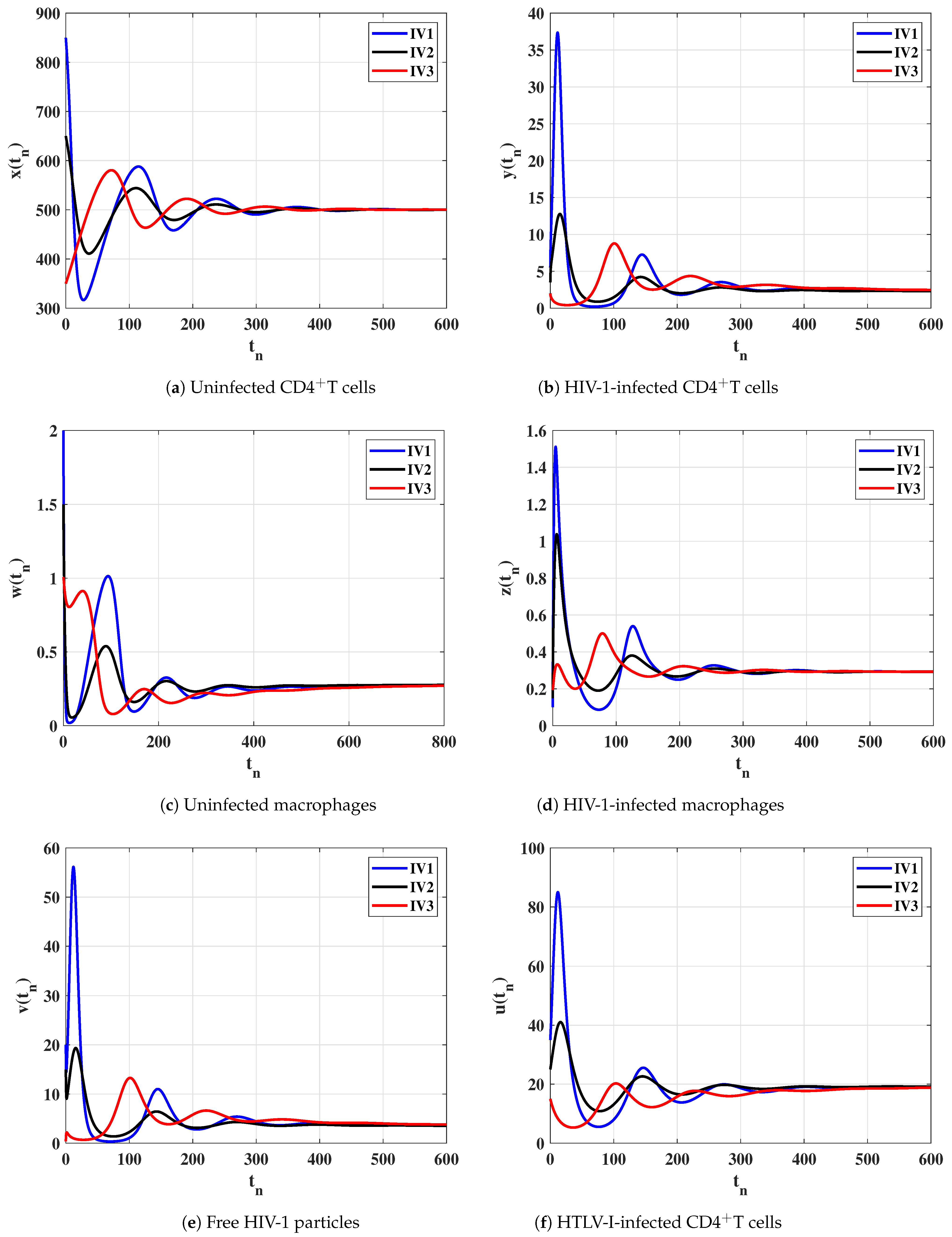
To demonstrate the global stability of the discrete-time model’s equilibria given in Theorems 1–4, we show that the solutions of the model converge to one of the four equilibria regardless of the selected initial conditions. Therefore, we choose three different initial values as

$$\begin{array}{lllllll}\mathrm{IV}1:& x_0=850,& y_0=5.5,\hfill & w_0=2,& z_0=0.1,& v_0=20,& u_0=35,\\ \mathrm{IV}2:& x_0=650,& y_0=3.5,\hfill & w_0=1.5,& z_0=0.15,& v_0=15,& u_0=25,\\ \mathrm{IV}3:& x_0=350,& y_0=2,\hfill & w_0=1,& z_0=0.2,& v_0=0.4& u_0=15.\end{array}$$

We choose ${\omega }_1,$ ${\omega }_2$ and ${\omega }_3$ as follows:

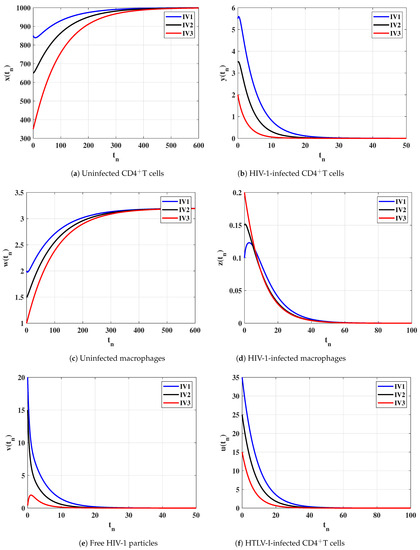
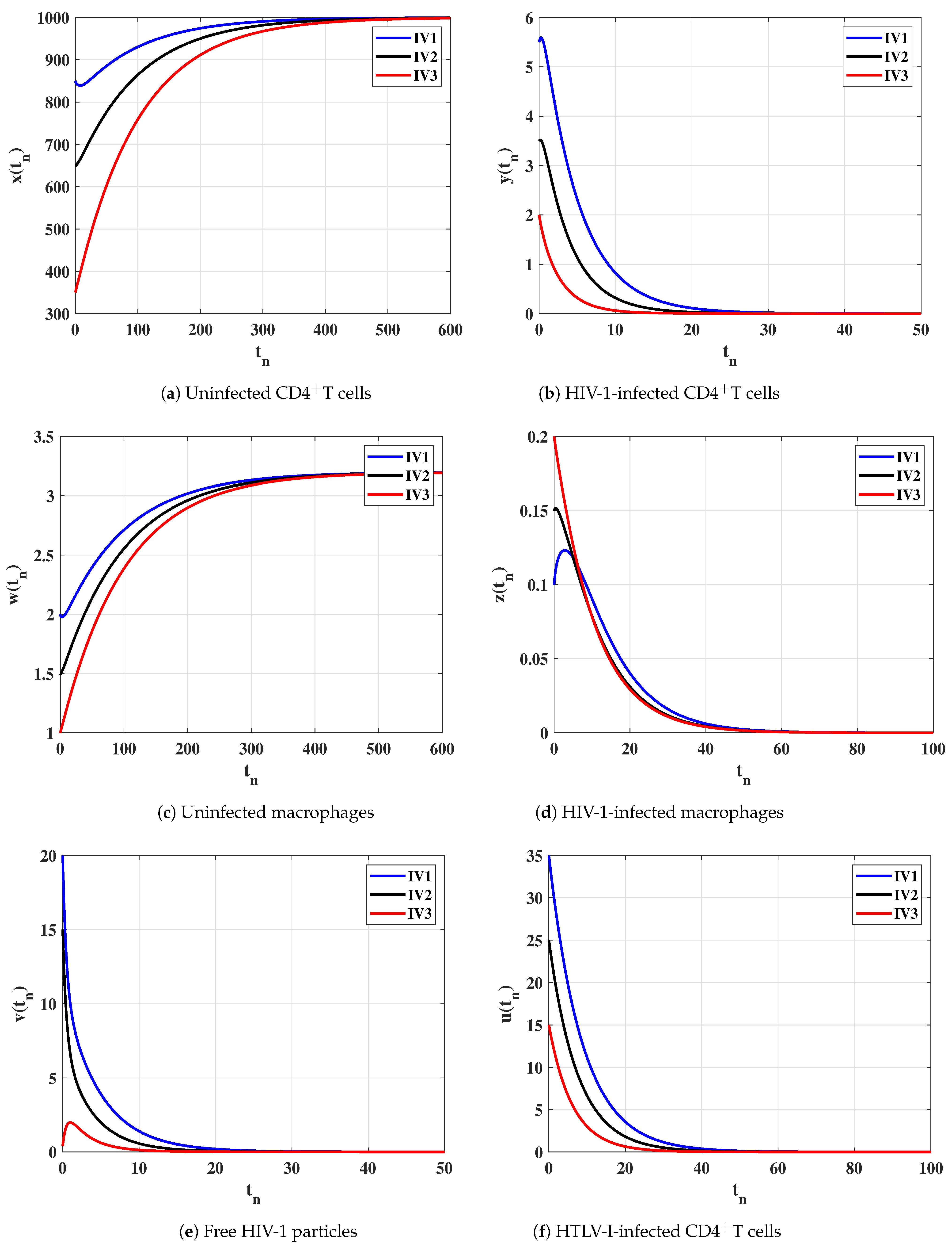
Case (I) ${\omega }_1=0.0002,$ ${\omega }_2=0.001$ and ${\omega }_3=0.0001$. This gives $R_0=0.6096\le 1$ and $R_1=0.5<1$. Figure 1 illustrates that the concentrations of uninfected CD4${}^{+}$T cells and uninfected macrophages increase and tend to the healthy values $x^0=1000$ and $w^0=3.1980$, while the concentrations of other compartments decrease and converge to zero. Therefore, $E{Q}_0$ is GAS and this agrees the result of Theorem 1. In this case, both HTLV-I and HIV-1 are cleared.

Figure 1. Solutions of model (10)–(15) with initial conditions IV1–IV3 in case of $R_0\le 1$ and $R_1\le 1$.

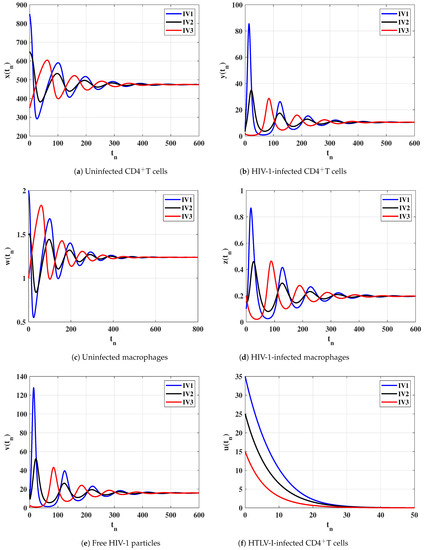
Case (II) ${\omega }_1=0.0007,$ ${\omega }_2=0.001$ and ${\omega }_3=0.0001$. These values give $R_0=2.109>1$ and $R_1=0.5<1$. From Figure 2, we see that the solutions of the discrete-time model tend to the equilibrium $E{Q}_1=(474.42,10.51,1.24,0.2,15.83,0)$. As a result, $E{Q}_1$ exists, and based on Theorem 2, it is GAS. This result shows that, the HIV-1 single-infection can be reached for all initial states.

Figure 2. Solutions of model (10)–(15) with initial conditions IV1-IV3 in case of $R_0>1$ and $R_1\le 1$.

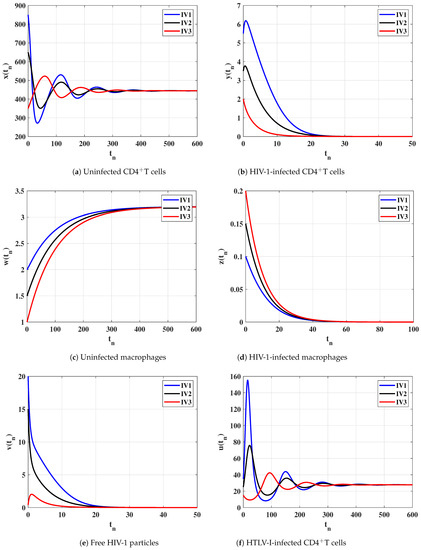
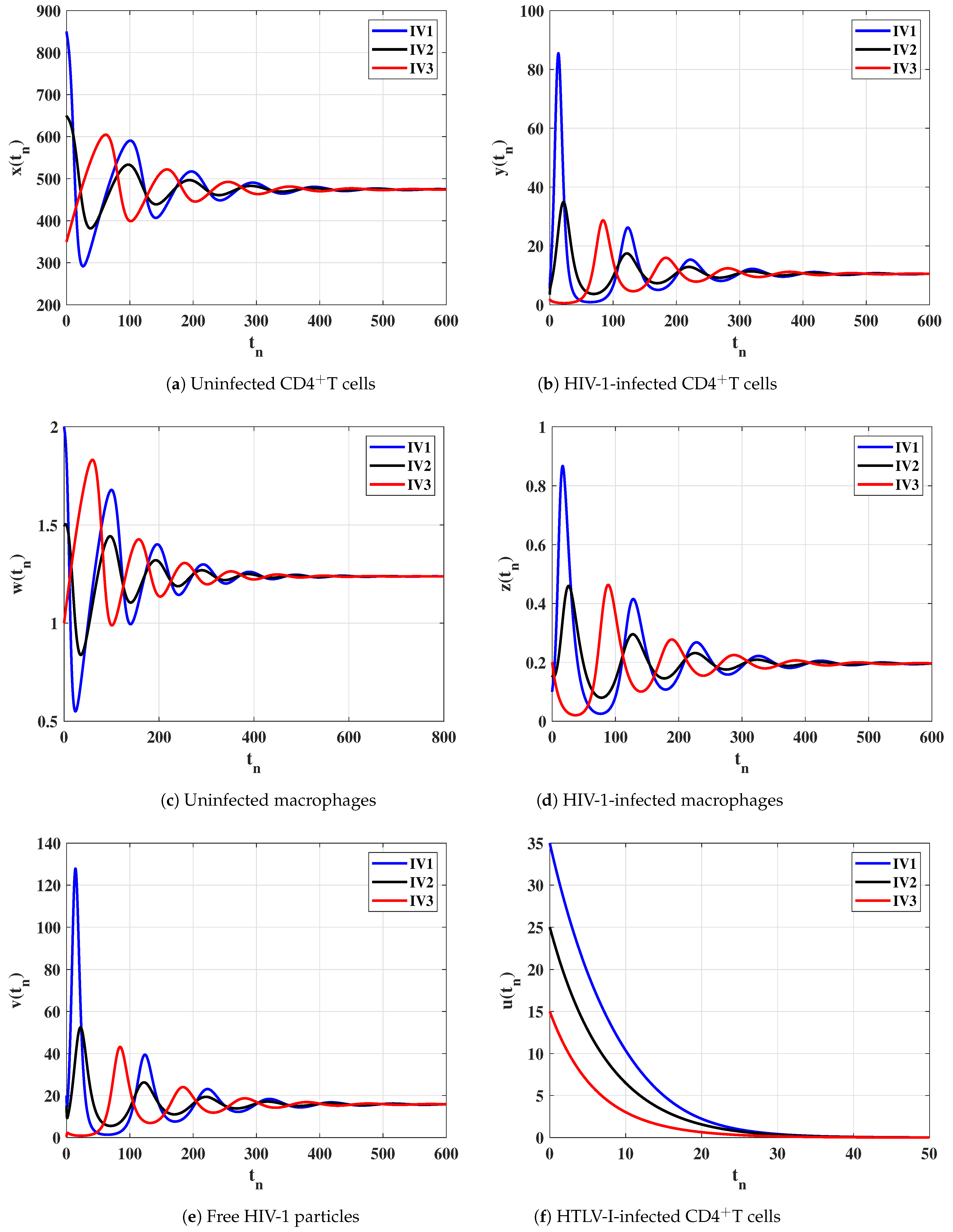
Case (III) ${\omega }_1=0.0003,$${\omega }_2=0.0001$ and ${\omega }_3=0.00045$, and then $R_1=2.25>1$ and $R_{02}+(R_{01}/R_1)=0.401<1$. Figure 3 clarifies that the solutions of the discrete-time model reach the equilibrium $E{Q}_2=(444.44,0,3.198,0,0,27.78)$ for all the initial states. According to Lemma 2 and Theorem 3, $E{Q}_2$ exists and it is GAS. This result shows that the HTLV-I single-infection can be reached for all initial states.

Figure 3. Solutions of model (10)–(15) with initial conditions IV1–IV3 in case of $R_1>1$ and $R_{02}+\frac{R_{01}}{R_1}\le 1$.

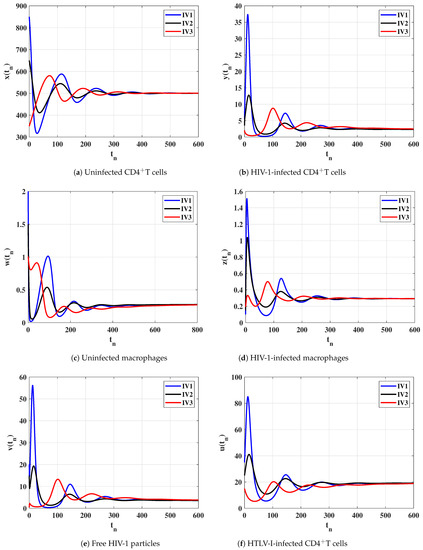
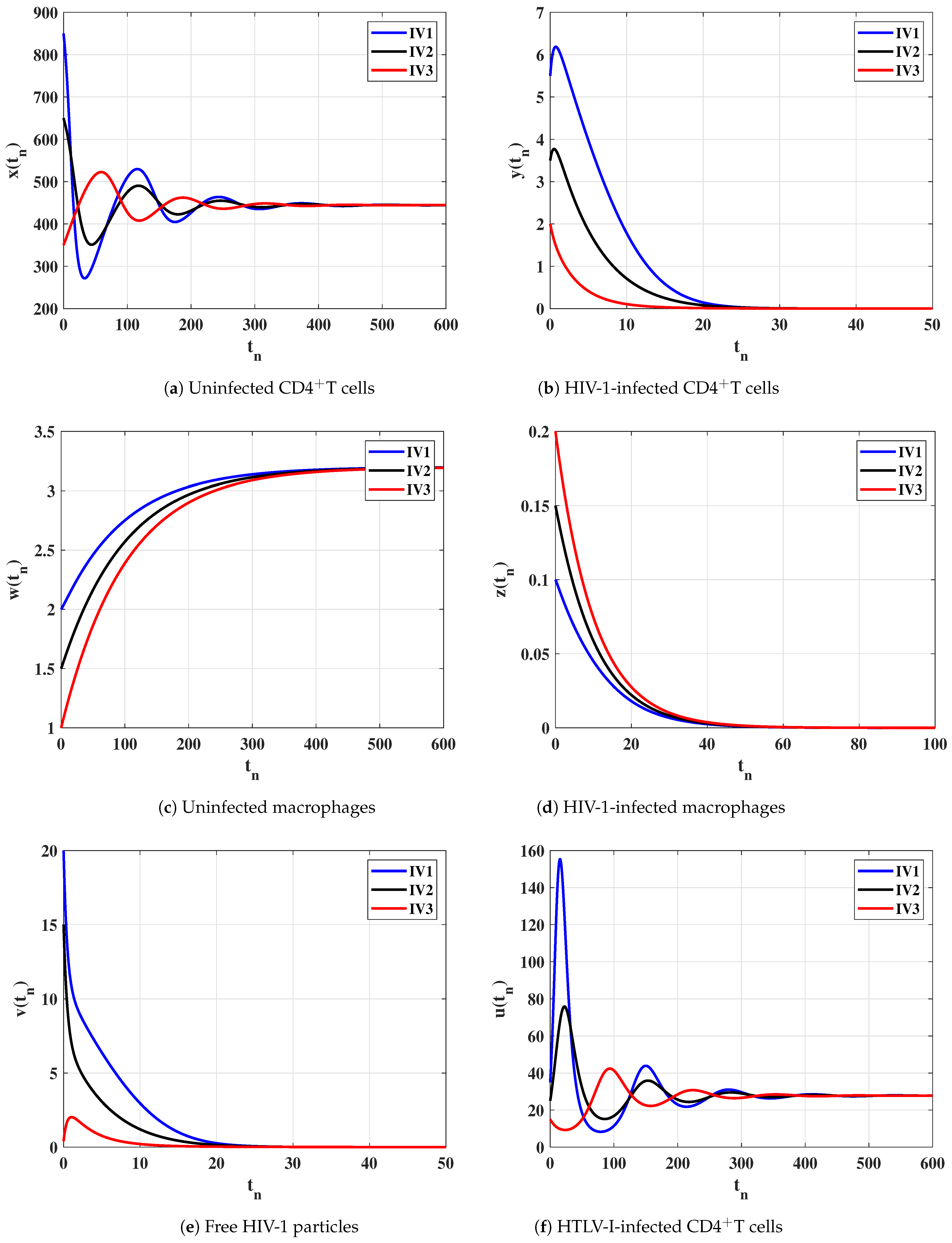
Case (IV) ${\omega }_1=0.00065,$ ${\omega }_2=0.03$ and ${\omega }_3=0.0004$, and thus, $R_1/R_{01}=1.0256>1,$ $R_2=11.5128>1$ and $R_3=4.3903>1$. Figure 4 illustrates that the solutions of the discrete-time model starting with initial values IV1-IV3 converge to the equilibrium $E{Q}_3=(500,2.28,0.28,0.29,3.5,19.31)$. Based on Lemma 2 and Theorem 4, $E{Q}_4$ exists and it is GAS. This result shows that the HTLV-I and HIV-1 co-infection can be reached for all initial states.

Figure 4. Solutions of model (10)–(15) with initial conditions IV1–IV3 in case of $\frac{R_1}{R_{01}}>1$, $R_2>1$ and $R_3>1$.

For more confirmation, we examine the local stability of the equilibria of the discrete-time model in cases (I)–(IV). The Jacobian matrix $J=J(x,y,w,z,v,u)$ of model (18)–(22) is calculated as

$$J=\left(\begin{array}{cccccc}{J}_{11}& 0& 0& 0& J_{15}& J_{16}\\ J_{21}& J_{22}& 0& 0& J_{25}& J_{26}\\ 0& 0& J_{33}& 0& J_{35}& 0\\ 0& 0& J_{43}& J_{44}& J_{45}& 0\\ J_{51}& J_{52}& J_{53}& J_{54}& J_{55}& J_{56}\\ J_{61}& 0& 0& 0& J_{65}& J_{66}\end{array}\right),$$

where

$$\begin{array}{cc}\hfill J_{11}& =\frac{1}{1+\Omega \left(h\right)({\gamma }_1+{\omega }_{1}v+{\omega }_{3}u)},J_{15}=-\frac{{\omega }_1\Omega \left(h\right)(x+{\xi }_1\Omega \left(h\right))}{{(1+\Omega \left(h\right)({\gamma }_1+{\omega }_{1}v+{\omega }_{3}u))}^2},\hfill \\ \hfill J_{16}& =-\frac{{\omega }_3\Omega \left(h\right)(x+{\xi }_1\Omega \left(h\right))}{{(1+\Omega \left(h\right)({\gamma }_1+{\omega }_{1}v+{\omega }_{3}u))}^2},J_{21}=\frac{{\omega }_1\Omega \left(h\right)v}{(1+{\alpha }_1\Omega \left(h\right))(1+\Omega \left(h\right)({\gamma }_1+{\omega }_{1}v+{\omega }_{3}u))},\hfill \\ \hfill J_{22}& =\frac{1}{1+{\alpha }_1\Omega \left(h\right)},J_{25}=\frac{{\omega }_1\Omega \left(h\right)(x+{\xi }_1\Omega \left(h\right))(1+{\gamma }_1\Omega \left(h\right)+{\omega }_3\Omega \left(h\right)u)}{(1+{\alpha }_1\Omega \left(h\right)){(1+\Omega \left(h\right)({\gamma }_1+{\omega }_{1}v+{\omega }_{3}u))}^2},\hfill \\ \hfill J_{26}& =-\frac{{\omega }_1{\omega }_3\Omega {\left(h\right)}^2(x+{\xi }_1\Omega \left(h\right))v}{(1+{\alpha }_1\Omega \left(h\right)){(1+\Omega \left(h\right)({\gamma }_1+{\omega }_{1}v+{\omega }_{3}u))}^2},J_{33}=\frac{1}{1+{\gamma }_2\Omega \left(h\right)+{\omega }_2\Omega \left(h\right)v},\hfill \\ \hfill J_{35}& =-\frac{{\omega }_2\Omega \left(h\right)(w+{\xi }_2\Omega \left(h\right))}{{(1+{\gamma }_2\Omega \left(h\right)+{\omega }_2\Omega \left(h\right)v)}^2},J_{43}=\frac{{\omega }_2\Omega \left(h\right)v}{(1+{\alpha }_2\Omega \left(h\right))(1+{\gamma }_2\Omega \left(h\right)+{\omega }_2\Omega \left(h\right)v)},\hfill \\ \hfill J_{44}& =\frac{1}{1+{\alpha }_2\Omega \left(h\right)},J_{45}=\frac{{\omega }_2\Omega \left(h\right)(1+{\gamma }_2\Omega \left(h\right))(w+{\xi }_2\Omega \left(h\right))}{(1+{\alpha }_2\Omega \left(h\right)){(1+{\gamma }_2\Omega \left(h\right)+{\omega }_2\Omega \left(h\right)v)}^2},\hfill \\ \hfill J_{51}& =\frac{{\alpha }_1{\beta }_1{\omega }_1{\Omega }^2\left(h\right)v}{(1+{\alpha }_1\Omega \left(h\right))(1+\theta \Omega \left(h\right))(1+\Omega \left(h\right)({\gamma }_1+{\omega }_{1}v+{\omega }_{3}u))},J_{52}=\frac{{\alpha }_1{\beta }_1\Omega \left(h\right)}{(1+{\alpha }_1\Omega \left(h\right))(1+\theta \Omega \left(h\right))},\hfill \\ \hfill J_{53}& =\frac{{\alpha }_2{\beta }_2{\omega }_2{\Omega }^2\left(h\right)v}{(1+{\alpha }_2\Omega \left(h\right))(1+\theta \Omega \left(h\right))(1+{\gamma }_2\Omega \left(h\right)+{\omega }_2\Omega \left(h\right)v)},J_{54}=\frac{{\alpha }_2{\beta }_2\Omega \left(h\right)}{(1+{\alpha }_2\Omega \left(h\right))(1+\theta \Omega \left(h\right))},\hfill \\ \hfill J_{55}& =\frac{1}{1+\theta \Omega \left(h\right)}+\frac{\Omega \left(h\right)}{1+\theta \Omega \left(h\right)}\left[\frac{{\omega }_2{\alpha }_2{\beta }_2\Omega \left(h\right)(1+{\gamma }_2\Omega \left(h\right))(w+{\xi }_2\Omega \left(h\right))}{(1+{\alpha }_2\Omega \left(h\right)){(1+{\gamma }_2\Omega \left(h\right)+{\omega }_2\Omega \left(h\right)v)}^2}\right.\hfill \\ \hfill & \left.+\frac{{\omega }_1{\alpha }_1{\beta }_1\Omega \left(h\right)(x+{\xi }_1\Omega \left(h\right))(1+{\gamma }_1\Omega \left(h\right)+{\omega }_3\Omega \left(h\right)u)}{(1+{\alpha }_1\Omega \left(h\right)){(1+\Omega \left(h\right)({\gamma }_1+{\omega }_{1}v+{\omega }_{3}u))}^2}\right],\hfill \\ \hfill J_{56}& =-\frac{{\omega }_1{\omega }_3{\alpha }_1{\beta }_1{\Omega }^3\left(h\right)(x+{\xi }_1\Omega \left(h\right))v}{(1+{\alpha }_1\Omega \left(h\right))(1+\theta \Omega \left(h\right)){(1+\Omega \left(h\right)({\gamma }_1+{\omega }_{1}v+{\omega }_{3}u))}^2},\hfill \\ \hfill J_{61}& =\frac{\Omega \left(h\right){\omega }_{3}u}{(1+\delta \Omega \left(h\right))(1+\Omega \left(h\right)({\gamma }_1+{\omega }_{1}v+{\omega }_{3}u))},\hfill \\ \hfill J_{65}& =-\frac{{\omega }_1{\omega }_3{\Omega }^2\left(h\right)(x+{\xi }_1\Omega \left(h\right))u}{(1+\delta \Omega \left(h\right)){(1+\Omega \left(h\right)({\gamma }_1+{\omega }_{1}v+{\omega }_{3}u))}^2},\hfill \\ \hfill J_{66}& =\frac{1}{1+\delta \Omega \left(h\right)}\left[1+\frac{{\omega }_3\Omega \left(h\right)(x+{\xi }_1\Omega \left(h\right))(1+{\gamma }_1\Omega \left(h\right)+{\omega }_1\Omega \left(h\right)v)}{{(1+\Omega \left(h\right)({\gamma }_1+{\omega }_{1}v+{\omega }_{3}u))}^2}\right].\hfill \end{array}$$

Then, we compute the eigenvalues ${\lambda }_j,$ $j=1,2,\dots ,6$ of the matrix $J,$ at each equilibrium. An equilibrium point of the discrete-time model is locally asymptotically stable (LAS) when $\left|{\lambda }_j\right|<1$, for all $j=1,2,\dots ,6$. We compute the eigenvalues of all nonnegative equilibria using the values of ${\omega }_1$, ${\omega }_2$ and ${\omega }_3$ given in Cases (I)-(IV). Table 2 contains the nonnegative equilibria, the absolute value of the eigenvalues and whether the equilibrium point is LAS or unstable. We note that when an equilibrium point is GAS, then it is also LAS, and all the other equilibria will be unstable.

Table 2. Local stability of equilibria.

Case	Steady State	$\left|{\mathit{\lambda }}_{\mathit{j}}\right|,$$\mathit{j}=1,2,\mathit{\dots },6$	Stability
Case (I)	$\begin{array}{c}E{Q}_0=\left(1000,0,3.20,0,0,0\right)\end{array}$	$\begin{array}{c}\left(0.999,0.999,0.991,0.990,0.983,0.807\right)\end{array}$	$\begin{array}{c}\hfill \mathrm{LAS}\hfill \end{array}$
Case (II)	$\begin{array}{c}E{Q}_0=\left(1000,0,3.20,0,0,0\right)\hfill \\ E{Q}_1=(474.42,10.51,1.24,0.2,15.83,0)\hfill \end{array}$	$\begin{array}{c}\left(1.037,0.999,0.999,0.990,0.990,0.765\right)\hfill \\ \left(0.999,0.999,0.997,0.990,0.985,0.794\right)\hfill \end{array}$	$\begin{array}{c}\mathrm{unstable}\hfill \\ \mathrm{LAS}\hfill \end{array}$
Case (III)	$\begin{array}{c}E{Q}_0=\left(1000,0,3.20,0,0,0\right)\hfill \\ E{Q}_2=(444.44,0,3.198,0,0,27.78)\hfill \end{array}$	$\begin{array}{c}\left(1.025,0.999,0.999,0.996,0.990,0.797\right)\hfill \\ \left(0.999,0.999,0.999,0.990,0.974,0.815\right)\hfill \end{array}$	$\begin{array}{c}\mathrm{unstable}\\ \multicolumn{1}{c}{\mathrm{LAS}}\end{array}$
Case (IV)	$\begin{array}{c}E{Q}_0=\left(1000,0,3.20,0,0,0\right)\hfill \\ E{Q}_1=\left(509.57,9.81,0.07,0.31,14.81,0\right)\hfill \\ E{Q}_2=\left(500,0,3.20,0,0,25\right)\hfill \\ E{Q}_3=(500,2.28,0.28,0.29,3.5,19.31)\hfill \end{array}$	$\begin{array}{c}\left(1.036,1.02,0.999,0.999,0.988,0.768\right)\hfill \\ \left(1.0004,0.999,0.999,0.990,0.957,0.794\right)\hfill \\ \left(1.006,0.999,0.999,0.999,0.985,0.793\right)\hfill \\ \left(0.999,0.999,0.999,0.992,0.987,0.794\right)\hfill \end{array}$	$\begin{array}{c}\mathrm{unstable}\\ \mathrm{unstable}\\ \multicolumn{1}{c}{\mathrm{unstable}}\\ \multicolumn{1}{c}{\mathrm{LAS}}\end{array}$

7. Conclusions

In this paper, we studied a discrete-time HTLV-I and HIV-1 co-infection model within a host. We discretized the continuous-time co.infection model by using the NSFD scheme. We proved the positivity and ultimate boundedness of the discrete-time model’s solutions. Then, we deduced that the model has four equilibria: infection-free equilibrium $E{Q}_0$, chronic HIV-1 single-infection equilibrium $E{Q}_1$, chronic HTLV-I single-infection equilibrium $E{Q}_2$ and chronic HTLV-I/HIV-1 co-infection equilibrium $E{Q}_3$. We showed that the existence and stability of equilibria are determined by four positive threshold parameters $R_j$, $j=0,1,2,3$. The global stability of all equilibria of the discrete-time model was examined by constructing Lyapunov functions. We obtained that $E{Q}_0$ is GAS, when $R_0\le 1$ and $R_1\le 1$. The equilibrium $E{Q}_1$ exists when $R_0>1$ and it is GAS when $R_0>1$ and $R_1\le 1$. When $R_1>1$, the equilibrium $E{Q}_2$ exists and it is GAS if $R_1>1$ and $R_{02}+\frac{R_{01}}{R_1}\le 1$. Finally, we found that the equilibrium $E{Q}_3$ exists and it is GAS when $\frac{R_1}{R_{01}}>1$, $R_2>1$ and $R_3>1$. We simulated the discrete-time model to confirm the theoretical results.

The model addressed in this article can be extended in several directions by including (i) time delay [5], (ii) memory effects [28], (iii) reaction–diffusion [53], and (iv) stochastic interactions [54]. These points are left for future works.