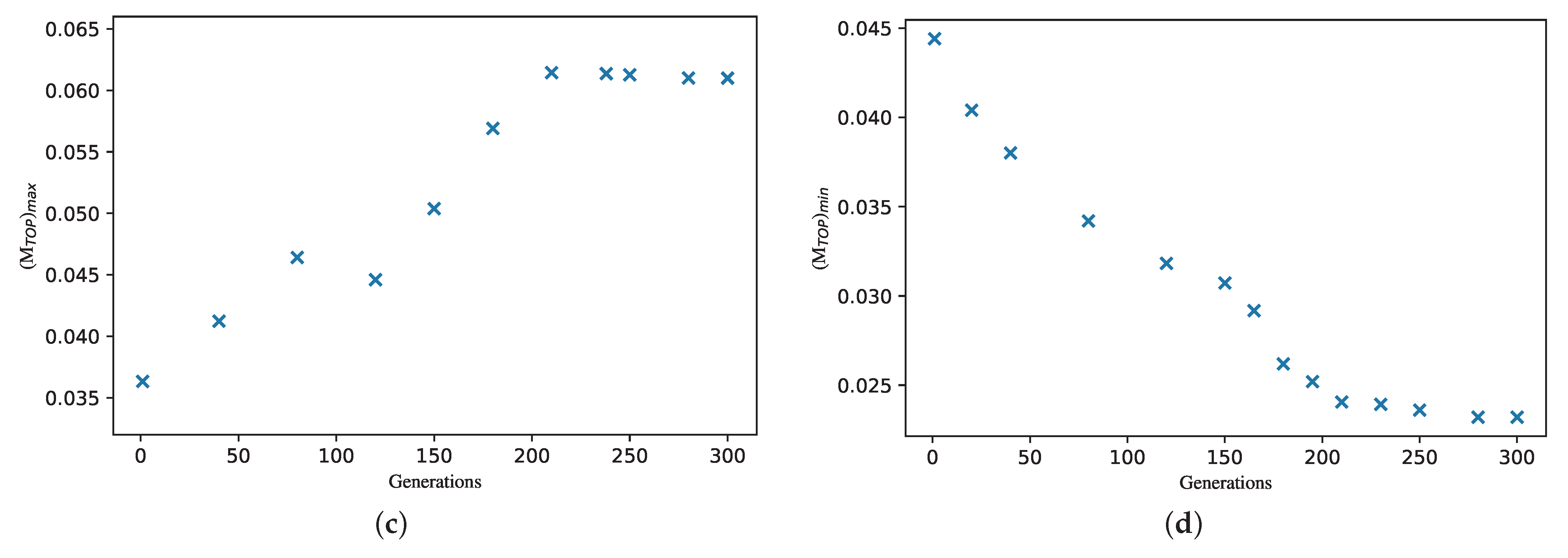Optimization of Leakage Risk and Maintenance Cost for a Subsea Production System Based on Uncertain Fault Tree

Abstract

Traditional fault tree analysis is an effective tool used to evaluate system risk if the required data are sufficient. Unfortunately, the operation and maintenance data of some complex systems are difficult to obtain due to economic or technical reasons. The solution is to invite experts to evaluate some critical aspect of the performance of the system. In this study, the belief degrees of the occurrence of basic events evaluated by experts are measured by an uncertain measure. Then, a system risk assessment method based on an uncertain fault tree is proposed, based on which two general optimization models are established. Furthermore, the genetic algorithm (GA) and the nondominated sorting genetic algorithm II (NSGA-II) are applied to solve the two optimization models, separately. In addition, the proposed risk assessment method is applied for the leakage risk evaluation of a subsea production system, and the two general optimization models are used to optimize the leakage risk and maintenance cost of the subsea production system. The optimization results provide a theoretical basis for practitioners to guarantee the safety of subsea production system.

1. Introduction

Optimization between risk and cost is an important topic in the field of industrial and systems engineering. In past decades, researchers have paid attention to risk assessment and optimization methods for complex systems based on probability theory, such as Faddoul et al. [1], Hong et al. [2], Liu et al. [3], Ma et al. [4] and Yousefi et al. [5]. However, to take probability theory as a mathematical basis for risk evaluation and optimization, three basic premises need to be met at the same time: events need to be clearly defined; there are a large number of samples; there is probability repeatability between samples. and In the field of engineering, it is difficult to obtain sufficient data. Therefore, experts are invited to evaluate the technical condition of systems, which are often described with ambiguous language. In 1965, Zadeh [6] proposed the concept of fuzzy set to deal with imprecise and subjective information. After that, researchers began to deal with various optimization problems in fuzzy environments, such as Mortazavi [7], Sayyaadi and Baghsheikhi [8], Yang et al. [9], Zhou et al. [10], and so on. Unfortunately, Liu [11] showed that fuzzy theory is unsuitable for modeling belief degree via a counter example of the strength of a bridge. A similar situation exists in the field of system risk evaluation. For example, system risk is evaluated by experts as approximately 0.0. If the system risk is regarded as a triangular fuzzy variable (0.005, 0.01, 0.015), it can be concluded that the possibility of the system risk is exactly 0.01 is 1 and the possibility of the system risk is not 0.01 is 1 based on the possibility measure. It is usually thought that the possibility of the system risk is exactly 0.01 is 0. In addition, the system risk is exactly 0.01 and the system risk is not 0.01 have the same possibility measure. This contradictory conclusion also shows that the belief degree of experts is unsuitable for modeling by the possibility measure because it does not have a duality property.

In order to measure belief degree, uncertainty theory was founded by Liu [12] and refined by Liu [13] based on normality, duality, subadditivity, and product measure axioms. In recent years, uncertainty theory has been widely used in various fields, such as reliability analysis [14], inference controller [15], risk assessment [16], and statistics [17]. In terms of optimization problems, uncertainty theory is still an effective mathematical modeling tool. For instance, Ke and Yao [18] regarded the units as uncertain variables and proposed a block replacement strategy in uncertain environments. Liu et al. [19] gave the upper and lower bounds of insurance premiums with uncertain random losses and established a mathematical model of an optimal insurance problem. Zhang and Peng [20] solved the uncertain optimal assignment problem by giving the uncertainty distribution of the optimal assignment profit. Li et al. [21] regarded the return rate of risky assets as an uncertain variable and established an uncertain model for portfolio optimization. Li et al. [22] provided a new reliability metric that encompassed two types of task time uncertainties and developed a multiple objective to maximize the reliability and efficiency of assembly lines. Wen et al. [23] presented the minimal expected backorder model and the minimal backorder rate model with the constraints of costs and supply availability based on an uncertain measure. Li et al. [24] derived some useful theorems related to the optimal solutions by modeling the uncertain task time. Guo et al. [25] established a multiechelon multi-indenture optimization LORA model that took the best cost-effectiveness ratio as the criterion.

GA and NSGA-II, as well-known evolutionary algorithms for solving optimization problems, have been successfully applied to different real-world applications, including reliability optimization.

Andrews and Bartlett [26] used GA for the single objective optimization of a firewater deluge system on an offshore platform, in which the system was presented with the structure of a fault tree. Pattison and Andrews [27] described a design optimization scheme for systems that require a high likelihood of functioning on demand by using GA. Cui et al. [28] proposed a novel reliability design and optimization method of planetary gears using the GA, based on the Kriging model. Ardakan and Rezvan [29] considered the multiobjective optimization of the reliability–redundancy allocation problem with a cold-standby strategy using NSGA-II. Bhattacharyya and Cheliyan [30] solved a subsea production system optimization problem by using GA and NSGA-II, in which the risk was evaluated with fault tree analysis. Due to the advantages of GA and NSGA-II, we continued to use the above two algorithms to solve optimization models.

Subsea production systems are mainly composed of Xmas trees, manifolds, jumper tubes, umbilical cables, pipelines, etc. [31]. With the increase in service time of subsea production systems, more and more safety problems have emerged, especially leakage. The leakage of subsea production systems results in serious environment pollution and significant economic losses. Therefore, it is essential to ensure the safety of subsea production systems. Additionally, the total maintenance cost is expected as low as possible. Bhattacharyya and Cheliyan [30] paid attention to such problems and optimized the cost and reliability of a subsea production system on the basis of a traditional fault tree. Unfortunately, it is difficult to obtain sufficient data to evaluate the risk of subsea production systems. In this situation, experts must evaluate the key performance indicators of a subsea production system. Then, Cheliyan and Bhattacharyya [32] assessed the leakage risk of a subsea production system based on a fuzzy fault tree, in which the epistemic uncertainty was modeled with fuzzy set theory. Because the possibility measure has no duality property, a self-dual measure is absolutely needed in both theory and practice.

The major contributions of this study are as follows: A risk assessment method for complex systems with insufficient data is proposed based on uncertain fault tree analysis; two general optimization models are established for complex systems with insufficient data, and the GA and NSGA-II are applied to solve the two optimization models, separately. Leakage risk is evaluated; two optimization models of the leakage risk and maintenance cost are established for a subsea production system. Then, the optimization results are discussed.

The remainder of this paper is organized as follows Section 2 proposes a risk assessment method for systems with insufficient data. Section 3 establishes two general optimization models based on uncertain fault tree and describes the algorithms for solving the two optimization models. Section 4 outlines a leakage risk evaluation for a subsea production system, establishes the optimization models of maintenance cost and leakage risk for the subsea production system, and we discuss the optimization results. In addition, the steps of GA and NSGA-II are provided in Appendix A.

2. Risk Assessment Method Based on Uncertain Fault Tree

A fault tree is called an uncertain fault tree if the occurrences of the input events are evaluated by the uncertain measure proposed by Liu [12]. The system risk is the belief degree of the occurrence of the top event; for the operation rules, refer to Liu [33].

Theorem 1. 

If ${\mathsf{\Lambda }}_i,i=1,2,\dots ,N$ are independent input events, the belief degree of the occurrence of output event Λ is

$$\mathcal{M}\{\mathsf{\Lambda }\}=\left\{\begin{array}{cc}{\displaystyle \underset{i=1}{\overset{N}{\bigwedge }}\mathcal{M}\left\{{\mathsf{\Lambda }}_i\right\},}& \mathit{for}“\mathit{AND}”\mathit{gate}\hfill \\ {\displaystyle \underset{i=1}{\overset{N}{\bigvee }}\mathcal{M}\left\{{\mathsf{\Lambda }}_i\right\},}& \mathit{for}“\mathit{OR}”\mathit{gate}.\hfill \end{array}\right.$$

(1)

Proof. 

If independent input events ${\mathsf{\Lambda }}_i,i=1,2,\dots ,N$ are connected by an “AND” gate, the belief degree of the occurrence of the output event $\mathsf{\Lambda }$ can be derived by

$$\begin{array}{cc}\hfill \mathcal{M}\{\mathsf{\Lambda }\}=& \mathcal{M}\left\{{\mathsf{\Lambda }}_1\cap {\mathsf{\Lambda }}_2\cap \cdots \cap {\mathsf{\Lambda }}_N\right\}\hfill \\ \hfill =& \mathcal{M}\left\{{\mathsf{\Lambda }}_1\right\}\wedge \mathcal{M}\left\{{\mathsf{\Lambda }}_2\right\}\wedge \cdots \wedge \mathcal{M}\left\{{\mathsf{\Lambda }}_N\right\}\hfill \\ \hfill =& {\displaystyle \underset{i=1}{\overset{N}{\bigwedge }}\mathcal{M}\left\{{\mathsf{\Lambda }}_i\right\}.}\hfill \end{array}$$

If independent input events ${\mathsf{\Lambda }}_i,i=1,2,\dots ,N$ are connected by an “OR” gate, the belief degree of the occurrence of the output event $\mathsf{\Lambda }$ can be derived by

$$\begin{array}{cc}\hfill \mathcal{M}\{\mathsf{\Lambda }\}=& \mathcal{M}\left\{{\mathsf{\Lambda }}_1\cup {\mathsf{\Lambda }}_2\cup ···\cup {\mathsf{\Lambda }}_N\right\}\hfill \\ \hfill =& \mathcal{M}\left\{{\mathsf{\Lambda }}_1\right\}\vee \mathcal{M}\left\{{\mathsf{\Lambda }}_2\right\}\vee \cdots \vee \mathcal{M}\left\{{\mathsf{\Lambda }}_N\right\}\hfill \\ \hfill =& {\displaystyle \underset{i=1}{\overset{N}{\bigvee }}\mathcal{M}\left\{{\mathsf{\Lambda }}_i\right\}.}\hfill \end{array}$$

The proof is completed. □

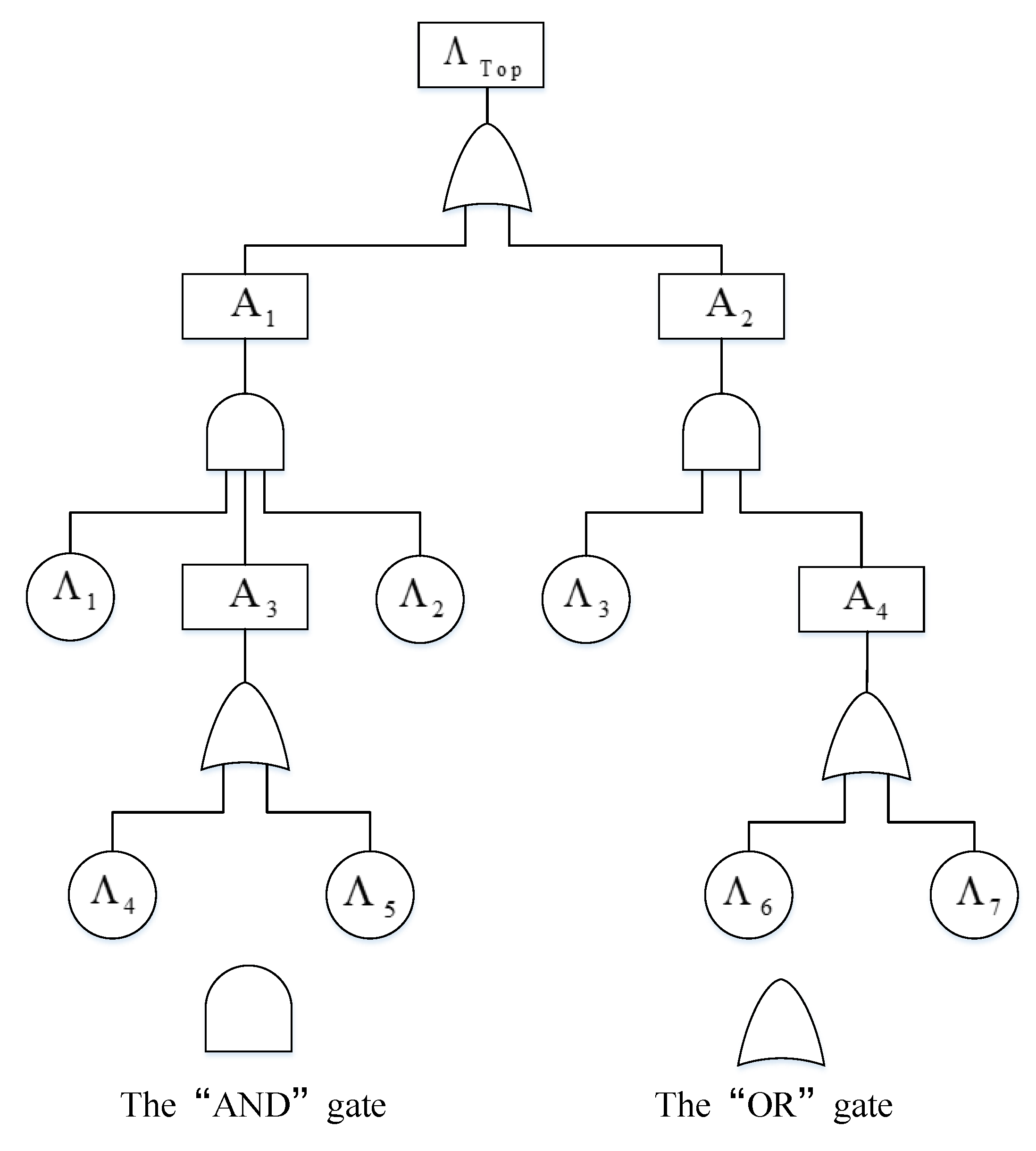
Example 1. 

The fault tree shown in Figure 1 describes the system risk. ${\mathsf{\Lambda }}_i$, $j=1,2,\dots ,7$ denote independent basic events, $A_k$, $k=1,2,3,4$ denote the intermediate events, and ${\mathsf{\Lambda }}_{Top}$ denotes the top event in the fault tree.

Table 1. The belief degrees of the occurrence of basic events.

Basic Events	${\mathbf{\Lambda }}_1$	${\mathbf{\Lambda }}_2$	${\mathbf{\Lambda }}_3$	${\mathbf{\Lambda }}_4$	${\mathbf{\Lambda }}_5$	${\mathbf{\Lambda }}_6$	${\mathbf{\Lambda }}_7$
Belief degree of occurrence	0.4	0.3	0.2	0.3	0.5	0.35	0.4

lists the belief degrees of the occurrence of the basic events.

As shown in Figure 1, the top event ${\mathsf{\Lambda }}_{Top}$ can be expressed as

$$\begin{array}{cc}\hfill {\mathsf{\Lambda }}_{Top}=& A_1\cup A_2\hfill \\ \hfill =& \left\{{\mathsf{\Lambda }}_1\cap A_3\cap {\mathsf{\Lambda }}_2\right\}\cup \left\{{\mathsf{\Lambda }}_3\cap A_4\right\}\hfill \\ \hfill =& \left\{{\mathsf{\Lambda }}_1\cap \left({\mathsf{\Lambda }}_4\cup {\mathsf{\Lambda }}_5\right)\cap {\mathsf{\Lambda }}_2\right\}\cup \left\{{\mathsf{\Lambda }}_3\cap \left({\mathsf{\Lambda }}_6\cup {\mathsf{\Lambda }}_7\right)\right\}.\hfill \end{array}$$

Then, the belief degree of occurrence of the top event ${\mathsf{\Lambda }}_{Top}$ can be determined, i.e., the risk of the top event ${\mathsf{\Lambda }}_{Top}$, namely,

$$\begin{array}{cc}\hfill \mathcal{M}\left\{{\mathsf{\Lambda }}_{Top}\right\}=& \mathcal{M}\left\{\left\{{\mathsf{\Lambda }}_1\cap \left({\mathsf{\Lambda }}_4\cup {\mathsf{\Lambda }}_5\right)\cap {\mathsf{\Lambda }}_2\right\}\cup \left\{{\mathsf{\Lambda }}_3\cap \left({\mathsf{\Lambda }}_6\cup {\mathsf{\Lambda }}_7\right)\right\}\right\}\hfill \\ \hfill =& \mathcal{M}\left\{{\mathsf{\Lambda }}_1\cap \left({\mathsf{\Lambda }}_4\cup {\mathsf{\Lambda }}_5\right)\cap {\mathsf{\Lambda }}_2\right\}\vee \mathcal{M}\left\{{\mathsf{\Lambda }}_3\cap \left({\mathsf{\Lambda }}_6\cup {\mathsf{\Lambda }}_7\right)\right\}\hfill \\ \hfill =& \left(\mathcal{M}\left\{{\mathsf{\Lambda }}_1\right\}\wedge \left(\mathcal{M}\left\{{\mathsf{\Lambda }}_4\right\}\vee \mathcal{M}\left\{{\mathsf{\Lambda }}_5\right\}\right)\wedge \mathcal{M}\left\{{\mathsf{\Lambda }}_2\right\}\right)\hfill \\ \hfill & \vee \left(\mathcal{M}\left\{{\mathsf{\Lambda }}_3\right\}\wedge \left(\mathcal{M}\left\{{\mathsf{\Lambda }}_6\right\}\vee \mathcal{M}\left\{{\mathsf{\Lambda }}_7\right\}\right)\right)\hfill \\ \hfill =& \left(0.4\wedge \left(0.3\vee 0.5\right)\wedge 0.3\right)\vee \left(0.2\wedge \left(0.35\vee 0.4\right)\right)\hfill \\ \hfill =& 0.3.\hfill \end{array}$$

If the belief degree is replaced by probability in Example 1, then the risk of the top event ${\mathsf{\Lambda }}_{Top}$ can be calculated with the probability method, namely,

$$\begin{array}{cc}\hfill P\left\{{\mathsf{\Lambda }}_{Top}\right\}=& P\left\{\left\{{\mathsf{\Lambda }}_1\cap \left({\mathsf{\Lambda }}_4\cup {\mathsf{\Lambda }}_5\right)\cap {\mathsf{\Lambda }}_2\right\}\cup \left\{{\mathsf{\Lambda }}_3\cap \left({\mathsf{\Lambda }}_6\cup {\mathsf{\Lambda }}_7\right)\right\}\right\}\hfill \\ \hfill =& \left(P\left\{{\mathsf{\Lambda }}_1\right\}·\left(P\left\{{\mathsf{\Lambda }}_4\right\}+P\left\{{\mathsf{\Lambda }}_5\right\}\right)·P\left\{{\mathsf{\Lambda }}_2\right\}\right)\hfill \\ \hfill & +\left(P\left\{{\mathsf{\Lambda }}_3\right\}·\left(P\left\{{\mathsf{\Lambda }}_6\right\}+P\left\{{\mathsf{\Lambda }}_7\right\}\right)\right)\hfill \\ \hfill =& \left(0.4·\left(0.3+0.5\right)·0.3\right)+\left(0.2·\left(0.35+0.4\right)\right)\hfill \\ \hfill =& 0.246.\hfill \end{array}$$

It can be seen that $P\left\{{\mathsf{\Lambda }}_{Top}\right\}$ and $\mathcal{M}\left\{{\mathsf{\Lambda }}_{Top}\right\}$ are different, which implies when the data are sufficient, traditional fault tree analysis is applied to evaluate the probability of the occurrence of the top event; when the data are insufficient, uncertain fault tree analysis is used to evaluate the belief degree of the occurrence of the top event.

By comparison of $\mathcal{M}\left\{{\mathsf{\Lambda }}_{Top}\right\}$ and $P\left\{{\mathsf{\Lambda }}_{Top}\right\}$ in Example 1, it can be seen that $\mathcal{M}\left\{{\mathsf{\Lambda }}_{Top}\right\}$ is larger than $P\left\{{\mathsf{\Lambda }}_{Top}\right\}$. However, this does not mean that $\mathcal{M}\left\{{\mathsf{\Lambda }}_{Top}\right\}$ is always larger than $P\left\{{\mathsf{\Lambda }}_{Top}\right\}$. For example, if $\mathcal{M}\left\{{\mathsf{\Lambda }}_2\right\}$ and $P\left\{{\mathsf{\Lambda }}_2\right\}$ change to $0.2$, then $\mathcal{M}\left\{{\mathsf{\Lambda }}_{Top}\right\}=0.2$ and $P\left\{{\mathsf{\Lambda }}_{Top}\right\}=0.214.$ Therefore, we cannot simply compare the values of $\mathcal{M}\left\{{\mathsf{\Lambda }}_{Top}\right\}$ and $P\left\{{\mathsf{\Lambda }}_{Top}\right\}$ without knowing the fault tree structure and the belief degrees and probabilities of the occurrence of all basic events.

3. General Optimization Models Based on Uncertain Fault Tree

In this section, an uncertain fault tree is used to evaluate system risk. Then, a single-objective optimization model and a multiobjective optimization model based on uncertain fault tree are separately established.

Consider an uncertain fault tree consisting of n independent basic events. Suppose that N ($N\le n$) basic events have a variety of maintenance techniques, and incomplete maintenance, denoted by ${\mathsf{\Lambda }}_i,i=1,2,\dots ,N$, is usually used. The maintenance cost $C_i$ of basic event ${\mathsf{\Lambda }}_i$ is related to its own risk; it can be expressed by

$$C_i=F_i\left(\mathcal{M}\left\{{\mathsf{\Lambda }}_i\right\}\right),i=1,2,\dots ,N,$$

(2)

where $F_i$ is called the risk–cost function. Usually, the risk–cost function is a monotonically decreasing function, that is, the lower the risk achieved through maintenance, the higher the maintenance cost to be invested. The total maintenance cost of the top event ${\mathsf{\Lambda }}_{Top}$ is

$$C_{Top}=\sum _{i=1}^N{C}_i=\sum _{i=1}^N{F}_i\left(\mathcal{M}\left\{{\mathsf{\Lambda }}_i\right\}\right).$$

(3)

3.1. Single-Objective Optimization Model

The aim of the single-objective optimization model is to determine the risk to be achieved after basic event maintenance when the total maintenance cost is minimized under the given system risk level. Decision variables are denoted by $\mathcal{M}\left\{{\mathsf{\Lambda }}_i\right\},i=1,2,\dots ,N$; the system risk, denoted by ${\mathcal{M}}_{Top}$, is the function of $\mathcal{M}\left\{{\mathsf{\Lambda }}_i\right\},i=1,2,\dots ,N$; and the total maintenance cost $C_{Top}$ is also a function of $\mathcal{M}\left\{{\mathsf{\Lambda }}_i\right\},i=1,2,\dots ,N$. Then, the single-objective optimization model can be expressed by the following mathematical programming

$$\left\{\begin{array}{c}Min{C}_{Top}\hfill \\ s.t.\hfill \\ {\mathcal{M}}_{Top}=\tau \hfill \\ {\mu }_i\le \mathcal{M}\left\{{\mathsf{\Lambda }}_i\right\}\le {\nu }_i,i=1,2,\dots ,N,\hfill \end{array}\right.$$

(4)

where ${\mu }_i$ and ${\nu }_i$ are the lower and upper bounds of decision variables $\mathcal{M}\left\{{\mathsf{\Lambda }}_i\right\},i=1,2,\dots ,N$, respectively. The range of $\tau$ is

$${\mathcal{M}}_{Top}({\mu }_1,{\mu }_2,\dots ,{\mu }_N)\le \tau \le {\mathcal{M}}_{Top}({\nu }_1,{\nu }_2,\dots ,{\nu }_N).$$

(5)

3.2. Multiobjective Optimization Model

The aim of the multiobjective optimization model is to determine the risk to be achieved after basic event maintenance when the total maintenance cost and the system risk are minimized at the same time. ${\mathcal{M}}_{Top}$ and $C_{Top}$ are the functions of decision variables $\mathcal{M}\left\{{\mathsf{\Lambda }}_i\right\},i=1,2,\dots ,N$. Then, the multiobjective optimization model can be expressed by the following mathematical programming

$$\left\{\begin{array}{c}Min{C}_{Top}\hfill \\ Min{\mathcal{M}}_{Top}\hfill \\ s.t.\hfill \\ {\mu }_i\le \mathcal{M}\left\{{\mathsf{\Lambda }}_i\right\}\le {\nu }_i,i=1,2,\dots ,N.\hfill \end{array}\right.$$

(6)

3.3. Solutions of Optimization Models

GA is a method to search the optimal solution by simulating natural evolution process. It is an effective and efficient algorithm to solve the single-objective optimization model. NSGA-II is used to solve the multiobjective optimization model since it can reduces the complexity of noninferior sorting genetic algorithm and has the advantages of fast running speed and good convergence of solution set. NSGA-II yields a non-dominated set of solutions known as the Pareto-optimal solutions. The steps of GA and NSGA-II are described in the Appendix A.

4. Optimization of Leakage Risk and Maintenance Cost for a Subsea Production System

The operation and maintenance data of subsea production systems are difficult to obtain due to the underwater environment, or the obtained data are often interpreted by experts. Therefore, evaluations of the leakage risk based on the traditional fault tree analysis method are limited. In this section, the leakage risk of the subsea production system is evaluated with uncertain fault tree analysis. Then, two optimization models of leakage risk and maintenance cost are established for subsea production systems. Finally, the optimization results are presented to show the optimal relationship between leakage risk and maintenance cost, and the risks of basic events to be achieved after maintenance are given.

4.1. Leakage Risk Assessment of Subsea Production System

Subsea production systems are the main lifeline of offshore oil and gas exploitation, which consist of Xmas trees, manifolds, jumper tubes, umbilical cables, pipelines, etc. The fault tree structure with subsea production system leakage as the top event was reported in Cheliyan and Bhattacharyya [32].

Table 2. Information of basic events.

BE	Description	BEs	Description
${\mathsf{\Lambda }}_1$	Overpressure in well	${\mathsf{\Lambda }}_{14}$	Defect in pipe manifold connector
${\mathsf{\Lambda }}_2$	Failure of control in well	${\mathsf{\Lambda }}_{15}$	Defect in pipe–PLET connector
${\mathsf{\Lambda }}_3$	Jumper puncture	${\mathsf{\Lambda }}_{16}$	Defect in pipe–PLEM connector
${\mathsf{\Lambda }}_4$	Jumper rupture	${\mathsf{\Lambda }}_{17}$	Failure of connector leakage control
${\mathsf{\Lambda }}_5$	Flowline puncture	${\mathsf{\Lambda }}_{18}$	Defect in X-tree
${\mathsf{\Lambda }}_6$	Flowline rupture	${\mathsf{\Lambda }}_{19}$	Failure of X-tree leakage control
${\mathsf{\Lambda }}_7$	Pipeline puncture	${\mathsf{\Lambda }}_{20}$	Defect in manifold
${\mathsf{\Lambda }}_8$	Pipeline rupture	${\mathsf{\Lambda }}_{21}$	Failure of manifold leakage control
${\mathsf{\Lambda }}_9$	Riser puncture	${\mathsf{\Lambda }}_{22}$	Defect in PLET
${\mathsf{\Lambda }}_{10}$	Riser rupture	${\mathsf{\Lambda }}_{23}$	Failure of PLET leakage control
${\mathsf{\Lambda }}_{11}$	Failure of leakage control of pipe	${\mathsf{\Lambda }}_{24}$	Defect in PLEM
${\mathsf{\Lambda }}_{12}$	Defect in X-tree wellhead connector	${\mathsf{\Lambda }}_{25}$	Failure of PLEM leakage control
${\mathsf{\Lambda }}_{13}$	Defect in pipe connector	${\mathsf{\Lambda }}_{26}$	Third-party damage

and

Table 3. Information of the top and intermediate events.

Event	Description	Gates	Connected Event
${\mathsf{\Lambda }}_{Top}$	Oil and gas leakage	OR	${\mathsf{\Lambda }}_{26},{\mathsf{\Lambda }}_{38},{\mathsf{\Lambda }}_{39},{\mathsf{\Lambda }}_{40}$
${\mathsf{\Lambda }}_{40}$	Leakage in key facilities	OR	${\mathsf{\Lambda }}_{32},{\mathsf{\Lambda }}_{33},{\mathsf{\Lambda }}_{34},{\mathsf{\Lambda }}_{35},{\mathsf{\Lambda }}_{37}$
${\mathsf{\Lambda }}_{39}$	Leakage in pipe	AND	${\mathsf{\Lambda }}_{11},{\mathsf{\Lambda }}_{36}$
${\mathsf{\Lambda }}_{38}$	Leakage in gas or oil well	AND	${\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2$
${\mathsf{\Lambda }}_{37}$	Connector leakage	AND	${\mathsf{\Lambda }}_{17},{\mathsf{\Lambda }}_{31}$
${\mathsf{\Lambda }}_{36}$	Defect in pipe	OR	${\mathsf{\Lambda }}_{27},{\mathsf{\Lambda }}_{28},{\mathsf{\Lambda }}_{29},{\mathsf{\Lambda }}_{30}$
${\mathsf{\Lambda }}_{35}$	PLEM leakage	AND	${\mathsf{\Lambda }}_{24},{\mathsf{\Lambda }}_{25}$
${\mathsf{\Lambda }}_{34}$	PLET leakage	AND	${\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{23}$
${\mathsf{\Lambda }}_{33}$	Manifold leakage	AND	${\mathsf{\Lambda }}_{20},{\mathsf{\Lambda }}_{21}$
${\mathsf{\Lambda }}_{32}$	X-tree leakage	AND	${\mathsf{\Lambda }}_{18},{\mathsf{\Lambda }}_{19}$
${\mathsf{\Lambda }}_{31}$	Defect in connector	OR	${\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{13},{\mathsf{\Lambda }}_{14},{\mathsf{\Lambda }}_{15},{\mathsf{\Lambda }}_{16}$
${\mathsf{\Lambda }}_{30}$	Defect in riser	OR	${\mathsf{\Lambda }}_9,{\mathsf{\Lambda }}_{10}$
${\mathsf{\Lambda }}_{29}$	Defect in pipeline	OR	${\mathsf{\Lambda }}_7,{\mathsf{\Lambda }}_8$
${\mathsf{\Lambda }}_{28}$	Defect in flowline	OR	${\mathsf{\Lambda }}_5,{\mathsf{\Lambda }}_6$
${\mathsf{\Lambda }}_{27}$	Defect in jumper	OR	${\mathsf{\Lambda }}_3,{\mathsf{\Lambda }}_4$

briefly describe the fault tree structure. All basic events (BEs) are described in Table 2. The description of the intermediate events and top event and their connectivity with events are shown in Table 3.

Based on the uncertain fault tree analysis, the leakage risk of the subsea production system (denoted by ${\mathcal{M}}_{Top}$) is

$$\begin{array}{cc}{\mathcal{M}}_{Top}\hfill & {\displaystyle =\mathcal{M}\left\{{\mathsf{\Lambda }}_{26}\right\}\vee \mathcal{M}\left\{{\mathsf{\Lambda }}_{38}\right\}\vee \mathcal{M}\left\{{\mathsf{\Lambda }}_{39}\right\}\vee \mathcal{M}\left\{{\mathsf{\Lambda }}_{40}\right\}}\hfill \\ \hfill & {\displaystyle =\mathcal{M}\left\{{\mathsf{\Lambda }}_{26}\right\}\vee \left(\mathcal{M}\left\{{\mathsf{\Lambda }}_1\right\}\wedge \mathcal{M}\left\{{\mathsf{\Lambda }}_2\right\}\right)\vee \left(\mathcal{M}\left\{{\mathsf{\Lambda }}_{11}\right\}\wedge \mathcal{M}\left\{{\mathsf{\Lambda }}_{36}\right\}\right)}\hfill \\ \hfill & {\displaystyle \vee \left(\mathcal{M}\left\{{\mathsf{\Lambda }}_{32}\right\}\vee \mathcal{M}\left\{{\mathsf{\Lambda }}_{33}\right\}\vee \mathcal{M}\left\{{\mathsf{\Lambda }}_{34}\right\}\vee \mathcal{M}\left\{{\mathsf{\Lambda }}_{35}\right\}\vee \mathcal{M}\left\{{\mathsf{\Lambda }}_{37}\right\}\right)}\hfill \\ \hfill & {\displaystyle =\left(\mathcal{M}\left\{{\mathsf{\Lambda }}_1\right\}\wedge \mathcal{M}\left\{{\mathsf{\Lambda }}_2\right\}\right)\vee \mathcal{M}\left\{{\mathsf{\Lambda }}_{26}\right\}}\hfill \\ \hfill & {\displaystyle \vee \left(\mathcal{M}\left\{{\mathsf{\Lambda }}_{11}\right\}\wedge \left(\mathcal{M}\left\{{\mathsf{\Lambda }}_{27}\right\}\vee \mathcal{M}\left\{{\mathsf{\Lambda }}_{28}\right\}\vee \mathcal{M}\left\{{\mathsf{\Lambda }}_{29}\right\}\vee \mathcal{M}\left\{{\mathsf{\Lambda }}_{30}\right\}\right)\right)}\hfill \\ \hfill & {\displaystyle \vee \left(\mathcal{M}\left\{{\mathsf{\Lambda }}_{18}\right\}\wedge \mathcal{M}\left\{{\mathsf{\Lambda }}_{19}\right\}\right)\vee \left(\mathcal{M}\left\{{\mathsf{\Lambda }}_{20}\right\}\wedge \mathcal{M}\left\{{\mathsf{\Lambda }}_{21}\right\}\right)\vee \left(\mathcal{M}\left\{{\mathsf{\Lambda }}_{22}\right\}\wedge \mathcal{M}\left\{{\mathsf{\Lambda }}_{23}\right\}\right)}\hfill \\ \hfill & {\displaystyle \vee \left(\mathcal{M}\left\{{\mathsf{\Lambda }}_{24}\right\}\wedge \mathcal{M}\left\{{\mathsf{\Lambda }}_{25}\right\}\right)\vee \left(\mathcal{M}\left\{{\mathsf{\Lambda }}_{17}\right\}\wedge \mathcal{M}\left\{{\mathsf{\Lambda }}_{31}\right\}\right)}\hfill \\ \hfill & {\displaystyle =\left(\mathcal{M}\left\{{\mathsf{\Lambda }}_1\right\}\wedge \mathcal{M}\left\{{\mathsf{\Lambda }}_2\right\}\right)\vee \left(\mathcal{M}\left\{{\mathsf{\Lambda }}_{18}\right\}\wedge \mathcal{M}\left\{{\mathsf{\Lambda }}_{19}\right\}\right)}\hfill \\ \hfill & {\displaystyle \vee \left(\mathcal{M}\left\{{\mathsf{\Lambda }}_{11}\right\}\wedge \left(\left(\mathcal{M}\left\{{\mathsf{\Lambda }}_3\right\}\vee \mathcal{M}\left\{{\mathsf{\Lambda }}_4\right\}\right)\vee \left(\mathcal{M}\left\{{\mathsf{\Lambda }}_5\right\}\vee \mathcal{M}\left\{{\mathsf{\Lambda }}_6\right\}\right)\right.\right.}\hfill \\ \hfill & {\displaystyle \left.\left.\vee \left(\mathcal{M}\left\{{\mathsf{\Lambda }}_7\right\}\vee \mathcal{M}\left\{{\mathsf{\Lambda }}_8\right\}\right)\vee \left(\mathcal{M}\left\{{\mathsf{\Lambda }}_9\right\}\vee \mathcal{M}\left\{{\mathsf{\Lambda }}_{10}\right\}\right)\right)\right)}\hfill \\ \hfill & {\displaystyle \vee \left(\mathcal{M}\left\{{\mathsf{\Lambda }}_{20}\right\}\wedge \mathcal{M}\left\{{\mathsf{\Lambda }}_{21}\right\}\right)\vee \left(\mathcal{M}\left\{{\mathsf{\Lambda }}_{22}\right\}\wedge \mathcal{M}\left\{{\mathsf{\Lambda }}_{23}\right\}\right)}\hfill \\ \hfill & {\displaystyle \vee \left(\mathcal{M}\left\{{\mathsf{\Lambda }}_{24}\right\}\wedge \mathcal{M}\left\{{\mathsf{\Lambda }}_{25}\right\}\right)\vee \mathcal{M}\left\{{\mathsf{\Lambda }}_{26}\right\}}\hfill \\ \hfill & {\displaystyle \vee \left(\mathcal{M}\left\{{\mathsf{\Lambda }}_{17}\right\}\wedge \left(\mathcal{M}\left\{{\mathsf{\Lambda }}_{12}\right\}\vee \mathcal{M}\left\{{\mathsf{\Lambda }}_{13}\right\}\vee \mathcal{M}\left\{{\mathsf{\Lambda }}_{14}\right\}\vee \mathcal{M}\left\{{\mathsf{\Lambda }}_{15}\right\}\vee \mathcal{M}\left\{{\mathsf{\Lambda }}_{16}\right\}\right)\right).}\hfill \end{array}$$

(7)

4.2. Single-Objective Optimization Model of Leakage Risk and Maintenance Cost for Subsea Production System

The fault tree of the subsea production system contains 26 basic events, in which 25 basic events require a variety of maintenance techniques. For all risk–cost functions, we used the data in [30]. Each risk–cost function is assumed to be two straight lines of different slopes and can be determined by three points $({\mathcal{M}}^1\left\{{\mathsf{\Lambda }}_i\right\},C_i^1)$, $({\mathcal{M}}^2\left\{{\mathsf{\Lambda }}_i\right\},C_i^2)$, $({\mathcal{M}}^3\left\{{\mathsf{\Lambda }}_i\right\},C_i^3)$, $i=1,2,\dots ,25$, in which

$${\mathcal{M}}^1\left\{{\mathsf{\Lambda }}_i\right\}=\frac{{\mathcal{M}}^2\left\{{\mathsf{\Lambda }}_i\right\}}{2},{\mathcal{M}}^3\left\{{\mathsf{\Lambda }}_i\right\}=2{\mathcal{M}}^2\left\{{\mathsf{\Lambda }}_i\right\},C_i^1=3C_i^2,C_i^3=\frac{C_i^2}{2}.$$

So, $({\mathcal{M}}^2\left\{{\mathsf{\Lambda }}_i\right\},C_i^2),i=1,2,\dots ,25$ need to be defined, which are shown in

Table 4. Information of risk–cost functions of basic events.

BEs	${\mathsf{\Lambda }}_1$	${\mathsf{\Lambda }}_2$	${\mathsf{\Lambda }}_3$	${\mathsf{\Lambda }}_4$	${\mathsf{\Lambda }}_5$
$({\mathcal{M}}^2\left\{{\mathsf{\Lambda }}_i\right\},C_i^2)$	(0.043, 2)	(0.0332, 2)	(0.0095, 0.15)	(0.0094, 0.15)	(0.007, 2.5)
BEs	${\mathsf{\Lambda }}_6$	${\mathsf{\Lambda }}_7$	${\mathsf{\Lambda }}_8$	${\mathsf{\Lambda }}_9$	${\mathsf{\Lambda }}_{10}$
$({\mathcal{M}}^2\left\{{\mathsf{\Lambda }}_i\right\},C_i^2)$	(0.095, 2.5)	(0.0078, 6)	(0.0103, 6)	(0.023, 3.5)	(0.0288, 3.5)
BEs	${\mathsf{\Lambda }}_{11}$	${\mathsf{\Lambda }}_{12}$	${\mathsf{\Lambda }}_{13}$	${\mathsf{\Lambda }}_{14}$	${\mathsf{\Lambda }}_{15}$
$({\mathcal{M}}^2\left\{{\mathsf{\Lambda }}_i\right\},C_i^2)$	(0.0538, 1)	(0.0195, 0.75)	(0.0205, 0.75)	(0.0193, 1.5)	(0.0175, 2)
BEs	${\mathsf{\Lambda }}_{16}$	${\mathsf{\Lambda }}_{17}$	${\mathsf{\Lambda }}_{18}$	${\mathsf{\Lambda }}_{19}$	${\mathsf{\Lambda }}_{20}$
$({\mathcal{M}}^2\left\{{\mathsf{\Lambda }}_i\right\},C_i^2)$	(0.0183, 1)	(0.0425, 0.25)	(0.0199, 2)	(0.032, 2)	(0.0204,6)
BEs	${\mathsf{\Lambda }}_{21}$	${\mathsf{\Lambda }}_{22}$	${\mathsf{\Lambda }}_{23}$	${\mathsf{\Lambda }}_{24}$	${\mathsf{\Lambda }}_{25}$
$({\mathcal{M}}^2\left\{{\mathsf{\Lambda }}_i\right\},C_i^2)$	(0.0223, 1.5)	(0.0189, 2)	(0.0214, 0.75)	(0.0189, 2)	(0.0214, 1.5)

. The unit cost of $C_i^2,i=1,2,\dots ,25$ is in million USD. The risk tolerance of basic events is 0.2.

From the single-objective optimization model described in (9), the optimization model of leakage risk and maintenance cost for the subsea production system can be expressed as

$$\left\{\begin{array}{c}Min{C}_{Top}\hfill \\ s.t.\hfill \\ {\mathcal{M}}_{Top}=\tau \hfill \\ 0\le \mathcal{M}\left\{{\mathsf{\Lambda }}_i\right\}\le 0.2,i=1,2,\dots ,25,\hfill \end{array}\right.$$

(8)

In which ${\mathcal{M}}_{Top}$ can be obtained from Formula (7) and

$$C_{Top}=\sum _{i=1}^{25}{C}_i=\sum _{i=1}^{25}{F}_i\left(\mathcal{M}\left\{{\mathsf{\Lambda }}_i\right\}\right).$$

(9)

Then, we solve the optimal risk level of all basic events after maintenance (denoted by ${\mathcal{M}}^{\ast }\left\{{\mathsf{\Lambda }}_i\right\}$, $i=1,2,\dots ,25$), so as to minimize the total maintenance cost under the allowable leakage risk of the subsea production system.

4.3. Multiobjective Optimization Model of Leakage Risk and Maintenance Cost for Subsea Production System

From the multiobjective optimization model described in (10), the optimization model of leakage risk and maintenance cost for the subsea production system can be expressed by

$$\left\{\begin{array}{c}Min{C}_{Top}\hfill \\ Min{\mathcal{M}}_{Top}\hfill \\ s.t.\hfill \\ 0\le \mathcal{M}\left\{{\mathsf{\Lambda }}_i\right\}\le 0.2,i=1,2,\dots ,25,\hfill \end{array}\right.$$

(10)

where ${\mathcal{M}}_{Top}$ and $C_{Top}$ can be calculated by (7) and (9). Then, we solve the optimal risk level of all basic events after maintenance (denoted by ${\mathcal{M}}^{\ast }\left\{{\mathsf{\Lambda }}_i\right\}$, $i=1,2,\dots ,25$), so as to minimize the total maintenance cost and leakage risk at the same time.

4.4. Results and Discussion

The single-objective optimization Model (8) can be solved by the GA described in Appendix A.1. The optimization solutions are obtained by running the GA multiple times because Min $C_{Top}$ converges with increasing generations, each time with a prescribed value of ${\mathcal{M}}_{Top}$. The key parameters of the GA were assigned as follows: the population size is 100, the crossover probability is 0.8, and the mutation probability is 0.04. As shown in Figure 2, if ${\mathcal{M}}_{Top}$ is assigned as 0.03, Min $C_{Top}$ converges when the number of generations reaches 130, and the total maintenance cost is USD 33.4456. The optimal risks of the basic events are presented in

Table 5. The optimized risk of basic events after maintenance.

${\mathcal{M}}^{\ast }\left\{{\mathsf{\Lambda }}_1\right\}$	${\mathcal{M}}^{\ast }\left\{{\mathsf{\Lambda }}_2\right\}$	${\mathcal{M}}^{\ast }\left\{{\mathsf{\Lambda }}_3\right\}$	${\mathcal{M}}^{\ast }\left\{{\mathsf{\Lambda }}_4\right\}$	${\mathcal{M}}^{\ast }\left\{{\mathsf{\Lambda }}_5\right\}$
0.086	0.029985	0.0019	0.0188	0.013999
${\mathcal{M}}^{\ast }\left\{{\mathsf{\Lambda }}_6\right\}$	${\mathcal{M}}^{\ast }\left\{{\mathsf{\Lambda }}_7\right\}$	${\mathcal{M}}^{\ast }\left\{{\mathsf{\Lambda }}_8\right\}$	${\mathcal{M}}^{\ast }\left\{{\mathsf{\Lambda }}_9\right\}$	${\mathcal{M}}^{\ast }\left\{{\mathsf{\Lambda }}_{10}\right\}$
0.019	0.0156	0.020599	0.029970	0.02999
${\mathcal{M}}^{\ast }\left\{{\mathsf{\Lambda }}_{11}\right\}$	${\mathcal{M}}^{\ast }\left\{{\mathsf{\Lambda }}_{12}\right\}$	${\mathcal{M}}^{\ast }\left\{{\mathsf{\Lambda }}_{13}\right\}$	${\mathcal{M}}^{\ast }\left\{{\mathsf{\Lambda }}_{14}\right\}$	${\mathcal{M}}^{\ast }\left\{{\mathsf{\Lambda }}_{15}\right\}$
0.10759	0.039	0.041	0.0386	0.034999
${\mathcal{M}}^{\ast }\left\{{\mathsf{\Lambda }}_{16}\right\}$	${\mathcal{M}}^{\ast }\left\{{\mathsf{\Lambda }}_{17}\right\}$	${\mathcal{M}}^{\ast }\left\{{\mathsf{\Lambda }}_{18}\right\}$	${\mathcal{M}}^{\ast }\left\{{\mathsf{\Lambda }}_{19}\right\}$	${\mathcal{M}}^{\ast }\left\{{\mathsf{\Lambda }}_{20}\right\}$
0.0366	0.029850	0.02995	0.064	0.0408
${\mathcal{M}}^{\ast }\left\{{\mathsf{\Lambda }}_{21}\right\}$	${\mathcal{M}}^{\ast }\left\{{\mathsf{\Lambda }}_{22}\right\}$	${\mathcal{M}}^{\ast }\left\{{\mathsf{\Lambda }}_{23}\right\}$	${\mathcal{M}}^{\ast }\left\{{\mathsf{\Lambda }}_{24}\right\}$	${\mathcal{M}}^{\ast }\left\{{\mathsf{\Lambda }}_{25}\right\}$
0.02999	0.0378	0.02998	0.0378	0.02999

. So, the number of generations was specified as 300 to ensure convergence. The optimization results, i.e., the relationship between ${\mathcal{M}}_{Top}$ and Min $C_{Top}$, are presented in

Table 6. The solution of the singe-objective optimization model.

${\mathcal{M}}_{\mathit{T}\mathit{o}\mathit{p}}$	0.0190	0.0200	0.0250	0.0300	0.0350
Min $C_{Top}$	53.3279	51.0307	40.6930	33.4456	30.7314
${\mathcal{M}}_{Top}$	0.0400	0.0450	0.0500	0.0550	0.0600
Min $C_{Top}$	29.1465	28.4458	27.9496	27.5289	26.8427

and Figure 3.

The multiobjective optimization Model (10) can be solved by the NSGA-II described in Appendix A.2. The key parameters of the NSGA-II were assigned as follows: the population size is 100, the crossover probability is 0.8, and the mutation probability is 0.04. Figure 4 shows a comparison between the Pareto front and the solutions of the initial population, 50th-generation population, 80th-generation population, and 180th-generation population. The values of $C_{Top}$ and ${\mathcal{M}}_{Top}$ almost converge when the number of generations reaches 180. The converge maximum and minimum values of $C_{Top}$ and ${\mathcal{M}}_{Top}$ are used to construct the ranges of the Pareto front.

As shown in Figure 4 and Figure 5, the maximum and minimum values of $C_{Top}$ and ${\mathcal{M}}_{Top}$ converge when the number of generations reaches 300. So, the number of generations was specified as 300 to ensure the Pareto front converged.

Table 7. The Pareto optimal solutions on the Pareto front.

No.	${\mathcal{M}}_{\mathit{Top}}$	${\mathit{C}}_{\mathit{Top}}$	No.	${\mathcal{M}}_{\mathit{Top}}$	${\mathit{C}}_{\mathit{Top}}$
1	0.0612638248	27.7478222	49	0.0310619046	34.0771521
2	0.0572564195	27.981213	50	0.0308524248	34.2760071
3	0.0567421952	28.021177	51	0.0303672445	34.278854
4	0.0564184552	28.0770276	52	0.0302840162	34.3660938
5	0.051710345	28.131183	53	0.030074754	34.5212012
6	0.0502892177	28.1920152	54	0.0299697184	34.6846129
7	0.0500242664	28.3133204	55	0.0299152533	35.037695
8	0.0482454929	28.3294124	56	0.0293061756	35.0816926
9	0.0482437703	28.5376517	57	0.0288337629	35.2052424
10	0.0479210354	28.6258182	58	0.0287993911	35.5243215
11	0.0447263397	28.7626312	59	0.0287770222	35.7700708
12	0.0434444279	28.9295184	60	0.0287535734	35.9526883
13	0.0429674306	29.0469512	61	0.0284638849	35.9577624
14	0.042370396	29.2535414	62	0.028078938	36.1577861
15	0.0423279743	29.269485	63	0.0277844038	36.1922948
16	0.0407881686	29.4583618	64	0.0277638228	36.3396034
17	0.0407879569	29.5225774	65	0.0276065402	36.4926474
18	0.0400557271	29.7408744	66	0.027548522	36.7284912
19	0.0398701558	29.9324046	67	0.0273572349	36.8581749
20	0.039714352	30.0555856	68	0.0273386922	36.9791893
21	0.0389417761	30.1112929	69	0.0268895798	37.1414137
22	0.0388453569	30.2700468	70	0.026788262	37.3833141
23	0.0386	30.4555862	71	0.0267640195	37.4583168
24	0.0377473361	30.5280521	72	0.0264837598	37.7025692
25	0.0375137475	30.5707205	73	0.0261634217	37.9739896
26	0.0368736655	30.7223616	74	0.0261046702	38.0523796
27	0.0367790343	30.8394166	75	0.0260608304	38.2207902
28	0.0367010545	31.0388581	76	0.0256734198	38.3436548
29	0.0364044443	31.1345122	77	0.0255414577	38.4349168
30	0.0363891864	31.3961569	78	0.0253661598	38.5428964
31	0.0360283388	31.4052595	79	0.0253507159	38.7729405
32	0.0358800828	31.4852581	80	0.0252378367	38.9022766
33	0.0358238913	31.644148	81	0.0251321018	39.1191081
34	0.0353863681	31.8501649	82	0.0247701335	39.1363357
35	0.0353751191	31.8641366	83	0.0247283539	39.3371158
36	0.0350310536	32.1544939	84	0.0244106642	39.575638
37	0.0349184312	32.3140202	85	0.0242506241	39.7369331
38	0.0343000317	32.5272719	86	0.0241255785	40.1756648
39	0.0342013048	32.6522411	87	0.0238315582	40.3140573
40	0.0340378531	32.7191019	88	0.0237934558	40.476925
41	0.0333494947	32.8159548	89	0.0237100284	40.5409006
42	0.0328617016	32.9674031	90	0.0234442516	40.6835945
43	0.0326773989	33.3421619	91	0.0233346572	40.6969574
44	0.0321136787	33.4693596	92	0.0232434981	41.1975037
45	0.0320822532	33.657781	93	0.0228107907	41.318251
46	0.0315062067	33.7166985	94	0.0227432198	41.4199314
47	0.0314511688	33.75349	95	0.0226151187	41.7470685
48	0.0310652585	33.912054	96	0.0226	41.7627859

shows the Pareto optimal solutions on the Pareto front. It is up to the decision maker to adopt a Pareto optimal solution that lies on this Pareto front.

The optimization results provide the theoretical basis for practitioners to guarantee the safety of subsea production systems when they do not have sufficient data, which can help practitioners determine the preliminary funds need required in consideration of the system risk and give the maintenance degree of basic events.

5. Conclusions

It is difficult to obtain operation and maintenance data of subsea production systems, and the obtained data are often interpreted by experts. Therefore, evaluations of leakage risk based on the traditional fault tree analysis method are limited. Although the fuzzy fault tree is also used to evaluate system risk under incomplete information, it often produces conflicting evaluation results because the possibility measure does not have a duality property. In this study, the belief degrees of occurrence of basic events were measured with an uncertain measure. Then, the leakage risk of a subsea production system was evaluated with uncertain fault tree analysis. Furthermore, optimization models were established to optimize the leakage risk and maintenance cost of a subsea production system. The specific contributions of this study are as follows:

(1)

The belief degrees of the occurrence of basic events evaluated by experts are measured with an uncertain measure. A risk assessment method for complex systems with insufficient data was proposed based on uncertain fault tree analysis.

(2)

Two general optimization models were established for complex systems with insufficient data, in which the system risk is evaluated by an uncertain fault tree. GA and NSGA-II were applied to solve the two optimization models, separately.

(3)

The leakage risk of the subsea production system was evaluated with the proposed risk assessment method. Based on the findings, two optimization models were proposed to optimize the leakage risk and maintenance cost of a subsea production system, and the optimization results were discussed.

In future research, the proposed risk assessment method and optimization models will be used in the risk assessment and optimization problems for other complex systems with insufficient data.