Mathematical Modeling of the Tumor–Immune System with Time Delay and Diffusion
Abstract
:1. Introduction
2. Model Formulation
3. Qualitative Analysis of the Model
3.1. Equilibria
- Free equilibrium (i.e., the absence of cancer cells and immune cells), .
- The axial equilibrium (i.e., the cancer cells exist),
- The interior equilibrium (i.e., the coexistence of cancer cells and immune cells),
3.2. Stability and Bifurcation Analysis
3.2.1. Stability of
3.2.2. Stability of
3.2.3. Stability and Bifurcation Analysis of the Interior Equilibrium
- If , equilibrium is unstable.
- If and , equilibrium is locally asymptotically stable.
- If , , and then the equilibrium is locally asymptotically stable.
- If , , and then the equilibrium is unstable.
- Has no positive roots if .
- Has one unique positive root, , if holds.
- Has two positive roots, , if holds.
- If is satisfied, then is locally asymptotically stable for all .
- If is satisfied, then is locally asymptotically stable for and unstable for and the system undergoes a Hopf bifurcation at and .
- If is satisfied, then there exists such that:
- (a)
- is locally asymptotically stable if
- (b)
- is unstable if .
- (c)
- System (1) undergoes a Hopf bifurcation at when , and .
4. Normal Form of Hopf Bifurcation
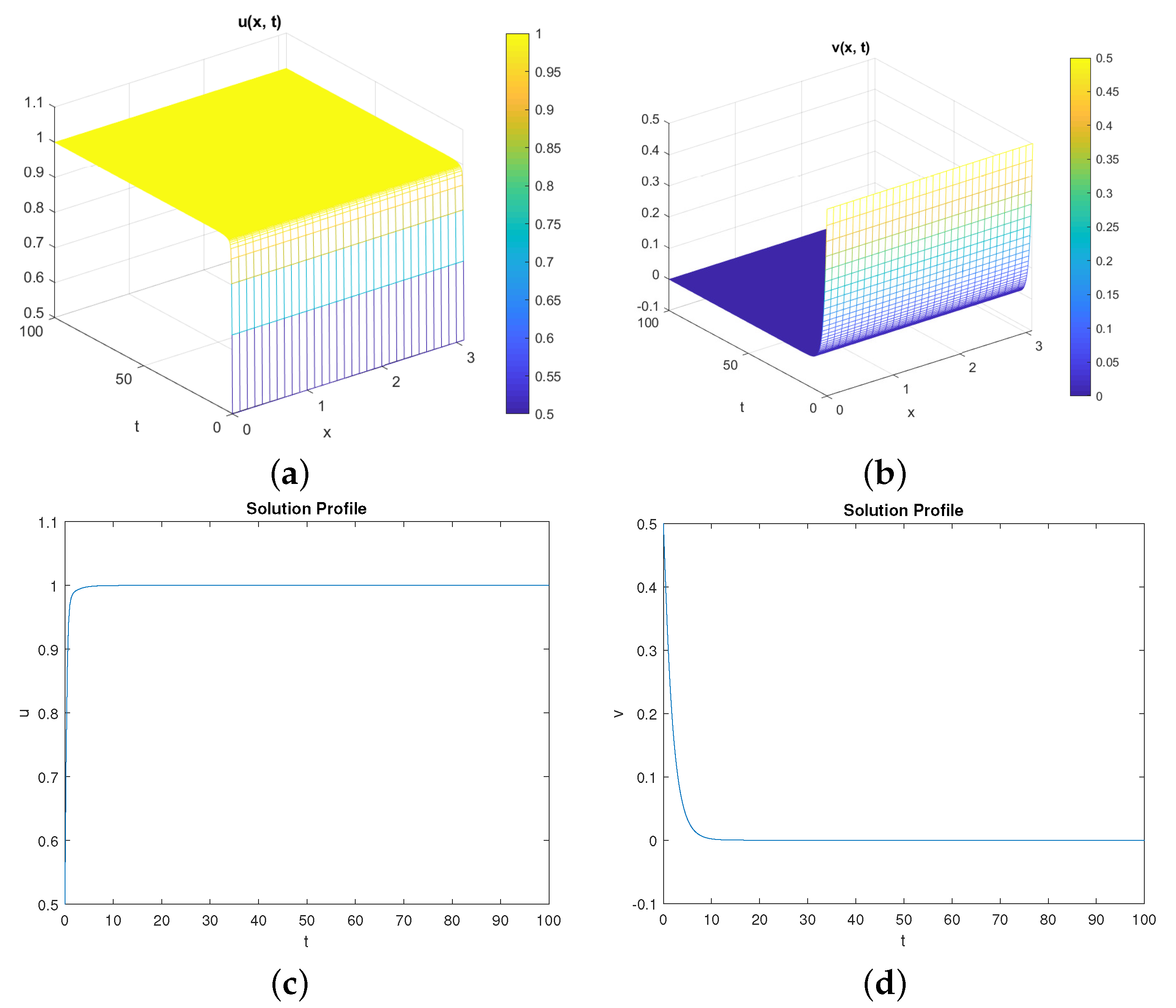
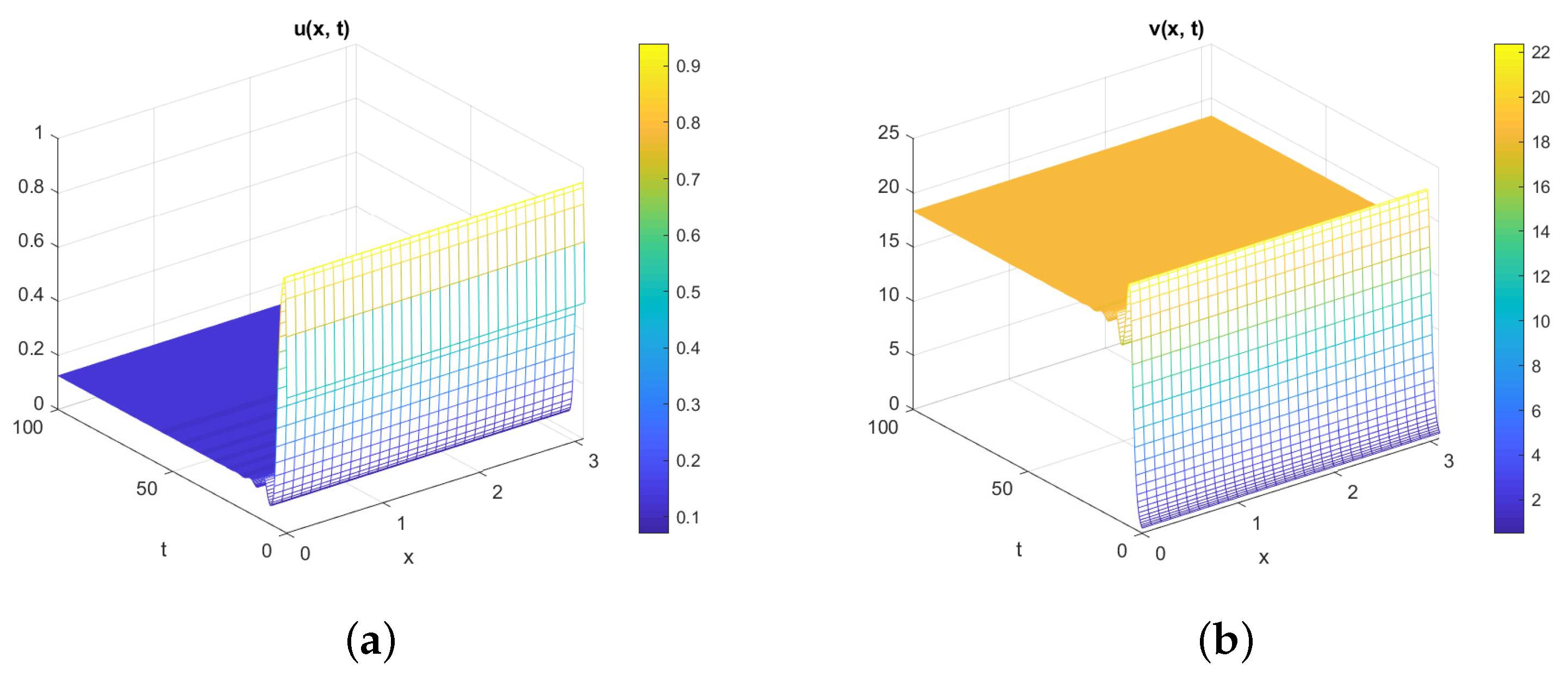
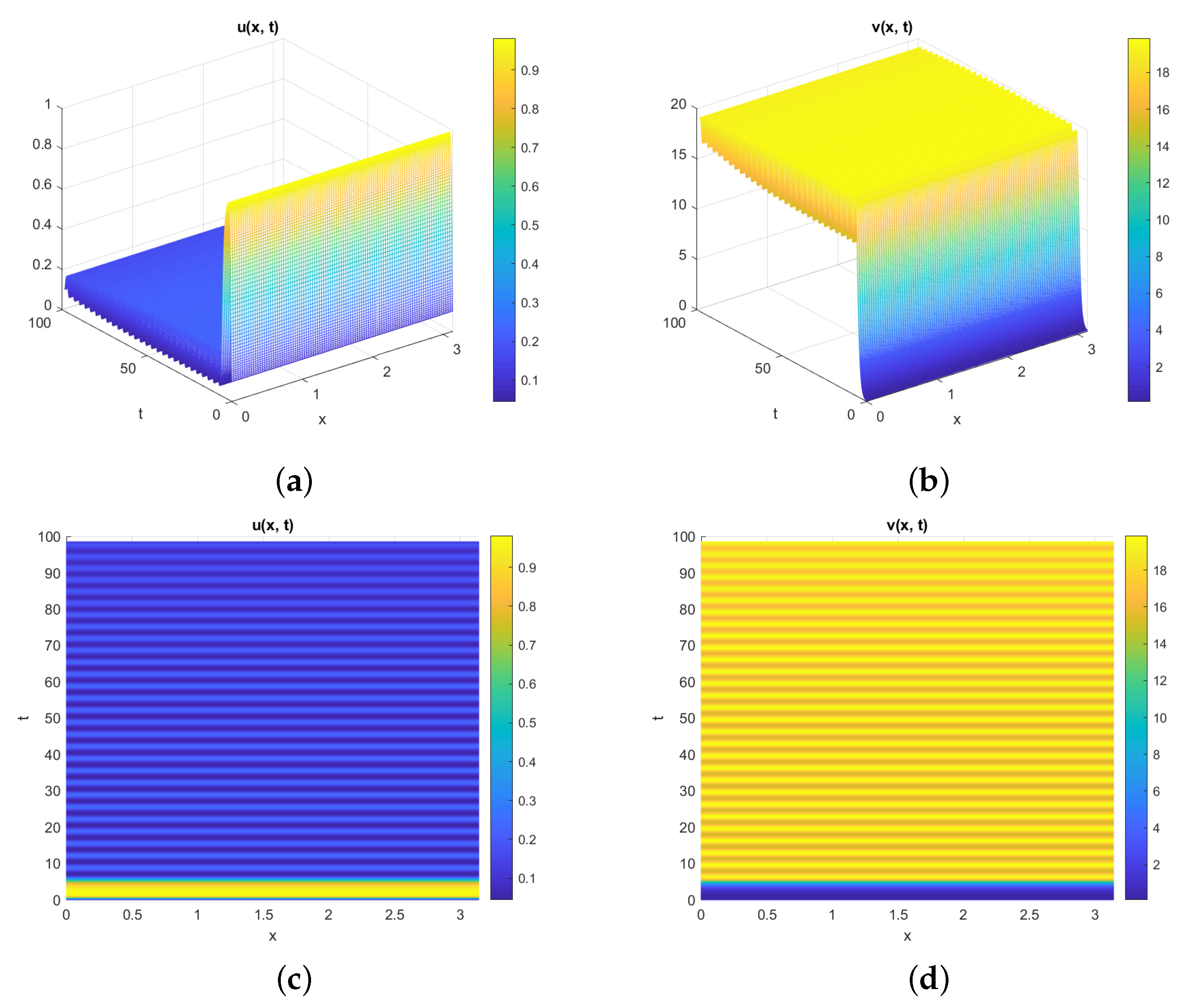
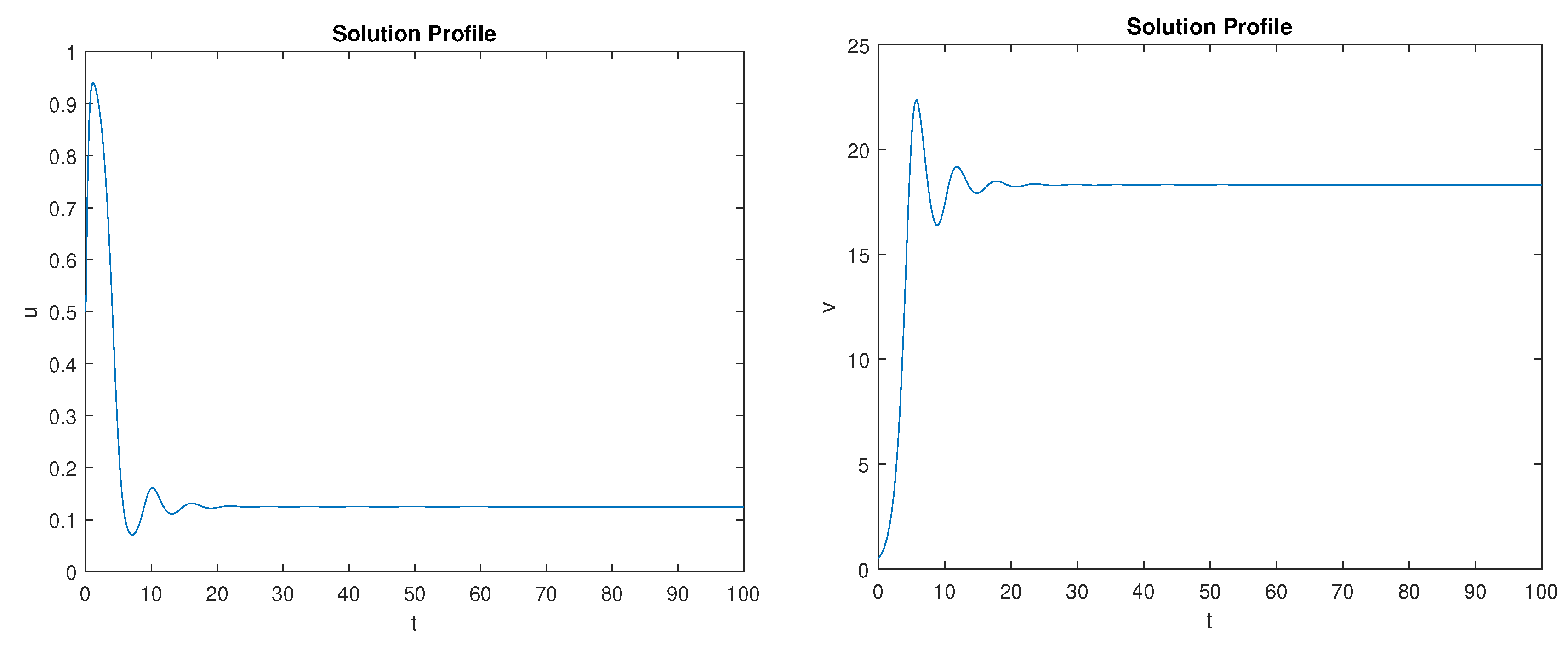
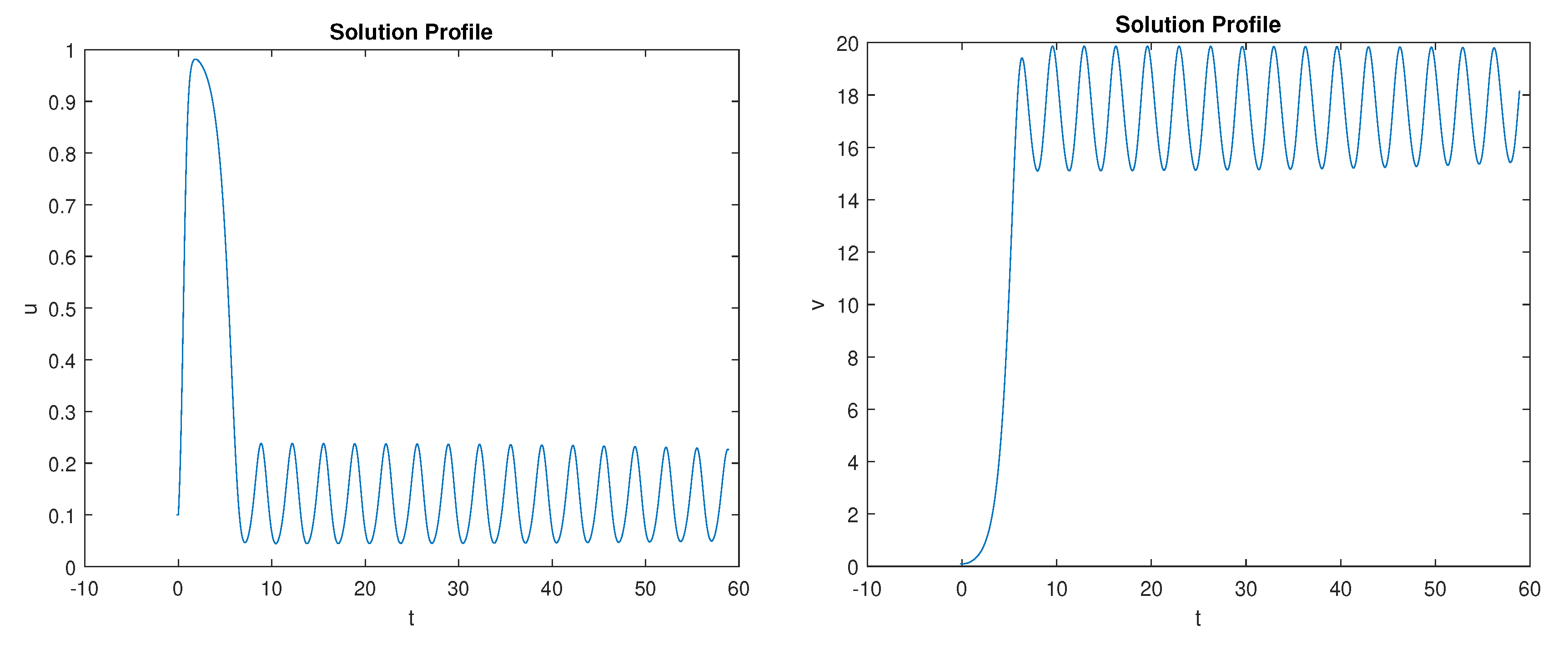
5. Numerical Simulations
Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ODEs | Ordinary differential equations |
| DDEs | Delay differential equations |
| PDEs | Partial differential equations |
References
- Eckert, A.W.; Wickenhauser, C.; Salins, P.C.; Kappler, M.; Bukur, J.; Seliger, B. Clinical relevance of the tumor microenvironment and immune escape of oral squamous cell carcinoma. J. Transl. Med. 2016, 14, 85. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.; Cheng, Q.; Hou, T.; Han, M.; Smbatyan, G.; Lang, J.E.; Epstein, A.L.; Lenz, H.J.; Zhang, Y. Genetically Engineered Cell-Derived Nanoparticles for Targeted Breast Cancer Immunotherapy. Mol. Ther. 2020, 28, 536–547. [Google Scholar] [CrossRef] [PubMed]
- Bidmon, N.; Kind, S.; Welters, M.; Joseph-Pietras, D.; Laske, K.; Maurer, D.; Hadrup, S.R.; Schreibelt, G.; Rae, R.; Sahin, U. Development of an RNA-based kit for easy generation of TCR-engineered lymphocytes to control T-cell assay performance. J. Immunol. Methods 2018, 458, 74–82. [Google Scholar] [CrossRef] [PubMed]
- Berzofsky, J.A.; Terabe, M.; Oh, S.; Belyakov, I.M.; Ahlers, J.D.; Janik, J.E.; Morris, J.C. Progress on new vaccine strategies for the immunotherapy and prevention of cancer. J. Clin. Investig. 2004, 113, 1515–1525. [Google Scholar] [CrossRef]
- Frhlich, F.; Loos, C.; Hasenauer, J. Scalable Inference of Ordinary Differential Equation Models of Biochemical Processes. In Gene Regulatory Networks: Methods and Protocols; Humana Press: New York, NY, USA, 2019. [Google Scholar]
- Xla, D.; Dwa, B.; Pza, B.; Yla, C. Recent advances in nanosized drug delivery systems for overcoming the barriers to anti-PD immunotherapy of cancer. Nano Today 2019, 29, 100801. [Google Scholar]
- Lai, X.; Friedman, A. Combination therapy of cancer with cancer vaccine and immune checkpoint inhibitors: A mathematical model. PLoS ONE 2017, 12, e0178479. [Google Scholar] [CrossRef]
- Wu, K.; Xiu, D. Data-Driven Deep Learning of Partial Differential Equations in Modal Space. J. Comput. Phys. 2020, 408, 109307. [Google Scholar] [CrossRef]
- Pettet, G.J.; Please, C.P.; Mcelwain, M. The migration of cells in multicell tumor spheroids. Bull. Math. Biol. 2001, 63, 231–257. [Google Scholar] [CrossRef]
- López, L.; Seoane, J.M.; Sanjuán, M. Dynamics of the cell-mediated immune response to tumour growth. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2017, 375, 20160291. [Google Scholar] [CrossRef]
- Kayan, E.; Merdan, H. An algorithm for Hopf bifurcation analysis of a general delayed reaction-diffusion model. Nonlinear Dyn. 2016, 89, 345–366. [Google Scholar] [CrossRef]
- Palencia, J.; González, J.; Rahman, S.U.; Redondo, A.N. Regularity, Asymptotic Solutions and Travelling Waves Analysis in a Porous Medium System to Model the Interaction between Invasive and Invaded Species. Mathematics 2022, 10, 1186. [Google Scholar] [CrossRef]
- Palencia, J. Invasive-invaded system of non-Lipschitz porous medium equations with advection. Int. J. Biomath. 2021, 14, 2150061. [Google Scholar] [CrossRef]
- Niu, H.L. Multidimensional stability of V-shaped traveling fronts in bistable reaction-diffusion equations with nonlinear convection. AIMS Math. 2021, 6, 314–332. [Google Scholar] [CrossRef]
- Chen, M.L. Dynamics of a HIV Infection Model with Delay in Immune Response. J. Biomath. 2009. [Google Scholar]
- Eladdadi, A.; Kim, P.; Mallet, D. Mathematical Models of Tumor-Immune System Dynamics; Springer: New York, NY, USA, 2014. [Google Scholar]
- D’Onofrio, A. Tumor-immune system interaction: Modeling the tumor-stimulated proliferation of effectors and immunotherapy. Math. Models Methods Appl. Sci. 2006, 16, 1375–1401. [Google Scholar] [CrossRef]
- Xie, J.H.; Zhao, T.J.; Hao, F.F.; He, F.; Science, S.O. The effect of time delay on tumor-immune system during tumor growth. J. Med. Biomech. 2017, 32, 319–324. [Google Scholar]
- Dong, Y.; Huang, G.; Miyazaki, R.; Takeuchi, Y. Dynamics in a tumor immune system with time delays. Appl. Math. Comput. 2015, 252, 99–113. [Google Scholar] [CrossRef]
- Babushkina, N.A.; Kuzina, E.A. Mathematical Modeling of Antitumor Viral Vaccine Therapy: From the Experiment to the Clinic. Adv. Syst. Sci. Appl. 2020, 20, 1–23. [Google Scholar]
- Yafia, R. Hopf bifurcation in a delayed model for tumor-immune system competition with negative immune response. Discret. Dyn. Nat. Soc. 2006, 2006, 095296. [Google Scholar] [CrossRef]
- Yusnaeni, A.; Kasbawati, K.; Syamsuddin, T. Analytical Study of the Existence of a Hopf Bifurcation in the Tumor Cell Growth Model with Time Delay. InPrime: Indonesian J. Pure Appl. Math. 2021, 3, 20–28. [Google Scholar] [CrossRef]
- Gurcan, F.; Kartal, S.; Ozturk, I.; Bozkurt, F. Stability and bifurcation analysis of a mathematical model for tumor-immune interaction with piecewise constant arguments of delay. Chaos Solitons Fractals 2014, 68, 169–179. [Google Scholar] [CrossRef]
- Sardar, M.; Khajanchi, S.; Biswas, S.; Abdelwahab, S.F.; Nisar, K.S. Exploring the dynamics of a tumor-immune interplay with time delay. AEJ—Alexandria Eng. J. 2021, 60, 4875–4888. [Google Scholar] [CrossRef]
- Soufiani, B.N.; Salamci, M.U. Effect of Delay of Immune System Response in Cancer Dynamics: Bifurcation and Chaos Analysis. In Proceedings of the 2018 26th Mediterranean Conference on Control and Automation (MED), Zadar, Croatia, 19–22 June 2018; pp. 765–770. [Google Scholar]
- Gaach, M. Dynamics of the tumor-immune system competition: The effect of time delay. Int. J. Appl. Math. Comput. Sci. 2003, 13, 395–406. [Google Scholar]
- Kuznetsov, V.A.; Makalkin, I.A.; Taylor, M.A.; Perelson, A.S. Nonlinear dynamics of immunogenic tumors: Parameter estimation and global bifurcation analysis. Bull. Math. Biol. 1994, 56, 295–321. [Google Scholar] [CrossRef] [PubMed]
| Parameters | Description |
|---|---|
| Diffusion rate of cancer cells | |
| Diffusion rate of immune cells | |
| The growth rate of cancer cells | |
| The coefficient of interaction between | |
| immune cells and tumor cells | |
| The production rate of immune cells | |
| stimulated by cancer cells | |
| The natural death rate of immune cells | |
| The number of cancer cells by which the immune system responds is half of its maximum | |
| The discrete time delay in interconnection terms |
| Parameter | |||||||
|---|---|---|---|---|---|---|---|
| Value |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cherraf, A.; Li, M.; Moulai-Khatir, A.; Hamidaoui, M. Mathematical Modeling of the Tumor–Immune System with Time Delay and Diffusion. Axioms 2023, 12, 184. https://doi.org/10.3390/axioms12020184
Cherraf A, Li M, Moulai-Khatir A, Hamidaoui M. Mathematical Modeling of the Tumor–Immune System with Time Delay and Diffusion. Axioms. 2023; 12(2):184. https://doi.org/10.3390/axioms12020184
Chicago/Turabian StyleCherraf, Amina, Mingchu Li, Anes Moulai-Khatir, and Meryem Hamidaoui. 2023. "Mathematical Modeling of the Tumor–Immune System with Time Delay and Diffusion" Axioms 12, no. 2: 184. https://doi.org/10.3390/axioms12020184
APA StyleCherraf, A., Li, M., Moulai-Khatir, A., & Hamidaoui, M. (2023). Mathematical Modeling of the Tumor–Immune System with Time Delay and Diffusion. Axioms, 12(2), 184. https://doi.org/10.3390/axioms12020184







