Novel Frequency-Based Approach to Analyze the Stability of Polynomial Fractional Differential Equations
Abstract
1. Introduction
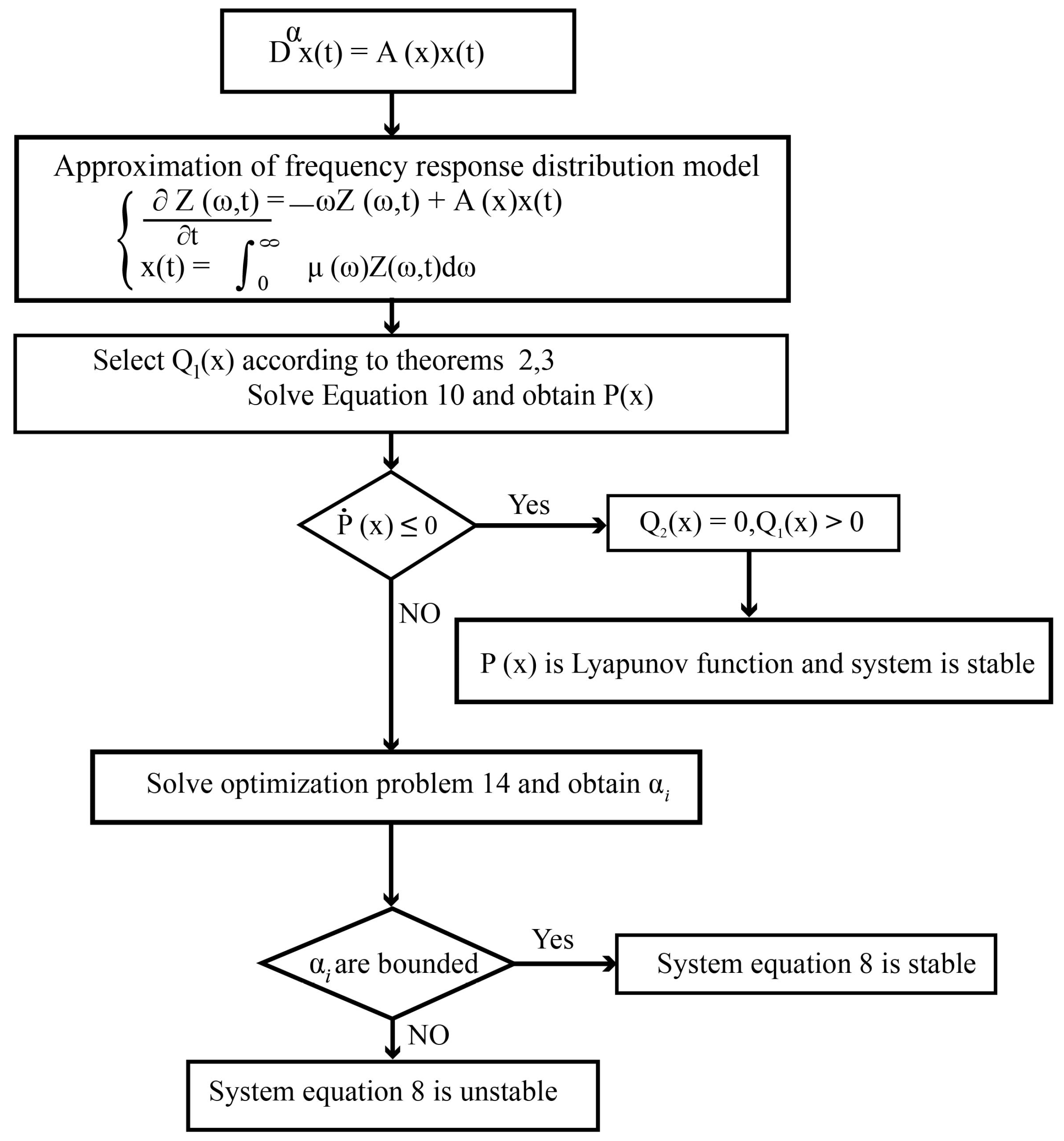
2. Principle
- ;
- ;
- .
The Positive Solutions for Operator Equation
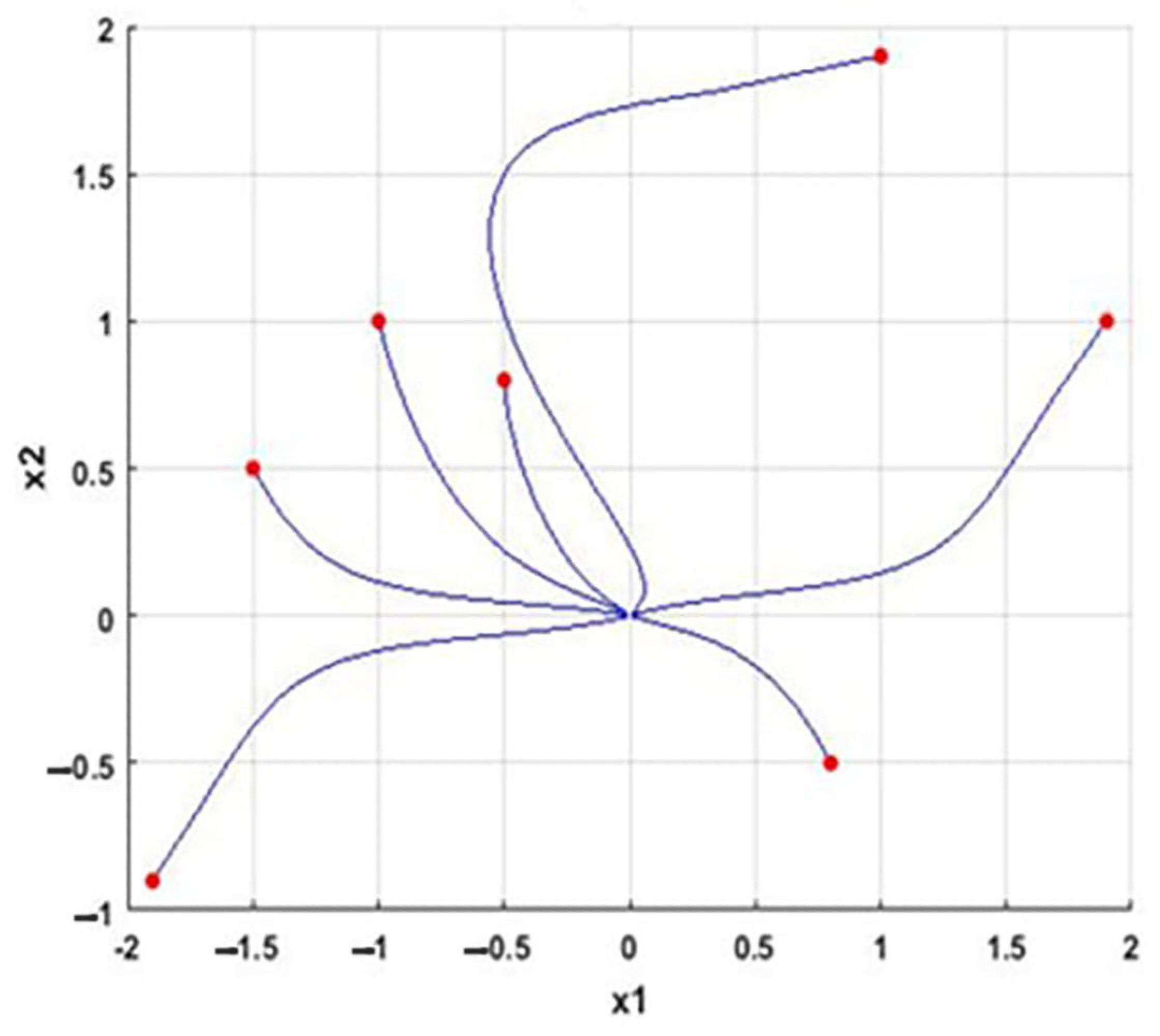
3. Main Theorem
4. Strengths and Future Research
- (1)
- It provides a new perspective on the stability analysis of SOS-based FOSs;
- (2)
- It is possible to determine a higher-order Lyapunov function;
- (3)
- The fractional-order system’s stability can be obtained despite an optimization problem’s bounded solution.
- (1)
- High computational volume in resolving optimization problems;
- (2)
- Absence of uncertainty in the proposed method.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ortigueira, M.D. Fractional Calculus for Scientists and Engineers; Springer Science & Business Media: Berlin, Germany, 2011; Volume 84. [Google Scholar]
- Hurwitz, A. Ueber die Bedingungen, unter welchen eine Gleichung nur Wurzeln mit negativen reellen Theilen besitzt. Math. Ann. 1985, 46, 273–284. [Google Scholar] [CrossRef]
- Chen, W.; Dai, H.; Song, Y.; Zhang, Z. Convex Lyapunov functions for stability analysis of fractional order systems. IET Control. Theory Appl. 2017, 11, 1070–1074. [Google Scholar] [CrossRef]
- Benzaouia, A.; Hmamed, A.; Mesquine, F.; Benhayoun, M.; Tadeo, F. Stabilization of continuous-time fractional positive systems by using a Lyapunov function. IEEE Trans. Autom. Control. 2014, 59, 2203–2208. [Google Scholar] [CrossRef]
- Matignon, D. Stability results for fractional differential equations with applications to control processing. Comput. Eng. Syst. Appl. 1996, 2, 963–968. [Google Scholar]
- Li, Y.; Chen, Y.; Podlubny, I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag–Leffler stability. Comput. Math. Appl. 2010, 59, 1810–1821. [Google Scholar] [CrossRef]
- Sabatier, J. On Stability and Performances of Fractional Order Systems. In Proceedings of the 3rd IFAC Symposium FDA’08, 2008, Ankara, Turkey.
- Trigeassou, J.C.; Maamri, N.; Sabatier, J.; Oustaloup, A. A Lyapunov approach to the stability of fractional differential equations. Signal Process. 2011, 91, 437–445. [Google Scholar] [CrossRef]
- Li, C.; Wang, J.; Lu, J. Observer-based robust stabilisation of a class of non-linear fractional-order uncertain systems: A linear matrix inequalitie approach. IET Control. Theory Appl. 2012, 6, 2757–2764. [Google Scholar] [CrossRef]
- Sadati, S.J.; Baleanu, D.; Ranjbar, A.; Ghaderi, R. Mittag-Leffler stability theorem for fractional nonlinear systems with delay. Abstr. Appl. Anal. 2010, 2010, 1–7. [Google Scholar] [CrossRef]
- Tuan, H.T.; Trinh, H. Stability of fractional-order nonlinear systems by Lyapunov direct method. IET Control. Theory Appl. 2018, 12, 2417–2422. [Google Scholar] [CrossRef]
- Boukal, Y.; Darouach, M.; Zasadzinski, M.; Radhy, N.E. Large-scale fractional-order systems: Stability analysis and their decentralised functional observers design. IET Control. Theory Appl. 2017, 12, 359–367. [Google Scholar] [CrossRef]
- Cong, N.D.; Doan, T.S.; Siegmund, S.; Tuan, H.T. Linearized asymptotic stability for fractional differential equations. arXiv 2015, arXiv:1512.04989. [Google Scholar] [CrossRef]
- Dai, H.; Chen, W. New power law inequalities for fractional derivative and stability analysis of fractional order systems. Nonlinear Dyn. 2017, 87, 1531–1542. [Google Scholar] [CrossRef]
- Aguila-Camacho, N.; Duarte-Mermoud, M.A.; Gallegos, J.A. Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2951–2957. [Google Scholar] [CrossRef]
- Badri, V.; Tavazoei, M.S. Stability analysis of fractional order time-delay systems: Constructing new Lyapunov functions from those of integer order counterparts. IET Control. Theory Appl. 2019, 13, 2476–2481. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Podlubny, I. Mittag–Leffler stability of fractional order nonlinear dynamic systems. Automatica 2009, 45, 1965–1969. [Google Scholar] [CrossRef]
- Thanh, N.T.; Trinh, H.; Phat, V.N. Stability analysis of fractional differential time-delay equations. IET Control. Theory Appl. 2017, 11, 1006–1015. [Google Scholar] [CrossRef]
- Lu, J.G.; Chen, G. Robust stability and stabilization of fractional-order interval systems: An LMI approach. IEEE Trans. Autom. Control. 2009, 54, 1294–1299. [Google Scholar]
- Li, B.; Zhang, X. Observer-based robust control of $(0\lt\alpha\lt 1) $(0< α< 1) fractional-order linear uncertain control systems. IET Control. Theory Appl. 2016, 10, 1724–1731. [Google Scholar]
- Heleschewitz, D.; Matignon, D. Diffusive realizations of fractional integral-differential operators: Structural analysis under approximation. IFAC Proc. Vol. 1998, 31, 227–232. [Google Scholar] [CrossRef]
- Laudebat, L.; Bidan, P.; Montseny, G. Modeling and optimal identification of pseudo-differential electrical dynamics by means of diffusive Representation-Part I: Modeling. IEEE Trans. Circuits Syst. I Regul. Pap. 2004, 51, 1801–1813. [Google Scholar] [CrossRef]
- Moghani, Z.N.; Karizaki, M.M.; Khanehgir, M. Solutions of the Sylvester equation in c*- modular operators. Ukrainian Mathematical Journal 2021, 73, 414–432. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yaghoubi, H.; Zare, A.; Rasouli, M.; Alizadehsani, R. Novel Frequency-Based Approach to Analyze the Stability of Polynomial Fractional Differential Equations. Axioms 2023, 12, 147. https://doi.org/10.3390/axioms12020147
Yaghoubi H, Zare A, Rasouli M, Alizadehsani R. Novel Frequency-Based Approach to Analyze the Stability of Polynomial Fractional Differential Equations. Axioms. 2023; 12(2):147. https://doi.org/10.3390/axioms12020147
Chicago/Turabian StyleYaghoubi, Hassan, Assef Zare, Mohammad Rasouli, and Roohallah Alizadehsani. 2023. "Novel Frequency-Based Approach to Analyze the Stability of Polynomial Fractional Differential Equations" Axioms 12, no. 2: 147. https://doi.org/10.3390/axioms12020147
APA StyleYaghoubi, H., Zare, A., Rasouli, M., & Alizadehsani, R. (2023). Novel Frequency-Based Approach to Analyze the Stability of Polynomial Fractional Differential Equations. Axioms, 12(2), 147. https://doi.org/10.3390/axioms12020147






