Abstract
This manuscript deals with a parameter estimation of a non-negative integer-valued (NNIV) time series based on the so-called probability generating function (PGF) method. The theoretical background of the PGF estimation technique for a very general, stationary class of NNIV time series is described, as well as the asymptotic properties of the obtained estimates. After that, a particular emphasis is given to PGF estimators of independent identical distributed (IID) and integer-valued non-negative autoregressive (INAR) series. A Monte Carlo study of the thus obtained PGF estimates, based on a numerical integration of the appropriate objective function, is also presented. For this purpose, numerical quadrature formulas were computed using Gegenbauer orthogonal polynomials. Finally, the application of the PGF estimators in the dynamic analysis of some actual data is given.
Keywords:
integer-valued time series; parameter estimation; probability generating functions; asymptotic properties; simulation; numerical integration; application MSC:
62M10; 65D30
1. Introduction
Non-negative integer-valued (NNIV) time series represent one of the most important stochastic models that have attracted the attention of numerous studies (for some more recent ones, see, e.g., [1,2,3,4,5,6,7]). Due to the specific structure of an NNIV series, the procedure for estimating their parameters may differ from that used for similar non-integer stochastic models. Thus, in the case of the most famous NNIV series, the so-called integer non-negative autoregressive (INAR) processes, various estimation techniques have been developed. For instance, in [8], conditional least square estimators were described, while in [9], estimators based on the conditional maximum likelihood method were discussed. On the other hand, the authors in [10,11] considered, among others, moment-based estimation techniques, i.e., the well-known Yule–Walker (YW) equations. Finally, some generalizations of these methods based on the high-order statistics can be found in [12,13].
However, in order to apply any of the mentioned methods, the estimation functions must usually be given in a finite, closed form and (most often) bounded within a certain parameter space. Unfortunately, sometimes, such conditions cannot be met, both in the case of independently identically distributed (IID) and stochastically dependent time series. Therefore, an estimation technique based on probability generating functions (PGFs) can be a useful alternative approach, since PGFs exist and are bounded for any NNIV time series, at least on the interval . Another advantage of PGF estimators is that the estimation procedure is close to the empirical characteristic function (ECF) method introduced in [14,15] and developed later in many studies, cf. [16,17,18]. Generally speaking, the idea behind the PGF method is based on the fact that PGF contains the same amount of information about the distribution of some random variable (RV) as the appropriate characteristic function (CF). Thus, it is expected that the minimization of ‘the distance’ between the PGF of some time series and its empirical PGF gives an efficient parameter estimator. In this way, the PGF method, similar to the ECF method for non-integer time series, could be applied to various kinds of stationary NNIV series. For these reasons, our main goal here is to obtain efficient PGF parameter estimates for the case of a rather general, stationary class of NNIV time series, with applications that will also be described in the following.
Let us point out that, to the best of our knowledge, there are only few studies where the PGF estimation procedure has been discussed so far. First, Esquivel [19] has shown the uniform laws of large numbers and the functional limit theorem for the empirical PGFs. Thereafter, Stojanović et al. [20] used a more general PGF estimation procedure, based on numerical integration techniques, in order to obtain parameter estimators of the so-called noise-indicator integer non-negative autoregressive (NIINAR) time series model. Our main motive here is to generalize these results, i.e., to give theoretical foundations of the PGF estimation procedure in the most general form. According to that, as it will be seen, the PGF estimates can be practically implemented in the estimation of some of the most important and often used NNIV times series, as well as in modelling the dynamics of an actual data set of the number of COVID-19 death cases.
For this purpose, in Section 2, we give some basic facts that are necessary to formulate the PGF estimation method. Additionally, under some regulatory conditions, we investigate the asymptotic properties and efficiency of the PGF estimators for an arbitrary stationary NNIV time series. After that, in Section 3, we analyze some specific PGF estimates for cases of independent identically distributed (IID) and integer-valued autoregressive (INAR) time series. For both types of time series, Monte Carlo simulations of the PGF estimates are computed and their asymptotic properties, such as efficiency and asymptotic normality, are examined too. Section 4 presents an application of the PGF method in parameters and distribution estimation of death cases in the period before and after the appearance of the SARS-CoV2 virus infection on the territory of the Republic of Serbia. Finally, Section 5 contains some concluding remarks.
2. PGF Estimates: Definition and Asymptotic Properties
Let , be a non-negative, integer-valued, and stationary time series with finite moments and probability mass distribution (PMF)
which depends on a vector of unknown parameters , . Additionally, let be some finite realization of the series , of the length T. In order to obtain the PGF estimates of , we introduce the following terms.
Let and , be the overlapping blocks of the process , and
be the r-dimensional PGF of the random vector . Due to the stationarity of series , it is obvious that the function in Equation (1) does not depend on the choice of overlapping blocks, i.e., moment of time t. The main aim of the PGF method is to minimize ‘the distance’ between the theoretical PGF, given by Equation (1), and the corresponding Empirical PGF (of order :
As the series is stationary, it follows that is an unbiased estimator of , i.e.,
where is the true (but unknown) value of parameter . It is also well-known that theoretical PGF is well defined at least for all values (see, e.g., [20]). Thus, the objective function can be defined as
where and is a weight function, integrable on . The PGF estimates will be obtained by minimizing the objective function in Equation (3) with respect to , i.e., they are solutions of the minimization equation
where is a parameter space. In order to solve this equation, we use numerical methods, i.e., procedures based on numerical integration, which is discussed in Section 3. In the sequel, we will examine strong consistency and asymptotic normality (AN) of the PGF estimators under some regularity conditions.
Theorem 1.
Let be the exact value of the parameter θ, and let , for an arbitrary , be the solutions of Equation (4). Additionally, let us suppose that the following regularity conditions are fulfilled:
- (A1)
- Θ is a compact set, where , and for T large enough.
- (A2)
- At the point functionhas a unique minimum .
- (A3)
- is a regular matrix.
- (A4)
- is a non-zero matrix, uniformly bounded by the strictly positive ω-integrable function .
- (A5)
- The covariance function of the seriesis absolutely summable when , i.e.,
At the same time, the integral in Equation (5) is non-singular and exists for each .Then, is a strictly consistent and AN estimator for θ.
Proof.
Firstly, we check the sufficient consistency conditions of the so-called extremum estimators (for more details, see Newey and McFadden [21]). According to given assumptions, the series is ergodic, so that Equation (2) and the strong law of large numbers (SLLN) give
where “as” denotes the almost sure convergence. Furthermore, according to assumption , the function is continuous on the compact , and is continuous on the compact . Hence, there exist constants such that the inequalities
hold. According to these, one obtains
so the last inequality and Equation (6) imply
Thus, uniformly converges almost surely toward . According to this, as well as the assumption and Theorem 1 in Newey and McFadden [21], it follows
i.e., is strictly consistent estimator for .
Furthermore, let us notice that function has continuous partial derivatives of the first and second orders, with respect to any component of the vector . Hence, the Taylor expansion of at gives
Substituting with , for a T large enough, under assumption and the fact that , we have
Furthermore, the function can be differentiated under the integral sign, i.e.,
Now, Equations (8) and (9) give
where
According to assumption , there exists an -integrable function such that
where is a matrix norm on . Hence, the inequalities
hold, so Equation (10) and the SLLN give
To prove the AN property, note that using Equations (5) and (8), we can write the gradient of as
Therefore, according to assumption , equality holds and it follows
Note that the last equality follows from Kronecker’s lemma (see, c.f. Fuller [22]). Thus, the proven convergence and Equation (12) imply
where “d” denotes the convergence in distribution. Now, applying the central limit theorem for stationary processes, as well as Equations (7), (11) and (13), one obtains
and the statement of theorem is completely proven. □
At the end of this section, we point out that PGF estimators of the r-dimensional parameter are usually obtained using overlapping blocks of the same dimensions. This is also consistent with some of the basic assumptions of the ECF method (for more details, see [14]). For these reasons, below, we examine in detail the PGF estimation procedures for the parameter order (as well as the corresponding PGFs order) and .
3. PGF Estimations of IID and INAR Time Series
In this section, we discuss the construction of PGF estimates for two important classes of stationary NNIV time series. First, using a very general form of the so-called power series (PS) distributions, the estimation procedure of independent identical distributed (IID) time series was examined. After that, using the obtained results, PGF estimators of integer-valued autoregressive (INAR) time series are considered.
3.1. Estimation of IID Time Series
The simplest case of the stationary NNIV time series are the IID series, which we denote as , . Similar to that in Stojanović et al. [20], and Bourguignon and Vasconcellos [23], we say that the series has a PS distribution if its PMF is given as follows:
Here, is the so-called discrete support of the RV and
- is a function that depends (only) on ;
- is a (one-dimensional) unknown parameter;
- is a function on , so that when , .
The expression given by Equation (14) represents the so-called PS distributions that, for some special choices of , and , allow for obtaining the most of the known distributions (see Table 1, below). In addition, according to assumption , it is obvious that, in fact, the power series converges on the interval . However, a common assumption is , so we say that power series converges on . Accordingly, the function is positive and increasing at this interval. Moreover, for an arbitrary , we denote by the PGF (of the first order) of RVs . Thus, according to Equation (14), one obtains
where the sum above converges when . Note that Equation (15) allows for a simple computation of first-order PGFs for some of the well-known NNIV distributions, which are also given in Table 1.

Table 1.
NNIV distributions, along with their PGFs, interpreted in the form of PS distributions.
Furthermore, let be the appropriate first-order empirical PGF of series , obtained by its realization . Thus, the objective function can be written as
where is the weight function. Finally, in this case, the minimization Equation (5) reads as follows
As an illustration, Figure 1 shows plots of the PGFs of some typical NNIV IID time series, along with their empirical PGFs.
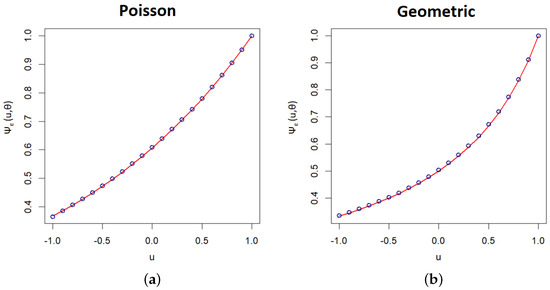
Figure 1.
Graphs of PGFs (lines) and empirical PGFs (dots) of the IID series: (a) Poisson distribution; (b) geometric distribution. (True parameter value is ).
In the following, we assume that , so the set will be a compact. Thus, assuming that other regularity conditions in Theorem 1 are fulfilled, we can apply the PGF method. For this purpose, we have taken two different types of distribution of the series . Firstly, we assume that is the IID series with Poisson distribution and, later, that it has a geometric distribution. In the both cases, for estimating the parameter , we generated independent Monte Carlo replications of the series , of the length . Note that this is close to the length of actual series of COVID-19 death cases, which will be considered in the following. To examine the convergence, i.e., the quality of the PGF estimators, the appropriate estimation errors will also be investigated.
The PGF estimates are computed according to a minimization of the integral in Equation (16). Note that it can be numerically approximated by using an N-point quadrature formula:
where are the quadrature nodes and , are the corresponding weight coefficients. In our simulation study, quadrature formulas based on Gegenbauer orthogonal polynomials, with weights and nodes, were used. More specifically, we consider Gaussian quadratures based on three well-known special cases of Gegenbauer polynomials, i.e., the appropriate weights:
- Chebyshev polynomials (of the first kind): ;
- Legendre polynomials: ;
- Chebyshev polynomials (of the second kind): .
The construction of all these quadrature formulas was realized using the Wolfram Mathematica package “OrthogonalPolinomials”, authored by Cvetković and Milovanović [24]. After that, the objective function in Equation (17) is minimized by the “R” procedure “optimize”, based on the Brent minimization algorithm [25] and realized by the authors’ original codes in “R”.
Summary statistics of the PGF estimates , , obtained with the appropriate weights and computed via aforementioned estimation procedure, are presented in Table 2. More precisely, it contains the mean values (Mean), minima (Min.), maxima (Max.), and the mean squared estimating errors (MSEE) of obtained PGF estimates of the IID series with Poisson and geometric distribution. (These two distributions are taken as an illustration of the application of the PGF method, that is, to describe the dynamics of actual data in Section 4, below). The values of objective functions , , as the reference estimation errors, are also shown. According to presented results, it is obvious that PGF estimates of both IID series are generally the efficient parameter estimators and have very similar properties. Slightly lower estimation errors are observed in the case of the Gauss–Chebyshev quadrature of the second type, i.e., the weight function . This is expected, since it is known that this weight forces the points around the coordinate origin and ignores those near the ends of the interval . On the other hand, the somewhat larger estimation error in the case of Gauss–Chebyshev quadrature of the first kind is a consequence of ‘forcing’ the ends of the interval , where the weight is infinite. In addition, the results of AN testing of the obtained PGF estimates are also presented in Table 2. For this purpose, the Anderson–Darling normality test was used and its test statistic (labelled as AD), along with the corresponding p-values, were calculated using the procedure from the R-package “nortest”, authored by Gross [26]. According to the values thus obtained, it is evident that the AN property is valid for all PGF estimators, which is in accordance with the previous theoretical results, i.e., the statement of Theorem 1.

Table 2.
Estimated parameters’ values of IID series series with Poisson and geometric distribution. (True parameter value is .)
3.2. Estimation of INAR Time Series
In this part of our work, using the previous assumptions, we define the integer-valued autoregressive process (of the first order) or, simply, INAR(1) process , by the recurrence relation
Here, is the IID series of RVs commonly called innovations, is an unknown parameter, and
is the so-called binomial thinning operator (for more details, see [27]). More precisely, X is an arbitrary NNIV RV such that, for any , the RVs are mutually independent (also independent of X) with Bernoulli’s distribution
In that way, it is simply shown that the INAR(1) process is stationary for each , with the autocorrelation function (ACF)
As an illustration, Figure 2 presents sample frequency distributions of the INAR(1) process , along with their corresponding innovations , for Poisson and geometric distributions. Furthermore, it will be of interest to use the first-order PGF of the RV . For that purpose, we prove the following simple statement:
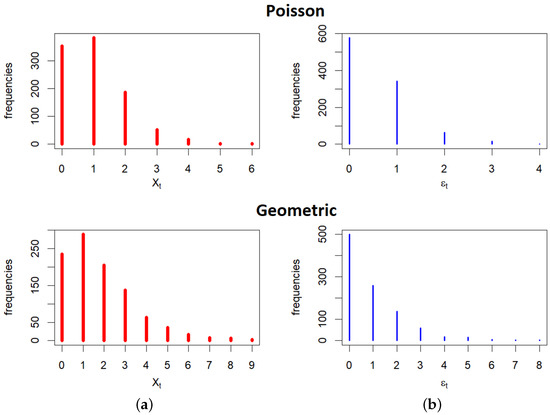
Figure 2.
Plots of the sample frequency distributions of INAR(1) processes (a) and their innovations (b) with Poisson distribution (plots above) and geometric distribution (plots below). True parameters’ values are .
Lemma 1.
For an arbitrary and NNIV RV X, the first-order PGF of the RV reads as follows:
Proof.
Let us also note that some of the important properties of the INAR(1) process can be found in many studies, cf. [29,30,31,32,33,34,35,36]. This kind of stochastic model was first introduced in the pioneer work of Al-Osh and Alzaid [37]. Here, among others, the first order PGF of the INAR(1) process was derived. In the case of PS-distributed innovations , we generalized this result in the following way:
Theorem 2.
Let us assume that the innovations of the INAR(1) process have the PS distribution given by Equation (14). Additionally, suppose that the function has a finite derivative, uniformly bounded on a finite interval . Then, an arbitrary INAR (1) series , given by Equation (19), has a PGF of the first order:
as well as PGFs of order :
Proof.
According to a definition of the PS-distributed RVs , given by Equation (14), as well as their first-order PGF, given by Equation (15), the mathematical expectation of the series can be obtained as follows:
Based on this and the assumptions of the theorem, for some constant and any , we have
where the sum above converges uniformly on . On the other hand, the sequence , is monotone and bounded, so Abel’s convergence criterion implies that, when uniformly on , the following is valid:
As it is known from Alzaid and Al-Osh [38], the inequality (25) represents a necessary and sufficient condition for the infinite-order integer moving average (INMA) representation of the series :
where the sum above converges almost surely. According to Equation (26) and the previous Lemma, we have the following:
and the product above converges absolutely at least for all . Hence, substituting Equation (15) in Equation (27), we have Equation (23). In order to prove the second part of the theorem, notice that, according to the definition (18) of the series , for an arbitrary , the following holds:
Substituting into Equation (28) and after some computation similar to the previous one, an explicit expression of the PGF in Equation (24) can be easily obtained. □
Remark 1.
Note that the distribution of the INAR(1) process depends on two unknown parameters . Therefore, in order to estimate them, it is of interest to determine the two-dimensional PGF of , which is simply obtained by replacing in Equation (24):
In the following, similar to the case of IID series, the procedure for estimating the parameters of the INAR(1) model with Poisson and geometric innovations will be described. Using Poisson distribution for series , as well as Equations (23) and (29), the one- and two-dimensional PGFs of the INAR(1) process , after some simple computations, can be obtained as follows:
In a similar way, for the appropriate PGFs of the INAR(1) process with geometric innovations, one obtains
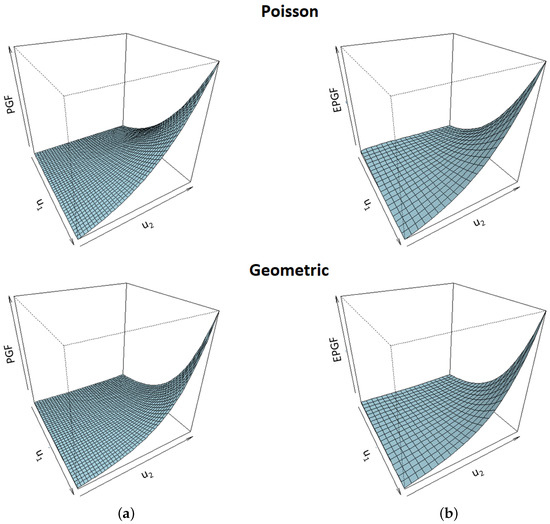
Three-dimensional plots of the theoretical and empirical PGFs of INAR(1) processes with Poisson and geometric innovations, respectively, are shown in Figure 3.

Figure 3.
Three-dimensional plots of the two-dimensional PGFs (a) and empirical PGFs (b) of the INAR(1) series with Poisson innovations (panels above) and geometric innovations (panels below). True parameters’ values are .
Therefore, notice that the PGFs of the INAR(1) process with geometric innovations are not in closed form. However, they depend on alternating sums and can be easily approximated by finite k-term sums. Thus, for instance, in the case of a one-dimensional PGF, the approximation error amounts to
Similar to that in the previous estimation procedure, the PGF estimates of unknown parameters are computed according to a minimization of the double integral
with respect to some weight function . Similar to earlier, the integral in (30) can be numerically approximated by using some N-point cubature formula:
where are the cubature nodes, and are the corresponding weight coefficients. In our simulations study, we used the same kind of (two-dimensional) weights as in the IID case, i.e., the Gaussian qubature formulas based on Gegenbauer orthogonal polynomials, with weights
and nodes. After that, the objective function (30) is minimized by “R” procedure for linearly constrained minimization “constrOptim”, based on the Nelder–Mead optimization method [39].
As the initial values of this estimation procedure, we used the Yule–Walker (YW) estimates, obtained by solving the equations
Here,
are, respectively, the mean and first autocorrelation of the INAR(1) series , while
are their sample estimators. Thus, in the case of Poisson distributed innovations , the YW estimators are obtained as follows:
Similarly, for geometric distributed innovations , the YW estimates are
Summary statistics of the PGF estimates , , obtained using the aforementioned numerical estimation procedure with the appropriate weights , , are presented in the following Table 3. Similar to in the IID case, two different types of innovations , with Poisson and geometric distributions, were used. Thus, in both cases, the unknown parameters were estimated through the set of independent Monte Carlo simulations of the innovation series and INAR(1) process of the length .

Table 3.
Estimated parameter values of the INAR(1) process with Poisson and geometric innovations. (True parameters’ values are ).
In the same way as before, Table 3 contains the mean values (Mean), minima (Min.), maxima (Max.), as well as the mean squared estimating errors (MSEE) and the objective function for all obtained PGF estimates. Notice that the thus obtained PGF estimators have very similar properties as in the one-dimensional case, with somewhat higher estimation errors, which is expected. Namely, they are computed using a two-step procedure, using the YW estimated values as the initial ones.
Similar to earlier, the summarized values of test statistics, along with the appropriate p-values, are also shown in Table 3. It can be seen that the AN property is confirmed in almost all cases, that is, for most of the PGF estimators of the parameters , as well as the corresponding weight functions . We assume, in the same way as it is shown in Stojanović et al. [40], that the variations that occur in some simulations, at the significant level of , are also reasonable as a consequence of this specific, two-stage estimation procedure.
4. Application of the PGF Estimates
In this section, we indicate some possibilities of the practical application of PGF estimators in stochastic modeling of real data. Additionally, our motivation is also to point out the different dynamics of time series of death cases in the time period before and after the emergence of the SARS-CoV2 virus. We emphasize that much attention has been paid to the COVID-19 disease, from the beginning of the pandemic until today. For these reasons, various theoretical models were proposed for research of this still current issue. Rigorous mathematical ones, usually based on solving coupled partial equations, have been proposed, e.g., in [41,42,43]. Some other authors [44,45,46] used both deterministic and stochastic approaches to predict the various effects caused by the COVID-19 pandemic. A particular interesting approach is given in [47,48] where the NNIV time series were used for modelling the dynamic of some the COVID-19 count data. In this regard, here, we explore some more possibilities in modeling the dynamics of such data.
More precisely, we observed two real data sets, one of which refers to the period before and the other after the appearance of the SARS-CoV2 virus infection on the territory of the Republic of Serbia. The first time series, labelled as Series A, contains the number of daily mortality in Niš, the third largest city in the Republic of Serbia, in the period from 1 January 2017 until 31 December 2019. The second one (Series B) contains the daily number of deaths per day in the Republic of Serbia, from 20 March 2020 (the date of the first death caused by the disease COVID-19) to 1 December 2022. Dynamics of the observed time series, lengths and , respectively, are shown on the left plots in Figure 4. On the other hand, the right plots in Figure 4 show the autocorrelation functions (ACFs) of these time series. In the case of Series A, it is obvious that there is a very weak correlation, so it can be seen as an IID time series. On the contrary, with Series B, it is evident that there is a positive and significant but exponentially decreasing correlation, depending on the lag . Therefore, in accordance with the previous theoretical results, primarily Equation (20), it could be expected that the INAR(1) process is an adequate stochastic model for describing the dynamics of the number of deaths caused by the COVID-19 disease.
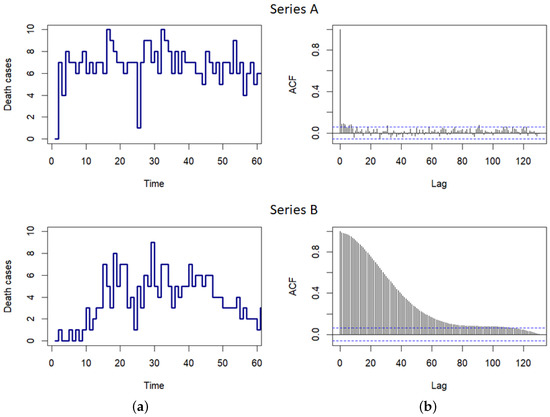
Figure 4.
(a) Dynamics of the number of deaths before and after the onset of the disease COVID-19 in Serbia. (b) The corresponding ACFs of the observed time series.
Some confirmation of these observations can also be seen in Table 4, where its upper part shows the basic descriptive statistical analysis of the both time series. In the case of Series A, the existence of an equal-dispersion property can be recognized through ’close’ values of its sample mean and variance. Thus, this series can be modeled with a Poisson distribution. On the other hand, with Series B, there is a wide range and variability of observed data. Additionally, it can be seen that frequencies of ‘smaller’ numerical values are emphasized (its mode equals 1). Therefore, it could be assumed that, in the INAR(1) model, innovations with a Poisson distribution (and a ‘small’ parameter ) can be taken, as well as with a geometric distribution. In accordance with the mentioned facts, we modeled the dynamics of the Series B by using the INAR(1) process with geometric distributed innovations . Finally, the lower part of Table 4 shows some of the estimated values for the ACFs of both observed time series. Obviously, the obtained autocorrelation values of Series A are not statistically significant, so it can be considered as an IID time series. Conversely, the estimated ACF values of Series B indicate the possibility of modeling the dynamics of this time series using the INAR(1) process.

Table 4.
Summary statistics of the total number of deaths per day before and after the appearance of the COVID-19 disease in the Republic of Serbia.
In the upper part of Table 5, the estimated values of parameter for Series A, as well as estimates of the INAR(1) process for Series B, are shown. As in the previous simulation study, PGF estimates for IID Series A were obtained using an unconstrained Brent’s optimization procedure. On the other hand, for Series B, PGF estimates were computed using the two-step estimation procedure described in the previous section, that is, by linearly constrained optimization and YW estimates as initial parameter values. In both cases, as before, weight functions , based on Gegenbauer orthogonal polynomials were used.

Table 5.
Estimated values of parameters, along with error and predictive statistics of the actual data.
It can be easily seen that in the case of Series A, estimated parameter is ’between’ to sample mean and variance, which is expected. For Series B, the estimated values of the parameter are relatively ‘small’. This is obviously a consequence of the emphasized frequencies of smaller integer values of the observed time series (which can also be seen in the following Figure 5). Conversely, the estimated values of the parameter are close to 1. This can also be explained by the previously described properties of this time series, which has a significantly high estimated value of the first correlation.
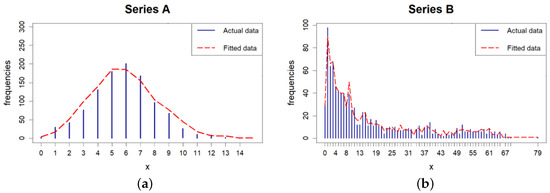
Figure 5.
Frequency distribution of the actual and fitted data, obtained by (a) IID Poisson process; (b) INAR(1) process with geometric innovations.
Furthermore, we analyzed the fitting efficiency for both time series, when all weights are applied. For this purpose, we generated 500 independent simulations for the IID Series A, as well as the INAR(1) model for Series B, for all estimated parameters’ values. In order to check the efficiency of proposed models, we computed two typical goodness-of-fit statistics: the mean squared estimation error (MSEE) and the Akaike information criterion (AIC). The mean values of these statistics are shown in the middle part of Table 5. It is noticeable that, in all the mentioned cases, the PGF estimates have similar efficiency because the MSEE and AIC statistics have relatively close and small estimated values.
Finally, an analysis of the forecast accuracy of models obtained with PGF estimates was also checked. For this purpose, we used the one-tailed Diebold–Mariano test [49] for prediction accuracy. The null hypothesis is that the fitted time series have the same accuracy as the actual data, while the alternative is that the series obtained by the PGF estimation procedure are less accurate. The test statistic (denoted as DM), as well as the corresponding p-values, were calculated using the R-package “forecast”, authored by Hyndman [50]. In the case of Series A, the data set from 1 January 2020 to 20 March 2020 was used, as a forecast horizon of length . For Series B, the forecast horizon from 1 December 2022 to 9 January 2023 was used, the length of which is equal to . As a result, it is noticeable that the realized values of the DM statistics, shown in the lower part of Table 5, indicate that all models fitted by PGF estimators have the same forecast accuracy as empirical data, i.e., the null hypothesis is valid. Some of these aforementioned facts can be also seen in Figure 5, where the empirical frequencies distribution, along with the appropriate distributions of IID and INAR(1) processes, are shown.
5. Conclusions
In this paper, an estimation method based on probability generating functions (PGFs) is proposed. For this purpose, the stochastic properties of this method were analyzed, as well as its application in estimating the parameters of some typical stationary time series. Notice that the PGF method, with certain modifications, may be suitable for estimating and fitting time series of a similar, or some other kind to those considered here. These can be, for instance, INAR processes with negative binomial thinning [51,52], integer generalized autoregressive (IN-GARCH) processes [53], or the so-called self-exciting processes [54]. Moreover, the application of the PGF estimates is also particularly interesting in the case of some non-linear time series, when the usual estimation methods cannot be used. We point out again that, in Stojanović et al. [20], the PGF method was applied in parameter estimation of the so-called noise-indicator INAR process. Consequently, the application of the PGF estimators presented here can be a starting point for some future research related to these estimators. Therefore, notice that, in the case of Series B, the estimated values of the parameter indicate that the hypothesis is potentially valid. This could indicate a possible non-stationarity in the dynamics of the observed time series and could be the subject of some further research.
Author Contributions
Conceptualization, V.S. and E.L.; methodology, V.S. and M.T.; software, V.S. and E.L.; validation, E.L.; formal analysis, V.S.; data curation, V.S. and M.T.; writing—original draft preparation, V.S., E.L. and M.T.; writing—review and editing, E.L.; visualization, V.S. and M.T.; supervision, V.S.; project administration, E.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Official data on deaths from the disease COVID-19 can be found on the website of the Office for IT and e-Government of the Republic of Serbia (http://covid19.data.gov.rs/?locale=en, accessed on 6 December 2022).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ACF | Auto Correlation Function |
| AD test | Anderson–Darling test |
| AIC | Akaike Information Criterion |
| AN | Asymptotic Normality |
| CF | Characteristic Function |
| ECF | Empirical Characteristic Function |
| IID series | Independent Identical Distributed series |
| INAR process | Integer-Valued Autoregressive process |
| INMA | Integer Moving Average |
| MSEE | Mean Squared Estimating Error |
| NIINAR process | Noise-Indicator Integer-Valued Autoregressive process |
| NNIV series | Non-Negative Integer-Valued series |
| PGF | Probability Generating Function |
| PMF | Probability Mass Distribution |
| PS | Power Series |
| RV | Random Variable |
| SLLN | Strong Law of Large Numbers |
| YW | Yule–Walker |
References
- Johnson, N.L.; Kemp, A.W.; Kotz, S. Univariate Discrete Distributions, 3rd ed.; Wiley Series in Probability and Statistics; Wiley: Washington, DC, USA, 2005. [Google Scholar]
- Xu, H.-Y.; Xie, M.; Goh, T.N.; Fu, X. A Model for Integer–Valued Time Series With Conditional Overdispersion. Comput. Stat. Data Anal. 2012, 56, 4229–4242. [Google Scholar] [CrossRef]
- Jazi, M.A.; Jones, G.; Lai, C.-D. First-Order Integer Valued AR Processes With Zero Inflated Poisson Innovations. J. Time Ser. Anal. 2012, 33, 954–963. [Google Scholar] [CrossRef]
- Weiß, C.H.; Pollet, P.K. Binomial Autoregressive Processes With Density-Dependent Thinning. J. Time Ser. Anal. 2014, 35, 115–132. [Google Scholar] [CrossRef]
- Graziadei, H.; Lijoi, A.; Lopes, H.F.; Marques, P.C.; Prünster, I. Prior Sensitivity Analysis in a Semi-Parametric Integer-Valued Time Series Model. Entropy 2020, 22, 69. [Google Scholar] [CrossRef] [PubMed]
- Khoo, W.C.; Ong, S.H.; Atanu, B. Coherent Forecasting for a Mixed Integer-Valued Time Series Model. Mathematics 2022, 10, 2961. [Google Scholar] [CrossRef]
- El-Morshedy, M. A Discrete Linear-Exponential Model: Synthesis and Analysis with Inference to Model Extreme Count Data. Axioms 2022, 11, 531. [Google Scholar] [CrossRef]
- Du, J.-G.; Li, Y. The Integer-Valued Autoregressive (INAR(p)) Model. J. Time Ser. Anal. 1991, 12, 129–142. [Google Scholar]
- Franke, J.; Seligmann, T.H. Conditional Maximum Likelihood Estimates for INAR(1) Processes and Their Application to Modelling Epileptic Seizure Counts. In Developments in Time Series; Chapman & Hall: London, UK, 1993; pp. 310–330. [Google Scholar]
- Latour, A. Existence and Stochastic Structure of a Non-negative Integer-valued Autoregressive Process. J. Time Ser. Anal. 1998, 19, 439–455. [Google Scholar] [CrossRef]
- Silva, I.; Silva, M.E. Asymptotic Distribution of the Yule-Walker Estimator for INAR(p) Processes. Stat. Prob. Lett. 2006, 76, 1655–1663. [Google Scholar] [CrossRef]
- Silva, I.; Silva, M.E. Parameter Estimation for INAR Processes Based on High-Order Statistics. Revstat 2009, 7, 105–117. [Google Scholar]
- Martin, V.L.; Tremayne, A.R.; Jung, R.C. Efficient Method of Moments Estimators for Integer Time Series Models. J. Time Ser. Anal. 2014, 35, 491–516. [Google Scholar] [CrossRef]
- Knight, J.L.; Yu, J. Empirical Characteristic Function in Time Series Estimation. Econom. Theory 2002, 18, 691–721. [Google Scholar] [CrossRef]
- Yu, J. Empirical Characteristic Function Estimation and Its Applications. Econom. Rev. 2004, 23, 93–123. [Google Scholar] [CrossRef]
- Kotchoni, R. Applications of the Characteristic Function-Based Continuum GMM in Finance. Comput. Stat. Data Anal. 2012, 56, 3599–3622. [Google Scholar] [CrossRef]
- Meintanis, S.G.; Swanepoel, J.; Allison, J. The probability weighted characteristic function and goodness-of-fit testing. J. Stat. Plan. Infer. 2014, 146, 122–132. [Google Scholar] [CrossRef]
- Stojanović, V.; Milovanović, G.V.; Jelić, G. Distributional Properties and Parameters Estimation of GSB Process: An Approach Based on Characteristic Functions. ALEA Lat. Am. J. Probab. Math. Stat. 2016, 13, 835–861. [Google Scholar] [CrossRef]
- Esquìvel, M.L. Some Applications of Probability Generating Function Based Methods to Statistical Estimation. Discuss. Math. 2009, 29, 131–153. [Google Scholar] [CrossRef]
- Stojanović, V.; Randjelović, D.; Kuk, K. Noise-Indicator Nonnegative Integer-Valued Autoregressive Time Series of the First Order. Braz. J. Probab. Stat. 2018, 32, 147–171. [Google Scholar] [CrossRef]
- Newey, W.K.; McFadden, D. Large Sample Estimation and Hypothesis Testing. In Handbook of Econometrics; Elsevier: Amsterdam, The Netherlands, 1994; Volume 4. [Google Scholar]
- Fuller, W.A. Introduction to Statistical Time Series; John Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
- Bourguignon, M.; Vasconcellos, K.L.P. First Order Non-Negative Integer Valued Autoregressive Processes With Power Series Innovations. Braz. J. Probab. Stat. 2015, 29, 71–93. [Google Scholar] [CrossRef]
- Cvetković, A.S.; Milovanović, G.V. The Mathematica Package “Orthogonal Polynomials”. Facta Univ. Ser. Math. Inform. 2004, 19, 17–36. [Google Scholar]
- Brent, R. Algorithms for Minimization Without Derivatives; Prentice-Hall: Englewood Cliffs, NJ, USA, 1973. [Google Scholar]
- Gross, L. Tests for Normality. R Package Version 1.0-2. 2013. Available online: http://CRAN.R-project.org/package=nortest (accessed on 6 December 2022).
- Weiß, C.H. Thinning Operations for Modelling Time Series of Counts—A Survey. Adv. Statist. Anal. 2008, 92, 319–341. [Google Scholar] [CrossRef]
- Billingsley, P. Probability and Measure; John Wiley & Sons: New York, NY, USA, 1995. [Google Scholar]
- Silva, M.E.; Oliveira, V.L. Difference Equations for the Higher-Order Moments and Cumulants of the INAR(1) Model. J. Time Ser. Anal. 2004, 25, 317–333. [Google Scholar] [CrossRef]
- Jung, R.C.; Ronning, G.; Tremayne, A.R. Estimation in Conditional First Order Autoregression with Discrete Support. Stat. Pap. 2005, 46, 195–224. [Google Scholar] [CrossRef]
- Ristić, M.M.; Nastić, A.S.; Miletić, A.V. A Geometric Time Series Model with Dependent Bernoulli Counting Series. J. Time Ser. Anal. 2013, 34, 466–476. [Google Scholar] [CrossRef]
- Schweer, S.; Weiß, C.H. Compound Poisson INAR(1) Processes: Stochastic Properties and Testing for Over-Dispersion. Comput. Stat. Data Anal. 2014, 77, 267–284. [Google Scholar] [CrossRef]
- Bermúdez, L.; Karlis, D. Multivariate INAR(1) Regression Models Based on the Sarmanov Distribution. Mathematics 2021, 9, 505. [Google Scholar] [CrossRef]
- Li, Q.; Chen, H.; Liu, X. A New Bivariate Random Coefficient INAR(1) Model with Applications. Symmetry 2022, 14, 39. [Google Scholar] [CrossRef]
- Maya, R.; Chesneau, C.; Krishna, A.; Irshad, M.R. Poisson Extended Exponential Distribution with Associated INAR(1) Process and Applications. Stats 2022, 5, 755–772. [Google Scholar] [CrossRef]
- Maya, R.; Irshad, M.R.; Chesneau, C.; Nitin, S.L.; Shibu, D.S. On Discrete Poisson–Mirra Distribution: Regression, INAR(1) Process and Applications. Axioms 2022, 11, 193. [Google Scholar] [CrossRef]
- Al-Osh, M.A.; Alzaid, A.A. First-Order Integer-Valued Autoregressive (INAR(1)) Process. J. Time Ser. Anal. 1987, 8, 261–275. [Google Scholar] [CrossRef]
- Alzaid, A.A.; Al-Osh, M.A. An Integer-Valued pth-order Autoregressive Structure (INAR(p)) Process. J. App. Prob. 1990, 27, 314–324. [Google Scholar] [CrossRef]
- Lange, K. Numerical Analysis for Statisticians. In Book Series: Statistics and Computing; Springer: New York, NY, USA, 2001. [Google Scholar]
- Stojanović, V.; Popović, B.Č.; Milovanović, G.V. The Split-SV model. Comput. Statist. Data Anal. 2016, 100, 560–581. [Google Scholar] [CrossRef]
- Vaz, S.; Torres, D.F.M. A Discrete-Time Compartmental Epidemiological Model for COVID-19 with a Case Study for Portugal. Axioms 2021, 10, 314. [Google Scholar] [CrossRef]
- Ghosh, S.; Volpert, V.; Banerjee, M. An Epidemic Model with Time Delay Determined by the Disease Duration. Mathematics 2022, 10, 2561. [Google Scholar] [CrossRef]
- Sivakumar, B.; Deepthi, B. Complexity of COVID-19 Dynamics. Entropy 2022, 24, 50. [Google Scholar] [CrossRef] [PubMed]
- Hassan, S.M.; Riveros Gavilanes, J.M. First to React Is the Last to Forgive: Evidence from the Stock Market Impact of COVID 19. J. Risk Financ. Manag. 2021, 14, 26. [Google Scholar] [CrossRef]
- Zakharov, V.; Balykina, Y.; Ilin, I.; Tick, A. Forecasting a New Type of Virus Spread: A Case Study of COVID-19 with Stochastic Parameters. Mathematics 2022, 10, 3725. [Google Scholar] [CrossRef]
- Jovanović, M.; Stojanović, V.; Kuk, K.; Popović, B.; Čisar, P. Asymptotic Properties and Application of GSB Process: A Case Study of the COVID-19 Dynamics in Serbia. Mathematics 2022, 10, 3849. [Google Scholar] [CrossRef]
- Stapper, M. Count Data Time Series Modelling in Julia—The CountTimeSeries.jl Package and Applications. Entropy 2021, 23, 666. [Google Scholar] [CrossRef]
- Eliwa, M.S.; Tyagi, A.; Almohaimeed, B.; El-Morshedy, M. Modelling Coronavirus and Larvae Pyrausta Data: A Discrete Binomial Exponential II Distribution with Properties, Classical and Bayesian Estimation. Axioms 2022, 11, 646. [Google Scholar] [CrossRef]
- Diebold, F.X.; Mariano, R.S. Comparing Predictive Accuracy. J. Bus. Econ. Stat. 1995, 13, 253–263. [Google Scholar]
- Hyndman, R. Forecasting Functions for Time Series and Linear Models. R Package Version 7.1. 2016. Available online: http://CRAN.R-project.org/package=forecast (accessed on 9 January 2023).
- Nastić, A.S.; Ristić, M.M.; Bakouch, H.S. A Combined Geometric INAR(p) Model Based on Negative Binomial Thinning. Math. Comput. Model. 2012, 55, 1665–1672. [Google Scholar] [CrossRef]
- Ristić, M.M.; Nastić, A.S.; Bakouch, H.S. Estimation in an Integer-Valued Autoregressive Process With Negative Binomial Marginals (NBINAR(1)). Comm. Stat. Theory Methods 2012, 41, 606–618. [Google Scholar] [CrossRef]
- Weiß, C. INGARCH Models for Count Time Series. In An Introduction to Discrete-Valued Time Series; Weiß, C., Ed.; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar] [CrossRef]
- Reinhart, A. A Review of Self-Exciting Spatio-Temporal Point Processes and Their Applications. Stat. Sci. 2018, 33, 299–318. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).