Abstract
A relevant problem in the development and improvement of numeric analytical methods for the research of structures, buildings and construction is studying the stress–strain state of structures and construction with boundaries that have complex shapes. Deformations and stresses arise in a domain with a geometrically non-linear shape of the boundary (cut-outs and cuts). These stresses and deformations have great values and gradients. Experiments carried out using the photoelasticity method show a change in the deformation order ratios for different subareas of the boundary cut-out area depending on proximity to the apex of the angular cut-out. Areas with minor deformations are observed, and areas where linear deformations and shears are more significant than rotations are also observed. In addition, areas where section rotations are more significant than linear and shear deformations are observed. According to the experimental data, the mathematical model of the SSS in the area of the apex of the cut-out of the domain boundary should take into account non-linear deformations. Hence, it is necessary to formulate the boundary value problem of the theory of elasticity, taking into account the geometrical non-linearity. The research aim of this paper is to formulate the problem of the elasticity theory taking into account the geometrical non-linearity in furtherance of the proposed mathematical model justified by the experimental data obtained using the photoelasticity method. The obtained formulation of the elasticity theory problem allows analyzing the form of the system of equations of the boundary value problem depending on the proximity of the considered area to the irregular point of the boundary, i.e., taking into account the difference in the effect of linear and shear deformations, rotations and forced deformations on the solution to the geometrically non-linear elastic problem dealing with forced deformations in the area of an angular cut-out of the boundary of the plane domain.
Keywords:
finite deformations; temperature deformations; photoelasticity method; mathematical model; boundary elasticity problem; polar coordinate system; angular cut-out of the boundary of the plane domain MSC:
74D05; 74D10; 74G55
1. Introduction
The stress–strain state of composite structures and construction is characterized by substantial concentrations of stresses in areas where elements of structures are connected with various items of boundary structural design: special lines, points, for example, a re-entrant corner, cuts, etc. The most intricate stress–strain state occurs in areas of stress and strain concentration resulting from the boundary shape or the ‘geometry factor’ and from the finite discontinuity of pre-set forced deformations, mechanical properties reaching an irregular point of the domain boundary.
Studying the stress–strain state of structures and construction with boundaries that have complex shapes is a relevant problem of development and elaboration of numeric analytical methods in the research of structures, buildings and construction.
The stress–strain state of structures and construction is studied using state-of-the-art software packages and mathematical tools; these studies deal with independent research undertakings implemented within the framework of numerous research projects and journals. However, they are beyond the scope of problems addressed in this article.
The purpose of this research project, addressed in this article, is to formulate the problem of the elasticity theory, taking into account geometrical non-linearity according to the proposed mathematical model justified by the experimental data obtained using the photoelasticity method.
The choice of mathematical model is substantiated by the characteristics of the continuum physical model. In the apex of the angular cut-out of the domain boundary, singular stresses and deformations are observed. They are reviewed in classical papers [1,2,3,4,5,6,7,8,9,10], and the stress–strain concentration factors are no longer relevant. The stress–strain intensity factors are determined more accurately the more detailed the stress–strain state is modeled in a certain approximate neighborhood of the domain boundary cut-out excluding the apex [3,11,12,13,14,15,16,17,18,19]. Therefore, the mathematical formulation of the elasticity problem in the domain of the boundary cut-out apex becomes relevant from the standpoint of practice if its geometrical non-linearity in the case of forced deformations is taken into account.
Values and gradients of stresses and deformations are great in a domain with geometrically non-linear shapes of the boundary (cut-outs, cuts) [1,2,3,4,7,8,9,10,11,12,13,14]. In such areas of the angular cut-out of the domain boundary, certain irregularities are experimentally identified in terms of the solution to the non-linear elasticity problem [15,16,17,18,19,20,21,22,23,24,25,26,27,28]. Displacements are continuous in the area of the boundary cut-out of the domain and in the cut-out apex itself [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. The growing rate of change in displacements results in an increase in stress and strain as the apex of the boundary angular cut-out becomes closer to the radius. In the process, not only first-order and second-order derivatives of displacements increase for small radii. The effect of forced deformations with a finite discontinuity along the contact line of the domain components extending into the cut-out apex at the boundary can result in an increase in first-order and second-order derivatives of displacements as the distance to the cut-out apex reduces along the radius, which is confirmed experimentally in [15,20,21,22,23,24,25,26,27,29]. Therefore, taking into account the second-order displacement derivatives in such areas will result in a more accurate elasticity problem statement, which justifies the need to take finite deformations into account.
The goal of this paper is to formulate the plane elasticity problem in the area of the domain boundary angular cut-out, taking into account the geometrical non-linearity and physical linearity under the action of forced deformations.
The paper’s objectives are:
- (1)
- To consider the geometrical relationships between deformations and displacements in the curvilinear orthogonal coordinate system, taking into account finite deformations and to derive the geometrical relationships in a polar coordinate system for the plane strain state in generalized strains;
- (2)
- To derive the equilibrium equations in the curvilinear orthogonal coordinate system and to derive the equilibrium equations in the polar coordinate system for the plane strain state in generalized strains;
- (3)
- To formulate the plane elasticity problem in the area of the domain boundary angular cut-out, taking into account the geometrical non-linearity, which is physically linear under the action of forced deformations or free thermal strains.
2. Materials and Methods
2.1. Experimental Modeling: Problem Statement
A plane area with an angular cut-out of the boundary is considered. Discontinuous forced deformations along the contact line of elements of the composite domain extend to the apex of the cut-out.
Experimental modeling of the plane problem of the elasticity theory with pre-set discontinuous forced deformations is performed using methods of photoelasticity and “unfreezing” of free thermal deformations [20,21,22,23,26,27,28,29].
The plane model has two elements. Forced thermal deformations are created in one of them; the other is free from loads. Further, the model elements are glued together, and the “unfreezing” of free thermal deformations is performed. As a result, the stress–strain state (SSS) is created in the model under the action of discontinuous forced deformations along the contact line of the model elements.
The homogeneous epoxy model’s length is 180 mm; its width is 50 (46) mm; the model’s material stress coefficient is = 0.341 kg/cm2; and its cross-sectional thickness t is 3 mm. Models of plane wedge-shaped areas with different angles of the boundary cut-out were investigated. Depending on the angle of the cut-out, the stress state of its apex develops a unique characteristic, which is visible as a concentrator of stresses in a model made of an optically sensitive material. During the experiment, substantial rotations of cross-sections were observed in the area of the apex of the boundary cut-out.
Figure 1 shows images of interference fringes of several models with a thickness of 3 mm, corresponding to the SSS triggered by the action of discontinuous thermal deformations in the area of the angular cut-out of the boundary at different angles of the cut-out: (a) ; (b) ; (c) ; (d) ; (e) , which means a narrow cut-out similar to a slot; (f) . In close proximity to the geometrical concentrator of stresses, which is the apex of the angular cut-out of the boundary, the experimental solution is not “legible” or poorly “legible” regardless of the magnification of the neighborhood fragment. At some small distance from the source of concentration and stresses, reliable experimental data are obtained; they change continuously and monotonically when approaching the irregular point of the boundary.

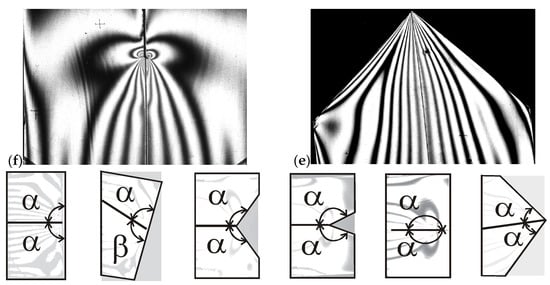
Figure 1.
Images of fringes in models with thickness t = 3 mm for different cases of the angular cut-out in the model: (a) ; (b) ; (c) ; (d) ; and (e) —this is a narrow slot-like cut-out; (f) .
In the area of the angular cut-out of the boundary of the domain, the experiment identifies several subareas in which the SSS is characterized by the extent of proximity to the apex of the cut-out of the boundary of the domain.
At a sufficient distance from the irregular point of the boundary, there is an area where small stresses are observed; here, stresses are explained by pre-set loads, and the SSS converges with the solution to a linear problem of the theory of elasticity.
Infinite stresses and strains are identified in the angular cut-out area of the boundary of the plane domain as the solution to homogeneous boundary value problems. The singularity of the solution to the problem depends on the type of homogeneous boundary conditions, mechanical characteristics of the domains, and angles of the boundary cut-out.
The area of elastic strains is observed close to the cut-out apex. Within the framework of a physically linear elastic problem, this area of elastic strains is characterized by the SSS featuring power-type singularity, which is identified by solving the homogeneous plane boundary problem of elasticity. At the same time, this power-type dependence is strictly observed for orders of fringes in a certain area. The dependence of stresses, strains, and fringe orders on radius is as follows in terms of power: .
As the irregular point of the boundary is approached from inside the domain, the gradients of strains, stresses, and orders of interference fringes increase. The character of the distribution of stresses is such that the orders of fringes have a “similar” form as in the case of the power dependence, and gradients of orders of fringes, stresses, and strains increase. If the order of change of linear strains is as follows: , then the order of non-linear strains is: , with linear strains becoming small in comparison with non-linear ones. Therefore, values of non-linear strains become greatest in a certain area of the irregular point of the boundary.
The experiment shows a change in the ratios of the order of strains for different subareas of the boundary cut-out area depending on the distance to the apex of the angular cut-out. Areas with small strains are observed; areas where linear strains and shears are more significant than rotations are observed; and the other observed areas are those where section rotations are significant with respect to linear and shear strains.
According to the experimental data, the mathematical model of the SSS in the area of the apex of the domain boundary cut-out should take into account non-linear deformations, which suggests that the formulation of the boundary value problem of the theory of elasticity must take into account the geometrical non-linearity.
2.2. Object of Study
The plane elasticity problem is considered for a domain that may have an angular cut-out at the domain boundary [1,4,15,18]. Volume forces may act in the plane domain (Figure 2), and forced deformations (free thermal strains ) are provided. In the domain, a jump (finite discontinuity) of forced deformations may be provided. A discontinuity of deformations, for example, occurs when thermal strains are provided for one of the subdomains of the domain , and the second subdomain is not loaded.
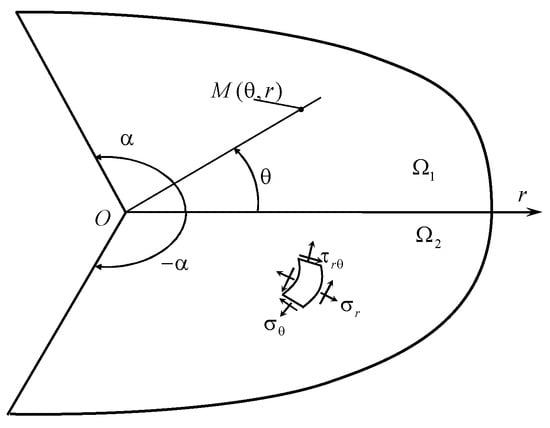
Figure 2.
The plane domain with forced deformations.
A homogeneous elastic body is in the plane strain state.
The domain has an elasticity modulus of E, a Poisson’s ratio of , the linear expansion coefficient of domains and is constant and equal to . The domain’s boundary conditions are homogeneous.
The state-of-the-art statement of the elasticity problem, taking into account finite deformations, was elaborated by V. Novozhilov in his Theory of Elasticity in 1958 [30]. The following definition of the deformation theory is used in this work. “The locations of continuum points before and after deformation are given; we need to determine the variation of the vector connecting two arbitrary infinitely near continuum points resulting from the deformation”. The measure of elongation is selected as the ratio of the segment’s elongation after the deformation of its initial length.
This problem statement of the deformation theory was reviewed and elaborated in many subsequent papers [31,32,33]. A detailed overview of works on geometrically and physically non-linear continuum mechanics is provided in [32]. In these papers, deformation ratios are derived in the Cartesian system. The polar coordinate system used for considering a domain with an angular boundary cut-out is a curvilinear coordinate system where the basis vectors and their derivatives vary from point to point. Therefore, deformation ratios were not written in the polar system due to the awkwardness of their derivation.
The objective is to consider and formulate the equations of the plane elasticity problem, taking into account the geometric non-linearity and physical non-linearity resulting from forced deformations or free thermal strains .
2.3. Taking Finite Deformations into Account for the Spatial Curvilinear Orthogonal and Polar Coordinate Systems
Figure 3 shows a curvilinear orthogonal coordinate system where the arbitrary point has coordinates and is identified by the radius of vector going from the origin. Unit vectors , tangential to coordinate lines , are directed towards the increase of these parameters and form the basis of space before the body deformation [29,30,32].
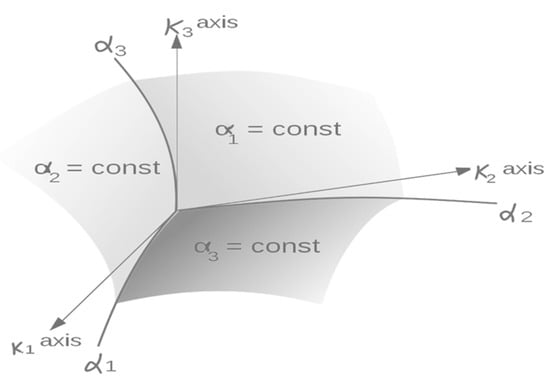
Figure 3.
Curvilinear orthogonal coordinate system, basis orthogonal unit vectors .
Basis vector directions change when moving from one point to another, and vector projections on the axis and derivatives also depend on coordinates . The Lamé parameters are as follows:
After deformation, point M will take the position of a point , which is determined by the radius–vector:
Here, values denote projections of the displacement vector on the axis of the local trihedron drawn at point M.
Before the deformation, the other point is determined by the vector . After the deformation, point N will change to the point , which is determined by the radius–vector:
Taking into account the differentiation of unit vectors [1,8,30,32], the resolution of the vector is obtained with the basis .
The relative elongation in point M is assumed as:
The difference between the squares of the segment lengths after and before the deformation , taking into account the relative elongation, will be written as:
Here, are the deformation components in the curvilinear coordinate system :
The polar coordinate system is considered as a special case of the curvilinear orthogonal system: , , ; the Lamé parameters are: .
The plane deformation state [2,3,4,34] is considered when points of an elastic body move in planes perpendicular to the OZ axis:
Then, parameters , , and deformation in the form of (6) and generalized stresses are reduced:
Non-linear deformations in the polar coordinate system will be written as:
2.4. Ratios for Generalized Stresses and Non-Linear Deformations
The physical ratios in the orthogonal curvilinear coordinate system, according to the works by V. Novozhilov [30] and according to [8,32,34], are written as:
where are the deformation deviator components, is Kronecker delta; .
Mixed invariants
characterize the properties of an elastic isotropic material. V. Novozhilov introduces the concepts of the generalized modulus of volume expansion , the generalized shear modulus and the similarity phase of deviators .
In expressions (12) and (13), are the invariants of the non-linear deformations tensor:
are the invariants of the generalized stresses tensor:
According to [8,30,32], it is assumed that the measure of deviation of an isotropic material from the law of similarity of stress and strain deviators (similarity phase of deviators) is equal to zero: .
For physically linear ratios (12) with constant characteristics (13): , , it is assumed that the relation form for generalized stresses and deformations is the same as in Hooke’s law between stresses and strains for small deformations [30,32,34].
Under the action of forced deformations (temperature deformations), the Dugamel–Neumann dependence is written as:
where is the deformation caused by generalized stresses , are free temperature strains, E is the elasticity modulus, , is the Poisson’s ratio, is the sum of normal generalized stresses, and is the linear expansion coefficient.
Taking into account (18), the stresses will be written as follows in the polar coordinate system:
Here, , , , , and deformations are defined in the form of (9) or (10).
2.5. Equilibrium Equations
In the spatial curvilinear orthogonal coordinate system [8,30,32] , i = 1, 2, 3, are basis vectors of the domain before deformation, a rectangular parallelepiped is considered with the pre-deformation edges , i = 1, 2, 3, where are Lamé’s parameters. After the deformation, a rectangular parallelepiped transforms into an oblique parallelepiped with edges , being relative elongations along the axes after deformation; are the domain basis vectors after deformation.
Making equilibrium equations of all forces acting on the oblique parallelepiped, we obtain [8,30,32,33]:
where are the generalized stresses on the faces of the oblique parallelepiped; are the area of the parallelepiped faces; are the generalized volume forces after deformation. Having written the forces on the parallelepiped faces after deformation in the vector initial basis , i = 1,2,3, before deformation, = Equation (21) can be written as:
Here, are the projections of the volume generalized force on directions .
Taking into account the curvilinear coordinates and Lamé parameters, the equilibrium Equations (22)–(24) are reduced:
where in Equations (25) and (26):
Generalized stresses are connected to stresses in the domain point by the ratios: .
Taking into account (27) and (28), equilibrium Equations (25) and (26) will be written as:
Note that the form of linear equations of equilibrium in generalized stresses in the polar coordinate system in the form (25) and (26) is similar to the “classical” equations of equilibrium for small deformations:
Taking into account (9), the equations of equilibrium in deformations under the action of temperature deformations have the form of:
In the absence of forced deformations and volumetric forces, the equations of equilibrium (33) and (34) will be rewritten as homogeneous equations:
Homogeneous boundary conditions are provided on the domain boundary (Figure 2):
where are the angles formed by the normal line to the square before deformation and by the unit vectors before deformation; hence , .
The boundary conditions (37) in the polar coordinate system take the form of:
or for angles :
If for one of the subdomains of the domain temperature strains are provided, and the second subdomain is not loaded (Figure 1), then the conditions of displacement and stress continuity orthogonal to the line of contact shall be true for the line of the domain contact.
3. Results
- (1)
- Geometrical relationships between deformations and displacements were provided in a curvilinear orthogonal coordinate system taking into account finite deformations (6); geometrical relationships were derived in the polar coordinate system for the plane deformation state taking into account non-linear deformations (9) and displacements (10);
- (2)
- Equations of equilibrium in the curvilinear orthogonal coordinate system (22), (23), and (24) were provided; equations of equilibrium in the polar coordinate system were derived for the plane deformation state in generalized stresses (25), (26), (27), and (28) and strains (33) and (34) under the action of forced temperature deformations .
- (3)
- The formulation of the plane elasticity problem in the angular boundary cut-out domain taking into account geometric non-linearity, physically linear under the action of forced deformations or free temperature deformations for the plane deformation state includes the following system of equations: geometrical relations (9), equilibrium equations (33) and (34), physical relations (19) and (20), homogeneous boundary conditions (39), and displacement and stress continuity conditions along the contact line of the composite domain in the presence of a finite discontinuity of the given forced deformations on the line of the domain contact. The continuity conditions for deformations are provided in [30].
4. Discussion
To justify the choice of a mathematical model of the SSS in the area of the angular cut-out of the boundary of the domain, experiments were conducted using methods of photoelasticity and “unfreezing” of free deformations. The author proposes a mathematical model characterizing the SSS in the area of the angular cut-out of the domain boundary subjected to discontinuous forced deformations on the basis of the data from experimental studies conducted using photo-elastic models.
The experimental data analysis made using the “microscope principle” and the “telescope principle” identified several subareas in which the SSS is determined by the degree of proximity to the apex of the cut-out of the domain boundary. Areas where small strains are observed, areas where linear strains and shears are more significant than rotations are observed, and areas where sectional rotations are significant with respect to linear and shear strains are observed. Thus, in some areas close to the apex of the boundary cut-out, rotations of sections are observed, which are absent at a distance from such an area, which confirms the need to take into account non-linear deformations. Therefore, the form of equilibrium equations must be modified to take into account the order ratios of linear strains, shear strains, and rotations.
For the proposed mathematical model of the SSS in the area of the boundary cut-out of the domain, the formulation of the elasticity theory problem for a plane domain with an angular boundary cut-out is obtained in the polar coordinate system for the post-deformation case, taking into account geometrical non-linearity, physical linearity under the action of thermal deformations. To derive the system of equations in the polar coordinate system, a curvilinear coordinate system is used, which takes into account a change in basis vectors due to the deformation of a solid body element. The equations are derived for the post-deformation state of an elastic solid body.
In further studies, numerical methods, the same as discrete methods, will allow us to (1) find the SSS in the area of the angular cut-out of the boundary on the basis of the formulated boundary value problem and (2) compare it with analytical and experimental data, which will be the subject of independent studies.
5. Conclusions
The author proposes a mathematical model for the study of the SSS in the angular cut-out area of the boundary of a plane domain. The validity of the choice of the mathematical model is determined by the characteristics of the physical model of the continuous medium. The existence of the area of an angular cut-out of the boundary of the domain with large gradients of stresses, strains, rotations, and different ratios of orders of their values is proven experimentally by the photoelasticity method. The SSS obtained using models of the photoelasticity method is continuous. If the irregular point of the boundary of the domain is excluded, or at some small distance from the source of stress concentration, there are valid experimental data, which change continuously and monotonically when approaching the irregular point of the boundary. For the proposed mathematical model in the area of the angular cut-out of the boundary, the boundary value problem of the theory is formulated, taking into account the geometrical non-linearity and physical linearity.
The obtained formulation of the problem of the theory of elasticity allows us (1) to analyze the form of the system of equations of the boundary value problem depending on the degree of proximity of the considered area to an irregular point of the boundary, and (2) to take into account the difference in the effect of linear, shear deformation, rotations, and forced deformations on the solution to the geometrically non-linear elastic problem with forced deformations in the area of the angular cut-out of the boundary of a plane domain.
The obtained homogeneous boundary value problem, taking into account geometrical non-linearity in the cut-out area of the boundary of the domain, will allow us to further improve the solution in this domain and analyze the effect of changes in the orders of deformation on the singularity of the solution in this domain. Therefore, the numerical implementation of the proposed formulation of the elasticity problem will allow us to clarify characteristics of stress and strain intensity coefficients in the area of the apex of the boundary cut-out, taking into account the geometrical non-linearity under the action of forced deformations.
The obtained formulation of the problem of the theory of elasticity for the plane domain, taking into account geometrical non-linearity, which is physically linear under the action of forced deformations, will further allow us to apply a mathematical model relevant to the behavior of structures with angular cut-outs on the boundary under the action of discontinuous thermal deformations.
Funding
This research received no external funding.
Data Availability Statement
All data generated or used during the study are available from the corresponding author by request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Parton, V.; Perlin, P. Methods of Mathematical Elasticity; Nauka: Moscow, Russia, 1981; 688p. [Google Scholar]
- Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity; New York Public Library: New York, NY, USA, 1944; 643p. [Google Scholar]
- Timoshenko, S.P.; Goodiear, J.N. Theory of Elasticity; McGRAW-HILL BOOK: New York, NY, USA; Toronto, ON, Canada; London, UK, 1951; 522p. [Google Scholar]
- Cherepanov, G. Brittle Destruction Mechanics; Nauka: Moscow, Russia, 1974; 640p. [Google Scholar]
- Cherepanov, G. On singular solutions in elasticity theory. In Mechanics of a Solid Deformed Body; Sudostroyenie: Leningrad, Russia, 1970; pp. 17–32. [Google Scholar]
- Lourier, A. Elasticity Theory; Nauka: Moscow, Russia, 1970; 940p. [Google Scholar]
- Kondratyev, V. Boundary value problems for elliptic equations in domains with conical or corner points. In Transactions of the Moscow Mathematical Society; MSU: Moscow, Russia, 1967; Volume 16, pp. 209–292. [Google Scholar]
- Rabotnov, Y. Mechanics of Deformable Solids; Nauka: Moscow, Russia, 1979; 744p. [Google Scholar]
- Kuliev, V. Singular Boundary Value Problems; Nauka: Moscow, Russia, 2005; 719p. [Google Scholar]
- Aksentjan, O. Features of the stress-strain state of the plate in the neighborhood of the edge. Appl. Math. Mech. 1967, 31, 178–186. [Google Scholar]
- Geen, A.E.; Rivlin, R.S. General Theory of Small Elastic Deformations. Proc. R. Soc. Lond. Ser. A 1952, 211, 128–154. [Google Scholar]
- Rivlin, R.S. The Solution of Problems in Second Order Elasticity Theory. J. Rat. Mech. Anal. 1953, 2, 53–81. [Google Scholar] [CrossRef]
- Toupin, R.A.; Rivlin, R.S. Dimensional Change in Crystals Caused by Dislocation. J. Math. Phys. 1960, 1, 8–15. [Google Scholar] [CrossRef]
- Adkins, J.E.; Geen, A.E.; Nicholas, G.C. Two–dimensional Theory of Elasticity for Finite deformations. Philos. Trans. R. Soc. Lond. Ser. A 1954, 247, 279–306. [Google Scholar]
- Makhutov, N.; Moskvichev, V.; Morozov, E.; Goldstein, R. Unification of computation and experimental methods of testing for crack resistance: Development of the fracture mechanics and new goals. Ind. Lab. Diagn. Mater. 2017, 83, 55–64. [Google Scholar] [CrossRef]
- Morozov, E.; Nikishkov, G. Finite Elements Method in Fracture Mechanics; Knizhny dom Librokom: Moscow, Russia, 2017; 256p. [Google Scholar]
- Kogaev, V.; Makhutov, N.; Gusenkov, A. Calculations of Machine Parts and Structures for Strength and Durability: Guidebook; Mashinostroyenie: Moscow, Russia, 1985; 224p. [Google Scholar]
- Matviyenko, Y. Fracture Mechanics Models and Criteria; Fizmatlit: Moscow, Russia, 2006; 328p. [Google Scholar]
- Frishter, L. Stress-strain state in structure angular zone taking into account differences between stress and deformation intensity factors. Adv. Intell. Syst. Comput. 2020, 982, 352–362. [Google Scholar] [CrossRef]
- Razumovskij, I. Interference-Optical Methods of Deformable Solid Mechanics; Bauman MSTU: Moscow, Russia, 2007; 240p. [Google Scholar]
- Hesin, G. The Photoelasticity Method; Stroyizdat: Moscow, Russia, 1975; Volume 3, 311p. [Google Scholar]
- Kobayashy, A.S.; Dally, J.W.; Atluri, S.N.; Riley, W.F.; Sirkis, J.S.; MCConnell, K.G.; Burger, C.P.; Parks, V.J.; Post, D.; Ranson, W.F.; et al. Handbook on Experimental Mechanics; Albert, S., Kobayashy, A.S., Eds.; University of Washington: Seattle, WA, USA, 1987; Volume 1. [Google Scholar]
- Kobayashy, A.S. (Ed.) Experimental Techniques in Fracture Mechanics 1 and 2; Iowa State University Press: Ames, IA, USA, 1975. [Google Scholar]
- Gourgiotis, P.A.; Georgiadis, H.G. The problem of sharp notch in couple-stress elasticity. Int. J. Solids Struct. 2011, 48, 2630–2641. [Google Scholar] [CrossRef]
- Sinclair, G.B. Stress singularities in classical elasticity. II: Asymptotic identification. Appl. Mech. Rev. 2004, 57, 385–439. [Google Scholar] [CrossRef]
- Pestrenin, V.; Pestrenina, I.; Landik, L.; Vestnik, T.G.U. Mathematics and Mechanics; TGU: Tomsk, Russia, 2013; Volume 4, pp. 80–87. [Google Scholar]
- Frishter, L. Photoelasticity-based study of stress-strain state in the area of the plain domain boundary cut-out area vertex. In Proceedings of the 19th International Scientific Conference Energy Management of Municipal Transportation Facilities and Transport EMMFT 2017, Khabarovsk, Russia, 10–13 April 2017; Advances in Intelligent Systems and Computing. Murgul, V., Popovic, Z., Eds.; Springer: Cham, Switzerland, 2017; Volume 692, pp. 836–844. [Google Scholar] [CrossRef]
- Tihomirov, V. Determination of stress intensity factors by the method of photoelasticity in three-dimensional problems of fracture mechanics. In Development of Methods of Experimental Mechanics; Makhutova, N., Ed.; IMASH RAN: Moscow, Russia, 2003; pp. 103–112. [Google Scholar]
- Kasatkin, B.; Kudrin, A.; Lobanov, L.M. Experimental Methods of Investigating Stresses and Strains; Reference Manual; Kasatkin, B., Ed.; Naukova Dumka: Kiyiv, Ukraine, 1981; 584p. [Google Scholar]
- Novozhilov, V.V. Theory of Elasticity; Pergamon Press: London, UK, 1961; 448p. [Google Scholar]
- Sedov, L. Continuum Mechanics, 6th ed.; Lan: Moscow, Russia, 2004; Volume 1, 528p, Volume 2, 560p. [Google Scholar]
- Bakushev, S. Geometrically and Physically Nonlinear Continuum Mechanics: The Plane Problem; Book House LIBROKOM: Moscow, Russia, 2013; 321p. [Google Scholar]
- Green, A.; Adkins, J. Large Elastic Deformations and Nonlinear Continuum Mechanics; Mir: Moscow, Russia, 1965; 456p. [Google Scholar]
- Vardanyan, G.; Andreev, V.; Atarov, N.; Gorshkov, A. Resistance of Materials with Fundamentals of Theory of Elasticity and Plasticity; ACB Publishers: Moscow, Russia, 1995; 568p. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).