A Comparative Study of the Explicit Finite Difference Method and Physics-Informed Neural Networks for Solving the Burgers’ Equation
Abstract
:1. Introduction
2. The Burgers’ Equation
3. Explicit Finite Difference Method
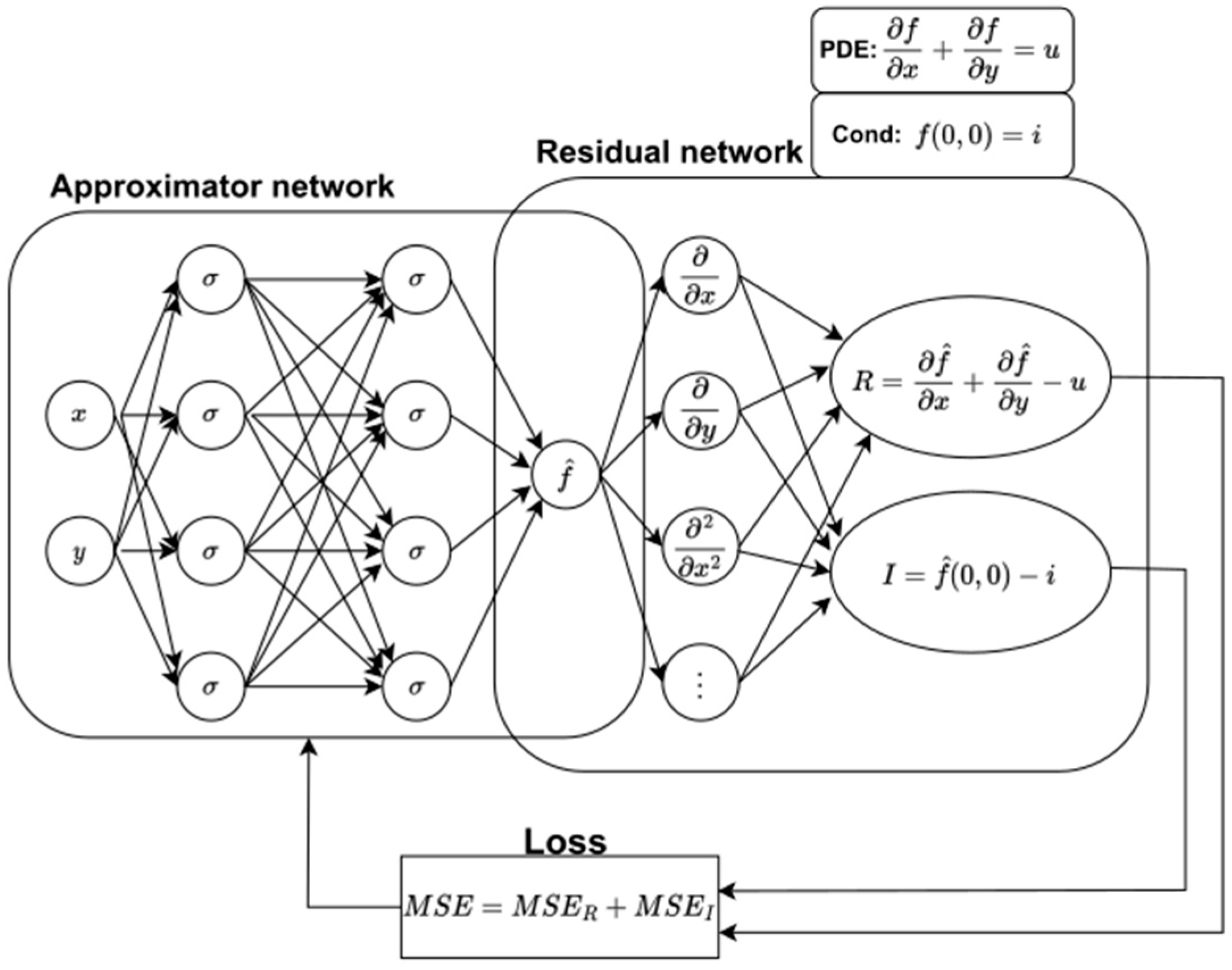
4. Physics-Informed Neural Networks
4.1. The Basic Concept of Physics-Informed Neural Networks in Solving PDEs
4.2. Implementation of PINN in Solving the Burgers’ Equation
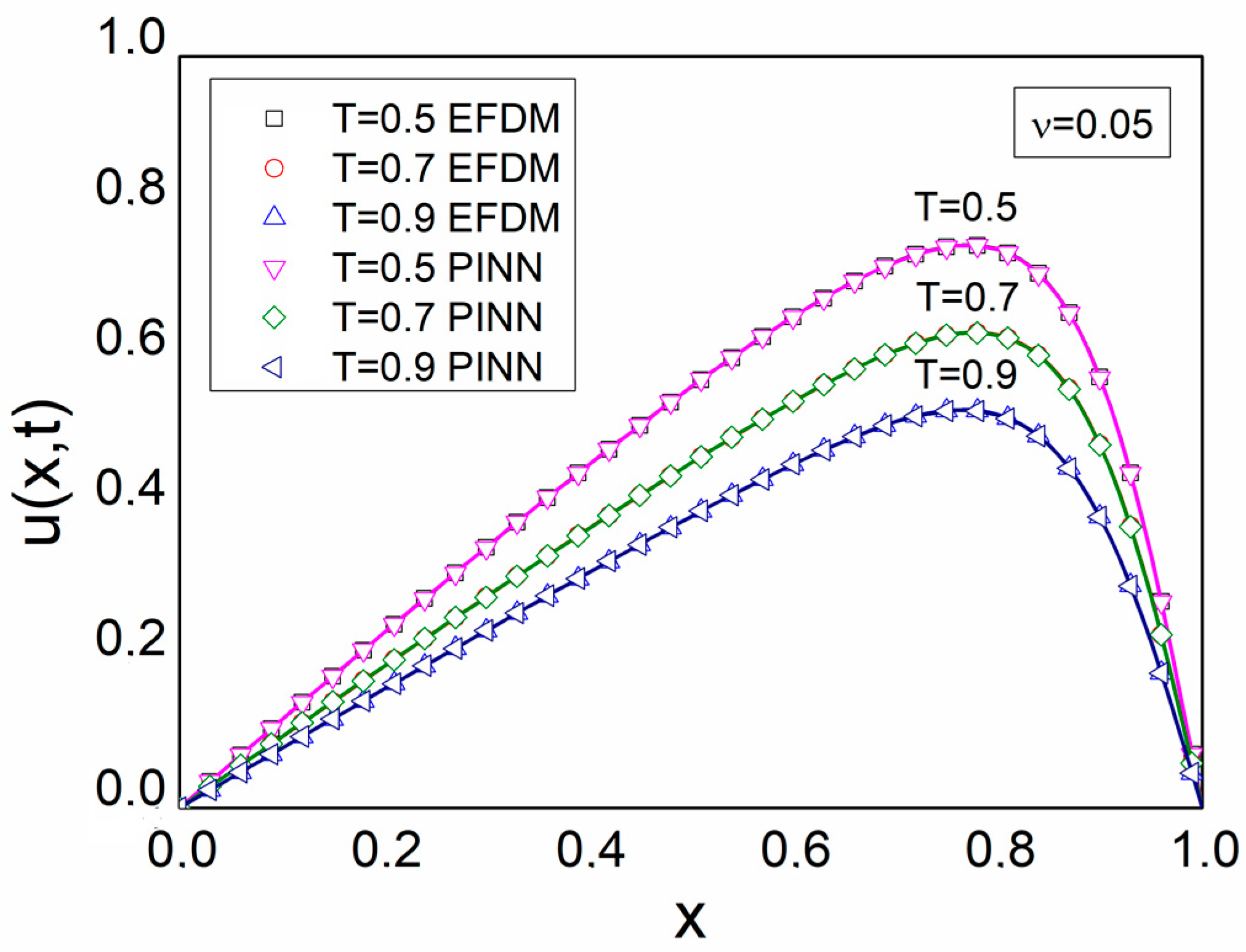
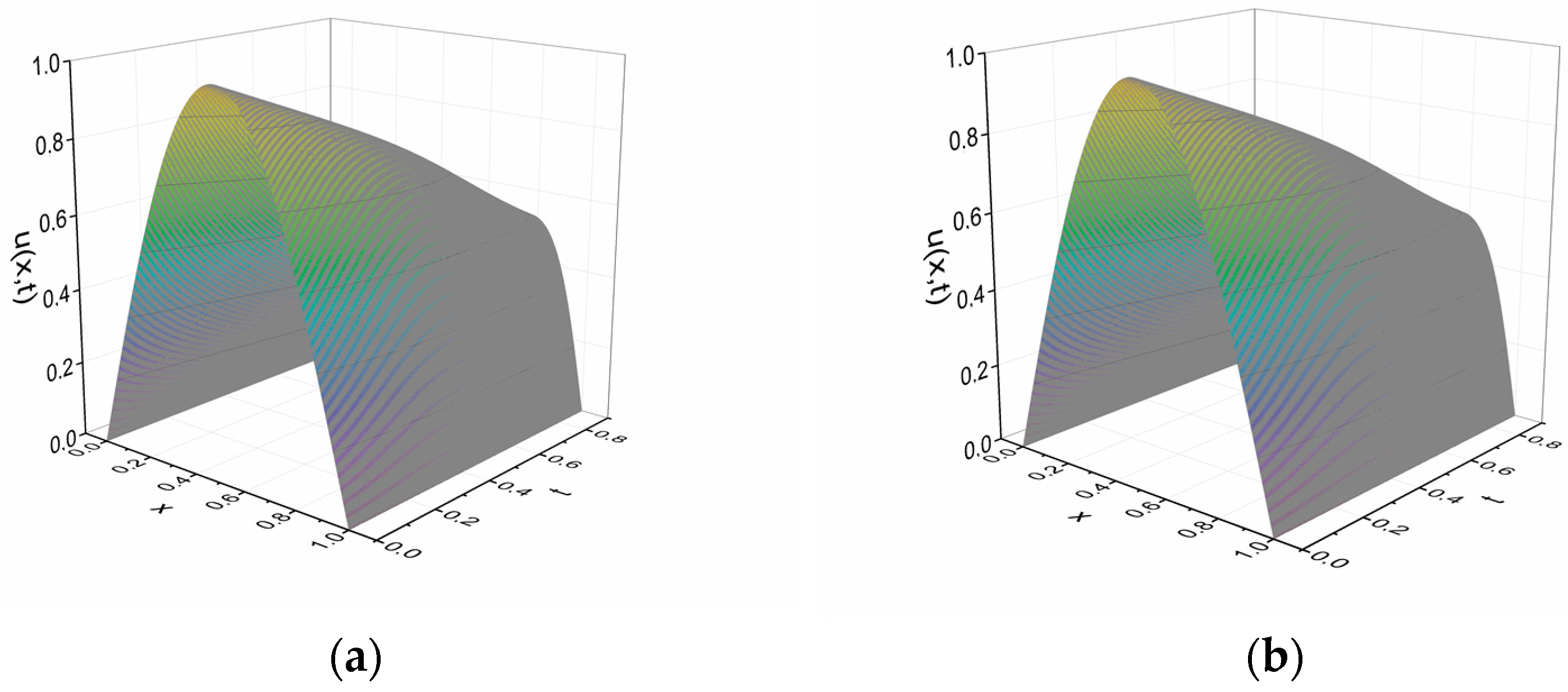
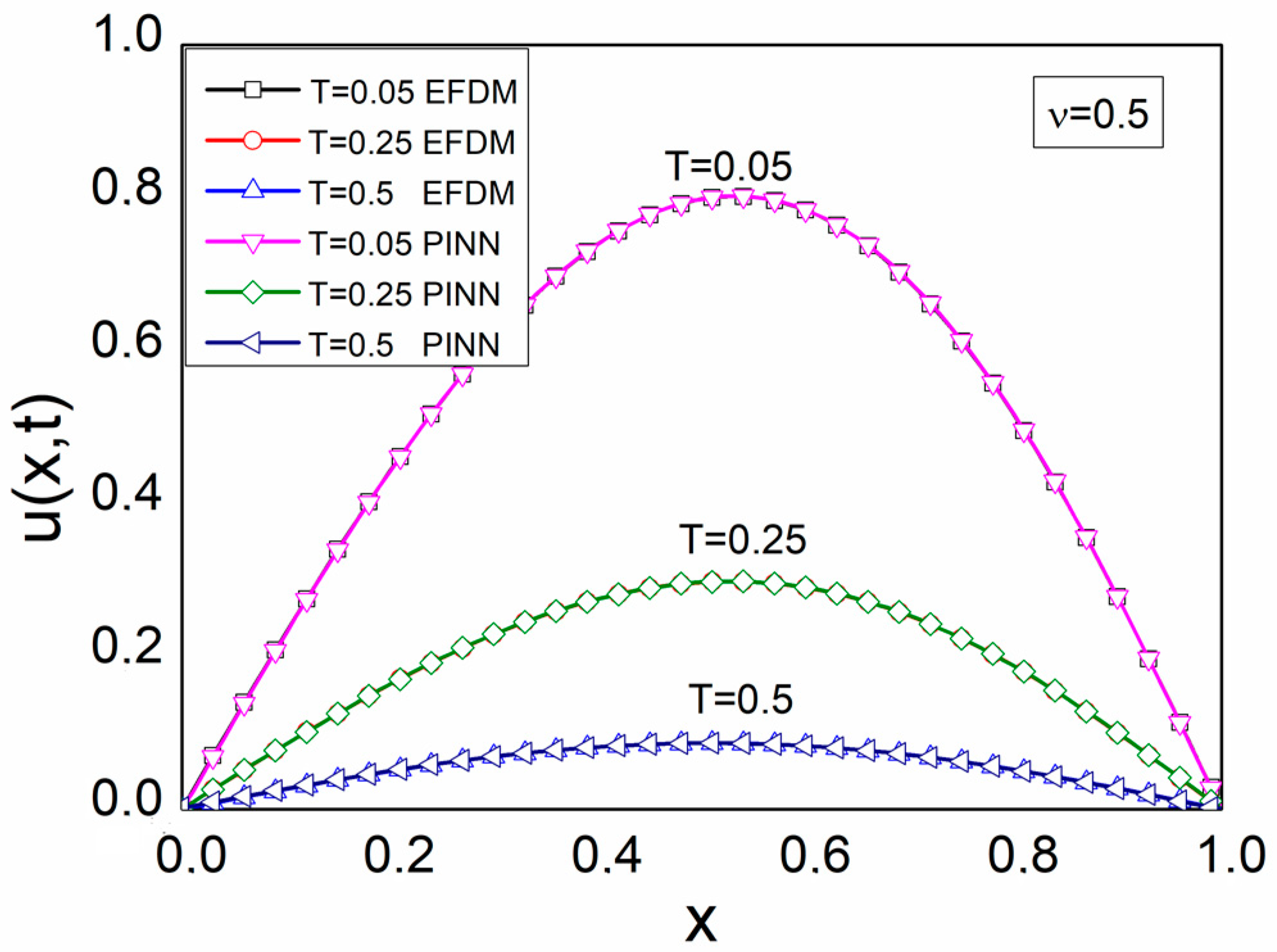
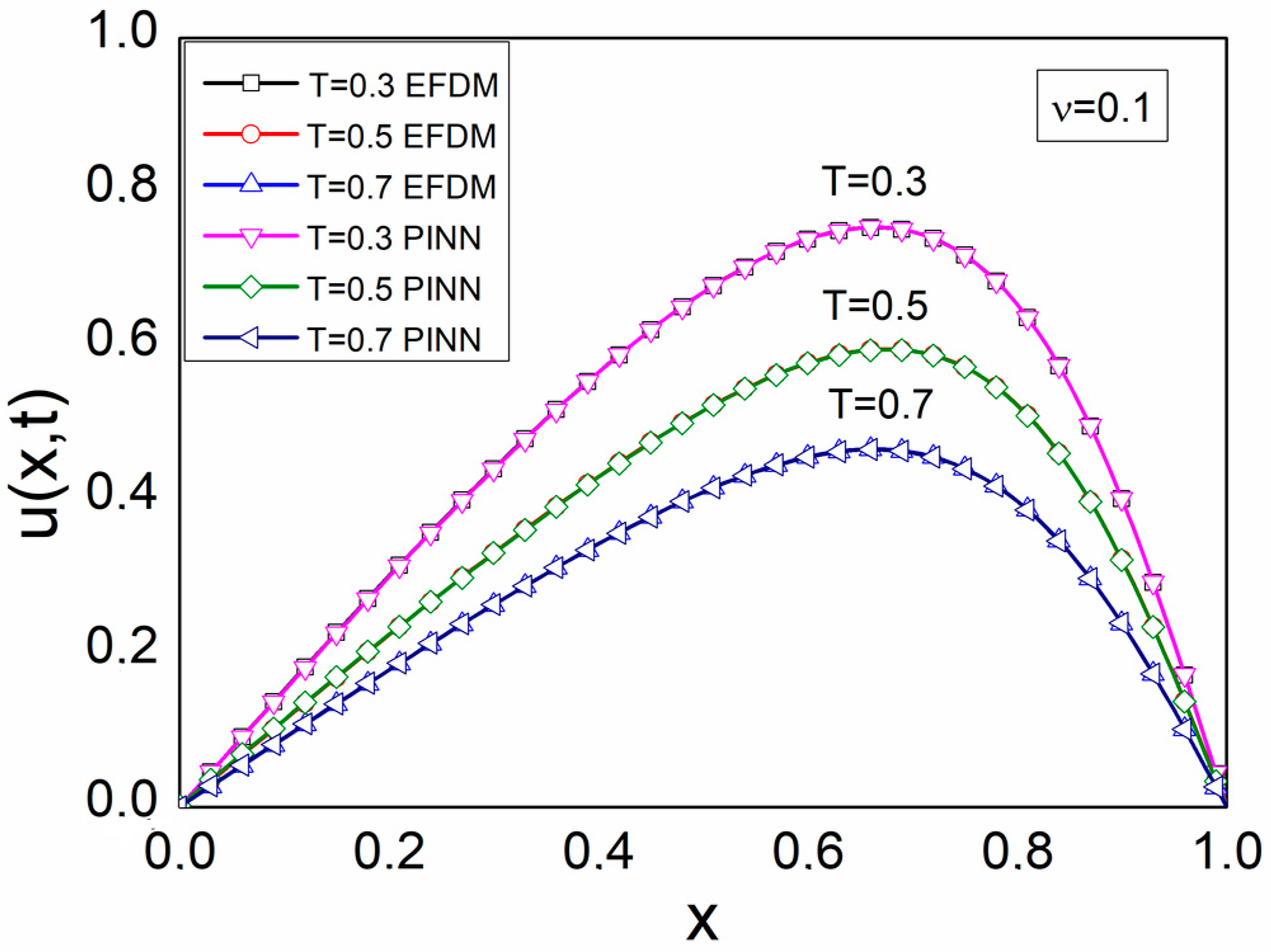
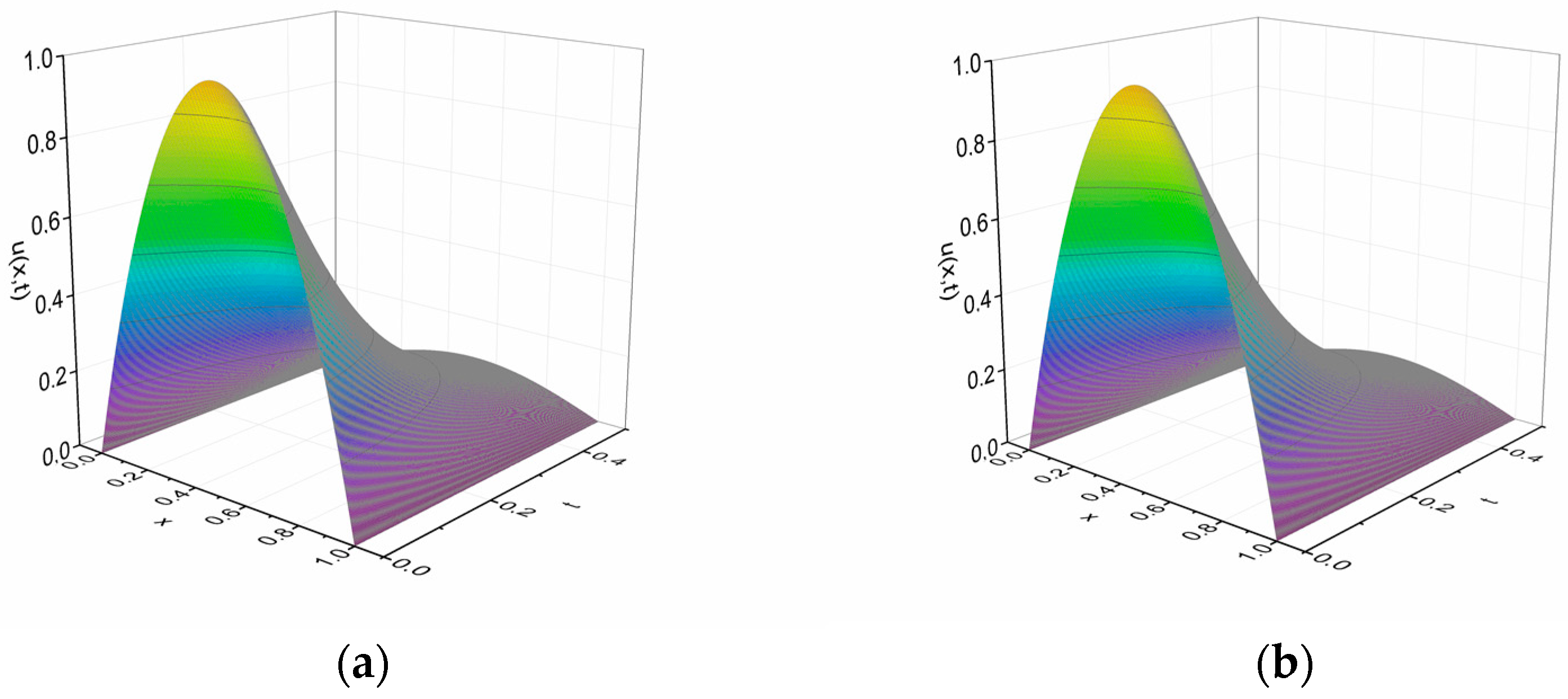
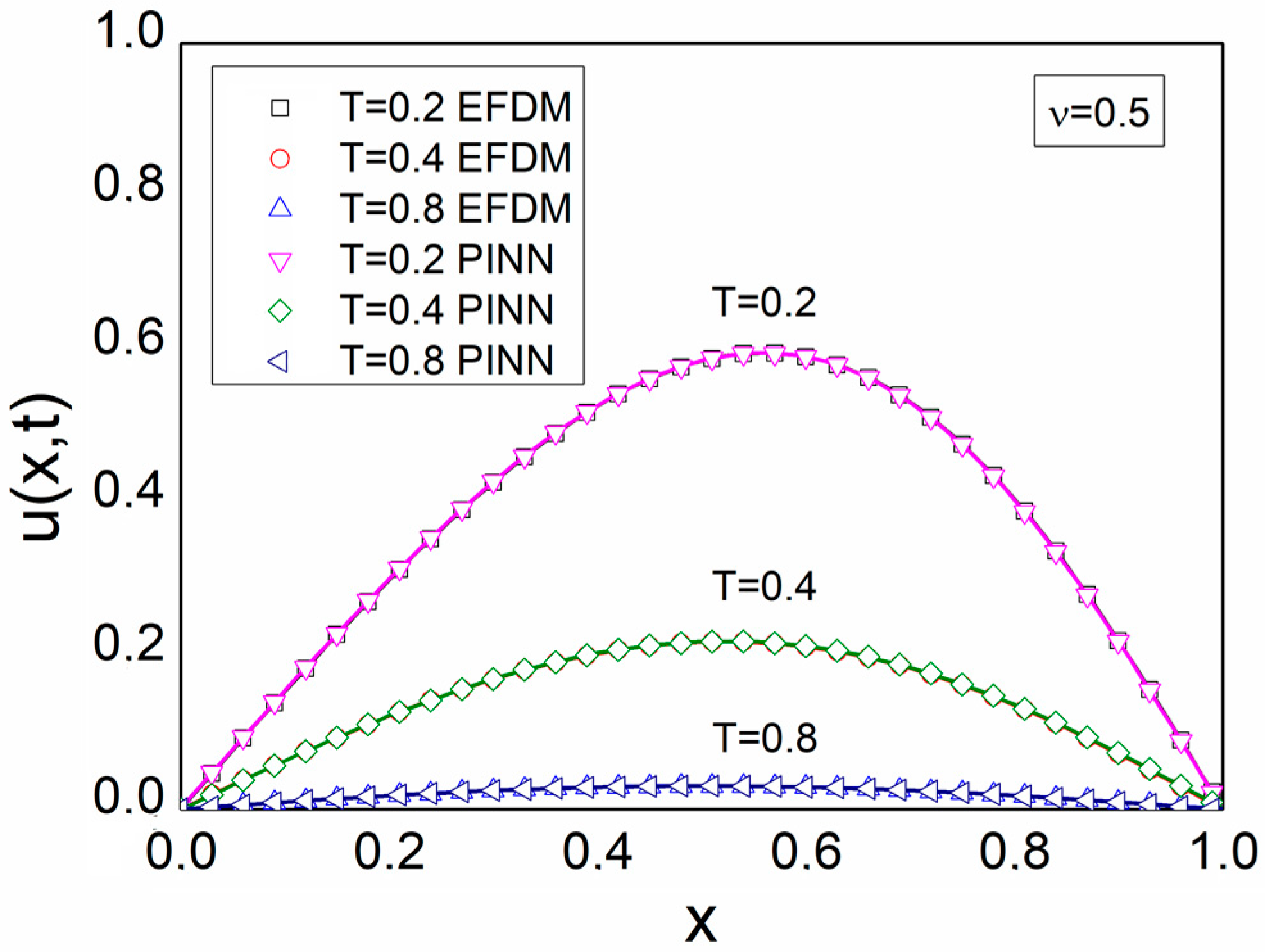
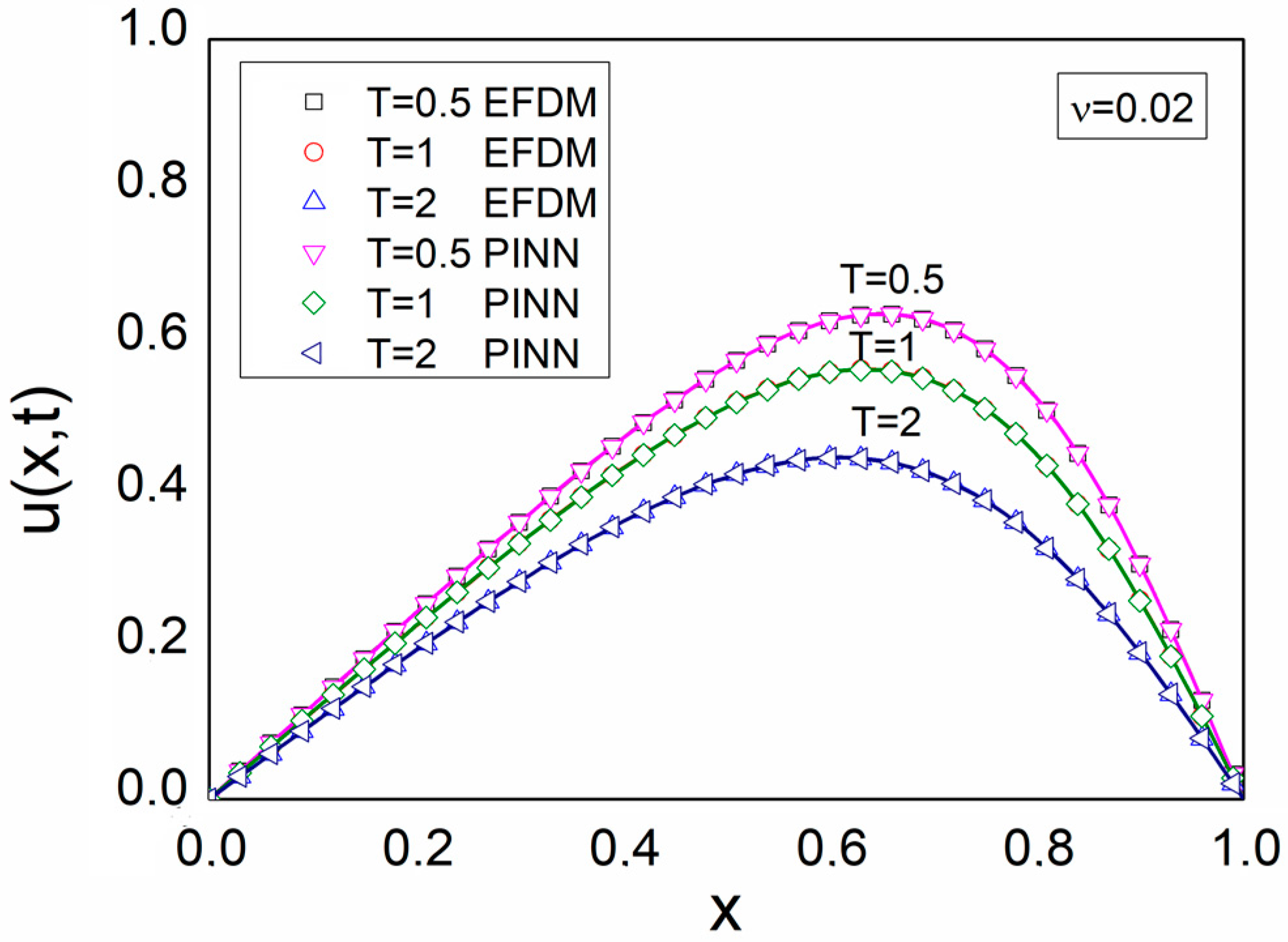
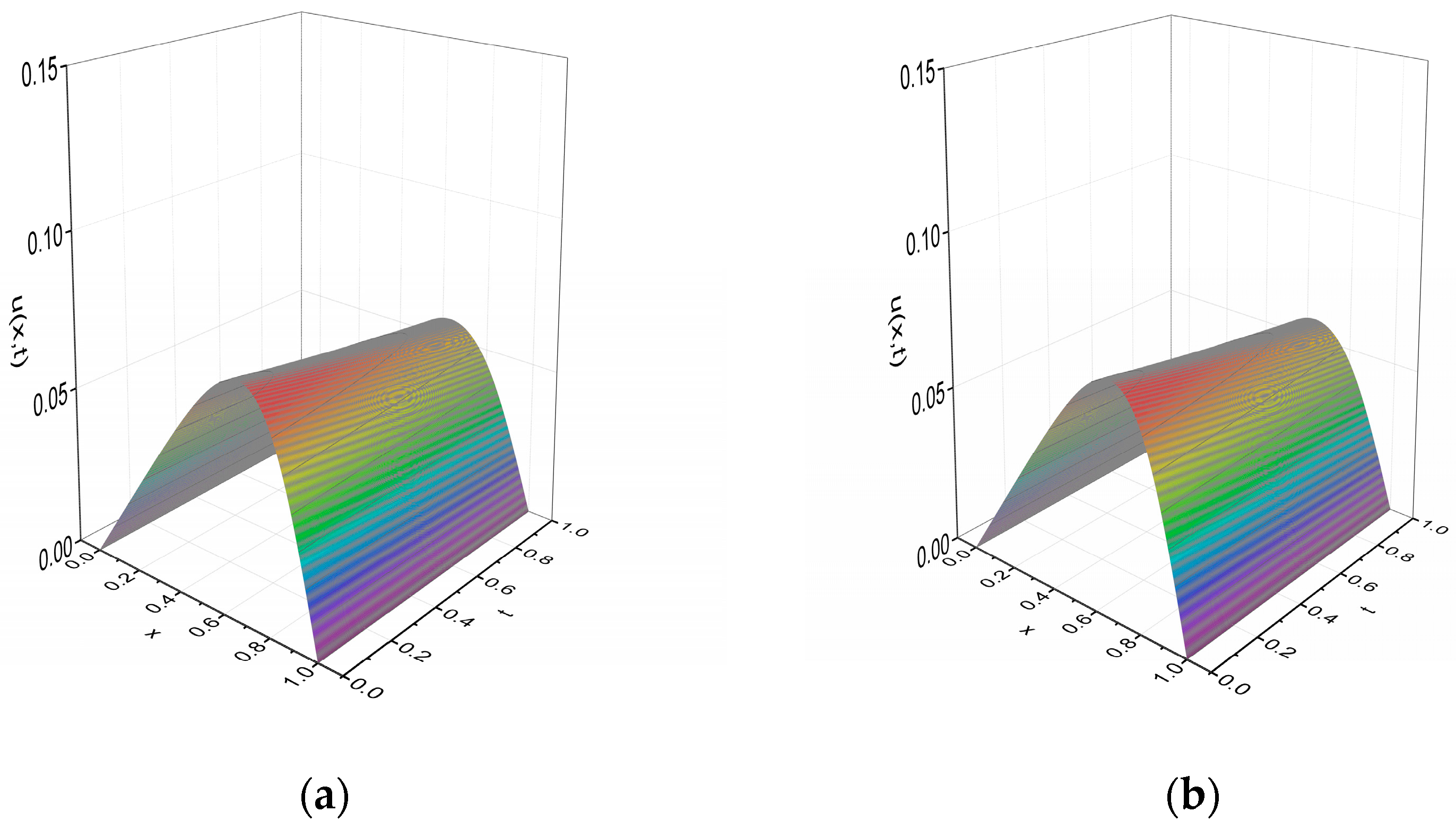
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Korshunova, A.A.; Rozanova, O.S. The Riemann Problem for the Stochastically Perturbed Non-Viscous Burgers Equation and the Pressureless Gas Dynamics Model. In Proceedings of the International Conference Days on Diffraction 2009, St. Petersburg, Russia, 26–29 May 2009. [Google Scholar]
- Hills, R.G. Model Validation: Model Parameter and Measurement Uncertainty. J. Heat Transf. 2005, 128, 339–351. [Google Scholar] [CrossRef]
- Sugimoto, N.; Kakutani, T. ‘Generalized Burgers’ Equation’ for Nonlinear Viscoelastic Waves. Wave Motion 1985, 7, 447–458. [Google Scholar] [CrossRef]
- Yonti Madie, C.; Kamga Togue, F.; Woafo, P. Numerical Solution of the Burgers’ Equation Associated with the Phenomena of Longitudinal Dispersion Depending on Time. Heliyon 2022, 8, e09776. [Google Scholar] [CrossRef] [PubMed]
- Rodin, E.Y. On Some Approximate and Exact Solutions of Boundary Value Problems for Burgers’ Equation. J. Math. Anal. Appl. 1970, 30, 401–414. [Google Scholar] [CrossRef]
- Benton, E.R.; Platzman, G.W. A Table of Solutions of the One-Dimensional Burgers Equation. Q. Appl. Math. 1972, 30, 195–212. [Google Scholar] [CrossRef]
- Wolf, K.B.; Hlavatý, L.; Steinberg, S. Nonlinear Differential Equations as Invariants under Group Action on Coset Bundles: Burgers and Korteweg-de Vries Equation Families. J. Math. Anal. Appl. 1986, 114, 340–359. [Google Scholar] [CrossRef]
- Nerney, S.; Schmahl, E.J.; Musielak, Z.E. Limits to Extensions of Burgers’ Equation. Q. Appl. Math. 1996, 54, 385–393. [Google Scholar] [CrossRef]
- Kudryavtsev, A.G.; Sapozhnikov, O.A. Determination of the Exact Solutions to the Inhomogeneous Burgers Equation with the Use of the Darboux Transformation. Acoust. Phys. 2011, 57, 311–319. [Google Scholar] [CrossRef]
- Kutluay, S.; Bahadir, A.R.; Özdeş, A. Numerical Solution of One-Dimensional Burgers Equation: Explicit and Exact-Explicit Finite Difference Methods. J. Comput. Appl. Math. 1999, 103, 251–261. [Google Scholar] [CrossRef]
- Hassanien, I.A.; Salama, A.A.; Hosham, H.A. Fourth-Order Finite Difference Method for Solving Burgers’ Equation. Appl. Math. Comput. 2005, 170, 781–800. [Google Scholar] [CrossRef]
- Bahadır, A.R. A Fully Implicit Finite-Difference Scheme for Two-Dimensional Burgers’ Equations. Appl. Math. Comput. 2003, 137, 131–137. [Google Scholar] [CrossRef]
- Kadalbajoo, M.K.; Sharma, K.K.; Awasthi, A. A Parameter-Uniform Implicit Difference Scheme for Solving Time-Dependent Burgers’ Equations. Appl. Math. Comput. 2005, 170, 1365–1393. [Google Scholar] [CrossRef]
- Mukundan, V.; Awasthi, A. Linearized Implicit Numerical Method for Burgers’ Equation. Nonlinear Eng. 2016, 5, 219–234. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-Informed Neural Networks: A Deep Learning Framework for Solving Forward and Inverse Problems Involving Nonlinear Partial Differential Equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics Informed Deep Learning (Part I): Data-Driven Solutions of Nonlinear Partial Differential Equations. arXiv 2017, arXiv:1711.10561. [Google Scholar]
- Lu, L.; Meng, X.; Mao, Z.; Karniadakis, G.E. DeepXDE: A Deep Learning Library for Solving Differential Equations. SIAM Rev. 2021, 63, 208–228. [Google Scholar] [CrossRef]
- Markidis, S. The Old and the New: Can Physics-Informed Deep-Learning Replace Traditional Linear Solvers? Front. Big Data 2021, 4, 669097. [Google Scholar] [CrossRef]
- Cole, J.D. On a Quasi-Linear Parabolic Equation Occurring in Aerodynamics. Q. Appl. Math. 1951, 9, 225–236. [Google Scholar] [CrossRef]
- Wood, W.L. An Exact Solution for Burger’s Equation. Commun. Numer. Methods Eng. 2006, 22, 797–798. [Google Scholar] [CrossRef]
- Winnicki, I.; Jasinski, J.; Pietrek, S. New approach to the Lax-Wendroff modified differential equation for linear and nonlinear advection. Numer. Methods Partial. Differ. Equ. 2019, 35, 2275–2304. [Google Scholar] [CrossRef]
- Savović, S.; Drljača, B.; Djordjevich, A. A comparative study of two different finite difference methods for solving advection–diffusion reaction equation for modeling exponential traveling wave. Ric. Mat. 2022, 71, 245–252. [Google Scholar] [CrossRef]
- Yang, X.; Ralescu, D.A. A Dufort–Frankel scheme for one-dimensional uncertain heat equation. Math. Comput. Simul. 2021, 181, 98–112. [Google Scholar] [CrossRef]
- Nagy, Á.; Omle, I.; Kareem, H.; Kovács, E.; Barna, I.F.; Bognar, G. Stable, Explicit, Leapfrog-Hopscotch Algorithms for the Diffusion Equation. Computation 2021, 9, 92. [Google Scholar] [CrossRef]
- Bakodah, H.O.; Al-Zaid, N.A.; Mirzazadeh, M.; Zhou, Q. Decomposition method for Solving Burgers’ Equation with Dirichlet and Neumann boundary conditions. Optik 2017, 130, 1339–1346. [Google Scholar] [CrossRef]

| T | Error (EFDM) | Error (PINN) | |
|---|---|---|---|
| ν = 0.5 | 0.02 | 5.14 × 10−7 | 2.56 × 10−5 |
| 0.05 | 5.07 × 10−7 | 4.96 × 10−5 | |
| 0.1 | 5.43 × 10−5 | 9.51 × 10−5 | |
| ν = 0.05 | 0.5 | 4.43 × 10−7 | 7.09 × 10−6 |
| 0.7 | 2.38 × 10−7 | 1.46 × 10−6 | |
| 0.9 | 7.03 × 10−8 | 1.02 × 10−6 |
| T | Error (EFDM) | Error (PINN) | |
|---|---|---|---|
| ν = 0.5 | 0.05 | 5.36 × 10−8 | 2.16 × 10−4 |
| 0.25 | 2.37 × 10−7 | 2.27 × 10−6 | |
| 0.5 | 1.14 × 10−7 | 1.57 × 10−4 | |
| ν = 0.1 | 0.3 | 3.80 × 10−9 | 9.09 × 10−7 |
| 0.5 | 6.19 × 10−7 | 1.65 × 10−4 | |
| 0.7 | 4.34 × 10−7 | 4.79 × 10−5 |
| T | Error (EFDM) | Error (PINN) | |
|---|---|---|---|
| ν = 0.5 | 0.2 | 6.05 × 10−5 | 9.72 × 10−4 |
| 0.4 | 6.07 × 10−5 | 7.56 × 10−4 | |
| 0.8 | 1.24 × 10−5 | 2.32 × 10−4 | |
| ν = 0.02 | 0.5 | 3.85 × 10−6 | 2.15 × 10−5 |
| 1 | 7.45 × 10−6 | 2.33 × 10−5 | |
| 2 | 1.12 × 10−5 | 3.27 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Savović, S.; Ivanović, M.; Min, R. A Comparative Study of the Explicit Finite Difference Method and Physics-Informed Neural Networks for Solving the Burgers’ Equation. Axioms 2023, 12, 982. https://doi.org/10.3390/axioms12100982
Savović S, Ivanović M, Min R. A Comparative Study of the Explicit Finite Difference Method and Physics-Informed Neural Networks for Solving the Burgers’ Equation. Axioms. 2023; 12(10):982. https://doi.org/10.3390/axioms12100982
Chicago/Turabian StyleSavović, Svetislav, Miloš Ivanović, and Rui Min. 2023. "A Comparative Study of the Explicit Finite Difference Method and Physics-Informed Neural Networks for Solving the Burgers’ Equation" Axioms 12, no. 10: 982. https://doi.org/10.3390/axioms12100982
APA StyleSavović, S., Ivanović, M., & Min, R. (2023). A Comparative Study of the Explicit Finite Difference Method and Physics-Informed Neural Networks for Solving the Burgers’ Equation. Axioms, 12(10), 982. https://doi.org/10.3390/axioms12100982










