An Emotionally Intuitive Fuzzy TODIM Methodology for Decision Making Based on Online Reviews: Insights from Movie Rankings

Abstract

With the burgeoning growth of the internet, online evaluation systems have become increasingly pivotal in shaping consumer decision making. In this context, this study introduces an intuitionistic fuzzy TODIM (an acronym in Portuguese for interactive and multicriteria decision making) methodology to rank products based on online reviews. Our approach aims to enhance user decision making efficiency and address the prevalent issue of information overload. Initially, we devised a product attribute emotion quantification framework within the confines of the intuitionistic fuzzy paradigm. This allows for the transformation of online reviews into exact functional outputs via our advanced intuitionistic fuzzy scoring mechanism and its associated precise function. Following this, we take into account the inherent correlation among product attributes, leading to the development of an attribute-associated intuitionistic fuzzy model. This model further ascertains the dominance degree of alternative products. Moreover, by integrating the risk aversion factor, we can derive a hierarchical structure for alternative products, aiding in the prioritization process. Finally, this paper validates the proposed method using movie sequencing as a case study. The results show that the proposed method, which takes into account the emotional tendencies of different attributes in a movie and the different preferences of viewers in the attribute weighting and movie selection process, is more reasonable than methods proposed in previous studies.

1. Introduction

The unprecedented growth of the Internet and social media platforms has led to the emergence of specialized websites, such as those dedicated to books and music, as well as e-commerce sites. As a result, user reviews have burgeoned as a primary conduit for information dissemination. A significant portion of the public now gravitates towards online platforms to voice their opinions, with experiential products like movies particularly benefiting from this trend [1]. Websites like Douban and Rotten Tomatoes have evolved into primary sources for audiences for movie details and reviews. Concurrently, there has been a noticeable uptick in the quality, expertise, and social interactivity of these reviews. The emotional slant of these reviews wields considerable influence over potential consumers’ decisions [2]. Factors such as online reviews, ratings, and extensive feedback play a pivotal role in influencing consumer decisions.

However, the deluge of reviews brings its own challenges, notably the phenomenon of information overload. Current recommendation systems falter in tailoring suggestions to individual genre preferences, highlighting the pressing need to deftly extract and harness the emotional nuances from multitudes of online reviews [3]. This extraction process aims to guide consumers towards more informed decisions.

While some review platforms showcase aggregate product ratings to circumvent the necessity of sifting through individual reviews, the text within reviews remains invaluable for potential consumers [4]. Therefore, efficiently pinpointing crucial information within these reviews is essential for refining consumer decision making. Notably, given that movies are experiential products, there is a surprising dearth of research on movie sorting. This paper seeks to bridge this gap and validate the proposed method by using movies as an example.

Historically, ranking methodologies grounded in online reviews have predominantly zeroed in on positive and negative sentiments, overlooking the nuances of neutral emotions [5,6,7,8,9,10]. Such oversights can lead to the omission of crucial information. Recent academic endeavors have harnessed multi-attribute decision making (MADM) methodologies for online product categorization. For instance, Fan et al. [11] derived a comparative superiority degree for various alternatives using the distribution percentages of specific features across distinct commodities, employing the PROMETHEE II (Preference Ranking Organization Method for Enrichment of Evaluations) method for comprehensive evaluation. In another study, Fan et al. [12] leveraged user ratings from online reviews to formulate two utility functions, with the subsequent application of the TOPSIS (Technique for Order Preference by Similarity to an Ideal Solution) method for holistic evaluation and ranking. Other notable works include Lee et al.’s [13] utilization of hierarchical deep neural networks (DNNs) for product ranking, and Wang et al.’s [14] user-centric commodity recommendation model. As a result of our research, we found that many extant studies exhibit a propensity to view products monolithically, often sidelining detailed attributes and features. Some product ranking methods based on online reviews only take into account the positive and negative affective tendencies of online reviews, ignoring the fact that the affective tendencies in the reviews can be neutral, i.e., ambiguous information, which can lead to a loss of information in the decision making process. Established models like TOPSIS and PROMETHEE II, premised on the notion of the decision maker’s absolute rationality, disregard the psychological intricacies underpinning the decision making process [11,12]. The TODIM method is appropriate for illustrating the psychological behavior of consumers during the product prioritization process [15,16]. Its central concept involves determining gain and loss values by comparing the characteristic values of each alternative product, and then calculating the dominance degree between every pair of alternatives and the overall prospect value of each product [17,18]. The alternative products are ranked based on their overall prospect value.

To address these lacunae, this paper embarks on an exploration of product ranking, leveraging online review data within an intuitionistic fuzzy framework. We introduce an intuitionistic fuzzy TODIM methodology, predicated on the multifaceted aspects of product reviews, particularly emphasizing the quantification of emotional tendencies across varying product attributes. This method encompasses the following:

(1)

The creation of a quantitative model for product attribute sentiment within an intuitionistic fuzzy paradigm. Recognizing the diverse preferences among consumers, we harness the Cemotion library, a sentiment analysis tool rooted in Bert, to discern nuanced emotional cues from reviews. Subsequently, we introduce the emotional intuition fuzzy value (E-IFV), which intuitively demonstrates the level of support for an attribute by integrating multidimensional eigenvalues of a product attribute with its emotional tendency.

(2)

An enhancement of the current intuitionistic fuzzy score function is presented. We analyze existing research to discern gaps in the current model. An augmented intuitionistic fuzzy score function, coupled with an exact function, is proposed, aiming to streamline decision making. This enhancement amalgamates concepts from hesitation allocation and voting models.

(3)

The integration of the TODIM approach to classify alternative products. The correlation among attributes is acknowledged, with the DEMATEL (Decision Making Trial and Evaluation Laboratory) method determining attribute weights for distinct product genres. These weights, in tandem with the loss aversion coefficients within the TODIM model, ascertain the relative prominence of alternative products. The final result is a personalized ranking, derived from consumer preferences, and a loss aversion risk factor.

By synthesizing information from online comments, likes, and comment volumes into intuitive fuzzy values, and aligning products with consumer attribute preferences, we aim to significantly augment the consumers’ decision making efficiency. In essence, our refined intuitionistic fuzzy TODIM product ranking method, rooted in multidimensional product review features, integrates diverse data sources, providing consumers with a tailored decision making guide.

2. Materials and Methods

This article introduces a novel methodology for product ranking by integrating insights from online reviews with inherent product attributes. In the intuitionistic fuzzy environment, the emotional tendency of product attributes is transformed into an emotional intuitionistic fuzzy value (E-IFV); in order to effectively compare the magnitude of intuitionistic fuzzy numbers, an intuitionistic fuzzy score function and an intuitionistic fuzzy exact function are proposed. Finally, a product ranking model based on online reviews is established by integrating the TODIM method. As this paper is based on the study of product ranking in an intuitionistic fuzzy environment, the intuitionistic fuzzy score function and the exact function are proposed, and the advantages of the intuitionistic fuzzy value (IFV) and intuitionistic fuzzy set (IFS) in terms of representing the affective tendencies of product features are considered. This section presents the literature related to intuitionistic fuzzy sets.

Zadeh [19], in 1965, introduced the fuzzy set (FS) theory. However, as fuzzy multi-attribute decision making paradigms evolved, it became evident that fuzzy sets were insufficient in capturing decision makers’ uncertainty comprehensively [20]. Addressing this, Atanassov [21] unveiled the intuitionistic fuzzy sets theory. This enhanced approach emphasized both membership and non-membership degrees, providing a richer representation of a decision maker’s hesitations. Later on, Liu et al. [22,23] built upon this theory by incorporating sentiment analysis, allowing online product reviews to be represented by intuitionistic fuzzy numbers. Furthermore, Roszkowska et al. [24,25,26] introduced a composite measure. This measure was tailored to the evaluation of complex social phenomena using questionnaires, refining the fuzzy set based on “objective” data. Specifically, research [24] advocated for the use of interval intuitionistic fuzzy sets (I-VIFS) to articulate the data from questionnaires. They crafted the I-VIFS composite measure and utilized the outcomes to stipulate the optimistic coefficients, thereby defining the bounds of the interval for the I-VIFS parameters. Meanwhile, other reserach [25] employed the intuitionistic fuzzy synthesis measure (IFSM) based on pattern object distance. They suggested translating ordered data using intuitionistic fuzzy sets and juxtaposed the results with traditional methods. Çalı and Balaman [27] used IFS to represent online ratings of hotel customers and used IF-ELECTRE to rank alternative hotels integrated with VIKOR. In this paper, we draw inspiration from the literature [24] and aim to augment the precision of product attributes tied to intuitionistic fuzzy values by formulating multidimensional eigenvalues for these attributes.

Upon this proposition, our subsequent focus revolved around refining the intuitionistic fuzzy multi-attribute decision theory to bolster decision making efficacy. Of paramount importance here is the intuitionistic fuzzy score function, pivotal for comparing and ranking intuitionistic fuzzy numbers. Despite significant contributions from scholars like Chen and HONG [28,29], certain aspects of these functions, such as the hesitancy degree’s impact on scheme ranking, remain under-explored.

While significant strides have been made in areas like text sentiment analysis and multi-attribute decision making using online reviews, specific challenges persist:

(1)

The existing research often overlooks neutral and ambiguous sentiments in reviews.

(2)

Most research presumes attribute independence, neglecting potential inter-attribute correlations.

(3)

Models like TOPSIS tend to assume complete decision maker rationality, sidelining psychological influences.

(4)

Research surrounding intuitive fuzzy score functions requires bolstering to achieve improved accuracy in intuitive fuzzy number discrimination.

Addressing these challenges, this paper presents a product-ranking model anchored in consumer preferences. By amalgamating sentiment analysis with intuitionistic fuzzy sets and integrating the TODIM multi-attribute decision making method, we aim to elevate decision making efficiency for consumers, as exemplified using data from the Douban (https://movie.douban.com (accessed on 13 May 2023)) platform.

3. Problem Description

Prior to finalizing a product selection, consumers frequently consult various online indicators including reviews, ratings, aggregate review counts, and other pertinent metrics. A substantial body of research corroborates the utility of these scoring data in facilitating informed decisions [30,31,32,33].

The primary challenge addressed in this study is to formulate a product ranking system that serves as a robust decision making tool for consumers. This ranking integrates data from online reviews and the associated engagement metrics—such as “likes” and comment counts—and takes into consideration consumers’ preferences related to specific product attributes. The overarching goal is to improve the decision making efficiency for potential consumers. The subsequent sections detail the representations and precise definitions of the sets and variables relevant to this problem.

Let $A=\{A_1,A_2,\cdots ,A_m\}$ be the set of products that the consumer is interested in choosing, where $A_i$ denotes the ith product, $i=1,2,\cdots ,m$.

Let $F=\{f_1,f_2,\cdots ,f_n\}$ be the set of n attributes of the alternative product, where $f_j$ denotes the jth attribute, $j=1,2,\cdots ,n$.

Let $w=\left[w_1,w_2,\cdots ,w_n\right]$ be a vector of product attribute weights, where $w_j$ is the weight corresponding to attribute $f_j$. $w_j\ge 0$, ${\displaystyle \sum _{j=1}^n{w}_j}=1$. The weights represent the differences in consumer preferences for product attributes.

Let $Q=\{q_1,q_2,\cdots ,q_n\}$ be the number of online reviews for the alternative product, where $q_i$ is the number of online reviews for product $A_i$, $i=1,2,\cdots ,n$.

The following collections will be described below:

Suppose $z_{p,q_i}^j$ denotes the number of “likes” for the qth comment under the jth attribute of product $A_i$. If the sentiment tendency of the qth comment is positive, then $z_{p,q_i}^j\in z_{pos}^{f_j}$, otherwise $z_{p,q_i}^j=0$;

Suppose $z_{n,q_i}^j$ denotes the number of “likes” for the qth comment under the jth attribute of product $A_i$. If the sentiment tendency of the qth comment is negative, then $z_{n,q_i}^j\in z_{neg}^{f_j}$, otherwise $z_{n,q_i}^j=0$;

Suppose $t_{p,q_i}^j$ denotes the number of words of the qth comment under the jth attribute of product $A_i$. If the sentiment tendency of the qth comment is positive, then $t_{p,q_i}^j\in t_{pos}^{f_j}$, otherwise $t_{p,q_i}^j=0$;

Suppose $t_{n,q_i}^j$ denotes the number of words of the qth comment under the jth attribute of product $A_i$. If the sentiment tendency of the qth comment is negative, then $t_{n,q_i}^j\in t_{neg}^{f_j}$, otherwise $t_{n,q_i}^j=0$;

Let $z_{pos}^{f_j}=\{z_{p,1}^j,z_{p,2}^j,\cdots ,z_{p,q_i}^j\}$ be the set consisting of the number of “likes” by consumers for the comments of product $A_i$ on attribute $f_j$ with a positive emotional tendency, where $z_{p,k}^j$ denotes the data of likes for the kth comment on product $A_i$ on attribute $f_j$, $k=1,2,\cdots ,q_i$, $i=1,2,\cdots ,m$.

Let $z_{neg}^{f_j}=\{z_{n,1}^j,z_{n,2}^j,\cdots ,z_{n,q_i}^j\}$ be the set consisting of the number of “likes” by consumers for the comments of product $A_i$ on attribute $f_j$ with a negative emotional tendency, where $z_{n,k}^j$ denotes the data of likes for the kth comment on product $A_i$ on attribute $f_j$, $k=1,2,\cdots ,q_i$, $i=1,2,\cdots ,m$.

Let $t_{pos}^{f_j}=\{t_{p,1}^j,t_{p,2}^j,\cdots ,t_{p,q_i}^j\}$ be the set consisting of the word counts of the consumer comments on the product $A_i$ on attribute $f_j$ with a positive affective tendency, where $t_{p,k}^j$ denotes the word count of the kth comment on the product $A_i$ on attribute $f_j$,$k=1,2,\cdots ,q_i$, $i=1,2,\cdots ,m$.

Let $t_{neg}^{f_j}=\{t_{n,1}^j,t_{n,2}^j,\cdots ,t_{n,q_i}^j\}$ be the set consisting of the word counts of the consumer’s comments on the product $A_i$ on attribute $f_j$ with a negative affective tendency, where $t_{n,k}^j$ denotes the word count of the kth comment on the product $A_i$ on attribute $f_j$, $k=1,2,\cdots ,q_i$, $i=1,2,\cdots ,m$.

The process of problem solving in this research is divided into two primary segments:

• Firstly, this investigation introduces a model tailored to the quantification of emotions within the realm of intuitionistic fuzzy contexts. The preliminary step involves the transformation of online product reviews into intuitionistic fuzzy numbers. Subsequently, using these comments, we propose an improved intuitionistic method for fuzzy and exact functions. This leads to the derivation of intuitionistic fuzzy exact functions anchored to specific product attributes.
• Secondly, the ranking of alternative products is executed via the enhanced intuitionistic fuzzy TODIM methodology, emphasizing attribute associations. Acknowledging the interdependencies among attributes, the DEMATEL approach is deployed to ascertain attribute weights. The dominance hierarchy amongst products is determined utilizing the intuitionistic fuzzy TODIM methodology. This hierarchy, when integrated with the risk tolerance parameters of the consumer, culminates in a bespoke product ranking schema.

The flowchart for solving the problem is shown in Figure 1.

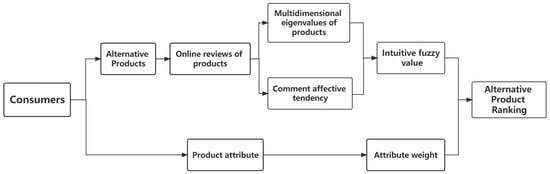
Figure 1. The process of problem solving.

4. A Quantitative Model of Product Attribute Sentiment in an Intuitively Ambiguous Environment

In order to solve the above problems, this section proposes a quantitative model of emotion based on product attributes in an intuitionistic fuzzy environment. The methodology comprises three parts:

• Identification of emotional tendencies in online product reviews;
• Multidimensional eigenvalue computation based on product attributes;
• Calculation of emotional intuition fuzzy values based on product attributes.

4.1. Identification of Emotional Tendencies in Online Product Reviews

This study uses Cemotion, a Chinese sentiment tendency analysis library based on Bert, to identify positive, neutral, and negative sentiment tendencies regarding alternative product attributes in online product reviews. Cemotion’s model is trained by a recurrent neural network, which returns a confidence level between 0 and 1 for the sentiment tendency of Chinese text and can accurately identify the sentiment tendency of online product reviews by linking them to the context of the online reviews.

Using the movie Titanic as an example, Table 1 presents some of the identified movie review data. In Figure 2, (a) illustrates the distribution of various attribute comments among online reviews of the movie Titanic, while (b) shows the proportion of the emotional tendency of the “Frame” attribute in those reviews.

Table 1. Partial movie review data obtained from emotional tendency recognition.

Review Text	Emotion Score	Analysis Result	Number of Favorable Reviews
The old couple who had no fear of death, the band who didn’t let the outside world interfere, the man who pretended to be a father for a living, the woman who whistled for her lover. All for a kind of spiritual attachment.	0.9961	positive	15,204
It will always be the film I have seen the most, the most moving and the best in the cinema	0.9942	positive	12,114
In the film organized by the school, people seemed to be curious about the love process between rose and jack. However, the scene that touched me was that the ship was about to sink, and the gentlemen of the sea band arranged their bow ties and played the last song solemnly. At that moment, it seemed to hear a soulless song ringing.	0.9996	positive	20,726

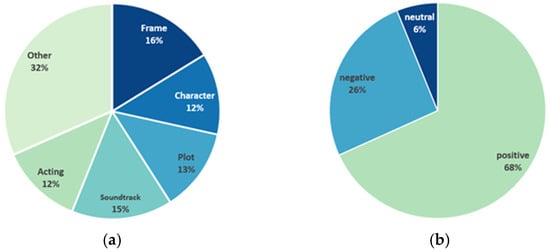
Figure 2. Relevant analysis of online reviews of the movie Titanic. (a) Distribution of attributes in reviews of the movie Titanic. (b) Percentage of emotional tendencies of “Frame” attributes of reviews of the movie Titanic.

4.2. Multidimensional Eigenvalue Computation Based on Product Attributes

Consumers usually refer to existing online reviews, ratings, the number of likes, the number of comments, and other information to make a comparative choice of products before making a decision [34,35]. Therefore, in this paper, multidimensional eigenvalues of products are introduced to improve the reasonableness of the ranking [36,37]. Since the credibility of a comment can be determined by the number of likes it receives [31], the length of the text [36,38,39], and the emotion it conveys, this study used the number of likes and the number of words in the text as indicators to evaluate the satisfaction of consumers with the product characteristics. The indicators will be described in more detail in the following sections.

Suppose there are m alternative products A_i and n decision attributes F = {f₁, f₂, ⋯, f_n}.

Definition 1.

“Positive Likes” is the ratio of the number of likes in the comments with positive emotional tendencies to the total number of likes in the comments of the corresponding attribute $f_j$ of the alternative product $A_i$.

• Positive liking rate:

$$Z_{pos}^{f_j}=\frac{1}{z_{f_j}}{\displaystyle \sum _{k=1}^{q_i}{z}_{p,k}^j},$$

(1)

where $Z_{pos}^{f_j}$ is the positive liking rate of the corresponding attribute $f_j$ of product $A_i$, and $z_{f_j}$ is the total number of likes of the alternative product $A_i$ on attribute $f_j$.

Definition 2.

“Negative Likes” is the ratio of the number of likes in the comments with negative emotional tendencies to the total number of likes in the comments of the corresponding attribute $f_j$ of the alternative product $A_i$.

• Negative liking rate:

$$Z_{neg}^{f_j}=\frac{1}{z_{f_j}}{\displaystyle \sum _{k=1}^{q_i}{z}_{n,k}^j},$$

(2)

where $Z_{neg}^{f_j}$ is the negative liking rate of the corresponding attribute $f_j$ of product $A_i$, and $z_{f_j}$ is the total number of likes of the alternative product $A_i$ on attribute $f_j$.

Definition 3.

“The Positive Text Rate” is the ratio of the number of words of text in the comments with positive emotional tendencies to the total number of words of text in the comments corresponding to attribute $f_j$ of alternative product $A_i$.

• Positive text rate:

$$T_{pos}^{f_j}=\frac{1}{t_{f_j}}{\displaystyle \sum _{k=1}^{q_i}{t}_{p,k}^j},$$

(3)

where $T_{pos}^{f_j}$ is the positive text rate of the corresponding attribute $f_j$ of product $A_i$, and $t_{f_j}$ is the total number of words for the alternative product $A_i$ on attribute $f_j$.

Definition 4.

“The Negative Text Rate” is the ratio of the number of words of text in the comments with negative emotional tendencies to the total number of words of text in the comments corresponding to attribute $f_j$ of alternative product $A_i$.

• Negative text rate:

$$T_{neg}^{f_j}=\frac{1}{t_{f_j}}{\displaystyle \sum _{k=1}^{q_i}{t}_{n,k}^j},$$

(4)

where $T_{neg}^{f_j}$ is the negative text rate of the corresponding attribute $f_j$ of product $A_i$, and $t_{f_j}$ is the total number of words for the alternative product $A_i$ on attribute $f_j$.

From Equations (1)–(4), we can obtain the text rate and like rate of the product $A_i$ corresponding to the attribute $f_j$. The multidimensional eigenvalue for the product attribute $f_j$ is obtained through further calculation:

Definition 5.

“The Positive Multidimensional Eigenvalue” $D_{pos}^{f_j}$ is the average of “The Positive Liking Rate” $Z_{pos}^{f_j}$ and “The Positive Text Rate” $T_{pos}^{f_j}$ of the attribute $f_j$ corresponding to product $A_i$.

• Positive multidimensional eigenvalues:

$$D_{pos}^{f_j}=\frac{Z_{pos}^{f_j}{+T}_{pos}^{f_j}}{2},$$

(5)

Definition 6.

“The Negative Multidimensional Eigenvalue” $D_{neg}^{f_j}$ is the average of “The Negative Liking Rate” $Z_{neg}^{f_j}$ and “The Negative Text Rate” $T_{neg}^{f_j}$ of the attribute $f_j$ corresponding to product $A_i$.

• Negative multidimensional eigenvalues:

$$D_{neg}^{f_j}=\frac{Z_{neg}^{f_j}{+T}_{neg}^{f_j}}{2},$$

(6)

4.3. Calculation of Sentiment Means for Product Attributes

The identification of affective tendencies for the products’ online product reviews through Section 4.1 yields positive, neutral, and negative affective tendencies regarding the attributes of the alternative products. The identified affective tendencies are further explained below.

Let ${\alpha }_{\mathrm{ik}}^{\mathrm{j}}$, ${\beta }_{\mathrm{ik}}^{\mathrm{j}}$, and ${\nu }_{\mathrm{ik}}^{\mathrm{j}}$ be the positive, negative, and neutral sentiment strengths of the kth comment by the consumer on attribute $f_j$ of the alternative product $A_i$, respectively. Since this study uses Cemotion, a Bert-based Chinese affective tendency analysis library, for identification, Cemotion returns an affective tendency confidence level between 0 and 1 for the Chinese text, so ${\alpha }_{\mathrm{ik}}^{\mathrm{j}},{\beta }_{\mathrm{ik}}^{\mathrm{j}},{\nu }_{\mathrm{ik}}^{\mathrm{j}}\in \left[0,1\right]$, and ${\alpha }_{\mathrm{ik}}^{\mathrm{j}}+{\beta }_{\mathrm{ik}}^{\mathrm{j}}+{\nu }_{\mathrm{ik}}^{\mathrm{j}}\in \left[0,1\right]$, $k=1,2,\cdots ,q_i$, $i=1,2,\cdots ,m$.

In the following, the mean values of positive, negative, and neutral emotions corresponding to attribute $f_j$ of alternative product $A_i$ will be calculated as follows:

$$p_{ij}^{pos}=\frac{1}{q_{f_j}}{\displaystyle \sum _{k=1}^{q_i}{\alpha }_{ik}^j},i=1,2,\cdots ,n,j=1,2\cdots ,m,$$

(7)

$$p_{ij}^{neg}=\frac{1}{q_{f_j}}{\displaystyle \sum _{k=1}^{q_i}{\beta }_{ik}^j},i=1,2,\cdots ,n,j=1,2\cdots ,m,$$

(8)

$$p_{ij}^{neu}=\frac{1}{q_{f_j}}{\displaystyle \sum _{k=1}^{q_i}{\nu }_{ik}^j},i=1,2,\cdots ,n,j=1,2\cdots ,m.$$

(9)

where $q_{f_i}$ is the total number of comments on attribute $f_j$ for alternative product $A_i$;

$p_{ij}^{pos}$ is the mean value of positive sentiment about attribute $f_j$ for alternative product $A_i$;

$p_{ij}^{neg}$ is the mean value of negative sentiment about attribute $f_j$ for alternative product $A_i$;

and $p_{ij}^{neu}$ is the mean value of neutral sentiment about attribute $f_j$ for alternative product $A_i$.

4.4. Calculation of Intuitional Fuzzy Values

In this section, leveraging the unique characteristics of product reviews and integrating the foundational principles of IFV, we propose the emotional intuitionistic fuzzy value (E-IFV) model for product attributes. The E-IFV serves as an intuitive representation of the emotional tendencies associated with attributes in product reviews.

The concept of the emotional intuitionistic fuzzy value introduced in this paper is rooted in the theory of intuitionistic fuzzy value, which will be elaborated upon in subsequent sections.

Definition 7.

Suppose $X$ is an argument. If there are two mappings ${\mu }_A:X\to \left[0,1\right]$ and ${\nu }_A:X\to \left[0,1\right]$ above $X$ so that

$$x\in X|\to {\mu }_A\left(x\right)\in \left[0,1\right],$$

(10)

and

$$x\in X|\to {\nu }_A\left(x\right)\in \left[0,1\right],$$

(11)

simultaneously satisfy condition

$$0\le {\mu }_A\left(x\right)+{\nu }_A\left(x\right)\le 1,$$

(12)

${\mu }_A$  and  ${\nu }_A$  are said to determine an intuitionistic fuzzy set on  $X$, which can be denoted as

$$A=\left\{⟨x,{\mu }_A\left(x\right),{\nu }_A\left(x\right)⟩|x\in X\right\},$$

(13)

 where   ${\mu }_A\left(x\right)$  and   ${\nu }_A\left(x\right)$ are referred to as the degree of affiliation and non-affiliation of x. The degree of hesitancy is defined as the following equation:

$${\pi }_A=1-{\mu }_A\left(x\right)-{\nu }_A\left(x\right).$$

(14)

 For any  $x\in X$, there is $0\le {\pi }_A\le 1$.

To facilitate the understanding and application of intuitionistic fuzzy sets, Xu [40] defines $\alpha =\left(\mu ,\nu \right)$ as an intuitionistic fuzzy number, where $\mu \ge 0$, $\nu \ge 0$, and $\mu +\nu \le 1$, and the degree of hesitation of intuitionistic fuzzy number $\alpha$ is ${\pi }_{\alpha }=1-\mu -\nu$.

From the aforementioned definition, it is evident that the intuitionistic fuzzy set (IFS) can encapsulate affirmative, negative, and hesitant attitudes simultaneously, minimizing the loss of emotional information. This makes it a robust tool for representing ambiguous and uncertain data. Given the intricate and subjective nature of emotions in online product reviews, factors such as online reviews, ratings, and particularly the emotional sentiments within these reviews, significantly influence consumers’ inclination to select alternative products. To enhance the applicability of the intuitionistic fuzzy value, this paper introduces the emotional intuitionistic fuzzy value (E-IFV). This is achieved by integrating the emotional mean with the multidimensional eigenvalue of product attributes, building upon the foundational intuitionistic fuzzy value. The subsequent sections detail the calculation methodology for E-IFV.

$${\mu }_{ij}=p_{pos}^{ij}\cdot D_{pos}^{ij},$$

(15)

$${\nu }_{ij}=p_{neg}^{ij}\cdot D_{neg}^{ij},$$

(16)

$${\pi }_{ij}=1-{\mu }_{ij}-{\nu }_{ij},$$

(17)

$x_{ij}=\left({\mu }_{ij},{\nu }_{ij}\right)$ denotes the E-IFV of alternative product $A_i$ on the attribute word $f_j$.

Where ${\mu }_{ij}$, ${\nu }_{ij}$, and ${\pi }_{ij}$ are the degree of affiliation, non-affiliation, and hesitation of the alternative product $A_i$ on attribute word $f_j$, i.e., the consumers’ support, opposition, and neutrality to attribute $f_j$ to alternative product $A_i$.

5. A Study on the Improved Intuitionistic Fuzzy TODIM Model Based on Attribute Association for Product Ranking

This paper proposes s an improved intuitionistic fuzzy TODIM model for the correlation of attributes to rank alternative products, taking into account that consumer attributes vary person-to-person and that correlations exist between them. The model comprises two primary segments:

• An improved intuitionistic fuzzy score function is proposed, based on which an exact function is determined to improve the accuracy of comparing intuitionistic fuzzy numbers.
• Since the attributes are correlated, instead of being independent of each other, the weights for different product types’ attributes are determined using the DEMATEL method. This study employs the TODIM method to determine the superiority of alternative products. The loss aversion coefficient $\theta$, which reflects the consumer’s risk appetite, is combined with the ranking to provide personalized decision making suggestions for the consumer.

5.1. The Available Intuitionistic Fuzzy Score Function

Establishing relative dominance (superiority and inferiority relationships) between intuitionistic fuzzy numbers is pivotal to intuitionistic fuzzy multi-attribute decision making. Existing research offers multiple methodologies for computing the score function of intuitionistic fuzzy values [17,18,28,29,41,42,43,44,45,46], such as

$$S\left(\alpha \right)=\frac{{\mu }_{\alpha }}{2}+\frac{3{\nu }_{\alpha }}{2}-1,$$

(18)

$$S_1\left(\alpha \right)={\mu }_{\alpha }-{\nu }_a-\frac{1-{\mu }_{\alpha }-{\nu }_a}{2}=\frac{3{\mu }_{\alpha }-{\nu }_a-1}{2},$$

(19)

$$S_2\left(\alpha \right)={\mu }_{\alpha }\left(1+{\pi }_{\alpha }\right)-{\pi }_{\alpha }{}^2,$$

(20)

etc, where Equations (18)–(20) belong to the literature [44,45,46] respectively.

These studies provide new ideas for the improvement of intuitionistic fuzzy functions, but at the same time, there are shortcomings.

Counterexample 1.

Taking Equation (18) [44] as an example, suppose $\alpha =\left({\mu }_{\alpha },{\nu }_{\alpha }\right)$ is an intuitionistic fuzzy number, then let

$$S\left(\alpha \right)=\frac{{\mu }_{\alpha }}{2}+\frac{3{\nu }_{\alpha }}{2}-1,$$

(21)

 be the score value of $\alpha$ and $S\left(\alpha \right)$ be the score function of $\alpha$. For any two intuitionistic fuzzy numbers ${\alpha }_1$ and ${\alpha }_2$, there is then

• If $S\left({\alpha }_1\right)＜S\left({\alpha }_2\right)$, ${\alpha }_1\prec {\alpha }_2$;
• If  $S\left({\alpha }_1\right)＞S\left({\alpha }_2\right)$,  ${\alpha }_1\succ {\alpha }_2$;
• If $S\left({\alpha }_1\right)=S\left({\alpha }_2\right)$, ${\alpha }_1\sim {\alpha }_2$.

Suppose two intuitionistic fuzzy numbers ${\alpha }_1=\left(0,0.2\right)$ and ${\alpha }_2=\left(0，0.3\right)$ exist, which can be obtained using Equation (18), $S\left({\alpha }_1\right)=-0.7$, $S\left({\alpha }_2\right)=-0.55$. Obviously, $S\left({\alpha }_1\right)＜S\left({\alpha }_2\right)$, i.e., ${\alpha }_1\prec {\alpha }_2$. However, in the actual decision making process, people tend to choose a small degree of opposition to ${\alpha }_1$. At this time, Equation (18) cannot judge the size of the two intuitionistic fuzzy numbers. (For a comparison of the arithmetic examples of different intuitionistic fuzzy score function ranking methods, see Table 2 in Summary 5.2).

Table 2. Comparison of different intuitionistic fuzzy score functions.

Example	Sorting Methods	Sorting Results
${\alpha }_1=\left(0,0\right)$, ${\alpha }_2=\left(0.5,0.5\right)$	[29]	${\alpha }_1\sim {\alpha }_2$
	[28]
	[45]
	[44]	${\alpha }_1\prec {\alpha }_2$
	[46]
	Methodology of the paper	${\alpha }_1\prec {\alpha }_2$
${\alpha }_3=\left(0.5,0.2\right)$, ${\alpha }_4=\left(0.3,0\right)$	[28]	${\alpha }_3\sim {\alpha }_4$
	[29]	${\alpha }_3\succ {\alpha }_4$
	[45]
	[44]
	[46]
	Methodology of the paper	${\alpha }_3\prec {\alpha }_4$
${\alpha }_5=\left(0.9,0.1\right)$, ${\alpha }_6=\left(0.8,0\right)$	[28]	${\alpha }_5\sim {\alpha }_6$
	[29]	${\alpha }_5\succ {\alpha }_6$
	[45]
	[44]
	[46]	${\alpha }_5\prec {\alpha }_6$
	Methodology of the paper	${\alpha }_5\prec {\alpha }_6$
${\alpha }_7=\left(0,0.2\right)$, ${\alpha }_8=\left(0,0.3\right)$	[29]	${\alpha }_7\succ {\alpha }_8$
	[28]
	[45]
	[44]	${\alpha }_7\prec {\alpha }_8$
	[46]
	Methodology of the paper	${\alpha }_7\succ {\alpha }_8$
${\alpha }_9=\left(0.5,0.2\right)$$, {\alpha }_{10}=\left(0.5,0.3\right)$	[29]	${\alpha }_9\succ {\alpha }_{10}$
	[28]
	[45]
	[44]	${\alpha }_9\prec {\alpha }_{10}$
	[46]	${\alpha }_9\sim {\alpha }_{10}$
	Methodology of the paper	${\alpha }_9\succ {\alpha }_{10}$

From this, it can be found that the existing intuitionistic fuzzy score function has the following problems:

(1)

The same result is obtained when calculating two different intuitionistic fuzzy numbers, and it is impossible to judge the size of two intuitionistic fuzzy numbers.

(2)

Owing to the inherent constraints of the score function, the derived results occasionally contradict real-world decision making scenarios.

To enhance the comparative efficacy of intuitionistic fuzzy numbers and, in turn, refine the product ranking model, this study introduces a refined intuitionistic fuzzy score function and an exact function. Subsequently, we provide proof for the formula of this newly formulated intuitionistic fuzzy score function.

5.2. Improved Intuitionistic Fuzzy Score Function

In this paper, we introduce the concept of the improved intuitionistic fuzzy score function using a voting model as an illustrative example.

In real life, when faced with indecision, people often choose to wait and see what others do before making a final decision. Thus, for the intuitionistic fuzzy number $\alpha =({\mu }_{\alpha },{\nu }_{\alpha })$, suppose that during the first vote, $\mu$ represents the proportion of those who voted in favor, $\nu$ represents the proportion of those who voted against, and $\pi$ represents the proportion of those who voted neutrally; and during the second vote, since the hesitant part of the first vote is affected by the first vote, that during the second vote ${\pi }_{\mu }$ represents the part of the vote that voted in favor, ${\pi }_{\nu }$ is the part of the vote that voted against, and ${\pi }^2$ is the part of the vote that continued to be neutral. The cycle continues in rounds, calculating the sum of the proportional parts in favor. The intuitionistic fuzzy score function considered in this paper is the sum of the final proportions in favor:

$$S_E=\mu +\pi \mu +{\pi }^2\mu +\cdots +{\pi }^{n-1}\mu =\frac{\mu \left(1-{\pi }^n\right)}{1-\pi }=\frac{\mu \left(1-{\pi }^n\right)}{\mu +\nu },$$

(22)

The following equation is obtained by taking the limit of the formula:

$$\underset{n\to \infty }{\lim }{S}_E=\underset{n\to \infty }{\lim }\frac{\mu \left(1-{\pi }^n\right)}{\mu +\nu }=\frac{\mu }{\mu +\nu },$$

(23)

Therefore, this paper proposes an improved intuitionistic fuzzy score function as shown in the following equation:

Theorem 1.

Suppose $\alpha =({\mu }_{\alpha },{\nu }_{\alpha })$ is an intuitionistic fuzzy number, then

$$S_E=\frac{\mu }{\mu +\nu },$$

(24)

 is the score function of the intuitionistic fuzzy number $\alpha =({\mu }_{\alpha },{\nu }_{\alpha })$. In particular, when $\mu =\nu =0$, we define $S\left(\alpha \right)=0$.

The equation above reveals that the intuitionistic fuzzy score function proposed in this paper has limitations, since the degree of affiliation of the intuitionistic fuzzy number cannot be 0. To address this issue, the paper introduces the intuitionistic fuzzy exact function. This paper presents a study on intuitionistic fuzzy exact functions as follows: for an intuitionistic fuzzy number, a larger degree of affiliation is considered better while a smaller degree of non-affiliation is preferred. If the hesitation degree is taken into account, the smaller the hesitation degree, the better. Building on the above concepts, this paper puts forward the subsequent equation:

$$h_E=\frac{\mu -\nu }{\pi +1}+1,$$

(25)

where, to avoid the case of $\pi =0$, the denominator of the formula is taken as $\pi +1$.

Further simplifying the formula, the new intuitionistic fuzzy exact function given in this paper is defined as follows:

Theorem 2.

Suppose $\alpha =(\mu ,\nu )$ is an intuitionistic fuzzy number, then

$$h_E=\frac{2-2\nu }{\pi +1},$$

(26)

 is said to be an exact function of the intuitionistic fuzzy number $\alpha =(\mu ,\nu )$.

After proposing the intuitionistic fuzzy score function and intuitionistic fuzzy exact function, this paper proposes the following new ranking method for intuitionistic fuzzy numbers:

Definition 8.

Suppose that for any two intuitionistic fuzzy numbers  ${\alpha }_1=({\mu }_{{\alpha }_1},{\nu }_{{\alpha }_1})$ and ${\alpha }_2=({\mu }_{{\alpha }_2},{\nu }_{{\alpha }_2})$, $S_E\left({\alpha }_1\right)$ and $h_E\left({\alpha }_1\right)$ are the values of the score function and the exact function for ${\alpha }_1$, and $S_E\left({\alpha }_2\right)$ and $h_E\left({\alpha }_2\right)$ are the values of the score function and the exact function for ${\alpha }_2$. Then

• If  $S_E\left({\alpha }_1\right)＜S_E\left({\alpha }_2\right)$, then  ${\alpha }_1\prec {\alpha }_2$;
• If  $S_E\left({\alpha }_1\right)＞S_E\left({\alpha }_2\right)$, then  ${\alpha }_1\succ {\alpha }_2$;
• If  $S_E\left({\alpha }_1\right)＝S_E\left({\alpha }_2\right)$, then
• when  $h_E\left({\alpha }_1\right)＜h_E\left({\alpha }_2\right)$,  ${\alpha }_1\prec {\alpha }_2$,
• when  $h_E\left({\alpha }_1\right)＞h_E\left({\alpha }_2\right)$,  ${\alpha }_1\succ {\alpha }_2$,
• when  $h_E\left({\alpha }_1\right)＝h_E\left({\alpha }_2\right)$,  ${\alpha }_1\sim {\alpha }_2$.

The properties of the intuitionistic fuzzy score function proposed in this paper are described and formulas are proved in the following:

Property 1.

The score function $S_E\left(\alpha \right)$ of an intuitionistic fuzzy number $\alpha =(\mu ,\nu )$ is monotonically increasing with respect to the degree of affiliation $\mu$ and monotonically decreasing with respect to the degree of non-affiliation $\nu$.

Proof of Property 1.

Since

$$\frac{\partial S_E\left(\mu ,\nu \right)}{\partial \mu }=\frac{\nu }{{\left(\mu ＋\nu \right)}^2},$$

(27)

and $0\le \mu ＋\nu \le 1$, so $\frac{\nu }{{\left(\mu ＋\nu \right)}^2}\ge 0$, the score function of the intuitionistic fuzzy number $\alpha =(\mu ,\nu )$ is monotonically increasing with respect to the degree of affiliation $\mu$;

similarly

$$\frac{\partial S_E\left(\mu ,\nu \right)}{\partial \nu }=\frac{-\mu }{{\left(\mu ＋\nu \right)}^2},$$

(28)

and $0\le \mu \le 1$ and $0\le \mu ＋\nu \le 1$, so that $\frac{-\mu }{{\left(\mu ＋\nu \right)}^2}\le 0$, so the score function of the intuitionistic fuzzy number $\alpha =(\mu ,\nu )$ is monotonically decreasing with respect to the unaffiliated degree $\nu$, which is proved. □

Property 2.

Intuitionistic fuzzy score function $S_E\left(\alpha \right)\in \left[0,1\right]$.

Proof of Property 2.

Since Formula (24), and $0\le \mu \le \mu +\nu \le 1$, $0\le \frac{\mu }{\mu +\nu }\le 1$.

• In particular,

(1)

when $\mu =0$, then $S_E\left(\alpha \right)=0$;

(2)

when $\nu =0$, then $S_E\left(\alpha \right)=1$;

(3)

when $\mu =\nu =0$, then $S_E\left(\alpha \right)=0$.

Proof is completed. □

Property 3.

Suppose two intuitionistic fuzzy numbers ${\alpha }_1=({\mu }_1,{\nu }_1)$ and ${\alpha }_2=({\mu }_2,{\nu }_2)$. If ${\mu }_1＞{\mu }_2$ and ${\nu }_1＜{\nu }_2$, then $S_E\left({\alpha }_1\right)＞S_E\left({\alpha }_2\right)$.

Proof of Property 3.

Because

• $S_E\left({\alpha }_1\right)-S_E\left({\alpha }_2\right)=\frac{{\mu }_1}{{\mu }_1+{\nu }_1}-\frac{{\mu }_2}{{\mu }_2+{\nu }_2}=\frac{{\mu }_1\left({\mu }_2+{\nu }_2\right)-{\mu }_2\left({\mu }_1+{\nu }_1\right)}{\left({\mu }_1+{\nu }_1\right)\left({\mu }_2+{\nu }_2\right)}=\frac{{\mu }_1{\nu }_2-{\mu }_2{\nu }_1}{\left({\mu }_1+{\nu }_1\right)\left({\mu }_2+{\nu }_2\right)}$
• and ${\mu }_1＞{\mu }_2$ and ${\nu }_1＜{\nu }_2$, then ${\mu }_1{\nu }_2-{\mu }_2{\nu }_1＞0$, $\left({\mu }_1+{\nu }_1\right)\left({\mu }_2+{\nu }_2\right)＞0$; then, $\frac{{\mu }_1{\nu }_2-{\mu }_2{\nu }_1}{\left({\mu }_1+{\nu }_1\right)\left({\mu }_2+{\nu }_2\right)}＞0$, i.e., $S_E\left({\alpha }_1\right)-S_E\left({\alpha }_2\right)＞0$.
• It is clear that $S_E\left({\alpha }_1\right)＞S_E\left({\alpha }_2\right)$. Proof is completed. □

The proposed intuitionistic fuzzy function and intuitionistic fuzzy exact function are compared and analyzed with the existing methods in the following, and the results of the comparative analysis are shown in Table 2.

5.3. DEMATEL Determines Attribute Weights

In problems involving multi-attribute decision making, calculating indicator weights through traditional methods is often based on subjective or objective criteria to reflect the attributes’ characteristics, but this ignores the correlation between them. This paper utilizes the DEMATEL method to analyze the mutual influence relationship between attributes and determine their respective weights. The traditional multi-attribute decision making approach, which does not consider attribute weights in relation to each other, is addressed. Because attribute weights vary between different types of products, experts are invited to score the attributes of each product type. The average of these scores is then calculated to obtain the relative weights of the attributes for each particular product type.

Assuming that the alternative product to be evaluated $A_i$$(i=1,2,\cdots ,m)$ belongs to a certain category of products, the evaluation of the product attribute is $f_j$$(j=1,2,\cdots ,n)$ and that the category of the product is t, and r experts are invited to use the linguistic scale evaluation for evaluation and scoring on a five-level scale, then, the DEMATEL method is used to calculate the attribute weight matrix $W_{t,n}^r$ given by the r experts under the different categories of the product, and the specific representation is as follows:

$$W_{{}_{t,n}}^r=\left|\begin{array}{cccc}{w}_{11,r}& w_{12,r}& \cdots & w_{1n,r}\\ w_{21,r}& \cdots & \cdots & w_{2n,r}\\ \cdots & \cdots & \cdots & \cdots \\ w_{t1,r}& \cdots & \cdots & w_{tn,r}\end{array}\right|,$$

(29)

where t denotes the number of product types, n is the number of attributes of the product, and r is the number of experts.

Finally, the weights obtained by r experts are averaged to obtain the attribute weight matrix for different types of products:

$$\overline{W_{t,n}}=\frac{1}{r}{\displaystyle \sum _{s=1}^r{W}_{{}_{t,n}}^s},$$

(30)

where r denotes the number of experts.

The alternative product average weight vector is calculated as follows:

$$\overline{W}=\frac{1}{t}{\displaystyle \sum _{z=1}^t\overline{W_{z,n}}},$$

(31)

where $\overline{W}$ denotes the vector of average weights of alternative products and t is the number of categories of products.

5.4. A Product Ranking Method Based on the Intuitionistic Fuzzy TODIM Model

Multi-attribute decision making refers to a process where a decision maker identifies the best solution among various alternatives based on selected attributes; the method ranks and selects solutions by calculating their perceived superiority relative to each other. When selecting a product, consumers often consider various attributes to make alternative choices. This paper presents an emotion quantification model for online reviews of products, constructed in an intuitionistic fuzzy environment. Product attributes are transformed into intuitionistic fuzzy values. The differences between attributes of different types of products and the correlation relationship between them are considered. The DEMATEL method is used to obtain the attribute weights of the correlations. Finally, identifying the degree of superiority of alternative products based on consumer preferences is achieved using the intuitionistic fuzzy TODIM model. A detailed description of the decision making steps is provided below.

• Decision step:

Assume that $A=\{A_i|i\in M\}$ is a limited number of alternative product scenarios and that $f=\{f_j|j\in N\}$ is a finite set of attributes, where $N=\left\{1,2,3,\cdots ,n\right\}$ and the weight of each attribute is $w={(w_1,w_2,\cdots ,w_n)}^T$, where ${\displaystyle \sum _{i=1}^n{w}_i}=1$. The alternative product $A_i$ has an evaluation value of $I_{ij}$ under the product attribute $f_j$, where $I_{ij}$ expresses the intuitionistic fuzzy set. This results in a decision matrix of $m$ decision scenarios under n decision attributes.

$$D=\left[\begin{array}{cccc}{I}_{11}& I_{12}& \cdots & I_{1n}\\ I_{21}& I_{22}& \cdots & I_{2n}\\ ⋮& ⋮& ⋮& ⋮\\ I_{m1}& I_{m2}& \cdots & I_{mn}\end{array}\right],$$

(32)

the specific decision making steps are as follows:

normalize the original decision matrix $D={\left[I_{ij}\right]}_{m\times n}$ to obtain $X={\left[x_{ij}\right]}_{n\times n}$, where $M=\left\{1,2,3,\cdots ,m\right\}$, $N=\left\{1,2,3,\cdots ,n\right\}$, and $i\in M$, $j\in N$.

Determine the attribute with the largest value as the reference attribute $f_j$ and calculate the ratio of each attribute relative to the reference attribute $w_{jr}$. The formula is

$$w_{jr}=\frac{f_j}{f_r},$$

(33)

where $w_{jr}=\max \left\{w_j|j\in N\right\}$.

The degree of dominance of Scenario $A_i$ over Scenario $A_k$ when the attribute is $f_j$ is calculated. The formula is

$${\Phi }_j\left(A_i,A_k\right)=\{\begin{array}{l}\sqrt{\frac{\left(x_{ij}-x_{kj}\right)w_{jr}}{{\displaystyle \sum _{j=1}^n{w}_{jr}}}}\\ 0\\ -\frac{1}{\theta }\sqrt{\frac{\left(x_{kj}-x_{ij}\right)\left({\displaystyle \sum _{j=1}^n{w}_{jr}}\right)}{w_{jr}}}\end{array}\begin{array}{l}{x}_{ij}-x_{kj}＞0\\ \\ x_{ij}-x_{kj}=0\\ \\ x_{ij}-x_{kj}＜0\end{array}.$$

(34)

Loss aversion coefficient $\theta$ can reflect the psychological behavior of decision makers; the smaller the value of $\theta$, the higher the risk tolerance of decision makers, and the larger the value of $\theta$, the lower the risk tolerance of decision makers. In the subsequent experiments, this paper will analyze the value of $\theta$ to confirm whether the size of $\theta$ will have an impact on the final ranking results.

Calculate the degree of dominance of Scenario $A_i$ over Scenario $A_k$ for all attributes; the formula is

$$\delta \left(A_i,A_k\right)={\displaystyle \sum _{j=1}^n\Phi }\left(A_1,A_k\right) i,k\in M,$$

(35)

Calculate the combined degree of dominance of all alternatives $A_i$ over the other alternatives. The formula is

$$\xi \left(A_i\right)=\frac{{\displaystyle \sum _{k=1}^m\delta \left(A_i,A_k\right)-\min \left\{{\displaystyle \sum _{k=1}^m\delta }\left(A_i,A_k\right)\right\}}}{\underset{i\in M}{\max }\left\{{\displaystyle \sum _{k=1}^m\delta }\left(A_i,A_k\right)\right\}-\underset{i\in M}{\min }\left\{{\displaystyle \sum _{k=1}^m\delta }\left(A_i,A_k\right)\right\}}, i\in M.$$

(36)

According to the above equation, the $\xi \left(A_i\right)$ of each scenario can be obtained, and the scenarios are ranked according to the size relationship of the $\xi \left(A_i\right)$. A larger value of $\xi \left(A_i\right)$ indicates a better scenario $A_i$.

6. Tests and Results

This section demonstrates the application of the proposed method through a case study where movies are ranked based on online reviews.

6.1. Problem Description and Data Source

With the development of the Internet, more and more viewers regularly use online reviews on relevant platforms as a decision making reference before making decisions. A viewer chooses $(A_1,A_2,A_3,A_4,A_5,A_6)$ as an alternative movie by referring to online reviews. The software used to process the data in this paper and the dates on which the data were analyzed are shown below in Table 3.

Table 3. Software for processing data and date of analysis.

Steps	Software	Date of Data Analysis
Crawling Movie Online Reviews	Python 3.9	5.13–5.15
Sentiment Analysis of Online Reviews	Python 3.9; The Bert-model-based Cemotion library	6.10–6.14
Calculation of the Degree of Dominance	Matlab R2022a	6.20–6.25

The movies selected are Titanic ($A_1$), Farewell My Concubine ($A_2$), The Shawshank Redemption ($A_3$), This Killer Is Not Too Cold ($A_4$), Green Book ($A_5$), and Le fabuleux destin d’Amélie Poulain ($A_6$). The classification of the movies reveals that the six selected films belong to three different genres, namely, romance, drama, and comedy. The evaluation panel, comprising five members, selected five attributes to assess the alternative movies by: these attributes are “Frame” ($f_1$), “Character” ($f_2$), “Plot” ($f_3$), “Soundtrack” ($f_4$), and “Acting” ($f_5$). Next, the proposed method is used in this study to rank the six movies mentioned above.

Step 1. We performed sentiment analysis on reviews of alternative movies to determine their tendencies of sentiments towards movie attributes. The affective tendencies of some of the movie attributes are shown in Table 1.

Step 2. The sentiment orientation of the reviews is acquired in Step 1, and the average sentiment value and multidimensional feature values of the movie attributes are calculated according to the content in Section 4.2. The results of the calculations are shown in Table 4 and Table 5.

Table 4. Mean values of sentiment corresponding to each attribute of the alternative movie.

Alternative Movie	Attribute	Frame	Character	Plot	Soundtrack	Acting
Titanic	Mean positive affect	0.8934	0.8814	0.8751	0.8975	0.8551
	Mean negative affect	0.4467	0.4331	0.4261	0.4131	0.4313
Farewell my concubine	Mean positive affect	0.8813	0.8931	0.8852	0.8834	0.8821
	Mean negative affect	0.4237	0.4424	0.4324	0.4541	0.4426
The Shawshank Redemption	Mean positive affect	0.8701	0.8835	0.8857	0.8921	0.8936
	Mean negative affect	0.4351	0.4234	0.4327	0.4353	0.4313
This killer’s not too cold	Mean positive affect	0.8831	0.8953	0.8924	0.8813	0.8854
	Mean negative affect	0.4353	0.4424	0.4345	0.4334	0.4313
Green book	Mean positive affect	0.8834	0.8924	0.8835	0.8834	0.8954
	Mean negative affect	0.4335	0.4324	0.4352	0.4315	0.4314
Le fabuleux destin d’Amélie Poulain	Mean positive affect	0.8741	0.8831	0.8937	0.8814	0.8764
	Mean negative affect	0.4324	0.4354	0.4334	0.4353	0.4375

Table 5. Multidimensional feature values corresponding to each attribute of the alternative movie.

Alternative Movie	Attribute	Frame	Character	Plot	Soundtrack	Acting
Titanic	Positive multidimensional eigenvalues	0.8272	0.8317	0.8264	0.8152	0.8366
	Negative multidimensional eigenvalues	0.1721	0.1673	0.1736	0.1843	0.1638
Farewell my concubine	Positive multidimensional eigenvalues	0.8253	0.8214	0.8124	0.8319	0.8132
	Negative multidimensional eigenvalues	0.1704	0.1786	0.1878	0.1631	0.1868
The Shawshank Redemption	Positive multidimensional eigenvalues	0.8232	0.8174	0.8236	0.8281	0.8233
	Negative multidimensional eigenvalues	0.1768	0.1821	0.1762	0.1718	0.1767
This killer’s not too cold	Positive multidimensional eigenvalues	0.8176	0.8231	0.8289	0.8219	0.8224
	Negative multidimensional eigenvalues	0.1804	0.1763	0.1711	0.1781	0.1776
Green book	Positive multidimensional eigenvalues	0.8193	0.8165	0.8151	0.8169	0.8319
	Negative multidimensional eigenvalues	0.1803	0.1835	0.1848	0.1836	0.1681
Le fabuleux destin d’Amélie Poulain	Positive multidimensional eigenvalues	0.8185	0.8187	0.8293	0.8109	0.8303
	Negative multidimensional eigenvalues	0.1814	0.1818	0.1706	0.1899	0.1697

Step 3. The intuitionistic fuzzy values for the movie attributes are calculated using Equations (15) and (16), and are shown in Table 6.

Table 6. Intuitive fuzzy values for movie attributes.

Alternative Movie	Intuitive Fuzzy Value	Frame	Character	Plot	Soundtrack	Acting
Titanic	Membership degree u	0.7367	0.7315	0.7189	0.7259	0.7113
	Degree of non-membership v	0.0774	0.0725	0.0729	0.0756	0.0702
Farewell my concubine	Membership degree u	0.7299	0.7314	0.7146	0.7358	0.7139
	Degree of non-membership v	0.0716	0.0785	0.0807	0.0737	0.0832
The Shawshank Redemption	Membership degree u	0.7244	0.7197	0.7249	0.7373	0.7327
	Degree of non-membership v	0.0762	0.0765	0.0757	0.0739	0.0759
This killer’s not too cold	Membership degree u	0.7198	0.7331	0.7377	0.7232	0.7241
	Degree of non-membership v	0.0782	0.0776	0.0735	0.0765	0.0761
Green book	Membership degree u	0.7212	0.7269	0.7173	0.7189	0.7402
	Degree of non-membership v	0.0775	0.0788	0.0794	0.0787	0.0723
Le fabuleux destin d’Amélie Poulain	Membership degree u	0.7203	0.7199	0.7381	0.7136	0.7306
	Degree of non-membership v	0.0781	0.0781	0.0733	0.0813	0.0729

Step 4. The improved intuitionistic fuzzy exact function Formula (26) is used to obtain the exact function values for each attribute of the movie, as shown in Table 7.

Table 7. Exact function values for movie attributes.

	Attribute	Frame	Character	Plot	Soundtrack	Acting
Movie
Titanic		1.5561	1.5511	1.5346	1.5426	1.5259
Farewell my concubine		1.5493	1.5481	1.5262	1.5562	1.5244
The Shawshank Redemption		1.5405	1.5343	1.5412	1.5576	1.5513
This killer’s not too cold		1.5337	1.5514	1.5587	1.5388	1.5401
Green book		1.5359	1.5427	1.5301	1.5324	1.5624
Le fabuleux destin d’Amélie Poulain		1.5346	1.5341	1.5593	1.5247	1.5497

Step 5. Five experts were invited to assess various types of movies based on the methodology used to establish attribute weights in Section 5.3. Expert 1 rated the attributes in the romance movie category, as illustrated in Table 8.

Table 8. Results of expert scoring of romance movies.

	Acting	Character	Plot	Soundtrack	Frame
Expert 1	$f_1$	$f_2$	$f_3$	$f_4$	$f_5$
C1	0	4	3	0	3
C2	4	0	3	2	2
C3	2	2	0	2	2
C4	2	0	3	0	2
C5	1	2	3	0	0

The weights $\omega$ of the attributes of the movies in the romance category evaluated by Expert 1 were obtained using the DEMATEL method, as shown in Table 9.

Table 9. Weights of attributes scored by Expert 1 for romance movies.

	${\mathit{f}}_1$	${\mathit{f}}_2$	${\mathit{f}}_3$	${\mathit{f}}_4$	${\mathit{f}}_5$
${\omega }_j$	7.6197	7.8342	7.7847	4.6162	6.2126
${\overline{\omega }}_j$	0.2237	0.2299	0.2285	0.1355	0.1824

Here, ${\omega }_j$ is the weight of each attribute obtained via DEMATEL after Expert 1 scored the movies in the romance category, and ${\overline{\omega }}_j$ is the weight of each attribute of the movies in the romance category after normalization.

Since the genres of the alternative films are romance, drama, and comedy, the attribute weights of the different genres of films obtained from the scoring of the three genres by the five experts according to Equation (30) are shown in Table 10.

Table 10. Attribute weights for different types of movies in the romance, drama, and comedy genres.

	Attribute	Frame	Character	Plot	Soundtrack	Acting
Movie Genre
Romance Movie		0.2026	0.2291	0.1932	0.2136	0.1615
Drama Movie		0.1956	0.2211	0.2134	0.1708	0.1991
Comedy Movie		0.2017	0.1934	0.2004	0.1936	0.2109

Step 6. Table 11 presents the average attribute weights for the three alternative movie types, as obtained using Equation (31).

Table 11. Average attribute weights for alternative movies.

	Attribute	Frame	Character	Plot	Soundtrack	Acting
Weight
Average weight of alternative movies		0.2053	0.2397	0.2159	0.1506	0.1885

Step 7. Construct the decision matrix for Scheme $A_i$ under attribute $f_j$ based on the exact function values in Table 7, as shown in Table 12.

Table 12. Judgment matrix of Scheme $A_i$ under attribute f_j.

	f1	f2	f3	f4	f5
A1	1.5562	1.5511	1.5347	1.5426	1.5259
A2	1.5494	1.5481	1.5263	1.5562	1.5245
A3	1.5405	1.5343	1.5412	1.5577	1.5513
A4	1.5337	1.5511	1.5587	1.5388	1.5405
A5	1.5359	1.5427	1.5301	1.5324	1.5624

Step 8. The total degree of dominance of scenario $A_i$ over scenario $A_I$ under all attributes is calculated using Equations (34) and (35). In this step, it is assumed that the loss recession factor $\theta =1$. Finally, based on Equation (36), we get the total dominance degree of scheme $A_i$ over scheme $A_I$ under all attributes $\Phi \left(A_i,A_I\right)$. The results are as follows:

$$\tilde{\Phi }\left(A_i,A_I\right)=\left[\begin{array}{cccccc}0& -0.8868& -3.7232& -2.7445& -1.0983& -2.4641\\ -3.3320& 0& -3.2042& -3.7951& -2.0809& -2.8380\\ -3.0381& -2.4698& 0& -2.8097& -1.8626& -0.8174\\ -2.3941& -2.7771& -3.5970& 0& -1.5087& -1.1336\\ -5.3305& -4.4661& -3.9319& -4.0953& 0& -1.1236\\ -5.3599& -5.3583& -4.1064& -3.3616& -4.1401& 0\end{array}\right].$$

(37)

Step 9. Normalize the total dominance degree of Scenario A:

$\tilde{\xi }(A_1)=1$, $\tilde{\xi }(A_2)=0.62$, $\tilde{\xi }(A_3)=0.99$, $\tilde{\xi }(A_4)=0.95$, $\tilde{\xi }(A_5)=0.29$, $\tilde{\xi }(A_6)=0$.

Based on the above results, the six alternative movies can be ranked in order: $A_6\prec A_5\prec A_2\prec A_4\prec A_3\prec A_1$.

From the above results, it is clear that movie $A_i$ has the largest $\tilde{\xi }(A_1)$ and is the best alternative movie for the audience.

6.2. Impact Analysis of Different Weights

To confirm the feasibility of the proposed method, we introduce identical attribute weights and objective weights to rank six alternative movies using the method described in this paper. We then compare these results with the rankings obtained from the paper. Equivalent attribute weights can be seen as disregarding certain movie attributes in online movie reviews, while objective weights exclude the influence of movie genres and viewer personality preferences. The ranking results are shown in Table 13.

Table 13. Alternative movie ranking results with different attribute weights.

Alternate Movie Sorting Results	Attribute Weight
	${\mathrm{w}}_1$	${\mathrm{w}}_2$	${\mathrm{w}}_3$	${\mathrm{w}}_4$	${\mathrm{w}}_5$
$A_1\succ A_3\succ A_4\succ A_2\succ A_5\succ A_6$	0.2053	0.2397	0.2159	0.1506	0.1885
$A_1\succ A_4\succ A_3\succ A_2\succ A_5\succ A_6$	0.1393	0.1173	0.2557	0.1936	0.2941
$A_1\succ A_4\succ A_3\succ A_2\succ A_5\succ A_6$	0.2000	0.2000	0.2000	0.2000	0.2000

The rankings resulting from the weightings proposed in this paper produce differences compared with the other two weightings. The results achieved through ranking by the equal and objective weights are identical. However, the ranking based on the weights proposed in this paper, which consider movie genres and attributes, produce similar but distinct ranking outcomes when compared with the other two weights. A comparison of the ranking results under different weights reveals the presence of personalized attribute preferences. The final ranking results of the scheme are subject to variation, based on the preferred attributes.

6.3. Impact Analysis of Different Parameters

The loss aversion parameter $\theta$ in the intuitionistic fuzzy TODIM method can reflect the decision maker’s psychological behavior. To examine whether the magnitude of $\theta$ affects the final ranking results, this section presents a sensitivity analysis of the $\theta$ parameter under the intuitionistic fuzzy TODIM method. The sensitivity analysis mainly involves selecting various values of $\theta$, calculating whether the final program rankings are consistent under these values, and analyzing the impact of $\theta$ on the rankings. Table 14 displays the results of ranking the schemes based on different parameters $\theta$.

Table 14. Alternative movie ranking results with different parameters $\theta$.

Specifies the Value of Parameter θ	Scheme Sorting Result
θ = 0.2	$$A_3\succ A_1\succ A_4\succ A_2\succ A_5\succ A_6$$
θ = 0.6	$$A_3\succ A_1\succ A_4\succ A_2\succ A_5\succ A_6$$
θ = 1	$$A_1\succ A_3\succ A_4\succ A_2\succ A_5\succ A_6$$
θ = 1.5	$$A_1\succ A_3\succ A_4\succ A_2\succ A_5\succ A_6$$
θ = 2	$$A_1\succ A_3\succ A_4\succ A_2\succ A_5\succ A_6$$
θ = 2.5	$$A_1\succ A_3\succ A_4\succ A_2\succ A_5\succ A_6$$
θ = 3	$$A_1\succ A_3\succ A_4\succ A_2\succ A_5\succ A_6$$

The sensitivity analysis results in Table 12 indicate a difference in the final ranking of scenarios when the parameter $\theta$ value is changed from 0.2 to 3. As $\theta$ increases, the scheme is ranked $A_3\succ A_1\succ A_4\succ A_2\succ A_5\succ A_6$ when $\theta$ is between 0.2 and 0.6 and $A_1\succ A_3\succ A_4\succ A_2\succ A_5\succ A_6$ when $\theta$ is between 1 and 3. It can be shown that the final ranking result of the scheme is sensitive to the values of the parameters.

7. Discussion

In this study, movies are systematically ranked while considering diverse weightage criteria, which is followed by a comparative analysis of the experimental outcomes. Notably, when movies are ranked using uniform and objective weights, the results display consistency. However, alterations in movie attribute weights $\omega$ lead to discernible variations in rankings. This accentuates the pivotal role that attribute weight preferences play in influencing ranking outcomes.

Our experimental framework provides a salient methodology that empowers viewers to obtain recommendations that are meticulously tailored to their individualistic preferences concerning diverse movie attributes. Through parameter sensitivity analysis, it has been discerned that the parameter value $\theta$ oscillates between 0.2 and 3. The chosen parameter value $\theta$ plays a pivotal role, inducing specific shifts in the final ranking algorithm.

The efficacy of the decision making approach developed in this paper is not merely theoretical; it finds practical resonance in real-world decision making paradigms. The underpinning rationale is that the parameter $\theta$ encapsulates the spectrum of risk preferences among decision makers, and such heterogeneity directly modulates the final ranking. This paradigm can be analogously understood in the context of audience movie preferences: those with a more eclectic taste, displaying an openness to diverse movie genres and attributes, exhibit higher risk tolerance. They are, in essence, more resilient to potential misalignments between movie preferences and actual viewings. Consequently, for such an audience demographic, a lower parameter value $\theta$ is apt, as it resonates with their higher risk tolerance threshold, suggesting they are more amenable to movie selections that might not align perfectly with their expectations. Conversely, an audience cohort with a pronounced predilection for movie personalization demonstrates reduced resilience to discrepancies in attribute preferences. Their diminished risk tolerance suggests the advisability of a higher parameter value $\theta$ when leveraging the model proposed for movie selections.

Furthermore, our empirical observations emphasize the inherent sensitivity of the ranking model to the parameter value. Variability in parameter preferences and weightage criteria culminates in diverse ranking outcomes. This underscores the burgeoning demand for bespoke movie recommendations, aligning seamlessly with nuanced viewer predilections.

8. Conclusions

This study presents a structured approach to extracting and processing product attribute reviews from digital platforms and subsequently converting them into evaluative metrics via intuitionistic fuzzy set principles. In this context, we established a quantitative model that adeptly encapsulates the emotional nuances of product attributes. Moreover, we have worked towards refining the prevalent scoring function for intuitionistic fuzzy numbers, enhancing the model’s accuracy and efficacy in decision making.

Our study further explores the relationship dynamics between product attributes, harnessing the DEMATEL methodology. This technique assists in determining attribute weights specific to individual product genres. Employing the multi-attribute decision making paradigm, based on TODIM, provides a sophisticated solution to modern product sequencing challenges and expands the use cases of the TODIM decision making model within an intuitionistic fuzzy framework. This study’s innovations can be articulated through three primary conclusions:

(1)

The introduction of a comprehensive product ranking methodology, attuned to the consumer’s genre and attribute preferences. The resulting rankings, molded by these unique inclinations, provide consumers with a more tailored decision making tool for product selection.

(2)

The systematic quantification of emotional weightage associated with product attributes in online dialogues using intuitionistic fuzzy techniques. We propose a refined quantitative model to decipher emotional tones within a fuzzy setting. The improved intuitionistic fuzzy scoring algorithm captures consumers’ emotional evaluations effectively. By leveraging multidimensional eigenvalues, the ranking’s foundation is further solidified. Our methodology, which prioritizes consumer feedback over traditional expert opinions, offers a more authentic and objective assessment. It presents a robust foundation for the product ranking algorithm, effectively handling vast online reviews and countering information overload.

(3)

A pioneering product ranking algorithm designed for recommendation systems. Although many existing recommendation systems offer basic sorting options, they often lack depth and refinement. Our approach, recognizing the multitude of attributes that consumers consider, can be smoothly integrated into digital platforms, providing users with a nuanced multi-attribute ranking tool, thereby enriching their browsing experience.

While this research heralds a notable advancement in product rankings based on digital reviews, some aspects could benefit from further development:

(1)

Scope of platforms: Although our methodology is tested on the Chinese platform Douban, there is a need to expand its applicability to global platforms like Rotten Tomatoes and IMDb, requiring adaptation to diverse linguistic contexts.

(2)

Decision maker’s risk aversion: Our framework incorporates a parameter reflecting the decision maker’s risk aversion. Determining its optimal value is crucial for accurate ranking and clear decision making guidance.

(3)

Focus on product attributes: While our method provides a comprehensive ranking based on product attributes, it may overlook potential correlations with other product features.

Building on the above, our proposed “Emotionally Intuitive Fuzzy TODIM Methodology for Decision-Making Based on Online Reviews” has distinct potential. However, its current testing is limited to movie rankings. A transition to other product arenas may necessitate deeper dives into consumer focus areas and nuanced object classifications. Future endeavors will delve into these areas, ensuring a broader applicability of our methodology.