Study of Rotavirus Mathematical Model Using Stochastic and Piecewise Fractional Differential Operators
Abstract
1. Introduction
2. Elementary Results
2.1. Some Fundamental Results about the Model (3)
2.2. Equilibrium Points and Basic Reproduction Number
3. Existence Theory
- (C1)
- If is constant, such that then
- (C2)
- For constants and we have
4. Numerical Scheme
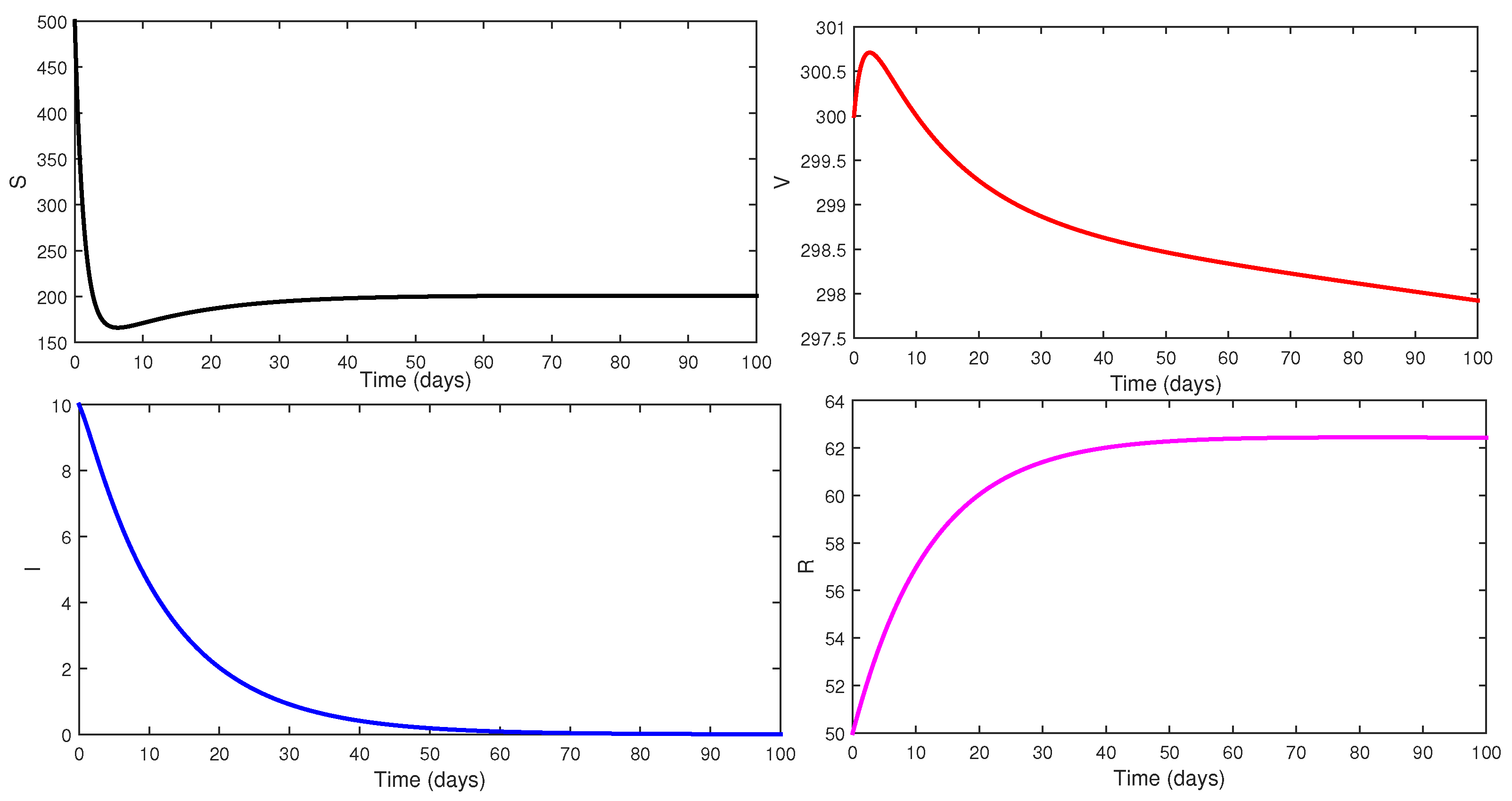
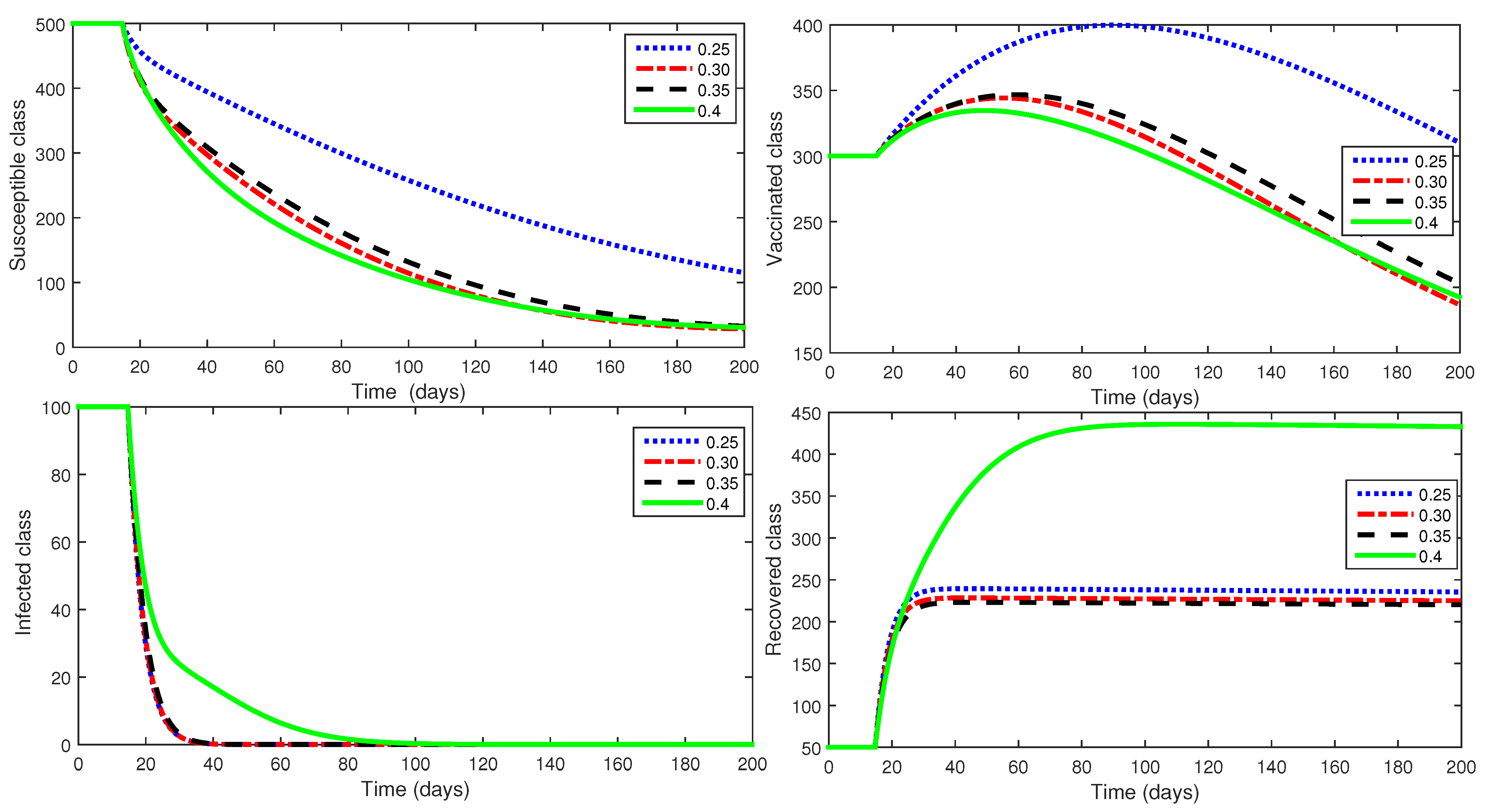
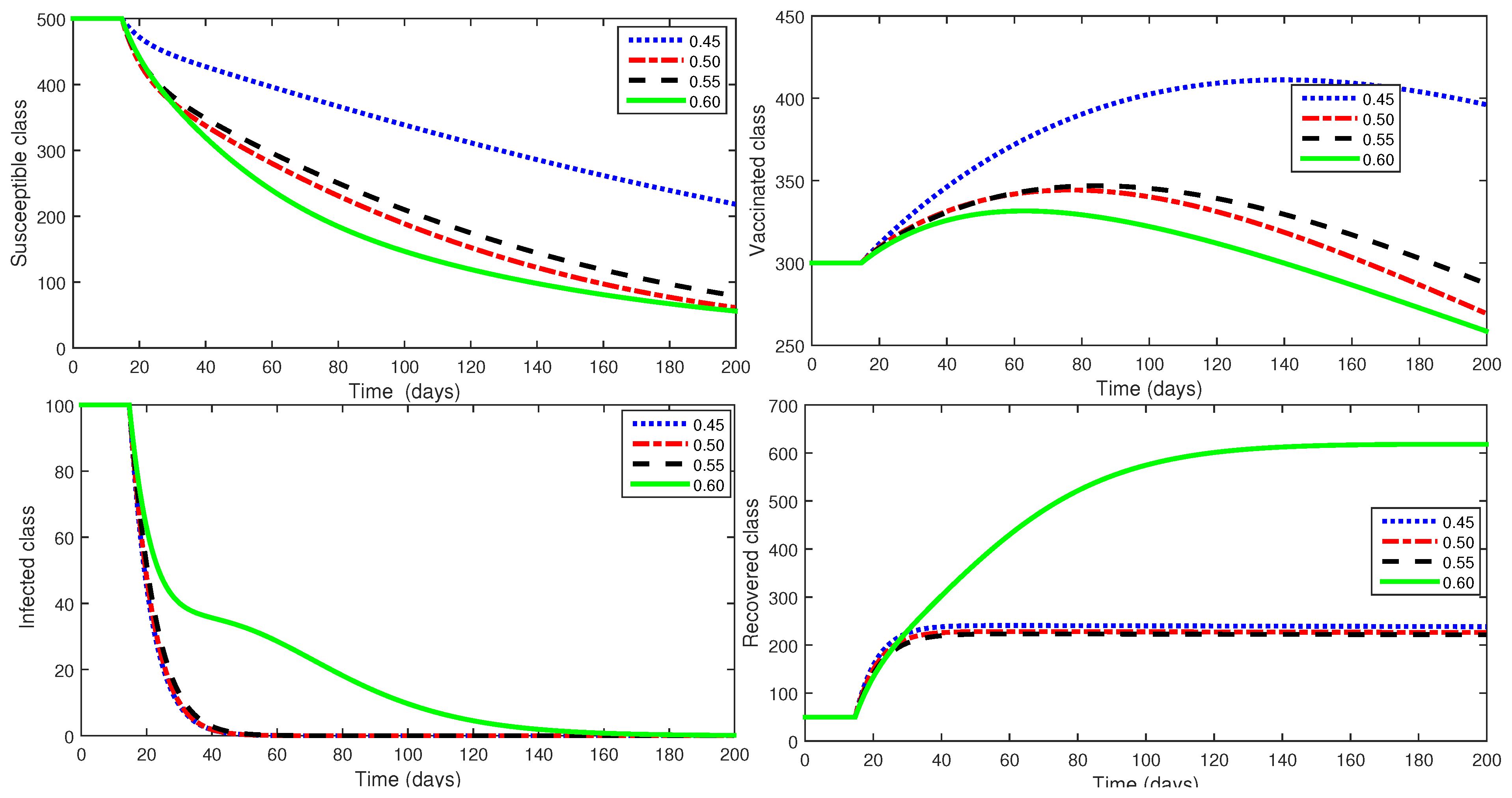
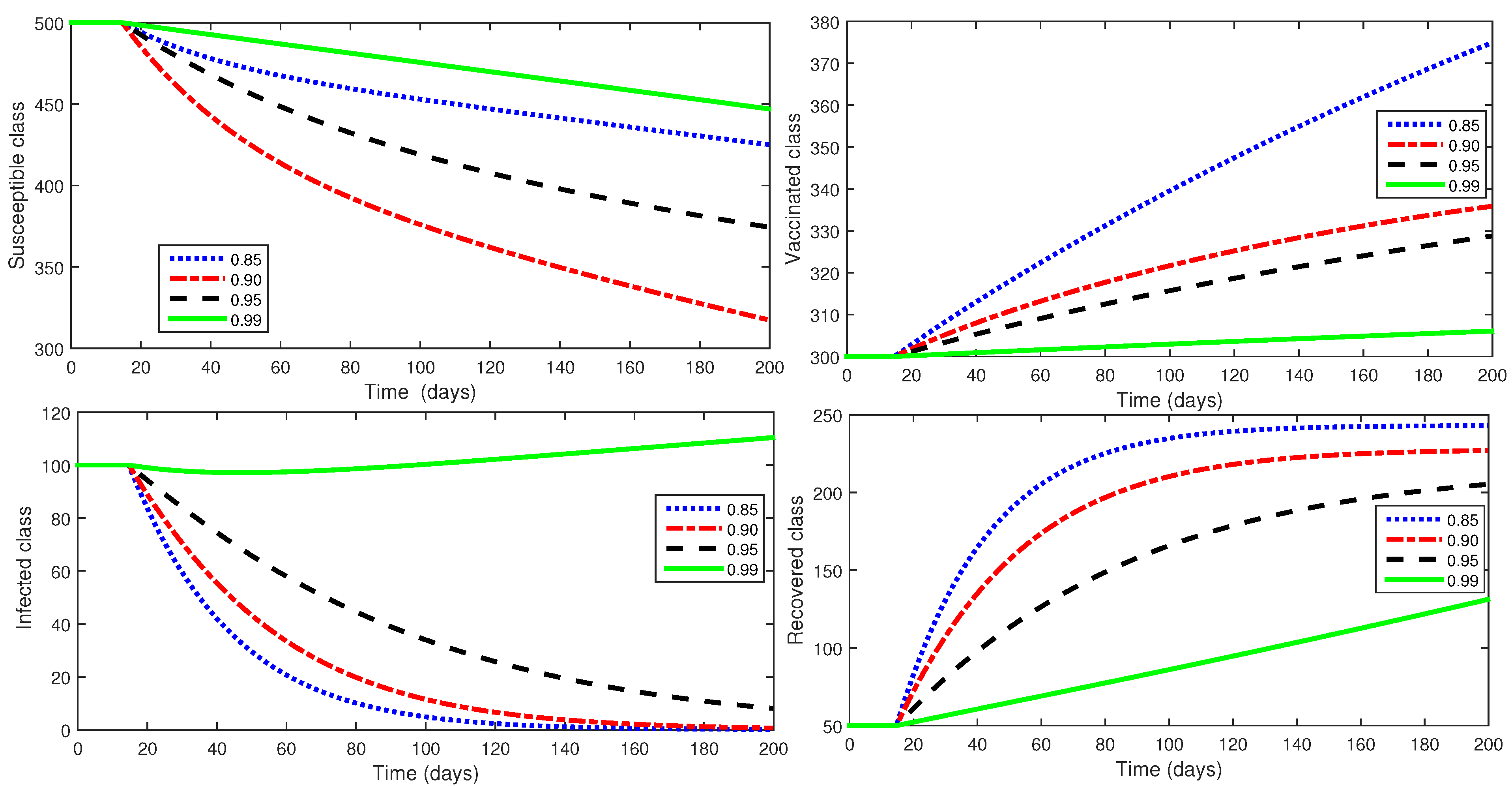
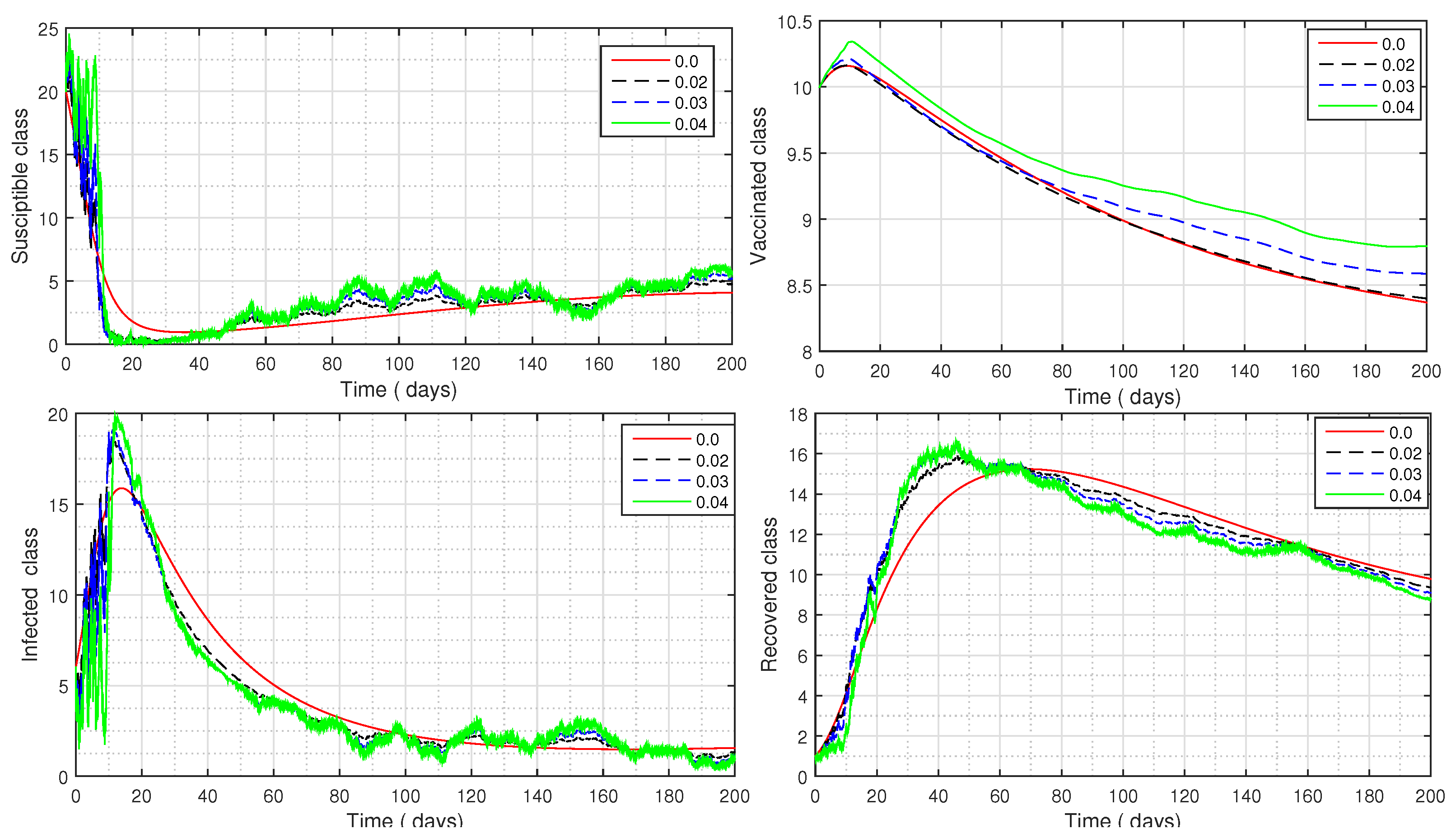
5. Simulations and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Health Organization. Generic Protocol for Monitoring Impact of Rotavirus Vaccination on Gastroenteritis Disease Burdenand Viral Strains; World Health Organization: Geneva, Switzerland, 2008. [Google Scholar]
- Ramig, R.F. Pathogenesis of intestinal and systemic rotavirus infection. J. Virol. 2004, 78, 10213–10220. [Google Scholar] [CrossRef]
- Muendo, C.; Laving, A.; Kumar, R.; Osano, B.; Egondi, T.; Njuguna, P. Prevalence of rotavirus infection among children with acute diarrhoea after rotavirus vaccine introduction in Kenya, a hospital cross-sectional study. BMC Pediatr. 2018, 18, 1–9. [Google Scholar] [CrossRef]
- Anderson, E.J.; Weber, S.G. Rotavirus infection in adults. Lancet Infect. Dis. 2004, 4, 91–99. [Google Scholar] [CrossRef]
- Bishop, R.F. Natural history of human rotavirus infection. Viral Gastroenteritis 1996, 119–128. [Google Scholar]
- Lambisia, A.W.; Onchaga, S.; Murunga, N.; Lewa, C.S.; Nyanjom, S.G.; Agoti, C.N. Epidemiological trends of five common diarrhea-associated enteric viruses pre-and post-rotavirus vaccine introduction in coastal Kenya. Pathogens 2020, 9, 660. [Google Scholar] [CrossRef]
- Shah, K.; Din, R.U.; Deebani, W.; Kumam, P.; Shah, Z. On nonlinear classical and fractional order dynamical system addressing COVID-19. Results Phys. 2021, 24, 104069. [Google Scholar] [CrossRef]
- Wang, Y.; Wei, Z.; Cao, J. Epidemic dynamics of influenza-like diseases spreading in complex networks. Nonlinear Dyn. 2020, 101, 1801–1820. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, J.A.P. Mathematical Epidemiology of Infectious Diseases: Model Building, Analysis and Interpretation; John Wiley & Sons: Hoboken, NJ, USA, 2020; Volume 5. [Google Scholar]
- Mondal, J.; Khajanchi, S. Mathematical modeling and optimal intervention strategies of the COVID-19 outbreak. Nonlinear Dyn. 2022, 109, 177–202. [Google Scholar] [CrossRef]
- Omondi, O.L.; Wang, C.; Xue, X.; Lawi, O.G. Modeling the effects of vaccination on rotavirus infection. Adv. Differ. Equ. 2015, 2015, 381. [Google Scholar] [CrossRef][Green Version]
- Ilmi, N.B.; Darti, I.; Suryanto, A. Dynamical Analysis of a rotavirus infection model with vaccination and saturation incidence rate. J. Phy. Conf. Ser. 2020, 1562, 012018. [Google Scholar] [CrossRef]
- Darti, I.; Suryanto, A.; Ilmi, N.B. Dynamical behavior of a rotavirus transmission model with an environmental effects. In AIP Conference Proceedings; AIP Publishing LLC.: Melville, NY, USA, 2020; p. 020001. [Google Scholar]
- Ahmad, S.; Ullah, A.; Arfan, M.; Shah, K. On analysis of the fractional mathematical model of rotavirus epidemic with the effects of breastfeeding and vaccination under atangana-baleanu (ab) derivative. Chaos Solitons Fractals 2020, 140, 110233. [Google Scholar] [CrossRef]
- Asare, E.O.; Al-Mamun, M.A.; Armah, G.E.; Lopman, B.A.; Parashar, U.D.; Binka, F.; Pitzer, V.E. Modeling of rotavirus transmission dynamics and impact of vaccination in ghana. Vaccine 2020, 38, 4820–4828. [Google Scholar] [CrossRef]
- Asamoah, J.K.K. A fractional mathematical model of heartwater transmission dynamics considering nymph and adult amblyomma ticks. Chaos Solitons Fractals 2023, 174, 113905. [Google Scholar] [CrossRef]
- Riewe, F. Mechanics with fractional derivatives. Phys. Rev. E 1997, 55, 3581. [Google Scholar] [CrossRef]
- Li, C.; Deng, W. Remarks on fractional derivatives. Appl. Math. Comput. 2007, 187, 777–784. [Google Scholar] [CrossRef]
- De Oliveira, E.C.; Tenreiro Machado, J.A. A review of definitions for fractional derivatives and integral. Math. Probl. Eng. 2014, 2014, 238459. [Google Scholar] [CrossRef]
- Magin, R. Fractional calculus in bioengineering, part 1. Crit. Rev. Biomed. Eng. 2004, 32, 1–104. [Google Scholar]
- Magin, R.L. Fractional calculus in bioengineering: A tool to model complex dynamics. In Proceedings of the 13th International Carpathian Control Conference (ICCC), Podbanske, Slovakia, 28–31 May 2012; pp. 464–469. [Google Scholar]
- Magin, R.L. Fractional calculus models of complex dynamics in biological tissues. Comput. Math. Appl. 2010, 59, 1586–1593. [Google Scholar] [CrossRef]
- Machado, J.T.; Kiryakova, V.; Mainardi, F. Recent history of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1140–1153. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F.; Razo-Hernández, R.; Granados-Lieberman, D. A physical interpretation of fractional calculus in observables terms: Analysis of the fractional time constant and the transitory response. Rev. Mex. Física 2014, 60, 32–38. [Google Scholar]
- Meral, F.C.; Royston, T.J.; Magin, R. Fractional calculus in viscoelasticity: An experimental study. Commun. Nonlinear Sci. Numer. Simul. 2014, 15, 939–945. [Google Scholar] [CrossRef]
- Wu, G.C.; Luo, M.; Huang, L.L.; Banerjee, S. Short memory fractional differential equations for new memristor and neural network design. Nonlinear Dyn. 2020, 100, 3611–3623. [Google Scholar] [CrossRef]
- Sang, Y.; Liang, S. Fractional Kirchhoff-Choquard equation involving Schrödinger term and upper critical exponent. J. Geom. Anal. 2022, 32, 5. [Google Scholar] [CrossRef]
- Zeb, A.; Atangana, A.; Khan, Z.A.; Djillali, S. A robust study of a piecewise fractional order COVID-19 mathematical model. Alex. Eng. J. 2022, 61, 5649–5665. [Google Scholar] [CrossRef]
- Atangana, A.; Araz, S.I. New concept in calculus: Piecewise differential and integral operators. Chaos Solitons Fractals 2021, 145, 110638. [Google Scholar] [CrossRef]
- Khalsaraei, M.M. An improvement on the positivity results for 2-stage explicit Runge–Kutta methods. J. Comput. Appl. Math. 2010, 235, 137–143. [Google Scholar] [CrossRef]
- Etemad, S.; Tellab, B.; Alzabut, J.; Rezapour, S.; Abbas, M.I. Approximate solutions and Hyers-Ulam stability for a system of the coupled fractional thermostat control model via the generalized differential transform. Adv. Differ. Equations 2021, 2021, 1–25. [Google Scholar] [CrossRef]
- Li, R.; Zhong, S.; Swartz, C. An improvement of the Arzela-Ascoli theorem. Topol. Its Appl. 2012, 159, 2058–2061. [Google Scholar] [CrossRef]
- Agarwal, R.P.; Arshad, S.; O’Regan, D.; Lupulescu, V. A Schauder fixed point theorem in semilinear spaces and applications. Fixed Point Theory Appl. 2013, 2013, 1–13. [Google Scholar] [CrossRef]
- Al Elaiw, A.; Hafeez, F.; Jeelani, M.B.; Awadalla, M.; Abuasbeh, K. Existence and uniqueness results for mixed derivative involving fractional operators. AIMS Math. 2023, 8, 7377–7393. [Google Scholar] [CrossRef]
- Jeelani, M.B. Stability and computational analysis of COVID-19 using a higher order galerkin time discretization scheme. Adv. Appl. Stat. 2023, 86, 167–206. [Google Scholar] [CrossRef]
- Moumen, A.; Shafqat, R.; Alsinai, A.; Boulares, H.; Cancan, M.; Jeelani, M.B. Analysis of fractional stochastic evolution equations by using Hilfer derivative of finite approximate controllability. AIMS Math. 2023, 8, 16094–16114. [Google Scholar] [CrossRef]
- Alharthi, N.H.; Jeelani, M.B. A fractional model of COVID-19 in the frame of environmental transformation with Caputo fractional derivative. Adv. Appl. Stat. 2023, 88, 225–244. [Google Scholar] [CrossRef]
- Alnahdi, A.S.; Jeelani, M.B.; Wahash, H.A.; Abdulwasaa, M.A. A Detailed Mathematical Analysis of the Vaccination Model for COVID-19. CMES-Comput. Model. Eng. Sci. 2023, 135, 1315–1343. [Google Scholar] [CrossRef]
- Dehingia, K.; Jeelani, M.B.; Das, A. Artificial Intelligence and Machine Learning: A Smart Science Approach for Cancer Control. In Advances in Deep Learning for Medical Image Analysis; CRC Press: Boca Raton, FL, USA, 2022; pp. 87–99. [Google Scholar]
- Shaikh, M.B.J. Some Application of Differential Transform Methods to Stiff Differential Equations. Int. J. Appl. Eng. Res. 2019, 14, 877–880. [Google Scholar]
- Shah, K.; Abdeljawad, T.; Alrabaiah, H. On coupled system of drug therapy via piecewise equations. Fractals 2022, 30, 2240206. [Google Scholar] [CrossRef]
- Banihashemi, S.; Jafari, H.; Babaei, A. A stable collocation approach to solve a neutral delay stochastic differential equation of fractional order. J. Comput. Appl. Math. 2022, 403, 113845. [Google Scholar] [CrossRef]
- Jumarie, G. Stochastic differential equations with fractional Brownian motion input. Int. J. Syst. Sci. 1993, 24, 1113–1131. [Google Scholar] [CrossRef]
- Shah, K.; Abdeljawad, T. Study of a mathematical model of COVID-19 outbreak using some advanced analysis. Waves Random Complex Media 2022, 1–18. [Google Scholar] [CrossRef]
- Platen, E. An introduction to numerical methods for stochastic differential equations. Acta Numer. 1999, 8, 197–246. [Google Scholar] [CrossRef]
- Khan, S.; Khan, Z.A.; Alrabaiah, H.; Zeb, S. On using piecewise fractional differential operator to study a dynamical system. Axioms 2023, 12, 292. [Google Scholar] [CrossRef]
- Kheyami, A.M.; Cunliffe, N.A.; Hart, C.A. Rotavirus infection in Saudi Arabia. Ann. Saudi Med. 2006, 6, 184–191. [Google Scholar] [CrossRef]
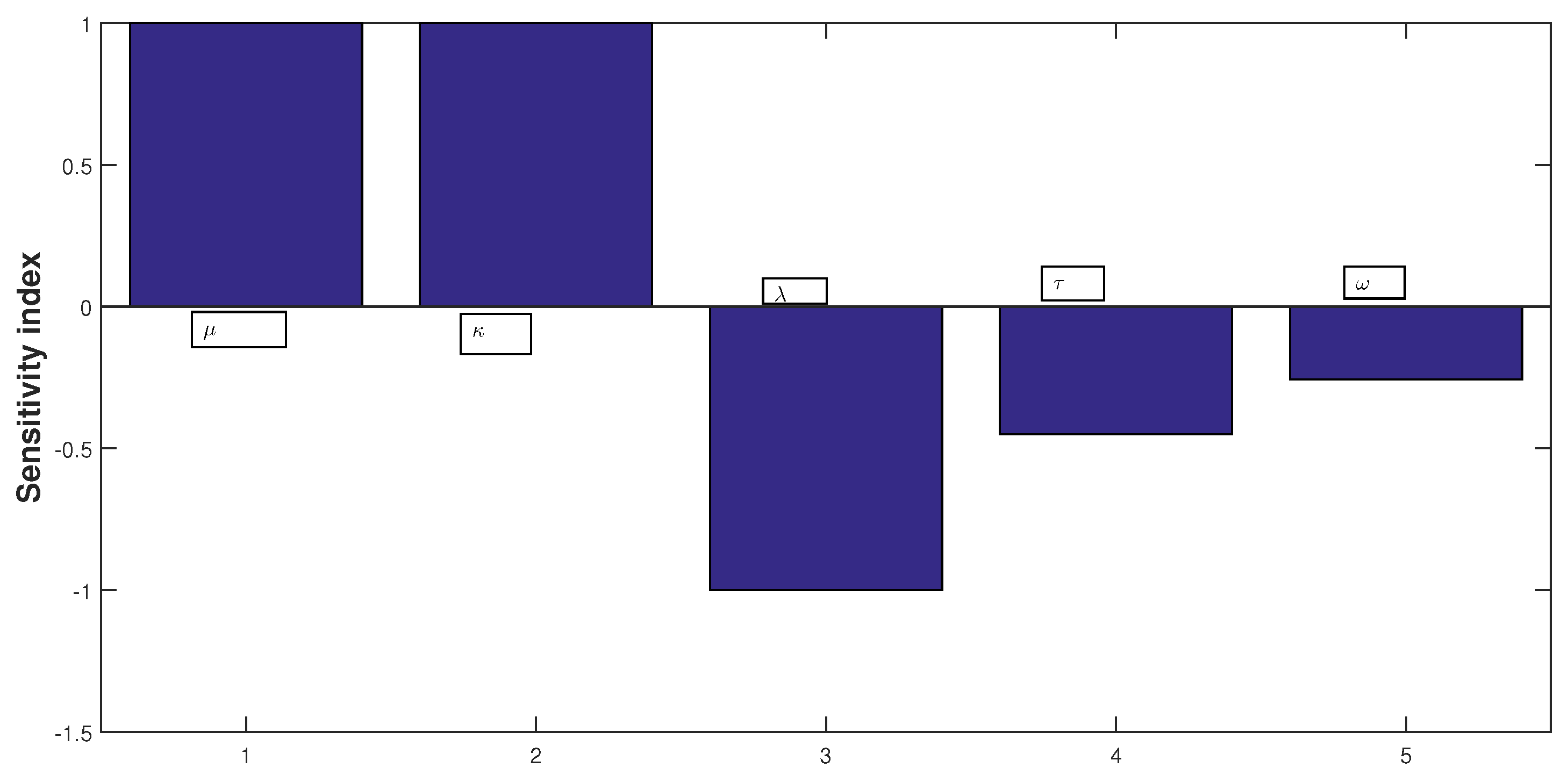

| Parameter | Sensitivity Index | Value | Parameter | Sensitivity Index | Value |
|---|---|---|---|---|---|
| 1 | −0.0004507 | ||||
| 1 | −0.00025608 | ||||
| −1.0002560 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alharthi, N.H.; Jeelani, M.B. Study of Rotavirus Mathematical Model Using Stochastic and Piecewise Fractional Differential Operators. Axioms 2023, 12, 970. https://doi.org/10.3390/axioms12100970
Alharthi NH, Jeelani MB. Study of Rotavirus Mathematical Model Using Stochastic and Piecewise Fractional Differential Operators. Axioms. 2023; 12(10):970. https://doi.org/10.3390/axioms12100970
Chicago/Turabian StyleAlharthi, Nadiyah Hussain, and Mdi Begum Jeelani. 2023. "Study of Rotavirus Mathematical Model Using Stochastic and Piecewise Fractional Differential Operators" Axioms 12, no. 10: 970. https://doi.org/10.3390/axioms12100970
APA StyleAlharthi, N. H., & Jeelani, M. B. (2023). Study of Rotavirus Mathematical Model Using Stochastic and Piecewise Fractional Differential Operators. Axioms, 12(10), 970. https://doi.org/10.3390/axioms12100970







