Modified Maximum Likelihood Estimation of the Inverse Weibull Model
Abstract
:1. Introduction
2. Modified MLE
3. Simulations
4. Applications
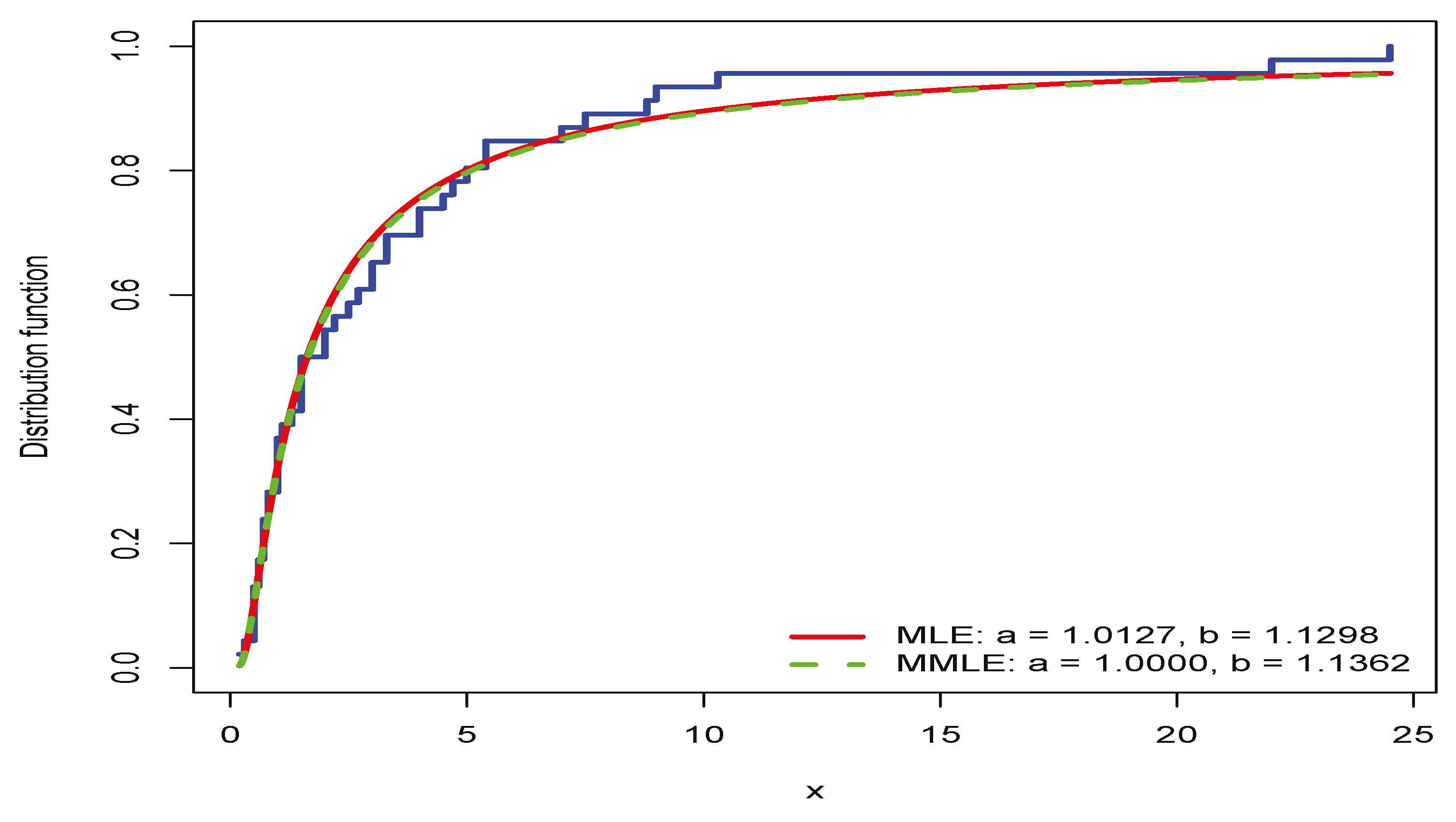
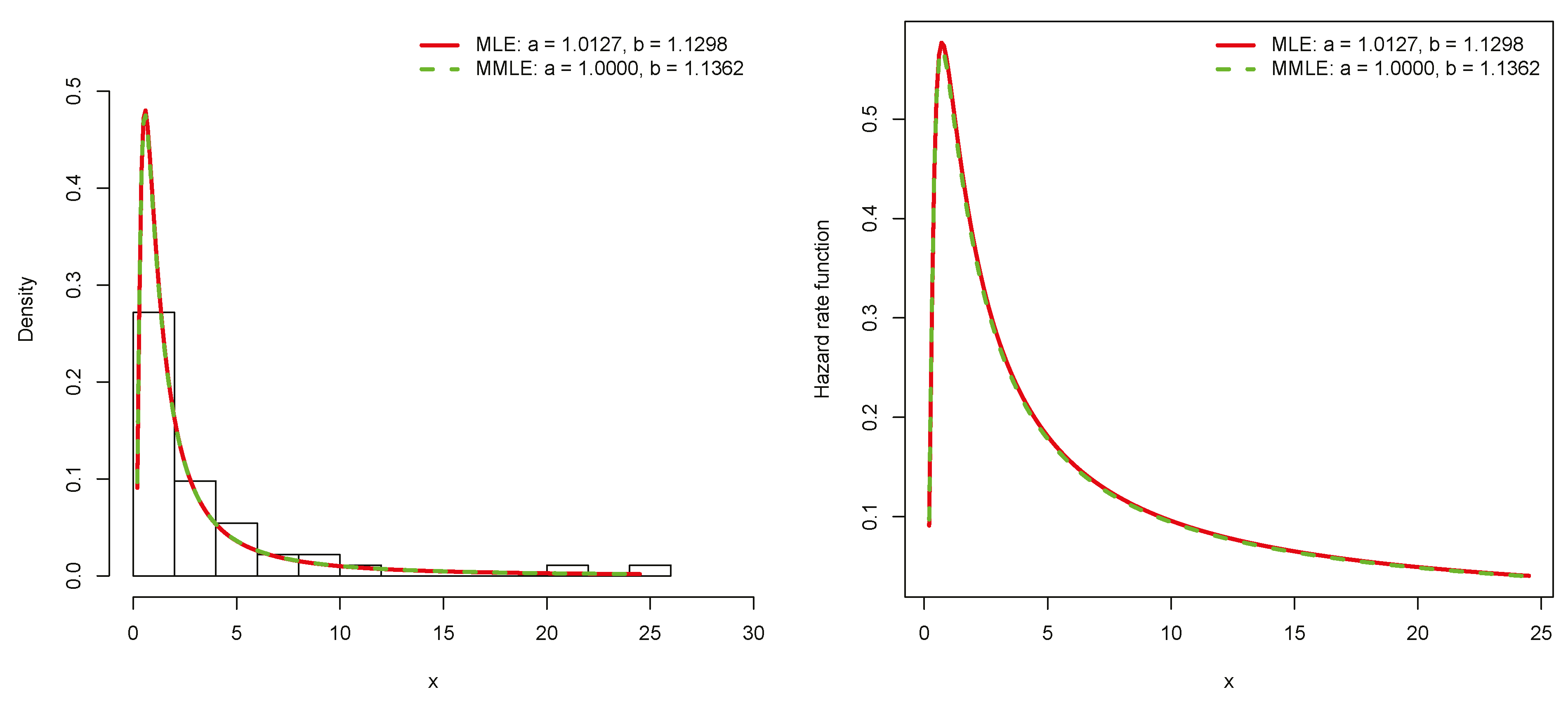
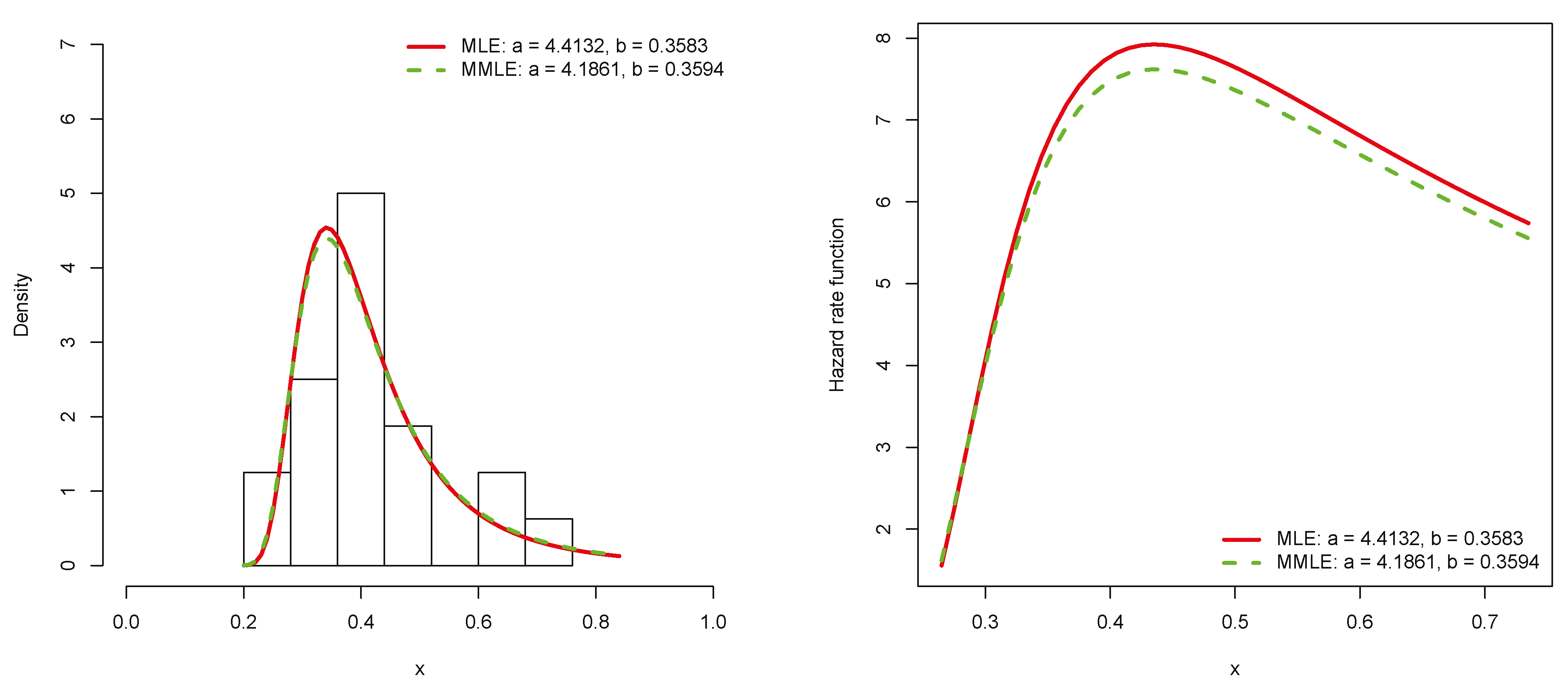
4.1. Repair Times of an Airborne Communication Transceiver
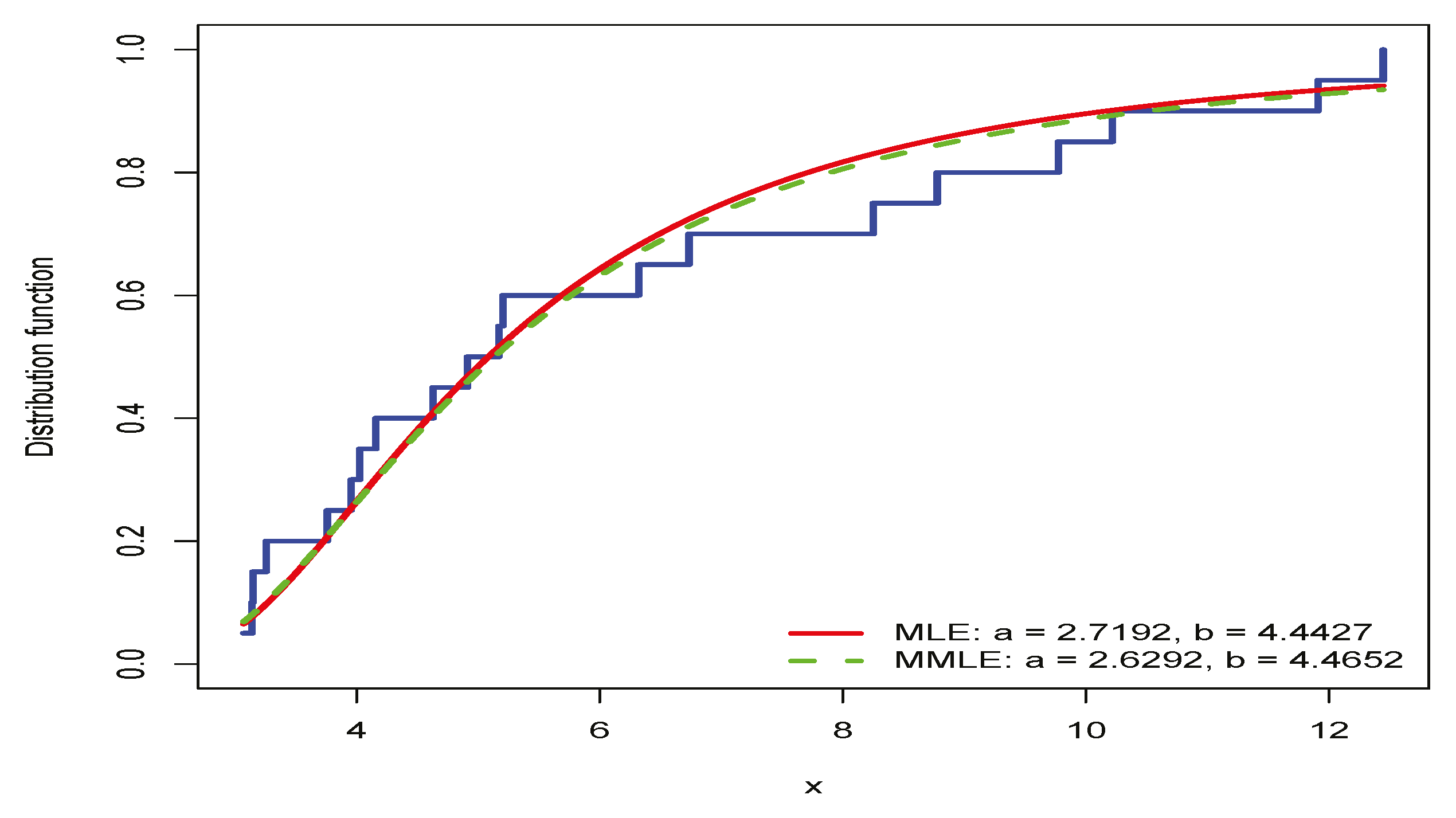
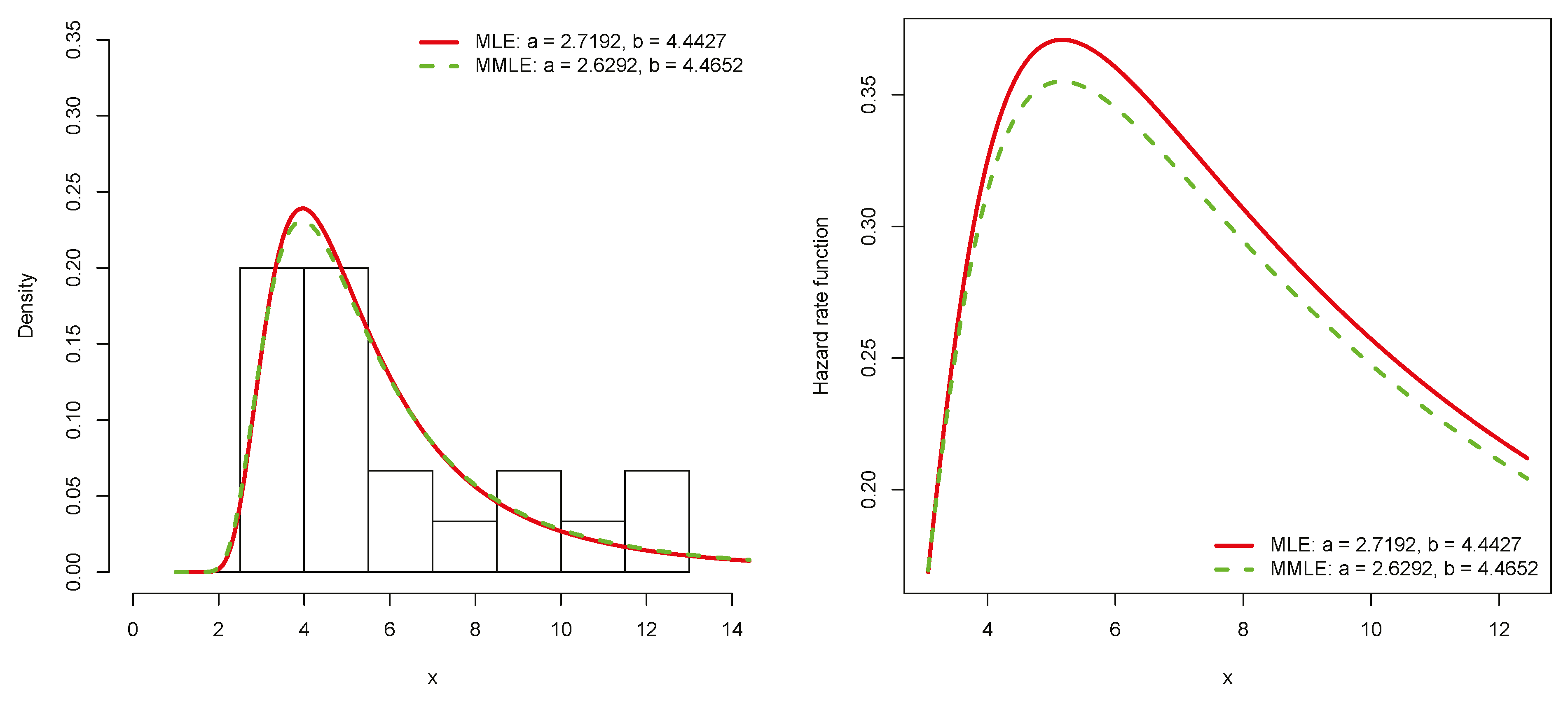
4.2. Maximum Flood Levels of the Susquehenna River
4.3. Duration of Remission Achieved by a Drug
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Jiang, R.; Ji, P.; Xiao, X. Aging property of unimodal failure rate models. Reliab. Eng. Syst. Saf. 2003, 79, 113–116. [Google Scholar] [CrossRef]
- Keller, A.Z.; Giblin, M.T.; Farnworth, N.R. Reliability analysis of commercial vehicle engines. Reliab. Eng. 1985, 10, 15–25. [Google Scholar] [CrossRef]
- Akgul, F.G.; Senoglu, B.; Arslan, T. An alternative distribution to Weibull for modeling the wind speed data: InverseWeibull distribution. Energy Convers. Manag. 2016, 114, 234–240. [Google Scholar] [CrossRef]
- Calabria, R.; Pulcini, G. Bayes 2-sample prediction for the inverse weibull distribution. Commun. Stat. Theory Methods 1994, 23, 1811–1824. [Google Scholar] [CrossRef]
- Jiang, R.; Murthy, D.N.P.; Ji, P. Models involving two inverse Weibull distributions. Reliab. Eng. Syst. Saf. 2001, 73, 73–81. [Google Scholar] [CrossRef]
- Mahmoud, M.A.W.; Sultan, K.S.; Amer, S.M. Order statistics from inverse weibull distribution and associated inference. Comput. Stat. Data Anal. 2003, 42, 149–163. [Google Scholar] [CrossRef]
- Sultan, K.S.; Ismail, M.A.; Al-Moisheer, A.S. Mixture of two inverse Weibull distributions: Properties and estimation. Comput. Stat. Data Anal. 2007, 51, 5377–5387. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Kateri, M. On the maximum likelihood estimation of Weibull distribution based on complete and censored data. Stat. Probab. Lett. 2008, 78, 2971–2975. [Google Scholar] [CrossRef]
- Kundu, D.; Howlader, H. Bayesian inference and prediction of the inverse Weibull distribution for Type-II censored data. Comput. Stat. Data Anal. 2010, 54, 1547–1558. [Google Scholar] [CrossRef]
- de Gusmão, F.R.S.; Ortega, E.M.M.; Cordeiro, G.M. The generalized inverse Weibull distribution. Stat. Pap. 2011, 52, 591–619. [Google Scholar] [CrossRef]
- Sultan, K.S.; Alsadat, N.H.; Kundu, D. Bayesian and maximum likelihood estimations of the inverse Weibull parameters under progressive type-II censoring. J. Stat. Comp. Simul. 2014, 84, 2248–2265. [Google Scholar] [CrossRef]
- Kim, D.H.; Lee, W.D.; Kang, S.G. Non-informative priors for the inverse Weibull distribution. J. Stat. Comp. Simul. 2014, 84, 1039–1054. [Google Scholar] [CrossRef]
- Loganathan, A.; Uma, M. Comparison of estimation methods for inverse Weibull parameters. Glob. Stoch. Anal. 2017, 4, 83–93. [Google Scholar]
- Ramos, P.L.; Nascimento, D.; Louzada, F. The long term fréchet distribution: Estimation, properties and its application. Biom. Biostat. Int. J. 2017, 6, 357–362. [Google Scholar] [CrossRef]
- Singh, S.; Tripathi, Y.M. Estimating the parameters of an inverse Weibull distribution under progressive type-I interval censoring. Stat. Pap. 2018, 59, 21–56. [Google Scholar] [CrossRef]
- Ramos, P.L.; Louzada, F.; Ramos, E.; Dey, S. The Fréchet distribution: Estimation and application—An overview. J. Stat. Manag. Syst. 2020, 23, 549–578. [Google Scholar] [CrossRef]
- Alkarni, S.; Afify, A.Z.; Elbatal, I.; Elgarhy, M. The Extended Inverse Weibull Distribution: Properties and Applications. Complexity 2020, 2020, 3297693. [Google Scholar] [CrossRef]
- Kazemi, M.; Azizpoor, M. Estimation of the inverse Weibull distribution parameters under Type-I hybrid censoring. Aust. J. Stat. 2021, 50, 38–51. [Google Scholar] [CrossRef]
- Nassar, M.; Abo-Kasem, O.E. Estimation of the inverse Weibull parameters under adaptive type-II progressive hybrid censoring scheme. J. Comp. App. Math. 2017, 315, 228–239. [Google Scholar] [CrossRef]
- Jana, N.; Bera, S. Estimation of parameters of inverse Weibull distribution and application to multi-component stress-strength model. J. App. Stat. 2022, 49, 169–194. [Google Scholar] [CrossRef] [PubMed]
- Jokiel-Rokita, A.; Piatek, S. Estimation of parameters and quantiles of the Weibull distribution. Stat. Papers 2022. [Google Scholar] [CrossRef]
- Alven, W.H. Reliability Engineering by ARINC; Prentice-Hall: Upper Saddle River, NJ, USA, 1964. [Google Scholar]
- Mead, M.; Nassar, M.M.; Dey, S. A Generalization of Generalized Gamma Distributions. Pak. J. Stat. Oper. Res. 2018, 14, 121–138. [Google Scholar] [CrossRef]
- Maswadah, M. Conditional confidence interval estimation for the inverse Weibull distribution based on censored generalized order statistics. J. Stat. Comput. Simul. 2003, 73, 887–898. [Google Scholar] [CrossRef]
- Wu, S.F.; Wu, C.C. Two stage multiple comparisons with the average for exponential location parameters under heteroscedasticity. J. Statist. Plan Inf. 2005, 134, 392–408. [Google Scholar] [CrossRef]
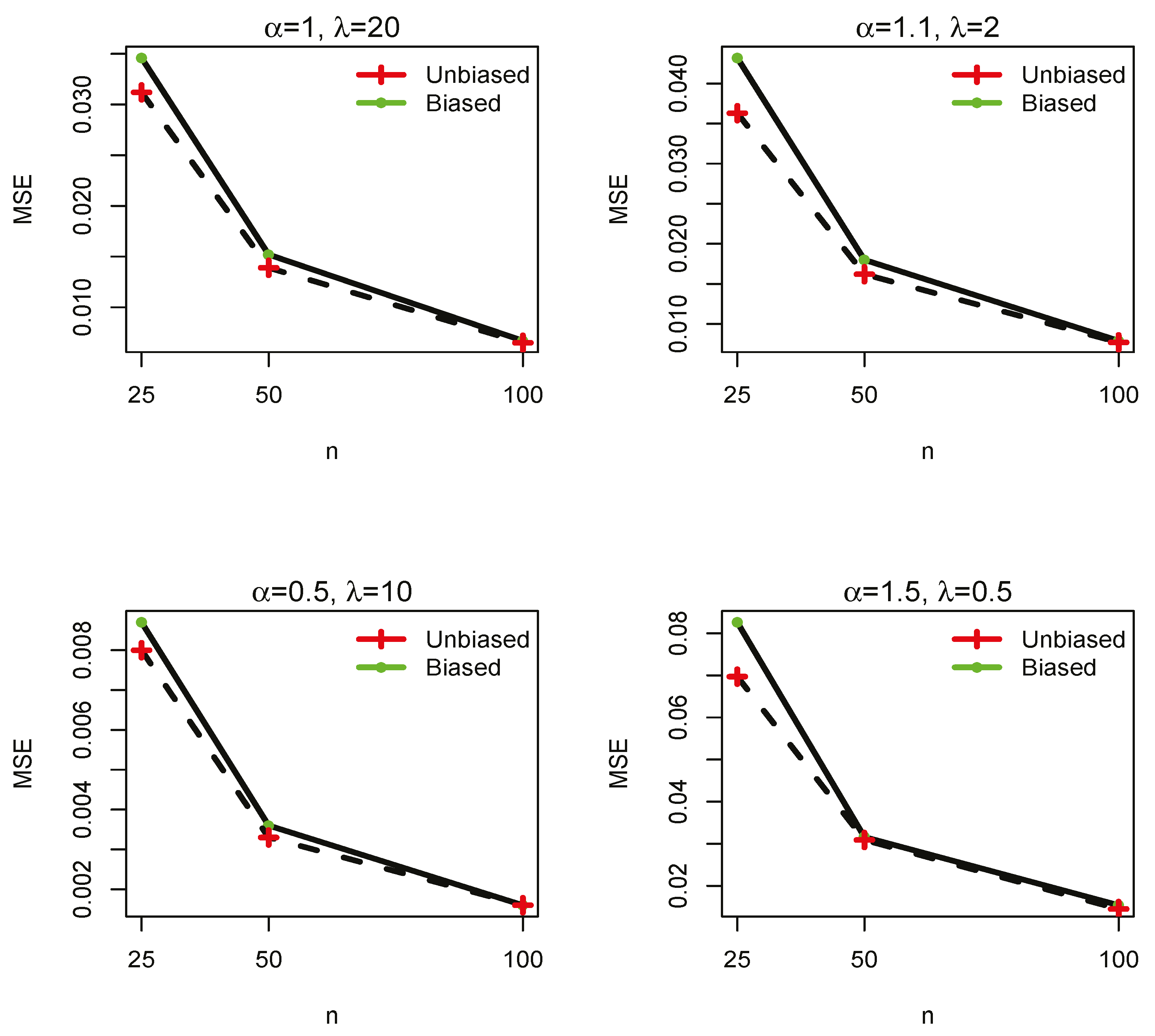
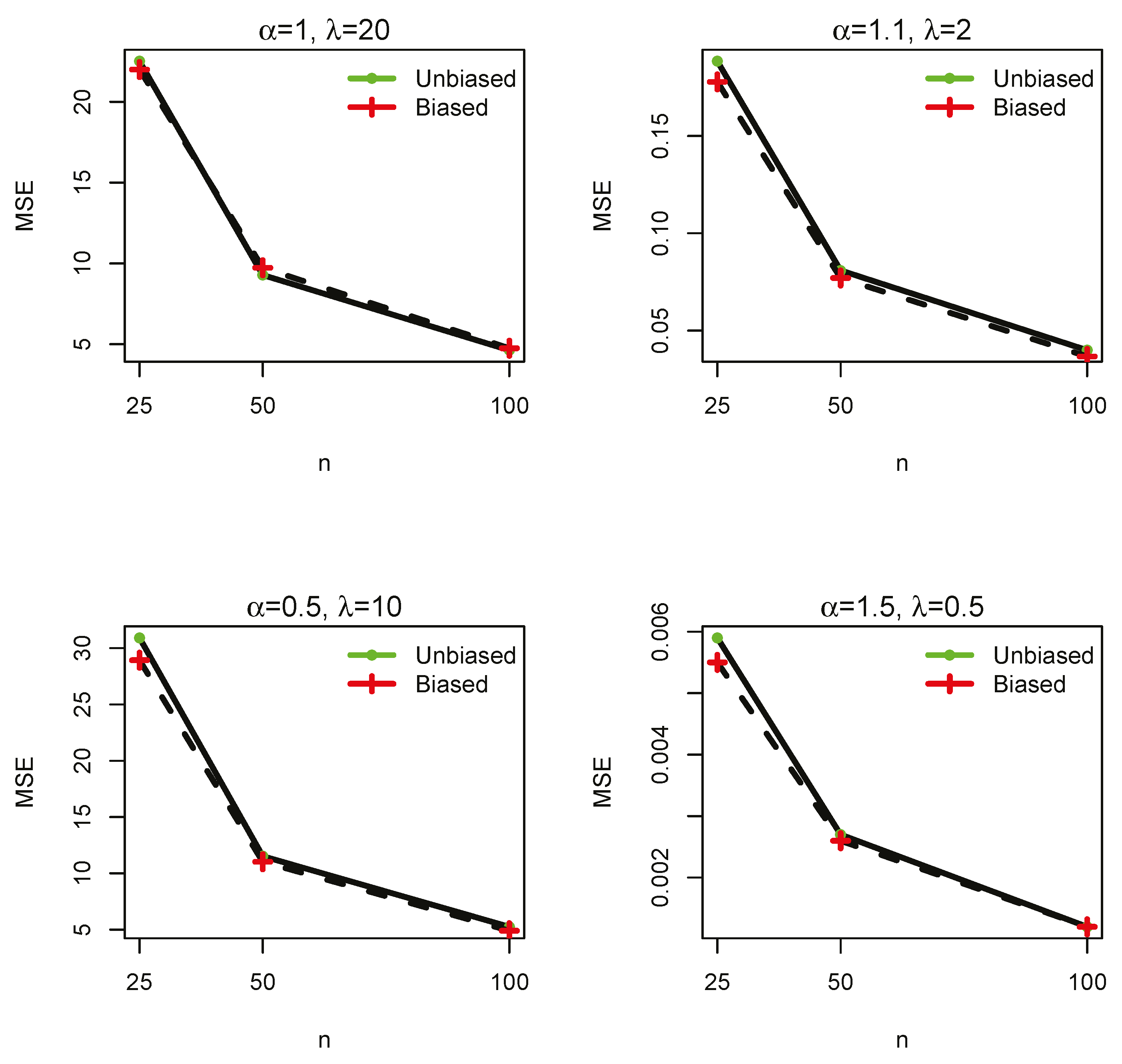

| Method | 25 | 50 | 100 | ||||
|---|---|---|---|---|---|---|---|
| B | MSE | B | MSE | B | MSE | ||
| MLE | 1, 20 | 0.0601 | 0.0346 | 0.0294 | 0.0152 | 0.0146 | 0.0067 |
| 0.8405 | 21.9961 | 0.3677 | 9.7325 | 0.1833 | 4.7483 | ||
| 1.1, 2 | 0.0684 | 0.0432 | 0.0313 | 0.0180 | 0.0153 | 0.0079 | |
| 0.0693 | 0.1778 | 0.0321 | 0.0770 | 0.0158 | 0.0367 | ||
| 0.5, 10 | 0.0300 | 0.0087 | 0.0141 | 0.0036 | 0.0067 | 0.0016 | |
| 1.2684 | 28.9262 | 0.6244 | 11.0262 | 0.2709 | 4.9036 | ||
| 1.5, 0.5 | 0.0928 | 0.0826 | 0.0373 | 0.0316 | 0.0217 | 0.0154 | |
| 0.0106 | 0.0055 | 0.0052 | 0.0026 | 0.0021 | 0.0012 | ||
| MMLE | 1, 20 | 0.0307 | 0.0312 | 0.0157 | 0.0139 | 0.0073 | 0.0065 |
| 0.8759 | 22.5114 | 0.4094 | 9.2799 | 0.2726 | 4.6273 | ||
| 1.1, 2 | 0.0350 | 0.0363 | 0.0161 | 0.162 | 0.0088 | 0.0077 | |
| 0.0894 | 0.1884 | 0.0440 | 0.0809 | 0.0186 | 0.0399 | ||
| 0.5, 10 | 0.0181 | 0.0080 | 0.0065 | 0.0033 | 0.0041 | 0.0016 | |
| 1.4493 | 30.9124 | 0.7504 | 11.5184 | 0.3412 | 5.2525 | ||
| 1.5, 0.5 | 0.0497 | 0.0697 | 0.0249 | 0.0309 | 0.0122 | 0.0145 | |
| 0.0137 | 0.0059 | 0.0085 | 0.0027 | 0.0035 | 0.0012 | ||
| n | ||||
|---|---|---|---|---|
| Method | 25 | 50 | 100 | |
| α, λ | Var | Var | Var | |
| MLE | 1, 20 | 0.0309, 21.2896 | 0.0143, 9.5972 | 0.0064, 4.7147 |
| 1.1, 2 | 0.0385, 0.1729 | 0.0170, 0.0759 | 0.0076, 0.0364 | |
| 0.5, 10 | 0.0078, 27.3173 | 0.0034, 10.6363 | 0.0015, 4.8302 | |
| 1.5, 0.5 | 0.0739, 0.0053 | 0.0302, 0.0025 | 0.0149, 0.0011 | |
| MMLE | 1, 20 | 0.0302, 21.7442 | 0.0136, 9.1122 | 0.0064, 4.5529 |
| 1.1, 2 | 0.0350, 0.1804 | 0.1617, 0.0789 | 0.0076, 0.0395 | |
| 0.5, 10 | 0.0076, 28.8119 | 0.0032, 10.9553 | 0.0015, 5.1360 | |
| 1.5, 0.5 | 0.0672, 0.0057 | 0.0302, 0.0026 | 0.0143, 0.0011 | |
| 0.2 | 0.3 | 0.5 | 0.5 | 0.5 | 0.5 | 0.6 | 0.6 | 0.7 | 0.7 |
| 0.7 | 0.8 | 0.8 | 1.0 | 1.0 | 1.0 | 1.0 | 1.1 | 1.3 | 1.5 |
| 0.5 | 1.5 | 1.5 | 2.0 | 2.0 | 2.2 | 2.5 | 2.7 | 3.0 | 3.0 |
| 0.3 | 3.3 | 4.0 | 4.0 | 4.5 | 4.7 | 5.0 | 5.4 | 5.4 | 7.0 |
| 0.5 | 8.8 | 9.0 | 10.3 | 22.0 | 24.5 |
| Model | Method | AIC | BIC | KS p-Value | CVM p-Value | AD p-Value | ||
|---|---|---|---|---|---|---|---|---|
| IW | MLE | 1.0127 | 1.1298 | 205.38 | 209.04 | 0.0807 0.9256 | 0.0510 0.8726 | 0.3570 0.8895 |
| IW | MMLE | 1.0000 | 1.1362 | 205.39 | 209.05 | 0.0760 0.9530 | 0.0470 0.8962 | 0.3461 0.8994 |
| Weibull | MLE | 0.8986 | 0.3337 | 212.93 | 216.59 | 0.1204 0.5170 | 0.1203 0.4956 | 0.8874 0.4214 |
| Gamma | MLE | 0.9324 | 0.2585 | 213.86 | 217.51 | 0.14545 0.2848 | 0.17532 0.3216 | 1.1042 0.3066 |
| Pareto | MLE | 0.2825 | 2.5981 | 209.90 | 213.56 | 0.1274 0.4442 | 0.0710 0.7478 | 0.6194 0.6289 |
| 0.654 | 0.613 | 0.315 | 0.449 | 0.297 | 0.402 | 0.379 | 0.423 | 0.379 | 0.324 |
| 0.269 | 0.740 | 0.418 | 0.412 | 0.494 | 0.416 | 0.338 | 0.392 | 0.484 | 0.265 |
| Model | Method | AIC | BIC | KS p-Value | CVM p-Value | AD p-Value | ||
|---|---|---|---|---|---|---|---|---|
| IW | MLE | 4.4132 | 0.3583 | −28.19 | −26.20 | 0.1560 0.7151 | 0.0546 0.8532 | 0.3104 0.9294 |
| IW | MMLE | 4.1861 | 0.3594 | −28.16 | −26.17 | 0.1488 0.7678 | 0.0520 0.8692 | 0.2973 0.9395 |
| Weibull | MLE | 3.5259 | 14.45 | −22.53 | −20.54 | 0.1987 0.4081 | 0.1400 0.4243 | 0.8215 0.4641 |
| Gamma | MLE | 13.44 | 31.77 | −26.62 | −24.63 | 0.1641 0.6538 | 0.0712 0.7498 | 0.4503 0.7958 |
| Pareto | MLE | 0.4239 | 9.5989 | 11.59 | 0.4647 0.0003 | 1.0582 0.0014 | 5.053 0.0027 |
| 0.158 | 4.025 | 5.170 | 11.909 | 4.912 | 4.629 | 3.955 | 6.735 | 3.140 | 12.446 |
| 0.777 | 6.321 | 3.256 | 8.250 | 3.759 | 5.205 | 3.071 | 3.147 | 9.773 | 10.218 |
| Model | Method | AIC | BIC | KS p-Value | CVM p-Value | AD p-Value | ||
|---|---|---|---|---|---|---|---|---|
| IW | MLE | 2.7192 | 4.4427 | 95.89 | 97.89 | 0.1304 0.8428 | 0.0555 0.8478 | 0.4292 0.8176 |
| IW | MMLE | 2.6292 | 4.4652 | 95.93 | 97.92 | 0.1195 0.9058 | 0.0503 0.8798 | 0.3884 0.8586 |
| Weibull | MLE | 2.2434 | 0.0128 | 101.06 | 103.06 | 0.1957 0.3783 | 0.1291 0.4633 | 0.7696 0.5017 |
| Gamma | MLE | 4.8300 | 0.7863 | 98.97 | 100.96 | 0.1792 0.4868 | 0.1140 0.5243 | 0.6937 0.5621 |
| Pareto | MLE | 6.1430 | 116.61 | 118.60 | 0.3934 0.0026 | 0.5500 0.0287 | 2.8692 0.0324 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kayid, M.; Alshehri, M.A. Modified Maximum Likelihood Estimation of the Inverse Weibull Model. Axioms 2023, 12, 961. https://doi.org/10.3390/axioms12100961
Kayid M, Alshehri MA. Modified Maximum Likelihood Estimation of the Inverse Weibull Model. Axioms. 2023; 12(10):961. https://doi.org/10.3390/axioms12100961
Chicago/Turabian StyleKayid, Mohamed, and Mashael A. Alshehri. 2023. "Modified Maximum Likelihood Estimation of the Inverse Weibull Model" Axioms 12, no. 10: 961. https://doi.org/10.3390/axioms12100961
APA StyleKayid, M., & Alshehri, M. A. (2023). Modified Maximum Likelihood Estimation of the Inverse Weibull Model. Axioms, 12(10), 961. https://doi.org/10.3390/axioms12100961








