Experimental Study of Void Fraction Measurement Using a Capacitance-Based Sensor and ANN in Two-Phase Annular Regimes for Different Fluids
Abstract
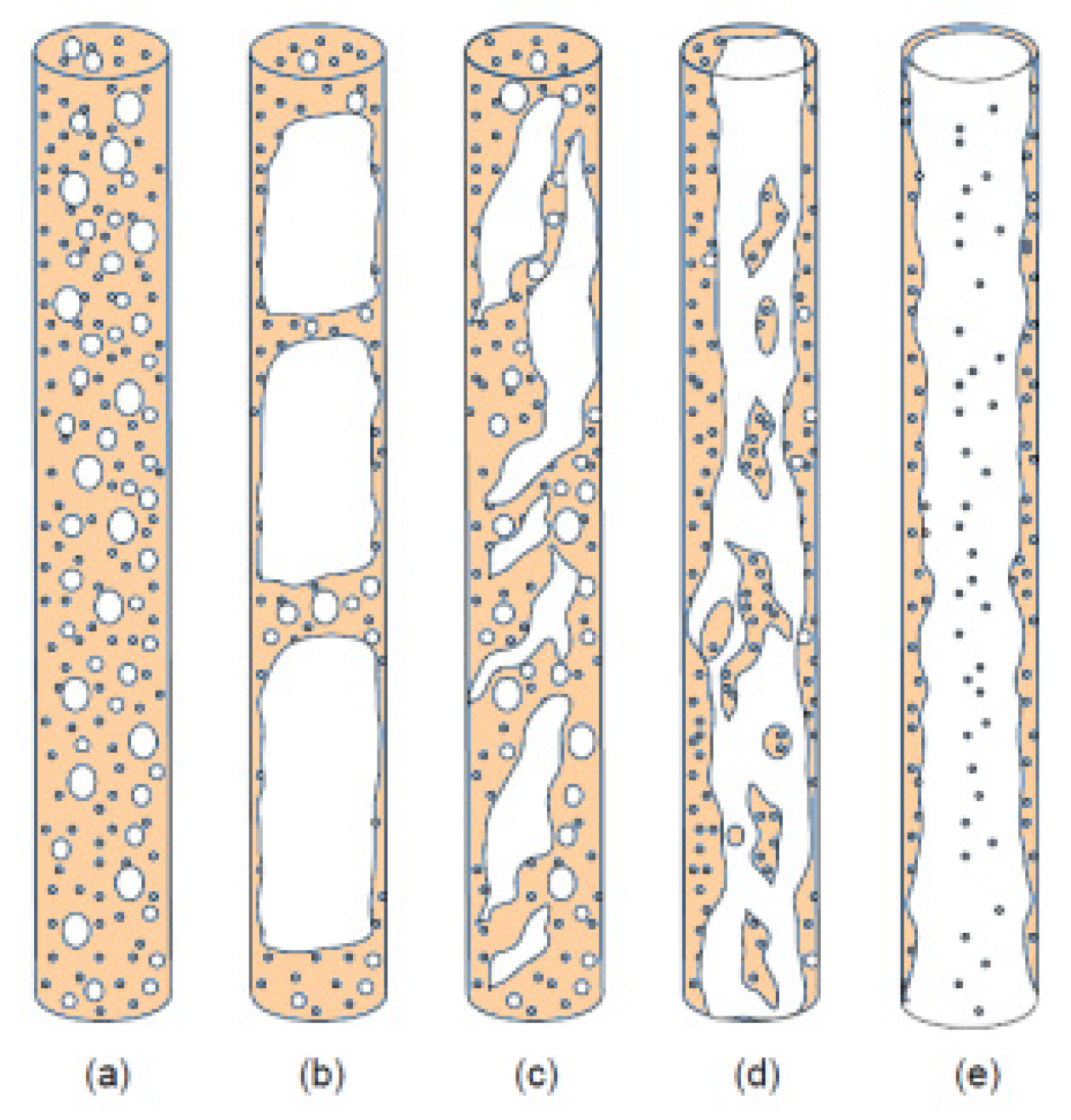
1. Introduction
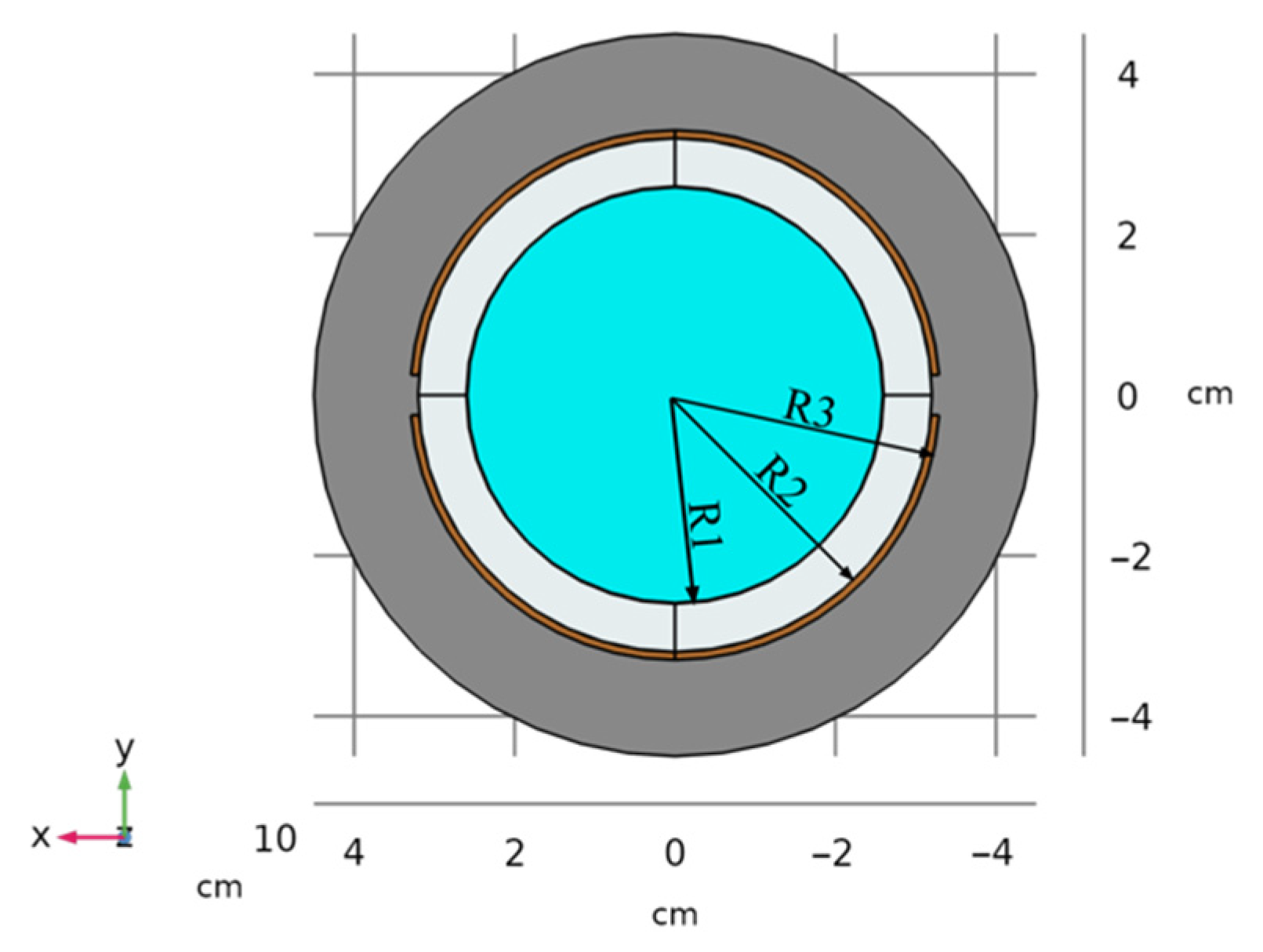
2. Experimental Setup of the Concave Capacitive Sensor and Measurements
3. Numerical Simulations
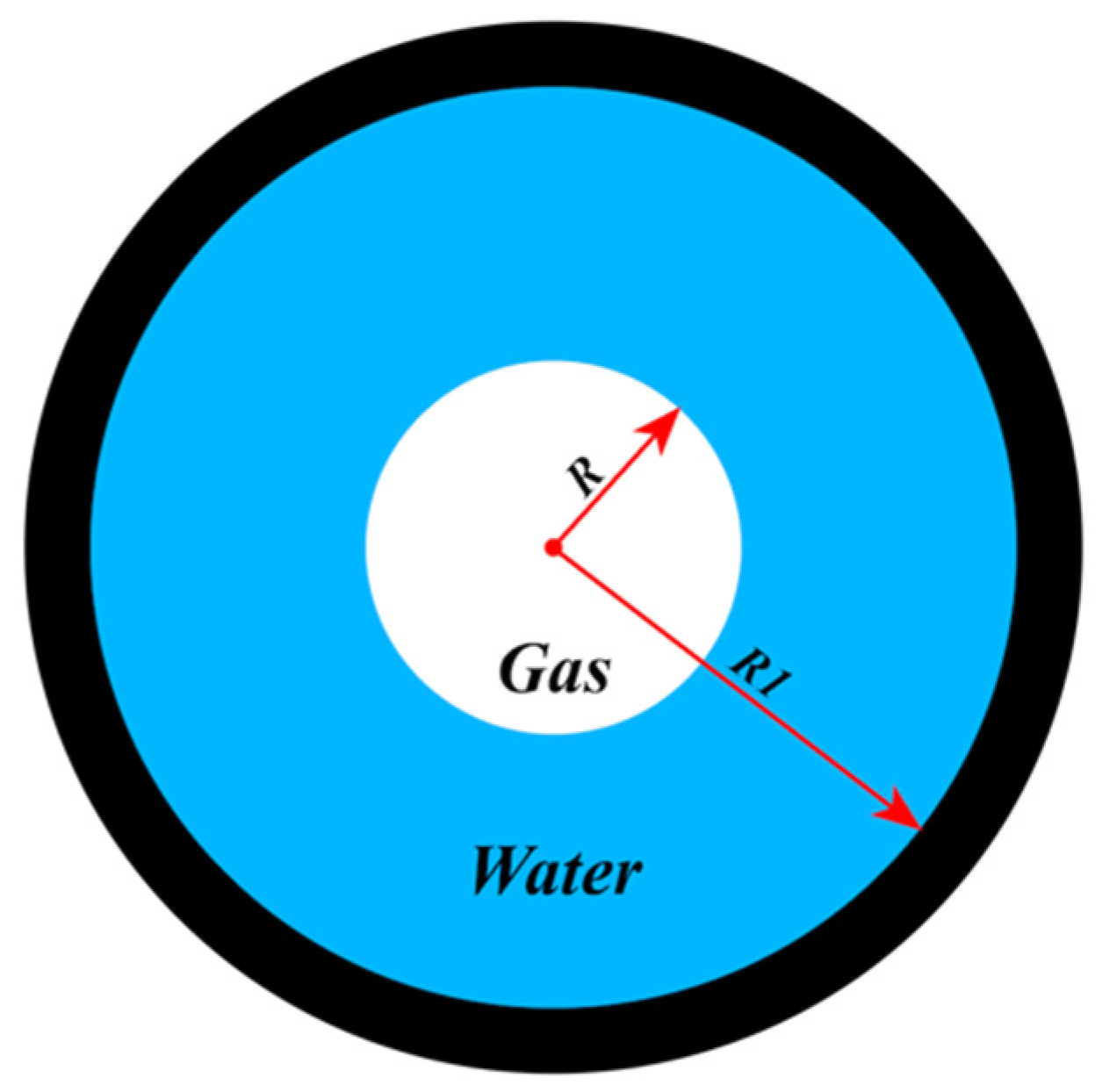
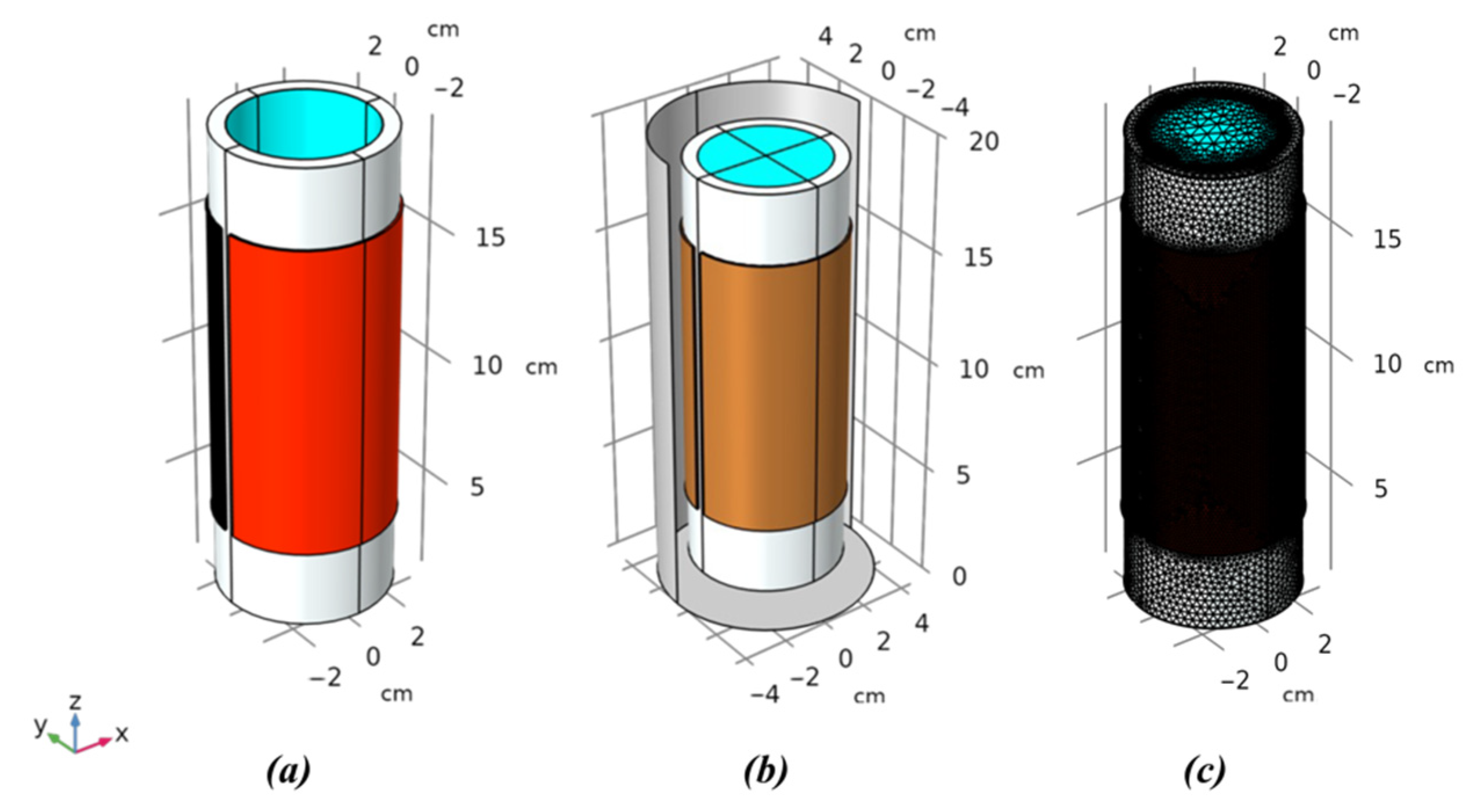
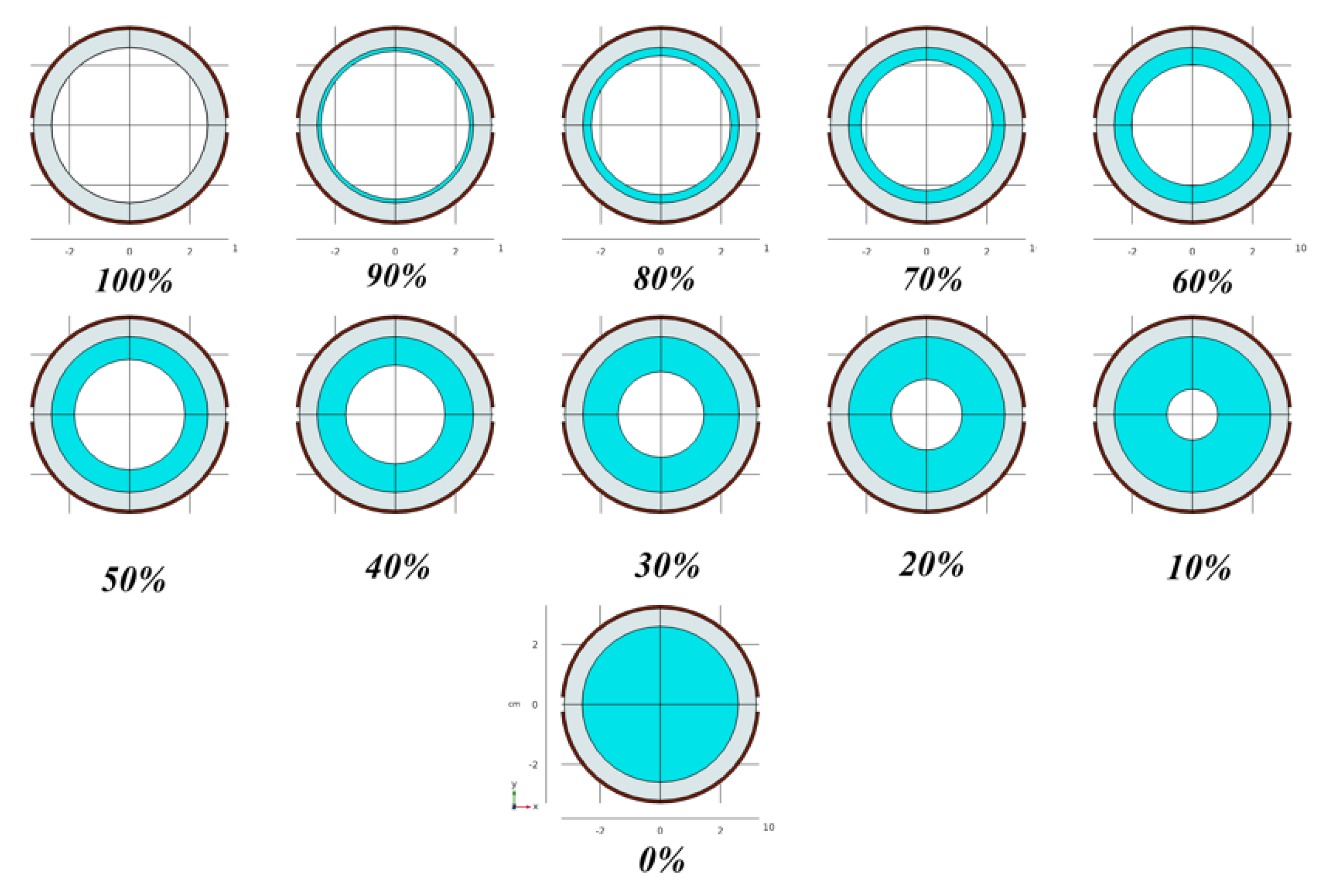
3.1. Modelled Configuration
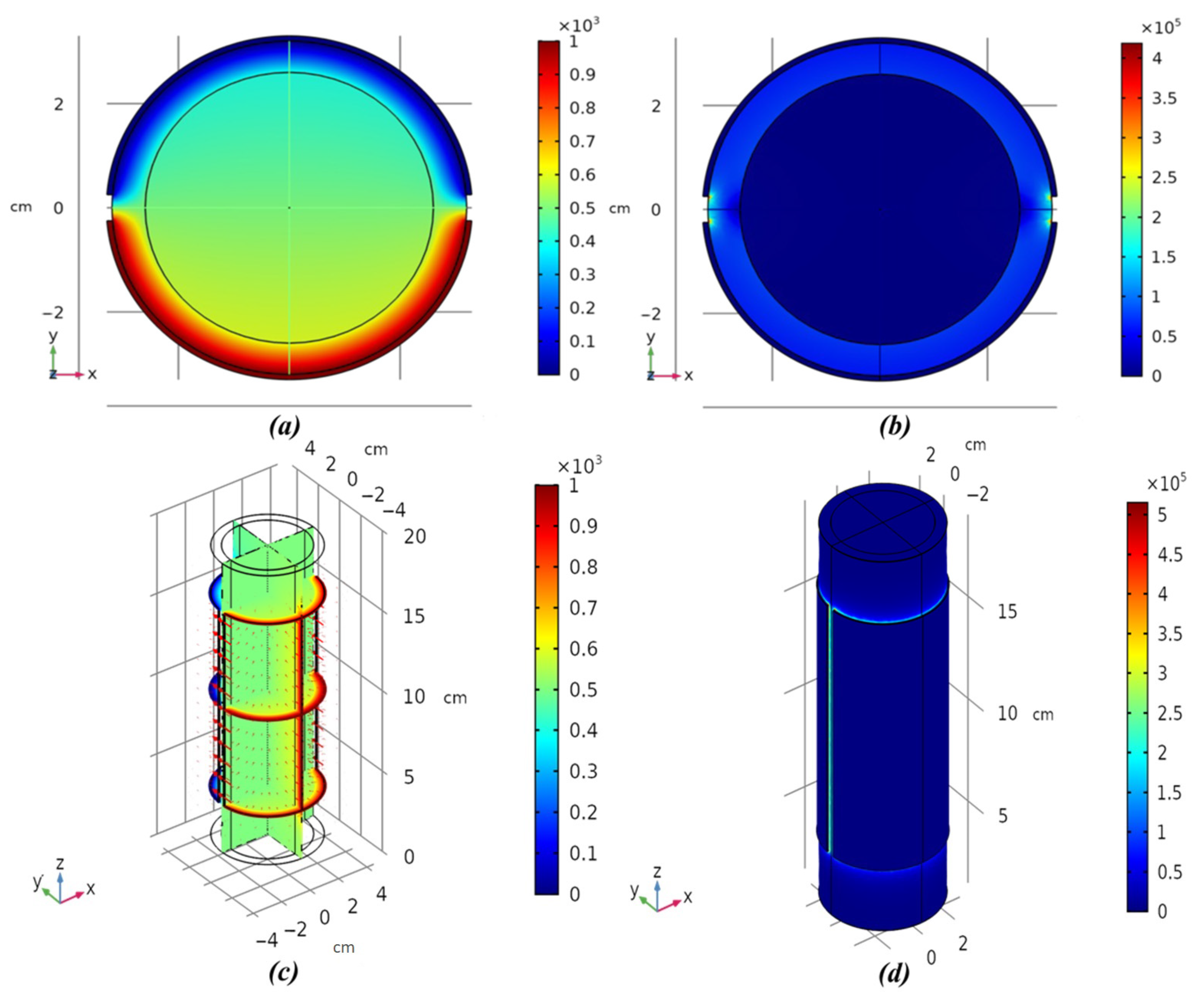
3.2. Validation of Simulations
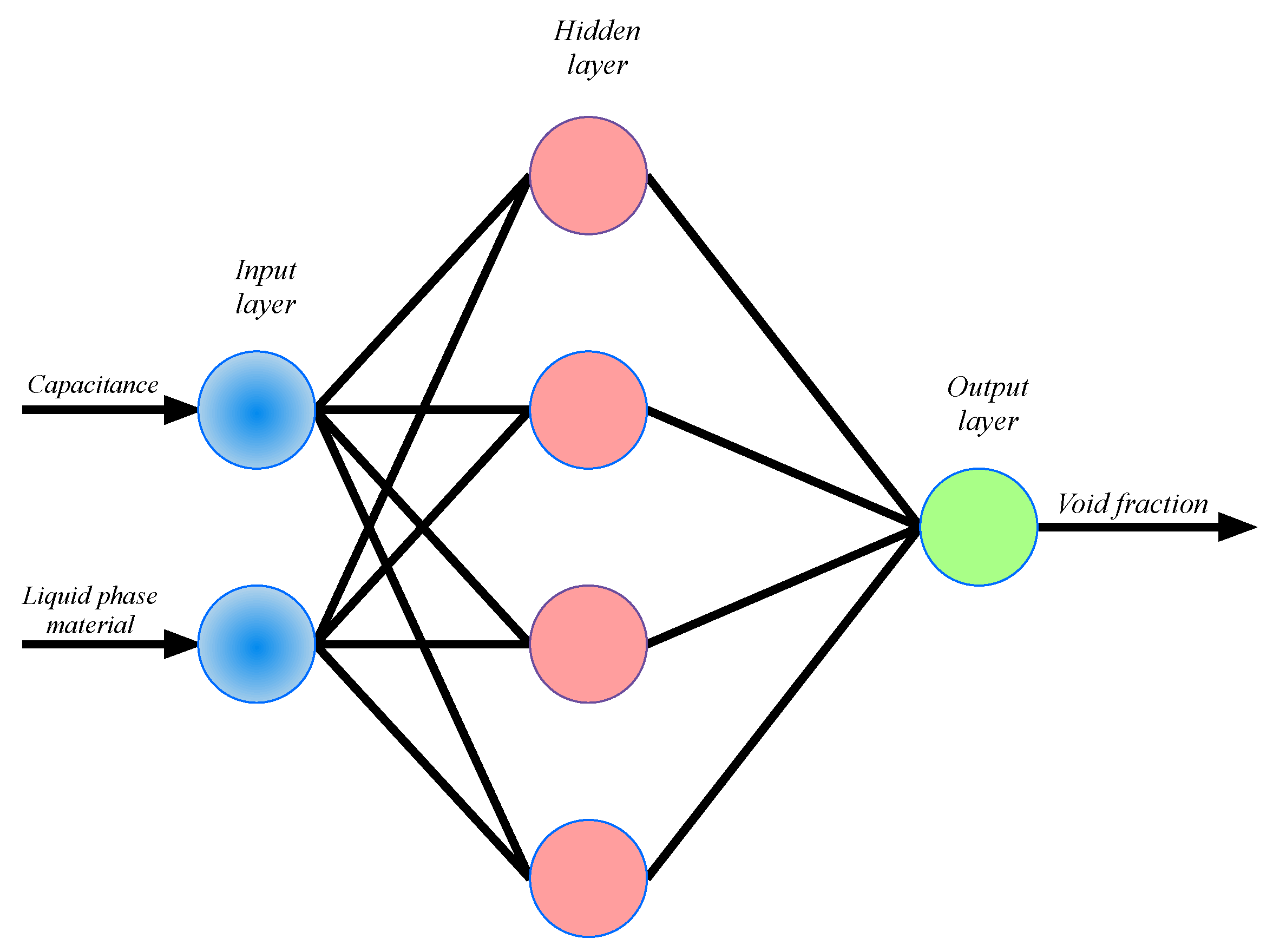
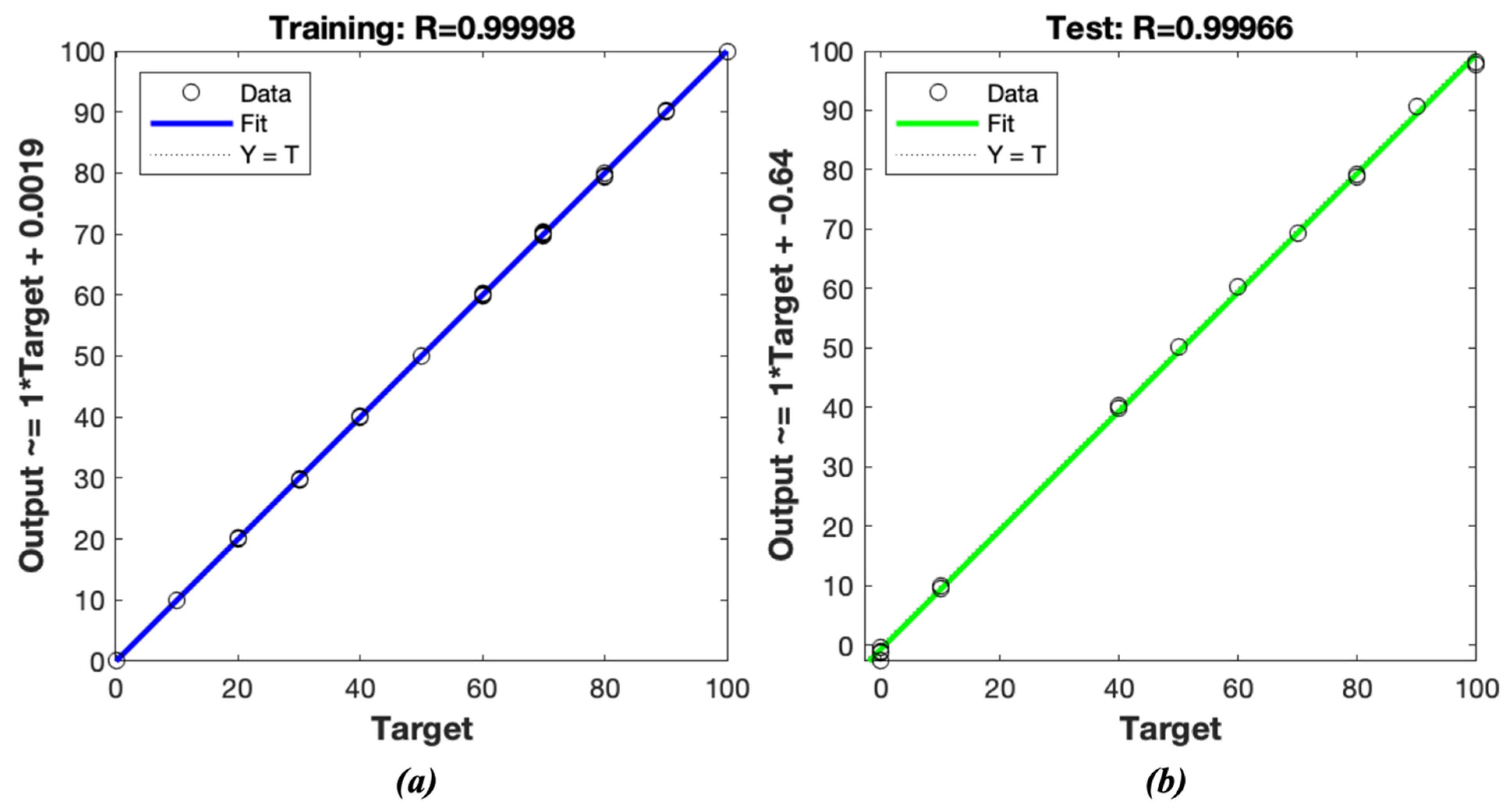
4. Artificial Neural Network
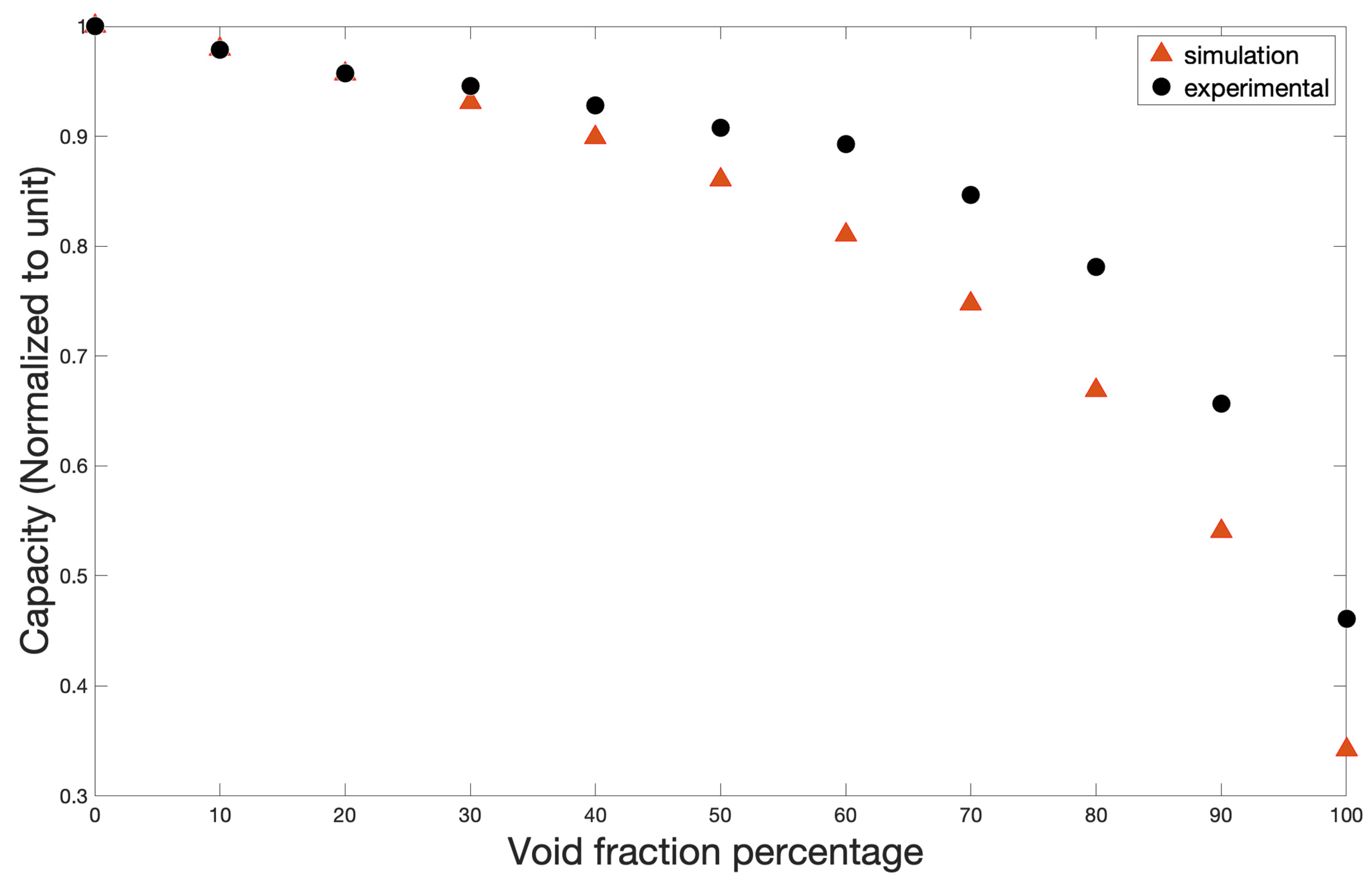
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, G.; Ji, H.; Huang, Z.; Wang, B.; Li, H. Flow regime identification of mini-pipe gas-liquid two-phase flow based on textural feature series. In Proceedings of the 2011 IEEE International Instrumentation and Measurement Technology Conference, Hangzhou, China, 10–12 May 2011; pp. 1–4. [Google Scholar]
- Hewitt, G.F. Developments in multiphase metering. In Proceedings of the Conference on Developments in Production Separation Systems, London, UK, 4 March 1993. [Google Scholar]
- Thorn, R.; Johansen, G.; Hammer, E. Recent developments in three-phase flow measurement. Meas. Sci. Technol. 1997, 8, 691–701. [Google Scholar] [CrossRef]
- Ismail, I.; Gamio, J.; Bukhari, S.A.; Yang, W. Tomography for multi-phase flow measurement in the oil industry. Flow Meas. Instrum. 2005, 16, 145–155. [Google Scholar] [CrossRef]
- Wang, D.; Liang, F.C.; Peng, Z.Q.; Wang, Y.G.; Lin, Z.H. Gas-liquid two-phase flow measurements by full stream batch sampling. Int. J. Multiph. Flow 2012, 40, 113–125. [Google Scholar] [CrossRef]
- Yang, H.; Kim, D.; Kim, M. Void fraction measurement using impedance method. Flow Meas. Instrum. 2003, 14, 151–160. [Google Scholar] [CrossRef]
- Lowe, D.; Rezkallah, K.S. A capacitance sensor for the characterization of microgravity two-phase liquid-gas flows. Meas. Sci. Technol. 1999, 10, 965–975. [Google Scholar] [CrossRef]
- Özgü, M.R.; Chen, J.C.; Eberhardt, N. A capacitance method for measurement of film thickness in two-phase flow. Rev. Sci. Instrum. 1973, 44, 1714–1716. [Google Scholar] [CrossRef]
- Reinecke, N.; Mewes, D. Recent developments and industrial/research applications of capacitance tomography. Meas. Sci. Technol. 1996, 7, 233–246. [Google Scholar] [CrossRef]
- Geraets, J.; Borst, J. A capacitance sensor for two-phase void fraction measurement and flow pattern identification. Int. J. Multiph. Flow 1988, 14, 305–320. [Google Scholar] [CrossRef]
- Strizzolo, C.N.; Converti, J. Capacitance sensors for measurement of phase volume fraction in two-phase pipelines. IEEE Trans. Instrum. Meas. 1993, 42, 726–729. [Google Scholar] [CrossRef]
- Yang, W.; Peng, L. Image reconstruction algorithms for electrical capacitance tomography. Meas. Sci. Technol. 2002, 14, R1–R13. [Google Scholar] [CrossRef]
- Olmos, A.M.; Carvajal, M.; Morales, D.; García, A.; Palma, A. Development of an electrical capacitance tomography system using four rotating electrodes. Sens. Actuators A Phys. 2008, 148, 366–375. [Google Scholar] [CrossRef]
- dos Reis, E.; Goldstein, L., Jr. A non-intrusive probe for bubble profile and velocity measurement in horizontal slug flows. Flow Meas. Instrum. 2005, 16, 229–239. [Google Scholar] [CrossRef]
- Dyakowski, T.; Edwards, R.; Xie, C.; Williams, R.A. Application of capacitance tomography to gas-solid flows. Chem. Eng. Sci. 1997, 52, 2099–2110. [Google Scholar] [CrossRef]
- Abouelwafa, M.S.A.; Kendall, E.J.M. The use of capacitance sensors for phase percentage determination in multiphase pipelines. IEEE Trans. Instrum. Meas. 1980, 29, 24–27. [Google Scholar] [CrossRef]
- Ahmed, H. Capacitance sensors for void-fraction measurements and flow-pattern identification in air–oil two-phase flow. IEEE Sens. J. 2006, 6, 1153–1163. [Google Scholar] [CrossRef]
- Demori, M.; Ferrari, V.; Strazza, D.; Poesio, P. A capacitive sensor system for the analysis of two-phase flows of oil and conductive water. Sens. Actuators A Phys. 2010, 163, 172–179. [Google Scholar] [CrossRef]
- Tollefsen, J.; Hammer, E.A. Capacitance sensor design for reducing errors in phase concentration measurements. Flow Meas. Instrum. 1998, 9, 25–32. [Google Scholar] [CrossRef]
- Salehi, S.M.; Karimi, H.; Dastranj, A.A. A capacitance sensor for gas/oil two-phase flow measurement: Exciting frequency analysis and static experiment. IEEE Sens. J. 2016, 17, 679–686. [Google Scholar] [CrossRef]
- Salehi, S.M.; Karimi, H.; Moosavi, R.; Dastranj, A.A. Different configurations of capacitance sensor for gas/oil two phase flow measurement: An experimental and numerical study. Exp. Therm. Fluid Sci. 2017, 82, 349–358. [Google Scholar] [CrossRef]
- Salehi, S.M.; Karimi, H.; Dastranj, A.A.; Moosavi, R. Twin rectangular fork-like capacitance sensor to flow regime identification in horizontal co-current gas–liquid two-phase flow. IEEE Sens. J. 2017, 17, 4834–4842. [Google Scholar] [CrossRef]
- Zych, M.; Petryka, L.; Kępński, J.; Hanus, R.; Bujak, T.; Puskarczyk, E. Radioisotope investigations of compound two-phase flows in an ope channel. Flow Meas. Instrum. 2014, 35, 11–15. [Google Scholar] [CrossRef]
- Chen, X.; Zheng, J.; Jiang, J.; Peng, H.; Luo, Y.; Zhang, L. Numerical Simulation and Experimental Study of a Multistage Multiphase Separation System. Separations 2022, 9, 405. [Google Scholar] [CrossRef]
- Rushd, S.; Gazder, U.; Qureshi, H.J.; Arifuzzaman, M. Advanced Machine Learning Applications to Viscous Oil-Water Multi-Phase Flow. Appl. Sci. 2022, 12, 4871. [Google Scholar] [CrossRef]
- Chala, G.T.; Negash, B.M. Artificial Neural Network and Regression Models for Predicting Intrusion of Non-Reacting Gases into Production Pipelines. Energies 2022, 15, 1725. [Google Scholar] [CrossRef]
- Ssebadduka, R.; Le, N.N.H.; Nguele, R.; Alade, O.; Sugai, Y. Artificial Neural Network Model Prediction of Bitumen/Light Oil Mixture Viscosity under Reservoir Temperature and Pressure Conditions as a Superior Alternative to Empirical Models. Energies 2021, 14, 8520. [Google Scholar] [CrossRef]
- Picha, T.; Papezova, S.; Picha, S. Evaluation of Relative Permittivity and Loss Factor of 3D Printing Materials for Use in RF Electronic Applications. Processes 2022, 10, 1881. [Google Scholar] [CrossRef]
- Kumbharkhane, A.; Puranik, S.; Mehrotra, S. Temperature dependent dielectric relaxation study of ethylene glycol-water mixtures. J. Solut. Chem. 1992, 21, 201–212. [Google Scholar] [CrossRef]
- Mukhlisin, M.; Saputra, A. Performance evaluation of volumetric water content and relative permittivity models. Sci. World J. 2013, 2013, 421762. [Google Scholar] [CrossRef]
- Roshani, G.; Feghhi, S.; Mahmoudi-Aznaveh, A.; Nazemi, E.; Adineh-Vand, A. Precise volume fraction prediction in oil–water–gas multiphase flows by means of gamma-ray attenuation and artificial neural networks using one detector. Measurement 2014, 51, 34–41. [Google Scholar] [CrossRef]
- Gallant, A.R.; White, H. On learning the derivatives of an unknown mapping with multilayer feedforward networks. Neural Netw. 1992, 5, 129–138. [Google Scholar] [CrossRef]
- Salgado, C.M.; Brandão, L.E.; Schirru, R.; Pereira, C.M.; da Silva, A.X.; Ramos, R. Prediction of volume fractions in three-phase flows using nuclear technique and artificial neural network. Appl. Radiat. Isot. 2009, 67, 1812–1818. [Google Scholar] [CrossRef]
- Roshani, G.H.; Roshani, S.; Nazemi, E.; Roshani, S. Online Measuring Density of Oil Products in Annular Regime of Gas-Liquid Two Phase Flows. Meas. J. Int. Meas. Confed. 2018, 129, 296–301. [Google Scholar] [CrossRef]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Balubaid, M.; Sattari, M.A.; Taylan, O.; Bakhsh, A.A.; Nazemi, E. Applications of discrete wavelet transform for feature extraction to increase the accuracy of monitoring systems of liquid petroleum products. Mathematics 2021, 9, 3215. [Google Scholar] [CrossRef]
- Hosseini, S.; Taylan, O.; Abusurrah, M.; Akilan, T.; Nazemi, E.; Eftekhari-Zadeh, E.; Bano, F.; Roshani, G.H. Application of Wavelet Feature Extraction and Artificial Neural Networks for Improving the Performance of Gas–Liquid Two-Phase Flow Meters Used in Oil and Petrochemical Industries. Polymers 2021, 13, 3647. [Google Scholar] [CrossRef]
- Alamoudi, M.; Sattari, M.A.; Balubaid, M.; Eftekhari-Zadeh, E.; Nazemi, E.; Taylan, O.; Kalmoun, E.M. Application of Gamma Attenuation Technique and Artificial Intelligence to Detect Scale Thickness in Pipelines in Which Two-Phase Flows with Different Flow Regimes and Void Fractions Exist. Symmetry 2021, 13, 1198. [Google Scholar] [CrossRef]





| Void Fraction (%) | Measured Capacitance (pF) |
|---|---|
| 100 | 27.21 |
| 90 | 44.73 |
| 80 | 53.19 |
| 70 | 57.65 |
| 60 | 60.83 |
| 50 | 61.80 |
| 40 | 63.22 |
| 30 | 64.38 |
| 20 | 65.23 |
| 10 | 66.65 |
| 0 | 68.11 |
| Void Fraction (%) | Simulated Capacitance (pF) |
|---|---|
| 100 | 10.067 |
| 90 | 15.317 |
| 80 | 18.957 |
| 70 | 21.178 |
| 60 | 22.967 |
| 50 | 24.391 |
| 40 | 25.481 |
| 30 | 26.389 |
| 20 | 27.113 |
| 10 | 27.749 |
| 0 | 28.341 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Veisi, A.; Shahsavari, M.H.; Roshani, G.H.; Eftekhari-Zadeh, E.; Nazemi, E. Experimental Study of Void Fraction Measurement Using a Capacitance-Based Sensor and ANN in Two-Phase Annular Regimes for Different Fluids. Axioms 2023, 12, 66. https://doi.org/10.3390/axioms12010066
Veisi A, Shahsavari MH, Roshani GH, Eftekhari-Zadeh E, Nazemi E. Experimental Study of Void Fraction Measurement Using a Capacitance-Based Sensor and ANN in Two-Phase Annular Regimes for Different Fluids. Axioms. 2023; 12(1):66. https://doi.org/10.3390/axioms12010066
Chicago/Turabian StyleVeisi, Aryan, Mohammad Hossein Shahsavari, Gholam Hossein Roshani, Ehsan Eftekhari-Zadeh, and Ehsan Nazemi. 2023. "Experimental Study of Void Fraction Measurement Using a Capacitance-Based Sensor and ANN in Two-Phase Annular Regimes for Different Fluids" Axioms 12, no. 1: 66. https://doi.org/10.3390/axioms12010066
APA StyleVeisi, A., Shahsavari, M. H., Roshani, G. H., Eftekhari-Zadeh, E., & Nazemi, E. (2023). Experimental Study of Void Fraction Measurement Using a Capacitance-Based Sensor and ANN in Two-Phase Annular Regimes for Different Fluids. Axioms, 12(1), 66. https://doi.org/10.3390/axioms12010066







