Computer-Aided Analysis of Solvable Rigid Lie Algebras with a Given Eigenvalue Spectrum
Abstract
1. Introduction
1.1. Generalities
1.2. Rigid Lie Algebras and Chevalley cohomology
- 1.
- The tangent Zariski space to at the point coincides with the space of 2 cocycles of the Chevalley cohomology.
- 2.
- The tangent space to the orbit coincides with the space of 2 coboundaries of the Chevalley cohomology.
2. Rigid Lie Algebras with Fixed Eigenvalue Spectrum
3. Rigid Algebras with Spectrum (13) and
- 1.
- Set for .
- 2.
- Start with .
- 3.
- In the main diagonal , set and for .
- 4.
- If the linear Equations (15) are incompatible, then replace q by and go to step 3.
- 5.
- If (15) is satisfied, evaluate the system formed by the Jacobi conditions for the triples with .
- 6.
- If the system admits no solution, then replace q by and go to step 3.
- 7.
- If the system admits a solution depending on one or more parameters , then replace q by and go to step 3.
- 8.
- If the system admits an isolated solution, let be the corresponding nilpotent Lie algebra.
- 9.
- Compute .
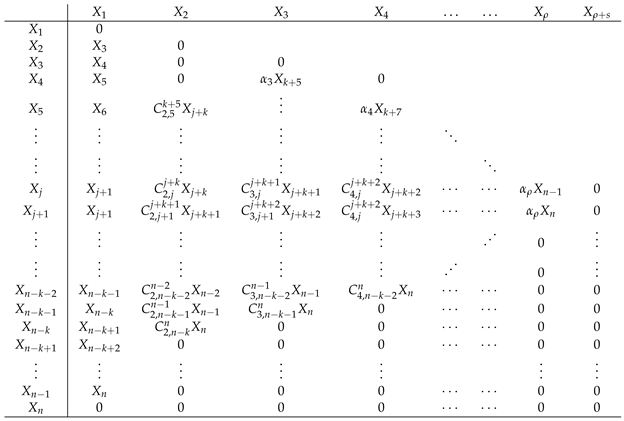
- 1.
- For , we obtain parametrised families with two or more parameters, so that no cohomologically rigid solution is obtained.
- 2.
- For , there are seven solutions, but none of the isolated ones has a vanishing cohomology.
- 3.
- For , there are six parametrised families and four isolated solutions. Among these, only two have a vanishing cohomology. The main diagonal is given by
- 4.
- For , there are nine solutions, four of which are isolated, and only two of these have vanishing cohomology. The diagonal is given by
- 5.
- For , there are five solutions, from which two are isolated with diagonals given, respectively, byAlthough the associated solvable Lie algebras satisfy in both cases , they are geometrically rigid, as can be shown by topological arguments (see, e.g., [30]).
- 6.
- For , there are six solutions, from which two are isolated with diagonals given, respectively, byAs before, for the associated solvable Lie algebras . Furthermore, in this case, these Lie algebras are geometrically rigid.
- 7.
- For , we find four solutions—one is isolated. It is cohomologically rigid with diagonal
- 8.
- For , we find five solutions—one isolated. It is cohomologically rigid with diagonal
- 9.
- For , we obtain at most four solutions, three of them parametrised and one isolated with vanishing cohomology. The precise structure of the resulting diagonal and the associated nilradical for this series will be described in the following paragraph.

3.1. Algebras with
3.1.1. k Even, n Odd
3.1.2. k Even, n Even
3.1.3. k Odd, n Odd
3.1.4. k Odd, n Even
4. Algebras with
4.1. Subcase 1: , ,
- 1.
- For odd values of n and , there exists an -dimensional cohomologically rigid Lie algebra, , for any .
- 2.
- For odd values of n and , there exists an -dimensional cohomologically rigid Lie algebra, , for any .
- 3.
- For odd values of n and either or , there do not exist cohomologically rigid solutions.
- 4.
- For even values of n and either or , there do not exist cohomologically rigid solutions.
- 5.
- For even values of n and , there exists an -dimensional cohomologically rigid Lie algebra, , for any .
- 6.
- For even values of n and , there exists an -dimensional cohomologically rigid Lie algebra, , for any .
4.2. Subcase 2: and
- 1.
- For odd values of n and , there exists an -dimensional cohomologically rigid Lie algebra, , for any and .
- 2.
- For even values of n and , there do not exist cohomologically rigid solutions.
- 3.
- For odd values of n and , there exists an -dimensional cohomologically rigid Lie algebra, , for any and .
- 4.
- For even values of n and , there exists an -dimensional cohomologically rigid Lie algebra, , for any and .
- 5.
- For odd values of n and , there do not exist cohomologically rigid solutions.
- 6.
- For even values of n and , there exists an -dimensional cohomologically rigid Lie algebra, , for any and .
- 7.
- For , there do not exist cohomologically rigid solutions, regardless of the parity on n.
4.3. Subcase 3: , and
- 1.
- For odd values of n and , there exists an -dimensional cohomologically rigid Lie algebra, , for any and .
- 2.
- For even values of n and , there do not exist cohomologically rigid solutions.
- 3.
- For odd values of n and , there exists an -dimensional cohomologically rigid Lie algebra, , for any and .
- 4.
- For even values of n and , there exists an -dimensional cohomologically rigid Lie algebra, , for any and .
- 5.
- For odd values of n and , there do not exist cohomologically rigid solutions.
- 6.
- For even values of n and , there exists an -dimensional cohomologically rigid Lie algebra, , for any and .
- 7.
- For , there do not exist cohomologically rigid solutions, regardless of the parity on n.
4.4. Subcase 4: and
- 1.
- For , there exists an -dimensional cohomologically rigid Lie algebra, , for any .
- 2.
- For , there exists an -dimensional cohomologically rigid Lie algebra, , for .
- 3.
- For , there exists an -dimensional cohomologically rigid Lie algebra, , for any .
- 4.
- For , there exists an -dimensional cohomologically rigid Lie algebra, , for any .
5. Cohomological Rigidity of the Families
- 1.
- For the nilradicals belonging to the subcase , the generic form of a cocycle is given byso that a basis of 2-cocycles is given by the cocycle classes of
- 2.
- For the remaining cases with , the cocycles adopt the formwith basis
Other Isolated Cohomologically Rigid Solutions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Frölicher, A.; Nijenhuis, A. A theorem on stability of complex structures. Proc. Natl. Acad. Sci. USA 1957, 3, 239–241. [Google Scholar] [CrossRef] [PubMed]
- Kodaira, K.; Spencer, D.C. On deformations of complex analytic structures I. Ann. Math. 1958, 67, 328–401. [Google Scholar] [CrossRef]
- Carles, R. Sur certaines classes d’orbites ouvertes dans les variétés d’algèbres de Lie. C. R. Acad. Sci. Paris 1981, 293, 545–547. [Google Scholar]
- Carles, R. Déformations et éléments nilpotents dans les schémas définis par les identités de Jacobi. C. R. Acad. Sci. Paris 1991, 312, 671–674. [Google Scholar]
- Carles, R.; Márquez García, M.C. Different methods for the study of obstructions in the schemes of Jacobi. Ann. Inst. Fourier 2011, 61, 453–490. [Google Scholar] [CrossRef]
- Richardson, R.W. On the rigidity of semi-direct products of Lie algebras. Pac. J. Math. 1967, 22, 329–344. [Google Scholar] [CrossRef]
- Page, S.S. A characterization of rigid algebras. J. Lond. Math. Soc. 1970, 2, 237–240. [Google Scholar] [CrossRef]
- Chevalley, C.; Eilenberg, S. Cohomology theory of Lie groups and Lie algebras. Trans. Amer. Math. Soc. 1948, 63, 85–124. [Google Scholar] [CrossRef]
- Tolpygo, A.K. On the cohomology of parabolic Lie algebras. Mat. Zamet. 1972, 12, 251–255. [Google Scholar] [CrossRef]
- Rauch, G. Effacement et déformation. Ann. Inst. Fourier 1972, 22, 239–269. [Google Scholar] [CrossRef]
- Rim, D.S. Deformation of transitive Lie algebras. Ann. Math. 1966, 83, 339–357. [Google Scholar] [CrossRef]
- Tôgô, S. Outer derivations of Lie algebras. Trans. Amer. Math. Soc. 1967, 128, 264–276. [Google Scholar] [CrossRef][Green Version]
- Bratzlavsky, F. Sur les algèbres admettant un tore d’automorphismes donné. J. Algebra 1974, 30, 305–316. [Google Scholar] [CrossRef]
- Favre, G. Système des poids sur une algèbre de Lie nilpotente. Manuscr. Math. 1973, 9, 53–90. [Google Scholar] [CrossRef]
- Ancochea, J.M.; Goze, M. Algorithme de construction des algèbres de Lie rigides. Publ. Math. Univ. Paris VII 1989, 31, 277–298. [Google Scholar]
- Goze, M. Critères cohomologiques pour la rigidité de lois algébriques. Bull. Soc. Math. Belg. 1991, 43, 33–42. [Google Scholar]
- Ancochea, J.M.; Goze, M. Le rang du système linéaire des racines d’une algèbre de Lie rigide résoluble complexe. Commun. Algebra 1992, 20, 875–887. [Google Scholar]
- Nelson, E. Internal set theory: A new approach to nonstandard analysis. Bull. Amer. Math. Soc. 1977, 83, 1165–1198. [Google Scholar] [CrossRef]
- Goze, M.; Ancochea, J.M. Algèbres de Lie rigides. Indag. Math. 1985, 47, 397–415. [Google Scholar] [CrossRef]
- Goze, M.; Ancochea, J.M. Algèbres de Lie rigides dont le nilradical est filiforme. C. R. Acad. Sci. Paris 1991, 312, 21–24. [Google Scholar]
- Goze, M.; Ancochea, J.M. On the classification of rigid Lie algebras. J. Algebra 2001, 245, 68–91. [Google Scholar] [CrossRef]
- Carles, R. Sur certaines classes d’algèbres de Lie rigides. Math. Ann. 1985, 272, 477–488. [Google Scholar] [CrossRef]
- Ancochea, J.M.; Campoamor-Stursberg, R. Classification of solvable real rigid Lie algebras with a nilradical of dimension n ≤ 6. Linear Algebra Appl. 2015, 451, 54–75. [Google Scholar] [CrossRef]
- Bouarroudj, S.; Navarro, R.M. Cohomologically rigid solvable Lie superalgebras with model filiform and model nilpotent nilradical. Commun. Algebra 2021, 49, 5061–5072. [Google Scholar] [CrossRef]
- Goze, M.; Hakimjanov, Y. Sur les algèbres de Lie nilpotentes admettant un tore de dérivations. Manuscr. Math. 1994, 84, 115–124. [Google Scholar] [CrossRef]
- Ancochea, J.M.; Campoamor-Stursberg, R. Cohomologically rigid solvable real Lie algebras with a nilradical of arbitrary characteristic sequence. Linear Algebra Appl. 2016, 488, 135–147. [Google Scholar] [CrossRef]
- Ancochea, J.M.; Campoamor-Stursberg, R. Rigidity-preserving and cohomology-decreasing extensions of solvable rigid Lie algebras. Linear Multilinear Algebra 2017, 66, 525–539. [Google Scholar] [CrossRef]
- Bérubé, D.; de Montigny, M. The computer calculation of graded contractions of Lie algebras and their representations. Comput. Phys. Commun. 1993, 76, 389–410. [Google Scholar] [CrossRef]
- Grozman, P.; Leites, D. MATHEMATICA aided study of Lie algebras and their cohomology. From supergravity to ballbearings and magnetic hydrodynamics. Trans. Eng. Sci. 1997, 15, 185–192. [Google Scholar]
- Ancochea, J.M.; Campoamor-Stursberg, R.; Oviaño García, F. New examples of rank one solvable real rigid Lie algebras possessing a nonvanishing Chevalley cohomology. Appl. Math. Comput. 2018, 339, 431–440. [Google Scholar]
- Carles, R. Sur la structure des algèbres de Lie rigides. Ann. Inst. Fourier 1984, 34, 65–82. [Google Scholar] [CrossRef]
- Carles, R. Un exemple d’algèbres de Lie résolubles rigides, au deuxième groupe de cohomologie non nul et pour lesquelles l’application quadratique de D.S. Rim est injective. C. R. Acad. Sci. Paris 1985, 300, 467–469. [Google Scholar]
- Carles, R. Sur la cohomologie d’une nouvelle classe d’algèbres de Lie qui généralisent les sous-algèbres de Borel. J. Algebra 1993, 154, 310–334. [Google Scholar] [CrossRef]
- Carles, R.; Petit, T. Versal deformations and versality in central extensions of Jacobi schemes. Transform. Groups 2009, 14, 287–317. [Google Scholar] [CrossRef]
- Campoamor-Stursberg, R.; Oviaño, F. Algorithmic construction of solvable rigid Lie algebras determined by generating functions. Linear Multilinear Algebra 2022, 70, 280–296. [Google Scholar] [CrossRef]
- Campoamor-Stursberg, R.; Oviaño, F. Some features of rank one real solvable cohomologically rigid Lie algebras with a nilradical contracting onto the model filiform Lie algebra Qn. Axioms 2019, 8, 10. [Google Scholar] [CrossRef]
- Mal’cev, A.I. Solvable Lie algebras. Izv. Akad. Nauk SSSR 1945, 9, 329–356. [Google Scholar]
- Šnobl, L.; Winternitz, P. Classification and Identification of Lie Algebras; CRC Monograph Series; American Mathematical Society: Providence, RI, USA, 2014; Volume 33. [Google Scholar]
- Fialowski, A. Deformations and contractions of algebraic structures. Proc. Steklov Inst. Math. 2014, 286, 240–252. [Google Scholar] [CrossRef]
- Rauch, G. Variations d’algébres de Lie résolubles. C. R. Acad. Sci. Paris 1969, 269, 285–288. [Google Scholar]
- Murray, F.J. Perturbation theory and Lie algebras. J. Math. Phys. 1962, 3, 89–105. [Google Scholar] [CrossRef]
- Gerstenhaber, M. On the deformations of rings and algebras. Ann. Math. 1964, 79, 59–103. [Google Scholar] [CrossRef]
- Nijenhuis, A.; Richardson, R.W. Cohomology and deformations of algebraic structures. Bull. Amer. Math. Soc. 1964, 70, 406–411. [Google Scholar] [CrossRef]
- Boyer, C.P. Deformations of Lie algebras and groups and their applications. Rev. Mex. Fis. 1974, 23, 99–122. [Google Scholar]
- Grunewald, F.; O’Halloran, J. Deformations of Lie algebras. J. Algebra 1993, 162, 210–224. [Google Scholar] [CrossRef][Green Version]
- Hochschild, G.; Serre, J.P. Cohomology of Lie algebras. Annals Math. 1953, 57, 591–603. [Google Scholar] [CrossRef]
| n | k | n | k | ||
|---|---|---|---|---|---|
| 21 | 5 | 29 | 5 | ||
| 22 | 5 | 29 | 6 | ||
| 23 | 5 | 29 | 7 | ||
| 24 | 5 | 29 | 8 | ||
| 24 | 6 | 30 | 5 | ||
| 25 | 5 | 30 | 6 | ||
| 25 | 6 | 30 | 7 | ||
| 25 | 7 | 31 | 5 | ||
| 26 | 5 | 31 | 6 | ||
| 26 | 6 | 31 | 7 | ||
| 26 | 7 | 32 | 5 | ||
| 27 | 5 | 32 | 6 | ||
| 27 | 6 | 32 | 7 | ||
| 27 | 7 | 32 | 8 | ||
| 28 | 5 | 33 | 5 | ||
| 28 | 6 | 33 | 6 | ||
| 28 | 7 | 33 | 7 | ||
| 28 | 8 | 33 | 8 |
| k | ||
|---|---|---|
| 24 | 6 | |
| 29 | 8 | |
| 31 | 9 | |
| 32 | 9 | |
| 33 | 9 | |
| 34 | 9 | |
| 34 | 10 | |
| 36 | 10 | |
| 38 | 10 | |
| 39 | 12 | |
| 41 | 12 | |
| 43 | 12 |
| k | ||
|---|---|---|
| 40 | 13 | |
| 40 | 13 | |
| 40 | 13 | |
| 42 | 13 | |
| 42 | 14 | |
| 42 | 14 | |
| 42 | 14 | |
| 44 | 14 | |
| 47 | 16 | |
| 47 | 16 | |
| 47 | 16 | |
| 47 | 16 |
| k | ||
|---|---|---|
| 40 | 13 | |
| 42 | 14 | |
| 47 | 16 | |
| 47 | 16 | |
| 49 | 17 | |
| 49 | 17 | |
| 50 | 17 | |
| 52 | 17 | |
| k | ||
|---|---|---|
| 28 | 8 | |
| 29 | 9 | |
| 31 | 9 | |
| 33 | 9 | |
| 34 | 10 | |
| 36 | 10 | |
| 38 | 10 | |
| 35 | 11 | |
| 37 | 11 | |
| 38 | 12 | |
| 40 | 12 | |
| 42 | 12 |
| k | ||
|---|---|---|
| 39 | 12 | |
| 40 | 13 | |
| 41 | 13 | |
| 42 | 13 | |
| 42 | 14 | |
| 44 | 14 | |
| 49 | 16 | |
| 51 | 16 | |
| 52 | 17 | |
| 53 | 17 | |
| 54 | 17 | |
| 54 | 18 | |
| 56 | 18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campoamor-Stursberg, R.; Oviaño García, F. Computer-Aided Analysis of Solvable Rigid Lie Algebras with a Given Eigenvalue Spectrum. Axioms 2022, 11, 442. https://doi.org/10.3390/axioms11090442
Campoamor-Stursberg R, Oviaño García F. Computer-Aided Analysis of Solvable Rigid Lie Algebras with a Given Eigenvalue Spectrum. Axioms. 2022; 11(9):442. https://doi.org/10.3390/axioms11090442
Chicago/Turabian StyleCampoamor-Stursberg, Rutwig, and Francisco Oviaño García. 2022. "Computer-Aided Analysis of Solvable Rigid Lie Algebras with a Given Eigenvalue Spectrum" Axioms 11, no. 9: 442. https://doi.org/10.3390/axioms11090442
APA StyleCampoamor-Stursberg, R., & Oviaño García, F. (2022). Computer-Aided Analysis of Solvable Rigid Lie Algebras with a Given Eigenvalue Spectrum. Axioms, 11(9), 442. https://doi.org/10.3390/axioms11090442







