On the Distribution of Kurepa’s Function

Abstract

Kurepa’s function and his hypothesis have been investigated by means of numerical simulation. Particular emphasis has been given to the conjecture on its distribution, that should be one of a random uniform distribution, which has been verified for large numbers. A convergence function for the two has been found.

1. Introduction

It has been more than fifty years since the introduction of the simple arithmetic function and the hypothesis related to it, the former being the Kurepa’s function and the latter known as the Kurepa’s hypothesis. This hypothesis has defied the resolution ever since.

Namely, in [1], Kurepa defined the function,

$$K\left(n\right)=!n=\sum _{i=0}^{n-1}i!,$$

(1)

for $n\in \mathbb{N}$ following his earlier works [2,3,4]. Kurepa himself called the function the left factorial, at present the function is also called Kurepa’s left factorial, or simply Kurepa’s function. He subsequently extended this function to the complex plane [5]

$$K\left(z\right)={\int }_0^{+\infty }{e}^{-t}\frac{t^z-1}{t-1}dt,$$

(2)

for $\Re \left(z\right)>0$. An important property of this function is the following:

$$\underset{x\to +\infty }{lim}\frac{K\left(x\right)}{\mathsf{\Gamma }\left(x\right)}=1,$$

(3)

where $\mathsf{\Gamma }\left(x\right)$ represents the Gamma function. For more details, see [6], for Kurepa’s selected papers with commentary on number theoretical problems, see [7], and regarding historical overview of the problem up to the fiftieth anniversary, see [8]. Some recent developments and further references could be found in [9,10].

In the same 1971 paper [1], Kurepa introduced his hypothesis on the function $K\left(n\right)$, which could be written in the following manner:

$$\mathrm{mod}\left(K\right(n),n)\not\equiv 0,n\in \mathbb{N},n>2,$$

(4)

where $\mathrm{mod}\left(K\right(n),n)$ signifies the remainder of the division of $K\left(n\right)$ by n. Up to today (2022), it has not been proved. In 2004, an attempt at a proof was presented in a paper that was later retracted by the authors [11,12]. In [13], the search for a counterexample of the hypothesis was performed, without success, for $n<2^{34}\approx 1.718\times {10}^{10}$ by means of GPU computing.

The aim of this work is not to try to solve the original Kurepa’s hypothesis, already discussed in great detail in [9,10], together with the properties of Kurepa’s function and its extension on the complex plane. The scope is to investigate the conjecture first presented in [13] about the distribution of Kurepa’s function as a function of $n\in \mathbb{N}$.

2. The Distribution Conjecture

While studying numerically the hypothesis, the authors of [13] made the following conjecture:

$$\mathrm{mod}\left(K\right(n),n)/n$$

(5)

is a random number in the range $[0,n]$ with uniform distribution in $(0,1)$. In this paper, we will further numerically investigate this conjecture. Previously, in [9,10], we did an analysis of (5) on prime numbers distribution up to the value of p = 116,447, that is, the 11,000th prime number, where it is clearly shown how the difference with a uniform random distribution in $(0,1)$ decreases with increasing number of prime numbers p considered.

Our new analysis is done with the software PARI/GP [14] for $n\in \mathbb{N}$ up to the value of $n=4\times {10}^6$, for which $K(4\times {10}^6)>{10}^{{10}^7}$. In the following figures, Figure 1a–d, we show the distribution of (5) for different ranges of n. As our largest n is $4\times {10}^6$, we have millions of points, so we could only present a small range for the distribution in order for the figure to be discernible from a black blob. The figures, for different ranges of n, visually do not appear to be different from a uniform random distribution in $(0,1)$, the so-called white noise. A different choice of n ranges and starting points does not present substantial modifications to the figures. Additionally, compare those results to the one obtained in [9,10] for different ranges of the arguments, which are quite similar. We could also observe how Kurepa’s hypothesis is satisfied, as there is no value of n in the investigated range for which $\mathrm{mod}\left(K\right(n),n)=0$.

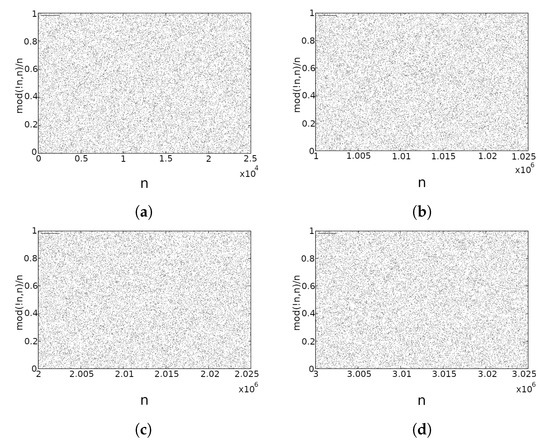
Figure 1. Distribution of $mod\left(K\right(n),n)/n$; (a) n in range $[0÷2.5]\times {10}^4$, (b) n in range $[1.0÷1.025]\times {10}^6$, (c) n in range $[2.0÷2.025]\times {10}^6$, and (d) n in range $[3.0÷3.025]\times {10}^6$.

In Figure 2, we show the comparison of the results of $\mathrm{mod}\left(K\right(n),n)/n$ with respect to a random uniform distribution in $(0,1)$ as a function of n, for the whole range of numbers considered, up to $n=4\times {10}^6$. We observe that this fluctuation, naturally defined as the difference of (5) from the average of a random distribution in (0,1), which is $1/2$, normalized to its average, that is

$$\mathrm{fluctuation}\left(n\right)=\left(\frac{\frac{\mathrm{mod}\left(K\right(n),n)}{n}-\frac{1}{2}}{\frac{1}{2}}\right),$$

(6)

as a function of n, stabilizes above a certain number and then starts decreasing with increasing n, providing more support to the conjecture presented in Equation (5), for which the relation

$$\underset{n\to +\infty }{lim}\mathrm{fluctuation}\left(n\right)=0,$$

(7)

holds true. Loosely speaking, it means that for large n, the average value of (5) is $1/2$. For n approximately larger than ${10}^6$, the fluctuation in percentage is less than 0.2 and decreasing, being lower than 0.1 when n crosses the value of $3\times {10}^6$.

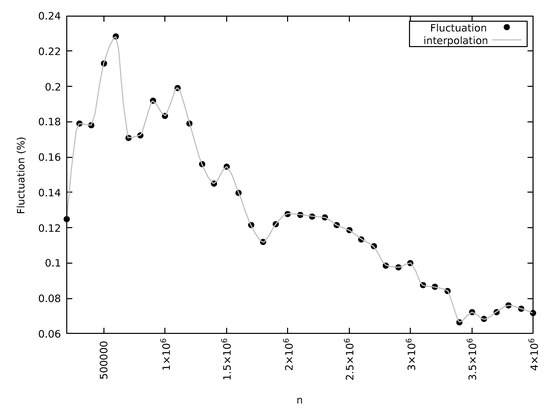
Figure 2. Difference of $\mathrm{mod}\left(K\right(n),n)/n$ from a random uniform distribution, in percentage.

To evaluate the speed at which the fluctuation decreases as a function of n, we have used a simple function:

$$Aexp(-n^{\alpha }),$$

(8)

where the parameters $A,\alpha$ have been fitted to the data points for $n>{10}^6$. The obtained results for the parameters in the range $n=[1\times {10}^6÷4\times {10}^6]$ are:

$$A=37.8409,\alpha =0.12034.$$

(9)

This fit is compared to data points in Figure 3, and it is possible to observe a very good agreement with the function (8). The fluctuation goes to zero with increasing n as a negative exponential function of a small power of n. The simplicity of Equation (8) also allows us to estimate the limit value of n above which the fluctuation F should be lower than a fixed value by means of the equation

$$Aexp(-n^{\alpha })=F\mathrm{implies}n=\sqrt[\alpha ]{ln\left(\frac{A}{F}\right)}.$$

(10)

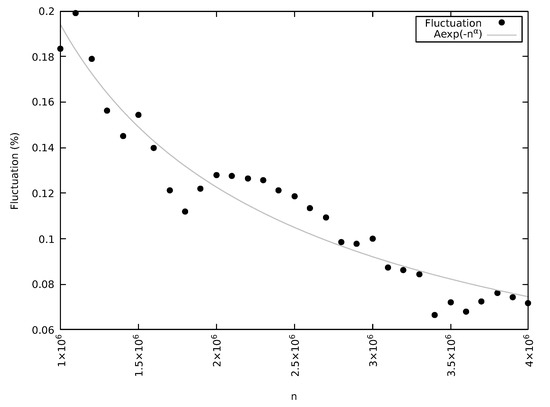
Figure 3. Fit of the function (8) to the data.

For instance, n should be approximately larger than $2.7\times {10}^6$ in order to obtain a fluctuation F smaller than 0.1%; $n>6.7\times {10}^6$ for $F<0.05\%$, and $n>40.7\times {10}^6$ for F < 0.01%.

3. Conclusions and Outlook

After more than half a century from the introduction of Kurepa’s hypothesis, there is still not even a hand-waving argument towards its possible solution. The best approach remains a numerical simulation that cannot provide a rigorous proof for its very nature. This fact also remains true for the distribution conjecture of Equation (5), which, curiously enough, is not due to Kurepa himself, but rather stemmed out from numerical simulations.

The present work did not solve the latter problem, but, for the first time, confirmed the conjecture, and as a byproduct Kurepa’s hypothesis as well, for the values up to $n=4\times {10}^6$. It also provides a convergence speed function given by an exponential of a mild power of n, Equation (8), a result not obtained previously. Moreover, this function shows convincingly that the behavior of Equation (7), the conjecture itself, should be true. Those results could help to indicate the path towards a formal and rigorous solution of Kurepa’s hypothesis and the conjecture on its distribution, which are both lacking after all this time.