Transposition Regular TA-Groupoids and Their Structures

Abstract

Tarski associative groupoid (TA-groupoid) is a kind of non-associative groupoid satisfying Tarski associative law. In this paper, the new notions of transposition regular TA-groupoid are proposed and their properties and structural characteristics are studied by using band and quasi-separativity. In particular, the following conclusions are strictly proved: (1) every left transposition regular TA-groupoid is a semigroup; (2) every left transposition regular TA-groupoid is the disjoint union of sub Abelian groups; and (3) a finite TA-groupoid with quasi-separativity and a finite left transposition regular TA-groupoid are equivalent.

1. Introduction

In mathematics, associative law or generalized associative law is a property that binary operations can have. The Tarski associative law is a kind of generalized associative law, which satisfies $(x\ast y)\ast z=x\ast (z\ast y)$.

As early as 1929, Suschkewitsch [1] studied the generalized associative law known as “Postulate A”. In a finite group $(G,\ast )$, for all $x,a,b\in G$, there exists $c\in G$, such that $(x\ast a)\ast b=x\ast c$, where the element c depends only on the elements a and b and not on x. When $c=b\ast a$, we can get the identity: $(x\ast a)\ast b=x\ast (b\ast a)$ (the Tarski associative law). When $c=a\ast b$, we can get another identity: $(x\ast a)\ast b=x\ast (a\ast b)$ (the associative law). Without much more effort, we can conclude that the Tarski associative law and associative law are two different generalized associative laws. In 1939, Bernstein [2] gave 20 sets of postulates for non-trivial Boolean groups. In the eleventh and sixteenth sets, the Tarski associative law was used. In 1954, Hosszú [3] first discussed function equations satisfying the Tarski associative law, and further studies of such function equations can be seen in [4,5]. A class of rings symmetric to the Tarski associative law was studied in [6]. Pushkashu [7] studied the properties of left (right) division groupoid with left (right) cancellation satisfying the Tarski associative law.

Groupoid is an algebraic structure on a set with a closure binary operator. Groupoids can be used not only as confidential storage systems, but also in cryptography theory, the construction of semiautomaton, and biology to describe certain aspects in the crossing of organisms in genetics and in considerations of metabolisms (see [8]). The concept of Tarski associative groupoid (TA-groupoid) was first given by Xiaohong Zhang et al. [9] in 2020. A groupoid is called a TA-groupoid if it holds the Tarski associative law.

In algebraic structures, the study of regularity [10,11,12,13,14] is an effective method. In [15], the cross-connection representation of a regular semigroup can be constructed directly from the inductive groupoid of the semigroup. Cattaneo and Contreras defined a regular relational symplectic groupoid and showed that every Poisson manifold arises as the “space of objects” of a regular relational symplectic groupoid in [16]. In [17], Xiaohong Zhang et al. proposed a new research method to study semigroups, that is, introducing the concepts of various transposition regular semigroups and studying their structures. The successful application of this new transposition regular research method in the Abel-Grassmann’s groupoid (AG-groupoid) [18] also prompted us to apply it to the TA-groupoid. As a continuation of [17,18], we propose the notions of transposition regular TA-groupoids and investigate their properties and structural characteristics. This is also the embodiment of the transposition regularity method in the TA-groupoid.

The rest of this paper is organized as follows. In Section 2, some definitions and properties on TA-groupoids are given. We give a test that a finite groupoid is a TA-groupoid in Section 3. In Section 4, we propose the new notions of transposition regular TA-groupoids and investigate their properties and their relationships with regular TA-groupoids and semigroups. The relationships between the left transposition regular TA-groupoids and the quasi-separative TA-groupoids are analyzed in depth in Section 5. Finally, Section 6 gives some conclusions and two future research goals.

2. Preliminaries

In this section, the related research and results of the TA-groupoids are presented. Some related notions are introduced first. A TA-groupoid $(G,\ast )$ is called monoassociative if for all $x\in G,(x\ast x)\ast x=x\ast (x\ast x).$ We can easily verify that each TA-groupoid is monoassociative.

Definition 1

([17]). Let $(G,\ast )$ be a groupoid, $x\in G$.

(1) 

If there exists $e\in G$ such that $e\ast x=x$, e is said to be a local left identity element of x. Dually, we can define a local right identity element of x such that $x\ast e=x$. If e is both a local left and right identity element, e is said to be a local identity element;

(2) 

Let e be a local left identity element/local right identity element/local identity element of x. If there exists$c\in G$such that$c\ast x=e$, c is said to be a local left inverse element of x relative to e. Dually, we can define a local right inverse element of x relative to e such that$x\ast c=e$. If c is both a local left and right inverse element of x relative to e, c is a local inverse element of it.

Definition 2

([17]). Let $(G,\ast )$ be a semigroup, $a\in G$. Element a is a L1-transposition regular element of G if there exists $x\in G$ such that $(x\ast a)\ast a=a=(a\ast x)\ast a$. The semigroup G is said to be L1-transposition regular if all its elements are L1-transposition regular.

Definition 3.

Let $(G,\ast )$ be a TA-groupoid, $a\in G$. Element a is a regular element of G if there exists $x\in G$ such that $a=a\ast (x\ast a)$. The TA-groupoid G is said to be regular if all its elements are regular.

Proposition 1

([9]). Let $(G,\ast )$ be a TA-groupoid. Then, for all $a,b,c,d\in G$, $(a\ast b)\ast (c\ast d)=(a\ast d)\ast (c\ast b).$

Proposition 2

([9]). Any commutative TA-groupoid is a commutative semigroup.

3. TA-Test for a Finite TA-Groupoid

Working out how to verify that a groupoid satisfies the Tarski associative law is the first thing we do in the study of TA-groupoid. In this section, we give a test that a finite groupoid is a TA-groupoid.

In [19], Protić and Stevanović proposed a method to test that a finite groupoid is an AG-groupoid. This method has modified by Iqbal et al. in [20] and can test that a finite groupoid is a cyclic associative groupoid (CA-groupoid). In view of the successful application of the test methods in [19,20] on finite groupoids, we propose a method to test that a finite groupoid is a TA-groupoid.

For a groupoid $(G,\ast )$, if we want to verify whether it satisfies the Tarski associative law, we will first define the following two binary operations • and ∘ on the G.

                          $a•b=a\ast (x\ast b),$

                          $a\circ b=(a\ast b)\ast x$,      for some fixed $x\in G.$

If $a•b=a\circ b$ is satisfied for all $x\in G$, then G is a TA-groupoid. For any fixed $x\in G$, we can easily create the • table and ∘ table through the ∗ table. We take the x-row in the ∗ table as the index row of the • table, and then the index row of the • table is left multiplied by the elements of the index column of the ∗ table to obtain respective rows of the • table for x. All elements in the ∗ table are right multiplied by x to get the ∘ table of x. We say that • coincides with ∘ if the • table and ∘ table coincide for all $x\in G$. When • coincides with ∘, it means that the groupoid satisfies the Tarski associative law. For the convenience of comparison, we write the ∘ tables below the • tables.

Example 1 will illustrate the testing process described above.

Example 1.

Consider the groupoid in

Table 1. A TA-groupoid of Example 1.

∗	1	2	3	4
1	1	1	1	1
2	1	2	3	1
3	1	3	2	1
4	4	4	4	4

. In order to check whether the groupoid given in Table 1 satisfies the Tarski associative law, we extended Table 1 in the above way to get

Table 2. Extended table of Example 1.

∗	1	2	3	4	1	1	1	1	1	2	3	1	1	3	2	1	4	4	4	4
1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
2	1	2	3	1	1	1	1	1	1	2	3	1	1	3	2	1	1	1	1	1
3	1	3	2	1	1	1	1	1	1	3	2	1	1	2	3	1	1	1	1	1
4	4	4	4	4	4	4	4	4	4	4	4	4	4	4	4	4	4	4	4	4
						1				2				3				4
					1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
					1	1	1	1	1	2	3	1	1	3	2	1	1	1	1	1
					1	1	1	1	1	3	2	1	1	2	3	1	1	1	1	1
					4	4	4	4	4	4	4	4	4	4	4	4	4	4	4	4

. The upper tables on the right of the original ∗ table are the constructed • operation, and the lower tables are the constructed ∘ operation. From Table 2, we can clearly draw the conclusion that • and ∘ coincide. Thus, the groupoid in Table 1 is a TA-groupoid.

When a groupoid is not a TA-groupoid, Example 2 gives the process of test failure.

Example 2.

Consider the groupoid in

Table 3. A groupoid of Example 2.

∗	1	2	3	4
1	1	1	1	1
2	1	2	3	1
3	1	3	2	1
4	4	4	4	1

. In order to check whether the groupoid given in Table 3 satisfies the Tarski associative law, we extended Table 3 in the above way to get

Table 4. Extended table of Example 2.

∗	1	2	3	4	1	1	1	1	1	2	3	1	1	3	2	1	4	4	4	1
1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
2	1	2	3	1	1	1	1	1	1	2	3	1	1	3	2	1	1	1	1	1
3	1	3	2	1	1	1	1	1	1	3	2	1	1	2	3	1	1	1	1	1
4	4	4	4	1	4	4	4	4	4	4	4	4	4	4	4	4	1	1	1	4
						1				2				3				4
					1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
					1	1	1	1	1	2	3	1	1	3	2	1	1	1	1	1
					1	1	1	1	1	3	2	1	1	2	3	1	1	1	1	1
					4	4	4	1	4	4	4	1	4	4	4	1	1	1	1	1

. The upper tables on the right of the original ∗ table are the constructed • operation, and the lower tables are the constructed ∘ operation. In Table 4, the last element in the first upper table to the right of the original ∗ table differs from the last one in the first lower table in the same place. It is easy to conclude that • and ∘ do not coincide. Thus, the groupoid in Table 3 is not a TA-groupoid.

Moreover, we analyzed the computational complexity of TA-test for a groupoid. Let $(G,\ast )$ be a finite goupoid, where $\left|G\right|=n,n\in Z^{+}.$ If we use the exhaustive test method to verify whether it satisfies the Tarski associative law, then take any three elements $a,b$, and c in G and verify that $a\ast (b\ast c)=(a\ast c)\ast b$. In the exhaustive test method, $a,b$, and c need to traverse all elements in G. A total of $4n^3$ ∗ operations and $n^3$ comparison operations are required. The biggest problem of the exhaustive test method is that it does not use the existing data in the Cayley’s tables, resulting in an increase in the number of ∗ operations. In the TA-test method, it takes $n^3$ ∗ operations to construct • table, just as it takes $n^3$ ∗ operations to construct ∘ table. A total of $2n^3$ ∗ operations and $n^3$ comparison operations are required. Through analysis and comparison, we can see that, compared with the exhaustive method, the TA-test method reduces $2n^3$ ∗ operations and improves the efficiency of the test.

4. Transposition Regular TA-Groupoids

In this section, we propose the new notions of transposition regular TA-groupoids and investigate their properties and their relations with regular TA-groupoids and semigroups.

Proposition 3.

Let $(G,\ast )$ be a regular TA-groupoid. Then, for all $a\in G$, there exists $x\in G$ such that for all $m\in Z^{+}$, $a^m\ast x^m=a\ast x$.

Proof. 

Suppose that $(G,\ast )$ is a regular TA-groupoid. For all $a\in G$, by Defintion 3, there exists $x\in G$, such that $a\ast (x\ast a)=a$. We have

$$\begin{array}{cc}\hfill a^2\ast x^2& =(a\ast a)\ast (x\ast x)\hfill \\ \hfill & =\left(\right(a\ast a)\ast x)\ast x\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =(a\ast (x\ast a\left)\right)\ast x\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =a\ast x.\hfill \end{array}$$

Since the TA-groupoid is monoassociative, we have $x^{m+1}=x\ast x^m=x^m\ast x$. When $m>2$, if $a^m\ast x^m=a\ast x$, we can determine that

$$\begin{array}{cc}\hfill a^{m+1}\ast x^{m+1}& =(a^m\ast a)\ast (x^m\ast x)\hfill \\ \hfill & =(a^m\ast a)\ast (x\ast x^m)(byx\ast x^m=x^m\ast x)\hfill \\ & =(a^m\ast x^m)\ast (x\ast a)(byProposition 1)\hfill \\ \hfill & =(a\ast x)\ast (x\ast a)(by{a}^m\ast x^m=a\ast x)\hfill \\ \hfill & =a^2\ast x^2 (byProposition 1)\hfill \\ \hfill & =a\ast x.\hfill \end{array}$$

By mathematical induction, the equation $a^m\ast x^m=a\ast x$ holds for any positive integer m.   □

Definition 4.

Let $(G,\ast )$ be a TA-groupoid, $a\in G$. Then a is a left transposition regular element of G if there exists $x\in G$ such that $(x\ast a)\ast a=a$. The TA-groupoid G is said to be the left transposition regular if all its elements are left transposition regular.

Example 3 illustrates the existance of left transposition regular TA-groupoid.

Example 3.

In

Table 5. A left transposition regular TA-groupoid of Example 3.

∗	a	b	c	d	e	f
a	a	b	c	a	a	a
b	b	c	a	b	b	b
c	c	a	b	c	c	c
d	a	b	c	d	d	d
e	a	b	c	e	e	e
f	a	b	c	e	e	f

, the left transposition regular TA-groupoid $(G,\ast )$ of order 6 is given. For element b, $b=(c\ast b)\ast b$, element b is a left transposition regular element. It is not difficult to verify that other elements are also left transposition regular elements.

Theorem 1.

Let $(G,\ast )$ be a left transposition regular TA-groupoid. Then, for all $a\in G$,

(1) 

there exists $e,x\in G$ such that $e\ast a=a\ast e=a$ and $x\ast a=a\ast x=e$. That is, element a has a local identity element and a local inverse element relative to e;

(2) 

$e\ast e=e$, and e is unique.

Proof. 

(1) Suppose that $(G,\ast )$ is a left transposition regular TA-groupoid. By Definition 4, for all $a\in G$, there exists $x\in G$ such that $(x\ast a)\ast a=a$. Let $e=x\ast a$, we have

$$\begin{array}{cc}\hfill a\ast x& =\left(\right(x\ast a)\ast a)\ast x\hfill \\ \hfill & =(x\ast a)\ast (x\ast a)\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =x\ast \left(\right(x\ast a)\ast a)\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =x\ast a\hfill \\ \hfill & =e,\hfill \end{array}$$

$$\begin{array}{cc}\hfill a\ast e& =(e\ast a)\ast e\hfill \\ \hfill & =e\ast (e\ast a)\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =e\ast a\hfill \\ \hfill & =a.\hfill \end{array}$$

Thus, e is a local identity element of a, and x is a local inverse element of a relative to e.

(2) $e\ast e=(x\ast a)\ast e=x\ast (e\ast a)=x\ast a=e$. If $e_1$ is another local identity element of a and $x_1$ is a local inverse element of a relative to $e_1$, then $e_1\ast a=a\ast e_1=a,$$x_1\ast a=a\ast x_1=e_1$. We have

$$\begin{array}{cc}\hfill e\ast e_1& =(x\ast a)\ast e_1\hfill \\ \hfill & =x\ast (e_1\ast a)\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =x\ast a\hfill \\ \hfill & =e,\hfill \end{array}$$

$$\begin{array}{cc}\hfill e\ast e_1& =e\ast (x_1\ast a)\hfill \\ \hfill & =(e\ast a)\ast x_1\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =a\ast x_1\hfill \\ \hfill & =e_1.\hfill \end{array}$$

Thus $e=e_1$, e is unique.  □

Proposition 4.

Let $(G,\ast )$ be a left transposition regular TA-groupoid. Then, for all $a\in G$, there exists $x\in G$ such that for all $m\in Z^{+}$, $a^m\ast x^m=x^m\ast a^m=x\ast a$.

Proof. 

Suppose that $(G,\ast )$ is a left transposition regular TA-groupoid. For all $a\in G$, by Defintion 4, there exists $x\in G$, such that $(x\ast a)\ast a=a$. By Theorem 1 (1), $a\ast x=x\ast a$. We have

$$\begin{array}{cc}\hfill x^2\ast a^2& =(x\ast x)\ast (a\ast a)\hfill \\ \hfill & =(x\ast a)\ast (a\ast x)(byProposition 1)\hfill \\ \hfill & =(x\ast a)\ast (x\ast a)(bya\ast x=x\ast a)\hfill \\ \hfill & =\left(\right(x\ast a)\ast a)\ast x\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =a\ast x\hfill \\ \hfill & =x\ast a,\hfill \end{array}$$

$$\begin{array}{cc}\hfill a^2\ast x^2& =(a\ast a)\ast (x\ast x)\hfill \\ \hfill & =(a\ast x)\ast (x\ast a)(byProposition 1)\hfill \\ \hfill & =(x\ast a)\ast (a\ast x)(bya\ast x=x\ast a)\hfill \\ \hfill & =x^2\ast a^2. (byProposition 1)\hfill \end{array}$$

Since the TA-groupoid is monoassociative, we have $a^{m+1}=a\ast a^m=a^m\ast a$ and $x^{m+1}=x\ast x^m=x^m\ast x$. When $m>2$, if $a^m\ast x^m=x^m\ast a^m=x\ast a$, we can determine that

$$\begin{array}{cc}\hfill x^{m+1}\ast a^{m+1}& =(x^m\ast x)\ast (a^m\ast a)\hfill \\ \hfill & =(x^m\ast x)\ast (a\ast a^m)(bya\ast a^m=a^m\ast a)\hfill \\ & =(x^m\ast a^m)\ast (a\ast x)(byProposition 1)\hfill \\ \hfill & =(x\ast a)\ast (x\ast a)(by{x}^m\ast a^m=x\ast aanda\ast x=x\ast a)\hfill \\ \hfill & =\left(\right(x\ast a)\ast a)\ast x\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =a\ast x\hfill \\ \hfill & =x\ast a,\hfill \end{array}$$

$$\begin{array}{cc}\hfill x^{m+1}\ast a^{m+1}& =(x^m\ast a^m)\ast (a\ast x)\hfill \\ \hfill & =(a^m\ast x^m)\ast (x\ast a)(by{x}^m\ast a^m=a^m\ast x^{m}anda\ast x=x\ast a)\hfill \\ \hfill & =(a^m\ast a)\ast (x\ast x^m)(byProposition 1)\hfill \\ \hfill & =a^{m+1}\ast x^{m+1}.(byx\ast x^m=x^{m+1})\hfill \end{array}$$

By mathematical induction, the equation $a^m\ast x^m=x^m\ast a^m=x\ast a$ holds for any positive integer m.   □

Theorem 2.

Let $(G,\ast )$ be a finite TA-groupoid. Then, G is a left transposition regular TA-groupoid iff for all $a\in G$ there exists $k\in Z^{+},k>1$ such that $a^k=a$.

Proof. 

Suppose that $(G,\ast )$ is a finite left transposition regular TA-groupoid. Then, for all $a\in G$, $n\in Z^{+},$ $a^n\in G$, and there exists $x\in G$ such that $a=(x\ast a)\ast a$. There exists two positive integers i and j such that $a^i=a^{i+j}$ because G is finite. Since TA-groupoid is monoassociative, we have $a^{i+j}=a^i\ast a^j=a^j\ast a^i$ and $a^{j+1}=a\ast a^j=a^j\ast a$. By Proposition 4, we can also obtain $x^i\ast a^i=x\ast a$. Then,

$$\begin{array}{cc}\hfill x\ast a& =x^i\ast a^i\hfill \\ \hfill & =x^i\ast a^{i+j}(by{a}^i=a^{i+j})\hfill \\ \hfill & =x^i\ast (a^j\ast a^i)(by{a}^j\ast a^i=a^{i+j})\hfill \\ \hfill & =(x^i\ast a^i)\ast a^j\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =(x\ast a)\ast a^j,(by{x}^i\ast a^i=x\ast a)\hfill \end{array}$$

$$\begin{array}{cc}\hfill a& =(x\ast a)\ast a\hfill \\ \hfill & =((x\ast a)\ast a^j)\ast a(byx\ast a=(x\ast a)\ast a^j)\hfill \\ \hfill & =(x\ast a)\ast (a\ast a^j)\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =(x\ast a)\ast (a^j\ast a)(bya\ast a^j=a^j\ast a)\hfill \\ \hfill & =((x\ast a)\ast a)\ast a^j\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =a\ast a^j(bya=(x\ast a)\ast a)\hfill \\ \hfill & =a^{j+1}.\hfill \end{array}$$

Set $k=j+1$, k is the positive integer we are looking for.

In contrast, suppose that $(G,\ast )$ is a finite TA-groupoid. For all $a\in G$, there exists $k\in Z^{+},k>1$ such that $a^k=a$. When $k=2$, a is an idempotent element. When $k>2$, we have $(a^{k-2}\ast a)\ast a=a$. It follows that a is a left transposition regular element and G is a left transposition regular TA-groupoid.   □

Definition 5.

Let $(G,\ast )$ be a TA-groupoid, $a\in G$. Element a is a right transposition regular element of G if there exists $x\in G$ such that $a\ast (a\ast x)=a$. The TA-groupoid G is said to be the right transposition regular if all its elements are right transposition regular.

Theorem 3.

A left transposition regular TA-groupoid and a right transposition regular TA-groupoid are equivalent.

Proof. 

First, by Theorem 1 (1), we can prove that a left transposition regular TA-groupoid is a right transposition regular TA-groupoid.

In contrast, if $(G,\ast )$ is a right transposition regular TA-groupoid and for all $a\in G$, there exists $x\in G$ such that $a\ast (a\ast x)=a$. Let $x_1=(a\ast x)\ast x$, we have

$$\begin{array}{cc}\hfill (x_1\ast a)\ast a& =\left(\right((a\ast x)\ast x)\ast a)\ast a\hfill \\ \hfill & =\left(\right(a\ast x)\ast (a\ast x\left)\right)\ast a\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =(a\ast x)\ast (a\ast (a\ast x\left)\right)\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =(a\ast x)\ast a(bya=a\ast (a\ast x\left)\right)\hfill \\ \hfill & =a\ast (a\ast x)\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =a.\hfill \end{array}$$

By Definition 4, G is a left transposition regular TA-groupoid.  □

Corollary 1.

A left transposition regular TA-groupoid is a regular TA-groupoid.

Proof. 

This is the corollary of Theorem 1 (1).   □

Example 4 shows that a regular TA-groupoid is not always a left transposition regular TA-groupoid.

Example 4.

In

Table 6. A regular TA-groupoid of Example 4.

∗	1	2	3	4	5	6
1	1	2	2	1	3	1
2	2	1	1	3	1	2
3	2	1	1	3	1	2
4	4	5	5	4	5	4
5	5	4	4	5	4	5
6	1	2	2	1	3	6

, the regular TA-groupoid $(G,\ast )$ of order 6 is given, where $G=\{1,2,3,4,5,6\}$. However, for element 3, there is no element $x\in G$ such that $3=(x\ast 3)\ast 3$. Thus, G is not a left transposition regular TA-groupoid. In addition, G is not a semigroup because $(1\ast 4)\ast 3=2\ne 3=1\ast (4\ast 3)$.

Example 5 shows that a TA-groupoid is not always a regular TA-groupoid.

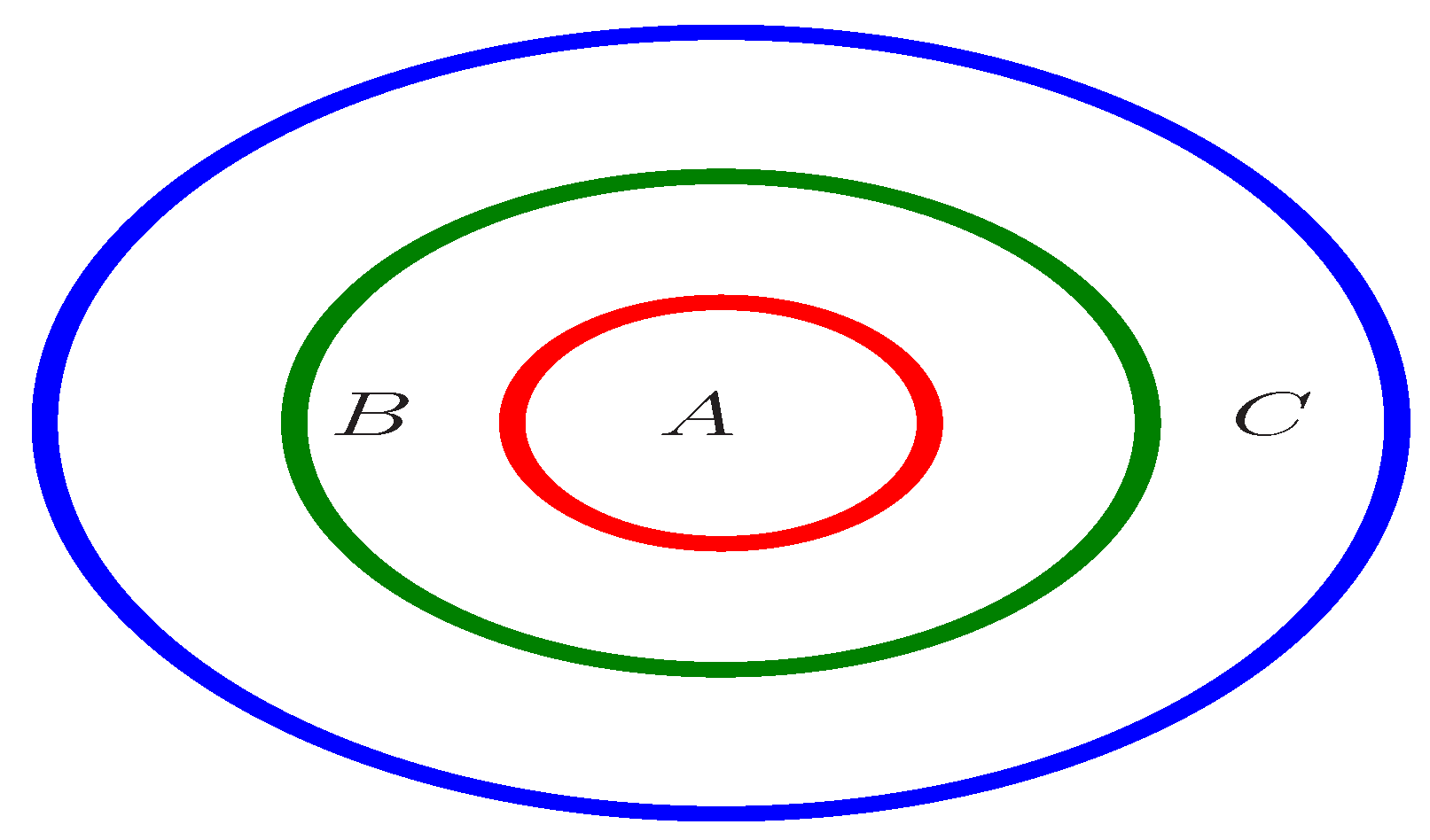
Example 5.

Consider the groupoid $(G,\ast )$ in

Table 7. A TA-groupoid of Example 5.

∗	a	b	c	d	e	f
a	a	c	a	a	c	a
b	b	b	b	b	b	b
c	a	c	a	a	c	a
d	a	c	a	c	d	a
e	b	b	b	b	e	b
f	a	c	a	a	f	a

, where $G=\{a,b,c,d,e,f\}$. By using the TA-test, we can verify that G is a TA-groupoid. However, there is no element $x\in G$ such that $f=f\ast (x\ast f).$ By Definition 3, G is not a regular TA-groupoid.

Figure 1 shows the relationships between the left transposition regular TA-groupoids and the regular TA-groupoids. There are three ellipses of different sizes and colors in the picture. Here, A, the smallest red ellipse, stands for the left transposition regular TA-groupoids; B, the ring between the red ellipse and the green ellipse, stands for the regular TA-groupoids shown in Example 4 rather than the left transposition regular TA-groupoids; and C, the ring between the green ellipse and the blue ellipse stands for the TA-groupoids shown in Example 5 rather than the regular TA-groupoids. A + B, the green ellipse, stands for the regular TA-groupoids; and A + B + C, the largest blue ellipse, stands for the TA-groupoids.

Proposition 5.

Let $(G,\ast )$ be a left transposition regular TA-groupoid. If $a,b\in G$ and $a^2=b^2$, then there exists $e,x_1,x_2\in G$, such that $e\ast a=a\ast e=a,e\ast b=b\ast e=b$ and $x_1\ast a=a\ast x_1=x_2\ast b=b\ast x_2=e$.

Proof. 

Suppose that $(G,\ast )$ is a left transposition regular TA-groupoid. If $a,b\in G$, by Theorem 1 (1), there exists $e_1,e_2,x_1,x_2\in G$ such that $e_1\ast a=a\ast e_1=a,e_2\ast b=b\ast e_2=b,$ $x_1\ast a=a\ast x_1=e_1,x_2\ast b=b\ast x_2=e_2$. We just need to prove that $e_1=e_2$ to finish the proof. For element $a^2$, we have

$$\begin{array}{cc}\hfill e_1\ast a^2& =e_1\ast (a\ast a)\hfill \\ \hfill & =(e_1\ast a)\ast a\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =a\ast a,\hfill \end{array}$$

$$\begin{array}{cc}\hfill a^2\ast e_1& =(a\ast a)\ast e_1\hfill \\ \hfill & =a\ast (e_1\ast a)\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =a\ast a,\hfill \end{array}$$

$$\begin{array}{cc}\hfill x_1^2\ast a^2& =(x_1\ast x_1)\ast (a\ast a)\hfill \\ \hfill & =(x_1\ast a)\ast (a\ast x_1)(byProposition 1)\hfill \\ \hfill & =e_1\ast e_1\hfill \\ \hfill & =e_1,(byTheorem 1\left(2\right))\hfill \end{array}$$

$$\begin{array}{cc}\hfill a^2\ast x_1^2& =(a\ast a)\ast (x_1\ast x_1)\hfill \\ \hfill & =(a\ast x_1)\ast (x_1\ast a)(byProposition 1)\hfill \\ \hfill & =e_1\ast e_1\hfill \\ \hfill & =e_1.(byTheorem 1\left(2\right))\hfill \end{array}$$

Similarly, we have $e_2\ast b^2=b^2\ast e_2=b^2$ and $x_2^2\ast b^2=b^2\ast x_2^2=e_2.$ Based on the existing assumption $a^2=b^2$, we can obtain that element $a^2$ has two local identity elements, as described in Theorem 1. However, this contradicts Theorem 1 (2). Thus, $e_1=e_2$, ending the proof.   □

In semigroups and other groupoids, scholars have studied quasi-separativity and separativity by establishing certain congruences in order to further reveal their intrinsic properties [21,22,23]. We will now discuss the quasi-separativity on the left transposition regular TA-groupoids.

Definition 6.

A TA-groupoid $(G,\ast )$ is called a quasi-separative TA-groupoid for all $a,b\in G$ if $a^2=a\ast b=b^2$ implies $a=b$.

Theorem 4.

A left transposition regular TA-groupoid has the quasi-separativity property.

Proof. 

Suppose that $(G,\ast )$ is a left transposition regular TA-groupoid. For all $a,b\in G$, if $a^2=b^2=a\ast b$, by Proposition 5, there exists $e,x_1,x_2\in G$, such that $e\ast a=a\ast e=a,e\ast b=b\ast e=b$ and $x_1\ast a=a\ast x_1=x_2\ast b=b\ast x_2=e$. We have

$$\begin{array}{cc}\hfill a& =e\ast a\hfill \\ \hfill & =(x_1\ast a)\ast a\hfill \\ \hfill & =(x_2\ast b)\ast a(by{x}_1\ast a=x_2\ast b)\hfill \\ \hfill & =x_2\ast (a\ast b)\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =x_2\ast (b\ast b)(bya\ast b=b^2)\hfill \\ \hfill & =(x_2\ast b)\ast b\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =e\ast b\hfill \\ \hfill & =b.\hfill \end{array}$$

Thus, by Definition 6, G has the quasi-separativity property.   □

One of the best ways to study one kind of algebraic structure is to connect it with another kind of better explored algebraic structure. By Proposition 2, we know that every commutative TA-groupoid is a commutative semigroup. On the Carley’s table, the commutative representation is the symmetry of the whole table. By Theorem 1, we know that each element in the left transposition regular TA-groupoid has a local identity element and a local inverse element relative to the local identity element. On the Carley’s table, this property is embodied as a local symmetry. To reveal the intrinsic connection between local and global symmetries, it is natural to study the relationship between the left transposition regular TA-groupoid and semigroup. As described in [1], we can get that the Tarski associative law and associative law are two different generalized associative laws. In addition, TA-groupoid is monoassociative. These clues will also lead us to study a common problem, that is, the relationship between the left transposition regular TA-groupoid and semigroup.

It is generally known that the semigroup has associativity properties and the TA-groupoid does not. After discussing quasi-separativity on the left transposition regular TA-groupoid, we use the following Theorem 5 to establish the relationship between left transposition regular TA-groupoid and seemingly unrelated semigroup.

Theorem 5.

Every left transposition regular TA-groupoid is a semigroup.

Proof. 

Suppose that $(G,\ast )$ is a left transposition regular TA-groupoid. For any $a,b,c\in G$, set $d=(a\ast b)\ast c$ and $f=a\ast (b\ast c)$, and we can get

$$\begin{array}{cc}\hfill d\ast d& =\left(\right(a\ast b)\ast c)\ast \left(\right(a\ast b)\ast c)\hfill \\ \hfill & =\left(\right((a\ast b)\ast c)\ast c)\ast (a\ast b)\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =\left(\right(a\ast b)\ast (c\ast c\left)\right)\ast (a\ast b)\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =((a\ast b)\ast c^2)\ast (a\ast b)\hfill \\ \hfill & =((a\ast b)\ast b)\ast (a\ast c^2)(byProposition 1)\hfill \\ \hfill & =(a\ast (b\ast b))\ast (a\ast c^2)\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =(a\ast b^2)\ast (a\ast c^2),\hfill \end{array}$$

$$\begin{array}{cc}\hfill f\ast f& =(a\ast (b\ast c\left)\right)\ast (a\ast (b\ast c\left)\right)\hfill \\ \hfill & =(a\ast (b\ast c\left)\right)\ast \left(\right(a\ast c)\ast b)\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =(a\ast b)\ast \left(\right(a\ast c)\ast (b\ast c\left)\right)(byProposition 1)\hfill \\ \hfill & =(a\ast b)\ast \left(\right((a\ast c)\ast c)\ast b)\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =(a\ast b)\ast \left(\right(a\ast (c\ast c))\ast b)\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =(a\ast b)\ast ((a\ast c^2)\ast b)\hfill \\ \hfill & =((a\ast b)\ast b)\ast (a\ast c^2)\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =(a\ast (b\ast b))\ast (a\ast c^2)\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =(a\ast b^2)\ast (a\ast c^2),\hfill \end{array}$$

$$\begin{array}{cc}\hfill d\ast f& =\left(\right(a\ast b)\ast c))\ast (a\ast (b\ast c))\hfill \\ \hfill & =\left(\right(a\ast b)\ast (b\ast c\left)\right)\ast (a\ast c)(byProposition 1)\hfill \\ \hfill & =\left(\right(a\ast c)\ast (b\ast b\left)\right)\ast (a\ast c)(byProposition 1)\hfill \\ \hfill & =((a\ast c)\ast b^2)\ast (a\ast c)\hfill \\ \hfill & =((a\ast c)\ast c)\ast (a\ast b^2)(byProposition 1)\hfill \\ \hfill & =(a\ast (c\ast c))\ast (a\ast b^2)\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =(a\ast c^2)\ast (a\ast b^2)\hfill \\ \hfill & =(a\ast b^2)\ast (a\ast c^2).(byProposition 1)\hfill \end{array}$$

By Theorem 4, we have $d=f$. Thus, $(a\ast b)\ast c=a\ast (b\ast c)$; that is, G is a semigroup.   □

Corollary 2.

A left transposition regular TA-groupoid is a L1-transposition regular semigroup.

Proof. 

It can be derived from Theorems 1 (1) and 5.   □

Example 6 shows that a L1-transposition regular semigroup is not always a left transposition regular TA-groupoid.

Example 6.

The L1-transposition regular semigroup of order 6, given in

Table 8. A L1-transposition regular semigroup of Example 6.

∗	${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{x}}_4$	${\mathit{x}}_5$	${\mathit{x}}_6$
$x_1$	$x_1$	$x_1$	$x_3$	$x_1$	$x_3$	$x_1$
$x_2$	$x_1$	$x_2$	$x_3$	$x_6$	$x_5$	$x_6$
$x_3$	$x_1$	$x_1$	$x_3$	$x_3$	$x_3$	$x_1$
$x_4$	$x_6$	$x_6$	$x_5$	$x_4$	$x_5$	$x_6$
$x_5$	$x_6$	$x_6$	$x_5$	$x_5$	$x_5$	$x_6$
$x_6$	$x_6$	$x_6$	$x_5$	$x_6$	$x_5$	$x_6$

, is not a left transposition regular TA-groupoid since $x_1\ast (x_2\ast x_3)=x_3\ne x_1=(x_1\ast x_3)\ast x_2$.

Proposition 6.

A regular TA-groupoid satisfying the associative law is a left transposition regular TA-groupoid.

Proof. 

Suppose that $(G,\ast )$ is a regular TA-groupoid. For all $a\in G$, there exists $x\in G$ such that $a\ast (x\ast a)=a$. We have

$$\begin{array}{cc}\hfill a& =a\ast (x\ast a)\hfill \\ \hfill & =(a\ast a)\ast x\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =a\ast (a\ast x).\left(bytheassociativelaw\right)\hfill \end{array}$$

By Definition 5, we can get that G is a right transposition regular TA-groupoid. By Theorem 3, G is a left transposition regular TA-groupoid.   □

Example 7 illustrates that a semigroup is not always a L1-transposition regular semigroup.

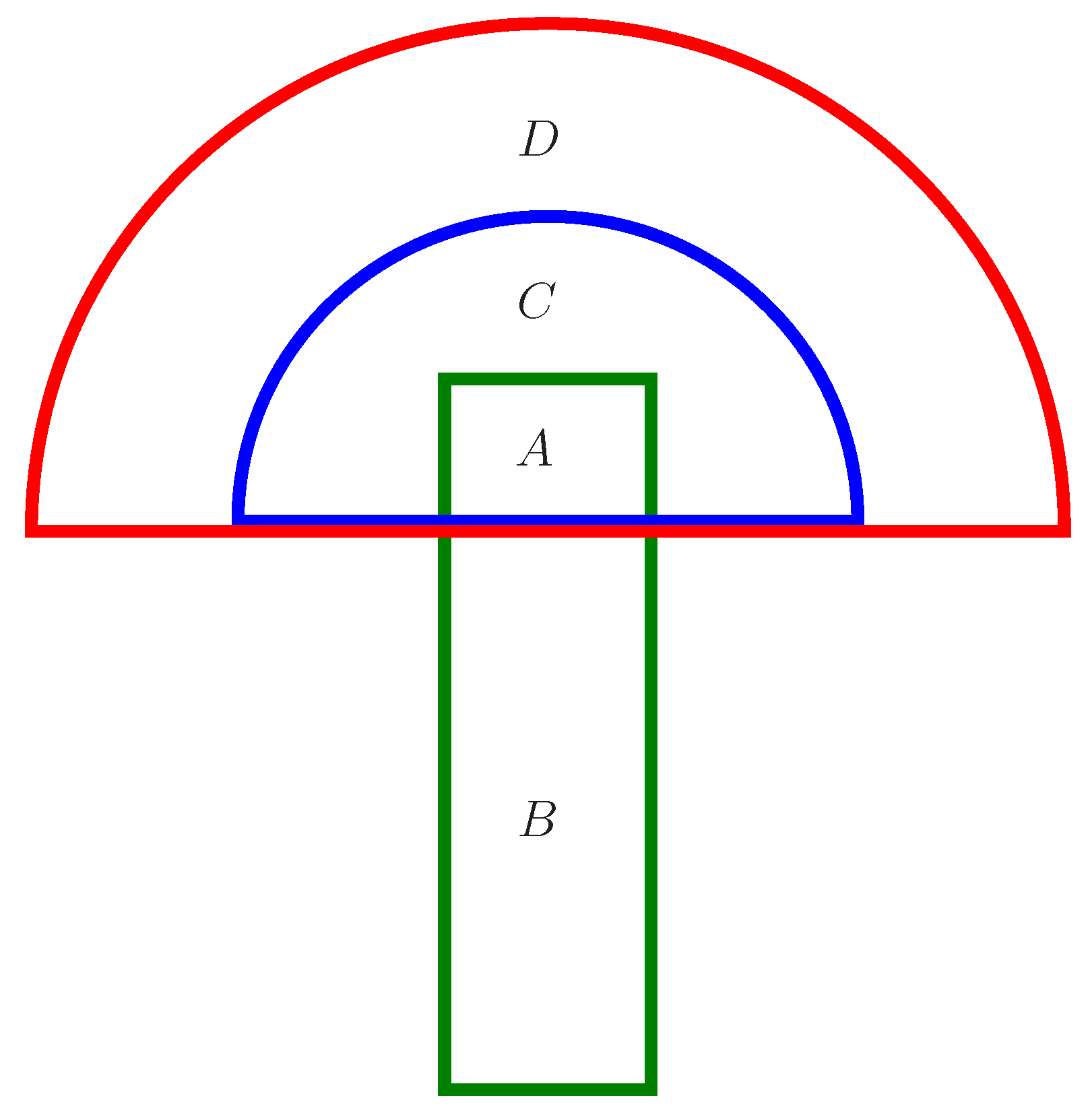
Example 7.

In

Table 9. A semigroup of Example 7.

∗	1	2	3	4	5	6
1	1	1	1	1	1	1
2	1	1	2	2	2	1
3	1	1	3	4	3	6
4	6	6	4	4	4	6
5	1	1	3	4	5	6
6	6	6	6	6	6	6

, the semigroup $(G,\ast )$ of order 6 is given, where $G=\{1,2,3,4,5,6\}$. However, for element 2, there is no element $x\in G$ such that $2=(x\ast 2)\ast 2$. Thus, G is not a L1-transposition regular semigroup.

Figure 2 shows the relationships between the regular TA-groupoids and the semigroups. There are two semicircles and a rectangle in different colors and sizes. Here, A, the intersection of a green rectangle and a blue semicircle, stands for the left transposition regular TA-groupoid; B stands for the regular TA-groupoid shown in Example 4 rather than the semigroup; C stands for the L1-transposition regular semigroup shown in Example 6 rather than the left transposition regular TA-groupoid; D stands for the semigroup shown in Example 7 rather than the L1-transposition regular semigroup. A + B, the green rectangle, stands for the regular TA-groupoid; A + C, the blue semicircle, stands for the L1-transposition regular semigroup; and A + C + D, the red semicircle, stands for the semigroup.

In [17], Xiaohong Zhang and Yudan Du investigated the decomposition of L1-transposition regular semigroups induced by an equivalence relation (see Theorem 6).

Theorem 6.

Let $(G,\ast )$ be a L1-transposition regular semigroup, and a binary ≈ on G is introduced as follows,

$$foralla,b\in G,a\approx b\iff e_a=e_b,$$

where $e_a$ is a local identity element of a. Then we have the following:

(1) 

The binary operation ≈ on G is an equivalence relation, and we denote the equivalent class contained x by ${\left[x\right]}_{\approx }$;

(2) 

for all $x\in G$, ${\left[x\right]}_{\approx }$ is a subgroup;

(3) 

$G={\bigcup }_{x\in G}{\left[x\right]}_{\approx }$, that is, every L1-transposition regular semigroup is the disjoint union of subgroups.

Let $(G,\ast )$ be a TA-groupoid, then a is an idempotent element in G if $a\in G,a^2=a$. The set of all idempotent elements in G is denoted by $E\left(G\right)$.

Proposition 7.

Let $(G,\ast )$ be a left transposition regular TA-groupoid. Then, for all $e\in E\left(G\right)$, $G\left(e\right)={\left[e\right]}_{\approx }$, where $G\left(e\right)=\{a\in G|e_a=e\}$, $e_a$ is a local identity element of a, and ${\left[e\right]}_{\approx }$ is defined in Theorem 6 (1).

Proof. 

Suppose that $(G,\ast )$ is a left transposition regular TA-groupoid. By Theorem 1, for all $a\in G$, a has a local identity element $e_a$ and $e_a$ is an idempotent. By Corollary 2, G is L1-transposition regular semigroup. For any $a\in G\left(e\right)$, $e_a=e$, since e is an idempotent element, we have $e_a=e_e\iff a\approx e$, that is $a\in {\left[e\right]}_{\approx }$. In contrast, for any $a\in {\left[e\right]}_{\approx }$, since e is an idempotent element, we have $a\approx e\iff e_a=e_e=e$, that is $a\in G\left(e\right)$. It follows that $G\left(e\right)={\left[e\right]}_{\approx }$ in G.   □

Since the left transposition regular TA-groupoid is a special L1-transposition regular semigroup, its decomposition theorem must have its particularity (see Theorem 7).

Theorem 7.

Let $(G,\ast )$ be a left transposition regular TA-groupoid. The set of all different idempotent elements in G is denoted as $E\left(G\right)$, for all $e\in E\left(G\right),G\left(e\right)=\{a\in G|e_a=e\}$. Then:

(1) 

$G\left(e\right)$ is a sub Abelian group of G;

(2) 

$G={\bigcup }_{e\in E\left(G\right)}G\left(e\right)$.

Proof. 

Suppose that $(G,\ast )$ is a left transposition regular TA-groupoid. By Proposition 7, $G\left(e\right)={\left[e\right]}_{\approx }$ in G. By Theorem 6, we can get that G is the disjoint union of $G\left(e\right)$. Then, as long as $G\left(e\right)$ is commutative, the proof can be completed. For any $a,b\in G\left(e\right)$, the local identity elements of a and b are both e, that is $e\ast a=a$ and $e\ast b=b$. Then, we have

$$\begin{array}{cc}\hfill a\ast b& =(e\ast a)\ast (e\ast b)\hfill \\ \hfill & =(e\ast b)\ast (e\ast a)\left(byProposition 1\right)\hfill \\ \hfill & =b\ast a.\hfill \end{array}$$

Thus, $G\left(e\right)$ is commutative, ending the proof.   □

Corollary 3.

Let $(G,\ast )$ be a left transposition regular TA-groupoid. The set of all different idempotent elements in G is denoted as $E\left(G\right)$, $E\left(G\right)=\{\alpha ,\beta \}$, then

(1) 

if $\alpha \ast \beta =\beta \ast \alpha$, there exists an identity element in G;

(2) 

if $\alpha \ast \beta \ne \beta \ast \alpha$, α and β are two right identity elements in G.

Proof. 

(1) Suppose that $G={\bigcup }_{e\in E\left(G\right)}G\left(e\right)$ is a left transposition regular TA-groupoid. By Theorem 5, G is a semigroup. Then we have

$$\begin{array}{cc}\hfill (\alpha \ast \beta )\ast (\alpha \ast \beta )& =(\alpha \ast (\beta \ast \alpha \left)\right)\ast \beta \left(bytheassociativelaw\right)\hfill \\ \hfill & =\left(\right(\alpha \ast \alpha )\ast \beta )\ast \beta \left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =(\alpha \ast \alpha )\ast (\beta \ast \beta )\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =\alpha \ast \beta .(by\alpha \ast \alpha =\alpha and\beta \ast \beta =\beta )\hfill \end{array}$$

Similarly, we have $(\beta \ast \alpha )\ast (\beta \ast \alpha )=\beta \ast \alpha$. Thus, $\alpha \ast \beta \in E\left(G\right)$ and $\beta \ast \alpha \in E\left(G\right)$. Let $a_{\alpha }\in G\left(\alpha \right)$, $b_{\beta }\in G\left(\beta \right)$ be two arbitrary elements, $a_{\alpha }=a_{\alpha }\ast \alpha =\alpha \ast a_{\alpha }$, $b_{\beta }=b_{\beta }\ast \beta =\beta \ast b_{\beta }$. According to the value of $\alpha \ast \beta$, we have two cases to discuss.

Case 1: $\alpha \ast \beta =\beta \ast \alpha =\beta$. We have

$$\begin{array}{cc}\hfill b_{\beta }\ast \alpha & =(b_{\beta }\ast \beta )\ast \alpha (by{b}_{\beta }=b_{\beta }\ast \beta )\hfill \\ \hfill & =b_{\beta }\ast (\alpha \ast \beta )\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =b_{\beta }\ast \beta (by\alpha \ast \beta =\beta )\hfill \\ \hfill & =b_{\beta },\hfill \end{array}$$

$$\begin{array}{cc}\hfill \alpha \ast b_{\beta }& =\alpha \ast (b_{\beta }\ast \beta )(by{b}_{\beta }=b_{\beta }\ast \beta )\hfill \\ \hfill & =(\alpha \ast \beta )\ast b_{\beta }\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =\beta \ast b_{\beta }(by\alpha \ast \beta =\beta )\hfill \\ \hfill & =b_{\beta }.\hfill \end{array}$$

Thus, $\alpha$ is the identity element of G.

Case 2: $\alpha \ast \beta =\beta \ast \alpha =\alpha$. Similar to Case 1, we can get $\beta$, which is the identity element of G.

(2) If $\alpha \ast \beta =\beta$ and $\beta \ast \alpha =\alpha$, we have

$$\begin{array}{cc}\hfill \alpha \ast \beta & =(\beta \ast \alpha )\ast (\alpha \ast \beta )(by\alpha \ast \beta =\beta and\beta \ast \alpha =\alpha )\hfill \\ \hfill & =(\beta \ast \beta )\ast (\alpha \ast \alpha )(byProposition 1)\hfill \\ \hfill & =\beta \ast \alpha .(by\beta \ast \beta =\beta and\alpha \ast \alpha =\alpha )\hfill \end{array}$$

This will lead to contradiction, so we can only discuss the situation when $\alpha \ast \beta =\alpha$ and $\beta \ast \alpha =\beta$. Then,

$$\begin{array}{cc}\hfill b_{\beta }\ast \alpha & =(b_{\beta }\ast \beta )\ast \alpha (by{b}_{\beta }=b_{\beta }\ast \beta )\hfill \\ \hfill & =b_{\beta }\ast (\beta \ast \alpha )\left(bytheassociativelaw\right)\hfill \\ \hfill & =b_{\beta }\ast \beta (by\beta \ast \alpha =\beta )\hfill \\ \hfill & =b_{\beta },\hfill \end{array}$$

$$\begin{array}{cc}\hfill a_{\alpha }\ast \beta & =(a_{\alpha }\ast \alpha )\ast \beta (by{a}_{\alpha }=a_{\alpha }\ast \alpha )\hfill \\ \hfill & =a_{\alpha }\ast (\alpha \ast \beta )\left(bytheassociativelaw\right)\hfill \\ \hfill & =a_{\alpha }\ast \alpha (by\alpha \ast \beta =\alpha )\hfill \\ \hfill & =a_{\alpha }.\hfill \end{array}$$

Thus, $\alpha$ and $\beta$ are two right identity elements in G.   □

Example 8 shows that a left transposition regular TA-groupoid with two idempotent elements has one identity element (corresponding to Corollary 3 (1)).

Example 8.

Table 10. A left transposition regular TA-groupoid with one identity element of Example 8.

∗	a	b	c	d	e	f	g	h
a	a	b	c	d	e	a	a	a
b	b	d	e	c	a	b	b	b
c	c	e	b	a	d	c	c	c
d	d	c	a	e	b	d	d	d
e	e	a	d	b	c	e	e	e
f	a	b	c	d	e	f	g	h
g	a	b	c	d	e	g	h	f
h	a	b	c	d	e	h	f	g

represents the left transposition regular TA-groupoid with two idempotent elements (element a and element f). In Table 10, we can see that $a\ast f=f\ast a=a$. What’s more, element f is the identity element.

Example 9 shows that a left transposition regular TA-groupoid with two idempotent elements has two right identity elements (corresponding to Corollary 3 (2)).

Example 9.

Table 11. A left transposition regular TA-groupoid with two right identity elements of Example 9.

∗	1	2	3	4	5	6
1	1	2	3	1	3	2
2	2	3	1	2	1	3
3	3	1	2	3	2	1
4	4	6	5	4	5	6
5	5	4	6	5	6	4
6	6	5	4	6	4	5

shows the left transposition regular TA-groupoid with two idempotent elements (element 1 and element 4). In Table 11, we can see that $1\ast 4=1\ne 4=4\ast 1$. By Corollary 3 (2), elements 1 and 4 are two right identity elements.

5. The Relationships between Left Transposition Regular TA-Groupoids and Quasi-Separative TA-Groupoids

In the previous section, we proved that every left transposition regular TA-groupoid has the quasi-separativity property (see Theorem 4), which is only a preliminary analysis of the relationships between the left transposition regular TA-groupoids and the quasi-separative TA-groupoids. In this section, we will make a more in-depth analysis of the relationships between the left transposition regular TA-groupoids and the quasi-separative TA-groupoids on the basis of the previous section. To achieve the goal of this section, we need a mathematical tool, which is band.

As one of the most effective methods to study non-associative algebra, bands, and band decompositions [24,25,26,27] were used by many scholars. In the left transposition regular TA-groupoids, we will study a special structure, in which the square of all its elements is idempotent. We name it as a kind of band (see Definiton 7).

For a TA-groupoid $(G,\ast )$, the set of all different idempotent elements in G is denoted as $E\left(G\right)$, for any $e\in E\left(G\right)$,$\sqrt{E\left(e\right)}=\{a\in G|a^2=e\}.$ We define the set $\sqrt{E\left(G\right)}=\{a\in G|a^2\ast a^2=a^2\}.$

Definition 7.

A TA-groupoid $(G,\ast )$ is called a TA-root of band if $\sqrt{E\left(G\right)}=G.$

Definition 8.

A TA-root of band $(G,\ast )$ is called a left transposition regular TA-root of band if all its elements are left transposition regular.

Example 10 illustrates the existance of left transposition regular TA-root of band.

Example 10.

In

Table 12. A left transposition regular TA-root of band of Example 10.

∗	${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{x}}_4$	${\mathit{x}}_5$	${\mathit{x}}_6$
$x_1$	$x_1$	$x_2$	$x_3$	$x_1$	$x_5$	$x_6$
$x_2$	$x_2$	$x_2$	$x_3$	$x_2$	$x_2$	$x_3$
$x_3$	$x_3$	$x_3$	$x_2$	$x_3$	$x_3$	$x_2$
$x_4$	$x_4$	$x_2$	$x_3$	$x_4$	$x_5$	$x_6$
$x_5$	$x_5$	$x_2$	$x_3$	$x_5$	$x_5$	$x_6$
$x_6$	$x_6$	$x_3$	$x_2$	$x_6$	$x_6$	$x_5$

, a left transposition regular TA-root of band of order 6 is given.

Theorem 8.

A finite TA-groupoid with quasi-separativity is equal to a finite left transposition regular TA-groupoid.

Proof. 

Suppose that $(G,\ast )$ is a finite TA-groupoid with quasi-separativity. Then, for all $a\in G$, $n\in Z^{+},$ $a^n\in G$. There exists two positive integers i and j such that $a^i=a^{i+j}$ because G is finite.

When $i=1$, we have $a=a^{j+1}$.

When $i=2$, we have $a^2=a^{2+j}$, $a^{j+1}\ast a^{j+1}=a^{2j+2}=a^2$ and $a\ast a^{j+1}=a^{2+j}=a^2$. Since G has the quasi-separativity property and $a\ast a=a\ast a^{j+1}=a^{j+1}\ast a^{j+1}$, we can get $a=a^{j+1}$.

When $i>2$, since $2i-2>i$, we can get ${\left(a^{i-1}\right)}^2={\left(a^{i+j-1}\right)}^2=a^{i-1}\ast a^{i+j-1}$. And then by quasi-separativity, we know that $a^{i-1}=a^{i-1+j}$. According to this recursion, we get $a=a^{j+1}$. By Theorem 2, G is a left transposition regular TA-groupoid.

In contrast, by Theorem 4, a left transposition regular TA-groupoid has the quasi-separativity property.   □

Proposition 8.

Let $(G,\ast )$ be a TA-root of band and e be an idempotent element of G. Then, $\sqrt{E\left(e\right)}=\{a\in G|a^2=e\}$ is a commutative sub TA-root of band if G has the quasi-separativity property.

Proof. 

Suppose that $(G,\ast )$ is a TA-root of band with quasi-separativity. By Definition 7, for all $a\in G$, there exists $e\in G$ such that $a\in \sqrt{E\left(e\right)}$. For any $a,b\in \sqrt{E\left(e\right)}$, $a^2=b^2=e^2=e$, we have

$$\begin{array}{cc}\hfill {(a\ast b)}^2& =(a\ast b)\ast (a\ast b)\hfill \\ \hfill & =a\ast \left(\right(a\ast b)\ast b)\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =a\ast (a\ast (b\ast b\left)\right)\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =a\ast (a\ast (a\ast a\left)\right)(bya\ast a=b\ast b)\hfill \\ \hfill & =a^4(SinceTA-groupoidismonoassociative)\hfill \\ \hfill & =e.\hfill \end{array}$$

Thus, $a\ast b\in \sqrt{E\left(e\right)}$, that is, $\sqrt{E\left(e\right)}$ is a sub TA-root of band. Similarly, we have ${(b\ast a)}^2=e$. In addition, $(a\ast b)\ast (b\ast a)=(a\ast a)\ast (b\ast b)=e$. Since G has the quasi-separativity property and ${(a\ast b)}^2={(b\ast a)}^2=(a\ast b)\ast (b\ast a)$, by Definition 6, we can obtain $a\ast b=b\ast a$. Thus, $\sqrt{E\left(e\right)}$ is commutative, ending the proof.   □

Theorem 9.

A TA-root of band with quasi-separativity is equal to a left transposition regular TA-root of band.

Proof. 

Suppose that $(G,\ast )$ is a TA-root of band with quasi-separativity. For all $a\in G$, there exists an idempotent element $e\in G$ such that $a\in \sqrt{E\left(e\right)}$, $a^2=e^2=e$. By Proposition 8, $\sqrt{E\left(e\right)}$ is closed and commutative. If $e\ast a=a$, we have $(a\ast a)\ast a=a$, a is a left transposition regular element. If $e\ast a\ne a$, since $\sqrt{E\left(e\right)}$ is closed, there exists $b\in \sqrt{E\left(e\right)}$ such that $e\ast a=b$. We can get

$$\begin{array}{cc}\hfill a\ast b& =a\ast (e\ast a)(bye\ast a=b)\hfill \\ \hfill & =(a\ast a)\ast e\left(bytheTarskiassociativelaw\right)\hfill \\ \hfill & =e\ast e(by{a}^2=e)\hfill \\ \hfill & =e.\hfill \end{array}$$

Since G has the quasi-separativity property and $a^2=b^2=a\ast b=e$, by Definition 6, we can obtain $a=b$. Thus, $e\ast a=b=a$, a is a left transposition regular element and G is a left transposition regular TA-root of band.

In contrast, by Theorem 4, a left transposition regular TA-root of band has the quasi-separativity property.   □

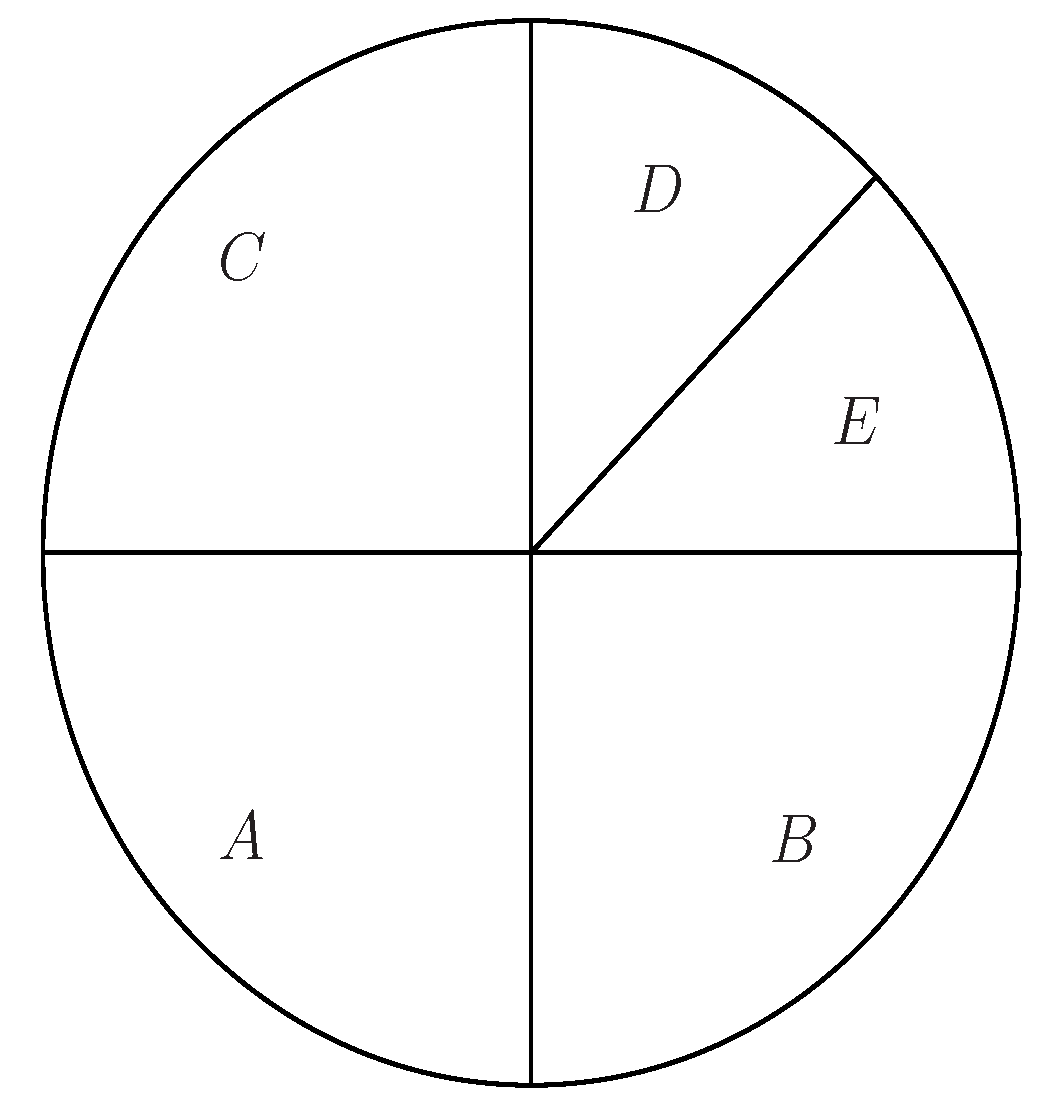
Figure 3 shows the relationships between the left transposition regular TA-groupoids and the quasi-separative TA-groupoids. Here, A, the lower left quarter circle, stands for the finite left transposition regular TA-root of band shown in Example 10; B, the lower right quarter circle, stands for the infinite left transposition regular TA-root of band; C, the upper left quarter circle, stands for the finite left transposition regular TA-groupoid shown in Example 9 rather than the TA-root of band; D, the sector at the top right, stands for the infinite left transposition regular TA-groupoid rather than the TA-root of band; and E, the sector at the top right, stands for the infinite TA-groupoid with quasi-separativity rather than the left transposition regular TA-groupoid. A + B + C + D + E, the whole circle, stands for the TA-groupoid with quasi-separativity. A + B + C + D stands for the left transposition regular TA-groupoid, and A + B + C + D is the complementary set of E, which shows that the left transposition regular TA-groupoid has the quasi-separativity property (see Theorem 4). A + B, the lower semicircle, stands for the left transposition regular TA-root of band. At the same time, A + B also stands for the TA-root of band with quasi-separativity, which shows that the TA-root of band with quasi-separativity and the left transposition regular TA-root of band are equivalent (see Theorem 9). A + C, the semicircle on the left, stands for the finite left transposition regular TA-groupoid. At the same time, A + C also stands for the finite TA-groupoid with quasi-separativity, which shows that the finite left transposition regular TA-groupoid and the finite quasi-separative TA-groupoid are equivalent (see Theorem 8). C + D + E, the upper semicircle, stands for the TA-groupoid with quasi-separativity rather than the TA-root of band; and B + D + E, the semicircle on the right, stands for the infinite TA-groupoid with quasi-separativity.

6. Conclusions

In this paper, we propose transposition regular TA-groupoids, study their properties, and analyze their relationships with other TA-groupoids. We prove that the left transposition regular TA-groupoid and the right transposition regular TA-groupoid are equivalent (see Theorem 3); that every left transposition regular TA-groupoid has the quasi-separativity property (see Theorem 4); that every left transposition regular TA-groupoid is a semigroup (see Theorem 5); and that every left transposition regular TA-groupoid is the disjoint union of sub Abelian groups (see Theorem 7). The relationships between the left transposition regular TA-groupoids, the regular TA-groupoids, and the semigroups have been discussed (see Figure 1 and Figure 2), thus clarifying the structure of the transposition regular TA-groupoids.

Furthermore, we prove that the finite TA-groupoid with quasi-separativity and the finite left transposition regular TA-groupoid are equivalent (see Theorem 8); and that the TA-root of band with quasi-separativity and the left transposition regular TA-root of band are equivalent (see Theorem 9). We investigate the relationships between the left transposition regular TA-groupoids and the quasi-separative TA-groupoids (see Figure 3). Figure 4 shows the main results of the TA-groupoids obtained in this paper.

In [28], Hwang et al. defined the levels of implicativities on the groupoid. In future research, we will use the levels of implicativities on the TA-groupoids to study the relationships between the TA-groupoids and the related logic algebras (as shown in [29,30]). In [31,32], Heidari and Cristea studied the breakable semihypergroups and the factorizable semihypergroups. We have proved that every left transposition regular TA-groupoid is a semigroup (see Theorem 5). It would be interesting to study semihypergroups on the transposition regular TA-groupoid.