Inertial Projection Algorithm for Solving Split Best Proximity Point and Mixed Equilibrium Problems in Hilbert Spaces

Abstract

The primary goal of this paper is to present and study an inertial projection algorithm for solving the split best proximity and mixed equilibrium problems. We find a solution of the best proximity problem in such a way that its image under a bounded linear operator is the solution of the mixed equilibrium problem under the setting of real Hilbert spaces. We construct an iterative algorithm for the proposed problem and prove a weak convergence theorem. Moreover, we deduce some consequences from the main convergence result. Finally, a numerical experiment is presented to demonstrate the convergence analysis of our algorithm. The methodology and results presented in this work improve and unify some previously published findings in this field.

1. Introduction

Let ${\mathcal{H}}_j$ for j = 1, 2 be two real Hilbert spaces with the inner product $⟨·,·⟩$ and the induced norm $\parallel ·\parallel$. Let ${\mathcal{C}}_j\subset {\mathcal{H}}_1$ for j=1,2 and $\mathcal{K}\subset {\mathcal{H}}_2$ be nonempty, closed and convex subsets of ${\mathcal{H}}_1$ and ${\mathcal{H}}_2$, respectively.

In 1994, Blum and Oettli [1] introduced and studied the following equilibrium problem (EP):

$$\mathrm{Find}{\mathfrak{q}}^{*}\in {\mathcal{C}}_1\mathrm{such}\mathrm{that}\psi ({\mathfrak{q}}^{*},\mathfrak{q})\ge 0,\forall \mathfrak{q}\in {\mathcal{C}}_1,$$

(1)

where $\psi :{\mathcal{C}}_1\times {\mathcal{C}}_1\to \mathbb{R}$ is a bifunction. We represent the solution set of problem (1) by EP($\psi )$.

The equilibrium problem is a generalization of many mathematical models such as the variational inequality problem, fixed point problem, certain optimization problem, Nash equilibrium problem, minimization problem and others; (see [1,2,3]).

In 2011, Moudafi [4] introduced and studied the following split equilibrium problem (SEP):

$$\mathrm{Find}{\mathfrak{q}}^{*}\in {\mathcal{C}}_1\mathrm{such}\mathrm{that}{\psi }_1({\mathfrak{q}}^{*},\mathfrak{q})\ge 0,\forall \mathfrak{q}\in {\mathcal{C}}_1,$$

(2)

$$\mathrm{and}{\mathfrak{u}}^{*}=\mathcal{B}{\mathfrak{q}}^{*}\in \mathcal{K}\mathrm{solves}{\psi }_2({\mathfrak{u}}^{*},\mathfrak{u})\ge 0,\forall \mathfrak{u}\in \mathcal{K},$$

(3)

where ${\psi }_1:{\mathcal{C}}_1\times {\mathcal{C}}_1\to \mathbb{R}$ and ${\psi }_2:\mathcal{K}\times \mathcal{K}\to \mathbb{R}$ are two bifunction and $\mathcal{B}:{\mathcal{H}}_1\to {\mathcal{H}}_2$ is a bounded linear operator. We represent the solution set of problem (2) and problem (3) with EP(${\psi }_1$) and EP(${\psi }_2$), respectively. An important generalization of SEP (2) and (3) is the split mixed equilibrium problem (SMEP):

$$\begin{array}{c}\hfill \mathrm{Find}{\mathfrak{q}}^{*}\in {\mathcal{C}}_1\mathrm{such}\mathrm{that}{\psi }_1({\mathfrak{q}}^{*},\mathfrak{q})+⟨\mathfrak{f}{\mathfrak{q}}^{*},\mathfrak{q}-{\mathfrak{q}}^{*}⟩\ge 0,\forall \mathfrak{q}\in {\mathcal{C}}_1\end{array}$$

(4)

$$\begin{array}{c}\hfill \mathrm{and}{\mathfrak{u}}^{*}=\mathcal{B}{\mathfrak{q}}^{*}\in \mathcal{K}\mathrm{solves}{\psi }_2({\mathfrak{u}}^{*},\mathfrak{u})+⟨\mathfrak{g}{\mathfrak{u}}^{*},\mathfrak{u}-{\mathfrak{u}}^{*}⟩\ge 0,\forall \mathfrak{u}\in \mathcal{K},\end{array}$$

(5)

where $\mathfrak{f}:{\mathcal{H}}_1\to {\mathcal{H}}_1$ and $\mathfrak{g}:{\mathcal{H}}_2\to {\mathcal{H}}_2$ be two nonlinear mappings. When we looked separately (4) is the mixed equilibrium problem that Moudafi and Thera [5] introduced and studied in 1999. We represent the solution set of problem (4) and problem (5) by MEP(${\psi }_1,\mathfrak{f}$) and MEP(${\psi }_2,\mathfrak{g}$), respectively.

In 2018, Kazmi et al. [6] proposed and studied the following iterative algorithm: For a given $x_0\in {\mathcal{H}}_1$, compute iterative sequence $\left\{x_m\right\}$ generated as follows:

$$\left\{\begin{array}{c}{u}_m=(1-{\zeta }_m)x_m+{\zeta }_m({\sigma }_m\mathcal{S}{x}_m+(1-{\sigma }_m)\mathcal{Q}{x}_m),\hfill \\ x_{m+1}=\mathcal{U}(x_m+\tau {\mathcal{B}}^{*}(\mathcal{V}-\mathcal{I})\mathcal{B}{x}_m),\hfill \end{array}\right.$$

(6)

where $\left\{{\zeta }_m\right\},\left\{{\sigma }_m\right\}$ are two real sequences in (0, 1), $\mathcal{U}={\mathcal{Q}}_{r_m}^{{\psi }_1}(\mathcal{I}-r_m\mathfrak{f})$, $\mathcal{V}={\mathcal{Q}}_{r_m}^{{\psi }_2}(\mathcal{I}-r_m\mathfrak{g})$, $\mathcal{S}$,$\mathcal{Q}:{\mathcal{C}}_1\to {\mathcal{C}}_1$ are two nonexpansive mappings and $\tau \in \left(0,\frac{1}{\parallel {\mathcal{B}}^{*}{\parallel }^2}\right)$. Under some mild conditions, they proved that the sequence $\left\{x_m\right\}$ induced by (6) converges weakly to an element of the solution set of the mixed equilibrium problem and hierarchical fixed point problem.

On the other hand, if ${\mathcal{C}}_1,{\mathcal{C}}_2\subset {\mathcal{H}}_1$ are two nonempty, closed and convex sets with $d({\mathcal{C}}_1,{\mathcal{C}}_2)=\inf \{\parallel c_1-c_2\parallel :c_1\in {\mathcal{C}}_1$ and $c_2\in {\mathcal{C}}_2\}$ and $\mathcal{S}:{\mathcal{C}}_1\to {\mathcal{C}}_2$ are a mapping. The best proximity problem (BPP) is defined as:

$$\mathrm{Find}{\mathfrak{q}}^{*}\in {\mathcal{C}}_1\mathrm{such}\mathrm{that}\parallel {\mathfrak{q}}^{*}-\mathcal{S}{\mathfrak{q}}^{*}\parallel =d({\mathcal{C}}_1,{\mathcal{C}}_2).$$

(7)

We represent the solution set of problem (7) by ${\mathrm{Best}}_{{\mathcal{C}}_1}\mathcal{S}$. The best proximity point problem for nonlinear mappings is an interesting topic in the optimization theory (see [7,8,9]). It is well known that the concept of a best proximity point includes that of a fixed point as a specific case. Some authors have developed some methods for solving the best proximity point problems (see [10,11]) and equilibrium problem (see [1,5,12,13,14,15]).

In 2016, Suantai et al. [16] proposed and studied the following iterative algorithm for solving split equilibrium problem and fixed point problem of non-spreading multivalued mapping in real Hilbert spaces:

$$\left\{\begin{array}{c}{x}_0\in {\mathcal{C}}_1,\hfill \\ y_m={\mathcal{Q}}_{r_m}^{{\psi }_1}(\mathcal{I}-\tau {\mathcal{B}}^{*}(\mathcal{I}-{\mathcal{Q}}_{r_m}^{{\psi }_2})\mathcal{B})x_m,\hfill \\ x_{m+1}={\zeta }_m{x}_m+(1-{\zeta }_m)\mathcal{S}{y}_m,\forall m\in \mathbb{N},\hfill \end{array}\right.$$

(8)

where $\left\{{\zeta }_m\right\}\subset$ (0, 1], $r_m\subset$ (0, ∞), $\mathcal{S}$ is a non-spreading multivalued mapping and $\tau \in \left(0,\frac{1}{\mathcal{L}}\right)$ such that $\mathcal{L}$ is the spectral radius of ${\mathcal{B}}^{*}\mathcal{B}$ where ${\mathcal{B}}^{*}$ is the adjoint of the bounded linear operator $\mathcal{B}$. Under some mild conditions, they proved that the sequence $\left\{x_m\right\}$ induced by (8) converges weakly to an element of the common solution of split equilibrium problem and fixed point problem.

In 2019, Tiammee and Suantai [17] proposed and studied the following iterative algorithm for solving the split best proximity point and equilibrium problems in Hilbert spaces:

$$\left\{\begin{array}{c}{x}_0\in {\mathcal{C}}_0,\hfill \\ y_m=(1-{\zeta }_m)x_m+{\zeta }_m{P}_{{\mathcal{C}}_1}\mathcal{S}{x}_m,\hfill \\ x_{m+1}=P_{{\mathcal{C}}_1}(y_m+\tau {\mathcal{B}}^{*}({\mathcal{Q}}_{r_m}^{{\psi }_2}-\mathcal{I})\mathcal{B}{y}_m),m\in \mathbb{N},\hfill \end{array}\right.$$

(9)

where $\left\{{\zeta }_m\right\}\subset$ (0,1], $r_m\subset$ (0, ∞), and $\tau \in \left(0,\frac{1}{\parallel {\mathcal{B}}^{*}{\parallel }^2}\right).$ Under some mild conditions, they proved that the sequence $\left\{x_m\right\}$ induced by (9) converges weakly to an element of the solution set $\mathsf{\Omega }=\{{\mathfrak{q}}^{*}\in {\mathrm{Best}}_{{\mathcal{C}}_1}\mathcal{S}:\mathcal{B}{\mathfrak{q}}^{*}\in \mathrm{EP}\left({\psi }_2\right)\}$.

In this paper, we introduce and study a new split problem, which is called a split best proximity problem and mixed equilibrium problem (SBPMEP). Let ${\mathcal{C}}_1,{\mathcal{C}}_2\subset {\mathcal{H}}_1$ be two nonempty, closed and convex subsets of ${\mathcal{H}}_1$ with $d({\mathcal{C}}_1,{\mathcal{C}}_2)=\inf \{\parallel c_1-c_2\parallel :c_1\in {\mathcal{C}}_1$ and $c_2\in {\mathcal{C}}_2\}.$ Let $\mathcal{K}\subset {\mathcal{H}}_2$ be a closed convex subset of ${\mathcal{H}}_2$ and $\mathcal{B}:{\mathcal{H}}_1\to {\mathcal{H}}_2$ be a bounded linear operator. Let $\mathcal{S}:{\mathcal{C}}_1\to {\mathcal{C}}_2$ be a mapping, $\psi :\mathcal{K}\times \mathcal{K}\to \mathbb{R}$ be a bifunction and $\mathfrak{g}:{\mathcal{H}}_2\to {\mathcal{H}}_2$ be a nonlinear mapping. Then SBPMEP is defined as:

$$\begin{array}{c}\hfill \mathrm{Find}{\mathfrak{q}}^{*}\in {\mathcal{C}}_1\mathrm{such}\mathrm{that}\parallel {\mathfrak{q}}^{*}-\mathcal{S}{\mathfrak{q}}^{*}\parallel =d({\mathcal{C}}_1,{\mathcal{C}}_2)\end{array}$$

(10)

$$\begin{array}{c}\hfill \mathrm{and}{\mathfrak{u}}^{*}=\mathcal{B}{\mathfrak{q}}^{*}\in \mathcal{K}\mathrm{solves}\psi ({\mathfrak{u}}^{*},\mathfrak{u})+⟨\mathfrak{g}{\mathfrak{u}}^{*},\mathfrak{u}-{\mathfrak{u}}^{*}⟩\ge 0,\forall \mathfrak{u}\in \mathcal{K}.\end{array}$$

(11)

We represent the solution set of SBPMEP by $\mathcal{J}=\{{\mathfrak{q}}^{*}\in {\mathrm{Best}}_{{\mathcal{C}}_1}\mathcal{S}:\mathcal{B}{\mathfrak{q}}^{*}\in \mathrm{MEP}(\psi ,\mathfrak{g})\}.$ When we looked separately (10) is a classical best proximity point problem and (11) is a classical mixed equilibrium problem (see [18,19,20]).

In particular, the term ${\vartheta }_m(x_m-x_{m-1})$, also known as the inertial extrapolation term was introduced as a useful tool for speeding up the convergence rate of iterative methods and many authors have investigated and improved the inertial type algorithm in various forms (see [21,22]).

Motivated and inspired by the work of Suantai et al. [16] and Tiammee and Suantai [17] and ongoing work in this direction, we propose and analyze an iterative algorithm for solving the SBPMEP (10) and (11) and establish a weak convergence theorem. The results obtained in this paper can be considered as the common solution of the best proximity point problem and mixed equilibrium problem and is a generalization of the recently published work by Tiammee and Suantai [17]. The iterative algorithm and results discussed in this paper are novel and can be viewed as a generalization and refinement of previously published work in this field.

The paper is organized as follows. In Section 1, we propose and formulate our problem and give a brief introduction of the work undertaken in this direction. In Section 2, we recall some concepts and results which are needed in proving the result presented in this paper. In Section 3, we prove a weak convergence theorem for an SBPMEP (10) and (11). In Section 4, we deduce some consequences from our main convergence theorem. In Section 5, we give a numerical example to justify our main convergence result while the conclusion is given in the last section.

2. Preliminaries

In this section, we need to review some basic definitions and lemmas that are required to prove our main convergence result. We denote the symbol ⇀ for weak convergence.

A mapping $\mathcal{Q}:{\mathcal{H}}_1\to {\mathcal{H}}_1$ is said to be

$\left(i\right)$

nonexpansive if

$$\parallel \mathcal{Q}{\mathfrak{u}}^{*}-\mathcal{Q}{\mathfrak{q}}^{*}\parallel \le \parallel {\mathfrak{u}}^{*}-{\mathfrak{q}}^{*}\parallel ,\forall {\mathfrak{u}}^{*},{\mathfrak{q}}^{*}\in {\mathcal{H}}_1;$$

$\left(ii\right)$

$\zeta$-inverse strongly monotone if there exists $\zeta >0$ such that

$$⟨\mathcal{Q}{\mathfrak{u}}^{*}-\mathcal{Q}{\mathfrak{q}}^{*},{\mathfrak{u}}^{*}-{\mathfrak{q}}^{*}⟩\ge \zeta {\parallel \mathcal{Q}{\mathfrak{u}}^{*}-\mathcal{Q}{\mathfrak{q}}^{*}\parallel }^2,\forall {\mathfrak{u}}^{*},{\mathfrak{q}}^{*}\in {\mathcal{H}}_1;$$

$\left(iii\right)$

quasi-nonexpansive if Fix($\mathcal{Q}$)$\ne \varphi$ and

$$\parallel \mathcal{Q}{\mathfrak{u}}^{*}-{\mathfrak{q}}^{*}\parallel \le \parallel {\mathfrak{u}}^{*}-{\mathfrak{q}}^{*}\parallel ,\forall {\mathfrak{u}}^{*}\in {\mathcal{H}}_1,{\mathfrak{q}}^{*}\in \mathrm{Fix}\left(\mathcal{Q}\right),$$

where Fix($\mathcal{Q})=\{{\mathfrak{q}}^{*}\in {\mathcal{C}}_1:\mathcal{Q}{\mathfrak{q}}^{*}={\mathfrak{q}}^{*}\}$. Observe that nonexpansive mappings are quasi-nonexpansive.

Let ${\mathcal{C}}_1$ and ${\mathcal{C}}_2$ be two nonempty, closed and convex subsets of ${\mathcal{H}}_1$. We define the following sets by ${\mathcal{C}}_0$ and ${\mathcal{D}}_0$

$${\mathcal{C}}_0=\{{\mathfrak{u}}^{*}\in {\mathcal{C}}_1:\parallel {\mathfrak{u}}^{*}-{\mathfrak{q}}^{*}\parallel =D({\mathcal{C}}_1,{\mathcal{C}}_2),\mathrm{for}\mathrm{some}{\mathfrak{q}}^{*}\in {\mathcal{C}}_2\}$$

and

$${\mathcal{D}}_0=\{{\mathfrak{q}}^{*}\in {\mathcal{C}}_2:\parallel {\mathfrak{u}}^{*}-{\mathfrak{q}}^{*}\parallel =D({\mathcal{C}}_1,{\mathcal{C}}_2),\mathrm{for}\mathrm{some}{\mathfrak{u}}^{*}\in {\mathcal{C}}_1\}.$$

A metric projection $P_{{\mathcal{C}}_1}\left({\mathfrak{u}}^{*}\right)$ of ${\mathfrak{u}}^{*}\in {\mathcal{H}}_1$ is defined by

$$P_{{\mathcal{C}}_1}\left({\mathfrak{u}}^{*}\right)=\mathrm{argmin}\{\parallel {\mathfrak{q}}^{*}-{\mathfrak{u}}^{*}\parallel :{\mathfrak{q}}^{*}\in {\mathcal{C}}_1\}.$$

The projection operator $P_{{\mathcal{C}}_1}:{\mathcal{H}}_1\to {\mathcal{C}}_1$ has the well known properties which are described in the following lemma.

Lemma 1

([23]). Let ${\mathcal{C}}_1$ be a nonempty, closed and convex subset of Hilbert space ${\mathcal{H}}_1$. Then ∀${\mathfrak{u}}^{*},{\mathfrak{q}}^{*}\in {\mathcal{H}}_1$ and ${\mathfrak{z}}^{*}\in {\mathcal{C}}_1$,

(a)

$⟨P_{{\mathcal{C}}_1}{\mathfrak{u}}^{*}-{\mathfrak{u}}^{*},{\mathfrak{z}}^{*}-P_{{\mathcal{C}}_1}{\mathfrak{u}}^{*}⟩\ge 0;$

(b)

$\parallel P_{{\mathcal{C}}_1}{\mathfrak{u}}^{*}-P_{{\mathcal{C}}_1}{\mathfrak{q}}^{*}{\parallel }^2\le ⟨P_{{\mathcal{C}}_1}{\mathfrak{u}}^{*}-P_{{\mathcal{C}}_1}{\mathfrak{q}}^{*},{\mathfrak{u}}^{*}-{\mathfrak{q}}^{*}⟩;$

(c)

$\parallel P_{{\mathcal{C}}_1}{\mathfrak{u}}^{*}-{\mathfrak{z}}^{*}{\parallel }^2\le \parallel {\mathfrak{u}}^{*}-{\mathfrak{z}}^{*}{\parallel }^2-{\parallel P_{{\mathcal{C}}_1}{\mathfrak{u}}^{*}-{\mathfrak{u}}^{*}\parallel }^2$;

(d)

$\parallel {\mathfrak{z}}^{*}-P_{{\mathcal{C}}_1}{\mathfrak{u}}^{*}{\parallel }^2+\parallel {\mathfrak{u}}^{*}-P_{{\mathcal{C}}_1}{\mathfrak{u}}^{*}{\parallel }^2\le {\parallel {\mathfrak{u}}^{*}-{\mathfrak{z}}^{*}\parallel }^2$.

A Hilbert space $\mathcal{H}$ is said to satisfy Opial’s condition if, for any sequence $\left\{x_m\right\}$ in $\mathcal{H}$ such that $x_m\rightharpoonup {\mathfrak{u}}^{*}$, we have

$$\underset{m\to \infty }{lim\; inf}\parallel x_m-{\mathfrak{u}}^{*}\parallel <\underset{m\to \infty }{lim\; inf}\parallel x_m-{\mathfrak{q}}^{*}\parallel ,\forall {\mathfrak{u}}^{*},{\mathfrak{q}}^{*}\in \mathbb{Y},{\mathfrak{u}}^{*}\ne {\mathfrak{q}}^{*}.$$

Lemma 2

([11]). Let ${\mathcal{C}}_1$ and ${\mathcal{C}}_2$ be two nonempty subsets of a uniformly convex Banach space $\mathbb{Y}$ such that ${\mathcal{C}}_1$ is closed and convex. Assume that $\mathcal{Q}:{\mathcal{C}}_1\to {\mathcal{C}}_2$ is a mapping such that $\mathcal{Q}\left({\mathcal{C}}_0\right)\subseteq {\mathcal{D}}_0$. Then Fix$\left(P_{{\mathcal{C}}_1}\mathcal{T}{|}_{{\mathcal{C}}_0}\right)$=${\mathrm{Best}}_{{\mathcal{C}}_1}\left(\mathcal{Q}\right)$.

Definition 1

([11]). Let $\mathcal{C}$ and $\mathcal{D}$ be two nonempty subsets of a real Hilbert space ${\mathcal{H}}_1$ and ${\mathcal{C}}_1$ a subset of $\mathcal{C}$. A mapping $\mathcal{Q}:\mathcal{C}\to \mathcal{D}$ is called ${\mathcal{C}}_1$-nonexpansive if

$$\parallel \mathcal{Q}{\mathfrak{u}}^{*}-\mathcal{Q}{\mathfrak{z}}^{*}\parallel \le \parallel {\mathfrak{u}}^{*}-{\mathfrak{z}}^{*}\parallel ,\forall {\mathfrak{u}}^{*}\in \mathcal{C},{\mathfrak{z}}^{*}\in {\mathcal{C}}_1.$$

If ${\mathcal{C}}_1={\mathrm{Best}}_{\mathcal{C}}\mathcal{Q}$, then $\mathcal{Q}$ is called a best proximally nonexpansive mapping.

Definition 2

([24]). Let ${\mathcal{C}}_1$ and ${\mathcal{C}}_2$ be two nonempty and closed subsets of a metric space $(\mathbb{Y},d)$. Then, ${\mathcal{C}}_1$ and ${\mathcal{C}}_2$ are said to satisfy the P-property if for ${\mathfrak{u}}_1,{\mathfrak{u}}_2\in {\mathcal{C}}_0$ and ${\mathfrak{q}}_1,{\mathfrak{q}}_2\in {\mathcal{D}}_0$, the following implication holds:

$$d({\mathfrak{u}}_1,{\mathfrak{q}}_1)=d({\mathfrak{u}}_2,{\mathfrak{q}}_2)=\mathrm{D}({\mathcal{C}}_1,{\mathcal{C}}_2)\to d({\mathfrak{u}}_1,{\mathfrak{u}}_2)=d({\mathfrak{q}}_1,{\mathfrak{q}}_2).$$

Notice that the P-property holds for any pair (${\mathcal{C}}_1,{\mathcal{C}}_2$) of nonempty, closed and convex subsets of ${\mathcal{H}}_1$.

Lemma 3

([10]). Let ${\mathcal{C}}_1$ and ${\mathcal{C}}_2$ be two nonempty subsets of a uniformly convex Banach space $\mathbb{Y}$ such that ${\mathcal{C}}_1$ is closed and convex. Suppose that $\mathcal{Q}:{\mathcal{C}}_1\to {\mathcal{C}}_2$ is mapping such that $\mathcal{Q}\left({\mathcal{C}}_0\right)\subseteq {\mathcal{D}}_0.$ Then ${\mathcal{Q}|}_{{\mathcal{C}}_0}$ satisfies the proximal property iff $(\mathcal{I}-P_{{\mathcal{C}}_1}\mathcal{Q}){|}_{{\mathcal{C}}_0}$ is demiclosed at zero.

Lemma 4

([1]). Let ${\mathcal{C}}_1$ be a nonempty, closed and convex subset of ${\mathcal{H}}_1$ and $\psi :{\mathcal{C}}_1\times {\mathcal{C}}_1\to \mathbb{R}$ be a bifunction satisfying the following conditions:

(B₁)

$\psi ({\mathfrak{u}}^{*},{\mathfrak{u}}^{*})=0,\forall {\mathfrak{u}}^{*}\in {\mathcal{C}}_1;$

(B₂)

ψ is monotone, i.e, $\psi ({\mathfrak{u}}^{*},{\mathfrak{q}}^{*})+\psi ({\mathfrak{q}}^{*},{\mathfrak{u}}^{*})\le 0,\forall {\mathfrak{u}}^{*},{\mathfrak{q}}^{*}\in {\mathcal{C}}_1;$

(B₃)

For each ${\mathfrak{u}}^{*},{\mathfrak{q}}^{*},{\mathfrak{z}}^{*}\in {\mathcal{C}}_1,\underset{\mathfrak{t}\to \infty }{lim\; sup}\psi (\mathfrak{t}{\mathfrak{z}}^{*}+(1-\mathfrak{t}){\mathfrak{u}}^{*},{\mathfrak{q}}^{*})\le \psi ({\mathfrak{u}}^{*},{\mathfrak{q}}^{*});$

(B₄)

For each ${\mathfrak{u}}^{*}\in {\mathcal{C}}_1$, ${\mathfrak{q}}^{*}\to \psi ({\mathfrak{u}}^{*},{\mathfrak{q}}^{*})$ is convex and lower semicontinuous.

Lemma 5

([14]). Let ${\mathcal{C}}_1$ be a nonempty, closed and convex subset of ${\mathcal{H}}_1$ and let $\psi :{\mathcal{C}}_1\times {\mathcal{C}}_1\to \mathbb{R}$ be a bifunction satisfying $\left({\mathcal{B}}_1\right)-\left({\mathcal{B}}_4\right)$. Define a mapping ${\mathcal{Q}}_r^{\psi }:{\mathcal{H}}_1\to {\mathcal{C}}_1$ is defined by

$${\mathcal{Q}}_r^{\psi }\left({\mathfrak{u}}^{*}\right)=\{{\mathfrak{z}}^{*}\in {\mathcal{C}}_1:\psi ({\mathfrak{z}}^{*},{\mathfrak{q}}^{*})+\frac{1}{r}⟨{\mathfrak{q}}^{*}-{\mathfrak{z}}^{*},{\mathfrak{z}}^{*}-{\mathfrak{u}}^{*}⟩\ge 0,\forall {\mathfrak{q}}^{*}\in {\mathcal{C}}_1\},r>0,\forall {\mathfrak{u}}^{*}\in {\mathcal{H}}_1.$$

Then the following results holds:

(a)

${\mathcal{Q}}_r^{\psi }$ is single-valued;

(b)

${\mathcal{Q}}_r^{\psi }$ is firmly-nonexpansive, i.e,

$$\parallel {\mathcal{Q}}_r^{\psi }\left({\mathfrak{u}}^{*}\right)-{\mathcal{Q}}_r^{\psi }\left({\mathfrak{q}}^{*}\right){\parallel }^2\le ⟨{\mathcal{Q}}_r^{\psi }\left({\mathfrak{u}}^{*}\right)-{\mathcal{Q}}_r^{\psi }\left({\mathfrak{q}}^{*}\right),{\mathfrak{u}}^{*}-{\mathfrak{q}}^{*}⟩,\forall {\mathfrak{u}}^{*},{\mathfrak{q}}^{*}\in {\mathcal{H}}_1;$$

(c)

Fix$({\mathcal{Q}}_r^{\psi })=\mathrm{EP}\left(\psi \right);$

(d)

Fix$({\mathcal{Q}}_r^{\psi })$ is closed and convex.

Lemma 6

([25]). $\left(a\right)$ For all ${\mathfrak{u}}^{*},{\mathfrak{q}}^{*}\in {\mathcal{H}}_1$, we have

$$\parallel {\mathfrak{u}}^{*}-{\mathfrak{q}}^{*}{\parallel }^2=\parallel {\mathfrak{u}}^{*}{\parallel }^2-{\parallel {\mathfrak{q}}^{*}\parallel }^2-2⟨{\mathfrak{u}}^{*}-{\mathfrak{q}}^{*},{\mathfrak{q}}^{*}⟩;$$

$\left(b\right)$ For any ${\mathfrak{u}}^{*},{\mathfrak{q}}^{*}\in {\mathcal{H}}_1$, we have

$$2⟨{\mathfrak{u}}^{*},{\mathfrak{q}}^{*}⟩=\parallel {\mathfrak{u}}^{*}{\parallel }^2+\parallel {\mathfrak{q}}^{*}{\parallel }^2-\parallel {\mathfrak{u}}^{*}-{\mathfrak{q}}^{*}{\parallel }^2=\parallel {\mathfrak{u}}^{*}+{\mathfrak{q}}^{*}{\parallel }^2-\parallel {\mathfrak{u}}^{*}{\parallel }^2-{\parallel {\mathfrak{q}}^{*}\parallel }^2.$$

Lemma 7

([26]). Let $\left\{{\delta }_m\right\}$ and $\left\{{\tau }_m\right\}$ be non-negative sequences satisfying

$$\sum _{m=0}^{\infty }{\delta }_m<+\infty \mathrm{and}{\tau }_{m+1}\le {\tau }_m+{\delta }_m,m=0,1,2,....$$

Then $\left\{{\tau }_m\right\}$ is a convergent sequence.

3. Main Result

In this section, we prove our main convergence result based on the proposed iterative algorithm for solving SBPMEP (10) and (11).

Theorem 1.

Let ${\mathcal{C}}_j\subset {\mathcal{H}}_1$ for j=1,2 and $\mathcal{K}\subset {\mathcal{H}}_2$ be nonempty, closed and convex subsets of ${\mathcal{H}}_1$ and ${\mathcal{H}}_2$, respectively. Let $\mathcal{B}:{\mathcal{H}}_1\to {\mathcal{H}}_2$ be a bounded linear operator with adjoint operator ${\mathcal{B}}^{*}$. Let $S:{\mathcal{C}}_1\to {\mathcal{C}}_2$ be best proximally nonexpansive mapping such that $\mathcal{S}\left({\mathcal{C}}_0\right)\subset {\mathcal{D}}_0$ with ${\mathrm{Best}}_{{\mathcal{C}}_1}\mathcal{S}$$\ne \varphi$. Let $\mathfrak{g}:{\mathcal{H}}_2\to {\mathcal{H}}_2$ be a ζ-inverse strongly monotone mapping and let $\psi :\mathcal{K}\times \mathcal{K}\to \mathbb{R}$ be a bifunction satisfying (${\mathcal{B}}_1)-\left({\mathcal{B}}_4\right)$ with $\mathrm{MEP}(\psi ,\mathfrak{g})\ne \varphi$. Suppose that $\mathcal{S}$ satisfies the proximal property. Let $\left\{x_m\right\}$ be a sequence generated by

$$\left\{\begin{array}{c}{x}_0,x_1\in {\mathcal{C}}_0,\hfill \\ w_m=x_m+{\vartheta }_m(x_m-x_{m-1}),\hfill \\ y_m=(1-{\zeta }_m)w_m+{\zeta }_m{P}_{{\mathcal{C}}_1}\mathcal{S}{w}_m,\hfill \\ x_{m+1}=P_{{\mathcal{C}}_1}(y_m+\tau {\mathcal{B}}^{*}(\mathcal{V}-\mathcal{I})\mathcal{B}{y}_m),m\in \mathbb{N},\hfill \end{array}\right.$$

(12)

where $\mathcal{V}={\mathcal{Q}}_{r_m}^{\psi }(\mathcal{I}-r_m\mathfrak{g}),\left\{{\zeta }_m\right\}\subset$ (0,1], $r_m\subset$ (0,∞), $\left\{{\vartheta }_m\right\}\subset [0,\vartheta ]$ for some $\vartheta \in [0,1)$ and $\tau \in \left(0,\frac{1}{\parallel {\mathcal{B}}^{*}{\parallel }^2}\right)$ is a constant. Suppose that $\mathcal{J}=\{{\mathfrak{q}}^{*}\in {\mathrm{Best}}_{{\mathcal{C}}_1}\mathcal{S}:\mathcal{B}{\mathfrak{q}}^{*}\in \mathrm{MEP}(\psi ,\mathfrak{g})\}\ne \varphi$. Moreover, let the following conditions be satisfied:

(i)

${\sum }_{m=0}^{\infty }{\vartheta }_m\parallel x_m-x_{m-1}\parallel <\infty ;$

(ii)

$\underset{m\to \infty }{lim\; sup}{\zeta }_m<1;$

(iii)

$\underset{m\to \infty }{lim\; inf}{r}_m>0.$

Then, the sequence $\left\{x_m\right\}$ converges weakly to $x^{*}\in \mathcal{J}.$

Proof. 

Let ${\mathfrak{q}}^{*}\in \mathcal{J}$. Since $\parallel P_{{\mathcal{C}}_1}\mathcal{S}{w}_m-\mathcal{S}{w}_m\parallel =D({\mathcal{C}}_1,{\mathcal{C}}_2)$ and $\parallel {\mathfrak{q}}^{*}-\mathcal{S}{\mathfrak{q}}^{*}\parallel =D({\mathcal{C}}_1,{\mathcal{C}}_2),$ using P-property, we have

$$\parallel P_{{\mathcal{C}}_1}\mathcal{S}{w}_m-{\mathfrak{q}}^{*}\parallel =\parallel \mathcal{S}{w}_m-\mathcal{S}{\mathfrak{q}}^{*}\parallel .$$

(13)

Since ${\mathfrak{q}}^{*}\in \mathcal{J}$, ${\mathfrak{q}}^{*}\in {\mathrm{Best}}_{{\mathcal{C}}_1}\mathcal{S}$. Now

$$\begin{array}{cc}\hfill \parallel w_m-{\mathfrak{q}}^{*}\parallel & =\parallel x_m+{\vartheta }_m(x_m-x_{m-1})-{\mathfrak{q}}^{*}\parallel \hfill \\ \hfill & =\parallel (x_m-{\mathfrak{q}}^{*})+{\vartheta }_m(x_m-x_{m-1})\parallel \hfill \\ \hfill & \le \parallel x_m-{\mathfrak{q}}^{*}\parallel +{\vartheta }_m\parallel x_m-x_{m-1}\parallel .\hfill \end{array}$$

(14)

Since $\mathcal{S}$ is a best proximally nonexpansive mapping, using (13), we have

$$\begin{array}{cc}\hfill \parallel y_m-{\mathfrak{q}}^{*}\parallel & =\parallel (1-{\zeta }_m)w_m+{\zeta }_m{P}_{{\mathcal{C}}_1}\mathcal{S}{w}_m-{\mathfrak{q}}^{*}\parallel \hfill \\ \hfill & =\parallel (1-{\zeta }_m)(w_m-{\mathfrak{q}}^{*})+{\zeta }_m(P_{{\mathcal{C}}_1}\mathcal{S}{w}_m-{\mathfrak{q}}^{*})\parallel \hfill \\ \hfill & \le (1-{\zeta }_m)\parallel w_m-{\mathfrak{q}}^{*}\parallel +{\zeta }_m\parallel P_{{\mathcal{C}}_1}\mathcal{S}{w}_m-{\mathfrak{q}}^{*}\parallel \hfill \\ \hfill & =(1-{\zeta }_m)\parallel w_m-{\mathfrak{q}}^{*}\parallel +{\zeta }_m\parallel \mathcal{S}{w}_m-\mathcal{S}{\mathfrak{q}}^{*}\parallel \hfill \\ \hfill & =(1-{\zeta }_m)\parallel w_m-{\mathfrak{q}}^{*}\parallel +{\zeta }_m\parallel w_m-{\mathfrak{q}}^{*}\parallel \hfill \\ \hfill & \le \parallel w_m-{\mathfrak{q}}^{*}\parallel .\hfill \end{array}$$

(15)

Moreover, since ${\mathfrak{q}}^{*}\in \mathcal{J}$, So ${\mathfrak{q}}^{*}\in {\mathrm{Best}}_{{\mathcal{C}}_1}\mathcal{S}$ and $\mathcal{B}{\mathfrak{q}}^{*}\in \mathrm{MEP}(\psi ,\mathfrak{g})$, we have

$$\begin{array}{cc}\hfill \parallel y_m-{\mathfrak{q}}^{*}{\parallel }^2& =(1-{\zeta }_m)\parallel w_m-{\mathfrak{q}}^{*}{\parallel }^2+{\zeta }_m\parallel P_{{\mathcal{C}}_1}\mathcal{S}{w}_m-{\mathfrak{q}}^{*}{\parallel }^2-{\zeta }_m(1-{\zeta }_m){\parallel P_{{\mathcal{C}}_1}\mathcal{S}{w}_m-w_m\parallel }^2\hfill \\ \hfill & \le (1-{\zeta }_m)\parallel w_m-{\mathfrak{q}}^{*}{\parallel }^2+{\zeta }_m\parallel w_m-{\mathfrak{q}}^{*}{\parallel }^2-{\zeta }_m(1-{\zeta }_m){\parallel P_{{\mathcal{C}}_1}\mathcal{S}{w}_m-w_m\parallel }^2\hfill \\ \hfill & \le \parallel w_m-{\mathfrak{q}}^{*}{\parallel }^2-{\zeta }_m(1-{\zeta }_m){\parallel P_{{\mathcal{C}}_1}\mathcal{S}{w}_m-w_m\parallel }^2.\hfill \end{array}$$

(16)

By Lemma 5 and ${\mathfrak{q}}^{*}\in \mathrm{MEP}(\psi ,\mathfrak{g})$, we have

$$\begin{array}{cc}\hfill \parallel \mathcal{V}\mathcal{B}{y}_m-\mathcal{B}{\mathfrak{q}}^{*}{\parallel }^2& =\parallel \mathcal{V}\mathcal{B}{y}_m-\mathcal{V}\mathcal{B}{\mathfrak{q}}^{*}{\parallel }^2\hfill \\ \hfill & \le ⟨\mathcal{V}\mathcal{B}{y}_m-\mathcal{V}\mathcal{B}{\mathfrak{q}}^{*},\mathcal{B}{y}_m-\mathcal{B}{\mathfrak{q}}^{*}⟩\hfill \\ \hfill & =\frac{1}{2}\left[\parallel \mathcal{V}\mathcal{B}{y}_m-\mathcal{V}\mathcal{B}{\mathfrak{q}}^{*}{\parallel }^2+\parallel \mathcal{B}{y}_m-\mathcal{B}{\mathfrak{q}}^{*}{\parallel }^2-{\parallel \mathcal{V}\mathcal{B}{y}_m-\mathcal{B}{y}_m\parallel }^2\right],\hfill \end{array}$$

which implies that

$$\begin{array}{cc}\hfill \parallel \mathcal{V}\mathcal{B}{y}_m-\mathcal{B}{\mathfrak{q}}^{*}{\parallel }^2& \le \parallel \mathcal{B}{y}_m-\mathcal{B}{\mathfrak{q}}^{*}{\parallel }^2-{\parallel \mathcal{V}\mathcal{B}{y}_m-\mathcal{B}{y}_m\parallel }^2.\hfill \end{array}$$

(17)

Now, using (17) and Lemma 6 (b), we calculate

$$\begin{array}{cc}\hfill 2\tau ⟨y_m-{\mathfrak{q}}^{*},{\mathcal{B}}^{*}(\mathcal{V}-\mathcal{I})\mathcal{B}{y}_m⟩& =2\tau ⟨\mathcal{B}{y}_m-\mathcal{B}{\mathfrak{q}}^{*},(\mathcal{V}-\mathcal{I})\mathcal{B}{y}_m⟩\hfill \\ \hfill & =2\tau ⟨\mathcal{B}{y}_m-\mathcal{B}{\mathfrak{q}}^{*}+(\mathcal{V}-\mathcal{I})\mathcal{B}{y}_m-(\mathcal{V}-\mathcal{I})\mathcal{B}{y}_m,(\mathcal{V}-\mathcal{I})\mathcal{B}{y}_m⟩\hfill \\ \hfill & =2\tau \{⟨\mathcal{V}\mathcal{B}{y}_m-\mathcal{B}{\mathfrak{q}}^{*},(\mathcal{V}-\mathcal{I})\mathcal{B}{y}_m⟩-\parallel (\mathcal{V}-\mathcal{I})\mathcal{B}{y}_m{\parallel }^2\}\hfill \\ \hfill & =\tau \{\parallel \mathcal{V}\mathcal{B}{y}_m-\mathcal{B}{\mathfrak{q}}^{*}{\parallel }^2+\parallel (\mathcal{V}-\mathcal{I})\mathcal{B}{y}_m{\parallel }^2-\parallel \mathcal{B}{y}_m-\mathcal{B}{\mathfrak{q}}^{*}{\parallel }^2\hfill \\ \hfill & -2\parallel (\mathcal{V}-\mathcal{I})\mathcal{B}{y}_m{\parallel }^2\}\hfill \\ \hfill & \le \tau \{\parallel \mathcal{B}{y}_m-\mathcal{B}{\mathfrak{q}}^{*}{\parallel }^2-\parallel \mathcal{B}{y}_m-\mathcal{B}{\mathfrak{q}}^{*}{\parallel }^2-\parallel (\mathcal{V}-\mathcal{I})\mathcal{B}{y}_m{\parallel }^2\}\hfill \\ \hfill & =-\tau \parallel (\mathcal{V}-\mathcal{I})\mathcal{B}{y}_m{\parallel }^2.\hfill \end{array}$$

(18)

From (18), we obtain

$$\begin{array}{cc}\hfill \parallel x_{m+1}-{\mathfrak{q}}^{*}{\parallel }^2& =\parallel P_{{\mathcal{C}}_1}(y_m+\tau {\mathcal{B}}^{*}(\mathcal{V}-\mathcal{I})\mathcal{B}{y}_m)-{\mathfrak{q}}^{*}{\parallel }^2\hfill \\ \hfill & =\parallel P_{{\mathcal{C}}_1}(y_m+\tau {\mathcal{B}}^{*}(\mathcal{V}-\mathcal{I})\mathcal{B}{y}_m)-P_{{\mathcal{C}}_1}{\mathfrak{q}}^{*}{\parallel }^2\hfill \\ \hfill & \le \parallel (y_m+\tau {\mathcal{B}}^{*}(\mathcal{V}-\mathcal{I})\mathcal{B}{y}_m)-{\mathfrak{q}}^{*}{\parallel }^2\hfill \\ \hfill & =\parallel y_m-{\mathfrak{q}}^{*}{\parallel }^2+{\tau }^2\parallel {\mathcal{B}}^{*}{\parallel }^2{\parallel (\mathcal{V}-\mathcal{I})\mathcal{B}{y}_m\parallel }^2+2\tau ⟨y_m-{\mathfrak{q}}^{*},{\mathcal{B}}^{*}(\mathcal{V}-\mathcal{I})\mathcal{B}{y}_m⟩\hfill \\ \hfill & \le \parallel y_m-{\mathfrak{q}}^{*}{\parallel }^2+{\tau }^2\parallel {\mathcal{B}}^{*}{\parallel }^2\parallel (\mathcal{V}-\mathcal{I})\mathcal{B}{y}_m{\parallel }^2-\tau {\parallel (\mathcal{V}-\mathcal{I})\mathcal{B}{y}_m\parallel }^2\hfill \\ \hfill & \le \parallel y_m-{\mathfrak{q}}^{*}{\parallel }^2-\tau (1-\tau \parallel {\mathcal{B}}^{*}{\parallel }^2)\parallel (\mathcal{V}-\mathcal{I})\mathcal{B}{y}_m{\parallel }^2.\hfill \end{array}$$

(19)

Since $0<\tau <\frac{1}{\parallel {\mathcal{B}}^{*}{\parallel }^2}\mathrm{and}\tau (1-\tau \parallel {\mathcal{B}}^{*}{\parallel }^2)>0,$ it follows from (14), (15) and (19) that

$$\parallel x_{m+1}-{\mathfrak{q}}^{*}\parallel \le \parallel y_m-{\mathfrak{q}}^{*}\parallel \le \parallel w_m-{\mathfrak{q}}^{*}\parallel \le \parallel x_m-{\mathfrak{q}}^{*}\parallel +{\vartheta }_m\parallel x_m-x_{m-1}\parallel .$$

(20)

Therefore, from Lemma 7, $\underset{m\to \infty }{lim}\parallel x_m-{\mathfrak{q}}^{*}\parallel =r\ge 0.$ Again by (20), we have $\underset{m\to \infty }{lim}\parallel w_m-{\mathfrak{q}}^{*}\parallel =\underset{m\to \infty }{lim}\parallel y_m-{\mathfrak{q}}^{*}\parallel =r.$ Consequently, $\left\{x_m\right\}$ is bounded. Hence, the sequences $\left\{w_m\right\}$ and $\left\{y_m\right\}$ are also bounded.

By (16), we have

$$\underset{m\to \infty }{lim}\parallel P_{{\mathcal{C}}_1}\mathcal{S}{w}_m-w_m\parallel =0.$$

(21)

From (12) and (21), we obtain

$$\underset{m\to \infty }{lim}\parallel y_m-w_m\parallel =0.$$

(22)

using (i) and we observe that

$$\underset{m\to \infty }{lim}\parallel w_m-x_m\parallel =\underset{m\to \infty }{lim}{\vartheta }_m\parallel x_m-x_{m+1}\parallel =0.$$

(23)

Since, by triangle inequality

$$\parallel y_m-x_m\parallel \le \parallel y_m-w_m\parallel +\parallel w_m-x_m\parallel ,$$

from (22) and (23), we obtain

$$\underset{m\to \infty }{lim}\parallel y_m-x_m\parallel =0.$$

(24)

As $\left\{w_m\right\}$ is bounded, $\left\{w_m\right\}$ has a weakly convergence subsequence $\left\{w_{m_j}\right\}$. Let us consider that $w_{m_j}\rightharpoonup x^{*}$ for some $x^{*}\in {\mathcal{C}}_1$. Then, $y_{m_j}\rightharpoonup x^{*}$ and $\mathcal{B}{y}_{m_j}\rightharpoonup \mathcal{B}{x}^{*}$ by (22) and $\mathcal{B}$ is a bounded linear operator.

Since $\underset{m\to \infty }{lim}\parallel y_m-{\mathfrak{q}}^{*}\parallel =\underset{m\to \infty }{lim}\parallel x_m-{\mathfrak{q}}^{*}\parallel =r,$ (19) implies that

$$\underset{m\to \infty }{lim}\parallel (\mathcal{V}-\mathcal{I})\mathcal{B}{y}_m\parallel =0.$$

(25)

Now, we prove that $x^{*}\in \mathcal{J}$, that is $x^{*}\in {\mathrm{Best}}_{{\mathcal{C}}_1}\mathcal{S}$ and $\mathcal{B}{x}^{*}\in \mathrm{MEP}(\psi ,\mathfrak{g})$. Since $\mathcal{S}$ satisfies proximal property, by Lemma 3, we have $(\mathcal{I}-P_{{\mathcal{C}}_1}\mathcal{S}){|}_{{\mathcal{C}}_0}$ is demiclosed at zero. It follows from (21) that $P_{{\mathcal{C}}_1}\mathcal{S}{x}^{*}=x^{*}$, i.e, $x^{*}\in {\mathrm{Best}}_{{\mathcal{C}}_1}\mathcal{S}$.

Now, we prove that $\mathcal{B}{x}^{*}\in \mathrm{MEP}(\psi ,\mathfrak{g})$. Since $\mathcal{B}$ is a bounded linear operator, we have $\mathcal{B}{y}_{m_j}\rightharpoonup \mathcal{B}{x}^{*}$. Setting $l_{m_j}=\mathcal{B}{y}_{m_j}-\mathcal{V}\mathcal{B}{x}^{*}$, we obtain $l_{m_j}\to 0$ and $\mathcal{B}{y}_{m_j}-l_{m_j}=\mathcal{V}\mathcal{B}{x}^{*}.$ Therefore, from Lemma 5, we have $\psi (\mathcal{B}{y}_{m_j}-l_{m_j},z)$+ $⟨\mathfrak{g}\mathcal{B}{y}_{m_j},z-(\mathcal{B}{y}_{m_j}-l_{m_j})⟩$

$$+\frac{1}{r_{m_j}}⟨z-(\mathcal{B}{y}_{m_j}-l_{m_j}),\mathcal{B}{y}_{m_j}-l_{m_j}-\mathcal{B}{y}_{m_j}⟩\ge 0,\forall z\in {\mathcal{C}}_2.$$

Since $\psi$ is upper semicontinuous in the first argument, taking limsup to the above inequality as $j\to \infty$ and using (iii), we obtain

$$\psi (\mathcal{B}{x}^{*},z)+⟨\mathfrak{g}\mathcal{B}{x}^{*},z-\mathcal{B}{x}^{*}⟩\ge 0,\forall z\in {\mathcal{C}}_2,$$

this implies that $\mathcal{B}{x}^{*}\in \mathrm{MEP}(\psi ,\mathfrak{g})$. This shows that $x^{*}\in \mathcal{J}.$ □

4. Consequences

In this section, we deduce some special cases from our main convergence theorem.

In Theorem 1, if we take $\mathfrak{g}\equiv 0$ and ${\vartheta }_m=0$, we have the following result for solving the split best proximity problem and equilibrium problem which was initially studied and analyzed by Tiammee and Suantai [17].

Corollary 1.

Let ${\mathcal{H}}_j$ for j = 1,2 be two real Hilbert spaces and let ${\mathcal{C}}_j\subset {\mathcal{H}}_1$ for j=1,2 and $\mathcal{K}\subset {\mathcal{H}}_2$ be nonempty, closed and convex subsets of ${\mathcal{H}}_1$ and ${\mathcal{H}}_2$, respectively. Let $\mathcal{B}:{\mathcal{H}}_1\to {\mathcal{H}}_2$ be a bounded linear operator with adjoint operator ${\mathcal{B}}^{*}$. Let $S:{\mathcal{C}}_1\to {\mathcal{C}}_2$ be best proximally nonexpansive mapping such that $\mathcal{S}\left({\mathcal{C}}_0\right)\subset {\mathcal{D}}_0$ with ${\mathrm{Best}}_{{\mathcal{C}}_1}\mathcal{S}$$\ne \varphi$. Let ${\psi }_2$: $\mathcal{K}\times \mathcal{K}\to \mathbb{R}$ be a bifunction satisfying (${\mathcal{B}}_1)-\left({\mathcal{B}}_4\right)$ with $\mathrm{EP}\left({\psi }_2\right)\ne \varphi$. Assume that $\mathcal{S}$ satisfies the proximal property. Let $\left\{x_m\right\}$ be a sequence generated by

$$\left\{\begin{array}{c}{x}_0\in {\mathcal{C}}_0,\hfill \\ y_m=(1-{\zeta }_m)w_m+{\zeta }_m{P}_{{\mathcal{C}}_1}\mathcal{S}{w}_m,\hfill \\ x_{m+1}=P_{{\mathcal{C}}_1}(y_m+\tau {\mathcal{B}}^{*}(T_{r_m}^{{\psi }_2}-\mathcal{I})\mathcal{B}{y}_m),m\in \mathbb{N},\hfill \end{array}\right.$$

(26)

where $\left\{{\zeta }_m\right\}\subset$ (0,1], $r_m\subset$ (0,∞) and $\tau \in \left(0,\frac{1}{\parallel {\mathcal{B}}^{*}{\parallel }^2}\right)$ is a constant. Suppose that $\mathsf{\Omega }=\{{\mathfrak{q}}^{*}\in {\mathrm{Best}}_{{\mathcal{C}}_1}\mathcal{S}:\mathcal{B}{\mathfrak{q}}^{*}\in \mathrm{EP}\left({\psi }_2\right)\}\ne \varphi$. Moreover, let the following conditions be satisfied:

(i)

$\underset{m\to \infty }{lim\; sup}{\zeta }_m<1;$

(ii)

$\underset{m\to \infty }{lim\; inf}{r}_m>0.$

Then, the sequence $\left\{x_m\right\}$ converges weakly to $x^{*}\in \mathsf{\Omega }.$

In Theorem 1, if ${\mathcal{H}}_1={\mathcal{H}}_2=\mathcal{H}$, $\mathcal{K}={\mathcal{C}}_1$ and $\mathcal{B}=\mathcal{I}$, the identity mapping on $\mathcal{H}$, then we have the following result to approximate a common solution of the best proximity problem (7) and mixed equilibrium problem (5).

Corollary 2.

Let $\mathcal{H}$ be a real Hilbert space and let ${\mathcal{C}}_j\subset \mathcal{H}$ for j = 1, 2 be two nonempty, closed and convex subsets of $\mathcal{H}$. Let $S:{\mathcal{C}}_1\to {\mathcal{C}}_2$ be best proximally nonexpansive mapping such that $\mathcal{S}\left({\mathcal{C}}_0\right)\subset {\mathcal{D}}_0$ with ${\mathrm{Best}}_{{\mathcal{C}}_1}\mathcal{S}$$\ne \varphi$. Let $\mathfrak{g}:\mathcal{H}\to \mathcal{H}$ be a ζ-inverse strongly monotone mapping and let ${\psi }_2$: ${\mathcal{C}}_1\times {\mathcal{C}}_1\to \mathbb{R}$ be a bifunction satisfying (${\mathcal{B}}_1)-\left({\mathcal{B}}_4\right)$ with $\mathrm{MEP}({\psi }_2,\mathfrak{g})\ne \varphi$. Assume that $\mathcal{S}$ satisfies the proximal property. Let $\left\{x_m\right\}$ be a sequence generated by

$$\left\{\begin{array}{c}{x}_0,x_1\in {\mathcal{C}}_0,\hfill \\ w_m=x_m+{\vartheta }_m(x_m-x_{m-1}),\hfill \\ y_m=(1-{\zeta }_m)w_m+{\zeta }_m{P}_{{\mathcal{C}}_1}\mathcal{S}{w}_m,\hfill \\ x_{m+1}=(1-\tau )y_m+\tau (\mathcal{V}-\mathcal{I})y_m,m\in \mathbb{N},\hfill \end{array}\right.$$

(27)

where $\mathcal{V}={\mathcal{Q}}_{r_m}^{{\psi }_2}(\mathcal{I}-r_m\mathfrak{g}),\left\{{\zeta }_m\right\}\subset$ (0,1], $r_m\subset$ (0,∞), $\left\{{\vartheta }_m\right\}\subset [0,\vartheta ]$ for some $\vartheta \in [0,1)$ and $\tau \in \left(0,\frac{1}{{\parallel \mathcal{I}\parallel }^2}\right)$. Suppose that ${\mathrm{Best}}_{{\mathcal{C}}_1}\mathcal{S}\cap \mathrm{MEP}({\psi }_2,\mathfrak{g})\ne \varphi$. Moreover, let the following conditions be satisfied:

(i)

${\sum }_{m=0}^{\infty }{\vartheta }_m\parallel x_m-x_{m-1}\parallel <\infty ;$

(ii)

$\underset{m\to \infty }{lim\; sup}{\zeta }_m<1;$

(iii)

$\underset{m\to \infty }{lim\; inf}{r}_m>0.$

Then, the sequence $\left\{x_m\right\}$ converges weakly to $x^{*}\in {\mathrm{Best}}_{{\mathcal{C}}_1}\mathcal{S}\cap \mathrm{MEP}({\psi }_2,\mathfrak{g}).$

In Theorem 1, if ${\mathcal{H}}_1={\mathcal{H}}_2=\mathcal{H}$, $\mathcal{K}={\mathcal{C}}_1$ and $\mathcal{B}=\mathcal{I}$, the identity mapping on $\mathcal{H}$ and $\mathfrak{g}\equiv 0$, then we have the following result for solving best proximity problem (7) and equilibrium problem (3).

Corollary 3.

Let $\mathcal{H}$ be a real Hilbert space and let ${\mathcal{C}}_j\subset \mathcal{H}$ for j=1,2 be two nonempty, closed and convex subsets of $\mathcal{H}$. Let $S:{\mathcal{C}}_1\to {\mathcal{C}}_2$ be best proximally nonexpansive mapping such that $\mathcal{S}\left({\mathcal{C}}_0\right)\subset {\mathcal{D}}_0$ with ${\mathrm{Best}}_{{\mathcal{C}}_1}\mathcal{S}$$\ne \varphi$. Let ${\psi }_2$: ${\mathcal{C}}_1\times {\mathcal{C}}_1\to \mathbb{R}$ be a bifunction satisfying (${\mathcal{B}}_1)-\left({\mathcal{B}}_4\right)$ with $\mathrm{EP}\left({\psi }_2\right)\ne \varphi$. Assume that $\mathcal{S}$ satisfies the proximal property. Let $\left\{x_m\right\}$ be a sequence generated by

$$\left\{\begin{array}{c}{x}_0,x_1\in {\mathcal{C}}_0,\hfill \\ w_m=x_m+{\vartheta }_m(x_m-x_{m-1}),\hfill \\ y_m=(1-{\zeta }_m)w_m+{\zeta }_m{P}_{{\mathcal{C}}_1}\mathcal{S}{w}_m,\hfill \\ x_{m+1}=(1-\tau )y_m+\tau {\mathcal{Q}}_{r_m}^{{\psi }_2}{y}_m,m\in \mathbb{N},\hfill \end{array}\right.$$

(28)

where $\left\{{\zeta }_m\right\}\subset$ (0,1], $r_m\subset$ (0,∞), $\left\{{\vartheta }_m\right\}\subset [0,\vartheta ]$ for some $\vartheta \in [0,1)$ and $\tau \in \left(0,\frac{1}{{\parallel \mathcal{I}\parallel }^2}\right)$. Suppose that ${\mathrm{Best}}_{{\mathcal{C}}_1}\mathcal{S}\cap \mathrm{EP}\left({\psi }_2\right)\ne \varphi$. Moreover, let the following conditions be satisfied:

(i)

${\sum }_{m=0}^{\infty }{\vartheta }_m\parallel x_m-x_{m-1}\parallel <\infty ;$

(ii)

$\underset{m\to \infty }{lim\; sup}{\zeta }_m<1;$

(iii)

$\underset{m\to \infty }{lim\; inf}{r}_m>0.$

Then, the sequence $\left\{x_m\right\}$ converges weakly to $x^{*}\in {\mathrm{Best}}_{{\mathcal{C}}_1}\mathcal{S}\cap \mathrm{EP}\left({\psi }_2\right).$

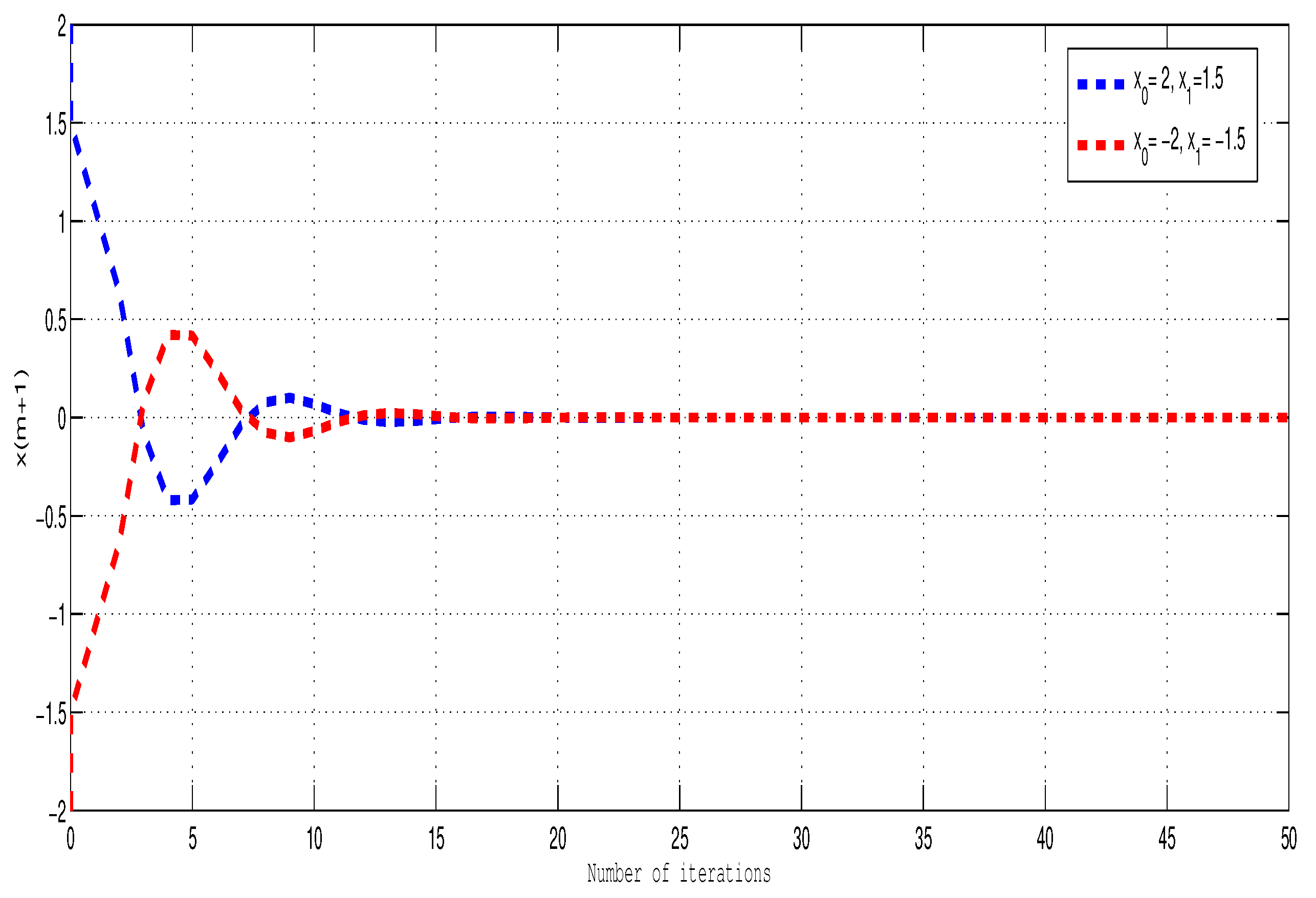
5. Numerical Experiment

In this section, we present a numerical experiment to justify our main convergence result.

Example 1.

Let ${\mathcal{H}}_1={\mathcal{H}}_2={\mathcal{C}}_1={\mathcal{C}}_2=\mathcal{K}=\mathbb{R},$ the set of real numbers, with the inner product defined by $⟨{\mathfrak{u}}^{*},{\mathfrak{q}}^{*}⟩={\mathfrak{u}}^{*}{\mathfrak{q}}^{*},\forall {\mathfrak{u}}^{*},{\mathfrak{q}}^{*}\in \mathbb{R}$, and induced usual norm $|·|$ and ${\mathcal{C}}_0=[-10,10].$ Let $\psi :\mathcal{K}\times \mathcal{K}\to \mathbb{R}$ be defined as $\psi ({\mathfrak{u}}^{*},{\mathfrak{q}}^{*})={\mathfrak{u}}^{*}{\mathfrak{q}}^{*}-{\mathfrak{u}}^{*}{}^2,\forall {\mathfrak{u}}^{*},{\mathfrak{q}}^{*}\in \mathcal{K}$ and $\mathfrak{g}:{\mathcal{H}}_2\to {\mathcal{H}}_2$ defined by $\mathfrak{g}\left({\mathfrak{u}}^{*}\right)=3{\mathfrak{u}}^{*},\forall {\mathfrak{u}}^{*}\in {\mathcal{H}}_2$. Let the mapping $\mathcal{B}:{\mathcal{H}}_1\to {\mathcal{H}}_2$ be defined by $\mathcal{B}\left({\mathfrak{u}}^{*}\right)=-\frac{9{\mathfrak{u}}^{*}}{4},\forall {\mathfrak{u}}^{*}\in {\mathcal{H}}_1$ and let the mapping $\mathcal{S}:{\mathcal{C}}_1\to {\mathcal{C}}_2$ be defined by $\mathcal{S}\left({\mathfrak{u}}^{*}\right)=\frac{{\mathfrak{u}}^{*}}{4},\forall {\mathfrak{u}}^{*}\in {\mathcal{C}}_1.$ For $r_m=\frac{1}{5}$, $\forall m$, we compute that

$${\mathcal{Q}}_{r_m}^{\psi }(\mathcal{I}-r_m\mathfrak{g})\left({\mathfrak{u}}^{*}\right)=\frac{12{\mathfrak{u}}^{*}}{25}.$$

It is easy to check that ψ satisfies $\left({\mathcal{B}}_1\right)-\left({\mathcal{B}}_4\right)$ and upper semicontinuous. $\mathcal{B}$ is a bounded linear operator on $\mathbb{R}$ with adjoint operator ${\mathcal{B}}^{*}$ and $\parallel \mathcal{B}\parallel =\parallel {\mathcal{B}}^{*}\parallel =\frac{9}{4},$ and hence, $\tau \in (0,\frac{16}{81})$. Therefore, we choose $\tau =\frac{1}{20}.$ Further, $\mathfrak{g}$ is $\frac{1}{3}$-inverse strongly monotone mapping and let us choose ${\zeta }_m=\frac{m}{2m+1},\forall m\ge 1.$ It is easy to prove that MEP$(\psi ,\mathfrak{g})=\left\{0\right\}$ and $\mathcal{S}$ is a best proximally nonexpansive mapping such that $\mathcal{S}\left({\mathcal{C}}_0\right)\subseteq {\mathcal{D}}_0$ with ${\mathrm{Best}}_{{\mathcal{C}}_1}\mathcal{S}=\left\{0\right\}.$ Therefore, $\mathcal{J}=\left\{0\right\}\ne \varphi .$

From Table 1 and Figure 1, it can be very well visualized that the sequence of iteration $\left\{x_m\right\}$ converges weakly to 0.

Table 1. Numerical experiment for two distinct initial values $x_0$ and $x_1$.

No. of Iterations	${\mathit{x}}_0=2,{\mathit{x}}_1=1.5$	${\mathit{x}}_0=-2,{\mathit{x}}_1=-1.5$
1	2.000000	−2.000000
4	−0.080913	0.080913
8	−0.039415	0.039415
12	0.022187	−0.022187
16	−0.008031	0.008031
20	0.002478	−0.002478
24	−0.000699	0.000699
28	0.000186	−0.000186
32	−0.000047	0.000047
36	0.000011	−0.000011
40	−0.000003	0.000003
44	0.000001	−0.000001
48	0.000000	0.000000
52	0.000000	0.000000

Figure 1. Convergence of sequence $\left\{x_m\right\}$.

6. Conclusions

In this paper, we suggest and analyze an inertial projection algorithm for solving the split best proximity and mixed equilibrium problems. We approximate a solution of the best proximity problem in such a way that its image under a bounded linear operator is the solution of the mixed equilibrium problem under the setting of real Hilbert spaces. We construct an iterative algorithm for the proposed problem and prove a weak convergence theorem. Further, we deduce some special cases from our main convergence result. Finally, a numerical experiment has been presented to justify the convergence analysis of the proposed iterative algorithm.