Ultimate Bounds for a Diabetes Mathematical Model Considering Glucose Homeostasis

Abstract

This paper deals with a recently reported mathematical model formulated by five first-order ordinary differential equations that describe glucoregulatory dynamics. As main contributions, we found a localization domain with all compact invariant sets; we settled on sufficient conditions for the existence of a bounded positively-invariant domain. We applied the localization of compact invariant sets and Lyapunov’s direct methods to obtain these results. The localization results establish the maximum cell concentration for each variable. On the other hand, Lyapunov’s direct method provides sufficient conditions for the bounded positively-invariant domain to attract all trajectories with non-negative initial conditions. Further, we illustrate our analytical results with numerical simulations. Overall, our results are valuable information for a better understanding of this disease. Bounds and attractive domains are crucial tools to design practical applications such as insulin controllers or in silico experiments. In addition, the model can be used to understand the long-term dynamics of the system.

1. Introduction

With high rates of mortality and morbidity, diabetes mellitus is considered a worldwide public health problem. Diabetes complications killed around 4.2 million adults between 20 and 79 years in 2019, which represents about 11% of deaths from all causes. On the other hand, 1.9 million of the diabetes mortalities (46%) happen in adults aged 60 or less [1,2]. There are two categories of diabetes mellitus: (i) Type-1 (T1DM) is considered an autoimmune disease that destroys insulin-producing pancreatic $\beta$-cells; it is normally juvenile-onset and commonly known as insulin-dependent diabetes. (ii) Type-2 (T2DM), develops usually in middle-aged or older people with insulin resistance; also called adult-onset diabetes.

1.1. Mathematical Modeling of Diabetes Mellitus

Diabetes mellitus is an open problem [3]. We have to understand the corresponding interactions and contributions in the parthenogenesis of this disease with respect to various defects of the glucose-insulin regulatory system associated with $\beta$-cells mass, the responsiveness level of $\beta$-cells to glucose, and the sensitivity of tissues to insulin. Regarding mathematical models based on T1DM and T2DM dynamical sense behavior, a realistic representation of the long-term physiological adaptation in developing insulin resistance is necessary for effectively design clinical trials and evaluate diabetes prevention or disease modification therapies [4,5]. During the past century, numerous mathematical models of the glucoregulatory system have been formulated or proposed in the field of diabetes with different purposes [6,7]. One of the main characteristics of these in silico models is dependence on the variability of their parameters. However, the main difficulty is dealing with many parameters, and complex metabolic studies are necessary to estimate them. These difficulties compel researchers to use approximations of the parameters’ values, decreasing the validity of models and their applicability. However, biomedical researchers are skeptical about utilizing mathematical modeling to investigate human diseases, so in silico experimentation is a powerful tool to reach this community [8]. A trustworthy understanding of diabetes progression is well known thanks to descriptive research by cross-sectional studies and rational extrapolation techniques. Nevertheless, the lack of a mathematical model interpretation by ordinary differential equations (ODEs) remains a research challenge [9]. In [10], authors provided a summary of how eight diabetes models match up to data from published clinical studies, to highlight differences between models, and to offer insights into the challenges facing diabetes models. They conclude that the used models predict well in typical cases, but fail with complicated scenarios, such as T2DM patients. In this direction, mathematical modeling gives us a reasonably precise means of approximating the phenomenon’s overall structure.

1.2. Recent Contributions, ODE Model Description, and Proposed Analysis

The Localization of Compact Invariant Sets (LCIS) is an analytical method applied to mathematical models described by first-order ODEs to provide bounding conditions for the state variables of a system; see [11,12]. Furthermore, related to diabetes, the LCIS method provides a broad understanding of $\beta$-cells behavior in the presence of glucose [13] or with the immunological response [14]. In this paper, we are interested in analyzing through the LCIS method an ODE mathematical model obtained by in vitro and in silico estimation. Therefore, results give us the solution using the considered variables over time based on upper bounds computation. The mathematical model we use was presented in [15]. The numerical values of parameters were estimated by in vivo experimentation; thus, background values were validated in vivo, showing a good approximation to the time-series of the real measurements of insulin levels and plasma glucose. Although this model was initially introduced in [16], it was used as a reference to evaluate the time series of glucose homeostasis in other kinds of studies [17,18]. Modeling, analysis, and in silico experimentation for diabetes mellitus are valuable tools that allows better understanding of the complicated nature of this disease. In particular, recently reported work in this direction offers valuable information with respect to specific aspects of the development of this disease. A strictly analytical mathematical tool, such as the method of LCIS, provides a way to understand the dynamical properties of a biological problem, revealing the non-intuitive properties of the system. However, Lyapunov’s theory allows us to determine sufficient conditions for the existence of the bounded positively invariant domain (BPID), which is an asymptotically attractive region including all the significant dynamics of the system; see Lemma 4.1 by Khalil at Section 4.2 in [19].

The organization of this paper is the following. The next section describes the system formulated by five first-order ODEs. Following that, the LCIS method is briefly discussed. Section 3 is devoted to applying the LCIS method to the system. Further, in this section we show that Lyapunov’s direct method allows calculating the BPID. Then, numerical simulations illustrate our results. Finally, the last section presents the conclusions of this research.

2. Materials and Methods

The mathematical model proposed in [15] is used as a baseline to study the T1DM and a T2DM. A previous version of this model was published in [16], where the authors aimed to create a very good glucoregulatory system description without involving a large number of mathematical equations; see [20,21]. That model consists of three ODEs with eight parameters describing the dynamic concentrations of blood insulin, blood glucose concentration, and glucose in the intestine. However, specialized control algorithms such as HOMA Calculator [22] and UVA/Padova [23] are included in the mathematical model under study in this work, and it is given as follows:

$$\begin{array}{lll}\frac{dI\left(t\right)}{dt}\hfill & =& -k_{6}I+k_{1}G+k_{7}Y,\hfill \end{array}$$

(1)

$$\begin{array}{lll}\frac{dY\left(t\right)}{dt}\hfill & =& -k_{8}Y,\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\frac{dD\left(t\right)}{dt}\hfill & =& -k_{a}D,\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\frac{dG\left(t\right)}{dt}\hfill & =& -k_4(I-I_{pi})-k_3-k_{2}I+k_{0}D-k_5(G-G_u)H,\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\frac{dU\left(t\right)}{dt}\hfill & =& k_5(G-G_u)H,\hfill \end{array}$$

(5)

where $I\left(t\right)$ represents the plasma insulin variation (pmol/l), $Y\left(t\right)$ is the amount of insulin in the subcutaneous compartment (UI), $D\left(t\right)$ is the amount of glucose in the digestive system (mg), $G\left(t\right)$ is the related plasma glucose level (mg/dl), and $U\left(t\right)$ is associated with the amount of glucose in the urine (mg). Equations (4) and (5) include a term H that is a function of glycaemia given in terms of G, as $H\left(G\right)$, given by Equation (6).

$$H\left(G\right)=\left\{\begin{array}{c}0ifG\le G_u,\\ 1ifG>G_u.\end{array}\right.$$

(6)

For the sake of the reader’s convenience, we include Figure 1 to interpret the contribution of each differential equation and its relationship with the parameters. The descriptions of the model and its parameters are presented in [15]; see

Table 1. Parameters reported in [15].

Parameter	T1DM	T2DM
$k_a$	$0.206$	$0.060$
$k_0$	$0.160$	$0.026$
$k_1$	$0.002$	$0.330$
$k_2$	$0.0067$	$0.000235$
$k_3$	$2.244$	$2.342$
$k_4$	$0.017$	$0.008$
$k_5$	$0.009$	$0.258$
$k_6$	$0.170$	$0.052$
$k_7$	$2.397$	-
$k_8$	$0.934$	-
$G_u$	$352.4$	$232.0$
$I_{pi}$	$156.3$	$1103.9$

.

The Localization of Compact Invariant Sets Method

The LCIS method proposed by Krishchenko and Starkov in [24,25] aims to understand the long-time dynamics of nonlinear systems formulated by autonomous and non-autonomous first-order ODEs. The later is achieved by computing both lower and upper bounds of the so-called localizing domain, which is a region in the state space ${\mathbf{R}}^n$ where all compact invariant sets of the system are located. Equilibrium points, periodic orbits, limit cycles, and chaotic attractors are examples of compact invariant sets. Localizing functions are selected by a heuristic process. This means that one may need to analyze several functions in order to find a proper set that will allow one to fulfill Theorem A1. The LCIS method is deeply described in Appendix A.

3. Results

3.1. Bounding the Diabetes Mathematical Model including Glucose Homeostasis Using LCIS Method

In this work, we apply the LCIS method to find the ultimate bounds of the system (1)–(6). Recently, the behavior of that model was studied in [15]. Moreover, the authors of that work claim that a deep understanding of the mathematical model can show how to reduce the flaws in strategies based on glucose control that use an insulin infusion pump. We now present the LCIS analysis to find the ultimate bounds of the system, which will allow us to have better background knowledge about the qualitative properties of the model. All parameters of the system are positive; their descriptions and values are given in Table 1; one can consult [15] for additional information about the model (1)–(5). Due to the biological meaning of the system, trajectories are confined to the non-negative orthant:

$${\mathbf{R}}_{+,0}^5=\left\{I\left(t\right)\ge 0,Y\left(t\right)\ge 0,G\left(t\right)\ge 0,D\left(t\right)\ge 0,U\left(t\right)\ge 0\right\},$$

(7)

which is possible if the next condition

$$k_4{I}_{pi}>k_3$$

(8)

is fulfilled, according to [16]. Clearly, $H\left(G\right)$ is a discontinuous function, which prevents analyzing the system with standard tools. We avoid that restriction by using instead of the Heaviside function (6), a sigmoid function given by Equation (9). Sigmoid monotonically increases, is continuous everywhere, and usually is interchangeable with the Heaviside function in biological modeling applications using the Hausdorff metric. Here we propose

$$H_1\left(G\right)=\epsilon +\frac{1}{1+{\mathrm{e}}^{-c_1\left(G-G_u\right)}},$$

(9)

where $c_1$ is a positive constant that allows changing the slope of the function (Hausdorff metric), and $\epsilon$ is an infinitesimal positive constant. Then,

$$\epsilon \le H_1\left(G\right)\le \left(1+\epsilon \right).$$

(10)

Now we define $H_{1min}:=\epsilon$ and $H_{1max}:=\left(1+\epsilon \right)$. These bounds of the $H_1\left(G\right)$ function allow us to take the constant $H_{1max}$ to find the upper bounds by applying the LCIS method. From this point we define $H_1:=H_1\left(G\right)\equiv H\left(G\right)$. Now we apply the first localizing function by considering a free positive parameter $q_1$:

$$h_1=G+q_{1}D.$$

(11)

The Lie derivative of (11) with respect to the system (1)–(5) is

$$L_f{h}_1=k_{0}D-k_{2}I-k_3-k_4(I-I_{pi})-k_5(G-G_u)H_1\left(G\right)-q_1{k}_{a}D$$

and the set $S\left(h_1\right)$ gives us the following mathematical expression:

$$h_1{\mid }_{S\left(h_1\right)}=k_5^{-1}{H}_{1max}^{-1}\left(k_5{G}_u+k_4{I}_{pi}-k_3-\left(q_1{k}_a-k_0-q_1{k}_5{H}_{1max}\right)D-(k_2+k_4)I\right).$$

Condition (8) must be fulfilled in order to take the following inequality:

$$k_a>k_5,$$

(12)

and our free parameter $q_1$ is given by

$$q_1\ge \frac{k_0}{k_a-k_5{H}_{1max}}.$$

(13)

Therefore, we can ensure an upper bound for the function $h_1$ if conditions (8), (12), and (13) are satisfied, hence,

$$\begin{array}{c}\hfill h_1{|}_{S\left(h_1\right)}\le \frac{k_4{I}_{pi}-k_3+k_5{G}_u}{k_5{H}_{1max}},\end{array}$$

(14)

implying that set $K_1$ is defined as follows:

$$\begin{array}{c}\hfill K_1=\left\{G+q_{1}D\le {\eta }_1:=\frac{k_4{I}_{pi}-k_3+k_5{G}_u}{k_5{H}_{1max}}\right\}.\end{array}$$

(15)

Thus, for the sake of notations, we define $G_{max}:={\eta }_1$ and $D_{max}:=\frac{{\eta }_1}{q_1}$.

On the other hand, the bound of $U\left(t\right)$ was mentioned in [16] with the following description: “when the plasma glucose level $G\le G_u$, then $H\left(G\right)=0$, and there is not renal glucose excretion; i.e., $U\left(t\right)=0$. On the other hand, when the plasma glucose level $G>G_u$, then $H\left(G\right)=1$, and the renal glucose excretion $U\left(t\right)$ depends on $(G-G_u)$." Then, taking our bound $G_{max}$ and considering the sigmoid function (9), we have the bound given by $U_{max}\le \left\{k_5{G}_{max}(1+\epsilon )\right\}$.

Now, let us propose a second localizing function with a free positive parameter $q_2$:

$$\begin{array}{c}\hfill h_2=I+q_{2}Y,\end{array}$$

(16)

where the Lie derivative of (11) with respect to the system (1)–(5) is

$$L_f{h}_2=k_{1}G-k_{6}I+k_{7}Y-q_2{k}_{8}Y,$$

(17)

leading to

$$h_2{|}_{S\left(h_2\right)}=k_6^{-1}\left(k_{1}G+k_{7}Y+q_2(k_6-k_8)Y\right),$$

(18)

when fulfilling the following condition:

$$k_6<k_8.$$

(19)

The free parameter of $q_2$ must fulfill the next condition:

$$q_2\ge \frac{k_7}{k_8-k_6}.$$

(20)

When applying the Iterative theorem to Equation (18) by considering the set $K_1$ through the upper bound of $G_{max}$, we have

$$h_2{|}_{S\left(h_2\right)}\cap K_1\le \frac{k_1}{k_6}{G}_{max},$$

(21)

implying that

$$K_2\cap K_1=\left\{I+q_{2}Y\le h_2{|}_{S\left(h_2\right)}\cap K_1:={\eta }_2=\frac{k_1}{k_6}{G}_{max}\right\}.$$

(22)

Then,

$$K_2=\left\{I+q_{2}Y\le {\eta }_2\right\},$$

(23)

with $I_{max}={\eta }_2$ and $Y_{max}=\frac{{\eta }_2}{q_2}.$ Hence, we derive the following theorem.

Theorem 1.

Suppose that conditions (8), (12), (13), (19), and (20) are fulfilled for a set of the parameters of the system (1)–(5). Let $K_1$ and $K_2$ be given by Equations (15) and (23), respectively. The set $K\left(h\right)$ defined by Equation (24) contains all compact invariant sets for the model (1)–(5), with

$$K\left(h\right)=K_1\cap K_2.$$

(24)

For the parameters given in Table 1, all the conditions (8), (12), (13), (19), and (20) are fulfilled.

3.2. Bounded Positively Invariant Domain

Now, let us consider a Lyapunov candidate function to define a BPID, ensuring that all trajectories of the system (1)–(5) that go inside of BPID will never leave this domain. In Equation (25) is proposed a function given the mathematical domain of the variables ${\mathbf{R}}_{+,0}^5$. Free positive parameters $q_4$ and $q_5$ are associated.

$$V=I+q_{4}Y+D+q_{5}G+U,$$

(25)

Then, the Lyapunov derivative is the following expression when ${\beta }_1=k_6+q_5(k_4+k_2)$ and ${\beta }_2=q_5(k_4{I}_{pi}-k_3+k_5{G}_u{H}_{1max})-k_5{G}_u{H}_{1max}.$

$$\begin{array}{c}\hfill \dot{V}=-{\beta }_{1}I-(q_5{k}_5{H}_{1max}-k_5{H}_{1max}-k_1)G\\ \hfill -(q_4{k}_8-k_7)Y-(k_a-q_5{k}_0)D+{\beta }_2.\end{array}$$

(26)

Given function $\dot{V}$ in (26), and if the following conditions are fulfilled

$$\begin{array}{c}\hfill q_4>\frac{k_6}{k_8},\end{array}$$

(27)

$$\begin{array}{c}\hfill \frac{k_5{H}_{1max}+k_1}{k_5{H}_{1max}}<q_5<\frac{k_a}{k_0},\end{array}$$

(28)

$$\begin{array}{c}\hfill k_4{I}_{pi}+k_5{G}_u>k_3,\end{array}$$

(29)

then with $\dot{V}=0$, the polytope (30)

$$\begin{array}{c}\hfill \left\{{\beta }_{1}I+(k_5{H}_{1max}(q_5-1)-k_1)G+(q_4{k}_8-k_7)Y+(k_a-q_5{k}_0)D\le {\beta }_2\right\}\end{array}$$

(30)

is obtained. From the expression (30), we can get that $\dot{V}<0$ outside this polytope. Therefore, for any ${\rho }_1>0$, the solid polytope (31)

$${\mathrm{\Xi }}_1\left({\rho }_1\right)=\left\{{\beta }_{1}I+(k_5{H}_{1max}(q_5-1)-k_1)G+(q_4{k}_8-k_7)Y+(k_a-q_5{k}_0)D\le {\beta }_2+{\rho }_1\right\}$$

(31)

is a positive invariant domain, i.e., each trajectory of the system (1)–(5) entering into ${\mathrm{\Xi }}_1\left({\rho }_1\right)$ remains there; see Lemma 4.1 by Khalil in [19]

Furthermore, every compact invariant set is contained in ${\mathrm{\Xi }}_1\left({\rho }_1\right)$. This result can be combined with $K\left(h\right)$ (24) to sharpen the BPID.

3.3. Analysis for the Model When a T2DM Case Is Considered

The model can be considered for a T2DM case if $Y\left(t\right)=0$ (where insulin into the subcutaneous compartment is not considered). Localization $K\left(h\right)$ of Equation (24) remains valid, so $I_{max}={\eta }_2$, $G_{max}={\eta }_1$, and $D_{max}=\frac{{\eta }_1}{q_1}$; and condition (20) must be eliminated.

On the other hand, the BPID can be calculated in a similar way, and is given by

$${\mathrm{\Xi }}_2\left({\rho }_2\right)=\left\{{\beta }_{1}I+(k_5{H}_{1max}(q_5-1)-k_1)G+(k_a-q_5{k}_0)D\le {\beta }_2+{\rho }_2\right\},$$

(32)

with ${\beta }_1$ and ${\beta }_2$ defined before. That means that for any ${\rho }_2>0$, the solid polytope (32) is a positive invariant domain; i.e., each trajectory of the system (1)–(5) entering into ${\mathrm{\Xi }}_2\left({\rho }_2\right)$ remains there; see Lemma 4.1 by Khalil in [19].

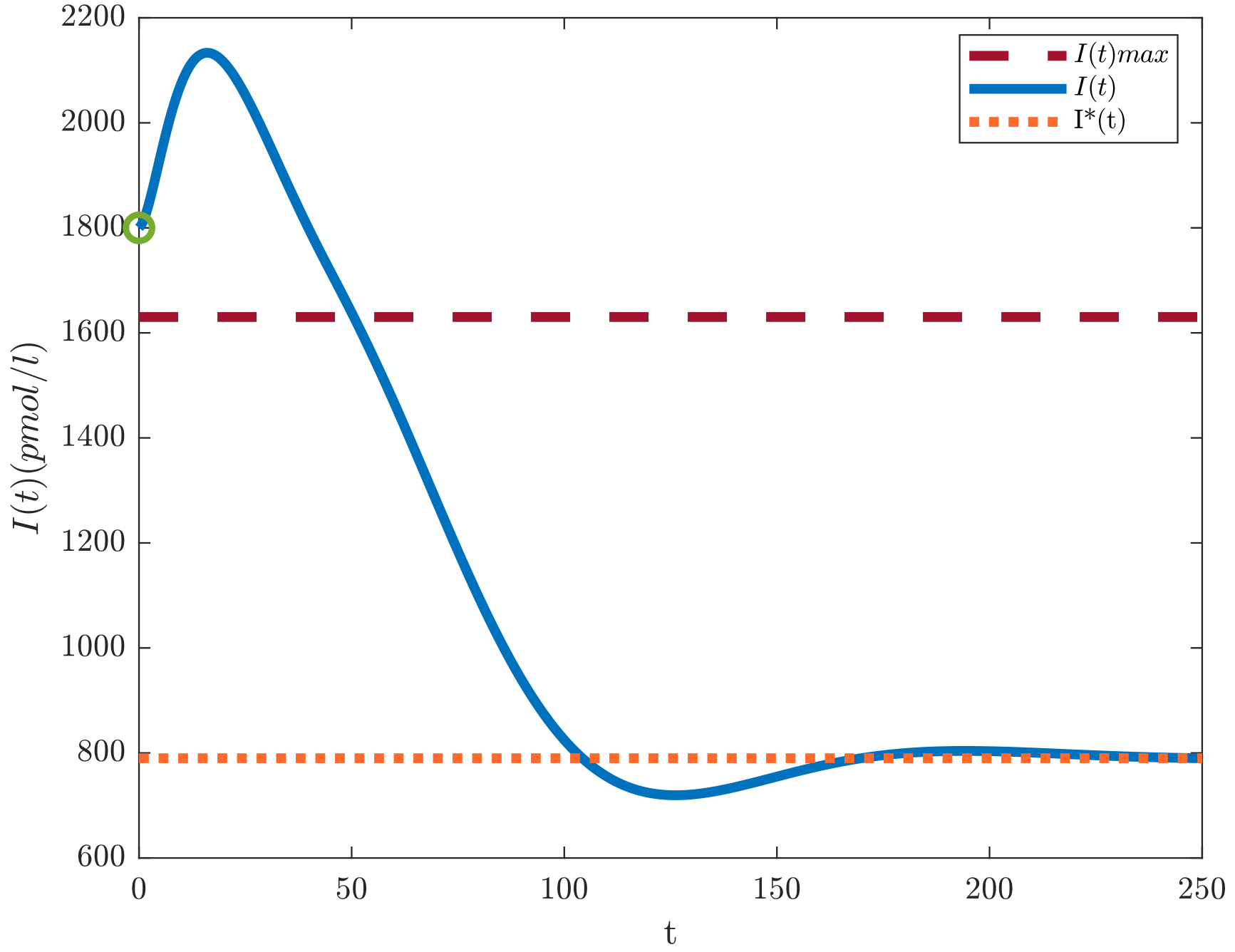
3.4. Numerical Simulations: In Silico Experimentation

This section includes numerical simulations as in silico experiments. Figures provide a visual way to interpret our results. We took the parameters of Table 1 to solve the system (1)–(5) with the Runge–Kutta method, using initial conditions outside of the BPID to show the attractiveness of that region. Here, Figure 2 and Figure 3 represent the simulation for the T1DM case. Moreover, Figure 4 and Figure 5 depict the curve when the T2DM case is considered. The trajectory goes inside the upper bounds $G_{max}$ and $I_{max}$ defined in (24), meaning that trajectories are going to the BPID. If the trajectories of $Y\left(t\right)$ and $D\left(t\right)$ are trivial (exponential type), then we do not show them here.

4. Discussion and Conclusions

This work focused on examining the ultimate bounds for a diabetes mathematical model, including glucose homeostasis. We applied the so-called method localization of compact invariant sets, which allowed us to determine the upper bounds for the system (1)–(5). On the other hand, we used a Lyapunov function to find a bounded positive invariant domain where the trajectories of the system are attracted. The original system contains a Heaviside function that limits the application of the LCIS method. We proposed a smooth function given by a sigmoid, which allowed us to solve the LCIS and BPID problems. The $I_{max},Y_{max},D_{max}$, and $G_{max}$ bounds were computed, and there are valid domains for both the T1DM and T2DM cases. These bounds were constructed with inequalities containing parameters of the system. Application of the localization theorem gave us some inequalities given by (8), (12), (13), (19), and (20), which are necessary assumptions for the existence of localization sets $K_1$ and $K_2$ given by Equations (15) and (23), respectively.

With respect to BPID, we obtained a solid polytope ${\mathrm{\Xi }}_1\left({\rho }_1\right)$, which attracts trajectories of the system with conditions (27)–(29). In both cases, (LCIS and BPID) conditions were fulfilled for the parameters of Table 1, and that could be used to apply our bounds in specific control problems. We performed numerical simulations to show the most relevant bounds $I_{max}$ and $G_{max}$.

Regarding biological implications, we found a BPID that depends directly on the parameters $k_5$ and $k_6$, which are related to insulin, plasma glucose level, and glucose in urine. If we can change at least one parameter externally, it is possible to have a smaller BPID. That implies in some cases, better health conditions for a patient. This kind of application is possible with a controller or observer design but is necessary to evaluate hardware and medical implications that are out of the reach of this paper.

Future work will be focused on the development of observers and controllers based on our bounds, which allows solving several problems, i.e., robustness of the closed-loop system, Lyapunov based controllers or observers.