Abstract
Truthteller liar puzzles are popular in science and also in recreational mathematics. In this paper, we compare five different types of puzzles. In each of our puzzles, the persons of the puzzle may state some statements about their types. In strong truthteller–strong liar puzzles (SS puzzles), each statement of a truthteller must be true and each statement of a liar must be false, and there is no third type of person in these puzzles. It is known that there is no good SS puzzle, where a puzzle is good if it has exactly one solution. In fact, because of symmetry, by flipping the type of person in a solution, another (dual) solution is obtained. Therefore, to break this symmetry, there are various ways to introduce a third type of person, e.g., Mutes and crazies. In SSS puzzles, crazy people may appear, each of whom can tell only a self-contradicting statement. In SSW puzzles, a crazy person may say some additional statements apart from his or her self-contradicting statement. In SSM puzzles, that we investigate here, there can also be some Mute people (as the third type together with truthtellers and liars). We differentiate two types of SSM puzzles. In SSMW puzzles a mute person may be a Mute (type), but he or she could also be either a truthteller or a liar (type). In SSMS puzzles, each person who did not say any statement must be a Mute in the solution. Various examples are presented and it is also highlighted how a puzzle changes from unsolvable to solvable or to a good puzzle when the interpretation, the type of the puzzle changes, i.e., shifted from one to other, and symmetry breaks. Among other data, the number of solvable and good puzzles are counted and compared for the five types when few people appear.
1. Introduction
Puzzles are known from ancient ages for entertaining, recreation and also for philosophical and reasoning points of view. Nowadays, puzzles could be related to different disciplines, since they motivate logical thinking and knowledge reasoning. Knight and knave puzzles are some of the popular puzzles that were investigated by Raymond Smullyan in depth [1,2,3,4,5,6]. Several papers have discussed the solvability of Smullyan’s puzzles [7,8,9,10], their applications [11,12,13] and the way of finding automatic solutions using different algorithms [14,15,16,17,18,19]. Basically, knights are truthtellers who (can) say only true statements and knaves are liars, who (can) tell only false statements. In some puzzles only short, so-called atomic statements are allowed, and they should be about the type of a person in the puzzle. These types are named as strong truthtellers and strong liars, respectively, to highlight that each (short) statement a person told is reflecting his or her type [20,21,22,23,24,25]. In the simplest class of puzzles, in the SS puzzles, only these two types of people may appear (the acronym comes from the word strong for both the truthtellers and liars). In general, a puzzle is good if it has a unique solution. On the other hand, it is known [20,23] that there is no good SS puzzle because of the symmetric roles of the two abovementioned types of people. Thus, we may need other types of people to appear in the puzzles, and, therefore, later on, more kinds of people were introduced in puzzles (not only knights and knaves). In [26,27,28,29], normal is a type of person who can say both true and false statements. KNK puzzles [29], i.e., puzzles with knights, knaves and normal persons, have always a trivial solution such that everybody is normal. Weak truthtellers and weak liars were also introduced and studied by denoting those persons by these terms who must have at least one true or at least one false (atomic) statement, respectively, if she or he says anything in the puzzle. This means that, e.g., if a weak truthteller says anything in the puzzle, then at least one of her or his atomic statements must be true. Thus, in SW puzzles [20,23], there are strong truthtellers and weak liars, i.e., it can also be understood as the conjunctive interpretation of the short statements: all must be true for a truthteller and at least one must be false for a liar. The dual puzzles, the WS type with weak truthtellers and strong liars, were also studied [30] and these puzzles are connected to the disjunctive interpretation of the statements. In this paper, however, we work with the simplest type of truthtellers and liars, the strong ones. Since there are no good SS puzzles, we may need to have types which can be used in the solutions as fixed points. Actually, since the usage of normal type leads to puzzles with a higher number of solutions, we are interested in expanding the possible types to the other direction. As we have mentioned the normal type may be used for people who can say both true and false statements. To complement this, there are two known ways to introduce a type for people who cannot tell true and cannot tell false statements. The first way we recall here is our recently introduced direction, which allows these people to say self-contradictory statements based on the ancient liar paradox. These people may say paradoxical statements that neither knights nor knaves can say in the puzzle. This type of statement defines a new type of puzzle, where the strong crazy type was initiated [21]. Strong crazy people are persons who can say only paradoxical statements. Various types of paradoxical statements and issues with self-reference in puzzles were also presented in [31,32,33,34,35,36,37,38,39]. Rather than strong types of crazy persons, we may also have the weak crazy type, similar to the already mentioned weak truthtellers and liars [22]. Generally, in the weak types, the person with the weak type should say at least one statement that reflects his or her type (if the person speaks anything). In contrast, in the strong types of persons, all statements said by those persons should reflect their types. The other, earlier used option for those who could not tell truth, nor could lie, is to introduce the type of Mutes [26]. In puzzles with Mutes, those who did not say anything in the puzzle, could be Mutes. However, it could also happen that some other people, e.g., truthtellers or liars remained silent. To resolve this ambiguity and provide some fix point for the solution, we also investigate puzzles, where only Mutes can remain silent, i.e., in the solution everybody is a Mute if and only if he or she is silent. Thus, in this paper, we compare five different types of puzzles regarding their solvability: SS, SSS, SSW, SSMW and SSMS puzzles. The first two letters, SS, representing that the truthtellers and liars are of the strong types in all of these puzzles. The third letter S or W stands for the possible type of crazy person who may appear. Letter M in the third position means that the introduced third type of person is a Mute. Since Mutes do not say any statement, there is no way to differentiate strong and weak Mutes. However, a somewhat similar thing gives us a way to refine the situation in SSM puzzles: we differentiate two types of puzzles with Mutes, thus expanding the horizons of these types of puzzles. Letter M with index W shows that in the puzzles the types are weak in the sense that anybody can be silent (i.e., mute), not only Mutes (the latter are defined to be mute and have to be mute), but also some truthtellers or liars can be accidentally mute in the puzzle if they do not say anything. (We refer to the type of Mute by writing it with capital letter ‘M’). On the other hand, by index S, we show that the types are also strong in the sense that each person can be identified by his or her statement, even if he or she does not say anything, i.e., by the lack of his or her statements. In this comparison, we are trying to figure out the possibility to have a good puzzle in a specific puzzle type, which puzzle type has the greatest number of solvable puzzles, what the maximum and the minimum number of statements are that can be said in a good puzzle and other brainstorming questions regarding different types of puzzles. Some statistics about SS puzzles were presented in [25], while some statistical comparisons between SS and SSS puzzles and between SS and SSW puzzles were presented in [21] and [22], respectively. In our work here, we do a more comprehensive comparison of five different types of puzzles in various aspects. One of our aims is to show how the symmetry of the truthtellers and liars can be broken by introducing a third type into the scope, and thus to have good puzzles. Another aim is to make more solvable and, if possible, good puzzles by shifting the interpretation, i.e., the possible types of the people appearing in it. We statistically compare the puzzles to see which way can be considered as the most efficient from these points of view. Actually, we introduce here two types of SSM puzzles (where the people can be strong truthtellers, strong liars and Mutes) by differentiating the muteness based on two different points of view as we have already mentioned, this way also complementing the earlier studies. Graph representations and diagrams are used to facilitate the interpretation of logical puzzles somewhat similarly as in [19,20,21,22,23,29]. Our puzzles can be linked easily to other scenarios, the persons are not necessarily always persons. Persons of our puzzles can simulate various peripherals or sensors in various types of networks which helps to define their identity, i.e., whether that device is a noisy device (crazy person), a defected or passive hacker device (Mute person) or an active hacking device (liar person). A similar scenario was introduced in [40] about satellites and messages between them about their status. Thus, some parts of our study may have applications beyond recreational mathematics and logic.
2. Preliminaries
Here, we will recall some definitions that are necessary for our investigation of the various types of puzzles and their solution(s). These definitions are common in all five types of puzzles we work on and some of these definitions are analogue to each other, that is depending on the type of the puzzle. In our work, we define the puzzle as a set of persons and statements said by those persons about each other and about themselves, where each person can say only one statement about any person in the puzzle. This type of statement is called atomic statement, and it comes in two forms: “A is a truthteller” or “A is a liar”, where A is a person in the puzzle [20,21]. Defining the solution(s) of the puzzle is always linked to the definition of the puzzle as models are connected to logic. Hence, the solution of the puzzle is defined as a function that specifies the type of each person in the puzzle, such that his/her type matches the statements that he/she said in the puzzle. In this manuscript, the puzzles are the same in terms of puzzle context, but they are different in terms of the solution(s) of the puzzle because we allow different types of persons in the solutions of the puzzles as it will be formally specified later. The puzzle is solvable if it has at least one solution. Moreover, the puzzle is good if it has a unique solution, whereas the puzzle is clear if it does not give any additional information to solve it; in a clear puzzle only the persons and their statements are provided to solve it. The number of true or false statements or the number of truth tellers or liars are possible examples of the additional information. However, in this paper, we deal with clear puzzles without any additional information.
As we have mentioned, we have different types of persons allowed in the solution(s) of different types of puzzles. To understand our comparison results, we need to recall these different types of persons. The strong truthteller and strong liar types are available in all types of puzzles we work with; therefore, we define them first based on [20,21,22,26].
Definition 1.
A strong truthteller is a person who says only true atomic statements if he/she says any statement, while strong liars are persons who say only false atomic statements if they say any statements in the puzzle.
Observe that in fact no people of the mentioned types are forced to say anything in a puzzle. They may remain silent. However, in some puzzles we will also work with Mutes, thus the following remark is important to distinguish some types of the puzzles.
Remark 1
. This definition for strong truthtellers and strong liars is applied for SS, SSS, SSW and SSMW puzzles, while it is applicable for SSMS puzzles with a further condition since in that type of puzzle, each strong truthteller, and each strong liar must say at least one statement.
In SSS and SSW puzzles crazy people may appear. Self-contradictory statements are crucial to define strong crazy and weak crazy types of persons that have already been discussed and defined in [21,22]. A self-contradictory statement is a statement that is neither true nor false independently of other statements if a strong truthteller or a strong liar would say it, i.e., both of these cases would lead to a contradiction.
Definition 2.
Any person in the SSS puzzle is a strong crazy if all his/her statements are self-contradictory statements if he/she said any statement in the puzzle. Furthermore, a person in the SSW puzzle is a weak crazy if at least one of his/her statements is a self-contradictory statement if he/she says any statement.
We have defined already one type of truthteller, one type of liar and two subtypes of crazies, now we recall the fourth type we are working with, the Mutes. They appear in puzzles in [26]. We differentiate here two subtypes of Mutes, and thus two types of puzzles with Mutes. An SSMW puzzle differs from the SSMS puzzle by how the Mute type is assigned to any person in the solution(s) of the puzzle.
Definition 3.
In SSM puzzles, Mute people may appear. In an SSMW puzzle, any person who does not say any statement in the puzzle can be a Mute person, but not necessarily, he or she still could be a strong truthteller or a strong liar in any solution of the puzzle depending on the statements that other persons say about him/her. Opposite to this, in an SSMS puzzle, every person who does not say any statement in the puzzle must be a Mute in every solution regardless of other persons and what they say about him/her.
Remark 2.
Note that in SSMS, if the Mute type is assigned to a person in one of the solutions, then he/she cannot have another type (such as a strong truthteller or strong liar) in other solutions of the puzzle.
In our statistics and comparisons on the various types of the puzzles, we will consider the graph representation of the puzzle as a visual representation of the puzzle as follows [21,22]:
- ▪
- Nodes represent persons of the puzzle.
- ▪
- Arrows represent the atomic statements of the puzzle
- ➢
- A solid arrow from A to B shows that A said that “B is a truthteller”.
- ➢
- A broken arrow from A to B represents that A said that “B is a liar”.
3. Puzzle Types
In this section in five subsections, we will reintroduce the formal definitions of the five different types of puzzles along with their solutions. Examples are also provided for better understanding.
3.1. SS Puzzles (Strong Truthteller and Strong Liar Puzzles)
In this type of puzzles, we initiate the simplest type of puzzles [20]. (In the name “SS puzzles”, the double S stands for strong type of truthtellers and liars, since weak truthteller and liar types were also defined in [20,23,30] for some other type of puzzles). Now we are ready to recall the definition of the SS puzzles.
Definition 4
. In SS puzzles, any person in the puzzle can either be a strong truthteller or a strong liar in the solution of the puzzle.
Now we recall the formal definition of the solution of SS puzzles.
Definition 5.
Let an SS puzzle with set N of people be given. The solution of the puzzle is a function N → {truthteller, liar}, such that for each person who claimed any statement in the puzzle the following holds:
- Personis truthteller if the following condition holds for every :ifclaimed that
- ➢
- “is a liar”, then is a liar (this atomic statement is true).
- ➢
- “is a truthteller”, then is a truthteller (this atomic statement is true).
- Person is a liar if the following condition holds for every :if claimed that
- ➢
- “is a liar”, then is a truthteller (the atomic statement is false).
- ➢
- “is a truthteller”, then is a liar (the atomic statement is false).
Based on what has been proven in [20], there is no good (and clear) SS puzzle, i.e., it is impossible to have an SS puzzle with a unique solution. In fact, each solution has a symmetric dual solution by changing the type of each person of the solution to the opposite type. The most important aim with the other type of puzzles we have introduced earlier and analyze here and with types we introduce in this paper is to break this symmetry and have puzzles with exactly one solution.
Example 1.
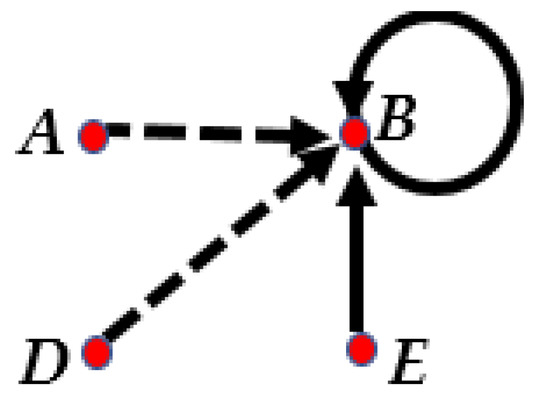
In the SS puzzle presented in Figure 1, A said that B is a liar, B said that he is a truthteller, D said that B is a liar, and E said that B is a truthteller. The problem is to decide whom of the four persons is a truthteller and liar.

Figure 1.
An SS puzzle with four persons (Example 1).
Based on Definition 5, this puzzle has two solutions, in the first solution A and D are liars and B and E are truthtellers. In the other solution, A and D are truthtellers and B and E are liars.
In the next type of puzzle, we have a new strong type of person which leads to such a scenario that there are good (and clear) puzzles.
3.2. SSS Puzzles (Strong Truthteller, Strong Liar and Strong Crazy Puzzles)
This type of puzzle was discussed and studied in [21]. First, we recall their definition.
Definition 6.
In SSS puzzles, each person may be a strong truthteller, strong liar or strong crazy in the solution of the puzzle.
Definition 7.
Let an SSS puzzle with set N of people be given. Its solution is a functionN→ {truthteller, liar, crazy}, such that for each person who claimed any statement in the puzzle the following holds:
- Personis a truthteller as in Definition 5.
- Person is a liar if the following condition holds for every :if claimed that
- ➢
- “is a liar”, thenis a truthteller or a crazy (the atomic statement is false).
- ➢
- “is a truthteller”, then is a liar or a crazy (the atomic statement is false).
- Person is a crazy if he/she says only self-contradictory statements in case he/she says anything in the puzzle.
Example 2.
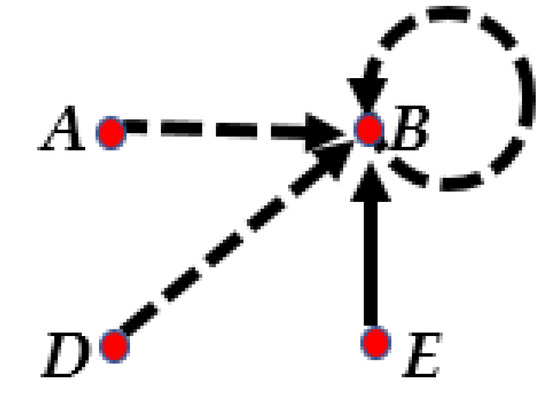
In the SSS puzzle presented in Figure 2, A said that B is a liar, B said that he is a liar, D said that B is a liar and E said that B is a truthteller. The problem is to decide who is the truthteller, liar and crazy.

Figure 2.
An SSS puzzle with four persons (Example 2).
Observe that the puzzle in Example 2 is almost the same as the puzzle presented in Example 1, with a small change that B said that he is a liar, while in Example 1 he said that he is a truthteller. If we consider the latter puzzle an SS puzzle, then it is unsolvable, since B said a self-contradictory statement. However, by interpreting it as an SSS puzzle, this puzzle becomes a good puzzle, since in the solution of the puzzle, B is a crazy person, while A, D and E are all liars and there is no other solution.
It was proven in [21] that the only statement that a strong crazy person can say is “I am a liar”, as that type of statement is the only self-contradictory statement in the puzzles. In the next, the third type of puzzle, a new variant of crazy person is used, the so-called weak crazy. As we have seen by the example shown, to include strong crazies in the puzzles could be a good way to break the symmetry of the strong truthtellers and strong liars by allowing statements about the crazy people that only strong liars may give.
3.3. SSW Puzzles (Strong Truthteller, Strong Liar and Weak Crazy Puzzles)
SSW puzzles were introduced and studied in [22]. We start again by recalling their definition.
Definition 8.
In SSW puzzles, any person may be a strong truthteller, a strong liar or a weak crazy in the solution of the puzzle.
Definition 9.
Let an SSW puzzle with set N of people be given. Its solution is a functionN→ {truthteller, liar, crazy}, such that for each person who claimed any statement in the puzzle the following holds:
- Person is truthteller as in Definition 5.
- Person is liar as in Definition 7.
- Person is crazy if at least one of his/her statements is a self-contradictory statement (in case he/she says anything in the puzzle).
Example 3.

In the SSW puzzle presented in Figure 3, A said that B is a liar, B said that he himself is a liar and A is a truthteller, D said that B is a liar and E said that B is a truthteller. The task is to decide who is the truthteller, liar and crazy.

Figure 3.
An SSW puzzle presented in Example 3.
If we consider the puzzle of Example 3 an SS puzzle or an SSS puzzle, then the puzzle is unsolvable, since B said a self-contradictory statement (B said that he is a liar) and a non-self-contradictory statement (B said A is a truthteller). Thus, B cannot be a strong crazy, a strong liar or a strong truthteller. However, the SSW puzzle, according to Definition 9, has a unique solution which is: A, D, and E are liars, while B is a weak crazy person. Observe that this puzzle is almost the same as the puzzle presented in Example 2, except adding one more statement from B about A. Thus, weak crazies can also be used to break the symmetry of strong truthtellers and liars in puzzles.
Based on the puzzles that were studied in [26], we consider two different types of Mute persons which leads to two different types of puzzles. In the sequel, we formally introduce these two types of new truthteller—liar puzzles in which the third, additional type of person is the Mutes. Observe that so far, any type of person may remain silent in a puzzle. This does not hold for SSMS puzzles, where all silent people must have the type Mute in the solution. Subsequently, the definition of a strong truthteller and strong liar is slightly modified by adding a condition in these puzzles. However, let us now continue with the SSMW puzzles.
3.4. SSMW Puzzles (Puzzles with Strong Truthtellers, Strong Liars and Mutes in a Weak Sense)
In this type of puzzle, the types of strong truthtellers and strong liars are the same as the ones defined in Definition 1 and have been used in the previous types of puzzles. Now we define our SSMW puzzles.
Definition 10.
In SSMW puzzles, any person in the puzzle may be a strong truthteller, a strong liar or a Mute in the solution of the puzzle. As the name indicates, if a person is a Mute, then he/she cannot say anything in the puzzle.
As the definition of Mutes in SSMW puzzles contains an “if” statement, we can infer that if a person is a Mute in the solution, then he/she must be silent in the puzzle. However, this is only an “if” statement and not an “if and only if” statement meaning that we may not use the induction backwards, i.e., silentness in the puzzle does not imply Muteness. Consequently, we may formally define the solution(s) of these puzzles as follows.
Definition 11.
The/a solution of an SSMW puzzle with set N of people is a function N→ {truthteller, liar, Mute}, such that for each person the following holds:
- Person is truthteller, as in Definition 5.
- Person is liar if the following condition holds for every :if claimed that
- ➢
- “ is a liar”, then is either a truthteller or a Mute (the atomic statement is false).
- ➢
- “ is a truthteller”, then is either a liar or a Mute (the atomic statement is false).
- If person is a Mute, then he/she does not say anything in the puzzle.
Example 4
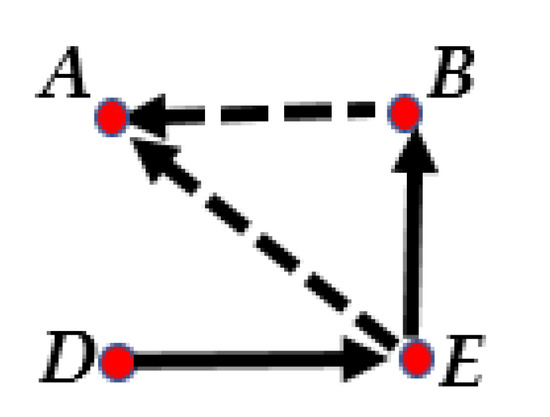
. In the SSMW puzzle presented in Figure 4, A does not say anything, B said that A is a liar, D said that E is a truthteller and E said that B is a truthteller and A is a liar. The task is to decide who is the truthteller, liar and Mute.

Figure 4.
An SSMW puzzle presented in Example 4.
If we assume that the previous puzzle is an SS puzzle then the puzzle has two solutions: in the first solution A is a truthteller, and B, D and E are liars. In the second solution, A is a liar, while B, D and E are truthtellers. Considering it as an SSS or an SSW puzzle, it has one more solution, that is, A is a crazy, while B, D and E are liars. Considering it as an SSMW puzzle, in addition to the solutions of the puzzle as an SS puzzle, it has one more, a third solution where A is a Mute, while B, D, and E are all liars. Therefore, as an SSMW puzzle, we have three solutions for this puzzle.
3.5. SSMS Puzzles (Puzzles with Strong Truthtellers, Strong Liars and Mutes in the Strong Sense)
In this type of puzzle, the definition of a strong truthteller and strong liar is slightly different as we mentioned in Remark 1. We are ready to give the definition of our last, fifth type of puzzle.
Definition 12.
In the SSMS puzzles, a strong truthteller is a person who must say only true atomic statements, whilst a strong liar is a person who says only false atomic statements. Any strong truthteller and any strong liar must say at least one statement in the puzzle. Finally, a person is a Mute if he or she does not say anything in the puzzle.
The main difference between SSMW puzzles and SSMS puzzles is that whilst in the former any type of people may remain silent, in the latter all truthtellers and liars must say something (evidently, their statements must reflect their types). Thus, there is an “if and only if” condition to characterize Mutes in the SSMS puzzles: a person is Mute if and only if he or she is silent (did not say anything in the puzzle). Thus, if there is person who does not say anything, we may infer its type in these puzzles. The formal definition of the solution(s) of these puzzles is thus written as follows.
Definition 13.
The/a solution of an SSMS puzzle with set N of people is a function of the form N → {truthteller, liar, Mute}, such that for each person the following holds:
+ Ifclaimed at least one statement in the puzzle, then
- Person is truthteller if the following condition holds for every :if claimed that
- ➢
- “is a liar”, then is a liar (the atomic statement is true).
- ➢
- “is a truthteller”, then is a truthteller (the atomic statement is true).
- Person is liar if the following holds for every :if claimed that
- ➢
- “is a liar”, then is either a truthteller or a Mute (the atomic statement is false).
- ➢
- “is a truthteller”, thenis either a liar or a Mute (the atomic statement is false).
- +
- If person does not say anything in the puzzle, then is a Mute person.
If we assume that the puzzle in Example 4 is an SSMS puzzle, then this puzzle is a good puzzle, since it has a unique solution, such that A is a Mute person and B, D and E are liars.
4. Some Properties of the Puzzles and Their Solutions
First, we consider some further examples to show how the solvability and the goodness property of a puzzle may change just by shifting from one type to another.
The solutions can be defined for the graph representation as well such that the solution(s) of the graph representation of an SS, an SSS or an SSW puzzle is/are exactly the same as the solution(s) of the puzzle itself [20,21,22]. Analogously, this can be carried out for other puzzle types, and thus the graph representation could be a useful tool to analyze puzzles.
Example 5.
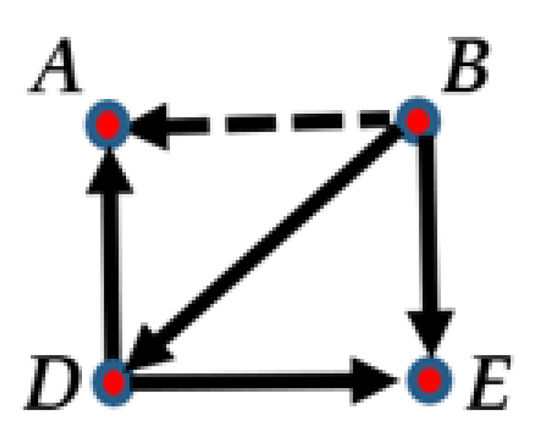
Let us consider the puzzle represented in Figure 5. In the puzzle, B said that A is a liar. Furthermore, he or she said that D and E are truthtellers, while D said that A and E are truthtellers. A and E do not say anything in the puzzle. What is/are the solution(s) of this puzzle if we consider it as an SS, SSS, SSW, SSMW or SSMS puzzle?

Figure 5.
A puzzle presented in Example 5.
First, if we consider the puzzle in Figure 5 as an SS-puzzle, then this puzzle has no solution. Next, if it is considered as an SSS-puzzle or an SSW-puzzle, then it has two solutions. In the first solution, A and E are crazy persons, B and D are liars, while in the second solution, A is a crazy person, B, D, and E are liars. Thirdly, let us assume that the puzzle is an SSMW-puzzle. Then, it has two solutions: in the first solution: A is a Mute person, B, D, and E are liars, while in the second solution, A and E are both Mute persons, B and D are liars. Finally, let us assume that the puzzle is an SSMS-puzzle. In this case, it is a good puzzle (it has a unique solution), where A and E are Mutes, and B and D are liars.
Example 6.
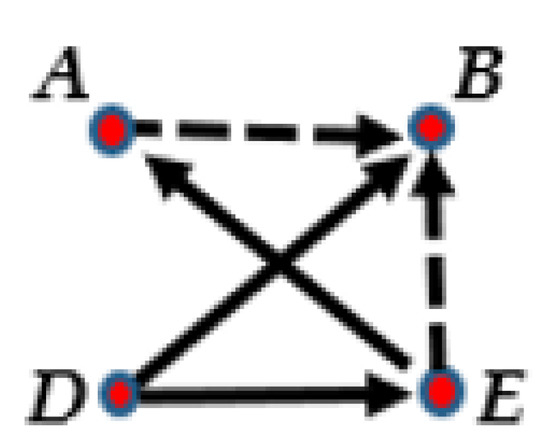
By considering the puzzle presented in Figure 6, A said that B is a liar, while D said that B and E are truthtellers. E said that B is a liar and A is a truthteller. B does not say anything in the puzzle. What is/are the solution(s) of this puzzle if we consider it as an SS-, SSS-, SSW-, SSMW- or SSMS-puzzle?

Figure 6.
A puzzle presented in Example 6.
First, if we consider the puzzle as an SS puzzle, then it has no solution. Next, if we consider this puzzle an SSS puzzle or an SSW puzzle, then it has a unique solution, which is A, D and E are liars, while B is a crazy person. Finally, if we assume that this puzzle is an SSMW puzzle or an SSMS puzzle, then this puzzle is again a good puzzle, since it has a unique solution, that is A, D, and E are liars and B is a Mute person. Thus, this example shows that all the possible extensions of SS puzzles may lead to good puzzles, i.e., by allowing crazy- or Mute-type people to appear in the solution.
All of the presented puzzles of the previous examples along with the numbers of their solutions are shown in Table 1. Each puzzle is considered to be each of the five different puzzle types analyzed. We may also conclude that by introducing (any of the types studied) Mutes we can also break the symmetry of the strong truthtellers and strong liars.

Table 1.
The number of solutions of the example puzzles considering them as an SS, an SSS, an SSW, an SSMW or an SSMS puzzle.
Theoretical Investigations
In this subsection, we recall and/or state some interesting relations of the types of the puzzles we studied. As one can recall from [20,24], there are no good SS puzzles. In fact, if only the statements of the people are given, then each solution s of an SS puzzle has a dual solution s’ by flipping the value assigned to each person, i.e., if a person is a truthteller in solution s, then he or she is a liar in s’, and if a person is a liar in s, then he or she is a truthteller in s’. Actually, as we have already mentioned, one of the aims of the newer types of puzzles was to break this symmetry between the two types of people.
In SSS and SSW puzzles, crazy people may appear in the solutions. As it was proven for these types of puzzles in [21] and [22], respectively, a crazy either gives a self-reference statement of the form “I am a liar” (maybe with some other statements in case of SSW puzzles, see [22]), or may not say anything in the puzzle. By observing the nature of these puzzles, we can establish the following fact.
Proposition 1.
Let a puzzle be given, if s is a solution of the puzzle when considering it as an SSS puzzle, then s is also its solution when it is considered as an SSW puzzle.
The proposition above is not if and only if, as we have already shown by the puzzle in Example 3, which has a solution as an SSW puzzle, but is unsolvable as an SSS puzzle. As we have seen, some crazy people may be silent in some puzzles, for silent people there is another special option to deal with: the symmetry of truthtellers and liars of SS puzzles can also be broken by using the type of Mutes. Actually, in SSMS puzzles, the Mute persons can easily be identified, and in this way, the symmetry is broken and one can have puzzles with a unique solution. Furthermore, we can also establish the following new result about SSM puzzles based on the fact that SSMS-type puzzles are restricted variants of the SSMW type.
Proposition 2.
Let a puzzle be given, if s is a solution of the puzzle when considering it as an SSMSpuzzle, then s is also a solution when it is considered as an SSMWpuzzle.
However, as we have seen in Examples 4–6, there are puzzles which have a greater number of solutions as SSMW puzzles than as SSMS puzzles. On the other hand, we have also seen an example for a good SSMW puzzle (see Example 6). Thus, it is proven that all types of extensions of the SS puzzles lead to some good puzzles and thus the aforementioned symmetry can be broken.
Furthermore, we are giving some interesting facts about the possible numbers of solutions of SSMS puzzles. For this, we will use the concept of connected puzzle. A puzzle is connected if its graph representation is weakly connected (by the usual meaning of directed graphs, i.e., the underlying undirected graph is connected). If a puzzle is not connected, then it can be seen as a union of some connected puzzles, defined by the maximal weakly connected components of the graph. Actually, in this latter case, one needs to solve these smaller puzzles independently. The number of solutions of the original puzzle will be the product of the numbers of solutions of these smaller component puzzles (defined by the maximal weakly connected components). Thinking about a puzzle as an SSMS puzzle, one can easily identify the Mute people and they and only they are the Mutes in every solution. If a connected puzzle (maybe the original one or one of the component puzzles) has at least one Mute, then it may have exactly 1 or maybe 0 solutions. Whenever a component has no Mute, its solutions are exactly the same as its solutions as an SS puzzle, and as it was shown (see also [20,24]) it has an even number of solutions. Thus, by applying the multiplication rule, we can state the following result.
Proposition 3.
Any solvable SSMS puzzle has either a unique solution (i.e., it is a good puzzle) or an even number of solutions.
5. Statistics and Comparison of Different Puzzle Types
In this section, various statistical results are presented to show the significance of the type of the puzzle when the set of solutions of the puzzle is obtained, since some puzzles may be unsolvable. One may also ask what is the chance for a “randomly generated” puzzle to be solvable or even to be good. Few statistics about the number of good, solvable and unsolvable SS, SSS and SSW puzzles generated by a computer program were already presented in [21,22,25], respectively. In this section, we expand the statistical analysis with some additional data, e.g., the number of good puzzles with the number of various types of people in their solution. Moreover, we also present some statistics about the newly studied puzzles, the SSM puzzles of both types. We give also some details on the possible numbers of arrows in the graphs of the puzzles which directly correspond to the numbers of the atomic statements made in the puzzle.
In our comparison, we use puzzles where each person can say at most one statement about each person (including her/himself) in the puzzle. Since in SS puzzles, if any person says both types of statements about a person in the puzzle, the puzzle is clearly unsolvable, we use this restriction for the puzzles included in our statistics. Thus, the total number of puzzles is calculated by considering that each person in the puzzle has three possibilities to state about any person in the puzzle:
- does not say anything about ;
- says that is a truthteller;
- says that is a liar.
Therefore, a matrix of size can represent how each person can talk about any person in the puzzle, which shows that the total number of possible puzzles is . With a computer program (using a brute force such as combinatorial strategy), we have created all those for a relatively small number of people (up to four) and checked their possible solutions. Because of the combinatorial explosion, it is not feasible to generate all puzzles with a large number of people. Our statistics are based on the results obtained by this measurement. In the rest of the section, we use some tables and column diagrams to show some statistical data and their comparisons of the different types of puzzles.
As it is shown in Table 2, the SSW type has both the maximum number of good and solvable puzzles, followed by SSS puzzles in each category. On the other hand, the SS-type puzzles have the smallest number of good (this value is actually always 0, as we have discussed before) and solvable puzzles. Observe that, on the one hand, the SSMW type has more solvable puzzles than the SSMS type (based on the fact shown in Proposition 2), but, on the other hand, the SSMS type has more good puzzles (see also Figure 7). Notice that for three- and four-person puzzles, the logarithmic scale is used to fit and compare all values, since some of the values are more than 100 times larger than others. One can see from the data presented that a puzzle needs to have at least three people to be good when it is interpreted as an SSMW puzzle.

Table 2.
The number of good, solvable (including good ones) and unsolvable SS, SSS, SSW, SSMW and SSMS puzzles with two, three and four people.

Figure 7.
Column diagrams represent the numbers of good, solvable and unsolvable puzzles of various types with two, three and four people (Same as the data in Table 2).
When we analyze solvable puzzles, we can differentiate them not only in two categories (good or not good), but more generally by their number of solutions. These data are displayed in Table 3. From them, one can also read that, for SSMS puzzles, it is impossible to have an odd number of solutions if it is greater than one, as we have shown in Proposition 3 (also see Figure 8 and Figure 9 for these comparisons. In the right diagram in the former one and also in the diagram for the latter one, the logarithmic scale is used due to the great variety of values to be displayed).

Table 3.
The number of SS, SSS, SSW, SSMW and SSMS puzzles with one, two, three, four, five or more solutions for puzzles with two, three and four people.
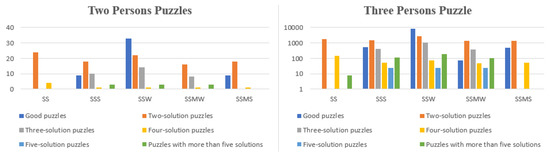
Figure 8.
Column diagrams represent the data shown in Table 3a: various number of various puzzles with the given number of solutions.

Figure 9.
Diagram representing the number of four-person puzzles with the given number of solutions (data from Table 3b).
As it is shown in Table 4a, in good puzzles with two persons, there are no truthtellers in the solution no matter how we interpret the puzzle, i.e., what type is used. This can also be seen by checking the possible cases: Any good SSS or SSW puzzle must have at least one crazy in its solution (this was proven in [21] and [22]), respectively). Then, with two persons (let us say, A and B), either there is exactly one crazy person or the solution has two crazy persons. In the latter case, clearly, there are no truthtellers. If the solution has one crazy person (let say A), then the other person B should say something about A (otherwise the puzzle is not good or both people are crazy). Thus, B must be a liar; therefore, there is not no truthteller in good SSS and SSW puzzles with two persons. One may apply a very similar argument about good two-person SSMS puzzles using Mutes instead of crazies in the previous argument. Moreover, as we have seen, there is no good SSMW puzzle with two people at all. Consequently, there are not any truthtellers occurring in any solution of a good puzzle of any of the studied types. Table 4a,b also shows the number of good puzzles of various types with a given number of truthtellers in their solutions. As one can see, there are good puzzles with at least one truthteller in their solutions if the number of people in the puzzle is at least four even in the case in SSMW puzzles.

Table 4.
The number of good SSS, SSW, SSMW and SSMS puzzles with one, two or three truthtellers in their solutions (puzzles with two, three and four people).
Table 5 shows that good SSW puzzles have the maximum number of liars, while in SSMW we can find the least number of liars, in general. Additionally, it is clearly shown that there is no good SSMW puzzle with exactly one liar.

Table 5.
The number of good SSS, SSW, SSMW and SSMS puzzles with one, two or three liars in their solutions (two-, three- and four-person puzzles).
Table 6 shows that, in general, the solution of a good SSW puzzle has a larger number of crazy persons compared to good SSS puzzles. This is due to the fact that every strong crazy is also a weak crazy, but not the other way around, i.e., there is a stronger restriction on the crazies in the SSS puzzles than in the SSW puzzles.

Table 6.
The number of good SSS and SSW puzzles with one, two, three or four crazies in their solutions.
As Table 7 shows, there are usually larger numbers of Mutes in the solutions of good SSMS puzzles than in the solutions of the good SSMW puzzles. However, as there are good SSMS puzzles where nobody says anything, these puzzles are not good SSMW puzzles; thus, there is no good SSMW puzzle where everybody in the solution is a Mute person. Moreover, we can see that there is no good SSMW puzzle with n = 2, 3, 4 persons where the number of Mutes in the solution is greater than n − 2. This gives us the conjecture that no such puzzle exists for any number of people.

Table 7.
The number of good SSMW and SSMS puzzles with one, two, three or four Mutes in their solutions.
Finally, we show some statistical data about the number of statements of good puzzles. These data correspond to the number of arrows in the graph representation. We also show results separately for the broken and solid arrows in Table 8.

Table 8.
The maximum and the minimum number of broken and solid arrows and the maximum and the minimum number of arrows altogether for good SSS, SSW, SSMW and SSMS puzzles with two, three and four people.
Observe that good SSW puzzles have the largest number of maximum number of arrows. On the other hand, notice that SSM puzzles (SSMW and SSMS) have the least maximum number of arrows. Furthermore, good SSMS puzzles have the least minimum number of arrows, since if there are no arrows in an SSMS puzzle, then the puzzle is good with the solution that all persons are Mutes. Regarding the minimum number of solid arrows in good SSMW puzzles, they should have at least one solid arrow in puzzles with four persons, while any good puzzles with three persons should have at least two solid arrows. Other types of puzzles do not have similar properties, since we have good SSS, SSW and SSMS puzzles with no solid arrows.
6. Conclusions
We have studied various truthteller–liar puzzles—in most cases also involving a third type of person in the solutions. The third type of person helped to break the symmetry of truthtellers and liars of the SS puzzles and thus remove some of the dual solutions. This way, we have shown that various SS puzzles become good puzzles (i.e., puzzle with a unique solution) if the interpretation, the possible solution is shifted by including third type of persons, e.g., crazies or Mutes, depending on the considered new type of the puzzle. This approach is related to the resolution of the liar paradox, by allowing more than two types of truth values. After giving some important relations among (the solutions of) these puzzles, we have presented various statistical data about them, mostly concentrating on relatively small size puzzles (in terms of the number of people in them). In our statistics, we found that SSW puzzles have the maximum number of good and solvable puzzles in comparison with other types of puzzles. Additionally, the majority of solvable SSW puzzles are good ones. Meanwhile, SSS comes in second place, followed next by SSMW and then SSMS puzzles, while SS puzzles come with the least number of solvable puzzles. We have also shown many other interesting comparisons between the five previously mentioned types of puzzles, e.g., maximum and minimum number of statements that the people can say in good puzzles, the number of good SSS, SSW, SSMS and SSMW puzzles with one, two, three or four liars, truthtellers, Mutes or crazies in the solution of the puzzle, etc. The statistics that were discussed in the paper are more general than the results presented in [21,22,25], as new views and new data are involved. Moreover, these results are complemented by data about SSM puzzles which were not studied before in this context.
We can conclude that some types of paradoxes, as well as the symmetry of the two-valued logic, can be broken if a kind of third value (e.g., contradictory such as a crazy, or none of the true or false, by a Mute) is assumed or directly introduced. This also highlights the necessity of many valued logics in various scenarios.
Puzzles can be used in recreational or educational studies and lectures. Some scenarios of the puzzles may reflect some real-life scenarios where good reasoning is needed to solve the case. As a further possible application of the studied types of puzzles, [40] mentions satellite systems, where each satellite sends messages about the status of other (neighbor) satellites to the administrative devices, whether they are defect, hacker or trusted satellites. Thus, we can mirror different puzzle types to address these trusting issues about other network devices.
As the future presents issues that need to be addressed, a comparison of other different puzzle types where any person of the puzzle can be a normal person, weak liar or weak truthteller. Additionally, the characterization of good, solvable and unsolvable puzzles of various other types of puzzles is an open question that needs to be discussed and addressed in the future.
Author Contributions
Writing—original draft preparation, L.A.; writing—review and editing, B.N.; supervision, B.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data used, the number of various puzzles, are of mathematical nature, based on the definitions anyone can reproduce them.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Smullyan, R. What Is the Name of This Book? The Riddle of Dracula and Other Logical Puzzles; Prentice-Hall: Englewood Cliffs, NJ, USA, 1978. [Google Scholar]
- Smullyan, R. The Lady or the Tiger? And Other Logic Puzzles; Alfred A. Knopf: New York, NY, USA, 1982. [Google Scholar]
- Smullyan, R. The Magic Garden of George B. and Other Logic Puzzles; Polimetrica S.A.S.: Milano, Italy, 2007. [Google Scholar]
- Smullyan, R. Logical Labyrinths; AK Peters: Natick, MA, USA; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Henle, J. The Entertainer. Math. Intell. 2018, 40, 76–80. [Google Scholar] [CrossRef]
- Holliday, R.L. Liars and Truthtellers: Learning Logic from Raymond Smullyan. Math Horiz. 2005, 13, 5–29. [Google Scholar] [CrossRef]
- Rahman, S.; Tulenheimo, T.; Genot, E. Unity, Truth and the Liar: The Modern Relevance of Medieval Solutions to the Liar Paradox; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; Volume 8. [Google Scholar]
- Frings, K.; Groot, P.; Hubbers, E. Formalizing and Proving Knights and Knaves Puzzles in Three Valued Logic in Coq. Bachelor’s Thesis, Radboud University, Nijmegen, The Netherlands, 17 January 2022. [Google Scholar]
- Ciraulo, F.; Maschio, S. Solving knights-and-knaves with one equation. Coll. Math. J. 2020, 51, 82–89. [Google Scholar] [CrossRef] [Green Version]
- Rosenhouse, J. Fuzzy knights and knaves. Math. Mag. 2016, 89, 268–280. [Google Scholar] [CrossRef]
- Chlond, M.J.; Toase, C.M. IP modeling and the logical puzzles of Raymond Smullyan. Trans. Educ. 2003, 3, 1–12. [Google Scholar] [CrossRef]
- Rips, L.J. The psychology of knights and knaves. Cognition 1989, 31, 85–116. [Google Scholar] [CrossRef]
- Johnson-Laird, P.N.; Byrne, R.M. Meta-logical problems: Knights, knaves, and Rips. Cognition 1990, 36, 69–84. [Google Scholar] [CrossRef]
- Aszalós, L. Automated puzzle solving. J. Appl. Non-Class. Log. 2002, 12, 99–116. [Google Scholar] [CrossRef] [Green Version]
- Chesani, F.; Mello, P.; Milano, M. Solving Mathematical Puzzles: A Challenging Competition for AI. AI Mag. 2017, 38, 83. [Google Scholar] [CrossRef] [Green Version]
- Kolany, A. A general method of solving Smullyan’s puzzles. Log. Log. Philos. 1996, 4, 97–103. [Google Scholar] [CrossRef]
- Lusk, E.; Wos, L.; Overbeek, R.; Boyle, J. Automated Reasoning: Introduction and Applications; McGraw-Hill: New York, NY, USA, 1992. [Google Scholar]
- Costa, J.F.; Poças, D. Solving Smullyan puzzles with formal systems. Axiomathes 2018, 28, 181–199. [Google Scholar] [CrossRef]
- Howse, J.; Stapleton, G.; Burton, J.; Blake, A. Picturing Problems: Solving Logic Puzzles Diagrammatically. In Proceedings of the International Workshop on Set Visualization and Reasoning (SetVR 2018), Edinburgh, UK, 18 June 2018; pp. 12–27. [Google Scholar]
- Nagy, B. Truth-teller, Liar puzzles and their graphs. Cent. Eur. J. Oper. Res. 2003, 11, 57–72. [Google Scholar]
- Alzboon, L.; Nagy, B. Truth-Teller–Liar Puzzles with Self-Reference. Mathematics 2020, 8, 190. [Google Scholar] [CrossRef] [Green Version]
- Alzboon, L.; Nagy, B. Crazy Truth-Teller–Liar Puzzles. Axiomathes 2021. (online first). [Google Scholar] [CrossRef]
- Nagy, B. SW puzzles and their graphs. Acta Cybernet. 2003, 16, 67–82. [Google Scholar]
- Nagy, B. SS-típusú igazmondó-hazug fejtörők gráfelméleti megközelítésben (SS-type truthteller-liar puzzles and their graphs, in Hungarian with English summary). Alkalm. Mat. Lapok 2006, 23, 59–72. [Google Scholar]
- Nagy, B.; Kósa, M. Logical Puzzles (Truth-tellers and liars). In Proceedings of the 5th International Conference on Applied Informatics, Eger, Hungary, 28 January–3 February 2001; pp. 105–112. [Google Scholar]
- Aszalós, L. The Logic of Knights, Knaves, Normals and Mutes. Acta Cybernet. 2000, 14, 533–540. [Google Scholar]
- Cook, R.T. Knights, knaves and unknowable truths. Analysis 2006, 66, 10–16. [Google Scholar] [CrossRef]
- Rosenhouse, J. Knights, knaves, normals, and neutrals. Coll. Math. J. 2014, 45, 297–306. [Google Scholar] [CrossRef]
- Nagy, B.; Allwein, G. Diagrams and Non-monotonicity in Puzzles. In Proceedings of the International Conference on Theory and Application of Diagram, Cambridge, UK, 22–24 March 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 82–96. [Google Scholar]
- Nagy, B. Duality of logical puzzles of type SW and WS—Their solution using graphs. Pure Math. Appl. 2005, 15, 235–252. [Google Scholar]
- Lukowski, P. Paradoxes; Springer: Dordrecht, The Netherlands, 2011. [Google Scholar]
- Henle, J. Romantic Mathematical Art: Part II. Math. Intell. 2020, 42, 57–64. [Google Scholar] [CrossRef]
- Yablo, S. Knights, Knaves, Truth, Truthfulness, Grounding, Tethering, Aboutness, and Paradox. In Raymond Smullyan on Self Reference; Springer: Cham, Switzerland, 2017; pp. 123–139. [Google Scholar]
- Priest, G. The structure of the paradoxes of self-reference. Mind 1994, 103, 25–34. [Google Scholar] [CrossRef]
- Cheruvalath, R. Analysing the Concept of “Paradox” in the Liar Paradox Arguments. Cultura 2020, 17, 87–98. [Google Scholar] [CrossRef]
- Barwise, J.; Etchemendy, J. The Liar: An Essay on Truth and Circularity; Oxford University Press: New York, NY, USA; Oxford, MS, USA, 1987. [Google Scholar]
- Benétreau-Dupin, Y. Buridan’s Solution to the Liar Paradox. Hist. Philos. Log. 2015, 36, 18–28. [Google Scholar] [CrossRef]
- Michael, E. Peirce’s paradoxical solution to the Liar’s Paradox. Notre Dame J. Form. Log. 1975, 16, 369–374. [Google Scholar] [CrossRef]
- Yablo, S. Paradox without self-reference. Analysis 1993, 53, 251–252. [Google Scholar] [CrossRef]
- Shasha, D.E. The Puzzling Adventures of Dr. Ecco; W.H. Freeman: New York, NY, USA, 1998. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).