Multitask Learning Based on Least Squares Support Vector Regression for Stock Forecast
Abstract
:1. Introduction
2. Least Squares Support Vector Regression
3. Extension of Multitask Learning Least Squares Support Vector Regression
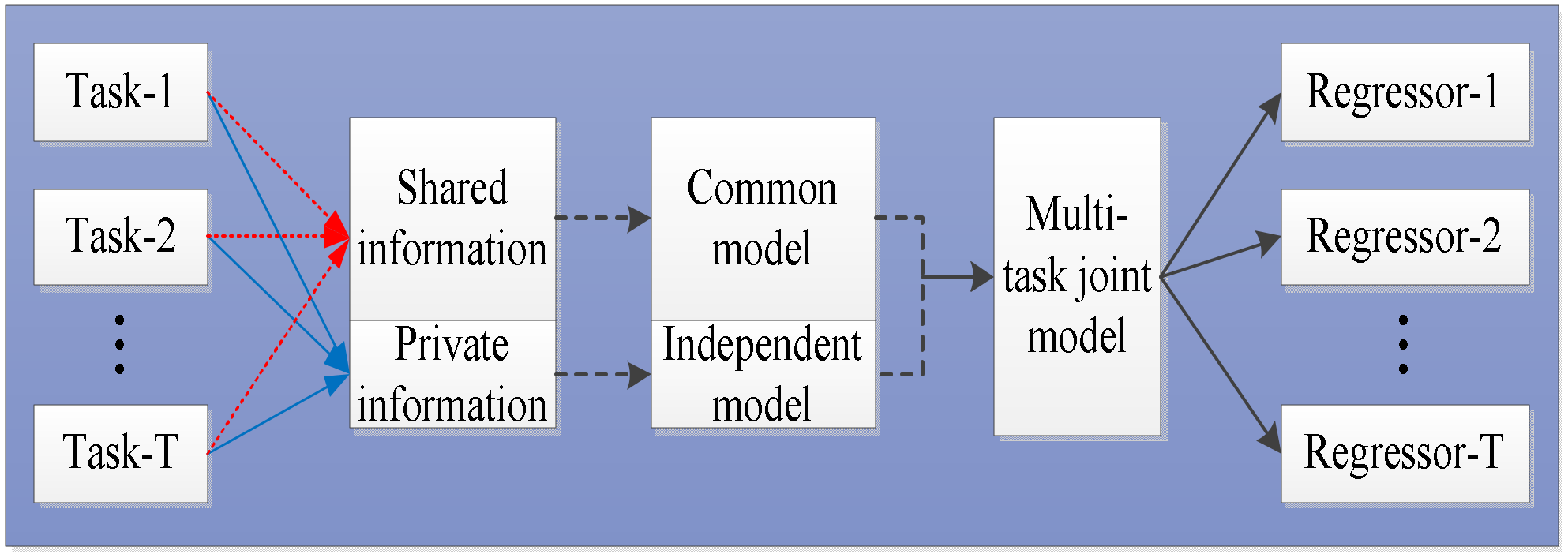
3.1. MTL-LS-SVR
3.2. EMTL-LS-SVR
3.3. Krylov-Cholesky Algorithm
- (1)
- Convert the linear system (7) or (13) to the following form using Krylov methods:where is a positive number. is a positive definite and symmetric matrix denoted as , and is an block-wise diagonal matrix;
- (2)
- Apply the Cholesky factorization method to decompose into , and the elements of the lower-triangular matrix can be determined from ;
- (3)
- Calculate , and thus , ;
- (4)
- Solve , from and , respectively, and record the corresponding solution and ;
- (5)
- Calculate ;
- (6)
- Obtain the optimal solution: and .
4. Experiments
- 1)
- is a linear kernel and is a polynomial kernel.
- 2)
- is a linear kernel and is a radial basis function kernel.
- 3)
- is a polynomial kernel and is a radial basis function kernel.
4.1. Parameter Selection
4.2. Evaluation Criteria
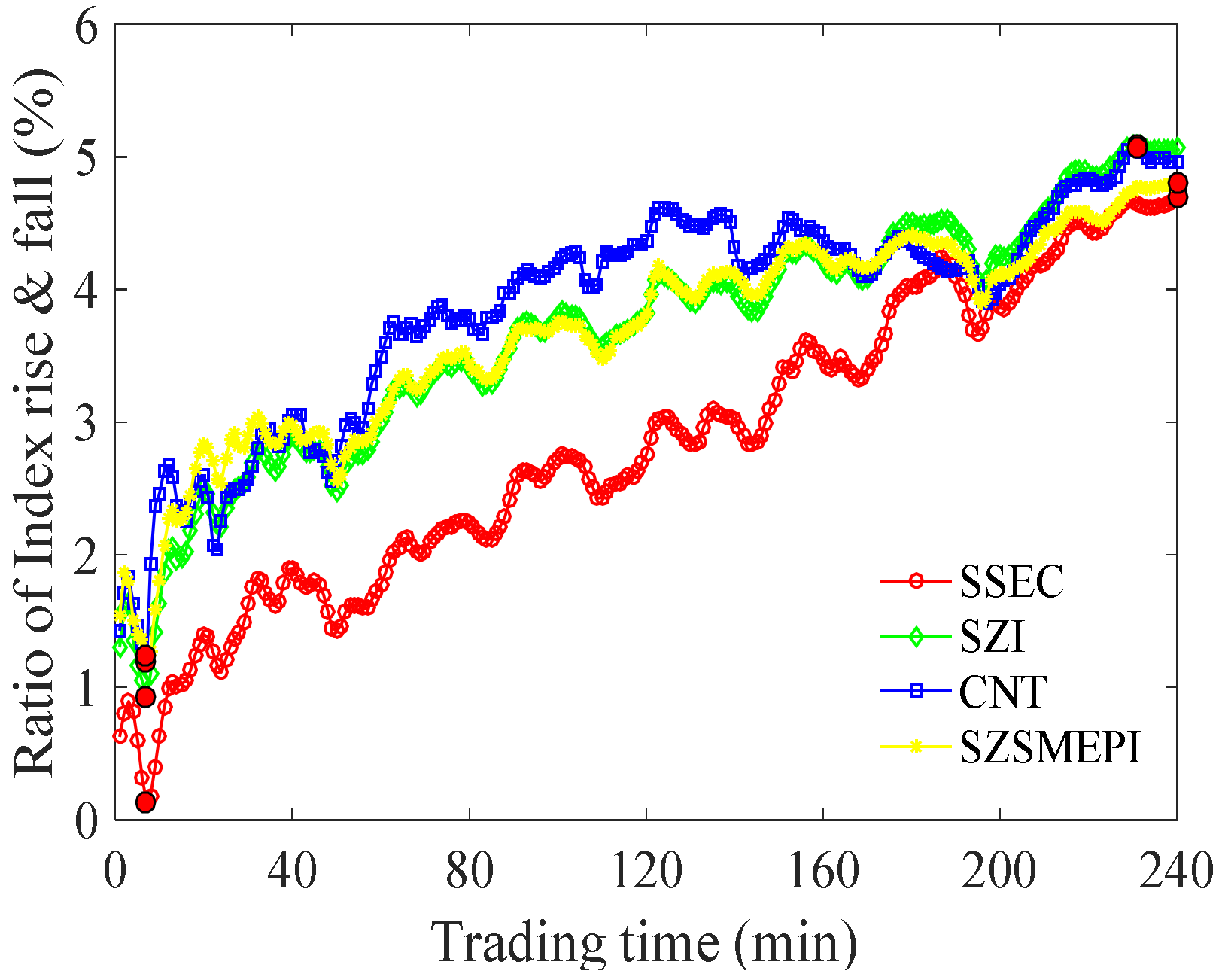
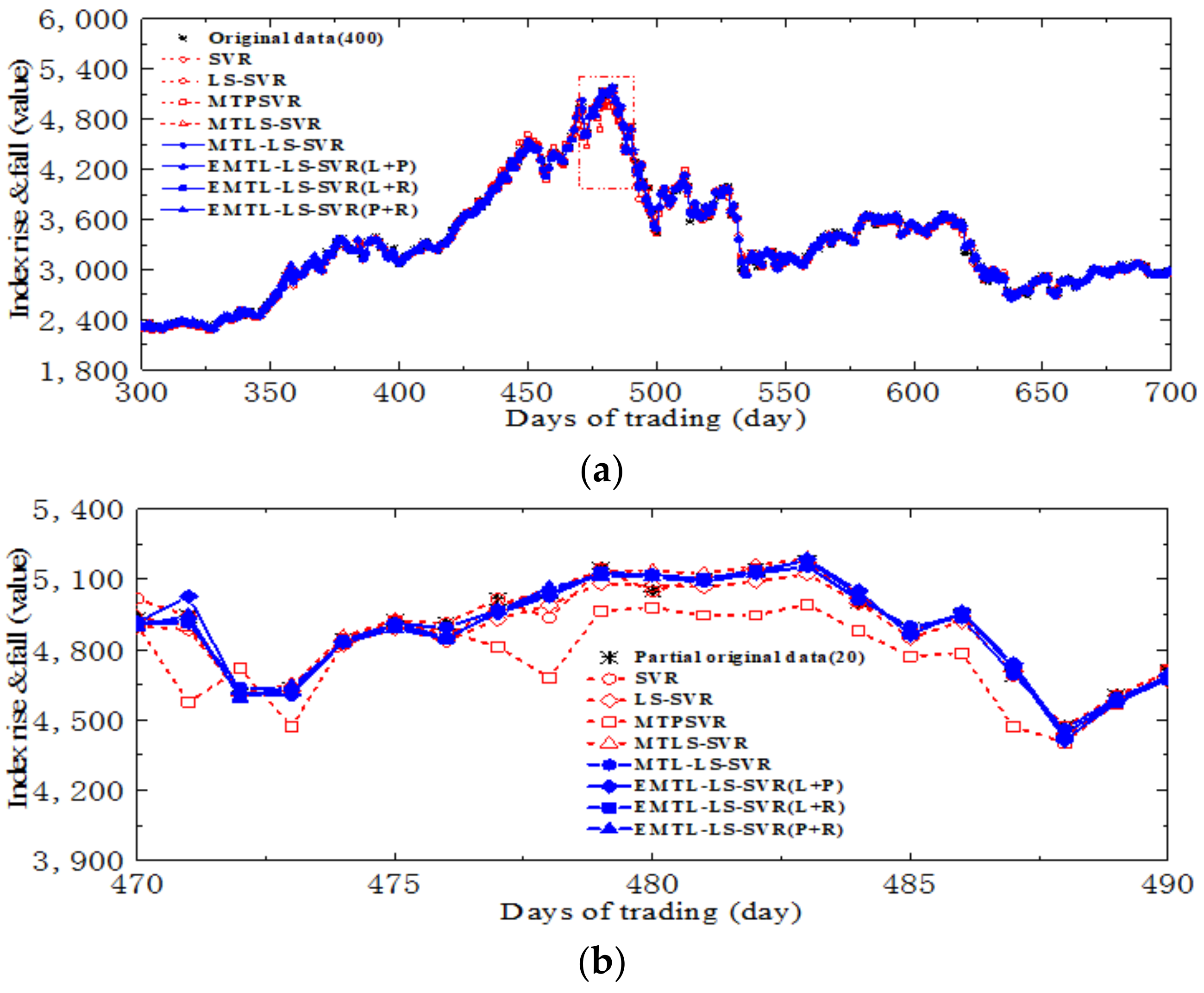
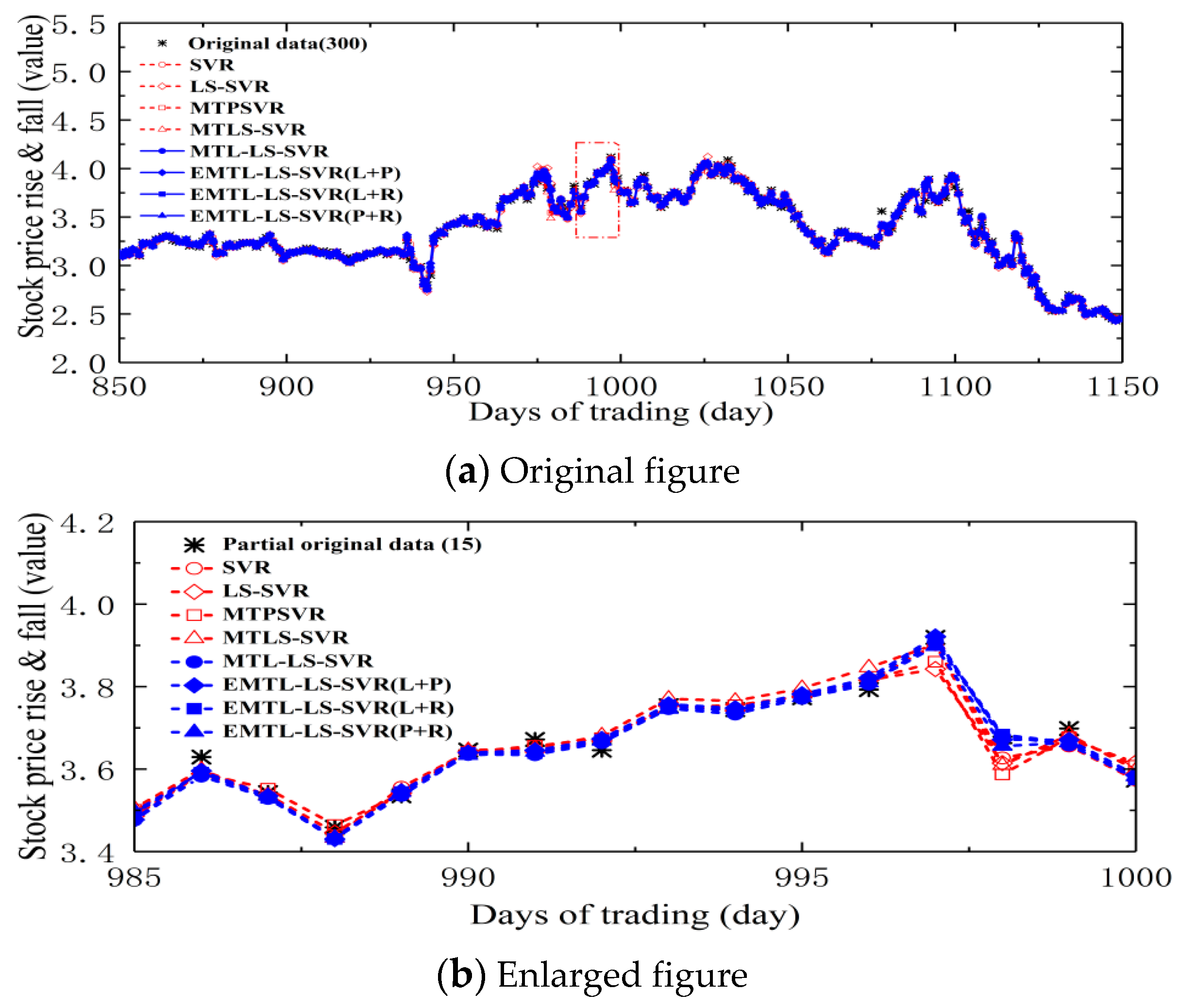
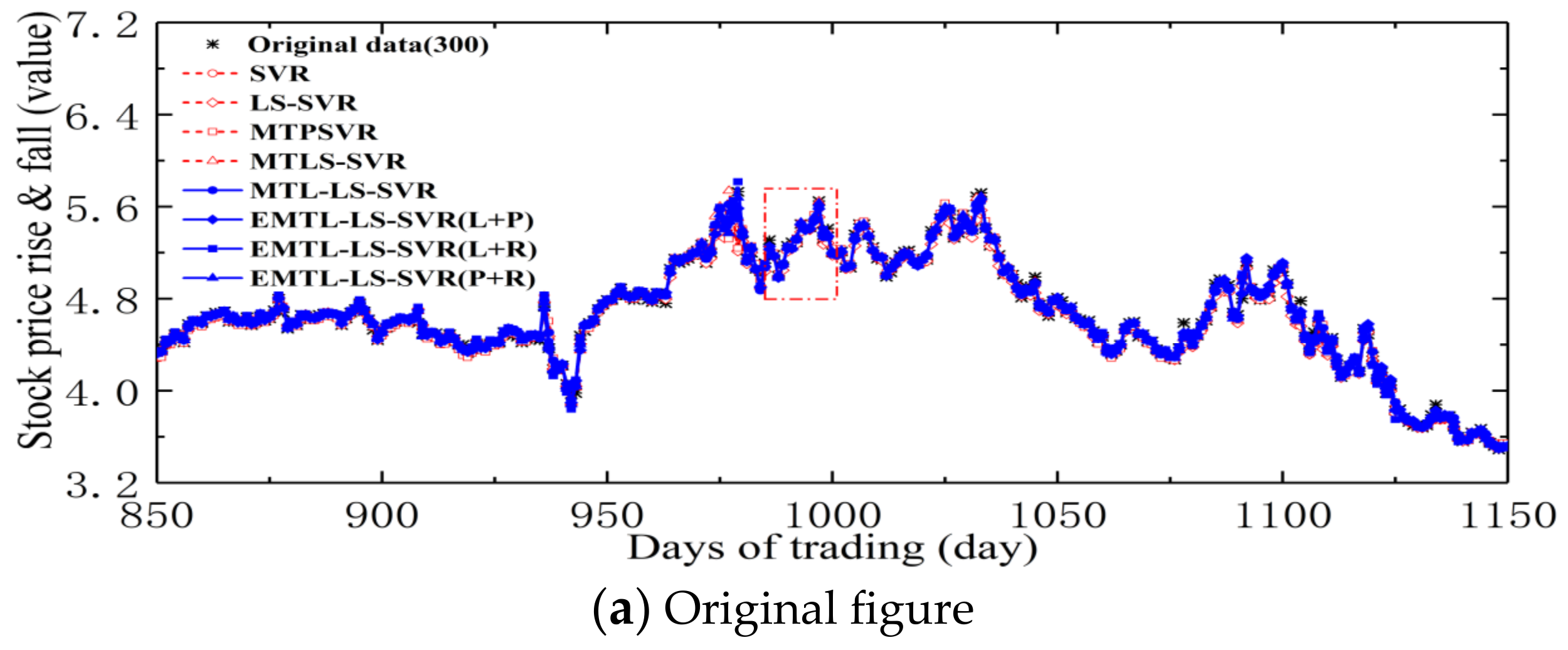
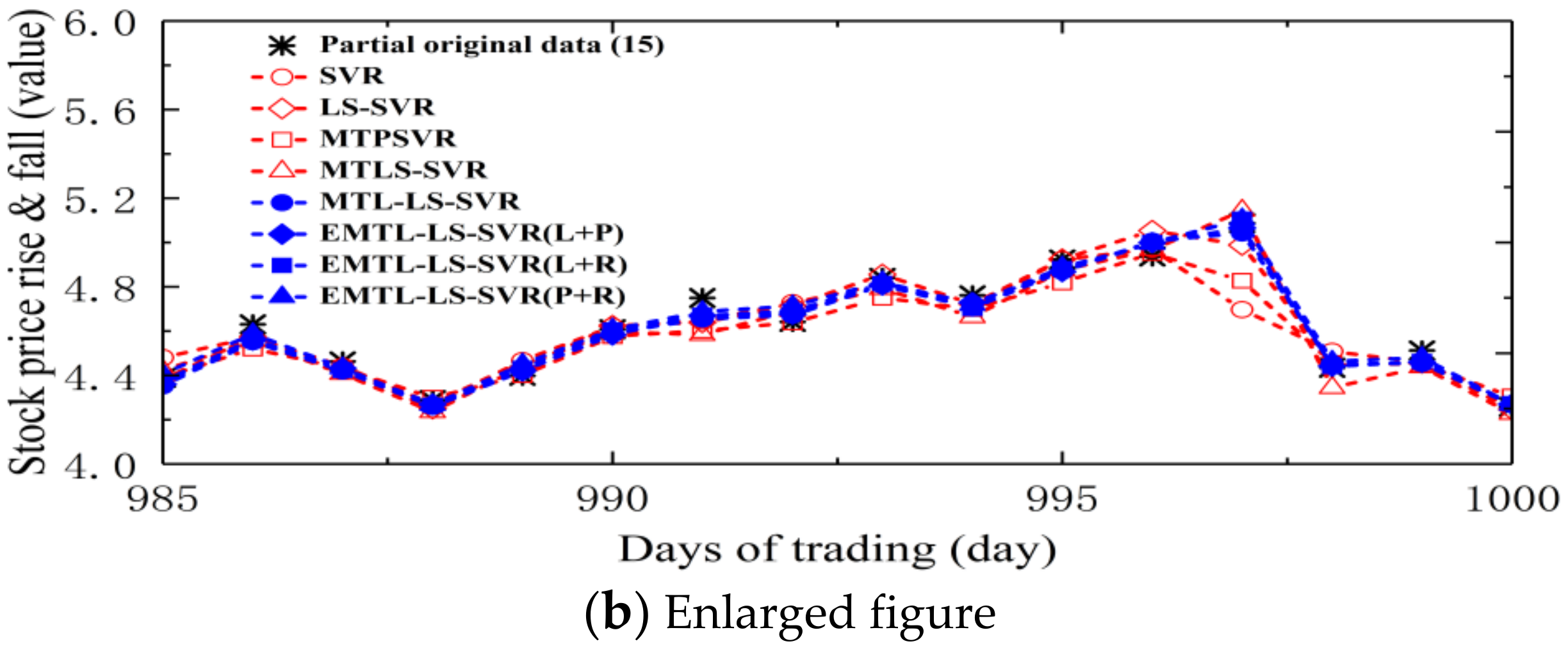
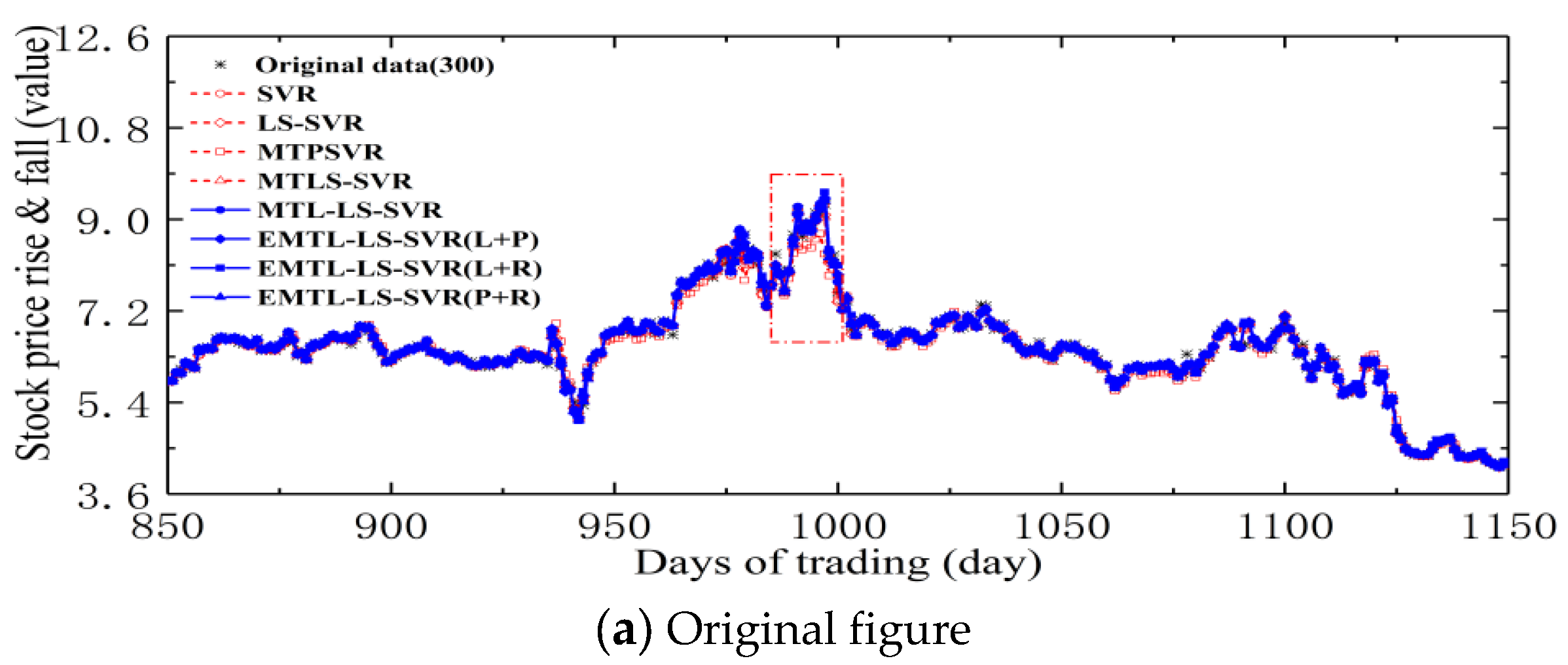
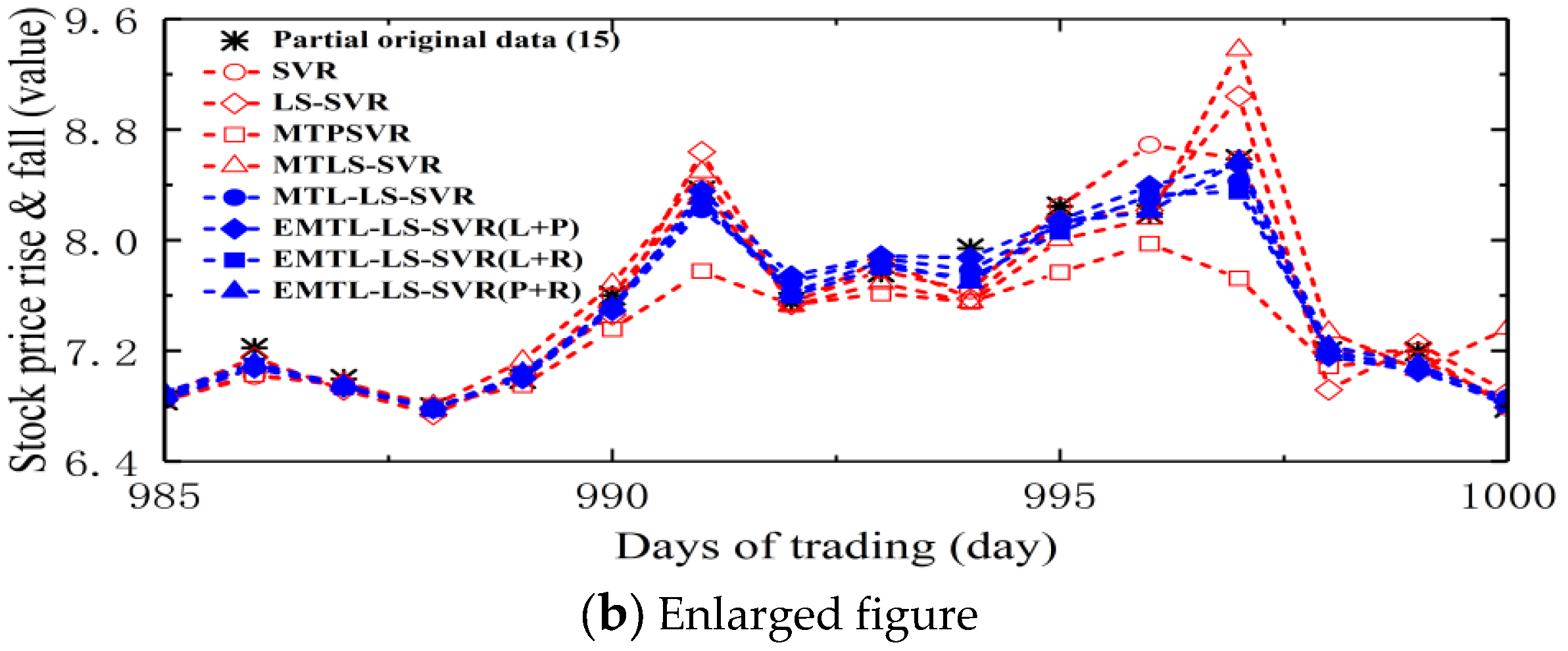
4.3. Forecast of Security of Stock Market Investment Environment
- a
- http://quotes.money.163.com/trade/lsjysj_zhishu_000001.html (accessed on 1 May 2021)
- b
- http://quotes.money.163.com/trade/lsjysj_zhishu_399001.html (accessed on 1 May 2021)
- c
- http://quotes.money.163.com/trade/lsjysj_zhishu_399006.html (accessed on 1 May 2021)
- d
- http://quotes.money.163.com/trade/lsjysj_zhishu_399005.html (accessed on 1 May 2021)
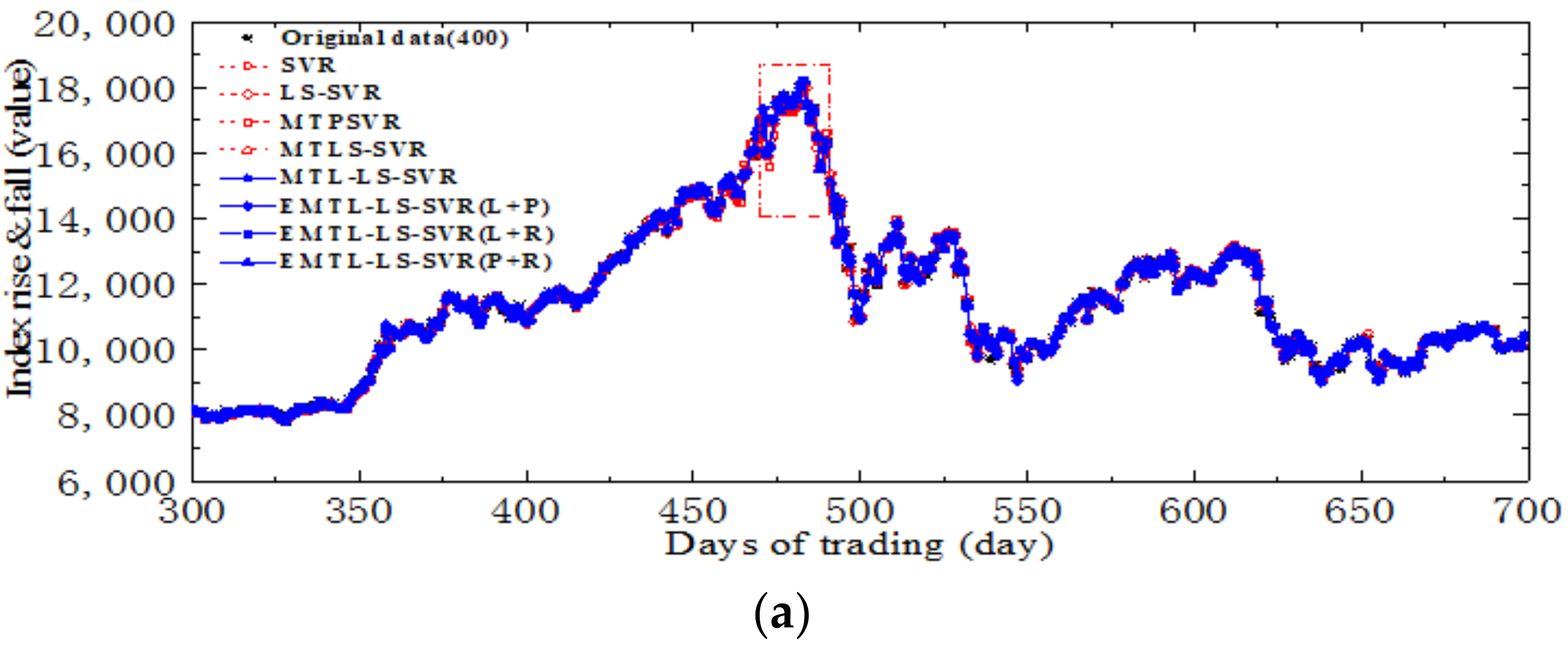
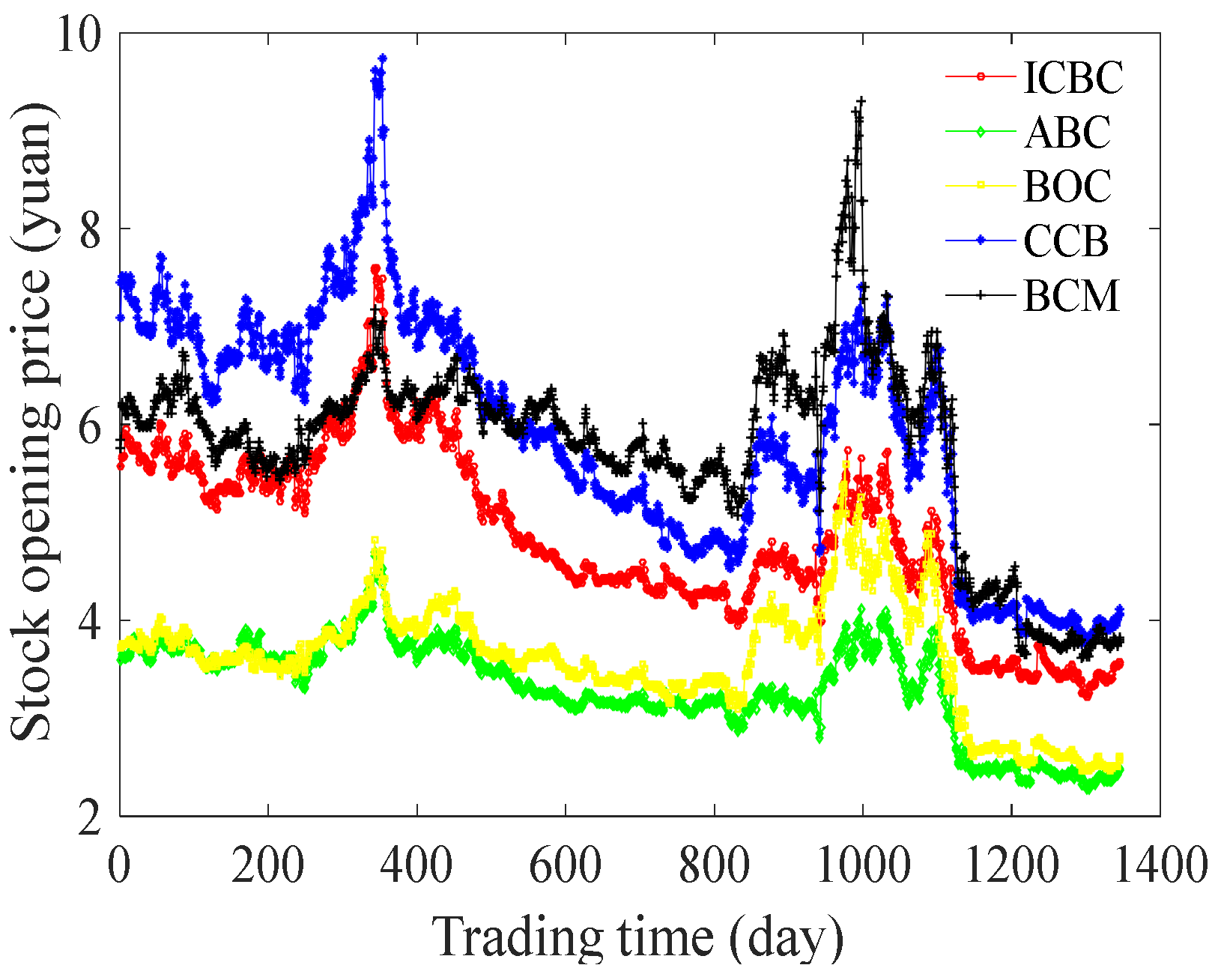
4.4. Forecasting Opening Prices of Five Major Banks
- e
- http://quotes.money.163.com/trade/lsjysj_601398.html (accessed on 1 May 2021)
- f
- http://quotes.money.163.com/trade/lsjysj_601288.html (accessed on 1 May 2021)
- g
- http://quotes.money.163.com/trade/lsjysj_601988.html (accessed on 1 May 2021)
- h
- http://quotes.money.163.com/trade/lsjysj_601939.html (accessed on 1 May 2021)
- i
- http://quotes.money.163.com/trade/lsjysj_601328.html (accessed on 1 May 2021)
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Park, H.J.; Kim, Y.; Kim, H.Y. Stock market forecasting using a multi-task approach integrating long short-term memory and the random forest framework. Appl. Soft Comput. 2022, 114, 108106. [Google Scholar] [CrossRef]
- Kumbure, M.M.; Lohrmann, C.; Luukka, P.; Porras, J. Machine learning techniques and data for stock market forecasting: A literature review. Expert Syst. Appl. 2022, 197, 116659. [Google Scholar] [CrossRef]
- Kao, L.J.; Chiu, C.C.; Lu, C.J.; Yang, J.L. Integration of nonlinear independent component analysis and support vector regression for stock price forecasting. Neurocomputing. 2013, 99, 534–542. [Google Scholar] [CrossRef]
- Liang, M.X.; Wu, S.C.; Wang, X.L.; Chen, Q.C. A stock time series forecasting approach incorporating candlestick patterns and sequence similarity. Expert Syst. Appl. 2022, 205, 117295. [Google Scholar] [CrossRef]
- Yang, X.L.; Zhu, Y.; Cheng, T.Y. How the individual investors took on big data: The effect of panic from the internet stock message boards on stock price crash. Pac. Basin Financ. J. 2020, 59, 101245. [Google Scholar] [CrossRef]
- Ghosh, I.; Jana, R.K.; Sanyal, M.K. Analysis of temporal pattern, causal interaction and predictive modeling of financial markets using nonlinear dynamics, econometric models and machine learning algorithms. Appl. Soft Comput. 2019, 82, 105553. [Google Scholar] [CrossRef]
- Yu, X.J.; Wang, Z.L.; Xiao, W.L. Is the nonlinear hedge of options more effective?—Evidence from the SSE 50 ETF options in China. North Am. J. Econ. Financ. 2019, 54, 100916. [Google Scholar] [CrossRef]
- Chen, Y.S.; Cheng, C.H.; Chiu, C.L.; Huang, S.T. A study of ANFIS-based multi-factor time series models for forecasting stock index. Appl. Intell. 2016, 45, 277–292. [Google Scholar] [CrossRef]
- Huang, L.X.; Li, W.; Wang, H.; Wu, L.S. Stock dividend and analyst optimistic bias in earnings forecast. Int. Rev. Econ. Financ. 2022, 78, 643–659. [Google Scholar] [CrossRef]
- Chalvatzis, C.; Hristu-Varsakelis, D. High-performance stock index trading via neural networks and trees. Appl. Soft Comput. 2020, 96, 106567. [Google Scholar] [CrossRef]
- Zhang, J.; Teng, Y.F.; Chen, W. Support vector regression with modified firefly algorithm for stock price forecasting. Appl. Intell. 2019, 49, 1658–1674. [Google Scholar] [CrossRef]
- Cao, J.S.; Wang, J.H. Exploration of stock index change prediction model based on the combination of principal component analysis and artificial neural network. Soft Comput. 2020, 24, 7851–7860. [Google Scholar] [CrossRef]
- Qiu, Y.; Yang, H.W.; Chen, W. A novel hybrid model based on recurrent neural networks for stock market timing. Soft Comput. 2020, 24, 15273–15290. [Google Scholar] [CrossRef]
- Song, Y.; Lee, J.W.; Lee, J. A study on novel filtering and relationship between input-features and target-vectors in a deep learning model for stock price prediction. Appl. Intell. 2019, 49, 897–911. [Google Scholar] [CrossRef]
- Ojo, S.O.; Owolawi, P.A.; Mphahlele, M.; Adisa, J.A. Stock Market Behaviour Prediction using Stacked LSTM Networks. Proceeding of the 2019 International Multidisciplinary Information Technology and Engineering Conference (IMITEC), Vanderbijlpark, South Africa, 21–22 November 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Li, X.D.; Xie, H.R.; Wang, R.; Cai, Y.; Cao, J.J.; Wang, F.; Min, H.Q.; Deng, X.T. Empirical analysis: Stock market prediction via extreme learning machine. Neural Comput. Appl. 2016, 27, 67–68. [Google Scholar] [CrossRef]
- Dash, R.; Dash, P.K. Efficient stock price prediction using a self evolving recurrent neuro-fuzzy inference system optimized through a modified differential harmony search technique. Expert Syst. Appl. 2016, 52, 75–90. [Google Scholar] [CrossRef]
- Kalra, S.; Prasad, J.S. Efficacy of news sentiment for stock market prediction. Proceeding of the 2019 International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon), Faridabad, India, 14–16 February 2019; pp. 491–496. [Google Scholar] [CrossRef]
- Lim, M.W.; Yeo, C.K. Harvesting social media sentiments for stock index prediction. Proceeding of the 2020 IEEE 17th Annual Consumer Communications & Networking Conference (CCNC), Las Vegas, NV, USA, 10–13 January 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Mohanty, D.K.; Parida, A.K.; Khuntia, S.S. Financial market prediction under deep learning framework using auto encoder and kernel extreme learning machine. Appl. Soft Comput. 2021, 99, 106898. [Google Scholar] [CrossRef]
- Mahmoud, R.A.; Hajj, H.; Karameh, F.N. A systematic approach to multi-task learning from time-series data. Appl. Soft Comput. 2020, 96, 106586. [Google Scholar] [CrossRef]
- Gao, P.X. Facial age estimation using clustered multi-task support vector regression machine. Proceeding of the 21st International Conference on Pattern Recognition (ICPR2012), Tsukuba, Japan, 11–15 November 2012; pp. 541–544. Available online: https://ieeexplore.ieee.org/document/6460191 (accessed on 29 April 2022).
- Li, Y.; Tian, X.M.; Song, M.L.; Tao, D.C. Multi-task proximal support vector machine. Pattern Recognit. 2015, 48, 3249–3257. [Google Scholar] [CrossRef]
- Xu, S.; An, X.; Qiao, X.D.; Zhu, L.J. Multi-task least-squares support vector machines. Multimed. Tools Appl. 2014, 71, 699–715. [Google Scholar] [CrossRef]
- Anand, P.; Rastogi, R.; Chandra, S. A class of new support vector regression models. Appl. Soft Comput. 2020, 94, 106446. [Google Scholar] [CrossRef]
- Hong, X.; Mitchell, R.; Fatta, G.D. Simplex basis function based sparse least squares support vector regression. Neurocomputing. 2019, 330, 394–402. [Google Scholar] [CrossRef] [Green Version]
- Choudhary, R.; Ahuja, K. Stability analysis of Bilinear Iterative Rational Krylov algorithm. Linear Algebra Its Appl. 2018, 538, 56–88. [Google Scholar] [CrossRef] [Green Version]
- Samar, M.; Farooq, A.; Li, H.Y.; Mu, C.L. Sensitivity analysis for the generalized Cholesky factorization. Appl. Math. Comput. 2019, 362, 124556. [Google Scholar] [CrossRef]
- Xue, Y.T.; Zhang, L.; Wang, B.J.; Zhang, Z.; Li, F.Z. Nonlinear feature selection using Gaussian kernel SVM-RFE for fault diagnosis. Appl. Intell. 2018, 48, 3306–3331. [Google Scholar] [CrossRef]
- Xu, Y.T.; Li, X.Y.; Pan, X.L.; Yang, Z.J. Asymmetric ν-twin support vector regression. Neural Comput. Appl. 2018, 30, 3799–3814. [Google Scholar] [CrossRef]
- Wang, E.; Wang, Z.Y.; Wu, Q. One novel class of Bézier smooth semi-supervised support vector machines for classification. Neural Comput. Appl. 2021, 33, 9975–9991. [Google Scholar] [CrossRef]
- Qin, W.T.; Tang, J.; Lu, C.; Lao, S.Y. A typhoon trajectory prediction model based on multimodal and multitask learning. Appl. Soft Comput. 2022, 122, 108804. [Google Scholar] [CrossRef]

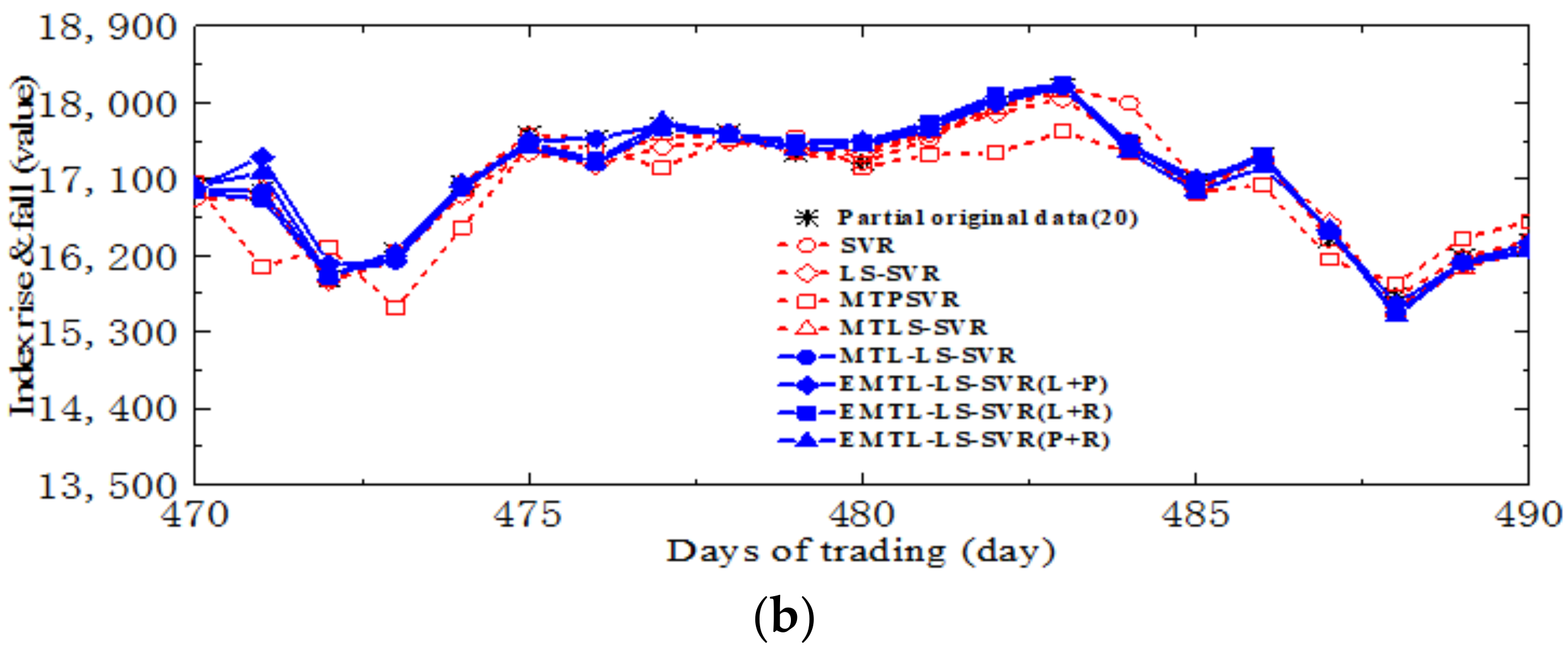
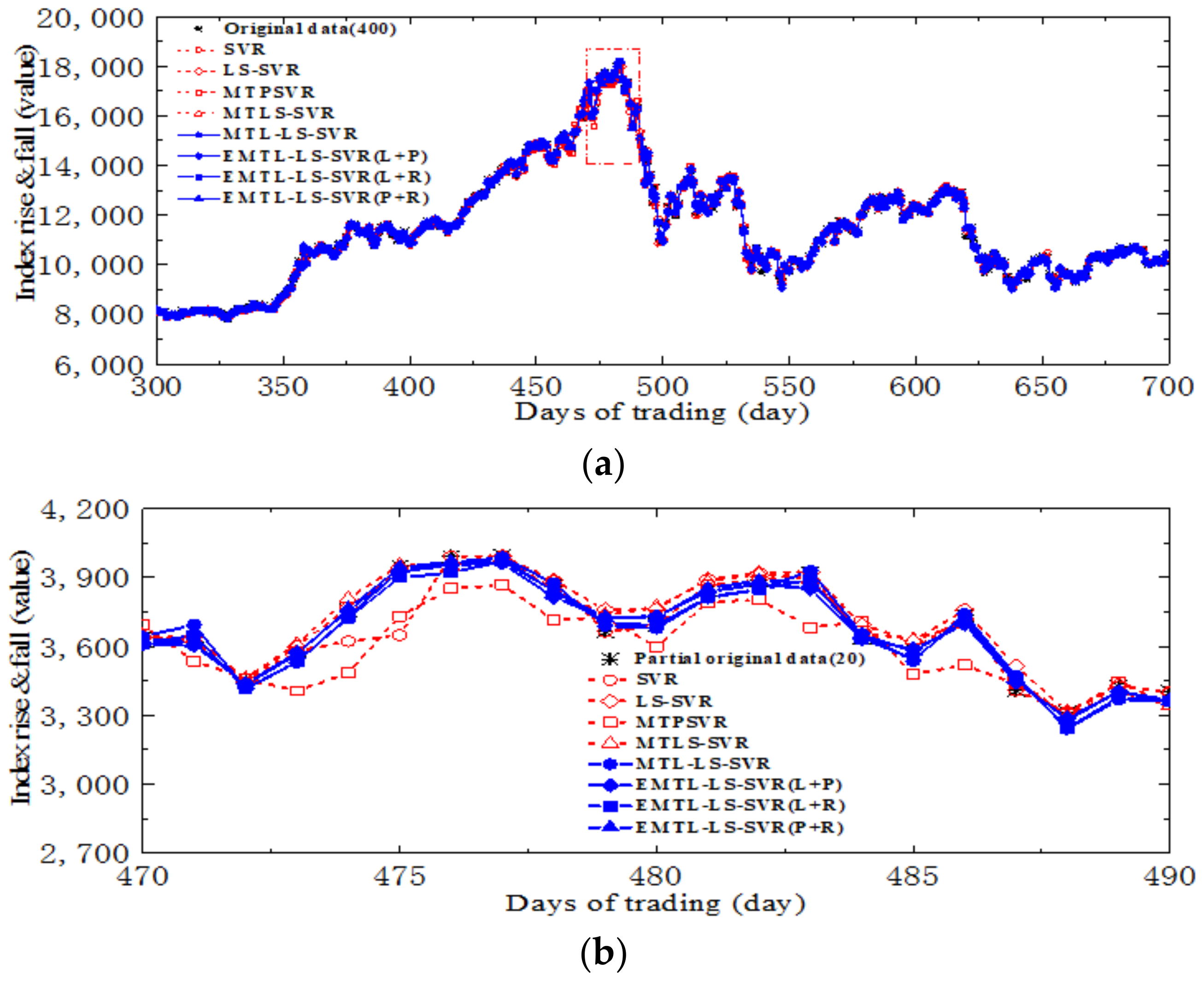


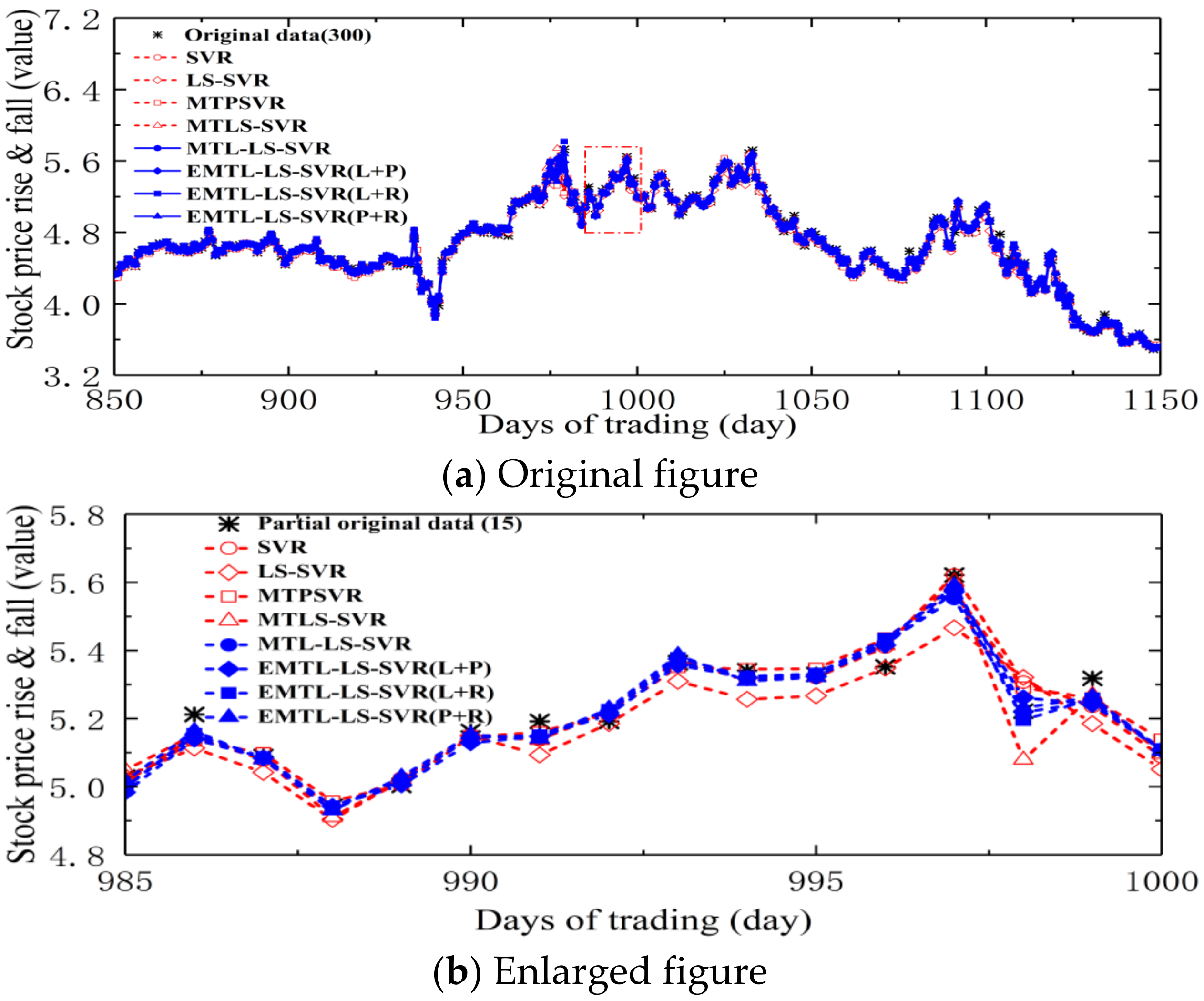

| Stock Index | Algorithm | MAE | RMSE | SSE/SST | SSR/SST | (C,σ,λ,d) |
|---|---|---|---|---|---|---|
| SSEC | SVR | 8.7363 ± 0.6100 | 15.0791 ± 2.9735 | 0.0007 ± 0.0003 | 0.9992 ± 0.0041 | (55,3.85,~,~) |
| LS-SVR | 9.8034 ± 0.9884 | 17.1879 ± 3.0598 | 0.0008 ± 0.0003 | 0.9961 ± 0.0064 | (100,1.85,~,~) | |
| MTPSVR | 10.299 ± 1.7081 | 18.9993 ± 2.9656 | 0.0010 ± 0.0003 | 0.9990 ± 0.0090 | (80,3.45,0.21,~) | |
| MTLS-SVR | 9.083 ± 1.8565 | 16.5463 ± 3.6839 | 0.0008 ± 0.0004 | 1.0038 ± 0.0070 | (70,2.65,1.26,~) | |
| MTL-LS-SVR | 7.0850 ± 1.2081 | 12.1375 ± 2.9656 | 0.0005 ± 0.0003 | 1.0134 ± 0.0090 | (100,2.25,0.11,~) | |
| EMTL-LS-SVR(L + P) | 8.7002 ± 1.8565 | 13.1821 ± 3.6839 | 0.0006 ± 0.0004 | 1.0180 ± 0.0070 | (85,~,1.81,2) | |
| EMTL-LS-SVR(L + R) | 8.2580 ± 0.9870 | 14.5139 ± 2.2211 | 0.0006 ± 0.0002 | 1.0152 ± 0.0067 | (95,2.65,1.31,~) | |
| EMTL-LS-SVR(P + R) | 7.9055 ± 1.4195 | 12.1985 ± 3.3330 | 0.0004 ± 0.0003 | 1.0147 ± 0.0065 | (100,1.85,0.86,2) | |
| SZI | SVR | 34.307 ± 3.2894 | 60.0911 ± 10.263 | 0.0010 ± 0.0003 | 1.0027 ± 0.0070 | (55,3.85,~,~) |
| LS-SVR | 39.772 ± 4.1398 | 65.2855 ± 10.649 | 0.0012 ± 0.0004 | 0.9983 ± 0.0066 | (85,0.65,~,~) | |
| MTPSVR | 41.355 ± 7.7932 | 70.3547 ± 14.535 | 0.0013 ± 0.0005 | 1.0042 ± 0.0101 | (80,3.45,0.21,~) | |
| MTLS-SVR | 35.049 ± 4.8879 | 58.0722 ± 7.9587 | 0.0010 ± 0.0002 | 1.0010 ± 0.0102 | (70,2.65,1.26,~) | |
| MTL-LS-SVR | 30.323 ± 7.7932 | 47.9612 ± 14.535 | 0.0008 ± 0.0005 | 1.0238 ± 0.0101 | (100,2.25,0.11,~) | |
| EMTL-LS-SVR(L + P) | 31.789 ± 4.8879 | 48.0880 ± 7.9587 | 0.0006 ± 0.0002 | 1.0305 ± 0.0102 | (85,~,1.81,2) | |
| EMTL-LS-SVR(L + R) | 31.278 ± 3.6882 | 50.9115 ± 6.5526 | 0.0007 ± 0.0002 | 1.0134 ± 0.0060 | (95,2.65,1.31,~) | |
| EMTL-LS-SVR(P + R) | 34.269 ± 6.7111 | 57.4735 ± 12.680 | 0.0008 ± 0.0005 | 1.0268 ± 0.0096 | (100,1.85,0.86,2) | |
| CNT | SVR | 6.6680 ± 0.6043 | 13.3354 ± 2.0972 | 0.0007 ± 0.0002 | 1.0035 ± 0.0081 | (65,3.05,~,~) |
| LS-SVR | 9.6897 ± 0.8728 | 17.6334 ± 2.2048 | 0.0012 ± 0.0003 | 0.9974 ± 0.0139 | (100,1.05,~,~) | |
| MTPSVR | 10.483 ± 1.5874 | 17.1729 ± 2.1407 | 0.0012 ± 0.0003 | 1.0006 ± 0.0088 | (80,3.45,0.21,~) | |
| MTLS-SVR | 9.3258 ± 1.2721 | 15.4848 ± 1.8014 | 0.0010 ± 0.0003 | 0.9985 ± 0.0090 | (70,2.65,1.26,~) | |
| MTL-LS-SVR | 8.8047 ± 1.5874 | 12.9715 ± 2.1407 | 0.0008 ± 0.0003 | 1.0121 ± 0.0088 | (100,2.25,0.11,~) | |
| EMTL-LS-SVR(L + P) | 7.5338 ± 1.2721 | 12.0025 ± 1.8014 | 0.0005 ± 0.0003 | 1.0152 ± 0.0090 | (85,~,1.81,2) | |
| EMTL-LS-SVR(L + R) | 7.6653 ± 0.7791 | 13.2993 ± 1.3632 | 0.0007 ± 0.0002 | 1.0170 ± 0.0095 | (95,2.65,1.31,~) | |
| EMTL-LS-SVR(P + R) | 8.1940 ± 1.8366 | 12.9907 ± 2.5260 | 0.0008 ± 0.0003 | 1.0162 ± 0.0110 | (100,1.85,0.86,2) | |
| SZSMEPI | SVR | 24.642 ± 1.6220 | 42.3225 ± 5.7639 | 0.0010 ± 0.0002 | 1.0015 ± 0.0058 | (80,1.45,~,~) |
| LS-SVR | 26.818 ± 1.7986 | 42.5460 ± 5.2053 | 0.0011 ± 0.0002 | 0.9979 ± 0.0068 | (100,0.95,~,~) | |
| MTPSVR | 28.393 ± 4.8609 | 47.7573 ± 10.486 | 0.0013 ± 0.0006 | 0.9975 ± 0.0100 | (80,3.45,0.21,~) | |
| MTLS-SVR | 25.043 ± 3.2029 | 42.4982 ± 7.4606 | 0.0011 ± 0.0003 | 1.0019 ± 0.0052 | (70,2.65,1.26,~) | |
| MTL-LS-SVR | 19.548 ± 2.3609 | 30.7638 ± 10.486 | 0.0006 ± 0.0006 | 1.0170 ± 0.0100 | (100,2.25,0.11,~) | |
| EMTL-LS-SVR(L + P) | 20.723 ± 3.2029 | 35.2842 ± 7.4606 | 0.0006 ± 0.0003 | 1.0105 ± 0.0052 | (85,~,1.81,2) | |
| EMTL-LS-SVR(L + R) | 22.228 ± 1.6492 | 34.3454 ± 3.9592 | 0.0007 ± 0.0001 | 1.0146 ± 0.0062 | (95,2.65,1.31,~) | |
| EMTL-LS-SVR(P + R) | 20.014 ± 4.2357 | 32.6555 ± 8.3170 | 0.0007 ± 0.0004 | 1.0157 ± 0.0071 | (100,1.85,0.86,2) |
| Bank Stock Price | Algorithm | MAE | RMSE | SSE/SST | SSR/SST | (C,σ,λ,d) |
|---|---|---|---|---|---|---|
| ICBC | SVR | 0.0144 ± 0.0012 | 0.0245 ± 0.0049 | 0.0008 ± 0.0003 | 0.9980 ± 0.0050 | (80,2.25,~,~) |
| LS-SVR | 0.0196 ± 0.0015 | 0.0276 ± 0.0070 | 0.0010 ± 0.0005 | 0.9968 ± 0.0070 | (70,0.65,~,~) | |
| MTPSVR | 0.0252 ± 0.0025 | 0.0263 ± 0.0060 | 0.0011 ± 0.0005 | 0.9939 ± 0.0124 | (75,2.25,0.06,~) | |
| MTLS-SVR | 0.0263 ± 0.0032 | 0.0278 ± 0.0075 | 0.0010 ± 0.0008 | 0.9978 ± 0.0157 | (75,3.05,1.81,~) | |
| MTL-LS-SVR | 0.0145 ± 0.0025 | 0.0220 ± 0.0060 | 0.0006 ± 0.0005 | 1.0109 ± 0.0124 | (90,3.45,0.91,~) | |
| EMTL-LS-SVR(L + P) | 0.0164 ± 0.0032 | 0.0230 ± 0.0075 | 0.0007 ± 0.0008 | 1.0487 ± 0.0157 | (100,~,1.61,2) | |
| EMTL-LS-SVR(L + R) | 0.0156 ± 0.0037 | 0.0232 ± 0.0092 | 0.0006 ± 0.0008 | 1.0088 ± 0.0115 | (100,1.45,1.41,~) | |
| EMTL-LS-SVR(P + R) | 0.0143 ± 0.0012 | 0.0203 ± 0.0063 | 0.0005 ± 0.0005 | 1.0146 ± 0.0086 | (85,1.45,0.46,2) | |
| ABC | SVR | 0.0098 ± 0.0009 | 0.0171 ± 0.0033 | 0.0013 ± 0.0005 | 0.9989 ± 0.0032 | (50,3.45,~,~) |
| LS-SVR | 0.0110 ± 0.0008 | 0.0184 ± 0.0027 | 0.0015 ± 0.0004 | 0.9964 ± 0.0046 | (90,1.45,~,~) | |
| MTPSVR | 0.0137 ± 0.0021 | 0.0211 ± 0.0040 | 0.0019 ± 0.0007 | 1.0038 ± 0.0216 | (75,2.25,0.06,~) | |
| MTLS-SVR | 0.0124 ± 0.0019 | 0.0216 ± 0.0062 | 0.0021 ± 0.0014 | 0.9975 ± 0.0101 | (75,3.05,1.81,~) | |
| MTL-LS-SVR | 0.0100 ± 0.0021 | 0.0150 ± 0.0040 | 0.0010 ± 0.0007 | 1.0505 ± 0.0216 | (90,3.45,0.91,~) | |
| EMTL-LS-SVR(L + P) | 0.0101 ± 0.0019 | 0.0147 ± 0.0028 | 0.0008 ± 0.0005 | 1.0141 ± 0.0101 | (100,~,1.61,2) | |
| EMTL-LS-SVR(L + R) | 0.0105 ± 0.0015 | 0.0167 ± 0.0034 | 0.0011 ± 0.0006 | 1.0130 ± 0.0117 | (100,1.45,1.41,~) | |
| EMTL-LS-SVR(P + R) | 0.0096 ± 0.0009 | 0.0149 ± 0.0033 | 0.0009 ± 0.0006 | 1.0253 ± 0.0111 | (85,1.45,0.46,2) | |
| BOC | SVR | 0.0120 ± 0.0013 | 0.0250 ± 0.0055 | 0.0019 ± 0.0008 | 0.9998 ± 0.0084 | (70,3.85,~,~) |
| LS-SVR | 0.0134 ± 0.0015 | 0.0262 ± 0.0056 | 0.0021 ± 0.0009 | 0.9973 ± 0.0069 | (95,2.25,~,~) | |
| MTPSVR | 0.0164 ± 0.0030 | 0.0278 ± 0.0061 | 0.0024 ± 0.0010 | 0.9991 ± 0.0210 | (75,2.25,0.06,~) | |
| MTLS-SVR | 0.0153 ± 0.0019 | 0.0272 ± 0.0060 | 0.0025 ± 0.0011 | 0.9971 ± 0.0122 | (75,3.05,1.81,~) | |
| MTL-LS-SVR | 0.0128 ± 0.0030 | 0.0189 ± 0.0061 | 0.0011 ± 0.0010 | 1.0424 ± 0.0210 | (90,3.45,0.91,~) | |
| EMTL-LS-SVR(L + P) | 0.0113 ± 0.0019 | 0.0177 ± 0.0060 | 0.0009 ± 0.0011 | 1.0209 ± 0.0122 | (100,~,1.61,2) | |
| EMTL-LS-SVR(L + R) | 0.0118 ± 0.0021 | 0.0190 ± 0.0070 | 0.0010 ± 0.0012 | 1.0159 ± 0.0176 | (100,1.45,1.41,~) | |
| EMTL-LS-SVR(P + R) | 0.0118 ± 0.0015 | 0.0182 ± 0.0062 | 0.0010 ± 0.0011 | 1.0433 ± 0.0162 | (85,1.45,0.46,2) | |
| CCB | SVR | 0.0203 ± 0.0018 | 0.0376 ± 0.0055 | 0.0010 ± 0.0003 | 0.9979 ± 0.0042 | (50,3.85,~,~) |
| LS-SVR | 0.0264 ± 0.0014 | 0.0510 ± 0.0048 | 0.0016 ± 0.0003 | 0.9946 ± 0.0048 | (85,0.65,~,~) | |
| MTPSVR | 0.0238 ± 0.0056 | 0.0432 ± 0.0070 | 0.0013 ± 0.0004 | 0.9956 ± 0.0246 | (75,2.25,0.06,~) | |
| MTLS-SVR | 0.0245 ± 0.0073 | 0.0509 ± 0.0142 | 0.0015 ± 0.0011 | 0.9961 ± 0.0133 | (75,3.05,1.81,~) | |
| MTL-LS-SVR | 0.0208 ± 0.0056 | 0.0327 ± 0.0070 | 0.0007 ± 0.0004 | 1.0558 ± 0.0246 | (90,3.45,0.91,~) | |
| EMTL-LS-SVR(L + P) | 0.0224 ± 0.0073 | 0.0330 ± 0.0142 | 0.0007 ± 0.0011 | 1.0134 ± 0.0133 | (100,~,1.61,2) | |
| EMTL-LS-SVR(L + R) | 0.0225 ± 0.0031 | 0.0374 ± 0.0055 | 0.0009 ± 0.0003 | 1.0098 ± 0.0121 | (100,1.45,1.41,~) | |
| EMTL-LS-SVR(P + R) | 0.0208 ± 0.0024 | 0.0316 ± 0.0046 | 0.0006 ± 0.0005 | 1.0118 ± 0.0097 | (85,1.45,0.46,2) | |
| BCM | SVR | 0.0204 ± 0.0021 | 0.0430 ± 0.0069 | 0.0021 ± 0.0006 | 0.9970 ± 0.0162 | (80,2.85,~,~) |
| LS-SVR | 0.0245 ± 0.0025 | 0.0483 ± 0.0067 | 0.0027 ± 0.0007 | 0.9924 ± 0.0154 | (75,1.85,~,~) | |
| MTPSVR | 0.0278 ± 0.0028 | 0.0565 ± 0.0082 | 0.0031 ± 0.0008 | 0.9916 ± 0.0205 | (75,2.25,0.06,~) | |
| MTLS-SVR | 0.0259 ± 0.0039 | 0.0418 ± 0.0121 | 0.0025 ± 0.0013 | 0.9996 ± 0.0163 | (75,3.05,1.81,~) | |
| MTL-LS-SVR | 0.0203 ± 0.0028 | 0.0333 ± 0.0082 | 0.0011 ± 0.0008 | 1.0370 ± 0.0205 | (90,3.45,0.91,~) | |
| EMTL-LS-SVR(L + P) | 0.0220 ± 0.0039 | 0.0352 ± 0.0121 | 0.0014 ± 0.0013 | 1.0404 ± 0.0163 | (100,~,1.61,2) | |
| EMTL-LS-SVR(L + R) | 0.0195 ± 0.0053 | 0.0308 ± 0.0103 | 0.0013 ± 0.0010 | 1.0270 ± 0.0187 | (100,1.45,1.41,~) | |
| EMTL-LS-SVR(P + R) | 0.0191 ± 0.0022 | 0.0278 ± 0.0089 | 0.0012 ± 0.0008 | 1.0242 ± 0.0138 | (85,1.45,0.46,2) |
| Algorithm | Metric | SSEC | SZI | CNT | SZSMEPI | ICBC | ABC | BOC | CCB | BCM | p-Value |
|---|---|---|---|---|---|---|---|---|---|---|---|
| SVR | MAE | 5 | 5 | 1 | 5 | 2 | 2 | 4 | 1 | 4 | 3.222 |
| RMSE | 5 | 6 | 5 | 5 | 5 | 5 | 5 | 5 | 6 | 5.222 | |
| LS-SVR | MAE | 7 | 7 | 7 | 7 | 6 | 6 | 6 | 8 | 6 | 6.667 |
| RMSE | 7 | 7 | 8 | 7 | 7 | 6 | 6 | 8 | 7 | 7 | |
| MTPSVR | MAE | 8 | 8 | 8 | 8 | 7 | 8 | 8 | 6 | 8 | 7.667 |
| RMSE | 8 | 8 | 7 | 8 | 6 | 7 | 8 | 6 | 8 | 7.333 | |
| MTLS-SVR | MAE | 6 | 6 | 6 | 6 | 8 | 7 | 7 | 7 | 7 | 6.667 |
| RMSE | 6 | 5 | 6 | 6 | 8 | 8 | 7 | 7 | 5 | 6.444 | |
| MTL-LS-SVR | MAE | 4 | 3 | 2 | 3 | 5 | 4 | 1 | 4 | 5 | 3.444 |
| RMSE | 3 | 2 | 1 | 4 | 3 | 1 | 1 | 3 | 4 | 2.444 | |
| EMTL-LS-SVR(L + P) | MAE | 3 | 2 | 3 | 4 | 4 | 5 | 3 | 5 | 2 | 3.444 |
| RMSE | 4 | 3 | 4 | 3 | 4 | 4 | 4 | 4 | 2 | 3.556 | |
| EMTL-LS-SVR(L + R) | MAE | 2 | 4 | 4 | 2 | 1 | 1 | 2 | 2 | 1 | 2.111 |
| RMSE | 2 | 4 | 3 | 2 | 1 | 2 | 2 | 1 | 1 | 2 | |
| EMTL-LS-SVR(P + R) | MAE | 1 | 1 | 5 | 1 | 3 | 3 | 5 | 3 | 3 | 2.778 |
| RMSE | 1 | 1 | 2 | 1 | 2 | 3 | 3 | 2 | 3 | 2 |
| Title 1 | MAE | Tag | RMSE | Tag |
|---|---|---|---|---|
| SVR | 1.111 | 0 | 3.222 | 1 * |
| LS-SVR | 4.556 | 1 ** | 5 | 1 *** |
| MTPSVR | 5.556 | 1 *** | 5.333 | 1 *** |
| MTLS-SVR | 4.556 | 1 ** | 4.444 | 1 ** |
| MTL-LS-SVR | 1.333 | 0 | 0.444 | 0 |
| EMTL-LS-SVR(L + P) | 1.333 | 0 | 1.556 | 0 |
| EMTL-LS-SVR(P + R) | 0.667 | 0 | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.-C.; Wu, Q.; Li, F.-Y.; Li, H. Multitask Learning Based on Least Squares Support Vector Regression for Stock Forecast. Axioms 2022, 11, 292. https://doi.org/10.3390/axioms11060292
Zhang H-C, Wu Q, Li F-Y, Li H. Multitask Learning Based on Least Squares Support Vector Regression for Stock Forecast. Axioms. 2022; 11(6):292. https://doi.org/10.3390/axioms11060292
Chicago/Turabian StyleZhang, Heng-Chang, Qing Wu, Fei-Yan Li, and Hong Li. 2022. "Multitask Learning Based on Least Squares Support Vector Regression for Stock Forecast" Axioms 11, no. 6: 292. https://doi.org/10.3390/axioms11060292
APA StyleZhang, H.-C., Wu, Q., Li, F.-Y., & Li, H. (2022). Multitask Learning Based on Least Squares Support Vector Regression for Stock Forecast. Axioms, 11(6), 292. https://doi.org/10.3390/axioms11060292






