Super Connected Direct Product of Graphs and Cycles
Abstract
1. Introduction
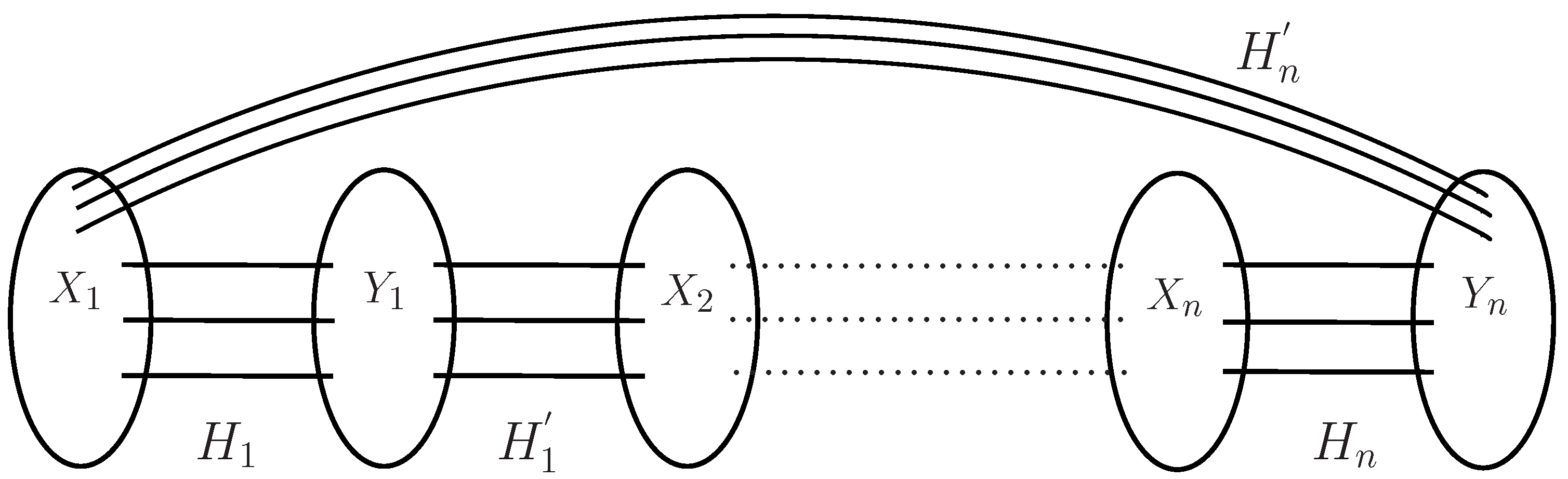
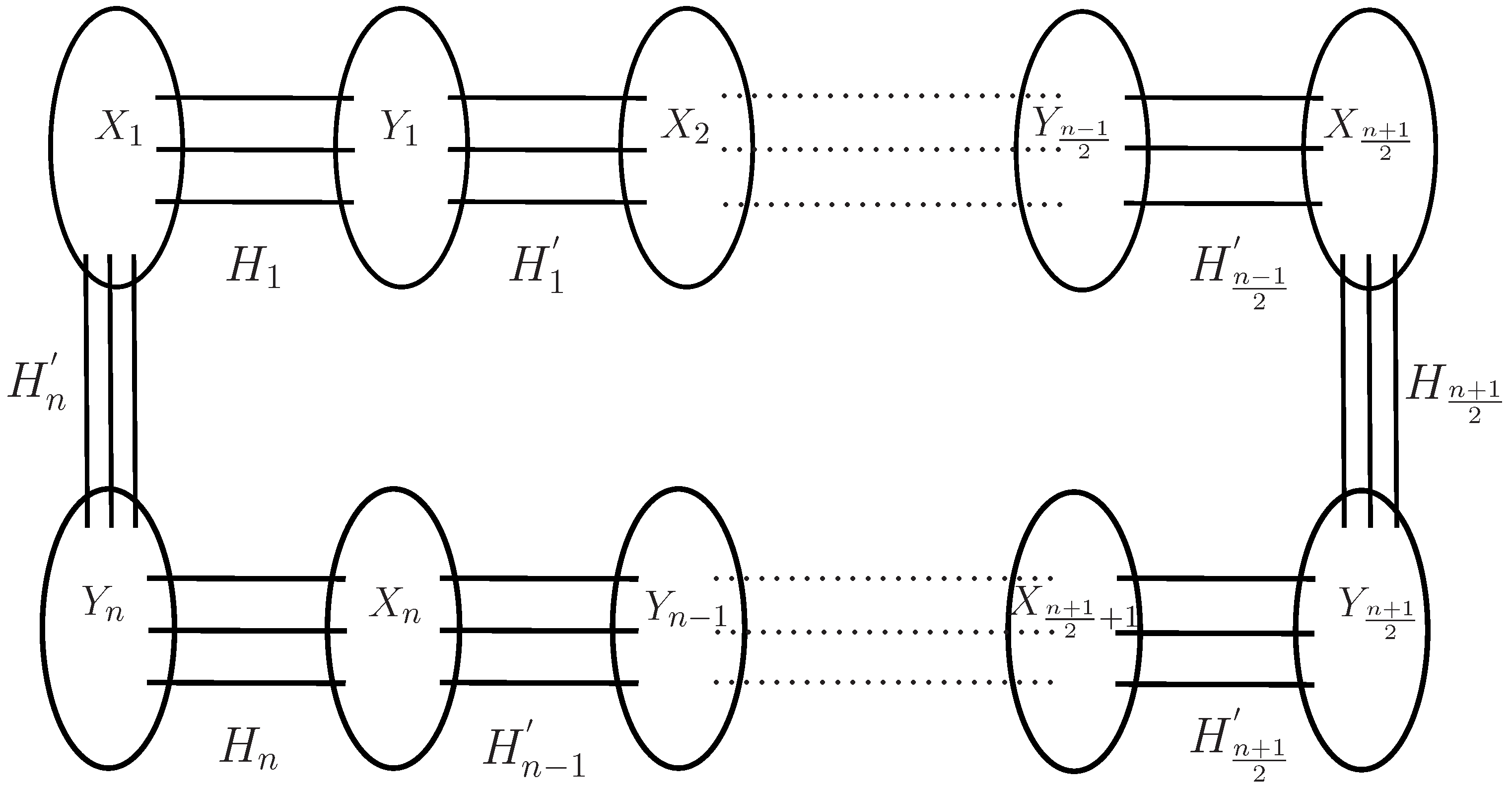
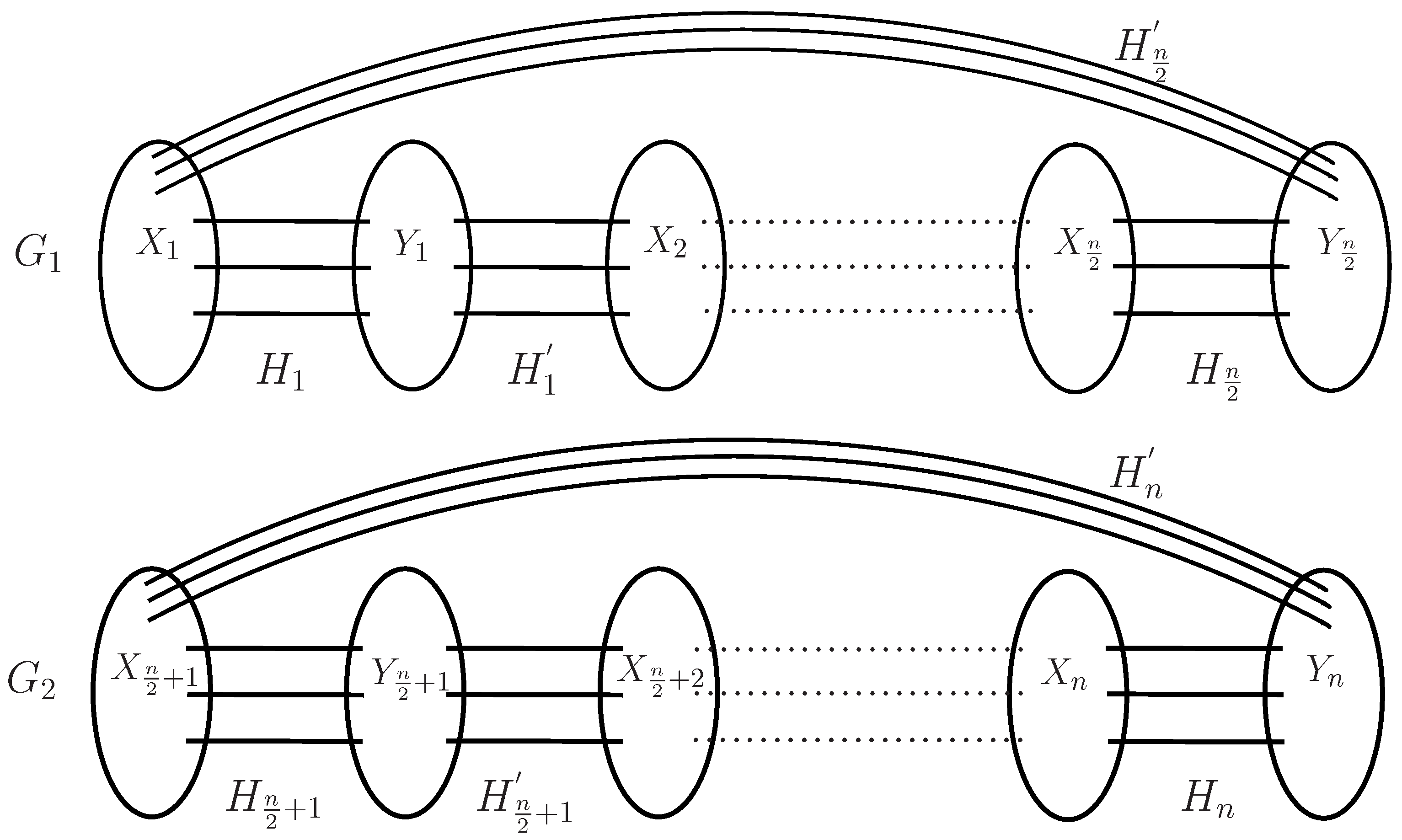
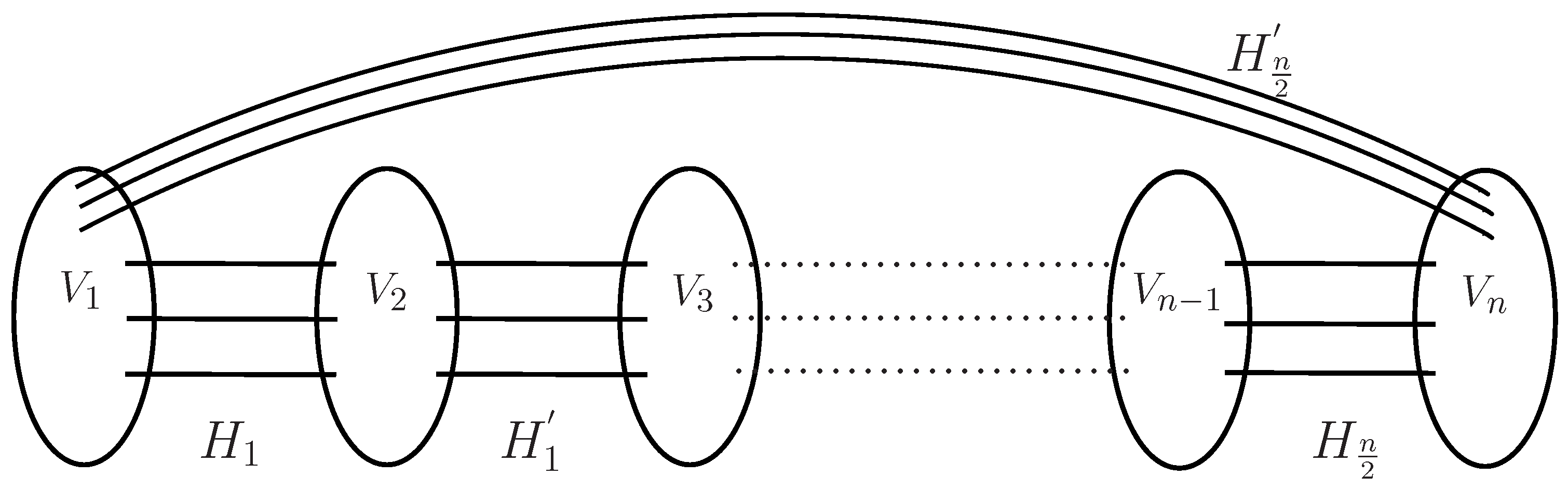
2. A Key Lemma
3. Main Results
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bondy, J.A.; Murty, U.S.R. Graph Theory, Graduate Texts in Mathematics 244; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Boesch, F. On unreliability polynomials and graph connectivity in reliable network synthesis. J. Graph Theory 1986, 10, 339–352. [Google Scholar] [CrossRef]
- Weichsel, P.M. The Kronecker product of graphs. Proc. Am. Math. Soc. 1962, 13, 47–52. [Google Scholar] [CrossRef]
- Brešar, B.; Špacapan, S. On the connectivity of the direct product of graphs. Australas. J. Combin. 2008, 41, 45–56. [Google Scholar]
- Cao, X.; Brglez, Š.; Špacapan, S.; Vumar, E. On edge connectivity of direct products of graphs. Inform. Process. Lett. 2011, 18, 899–902. [Google Scholar] [CrossRef]
- Špacapan, S. A characterization of the edge connectivity of direct products of graphs. Discrete Math. 2013, 313, 1385–1393. [Google Scholar] [CrossRef]
- Mamut, A.; Vumar, E. Vertex vulnerability parameters of Kronecker product of complete graphs. Inform. Process. Lett. 2008, 106, 258–262. [Google Scholar] [CrossRef]
- Guji, R.; Vumar, E. A note on the connectivity of Kronecker products of graphs. Appl. Math. Lett. 2009, 22, 1360–1363. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, B. Proof of a conjecture on connectivity of Kronecker product of graphs. Discrete Math. 2011, 311, 2563–2565. [Google Scholar] [CrossRef]
- Wang, W.; Xue, N. Connectivity of direct products of graphs. Ars Combin. 2011, 100, 107–111. [Google Scholar]
- Wang, W.; Yan, Z. Connectivity of Kronecker products by K2. Appl. Math. Lett. 2012, 25, 172–174. [Google Scholar] [CrossRef]
- Sonawane, A.V.; Borse, Y.M. Connectivity of the Tensor product of graphs and cycles. J. Ramanujan Math. Soc. 2021, 36, 325–330. [Google Scholar]
- Guo, L.; Qin, C.; Guo, X. Super connectivity of Kronecker product of graphs. Inform. Process. Lett. 2010, 110, 659–661. [Google Scholar] [CrossRef]
- Wang, H.; Shan, E.; Wang, W. On the super connectivity of Kronecker product of graphs. Inform. Process. Lett. 2012, 112, 402–405. [Google Scholar] [CrossRef][Green Version]
- Zhou, J. Super connectivity of Direct product of graphs. Ars Math. Contemp. 2014, 8, 235–244. [Google Scholar] [CrossRef]
- Wu, L.; Tian, Y. The super connectedness of Kronecker product graphs of paths, cycles and cycles. J. Xinjiang Univ. 2022, 39, 176–181. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, J.; Tian, Y. Super Connected Direct Product of Graphs and Cycles. Axioms 2022, 11, 277. https://doi.org/10.3390/axioms11060277
Yin J, Tian Y. Super Connected Direct Product of Graphs and Cycles. Axioms. 2022; 11(6):277. https://doi.org/10.3390/axioms11060277
Chicago/Turabian StyleYin, Jiaqiong, and Yingzhi Tian. 2022. "Super Connected Direct Product of Graphs and Cycles" Axioms 11, no. 6: 277. https://doi.org/10.3390/axioms11060277
APA StyleYin, J., & Tian, Y. (2022). Super Connected Direct Product of Graphs and Cycles. Axioms, 11(6), 277. https://doi.org/10.3390/axioms11060277




