Bounds for Quotients of Inverse Trigonometric and Inverse Hyperbolic Functions

Abstract

We establish new simple bounds for the quotients of inverse trigonometric and inverse hyperbolic functions such as $\frac{{sin}^{-1}x}{{sinh}^{-1}x}$ and $\frac{{tanh}^{-1}x}{{tan}^{-1}x}$. The main results provide polynomial bounds using even quadratic functions and exponential bounds under the form $e^{a{x}^2}.$ Graph validation is also performed.

1. Introduction

As discussed in [1], functions whose graphs are similar to bell-shaped curves should be studied, and one of the aspects is to investigate the bounds of such functions. For the bounds of this type of functions involving inverse trigonometric and inverse hyperbolic functions, we refer the reader to [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20] and references therein. Chesneau and Bagul [1] investigated the sharp bounds for ratio functions $\frac{cosx}{coshx}$ and $\frac{sinx}{sinhx}$. These inequalities were carefully studied and generalized by Kostić et al. [21] to get several types of bounds using infinite products.

Recently, Bagul et al. [22] corroborated the following double inequalities involving exponential bounds.

Proposition 1

([22] Proposition 1). For $x\in [0,\alpha ],$ where $\alpha \in \left(0,\frac{\pi }{2}\right)$, the inequalities

$$\begin{array}{c}\hfill e^{-a_1{x}^2}\le \frac{cosx}{coshx}\le e^{-a_2{x}^2}\end{array}$$

(1)

hold with the best possible constants $a_1={\alpha }^{-2}ln\left(\frac{cosh\alpha }{cos\alpha }\right)$ and $a_2=1.$

Proposition 2

([22] Proposition 2). For $x\in \left(0,\frac{\pi }{2}\right),$ the inequalities

$$\begin{array}{c}\hfill e^{-b_1{x}^2}<\frac{sinx}{sinhx}<e^{-b_2{x}^2}\end{array}$$

(2)

hold with the best possible constants $b_1=4{\pi }^{-2}ln\left[sinh\left(\frac{\pi }{2}\right)\right]\approx 0.337794$ and $b_2=\frac{1}{3}.$

Proposition 3

([22] Proposition 4). For $x\in (0,\alpha ],$ where $\alpha \in \left(0,\frac{\pi }{2}\right),$ the inequalities

$$\begin{array}{c}\hfill e^{-c_1{x}^2}<\frac{tanhx}{tanx}<e^{-c_2{x}^2}\end{array}$$

(3)

hold with the best possible constants $c_1={\alpha }^{-2}ln\left(\frac{tan\alpha }{tanh\alpha }\right)$ and $c_2=\frac{2}{3}.$

We contribute to the subject by establishing polynomial and exponential bounds for the functions $\frac{{sin}^{-1}x}{{sinh}^{-1}x}$ and $\frac{{tanh}^{-1}x}{{tan}^{-1}x}$, which are motivated by these works. In the whole paper, it is to be noted that the superscript “−” for trigonometric and hyperbolic functions is used for their inverses.

2. Main Theorems

2.1. Statements

Our main results are the following theorems.

Theorem 1.

${\eta }_1=\frac{1}{3}$ and ${\eta }_2=\frac{\pi }{ln(3+2\sqrt{2})}-1\approx 0.78221397$ are the best possible constants such that the inequalities

$$\begin{array}{c}\hfill 1+{\eta }_1{x}^2<\frac{{sin}^{-1}x}{{sinh}^{-1}x}<1+{\eta }_2{x}^2;x\in (0,1)\end{array}$$

(4)

hold.

Theorem 2.

If $x\in (0,r)$ and r is any real number in $(0,1)$, then the inequalities

$$\begin{array}{c}\hfill 1+{\theta }_1{x}^2<\frac{{tanh}^{-1}x}{{tan}^{-1}x}<1+{\theta }_2{x}^2\end{array}$$

(5)

hold with the best possible constants ${\theta }_1=\frac{2}{3}$ and ${\theta }_2=\frac{{tanh}^{-1}r-{tan}^{-1}r}{r^2\dot{{tan}^{-1}}r}.$

Theorem 3.

${\mu }_1=\frac{1}{3}$ and ${\mu }_2=ln\left(\frac{\pi }{2{sinh}^{-1}1}\right)\approx 0.57785639$ are the best possible constants such that the inequalities

$$\begin{array}{c}\hfill e^{{\mu }_1{x}^2}<\frac{{sin}^{-1}x}{{sinh}^{-1}x}<e^{{\mu }_2{x}^2};x\in (0,1)\end{array}$$

(6)

hold.

Theorem 4.

If $x\in (0,r)$ and r is any real number in $(0,1)$, then the inequalities

$$\begin{array}{c}\hfill e^{{\nu }_1{x}^2}<\frac{{tanh}^{-1}x}{{tan}^{-1}x}<e^{{\nu }_2{x}^2}\end{array}$$

(7)

hold with the best possible constants ${\nu }_1=\frac{2}{3}$ and ${\nu }_2=\frac{ln\left({tanh}^{-1}r\right)-ln\left({tan}^{-1}r\right)}{r^2}.$

Since ${\eta }_1={\mu }_1$ and ${\theta }_1={\nu }_1,$ by the well-known inequality $1+y\le e^y,$ it is not difficult to see that the lower bounds of (6) and (7) are sharper than those of (4) and (5), respectively.

Corollary 1.

If $x\in (0,1),$ then we have

$$\begin{array}{c}\hfill \frac{{sin}^{-1}x}{{sinh}^{-1}x}<\frac{{tanh}^{-1}x}{{tan}^{-1}x}.\end{array}$$

(8)

2.2. Graphical Illustrations

In this part, we compare the obtained bounds by the means of graphics, with a discussion.

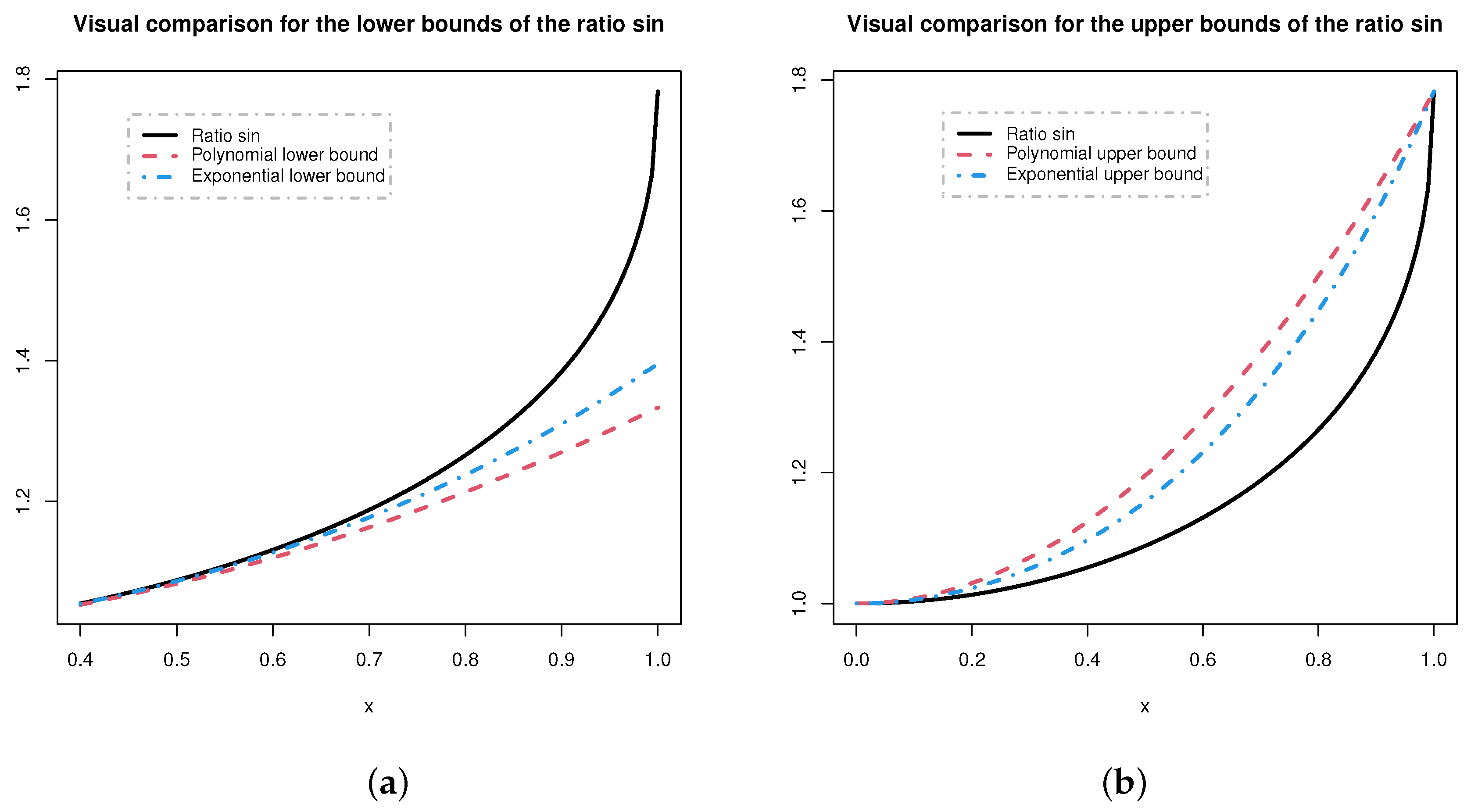
Figure 1 presents the bounds obtained in Theorems 1 and 3 for the “ratio sin” function defined by $\frac{{sin}^{-1}x}{{sinh}^{-1}x}$.

Figure 1. Visual comparison of the bounds for $\frac{{sin}^{-1}x}{{sinh}^{-1}x}$: (a) lower bounds with $x\in [0.4,1]$, and (b) upper bounds for $x\in [0,1]$.

It can be observed that the exponential bounds are sharper.

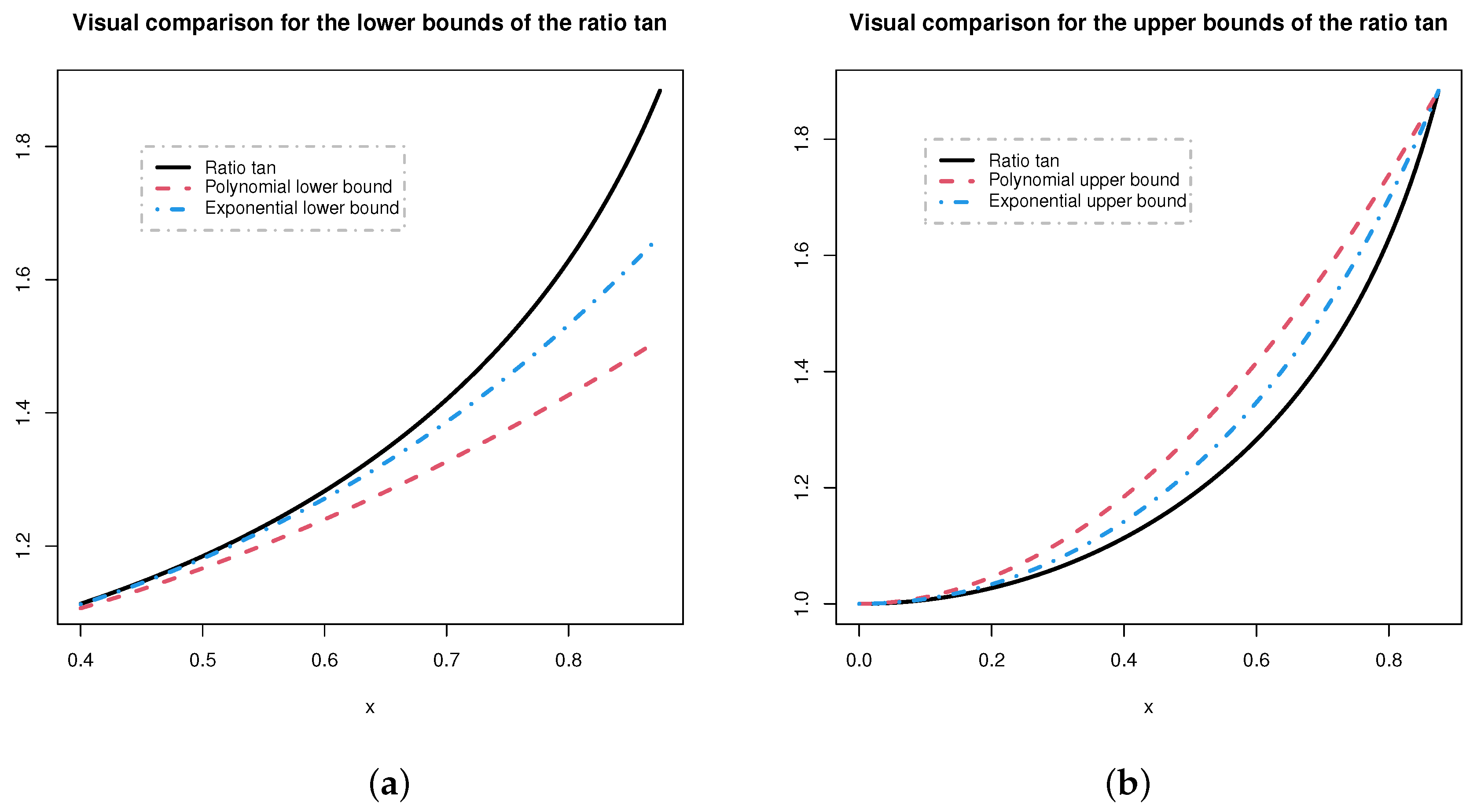
Figure 2 displays the bounds obtained in Theorems 1 and 3 for the “ratio tan” function defined by $\frac{{tanh}^{-1}x}{{tan}^{-1}x}$.

Figure 2. Visual comparison of the bounds for $\frac{{tanh}^{-1}x}{{tan}^{-1}x}$: (a) lower bounds with $x\in [0.4,r]$, and (b) upper bounds for $x\in [0,r]$, with $r=\frac{7}{8}$ (arbitrarily taken into $(0,1)$).

Again, it can be observed that the exponential bounds are sharper.

Thus, the graphical illustrations reveal that the upper bounds of (6) and (7) are sharper than those of (4) and (5), respectively.

We end by illustrating the ratio comparison states in Corollary 1 in Figure 3.

Figure 3. Visual comparison between $\frac{{sin}^{-1}x}{{sinh}^{-1}x}$ and $\frac{{tanh}^{-1}x}{{tan}^{-1}x}$.

3. Auxiliary Results

In order to prove our main results, we need the following lemmas from the existing literature.

Lemma 1

([23] L’Hôpital’s rule of monotonicity). Let $f,g$ be two real-valued functions which are continuous on $[a,b]$ and differentiable on $(a,b)$, where $-\infty <a<b<\infty$ and $g^{\prime }\left(x\right)\ne 0,$ for $\forall x\in (a,b).$ Let,

$$r_1\left(x\right)=\frac{f\left(x\right)-f\left(a\right)}{g\left(x\right)-g\left(a\right)}and{r}_2\left(x\right)=\frac{f\left(x\right)-f\left(b\right)}{g\left(x\right)-g\left(b\right)}.$$

Then,

(i) 

$r_1\left(x\right)$ and $r_2\left(x\right)$ are increasing on $(a,b)$ if $\frac{f^{\prime }}{g^{\prime }}$ is increasing on $(a,b)$; and

(ii) 

$r_1\left(x\right)$ and $r_2\left(x\right)$ are decreasing on $(a,b)$ if $\frac{f^{\prime }}{g^{\prime }}$ is decreasing on $(a,b).$

The strictness of the monotonicity of $r_1\left(x\right)$ and $r_2\left(x\right)$ depends on the strictness of the monotonicity of $\frac{f^{\prime }}{g^{\prime }}.$

Lemma 2

([2] Lemma 2). For $0<\left|x\right|<1,$ we have

$${\left({sin}^{-1}x\right)}^2=\sum _{n=0}^{\infty }\frac{2^{2n+1}·{(n!)}^2}{(2n+2)!}{x}^{2n+2}$$

and

$${\left({sinh}^{-1}x\right)}^2=\sum _{n=0}^{\infty }{(-1)}^n\frac{2^{2n+1}·{(n!)}^2}{(2n+2)!}{x}^{2n+2}.$$

The series for (sin⁻¹ x)² can also be found in [24]. For series expansions of powers of ${sin}^{-1}x$ we refer to [25] and references therein.

We also prove some other lemmas that are required to prove our main results.

Lemma 3.

The following inequality is true.

$$\begin{array}{c}\hfill \frac{{sin}^{-1}x}{x}<\frac{3}{(3+x^2)\sqrt{1-x^2}};x\in (0,1).\end{array}$$

(9)

Proof. 

Let

$$\varphi \left(x\right)=3x-(3+x^2)\sqrt{1-x^2}{sin}^{-1}x;x\in (0,1).$$

Differentiation gives

$$\begin{array}{cc}\hfill {\varphi }^{\prime }\left(x\right)& =3-(3+x^2)-2x\sqrt{1-x^2}{sin}^{-1}x+\frac{x(3+x^2){sin}^{-1}x}{\sqrt{1-x^2}}\hfill \\ \hfill & =\frac{x(3+x^2){sin}^{-1}x-2x(1-x^2){sin}^{-1}x}{\sqrt{1-x^2}}-x^2\hfill \\ \hfill & =\frac{x(1+3x^2){sin}^{-1}x}{\sqrt{1-x^2}}-x^2\hfill \\ \hfill & =x\left[\frac{(1+3x^2){sin}^{-1}x-x\sqrt{1-x^2}}{\sqrt{1-x^2}}\right].\hfill \end{array}$$

Since $\sqrt{1-x^2}<1+3x^2$ and $x<{sin}^{-1}x$, clearly, for $x\in (0,1)$, we get

$$\frac{\sqrt{1-x^2}}{1+3x^2}<1<\frac{{sin}^{-1}x}{x},$$

which results in ${\varphi }^{\prime }\left(x\right)>0.$ So $\varphi \left(x\right)$ is strictly increasing in $(0,1)$ and we have $\varphi \left(x\right)>\varphi \left(0\right)=0.$ □

Note 1.

The inequality (9) is a refinement of the inequality

$$\frac{{sin}^{-1}x}{x}<\frac{1}{\sqrt{1-x^2}};x\in (0,1).$$

See, for instance, [5].

Lemma 4.

For $x\in (0,1),$ the inequality

$$\begin{array}{c}\hfill {\left(\frac{{sinh}^{-1}x}{x}\right)}^2>\sqrt{1-x^2}·\frac{{sin}^{-1}x}{x}\end{array}$$

(10)

is true.

Proof. 

From Theorem 2.2 of [6], we have

$${\left(\frac{{sinh}^{-1}x}{x}\right)}^2>\frac{3}{3+x^2}.$$

Combining this inequality with (1), we get the desired inequality (10). □

Lemma 5.

For $x\in (0,1),$ it holds that

$$\begin{array}{c}\hfill \frac{{sinh}^{-1}x}{\sqrt{1-x^2}}>\frac{{sin}^{-1}x}{\sqrt{1+x^2}}.\end{array}$$

(11)

Proof. 

A combination of inequalities (1.1) of [5] and (1.1) of [6] gives (11). □

Lemma 6.

The inequality

$$\begin{array}{c}\hfill \frac{{tanh}^{-1}x}{{tan}^{-1}x}<\frac{\sqrt{1+x^2}}{\sqrt{1-x^2}}\end{array}$$

(12)

holds in $(0,1).$

Proof. 

From Theorem 4 (inequality (2.12)) of [5], we have

$$\begin{array}{c}\hfill \frac{{tan}^{-1}x}{x}>\frac{1}{\sqrt{1+x^2}};x>0\end{array}$$

(13)

and from Theorem 2.4 (inequality (2.4)) of [6], we have

$$\frac{{tanh}^{-1}x}{x}<\frac{1}{\sqrt[3]{1-x^2}};x\in (0,1).$$

Since $\frac{1}{\sqrt[3]{1-x^2}}<\frac{1}{\sqrt{1-x^2}},$ the above inequality can be written as

$$\begin{array}{c}\hfill \frac{x}{{tanh}^{-1}x}>\sqrt{1-x^2};x\in (0,1).\end{array}$$

(14)

The required inequality (12) follows from inequalities (13) and (14). □

Remark 1.

It is worth noting that an upper bound of $\frac{{tanh}^{-1}x}{{tan}^{-1}x}$ in (12) is sharper than those in (5) and (7) as $r\to 1.$

Lemma 7.

For $x\in (0,1),$ we have

$$\begin{array}{c}\hfill \frac{x}{{tan}^{-1}x}+\frac{x}{{tanh}^{-1}x}<2.\end{array}$$

(15)

Proof. 

By Proposition 3 of [5], we have

$$\frac{x}{{tan}^{-1}x}<1+\frac{x^2}{3};x>0.$$

Similarly, from Theorem 2.3 (inequality (2.3)) of [6], we write

$$\frac{x}{{tanh}^{-1}x}<1-\frac{x^2}{3};x\in (0,1).$$

By simply adding these inequalities we get the required inequality (14). □

4. Proofs of Theorems

Proof of Theorem 1.

Let us set

$${\displaystyle f\left(x\right)=\frac{{sin}^{-1}x-{sinh}^{-1}x}{x^2{sinh}^{-1}x}:=\frac{f_1\left(x\right)}{f_2\left(x\right)},}$$

where $f_1\left(x\right)={sin}^{-1}x-{sinh}^{-1}x$ and $f_2\left(x\right)=x^2{sinh}^{-1}x$ with $f_1\left(0\right)=0$ and $f_2\left(0\right)=0$. By differentiating with respect to x, we obtain

$$\frac{f_1^{\prime }\left(x\right)}{f_2^{\prime }\left(x\right)}=\frac{\frac{1}{\sqrt{1-x^2}}-\frac{1}{\sqrt{1+x^2}}}{2x{sinh}^{-1}x+\frac{x^2}{\sqrt{1+x^2}}}:=\frac{f_3\left(x\right)}{f_4\left(x\right)},$$

where $f_3\left(x\right)=\frac{1}{\sqrt{1-x^2}}-\frac{1}{\sqrt{1+x^2}}$ and $f_4\left(x\right)=2x{sinh}^{-1}x+\frac{x^2}{\sqrt{1+x^2}}$ with $f_3\left(0\right)=0$ and $f_4\left(0\right)=0$. By differentiating again with respect to x, we get

$$\frac{f_3^{\prime }\left(x\right)}{f_4^{\prime }\left(x\right)}=\frac{x\left[{(1-x^2)}^{-3/2}+{(1+x^2)}^{-3/2}\right]}{2{sinh}^{-1}x+\frac{4x}{\sqrt{1+x^2}}-x^3{(1+x^2)}^{-3/2}}:=\frac{f_5\left(x\right)}{f_6\left(x\right)},$$

where $f_5\left(x\right)=x\left[{(1-x^2)}^{-3/2}+{(1+x^2)}^{-3/2}\right]$ and $f_6\left(x\right)=2{sinh}^{-1}x+\frac{4x}{\sqrt{1+x^2}}-x^3{(1+x^2)}^{-3/2}$ with $f_5\left(0\right)=0$ and $f_6\left(0\right)=0$. Then,

$$\begin{array}{cc}\hfill \frac{f_5^{\prime }\left(x\right)}{f_6^{\prime }\left(x\right)}& =\frac{(1+2x^2){\left(\frac{1+x^2}{1-x^2}\right)}^{5/2}+(1-2x^2)}{6+5x^2+2x^4}\hfill \\ \hfill & :=\frac{(1+2x^2)f_7\left(x\right)+(1-2x^2)}{6+5x^2+2x^4}:=f_8\left(x\right),\hfill \end{array}$$

where $f_7\left(x\right)={\left(\frac{1+x^2}{1-x^2}\right)}^{5/2}$ with $f_7^{\prime }\left(x\right)=\frac{10x}{{(1-x^2)}^2}{\left(\frac{1+x^2}{1-x^2}\right)}^{3/2}.$ Now we need to show that $f_8\left(x\right)$ is strictly increasing on $(0,1).$ To demonstrate the required monotonicity of $f_8\left(x\right),$ we must prove that $f_8^{\prime }\left(x\right)>0$. First, we show that the numerator in $f_8^{\prime }\left(x\right)$, say $N_1$, is positive on $(0,1).$ We have

$$\begin{array}{c}\hfill N_1=(6+5x^2+2x^4)\left[(1+2x^2)f_7^{{}^{\prime }}\left(x\right)+4x{f}_7\left(x\right)-4x\right]\\ \hfill -\left[(1+2x^2)f_7\left(x\right)+(1-2x^2)\right](10x+8x^3).\end{array}$$

Simplifying the above expression we get the following

$$\begin{array}{cc}\hfill N_1& =\frac{60x+170x^3+120x^5+40x^7}{{(1-x^2)}^2}{\left(\frac{1+x^2}{1-x^2}\right)}^{3/2}\hfill \\ \hfill & +(14x-8x^3-8x^5){\left(\frac{1+x^2}{1-x^2}\right)}^{5/2}-34x-8x^3+8x^5\hfill \\ \hfill & =\frac{60x+170x^3+120x^5+40x^7+(14x-8x^3-8x^5)(1-x^4)}{{(1-x^2)}^2}{\left(\frac{1+x^2}{1-x^2}\right)}^{3/2}\hfill \\ \hfill & -34x-8x^3+8x^5\hfill \\ \hfill & >\frac{74x+162x^3+98x^5+48x^7+8x^9}{{(1-x^2)}^2}-34x-8x^3+8x^5\hfill \end{array}$$

due to the fact that ${\displaystyle {\left(\frac{1+x^2}{1-x^2}\right)}^{3/2}>1.}$ Thus,

$$\begin{array}{cc}\hfill {(1-x^2)}^2{N}_1& >(74x+162x^3+98x^5+48x^7+8x^9)\hfill \\ \hfill & -(34x+8x^3-8x^5){(1-x^2)}^2\hfill \\ \hfill & =40x+222x^3+88x^5+24x^7+16x^9>0.\hfill \end{array}$$

So $N_1>0$ and hence $f_8^{\prime }\left(x\right)$ is positive. As a result, $f_8\left(x\right)$ is strictly increasing on $(0,1)$. By successive application of Lemma 1, we conclude that $f\left(x\right)$ is strictly increasing on $(0,1)$. Therefore, $f\left(0^{+}\right)<f\left(x\right)<f\left(1\right)$, where ${\eta }_1=f\left(0^{+}\right)=\frac{1}{3}$ and ${\eta }_2=f\left(1\right)=\frac{\pi }{ln(3+2\sqrt{2})}-1$. This completes the proof of Theorem 1. □

Proof of Theorem 2.

Let

$$g\left(x\right)=\frac{{tanh}^{-1}x-{tan}^{-1}x}{x^2{tan}^{-1}x}:=\frac{g_1\left(x\right)}{g_2\left(x\right)},$$

where $g_1\left(x\right)={tanh}^{-1}x-{tan}^{-1}x$ and $g_2\left(x\right)=x^2{tan}^{-1}x,$ satisfying $g_1\left(0\right)=0=g_2\left(0\right).$ By differentiating with respect to x, we have

$$\frac{g_1^{\prime }\left(x\right)}{g_2^{\prime }\left(x\right)}=\frac{\frac{1}{1-x^2}-\frac{1}{1+x^2}}{2x{tan}^{-1}x+\frac{x^2}{1+x^2}}:=\frac{g_3\left(x\right)}{g_4\left(x\right)},$$

where $g_3\left(x\right)=\frac{1}{1-x^2}-\frac{1}{1+x^2}$ and $g_4\left(x\right)=2x{tan}^{-1}x+\frac{x^2}{1+x^2}$ with $g_3\left(0\right)=0=g_4\left(0\right).$ Differentiation gives us

$$\frac{g_3^{\prime }\left(x\right)}{g_4^{\prime }\left(x\right)}=\frac{x\left({(1-x^2)}^{-2}+{(1+x^2)}^{-2}\right)}{{tan}^{-1}x+\frac{2x}{1+x^2}-\frac{x^3}{{(1+x^2)}^2}}:=\frac{g_5\left(x\right)}{g_6\left(x\right)},$$

where $g_5\left(x\right)=x\left({(1-x^2)}^{-2}+{(1+x^2)}^{-2}\right)$ and $g_6\left(x\right)={tan}^{-1}x+\frac{2x}{1+x^2}-\frac{x^3}{{(1+x^2)}^2}$ are such that $g_5\left(0\right)=0$ and $g_6\left(0\right)=0.$ Differentiating again with respect to x, we get

$$\begin{array}{cc}\hfill \frac{g_5^{\prime }\left(x\right)}{g_6^{\prime }\left(x\right)}& =\frac{(1+3x^2){\left(\frac{1+x^2}{1-x^2}\right)}^3+(1-3x^2)}{3-x^2}\hfill \\ \hfill & :=\frac{(1+3x^2)g_7\left(x\right)+(1-3x^2)}{3-x^2}:=g_8\left(x\right),\hfill \end{array}$$

where $g_7\left(x\right)={\left(\frac{1+x^2}{1-x^2}\right)}^3$ with $g_7^{\prime }\left(x\right)=\frac{12x}{{(1-x^2)}^2}{\left(\frac{1+x^2}{1-x^2}\right)}^2.$ We show that $g_8\left(x\right)$ is strictly increasing on $(0,1).$ We demonstrate the positivity of $g_8^{\prime }\left(x\right)$ by showing that the numerator of $g_8^{\prime }\left(x\right)$, say $N_2$, is positive. We have

$$\begin{array}{c}\hfill N_2=(3-x^2)\left((1+3x^2)g_7^{\prime }\left(x\right)+6x{g}_7\left(x\right)-6x\right)\\ \hfill +2x\left((1+3x^2)g_7\left(x\right)+(1-3x^2)\right).\end{array}$$

Simplifying the above as in the proof of Theorem 2 and using the fact that ${\left(\frac{1+x^2}{1-x^2}\right)}^3>1$, we get

$$N_2>\frac{40x+88x^3-32x^5}{{(1-x^2)}^2}=\frac{40x+8x^3(11-4x^2)}{{(1-x^2)}^2}>0.$$

Therefore, $g_8\left(x\right)$ is increasing. By Lemma 1, it is concluded that $g\left(x\right)$ is strictly increasing in $(0,r)$. Consequently, $g\left(0^{+}\right)<g\left(x\right)<g\left(r\right).$ The inequalities (5) follow due to the limits $g\left(0^{+}\right)=\frac{2}{3}$ and $g\left(r\right)=\frac{{tanh}^{-1}r-{tan}^{-1}r}{r^2{tan}^{-1}r}.$ □

Proof of Theorem 3.

Let us set

$$F\left(x\right)=\frac{ln\left(\frac{{sin}^{-1}x}{{sinh}^{-1}x}\right)}{x^2}:=\frac{F_1\left(x\right)}{F_2\left(x\right)};x\in (0,1).$$

By differentiation, we obtain

$$\begin{array}{cc}\hfill \frac{F_1^{\prime }\left(x\right)}{F_2^{\prime }\left(x\right)}& =\frac{1}{2}\frac{1}{\sqrt{1-x^4}}·\frac{\sqrt{1+x^2}{sinh}^{-1}x-\sqrt{1-x^2}{sin}^{-1}x}{x{sin}^{-1}x{sinh}^{-1}x}\hfill \\ \hfill & :=\frac{1}{2}{F}_3\left(x\right)·F_4\left(x\right),\hfill \end{array}$$

where $F_3\left(x\right)=\frac{1}{\sqrt{1-x^4}}$ is strictly positively increasing in $(0,1)$ and

$$F_4\left(x\right)=\frac{\sqrt{1+x^2}{sinh}^{-1}x-\sqrt{1-x^2}{sin}^{-1}x}{x{sin}^{-1}x{sinh}^{-1}x}>0$$

due to Lemma 5. We prove that $F_4\left(x\right)$ is strictly monotonically increasing in $(0,1).$ We differentiate $F_4\left(x\right)$ with respect to x to get

$$\begin{array}{cc}\hfill F_4^{\prime }\left(x\right){\left(x{sin}^{-1}x{sinh}^{-1}x\right)}^2& =x{sin}^{-1}x{sinh}^{-1}x\left(\frac{x{sinh}^{-1}x}{\sqrt{1+x^2}}+\frac{x{sin}^{-1}x}{\sqrt{1-x^2}}\right)\hfill \\ \hfill & -\left(\sqrt{1+x^2}{sinh}^{-1}x-\sqrt{1-x^2}{sin}^{-1}x\right)\hfill \\ \hfill & \times \left({sin}^{-1}x{sinh}^{-1}x+\frac{x{sinh}^{-1}x}{\sqrt{1-x^2}}+\frac{x{sin}^{-1}x}{\sqrt{1+x^2}}\right).\hfill \end{array}$$

After some calculations, we get

$$\begin{array}{cc}\hfill & F_4^{\prime }\left(x\right){\left(x{sin}^{-1}x{sinh}^{-1}x\right)}^2\hfill \\ \hfill & =\frac{1}{\sqrt{1+x^2}}\left[x\sqrt{1-x^2}{\left({sin}^{-1}x\right)}^2+x^2{sin}^{-1}x{\left({sinh}^{-1}x\right)}^2-(1+x^2){sin}^{-1}x{\left({sinh}^{-1}x\right)}^2\right]\hfill \\ \hfill & +\frac{1}{\sqrt{1-x^2}}\left[x^2{\left({sin}^{-1}x\right)}^2{sinh}^{-1}x+(1-x^2){\left({sin}^{-1}x\right)}^2{sinh}^{-1}x-x\sqrt{1+x^2}{\left({sinh}^{-1}x\right)}^2\right]\hfill \\ \hfill & =\frac{{sin}^{-1}x}{\sqrt{1+x^2}}\left[x\sqrt{1-x^2}{sin}^{-1}x-{\left({sinh}^{-1}x\right)}^2\right]+\frac{{sinh}^{-1}x}{\sqrt{1-x^2}}\left[{\left({sin}^{-1}x\right)}^2-x\sqrt{1+x^2}{sinh}^{-1}x\right]\hfill \\ \hfill & >\frac{{sinh}^{-1}x}{\sqrt{1-x^2}}\left[x\sqrt{1-x^2}{sin}^{-1}x-{\left({sinh}^{-1}x\right)}^2\right]+\frac{{sinh}^{-1}x}{\sqrt{1-x^2}}\left[{\left({sin}^{-1}x\right)}^2-x\sqrt{1+x^2}{sinh}^{-1}x\right]\hfill \end{array}$$

due to Lemmas 4 and 5. Then, we have

$$F_4^{\prime }\left(x\right){\left(x{sin}^{-1}x{sinh}^{-1}x\right)}^2>\frac{{sinh}^{-1}x}{\sqrt{1-x^2}}·\psi \left(x\right),$$

where $\psi \left(x\right)={\left({sin}^{-1}x\right)}^2-{\left({sinh}^{-1}x\right)}^2+x\sqrt{1-x^2}{sin}^{-1}x-x\sqrt{1+x^2}{sinh}^{-1}x.$ Let us now consider

$$\begin{array}{cc}\hfill & {\psi }^{\prime }\left(x\right)\hfill \\ \hfill & =2\frac{{sin}^{-1}x}{\sqrt{1-x^2}}-2\frac{{sinh}^{-1}x}{\sqrt{1+x^2}}+\sqrt{1-x^2}{sin}^{-1}x-\frac{x^2{sin}^{-1}x}{\sqrt{1-x^2}}-\frac{x^2{sinh}^{-1}x}{\sqrt{1+x^2}}-\sqrt{1+x^2}{sinh}^{-1}x.\hfill \end{array}$$

Therefore,

$$\begin{array}{cc}\hfill {\psi }^{\prime }\left(x\right)\sqrt{1-x^4}& =2\sqrt{1+x^2}{sin}^{-1}x-2\sqrt{1-x^2}{sinh}^{-1}x+(1-x^2)\sqrt{1+x^2}{sin}^{-1}x\hfill \\ \hfill & -x^2\sqrt{1+x^2}{sin}^{-1}x-x^2\sqrt{1-x^2}{sinh}^{-1}x-(1+x^2)\sqrt{1-x^2}{sinh}^{-1}x\hfill \\ \hfill & =\sqrt{1+x^2}(3-2x^2){sin}^{-1}x-\sqrt{1-x^2}(3+2x^2){sinh}^{-1}x.\hfill \end{array}$$

Next, we prove that

$$\sqrt{1+x^2}(3-2x^2){sin}^{-1}x>\sqrt{1-x^2}(3+2x^2){sinh}^{-1}x.$$

Equivalently,

$$(1+x^2){(3-2x^2)}^2{\left({sin}^{-1}x\right)}^2>(1-x^2){(3+2x^2)}^2{\left({sinh}^{-1}x\right)}^2$$

or

$$(4x^6-8x^4-3x^2+9){\left({sin}^{-1}x\right)}^2+(4x^6+8x^4-3x^2-9){\left({sinh}^{-1}x\right)}^2>0,$$

i.e.,

$$\phi \left(x\right):=(4x^6-3x^2)\left[{\left({sin}^{-1}x\right)}^2+{\left({sinh}^{-1}x\right)}^2\right]+(9-8x^4)\left[{\left({sin}^{-1}x\right)}^2-{\left({sinh}^{-1}x\right)}^2\right]>0.$$

Making use of Lemma 2, we write

$$\begin{array}{cc}\hfill \phi \left(x\right)& =(4x^6-3x^2)\sum _{n=0}^{\infty }\left(1+{(-1)}^n\right)\frac{2^{2n+1}{(n!)}^2}{(2n+2)!}{x}^{2n+2}\hfill \\ \hfill & +(9-8x^4)\sum _{n=0}^{\infty }\left(1-{(-1)}^n\right)\frac{2^{2n+1}{(n!)}^2}{(2n+2)!}{x}^{2n+2}\hfill \\ \hfill & =\sum _{n=0}^{\infty }4\left(1+{(-1)}^n\right)\frac{2^{2n+1}{(n!)}^2}{(2n+2)!}{x}^{2n+8}-\sum _{n=0}^{\infty }8\left(1-{(-1)}^n\right)\frac{2^{2n+1}{(n!)}^2}{(2n+2)!}{x}^{2n+6}\hfill \\ \hfill & -\sum _{n=0}^{\infty }3\left(1+{(-1)}^n\right)\frac{2^{2n+1}{(n!)}^2}{(2n+2)!}{x}^{2n+4}+\sum _{n=0}^{\infty }9\left(1-{(-1)}^n\right)\frac{2^{2n+1}{(n!)}^2}{(2n+2)!}{x}^{2n+2}\hfill \\ \hfill & =\sum _{n=3}^{\infty }4(1+{(-1)}^{n-3})\frac{2^{2n-5}{((n-3)!)}^2}{(2n-4)!}{x}^{2n+2}-\sum _{n=2}^{\infty }8(1-{(-1)}^{n-2})\frac{2^{2n-3}{((n-2)!)}^2}{(2n-2)!}{x}^{2n+2}\hfill \\ \hfill & -\sum _{n=1}^{\infty }3(1+{(-1)}^{n-1})\frac{2^{2n-1}{((n-1)!)}^2}{\left(2n\right)!}{x}^{2n+2}+\sum _{n=0}^{\infty }9(1-{(-1)}^n)\frac{2^{2n+1}{(n!)}^2}{(2n+2)!}{x}^{2n+2}\hfill \\ \hfill & :=\sum _{n=3}^{\infty }{a}_n{x}^{2n+2},\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill a_n& =4(1+{(-1)}^{n-3})\frac{2^{2n-5}{((n-3)!)}^2}{(2n-4)!}-8(1-{(-1)}^{n-2})\frac{2^{2n-3}{((n-2)!)}^2}{(2n-2)!}\hfill \\ \hfill & -3(1+{(-1)}^{n-1})\frac{2^{2n-1}{((n-1)!)}^2}{(2n)!}+9(1-{(-1)}^n)\frac{2^{2n+1}{(n!)}^2}{(2n+2)!},n=3,4,5,\cdots .\hfill \end{array}$$

Clearly, $a_n=0,$ for $n=4,6,8,\cdots .$ For $n=3,5,7,\cdots ,$ we write

$$a_n=\frac{2^{2n}{((n-3)!)}^2}{(2n+2)!}·b_n,$$

where

$$\begin{array}{cc}\hfill b_n& =n(n+1)(2n+1)(2n-1)(2n-2)(2n-3)-8n(n+1)(2n+1)(2n-1){(n-2)}^2\hfill \\ \hfill & -6(n+1)(2n+1){(n-1)}^2{(n-2)}^2+36n^2{(n-1)}^2{(n-2)}^2\hfill \\ \hfill & =(n^2+n)(4n^2-1)(-4n^2+22n-26)+6(n^2-2n+1)(n^2-4n+4)(4n^2-3n-1)\hfill \\ \hfill & =8n^6-90n^5+402n^4-608n^3+238n^2+26n-24.\hfill \end{array}$$

Now it is very easy to prove that $b_n>0$ for $n\ge 3$ and hence $a_n\ge 0$ for $n=3,5,7,\cdots .$ This shows that $a_n\ge 0$ for $n=3,4,5,\cdots$, implying that $\phi \left(x\right)>0$ and ${\psi }^{\prime }\left(x\right)>0$, which further implies $\psi \left(x\right)>\psi \left(0\right)=0$ and $F_4^{\prime }\left(x\right)>0.$ Then $F_4\left(x\right)$ is strictly monotonically increasing in $(0,1),$ as $F_3\left(x\right)$ and $F_4\left(x\right)$ both are monotonically increasing in $(0,1)$. Thus, $\frac{F_1^{\prime }\left(x\right)}{F_2^{\prime }\left(x\right)}$ and thus, according to Lemma 1, $F\left(x\right)$ is also monotonically increasing in $(0,1).$ As a result, $F(0+)<F\left(x\right)<F\left(1\right).$ The limits $F(0+)=\frac{1}{3}$ and $F\left(1\right)=ln\left(\frac{\pi }{2{sinh}^{-1}1}\right)$ give the required inequalities (6). □

Proof of Theorem 4.

Let us set

$$G\left(x\right)=\frac{ln\left(\frac{{tanh}^{-1}x}{{tan}^{-1}x}\right)}{x^2}:=\frac{G_1\left(x\right)}{G_2\left(x\right)};x\in (0,r)\mathrm{and}r\in (0,1).$$

After differentiation, we obtain

$$\begin{array}{cc}\hfill \frac{G_1^{\prime }\left(x\right)}{G_2^{\prime }\left(x\right)}& =\frac{1}{2}\frac{(1+x^2){tan}^{-1}x-(1-x^2){tanh}^{-1}x}{x(1-x^4){tan}^{-1}x{tanh}^{-1}x}\hfill \\ \hfill & =\frac{1}{2}\frac{(1+x^2){tan}^{-1}x-(1-x^2){tanh}^{-1}x}{x^3}·\frac{x^2}{(1-x^4){tan}^{-1}x{tanh}^{-1}x}\hfill \\ \hfill & :=\frac{1}{2}{G}_3\left(x\right)·G_4\left(x\right).\hfill \end{array}$$

Consider

$$G_3\left(x\right)=\frac{(1+x^2){tan}^{-1}x-(1-x^2){tanh}^{-1}x}{x^3}:=\frac{G_5\left(x\right)}{G_6\left(x\right)},$$

where $G_5\left(x\right)=(1+x^2){tan}^{-1}x-(1-x^2){tanh}^{-1}x$ and $G_6\left(x\right)=x^3$ satisfying $G_5\left(0\right)=0=G_6\left(0\right).$ Differentiation gives

$$\frac{G_5^{\prime }\left(x\right)}{G_6^{\prime }\left(x\right)}=\frac{2}{3}·\frac{{tan}^{-1}x+{tanh}^{-1}x}{x}:=\frac{2}{3}·\frac{G_7\left(x\right)}{G_8\left(x\right)},$$

where $G_7\left(x\right)={tan}^{-1}x+{tanh}^{-1}x$ and $G_8\left(x\right)=x$ with $G_7\left(0\right)=0=G_8\left(0\right).$ Differentiating again, we get

$$\frac{G_7^{\prime }\left(x\right)}{G_8^{\prime }\left(x\right)}=\frac{1}{1+x^2}+\frac{1}{1-x^2}=\frac{2}{1-x^4},$$

which is strictly increasing in $(0,r).$ By Lemma 1, $G_3\left(x\right)$ is strictly increasing in $(0,r).$ In addition, by Lemma 6 and the fact that

$$\frac{\sqrt{1-x^2}}{\sqrt{1+x^2}}>\frac{1-x^2}{1+x^2},$$

we get that $G_3\left(x\right)$ is positive in $(0,r).$

Now, consider

$$G_4\left(x\right)=\frac{x^2}{(1-x^4){tan}^{-1}x{tanh}^{-1}x};x\in (0,r).$$

Then, we have

$$\begin{array}{cc}\hfill G_4^{\prime }\left(x\right){\left((1-x^4){tan}^{-1}x{tanh}^{-1}x\right)}^2& =2x(1-x^4){tan}^{-1}x{tanh}^{-1}x+4x^5{tan}^{-1}x{tanh}^{-1}x\hfill \\ \hfill & -x^2(1-x^2){tanh}^{-1}-x^2(1+x^2){tan}^{-1}x\hfill \\ \hfill & =2x{tan}^{-1}x{tanh}^{-1}x+2x^5{tan}^{-1}x{tanh}^{-1}x-x^2{tanh}^{-1}x\hfill \\ \hfill & -x^2{tan}^{-1}x+x^4({tanh}^{-1}x-{tan}^{-1}x)\hfill \\ \hfill & >2x{tan}^{-1}x{tanh}^{-1}x+2x^5{tan}^{-1}x{tanh}^{-1}x-x^2{tanh}^{-1}x\hfill \\ \hfill & -x^2{tan}^{-1}x\hfill \\ \hfill & =x{tan}^{-1}x{tanh}^{-1}x\left(2+2x^4-\frac{x}{{tan}^{-1}x}-\frac{x}{{tanh}^{-1}x}\right)>0,\hfill \end{array}$$

by Lemma 7. Therefore $G_4\left(x\right)$ is strictly increasing in $(0,1).$ Thus, since $\frac{G_1^{\prime }\left(x\right)}{G_2^{\prime }\left(x\right)}$ is the product of two positively increasing functions, it is increasing in $(0,r).$ By Lemma 1, $G\left(x\right)$ is strictly increasing in $(0,r).$ Consequently, we have

$$G(0+)<G\left(x\right)<G\left(r\right).$$

The desired inequalities (7) follow due to the limits $G(0+)=\frac{2}{3}$ and $G\left(r\right)=\frac{ln\left({tanh}^{-1}r\right)-ln\left({tan}^{-1}r\right)}{r^2}.$ □

Remark 2.

From the proofs of Theorems 2 and 4, it is clear that the rightmost inequalities of (5) and (7) are, in fact, true in $(0,1).$

Proof of Corollary 1.

It is an immediate consequence of Theorems 1 and 2, and Remark 2. □

Remark 3.

A better upper bound for $\frac{{tanh}^{-1}x}{{tan}^{-1}x}$ in $(0,1)$ can be found in Lemma 6, as stated in Remark 1.

5. Conclusions and Direction for Further Research

Polynomial and exponential bounds for bell-shaped functions involving only trigonometric or only hyperbolic functions or their inverses are present in the literature. Recently, these types of bounds have been obtained for the quotients of trigonometric and hyperbolic functions. We contributed to the field by establishing similar bounds for the quotients of inverse trigonometric and inverse hyperbolic functions, which can be useful in the theory of analytical inequalities. The exponential bounds were sharper than the polynomial bounds.

Wilker-type and Huygens-type inequalities for inverse trigonometric and inverse hyperbolic function quotients may also be obtained.