Investigation into the Explicit Solutions of the Integrable (2+1)—Dimensional Maccari System via the Variational Approach

Abstract

In this paper, the integrable (2+1)-dimensional Maccari system (MS), which can model many complex phenomena in hydrodynamics, plasma physics and nonlinear optics, is investigated by the variational approach (VA). This proposed approach that based on the variational theory and Ritz-like method can construct the explicit solutions via the stationary conditions only taking two steps. Finally, the dynamic behaviors of the solutions are exhibited by choosing the appropriate parameters through the 3-D and density plots. It can be seen that the proposed method is concise and straightforward, and can be adopted to study the travelling wave theory in physics.

1. Introduction

Many significant natural science and engineering problems arising in circuits [1,2,3] hydrodynamics [4,5,6], plasma physics [7,8,9], optics [10,11,12,13,14,15], biomedical science [16,17,18,19], vibration [20,21,22,23,24], chemistry [25,26] and so on can be attributed to the study of nonlinear partial differential equations (NPDEs). The study of NPDEs is of great value in theory and application, and can well explain various natural phenomena. In this work, we mainly study the (2+1)-dimensional MS that reads as [27,28]:

$$\{\begin{array}{l}i{p}_t+p_{xx}+pq=0\\ q_t+q_y+{\left({\left|p\right|}^2\right)}_x=0\end{array},$$

(1)

where $p=p\left(x,y,t\right)$ represents the complex scalar field and $q=q\left(x,y,t\right)$ indicates the real scalar field. x, y and t are the independent spatial variables and temporal variable, respectively. The (2+1)-dimensional MS can model many complex phenomenon arising in hydrodynamics, plasma physics, nonlinear optics and so on. In addition, the study of its travelling wave solution is important. Here in this work, we aim to search for the solitary and periodic wave solutions of coupled system via the VA. The rest of this article is arranged as follows: In Section 2, the variational principle (VP) is established by means of the semi-inverse method (SIM). In Section 3 and Section 4, we attain the periodic wave solution (PWS) and solitary wave solution (SWS) by applying the VA, respectively. In Section 5, the numerical results and discussion are given. Finally, we present the conclusion in Section 6.

2. The VP

To solve the coupled model, we first derive the VP in this section. To this end, the following wave transformation is introduced:

$$p\left(x,y,t\right)=e^{i\varphi }p\left(\xi \right), q\left(x,y,t\right)=q\left(\xi \right),$$

(2)

where,

$$\xi ={\gamma }_{1}x+{\gamma }_{2}y+{\gamma }_{3}t, \varphi ={\epsilon }_{1}x+{\epsilon }_{2}y+{\epsilon }_{3}t,$$

(3)

where γ₁, γ₂, γ₃, ε₁, ε₂ and ε₃ are arbitrary constants.

Using Equations (2) and (3), we have:

$$\begin{array}{l}i{p}_t=i\left[i{\epsilon }_3{e}^{i\varphi }p\left(\xi \right)+{\gamma }_3{e}^{i\varphi }{p}^{\prime }\left(\xi \right)\right]=-{\epsilon }_3{e}^{i\varphi }p\left(\xi \right)+i{\gamma }_3{e}^{i\varphi }{p}^{\prime }\left(\xi \right),\\ p_{xx}={\left[i{\epsilon }_1{e}^{i\varphi }p\left(\xi \right)+{\gamma }_1{e}^{i\varphi }{p}^{\prime }\left(\xi \right)\right]}_x=-{\epsilon }_1^2{e}^{i\varphi }p\left(\xi \right)+2i{\epsilon }_1^{}{\gamma }_1{e}^{i\varphi }{p}^{\prime }\left(\xi \right)+{\gamma }_1^2{e}^{i\varphi }{p}^{″}\left(\xi \right),\\ q_t={\gamma }_3{q}^{\prime }\left(\xi \right),\\ q_y={\gamma }_2{q}^{\prime }\left(\xi \right),\\ {\left({\left|p\right|}^2\right)}_x={\left(p^2\right)}_x={\gamma }_1{\left(p^2\right)}^{\prime },\end{array}$$

Taking above results into Equation (1), Equation (1) can be transformed into the following equations:

$$i{\gamma }_3{p}^{\prime }-{\epsilon }_{3}p-{\epsilon }_1^{2}p+2i{\epsilon }_1{\gamma }_1{p}^{\prime }+{\gamma }_1^2{p}^{″}+pq=0,$$

(4)

$$\left({\gamma }_2+{\gamma }_3\right)q^{\prime }+{\gamma }_1{\left(p^2\right)}^{\prime }=0,$$

(5)

where $p^{\prime }=\frac{dp}{d\xi }$, $p^{″}=\frac{d^{2}p}{d{\xi }^2}$, $q^{\prime }=\frac{dq}{d\xi }$, ${\left(p^2\right)}^{\prime }=\frac{d\left(p^2\right)}{d\xi }$.

Integrating Equation (5) about ξ once and setting the integration constant to zero, it gives:

$$\mathsf{\eta } q=\left(-\frac{{\gamma }_1}{{\gamma }_2+{\gamma }_3}\right)p^2.$$

(6)

Equation (4) can be separated into the real part and imaginary part, respectively, as:

$${\gamma }_1^2{p}^{″}-\left({\epsilon }_3+{\epsilon }_1^2\right)p+pq=0,$$

(7)

$$\left({\gamma }_3+2{\epsilon }_1{\gamma }_1\right)p^{\prime }=0.$$

(8)

Obviously, we can have the following expression in the view of Equation (8):

$${\gamma }_3=-2{\epsilon }_1{\gamma }_1.$$

(9)

Substituting Equations (6) and (9) into Equation (7) yields:

$${\gamma }_1^2{p}^{″}-\left(\frac{{\gamma }_1}{{\gamma }_2-2{\epsilon }_1{\gamma }_1}\right)p^3-\left({\epsilon }_3+{\epsilon }_1^2\right)p=0.$$

(10)

By the SIM [29,30,31,32,33,34,35,36,37], the VP of Equation (10) can be found as:

$$J\left(p\right)={\displaystyle \int \left\{-\frac{1}{2}{\gamma }_1^2{\left(p^{\prime }\right)}^2-\frac{1}{4}\left(\frac{{\gamma }_1}{{\gamma }_2-2{\epsilon }_1{\gamma }_1}\right)p^4-\frac{1}{2}\left({\epsilon }_3+{\epsilon }_1^2\right)p^2\right\}d\xi }.$$

(11)

To facilitate the calculation, we can re-express Equation (11) as:

$$J\left(p\right)={\displaystyle \int \left\{{\alpha }_1{\left(p^{\prime }\right)}^2-{\alpha }_2{p}^4-{\alpha }_3{p}^2\right\}d\xi },$$

(12)

where,

$${\alpha }_1=-\frac{1}{2}{\gamma }_1^2, {\alpha }_2=\frac{1}{4}\left(\frac{{\gamma }_1}{{\gamma }_2-2{\epsilon }_1{\gamma }_1}\right), {\alpha }_3=\frac{1}{2}\left({\epsilon }_3+{\epsilon }_1^2\right).$$

(13)

Comparing Equation (11) with Equation (10), it is easy to see that that the order of Equation (10) has been reduced through the VP, which makes the equation more simple. In addition, the obtained VP can imply the structural form of the solution. Next, we will find the PWS and SWS based on Equation (12) via the VA.

3. The PWSs

The target of this section is to seek the PWSs of Equation (1) by the VA [38,39,40,41]. In order to achieve this goal, we can assume Equation (10) has the following periodic solution:

$$p\left(\xi \right)=\mathrm{\Lambda }\cos \left(\varpi \xi \right), \varpi >0.$$

(14)

Substituting the above into the Equation (12) yields:

$$\begin{array}{ll}J\left(p\right)& ={\displaystyle {\int }_0^{\frac{T}{4}}\left\{{\alpha }_1{\left[-\mathrm{\Lambda }\varpi \sin \left(\varpi \xi \right)\right]}^2-{\alpha }_2{\left[\mathrm{\Lambda }\cos \left(\varpi \xi \right)\right]}^4-{\alpha }_3{\left[\mathrm{\Lambda }\cos \left(\varpi \xi \right)\right]}^2\right\}}d\xi \\ & ={\displaystyle {\int }_0^{\frac{T}{4}}\left\{{\alpha }_1{\mathrm{\Lambda }}^2{\varpi }^2{\sin }^2\left(\varpi \xi \right)-{\alpha }_2{\mathrm{\Lambda }}^4{\cos }^4\left(\varpi \xi \right)-{\alpha }_3{\mathrm{\Lambda }}^2{\cos }^2\left(\varpi \xi \right)\right\}}d\xi \\ & ={\displaystyle {\int }_0^{\frac{T}{4}}{\alpha }_1{\mathrm{\Lambda }}^2{\varpi }^2{\sin }^2\left(\varpi \xi \right)d\xi }-{\displaystyle {\int }_0^{\frac{T}{4}}{\alpha }_2{\mathrm{\Lambda }}^4{\cos }^4\left(\varpi \xi \right)d\xi }-{\displaystyle {\int }_0^{\frac{T}{4}}{\alpha }_3{\mathrm{\Lambda }}^2{\cos }^2\left(\varpi \xi \right)d\xi }\\ & ={\displaystyle {\int }_0^{\frac{\pi }{2}}{\alpha }_1{\mathrm{\Lambda }}^2\varpi {\sin }^2\left(\psi \right)d\psi }-{\displaystyle {\int }_0^{\frac{T}{4}}\frac{{\alpha }_2{\mathrm{\Lambda }}^4}{\varpi }{\cos }^4\left(\psi \right)d\psi }-{\displaystyle {\int }_0^{\frac{T}{4}}\frac{{\alpha }_3{\mathrm{\Lambda }}^2}{\varpi }{\cos }^2\left(\psi \right)d\psi }\\ & =-\frac{{\mathrm{\Lambda }}^2\left(4{\alpha }_3-4{\varpi }^2{\alpha }_1+3{\mathrm{\Lambda }}^2{\alpha }_2\right)\pi }{16\varpi }\end{array}$$

(15)

By the Ritz-like method, there is:

$$\frac{\partial J}{\partial \mathrm{\Lambda }}=0,$$

(16)

which leads to:

$$-\frac{\mathrm{\Lambda }\left(2{\alpha }_3-2{\varpi }^2{\alpha }_1+3{\mathrm{\Lambda }}^2{\alpha }_2\right)\pi }{4\varpi }=0.$$

(17)

Solving above equation, we obtain:

$$\varpi =\sqrt{\frac{2{\alpha }_3+3{\mathrm{\Lambda }}^2{\alpha }_2}{2{\alpha }_1}}>0.$$

(18)

Substituting Equation (13) into above equation, we acquire:

$$\varpi =\sqrt{-\frac{2\left({\epsilon }_3+{\epsilon }_1^2\right)\left({\gamma }_2-2{\epsilon }_1{\gamma }_1\right)+3{\mathrm{\Lambda }}^2{\gamma }_1}{2{\gamma }_1^2\left({\gamma }_2-2{\epsilon }_1{\gamma }_1\right)}}>0.$$

(19)

So the periodic solution of Equation (10) is attained as:

$$p\left(\xi \right)=\mathrm{\Lambda }\cos \left(\sqrt{-\frac{2\left({\epsilon }_3+{\epsilon }_1^2\right)\left({\gamma }_2-2{\epsilon }_1{\gamma }_1\right)+3{\mathrm{\Lambda }}^2{\gamma }_1}{2{\gamma }_1^2\left({\gamma }_2-2{\epsilon }_1{\gamma }_1\right)}}\xi \right).$$

(20)

In light of Equations (2) and (3), the PWS of Equation (1) can be obtained as:

$$p\left(x,y,t\right)=\mathrm{\Lambda }\cos \left[\sqrt{-\frac{2\left({\epsilon }_3+{\epsilon }_1^2\right)\left({\gamma }_2-2{\epsilon }_1{\gamma }_1\right)+3{\mathrm{\Lambda }}^2{\gamma }_1}{2{\gamma }_1^2\left({\gamma }_2-2{\epsilon }_1{\gamma }_1\right)}}\left({\gamma }_{1}x+{\gamma }_{2}y-2{\epsilon }_1{\gamma }_{1}t\right)\right]e^{i\left({\epsilon }_{1}x+{\epsilon }_{2}y+{\epsilon }_{3}t\right)}.$$

(21)

With help of Equations (6) and (9), we have:

$$q\left(x,y,t\right)=\left(-\frac{{\gamma }_1}{{\gamma }_2-2{\epsilon }_1{\gamma }_1}\right){\mathrm{\Lambda }}^2{\cos }^2\left[\sqrt{-\frac{2\left({\epsilon }_3+{\epsilon }_1^2\right)\left({\gamma }_2-2{\epsilon }_1{\gamma }_1\right)+3{\mathrm{\Lambda }}^2{\gamma }_1}{2{\gamma }_1^2\left({\gamma }_2-2{\epsilon }_1{\gamma }_1\right)}}\left({\gamma }_{1}x+{\gamma }_{2}y-2{\epsilon }_1{\gamma }_{1}t\right)\right]e^{2i\left({\epsilon }_{1}x+{\epsilon }_{2}y+{\epsilon }_{3}t\right)}$$

(22)

Note: We can also obtain the other different PWSs via supposing $p\left(\xi \right)=\mathrm{\Lambda }\sin \left(\varpi \xi \right)$, $p\left(\xi \right)=\mathrm{\Lambda }{\cos }^2\left(\varpi \xi \right)$ and so on.

4. The SWSs

This section will apply the VA to derive the SWSs. For this end, we make a assumption that the solution of Equation (10) is:

$$p\left(\xi \right)=A\sec h\left(B\xi \right), B>0$$

(23)

where A and B are constants that to be determined later. Taking Equation (23) into Equation (12) gives:

$$\begin{array}{ll}J\left(A,B\right)& ={\displaystyle {\int }_0^{\infty }\left\{{\alpha }_1{\left[-AB\sec h\left(B\xi \right)\tanh \left(B\xi \right)\right]}^2-{\alpha }_2{\left[A\sec h\left(B\xi \right)\right]}^4-{\alpha }_3{\left[A\sec h\left(B\xi \right)\right]}^2\right\}d\xi }\\ & ={\displaystyle {\int }_0^{\infty }\left\{{\alpha }_1{A}^2{B}^2\sec h^2\left(B\xi \right){\tanh }^2\left(B\xi \right)-{\alpha }_2{A}^4\sec h^4\left(B\xi \right)-{\alpha }_3{A}^2\sec h^2\left(B\xi \right)\right\}d\xi }\\ & ={\displaystyle {\int }_0^{\infty }\left\{{\alpha }_1{A}^{2}B\sec h^2\left(\mathrm{\Xi }\right){\tanh }^2\left(\mathrm{\Xi }\right)-\frac{{\alpha }_2{A}^4}{B}\sec h^4\left(\mathrm{\Xi }\right)-\frac{{\alpha }_3{A}^2}{B}\sec h^2\left(\mathrm{\Xi }\right)\right\}d\mathrm{\Xi }}\\ & =\frac{A^2\left(B^2{\alpha }_1-2A^2{\alpha }_2-3{\alpha }_3\right)}{3B}\end{array}$$

(24)

According to Ritz-like method [42,43,44,45], the following expressions can be obtained via the stationary conditions:

$$\frac{\partial J\left(A,B\right)}{\partial A}=0,$$

(25)

$$\frac{\partial J\left(A,B\right)}{\partial B}=0.$$

(26)

From which, we have:

$$-\frac{2A\left(-B^2{\alpha }_1+4A^2{\alpha }_2+3{\alpha }_3\right)}{3B}=0,$$

(27)

$$\frac{A^2\left(B^2{\alpha }_1+2A^2{\alpha }_2+3{\alpha }_3\right)}{3B^2}=0.$$

(28)

which results in:

$$A=\sqrt{-\frac{{\alpha }_3}{{\alpha }_2}}, B=\sqrt{-\frac{{\alpha }_3}{{\alpha }_1}}.$$

(29)

Or,

$$A=-\sqrt{-\frac{{\alpha }_3}{{\alpha }_2}}, B=\sqrt{-\frac{{\alpha }_3}{{\alpha }_1}}.$$

(30)

In the view of Equation (13), we have:

$$A=\sqrt{-\frac{2\left({\epsilon }_3+{\epsilon }_1^2\right)\left({\gamma }_2-2{\epsilon }_1{\gamma }_1\right)}{{\gamma }_1}}, B=\sqrt{\frac{{\epsilon }_3+{\epsilon }_1^2}{{\gamma }_1^2}},$$

(31)

or,

$$A=-\sqrt{-\frac{2\left({\epsilon }_3+{\epsilon }_1^2\right)\left({\gamma }_2-2{\epsilon }_1{\gamma }_1\right)}{{\gamma }_1}}, B=\sqrt{\frac{{\epsilon }_3+{\epsilon }_1^2}{{\gamma }_1^2}}.$$

(32)

Thus, we can acquire the solution of Equation (10) as:

$$p\left(\xi \right)=\sqrt{-\frac{2\left({\epsilon }_3+{\epsilon }_1^2\right)\left({\gamma }_2-2{\epsilon }_1{\gamma }_1\right)}{{\gamma }_1}}\sec h\left(\sqrt{\frac{{\epsilon }_3+{\epsilon }_1^2}{{\gamma }_1^2}}\xi \right),$$

(33)

Or,

$$p\left(\xi \right)=-\sqrt{-\frac{2\left({\epsilon }_3+{\epsilon }_1^2\right)\left({\gamma }_2-2{\epsilon }_1{\gamma }_1\right)}{{\gamma }_1}}\sec h\left(\sqrt{\frac{{\epsilon }_3+{\epsilon }_1^2}{{\gamma }_1^2}}\xi \right).$$

(34)

By the transform given in Equations (2) and (3), we have:

$$p\left(x,y,t\right)=\sqrt{-\frac{2\left({\epsilon }_3+{\epsilon }_1^2\right)\left({\gamma }_2-2{\epsilon }_1{\gamma }_1\right)}{{\gamma }_1}}\sec h\left[\sqrt{\frac{{\epsilon }_3+{\epsilon }_1^2}{{\gamma }_1^2}}\left({\gamma }_{1}x+{\gamma }_{2}y-2{\epsilon }_1{\gamma }_{1}t\right)\right]e^{i\left({\epsilon }_{1}x+{\epsilon }_{2}y+{\epsilon }_{3}t\right)},$$

(35)

or

$$p\left(x,y,t\right)=-\sqrt{-\frac{2\left({\epsilon }_3+{\epsilon }_1^2\right)\left({\gamma }_2-2{\epsilon }_1{\gamma }_1\right)}{{\gamma }_1}}\sec h\left[\sqrt{\frac{{\epsilon }_3+{\epsilon }_1^2}{{\gamma }_1^2}}\left({\gamma }_{1}x+{\gamma }_{2}y-2{\epsilon }_1{\gamma }_{1}t\right)\right]e^{i\left({\epsilon }_{1}x+{\epsilon }_{2}y+{\epsilon }_{3}t\right)}.$$

(36)

In the view of Equation (6), we have:

$$q\left(x,y,t\right)=\frac{2\left({\epsilon }_3+{\epsilon }_1^2\right)\left({\gamma }_2-2{\epsilon }_1{\gamma }_1\right)}{{\gamma }_2+{\gamma }_3}\sec h^2\left[\sqrt{\frac{{\epsilon }_3+{\epsilon }_1^2}{{\gamma }_1^2}}\left({\gamma }_{1}x+{\gamma }_{2}y-2{\epsilon }_1{\gamma }_{1}t\right)\right]e^{2i\left({\epsilon }_{1}x+{\epsilon }_{2}y+{\epsilon }_{3}t\right)}.$$

(37)

Thus, we can acquire the SWSs of Equation (1) as:

Family one:

$$p\left(x,y,t\right)=\sqrt{-\frac{2\left({\epsilon }_3+{\epsilon }_1^2\right)\left({\gamma }_2-2{\epsilon }_1{\gamma }_1\right)}{{\gamma }_1}}\sec h\left[\sqrt{\frac{{\epsilon }_3+{\epsilon }_1^2}{{\gamma }_1^2}}\left({\gamma }_{1}x+{\gamma }_{2}y-2{\epsilon }_1{\gamma }_{1}t\right)\right]e^{i\left({\epsilon }_{1}x+{\epsilon }_{2}y+{\epsilon }_{3}t\right)}$$

(38)

$$q\left(x,y,t\right)=\frac{2\left({\epsilon }_3+{\epsilon }_1^2\right)\left({\gamma }_2-2{\epsilon }_1{\gamma }_1\right)}{{\gamma }_2+{\gamma }_3}\sec h^2\left[\sqrt{\frac{{\epsilon }_3+{\epsilon }_1^2}{{\gamma }_1^2}}\left({\gamma }_{1}x+{\gamma }_{2}y-2{\epsilon }_1{\gamma }_{1}t\right)\right]e^{2i\left({\epsilon }_{1}x+{\epsilon }_{2}y+{\epsilon }_{3}t\right)}.$$

(39)

Family two:

$$p\left(x,y,t\right)=-\sqrt{-\frac{2\left({\epsilon }_3+{\epsilon }_1^2\right)\left({\gamma }_2-2{\epsilon }_1{\gamma }_1\right)}{{\gamma }_1}}\sec h\left[\sqrt{\frac{{\epsilon }_3+{\epsilon }_1^2}{{\gamma }_1^2}}\left({\gamma }_{1}x+{\gamma }_{2}y-2{\epsilon }_1{\gamma }_{1}t\right)\right]e^{i\left({\epsilon }_{1}x+{\epsilon }_{2}y+{\epsilon }_{3}t\right)},$$

(40)

$$q\left(x,y,t\right)=\frac{2\left({\epsilon }_3+{\epsilon }_1^2\right)\left({\gamma }_2-2{\epsilon }_1{\gamma }_1\right)}{{\gamma }_2+{\gamma }_3}\sec h^2\left[\sqrt{\frac{{\epsilon }_3+{\epsilon }_1^2}{{\gamma }_1^2}}\left({\gamma }_{1}x+{\gamma }_{2}y-2{\epsilon }_1{\gamma }_{1}t\right)\right]e^{2i\left({\epsilon }_{1}x+{\epsilon }_{2}y+{\epsilon }_{3}t\right)}.$$

(41)

It should be noted that another SWSs can be obtained by assuming $p\left(\xi \right)=A\sec h^2\left(B\xi \right)$, $p\left(\xi \right)=A\sec h^3\left(B\xi \right)$ and so on.

5. Numerical Results and Discussion

The goal of this section is to ascertain the correctness and effectiveness of the VA through one example. We choose the parameters as γ₁ = −1, γ₂ = 1, γ₃ = 1, ε₁ = 1, ε₂ = 1, ε₃ = 1.

For $\mathrm{\Lambda }=3$, the PWSs of Equation (1) can be obtained by using Equations (21) and (22) as:

$$\{\begin{array}{l}p\left(x,y,t\right)=3\cos \left[\sqrt{\frac{5}{2}}\left(-x+y+2t\right)\right]e^{i\left(x+y+t\right)}\\ q\left(x,y,t\right)=3{\cos }^2\left[\sqrt{\frac{5}{2}}\left(-x+y+2t\right)\right]e^{2i\left(x+y+t\right)}\end{array}$$

(42)

We plot the absolute part (AP), real part (RP) and imaginary part (IP) of the PWSs given by Equation (42) through 3-D polt and density contours in Figure 1 for $t=1$. Obviously, the AP, RP and IP of the solutions all have perfect periodic characteristics, that is, the profile of AP is a perfect wave, on the hand, the contours of the RP and IP are the kinky-perfect waves. They represent the periodic wave propagating along the x-axis and y-axis.

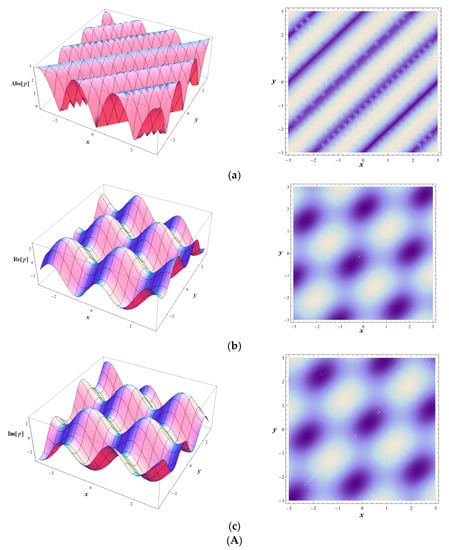
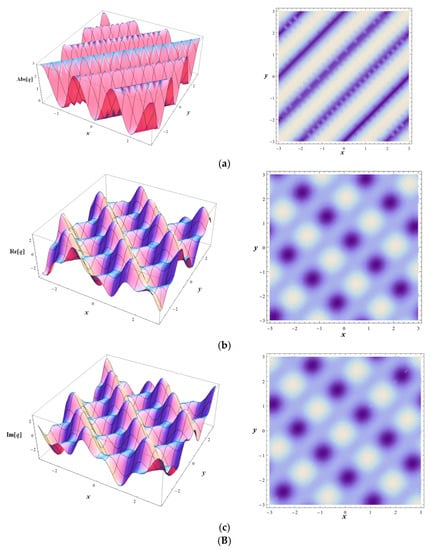
Figure 1. The AP, RP and IP of the PWS given by Equation (42) at t = 1. (A) The performance of $p\left(x,y,t\right)$. (Aa) The 3-D plot and density contour of the AP. (Ab) The 3-D plot and density contour of the RP. (Ac) The 3-D plot and density contour of the IP. (B) The performance of $q\left(x,y,t\right)$. (Ba) The 3-D plot and density contour of the AP. (Bb) The 3-D plot and density contour of the RP. (Bc) The 3-D plot and density contour of the IP.

On basis of Equations (38)–(41), we can acquire the SWSs of Equation (1) as:

Family one:

$$\{\begin{array}{l}p\left(x,y,t\right)=2\sqrt{3}\sec h\left[\sqrt{2}\left(-x+y+2t\right)\right]e^{i\left(x+y+t\right)}\\ q\left(x,y,t\right)=6\sec h^2\left[\sqrt{2}\left(-x+y+2t\right)\right]e^{2i\left(x+y+t\right)}\end{array}$$

(43)

Family two:

$$\{\begin{array}{l}p\left(x,y,t\right)=-2\sqrt{3}\sec h\left[\sqrt{2}\left(-x+y+2t\right)\right]e^{i\left(x+y+t\right)}\\ q\left(x,y,t\right)=6\sec h^2\left[\sqrt{2}\left(-x+y+2t\right)\right]e^{2i\left(x+y+t\right)}\end{array}$$

(44)

The AP, RP and IP of the SWSs obtained by Equations (43) and (44) are described in Figure 2 and Figure 3, respectively, at t = 2. Obviously, the AP shown in Figure 2a and Figure 3a are the bright solitary waves. In addition, the RP and IP of Equations (43) and (44) that plotted in Figure 2b,c and Figure 3b,c are the breathe-like waves, which have breathe wave characteristics.

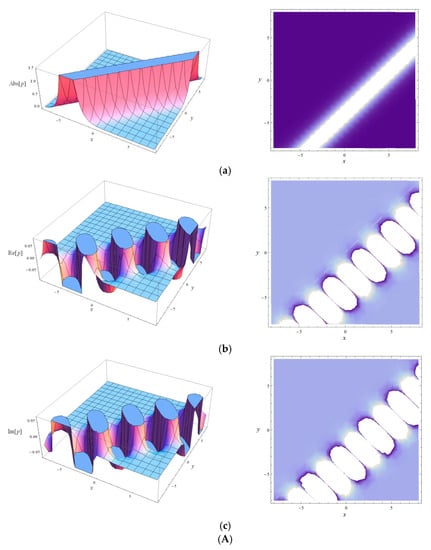
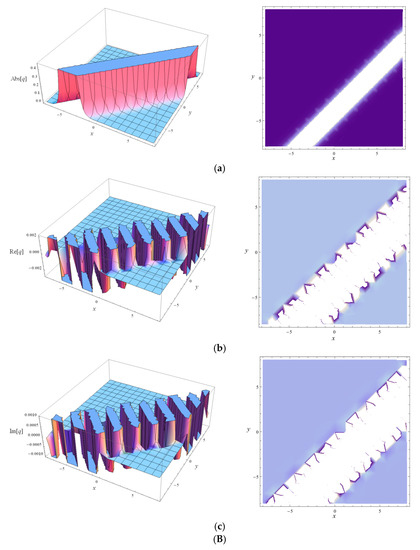
Figure 2. The AP, RP and IP of the SWS given by Equation (43) at t = 2. (A) The performance of $p\left(x,y,t\right)$. (Aa) The 3-D plot and density contour of the AP. (Ab) The 3-D plot and density contour of the RP. (Ac) The 3-D plot and density contour of the IP. (B) The performance of $q\left(x,y,t\right)$. (Ba) The 3-D plot and density contour of the AP. (Bb) The 3-D plot and density contour of the RP. (Bc) The 3-D plot and density contour of the IP.

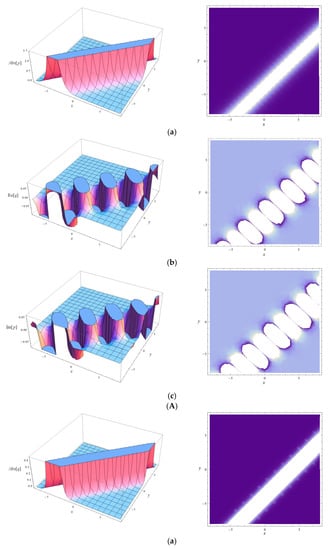
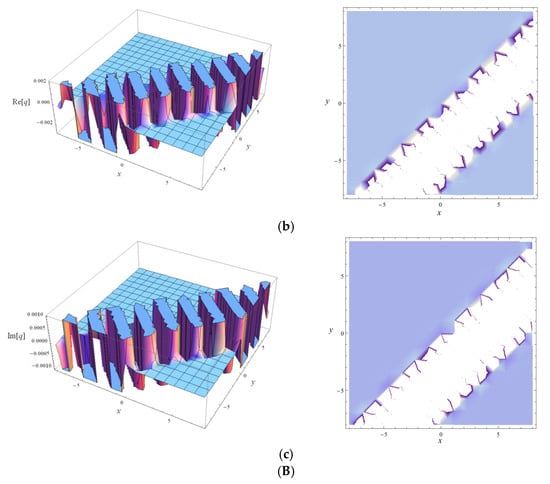
Figure 3. The AP, RP and IP of the SWS given by Equation (44) at t = 2. (A) The performance of $p\left(x,y,t\right)$. (Aa) The 3-D plot and density contour of the AP. (Ab) The 3-D plot and density contour of the RP. (Ac) The 3-D plot and density contour of the IP. (B) The performance of $q\left(x,y,t\right)$. (Ba) The 3-D plot and density contour of the AP. (Bb) The 3-D plot and density contour of the RP. (Bc) The 3-D plot and density contour of the IP.

6. Conclusions and Future Research

In this paper, some explicit exact solutions of the integrable (2+1)-dimensional MS such as PWS and SWS are obtained by utilizing the VA. This method can simplify the equation via reducing the order of the differential equation, avoid the tedious solving process, and obtain the optimal solution through the stationary conditions. The AP, RP and IP of the solutions are illustrated by using proper parameters via the 3-D plot and density contour. The calculations demonstrate that the proposed method is simple, straightforward and effective, which is expected to bring some new inspiration to the study of the travelling wave solutions.

Recently, the fractional and fractal calculus [46,47,48,49,50,51,52,53] have attracted extensive attention in many different fields involving in physics, filter, biological, circuit and so on. How to apply the VA to the fractional and fractal calculus is worthy of consideration and in-depth study.