Countermeasures of Double Carbon Targets in Beijing–Tianjin–Hebei Region by Using Grey Model
Abstract
:1. Introduction
2. Introduction to the Research Area and Data Sources
3. Prediction of Carbon Peak Period in Beijing–Tianjin–Hebei Region
3.1. FGM (1,1) Model
3.2. The Calculation Process
- (1)
- The initial dataset isIn MATLAB (R2018a), a particle swarm optimization algorithm was used to obtain the optimal order of the FGM (1,1) model. Thus, the -order cumulative sequence can be obtained as,Use the least square method to calculate and ,where , . Thus, the .
- (2)
- Put and into ; we can establish that, and
- (3)
- Then, we can establish that the predictive sequence is
- (4)
3.3. Validation of the Model
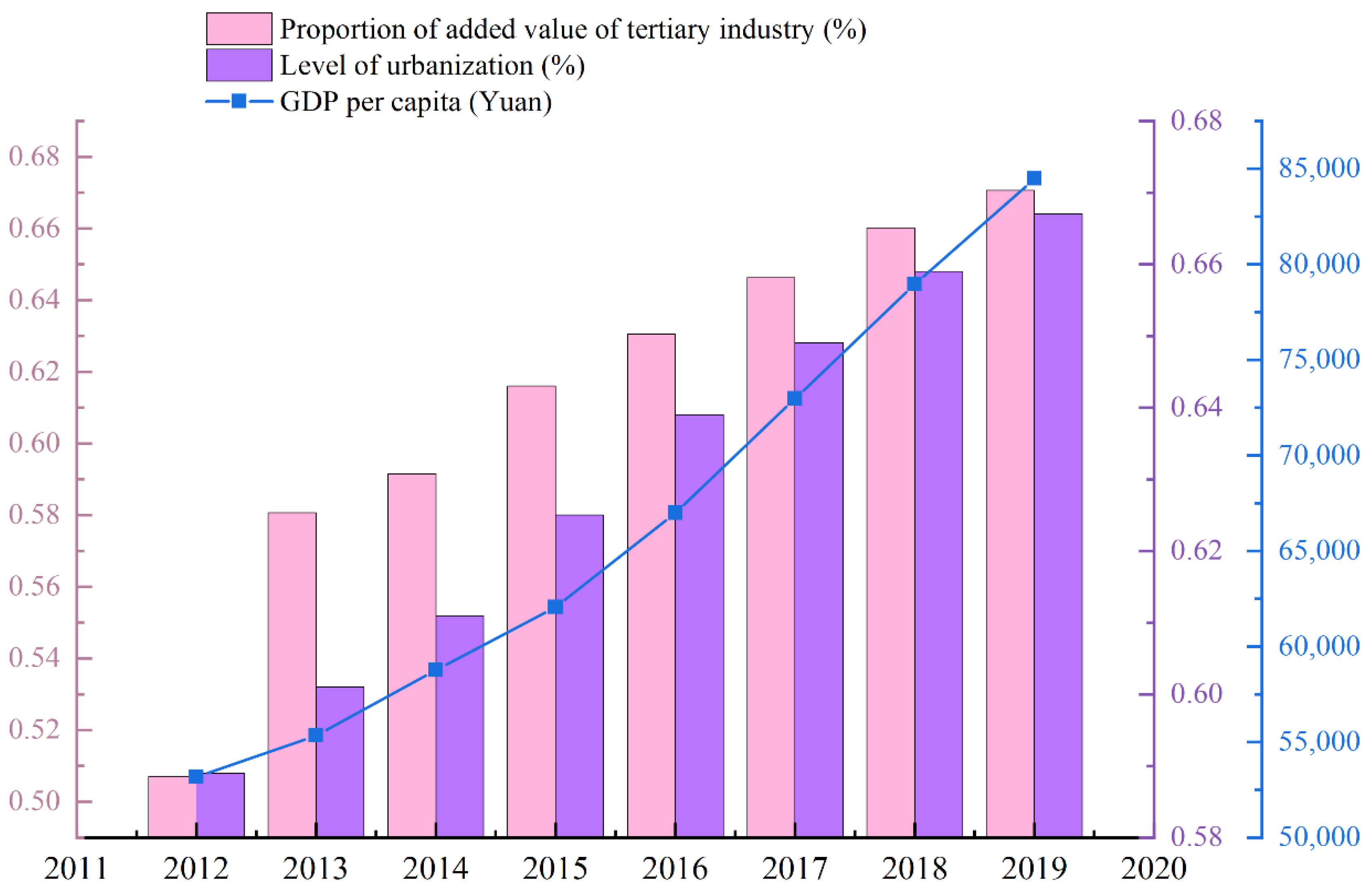
3.4. Index Prediction and Carbon Peak Time Prediction Result Analysis
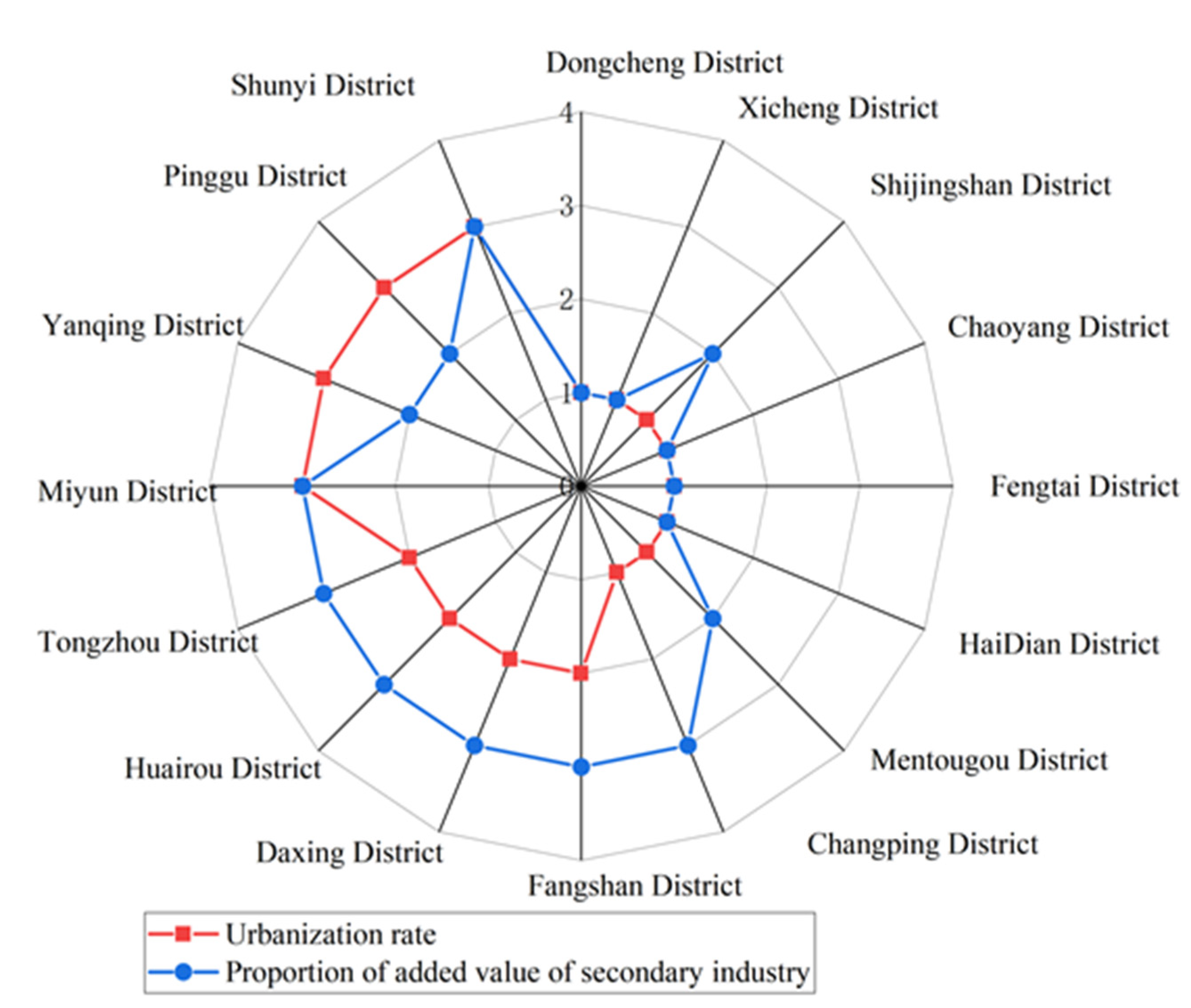
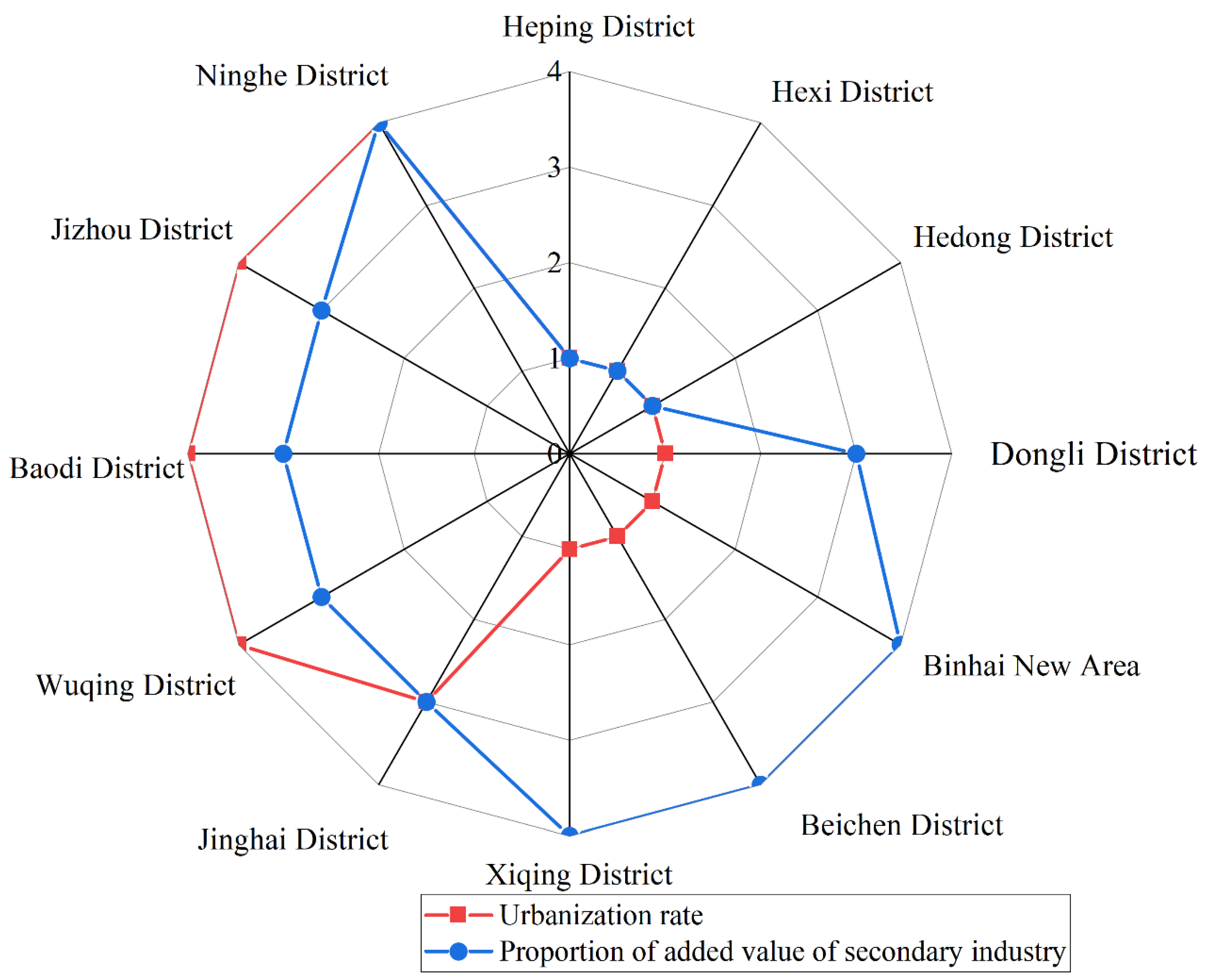
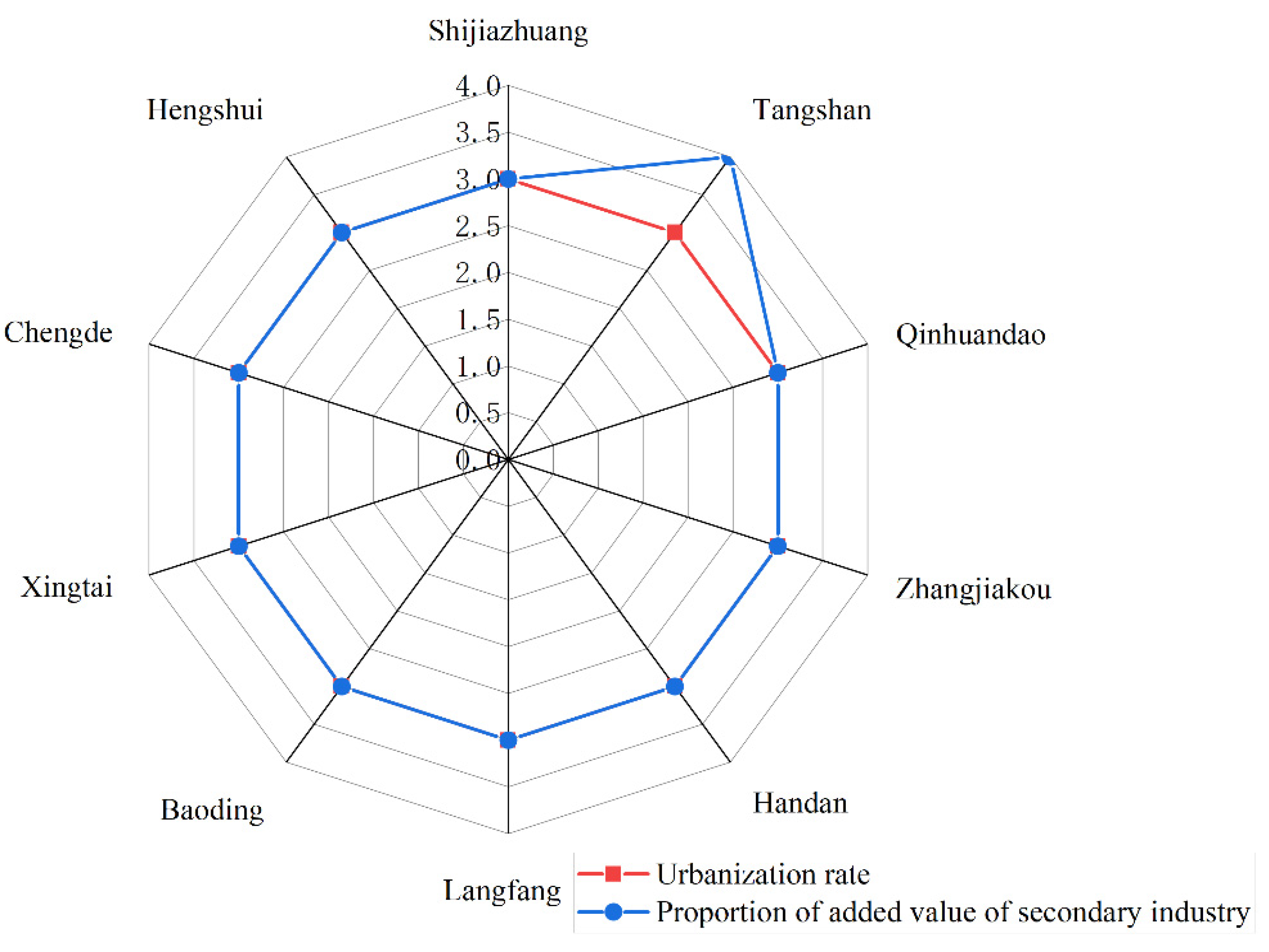
4. Spatial Differentiation Analysis of Carbon Peak in Beijing–Tianjin–Hebei Region
5. Conclusions and Countermeasures to Speed up the Realization of the Dual Carbon Goal in the Beijing–Tianjin–Hebei Region
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fang, D.; Zhang, X.; Yu, Q.; Jin, T.C.; Tian, L. A novel method for carbon dioxide emission forecasting based on improved Gaussian processes regression. J. Clean. Prod. 2018, 173, 143–150. [Google Scholar] [CrossRef]
- Yan, W.; Huang, Y.; Dong, H. Carbon emission prediction of Shandong peninsula blue economic zone based on STIRPAT model. J. Univ. Jinan (Sci. Technol.) 2021, 35, 125–131. [Google Scholar]
- Zhang, Z.; Ren, Y.; Dong, H. Urban carbon emission peaking and low-carbon development: A case study of Shanghai. Environ. Eng. 2020, 38, 12–18. [Google Scholar]
- Liu, X.; Meng, X.; Wang, X. Carbon Emissions Prediction of Jiangsu Province Based on Lasso-BP Neural Network Combined Model. In The IOP Conference Series: Earth and Environmental Science, Proceedings of Carbon Emissions Prediction of Jiangsu Province Based on Lasso-BP Neural Network Combined Model; IOP: Bristol, UK, 2021; Volume 769, No. 2; p. 022017. [Google Scholar]
- Wang, K.; Niu, D.; Zhen, H.; Sun, L.; Xu, X. Carbon emission forecasting in China based on WOA-ELM Model. Ecol. Econ. 2020, 36, 20–27. [Google Scholar]
- Zhu, C.; Wang, M.; Du, W.; Dolezel, P. Prediction on Peak Values of Carbon Dioxide Emissions from the Chinese Transpor-tation Industry Based on the SVR Model and Scenario Analysis. J. Adv. Transp. 2020, 2020, 8848149. [Google Scholar] [CrossRef]
- Ding, S.; Xu, N.; Ye, J.; Zhou, W.; Zhang, X. Estimating Chinese energy-related CO2 emissions by employing a novel discrete grey prediction model. J. Clean. Prod. 2020, 259, 120793. [Google Scholar] [CrossRef]
- Liang, Y.; Lei, S. Analysis and trend forecast of carbon emission factors in the six provinces of central China—An empirical study based on STIRPAT and Grey GM(1,1) Model. Value Eng. 2019, 38, 11–14. [Google Scholar]
- Gao, M.; Yang, H.; Xiao, Q.; Goh, M. A novel method for carbon emission forecasting based on Gompertz’s law and fractional grey model: Evidence from American industrial sector. Renew. Energy 2022, 181, 803–819. [Google Scholar] [CrossRef]
- Gao, M.; Yang, H.; Xiao, Q.; Goh, M. A novel fractional grey Riccati model for carbon emission prediction. J. clean. prod. 2021, 282, 124471. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, L.; Wu, L. Forecasting the carbon dioxide emissions in 53 countries and regions using a non-equigap grey model. Environ. Sci. Pollut. Res. Int. 2021, 28, 15659–15672. [Google Scholar] [CrossRef]
- Xiang, X.; Cai, Y.; Xie, S. Application of a new information priority accumulated grey model with simpson to forecast carbon dioxide emission. J. Adv. Math. Comput. Sci. 2020, 70–83. [Google Scholar] [CrossRef] [Green Version]
- Duan, H.; Wang, D.; Pang, X.; Liu, Y.; Zeng, S. A novel forecasting approach based on multi-kernel nonlinear multivariable grey model: A case report. J. Clean. Prod. 2020, 260, 120929. [Google Scholar] [CrossRef]
- Xu, G.; Schwarz, P.; Yang, H. Adjusting energy consumption structure to achieve China’s CO2 emissions peak. Renew. Sustain. Energy Rev. 2020, 122, 109737. [Google Scholar] [CrossRef]
- Boamah, K.B.; Du, J.; Adu, D.; Mensah, C.N.; Dauda, L.; Khan, M.A.S. Predicting the carbon dioxide emission of China using a novel augmented hypo-variance brain storm optimization and the impulse response function. Environ. Technol. 2021, 42, 4342–4354. [Google Scholar] [CrossRef] [PubMed]
- Cui, G.; Yu, Y.; Zhou, L.; Zhang, H. Driving forces for carbon emissions changes in Beijing and the role of green power. Sci. Total Environ. 2020, 728, 138688. [Google Scholar] [CrossRef] [PubMed]
- Ye, L.; Xie, N.; Hu, A. A novel time-delay multivariate grey model for impact analysis of CO2 emissions from China’s transportation sectors. Appl. Math. Model. 2021, 91, 493–507. [Google Scholar] [CrossRef]
- Yang, X.; Meng, C.; Lin, J. Research on the Spatio-temporal evolution and regional heterogeneity of carbon emissions in Beijing’s four functional zones. J. China Univ. Geosci. (Soc. Sci. Ed.) 2021, 21, 77–90. [Google Scholar]
- Xu, G.; Cai, Z.; Feng, S. Research on the temporal and spatial differences of carbon emissions and influencing factors based on the two-stage LMDI Model—Taking Jiangsu Province as an example. Soft Sci. 2021, 35, 107–113. [Google Scholar] [CrossRef]
- Yang, X.; Jia, Z.; Yang, Z.; Yuan, X. The effects of technological factors on carbon emissions from various sectors in China—A spatial perspective. J. Clean. Prod. 2021, 301, 126949. [Google Scholar] [CrossRef]
- Zhao, Z.Y.; Yuan, S.G.; Fu, Y.; Wang, Y.; Li, H. Analysis of the Spatial and Temporal Differences of China’s Power Carbon Footprint. J. Electr. Comput. Eng. 2020, 2020, 3701939. [Google Scholar] [CrossRef] [Green Version]
- Xu, Q.; Dong, Y.X.; Yang, R.; Zhang, H.O.; Wang, C.J.; Du, Z.W. Temporal and spatial differences in carbon emissions in the Pearl River Delta based on multi-resolution emission inventory modeling. J. Clean. Prod. 2019, 214, 615–622. [Google Scholar] [CrossRef]
- Wang, R.; Feng, Y. Research on China’s agricultural carbon emission efficiency evaluation and regional differentiation based on DEA and Theil models. Int. J. Environ. Sci. Technol. 2021, 18, 1453–1464. [Google Scholar] [CrossRef]
- Liu, H.; Song, Y. Financial development and carbon emissions in China since the recent world financial crisis: Evidence from a spatial-temporal analysis and a spatial Durbin model. Sci. Total Environ. 2020, 715, 136771. [Google Scholar] [CrossRef] [PubMed]
- Bai, C.; Zhou, L.; Xia, M.; Feng, C. Analysis of the spatial association network structure of China’s transportation carbon emissions and its driving factors. J. Environ. Manag. 2020, 253, 109765. [Google Scholar] [CrossRef]
- Ding, B.; Zhao, Y.; Deng, J. Research on Measurement, Decoupling Characteristics and Driving Factors of Carbon Emissions from China’s Planting Industry. J. China Agric. Resour. Reg. Plan. 2021, 1–14. [Google Scholar]
- Cao, J.; Zhou, L. Research on the Spatial and Temporal Distribution of Carbon Emissions of Logistics Industry in the Yang-tze River Delta and Its Influencing Factors. Stat. Decis. 2021, 37, 79–83. [Google Scholar]
- Wang, X.X.; He, A.Z.; Zhao, J. Regional disparity and dynamic evolution of carbon emission reduction maturity in China’s service industry. J. Clean. Prod. 2020, 244, 118926. [Google Scholar] [CrossRef]
- Tang, C.; Wan, Z.; Ng, P.; Dai, X.; Sheng, Q.; Chen, D. Temporal and Spatial Evolution of Carbon Emissions and Their Influencing Factors for Tourist Attractions at Heritage Tourist Destinations. Sustainability 2019, 11, 5944. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Xiao, Q. An empirical analysis on spatial correlation investigation of industrial carbon emissions using SNA-ICE model. Energy 2021, 224, 120183. [Google Scholar] [CrossRef]
- Wu, L.; Liu, S.; Yao, L.; Yan, S.; Liu, D. Grey system model with the fractional order accumulation. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 1775–1785. [Google Scholar] [CrossRef]
- Zhang, Y.; Luo, H.; Wang, C. International Trend Analysis of Carbon Neutrality Action. Adv. Clim. Chang. Res. 2021, 17, 88–97. [Google Scholar]
- Zang, H.; Yang, W.; Zhang, J. Research on peak carbon dioxide emissions in Beijing-Tianjin-Hebei urban agglomeration. Environ. Eng. 2020, 38, 19–24. [Google Scholar]
- Li, J.; Gu, A.; Zhang, C. “Fourteenth Five-Year Plan” China’s provincial economic development, energy demand and carbon emissions prospects-based on the analysis of the CMRCGE model. Adv. Clim. Chang. Res. 2019, 15, 649–659. [Google Scholar]
- Qi, W.; Li, G. Residential carbon emission embedded in China’s inter-provincial population migration. Energy Policy 2020, 136, 111065. [Google Scholar] [CrossRef]
| Year | Real Value | FGM (1,1) | GM (1,1) |
|---|---|---|---|
| 2012 | 38,596.63 | 38,596.63 | 38,596.63 |
| 2013 | 39,845.88 | 39,300.40 | 40,572.05 |
| 2014 | 40,143.33 | 41,847.95 | 41,860.43 |
| 2015 | 42,607.35 | 43,923.47 | 43,189.74 |
| 2016 | 47,827.52 | 45,402.46 | 44,561.25 |
| 2017 | 47,985.00 | 46,370.29 | 45,976.32 |
| 2018 | 47,772.00 | 46,931.12 | 47,436.32 |
| 2019 | 46,348.00 | 47,176.44 | 48,942.69 |
| MAPE | 2.59% | 3.1% |
| Area | GDP Per Capita/(Yuan/person) | Level of Urbanization/% | Proportion of Added Value of Tertiary Industry/% | |
|---|---|---|---|---|
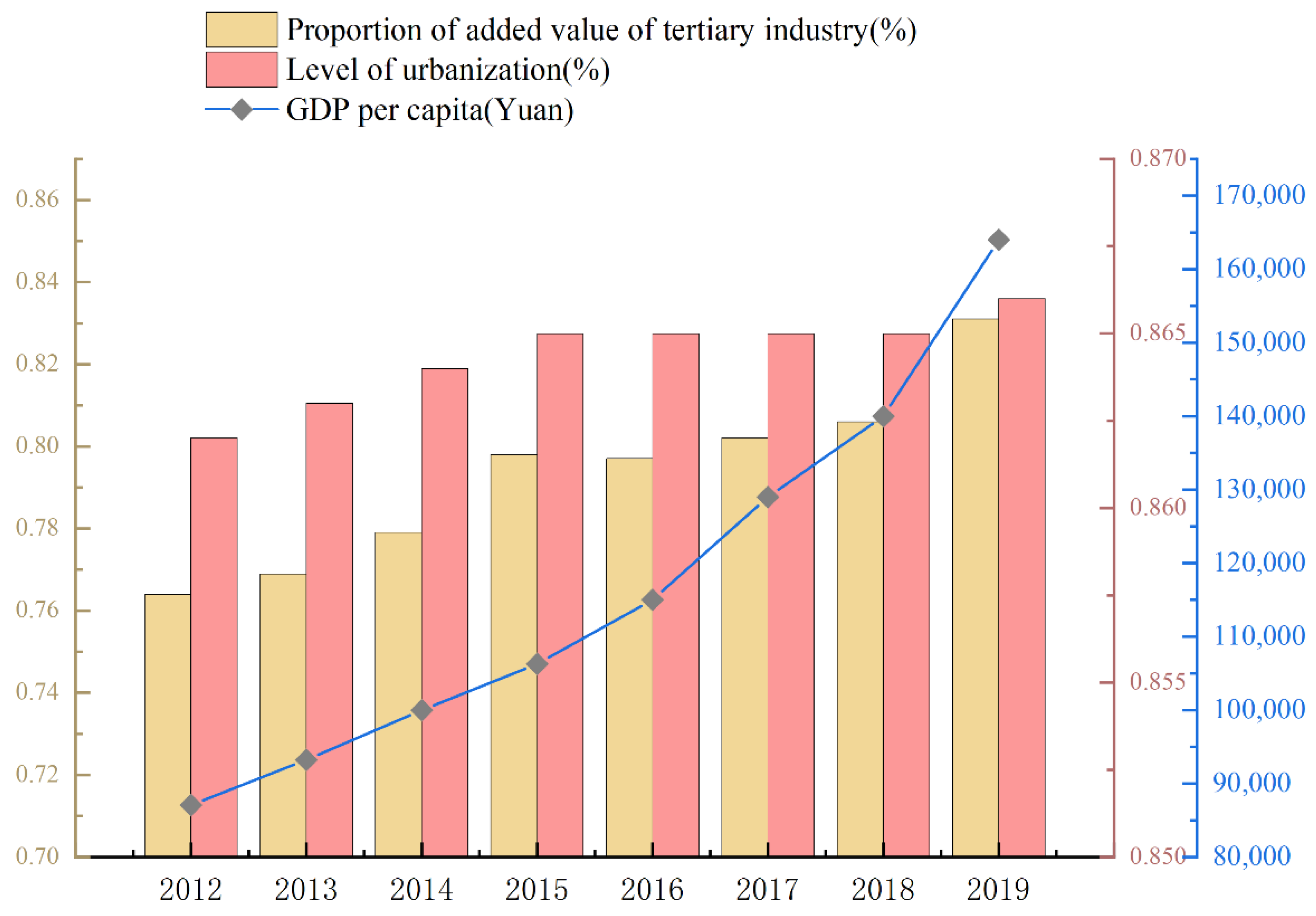
| Beijing | 2019 | 164,000 | 86.60% | 83.10% |
| Estimated realization time | (129,000) 2018 | Implemented | Implemented | |
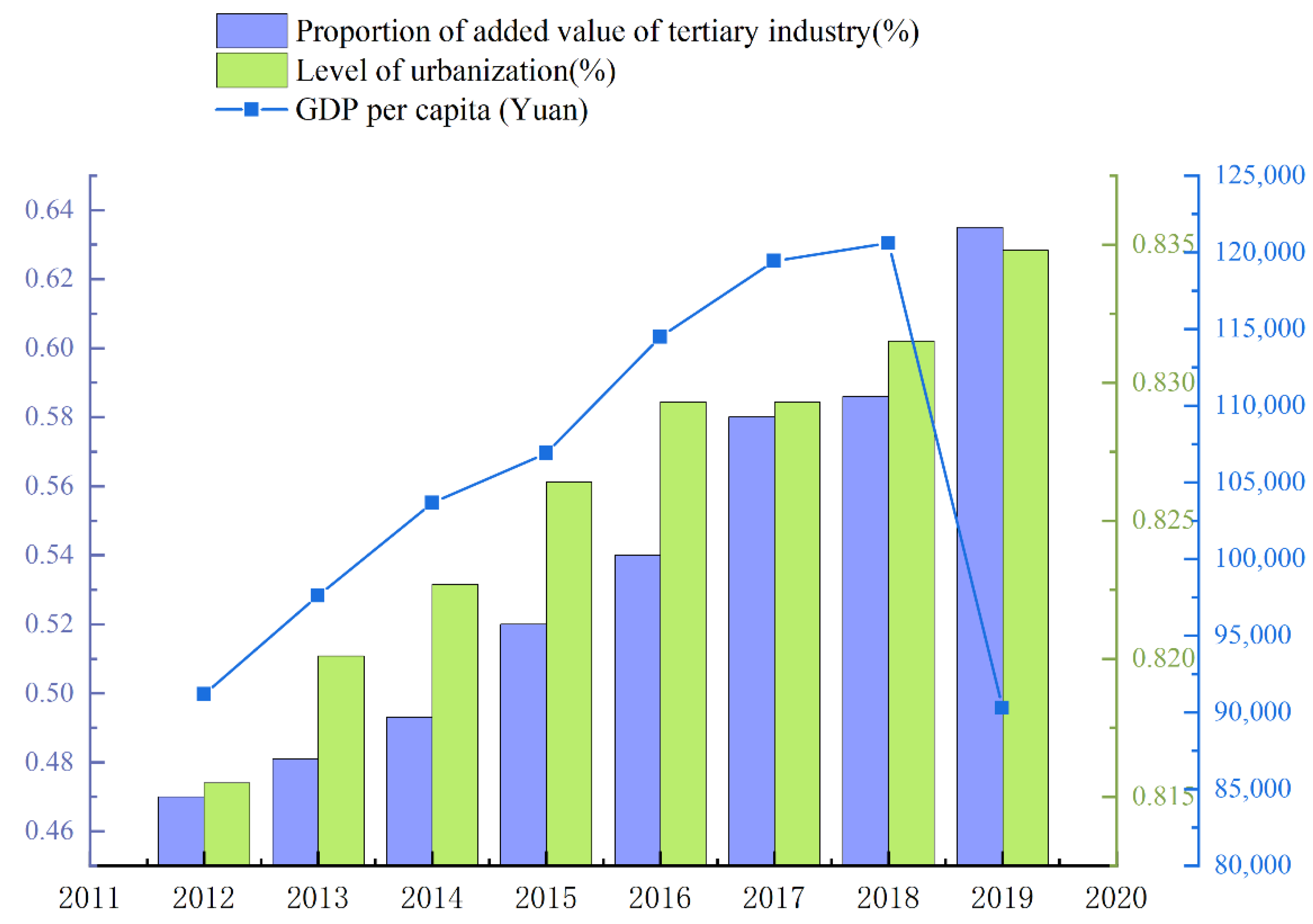
| Tianjin | 2019 | 90,306.12 | 83.48% | 63.50% |
| Estimated realization time | (129,000) 2028 | Implemented | (65%)2020 | |
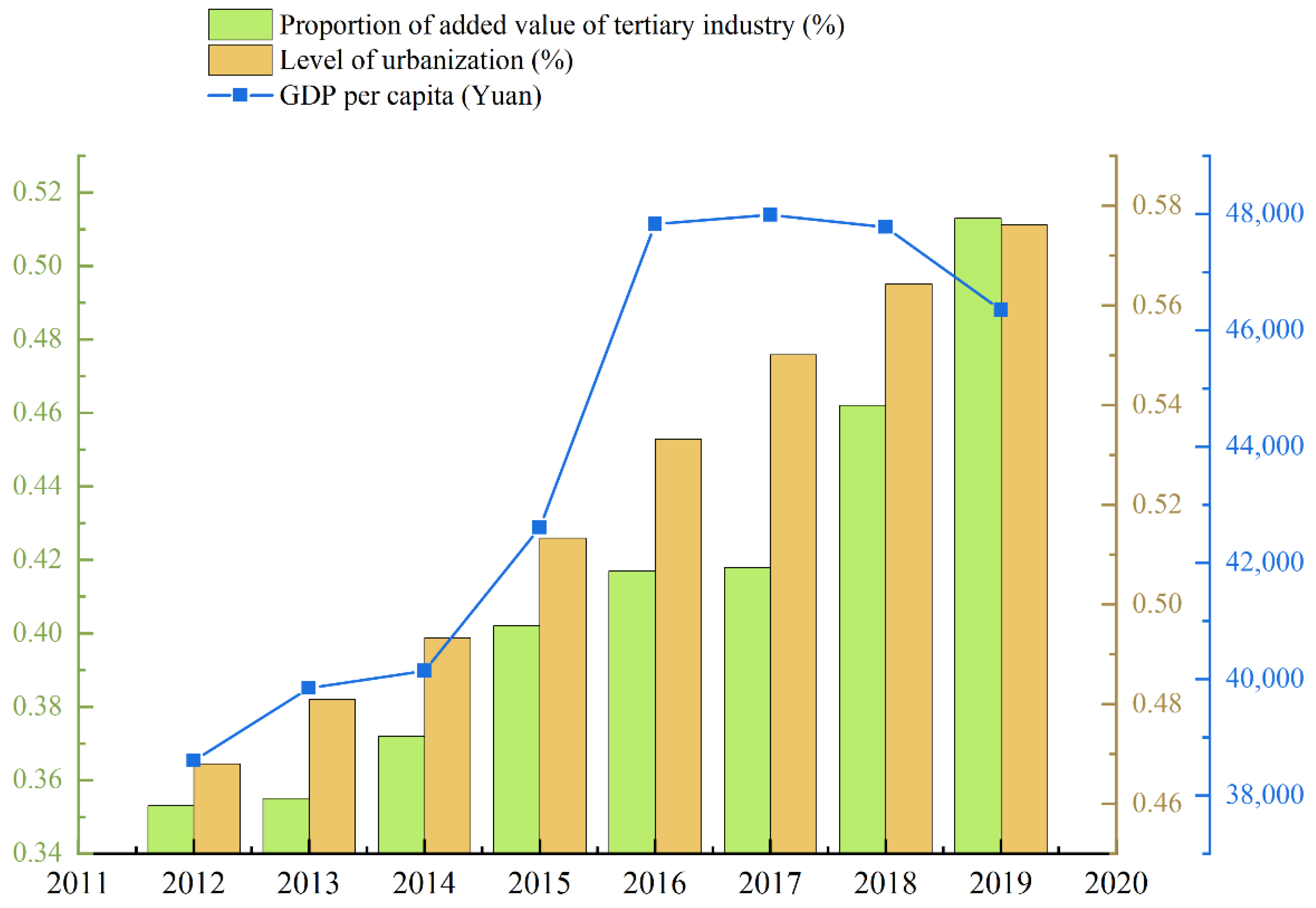
| Hebei | 2019 | 46,348 | 57.62 | 51.03% |
| Estimated realization time | (129,000) 2053 | (75%)2027 | (65%)2027 | |
| Beijing–Tianjin–Hebei Region | 2019 | 84,479.23 | 66.7 | 67.06% |
| Estimated realization time | (129,000) 2025 | (75%) 2044 | (65%)2018 | |
| Region | Implementation of the Main Body | Corresponding Suggestions | Corresponding Region |
|---|---|---|---|
| First reach peak area | Urban government, Ecological environment administration, Energy department, Transportation management department, Development and Reform Commission |
| Dongcheng District, Xicheng District, Shijingshan District, Chaoyang District, Fengtai District, Haidian District, Mentougou District, Heping District, Hexi District, Hedong District, Nankai District, Hongqiao District |
| Region | Implementation of the Main Body | Corresponding Suggestions | Corresponding Region |
|---|---|---|---|
| Easy to peak on schedule | Urban government, Ecological environment administration, Development and Reform Commission |
| Changping District, Fangshan District, Daxing District, Huairou District, Tongzhou District, Yanqing, Pinggu, Miyun District, Shunyi District, Binhai New District, Beichen District, Dongli District, Xiqing District, Shijiazhuang |
| Region | Implementation of the Main Body | Corresponding Suggestions | Corresponding Region |
|---|---|---|---|
| Generally easy to peak on schedule | Ecological environment administration agency, District (city) government, Development and Reform Commission |
| Wuqing District, Baodi District, Jinghai District, Tangshan, Qinhuangdao, Handan, Xingtai, Baoding, Zhangjiakou, Chengde, Langfang, Hengshui |
| Region | Implementation of the Main Body | Corresponding Suggestions | Corresponding Region |
|---|---|---|---|
| May reach peak overdue | Municipal ecological environment administration agency, Development and Reform Commission |
| Jizhou District, Ninghe District |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Wang, M.; Wu, L. Countermeasures of Double Carbon Targets in Beijing–Tianjin–Hebei Region by Using Grey Model. Axioms 2022, 11, 215. https://doi.org/10.3390/axioms11050215
Liu Z, Wang M, Wu L. Countermeasures of Double Carbon Targets in Beijing–Tianjin–Hebei Region by Using Grey Model. Axioms. 2022; 11(5):215. https://doi.org/10.3390/axioms11050215
Chicago/Turabian StyleLiu, Zhenxiu, Meng Wang, and Lifeng Wu. 2022. "Countermeasures of Double Carbon Targets in Beijing–Tianjin–Hebei Region by Using Grey Model" Axioms 11, no. 5: 215. https://doi.org/10.3390/axioms11050215
APA StyleLiu, Z., Wang, M., & Wu, L. (2022). Countermeasures of Double Carbon Targets in Beijing–Tianjin–Hebei Region by Using Grey Model. Axioms, 11(5), 215. https://doi.org/10.3390/axioms11050215






