A Distinguished Subgroup of Compact Abelian Groups
Abstract
:1. Introduction
- (FD1)
- It contains , is dense in G, and is torsion-free and divisible (Theorem 6(2),(4),(6) and Theorem 10(2)).
- (FD2)
- If G is not totally disconnected, then is a proper subgroup of G, and hence is not locally compact (Proposition 6(1)).
- (FD3)
- is zero-dimensional (Theorem 19), and contains every closed totally disconnected subgroup of G (Proposition 5).
- (FD4)
- Fat Delta is a functorial subgroup in the sense that for any morphism we have (Corollary 3, Proposition 10(1)), moreover if f is surjective (Proposition 10(2)).
- (FD5)
- The Fat Delta of a product is the product of the Fat Deltas of the factors (Theorem 10(4), Proposition 10(4)).
- (FD6)
- If is a compact group, then (see Theorem 10(1) for a more rigorous formulation).
- (FD7)
- determines G up to topological isomorphism (Theorem 12).
2. Notation and Background
- The category of discrete abelian groups with morphisms algebraic homomorphisms, ≅ denoting isomorphism in this category, also called algebraic isomorphism;
- is the category of topological abelian groups with morphisms continuous algebraic homomorphisms, denoting isomorphism in this category;
- is as usual the full subcategory of consisting of locally compact Hausdorff groups.
- (1)
- Suppose that φ is continuous and K is dense in G. Then H is indiscrete.
- (2)
- Suppose that φ is an open map and H is indiscrete. Then K is dense in G.
- (3)
- Suppose that H is indiscrete and is endowed with the compact-open topology. Then is indiscrete.
3. The Meet Semi-Lattice of Full Free Subgroups in AG
- (1)
- is a linearly independent set in A if and only if is a linearly independent set in . Moreover, is maximal linearly independent if and only if is maximal linearly independent.
- (2)
- If is a (maximal) linearly independent set in A and , then is a (maximal) linearly independent subset of A.
- (3)
- Every linearly independent set extends to a maximal linearly independent set. In particular, every torsion-free element in A is contained in a maximal linearly independent subset.
- (4)
- If is a maximal linearly independent subset of A, then is a full free subgroup of A. Conversely, if is a full free subgroup of A, then is a maximal linearly independent subset of A.
- (5)
- If , then and , , and .
- (6)
- Given , there exists such that and . If and , then there is such that . Note that
- (7)
- A maximal linearly independent subset of is a –basis of .
- (8)
- If is a –basis of , then there exist positive integers such that and is a full free subgroup of A.
- (1)
- Let . Then .
- (2)
- If , and is a torsion group, then .
- (3)
- If , then and .
- (4)
- . If then and .
- (5)
- is a meet semi-lattice with meet ∩.
- (6)
- Let . Then for some , and . If A is torsion-free, then .
4. The Semi-Lattices and
- is a join semi-lattice with join +.
- ; if , then ; .
- (1)
- is a join semi-lattice with join +. Hence, .
- (2)
- is dense in G, while if , otherwise .
- (3)
- Let and and assume that . Then and .
- (4)
- If , then for any . Hence, and .
- (5)
- Let and . Then there is such that . If A is torsion-free, then .
- (6)
- is torsion-free.

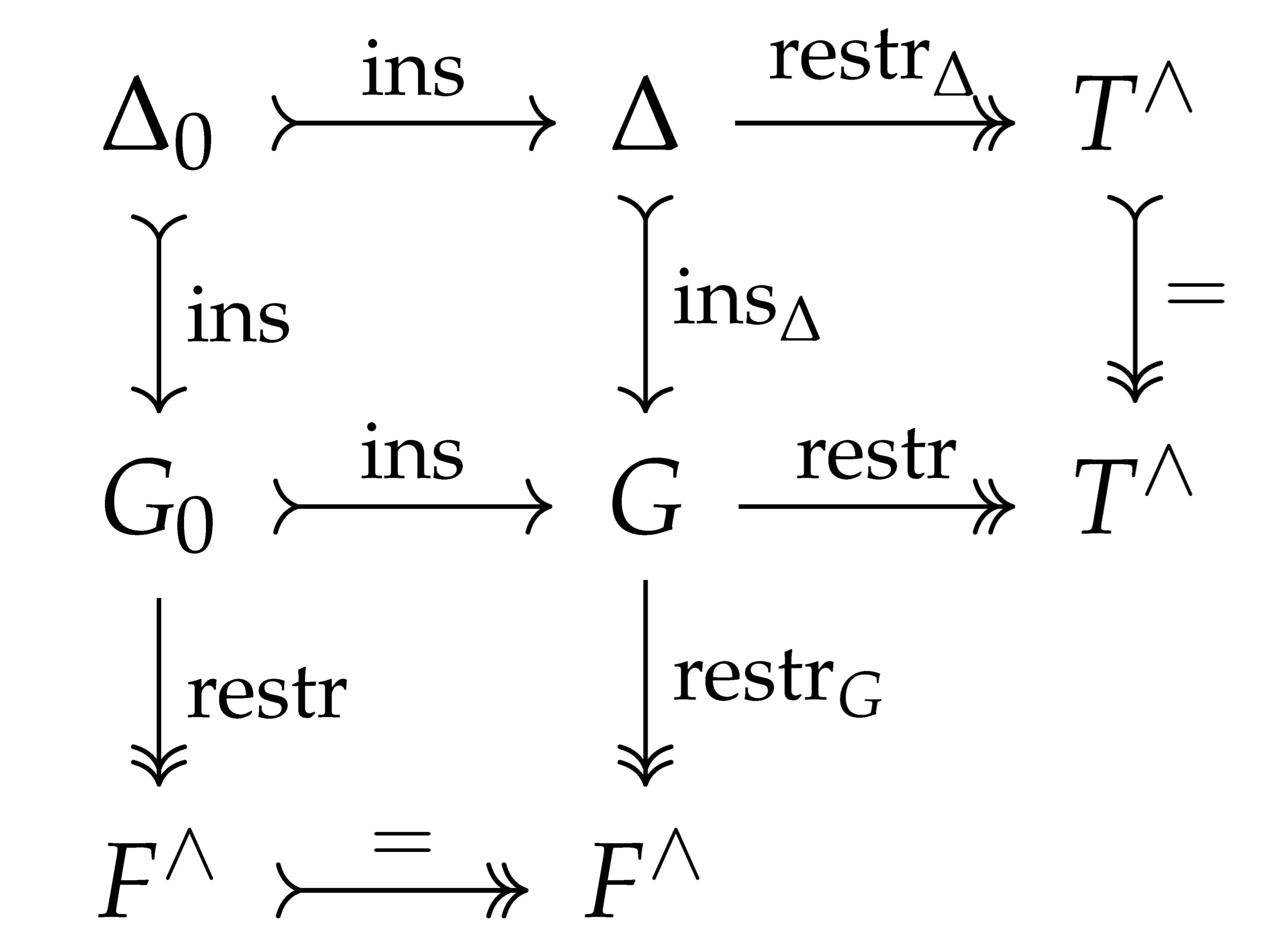
- (1)
- coincides with the 0–component of G.
- (2)
- is divisible and so, algebraically, and if and only if A splits, i.e., .
- (3)
- . Thus , , and is closed in .
- (4)
- and .
- (5)
- and .
- (6)
- With the established notation is divisible and hence algebraically a direct summand of .
- (7)
- There is a topological isomorphism .
- (1)
- Suppose that D is a closed subgroup of G such that is a torus. Then there exists such that . In particular, for every , there is such that .
- (2)
- There exists such that is torsion-free.
- (1)
- Suppose that D is a subgroup of G such that is a torus. Then there exists a subgroup of G such that and is a torus. In particular, for every , there is such that .
- (2)
- There exists a torsion-free .
5. The Fat Delta of Compact Groups
- ,
- is dense in G,
- and is torsion-free.
- is divisible.
- (1)
- If G is totally disconnected, then so is H.
- (2)
- If G is a torus, then so is H.
- (1)
- is zero-dimensional, in particular totally disconnected (Theorem 19). Consequently, if G is not totally disconnected, then and hence is not a locally compact subgroup of G.
- (2)
- Any countable extension of is zero-dimensional (in particular totally disconnected) as well (Proposition 11).
- (1)
- Suppose that H is a topological subgroup of K such that for all we have . Let be the insertion. Then is a topological isomorphism.
- (2)
- Suppose that is a short exact sequence in , α is proper, and G is some other topological group. Thenis an exact sequence in and is proper. The map is not claimed to be surjective.
- (3)
- Let be a short exact sequence of discrete groups and let G be a divisible topological group. Thenis an exact sequence of topological groups. In addition, is proper.
- (4)
- For a discrete torsion group , we have , the topological isomorphism being , and where .

- (1)
- By standard discrete homological algebra the diagram is commutative and rows and columns are exact.
- (2)
- All the domains of the Hom groups carry the discrete topology, hence in all cases.
- (3)
- All Hom groups in the diagram carry the compact-open topology. It follows from Lemma 8(2) that all the maps are continuous. It follows from Lemma 8(3) that all the maps are continuous.
- (4)
- By Lemma 8(1) the left most is a topological isomorphism.
- (5)
- By Lemma 8(2) columns 2 and 3 are exact in .
- (6)
- By Lemma 8(3) the three rows are exact in .
- (7)
- The situation of Lemma 9 matches the top part of (5) and we conclude that is a quotient map. It is easy to see that is an isomorphism. Since both groups are indiscrete (by Lemma 2(3)), this is a topological isomorphism.
- (1)
- where .
- (2)
- . Algebraically, where .
- (3)
- If where , then .
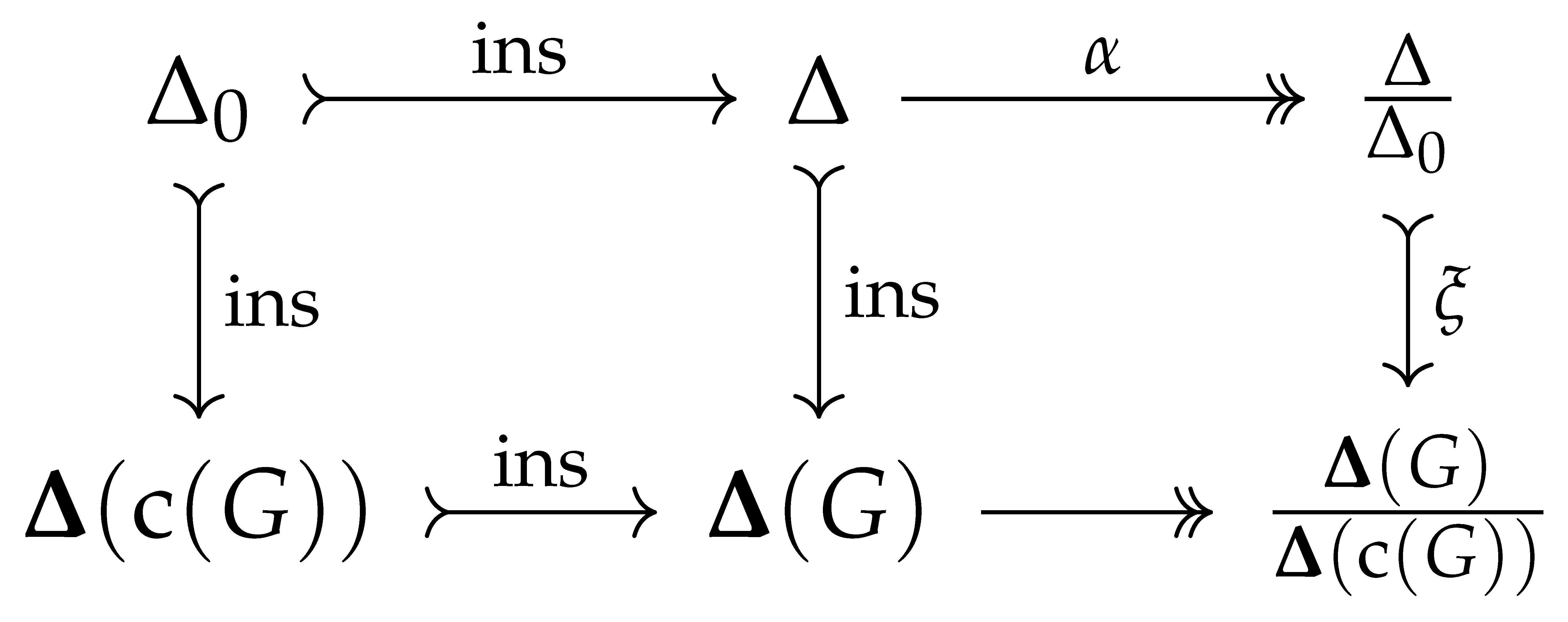
- (1)
- Let G and H be compact abelian groups and . Then ; in particular is fully invariant in G and if , then .
- (2)
- Let be compact abelian groups. Suppose that is a short exact sequence in . Then is a short exact sequence in .
- (1)
- D is totally disconnected and zero-dimensional (Proposition 11).
- (2)
- The completion of D is compact (i.e., D is precompact), and .
- (3)
- D contains a directed family of compact totally disconnected subgroups such that .
- (4)
- if and only if is totally disconnected, and, if so, is compact.
- (5)
- D is totally minimal (Theorem 19).
- (1)
- is a divisible hull of X,
- (2)
- ,
- (3)
- .
- (1)
- Let . Then there exist values such thatFor , one has if and only if .
- (2)
- Let and . Then (with a harmless identification) , and where is the group of p-adic integers and is the cyclic group of order for . Furthermore, Σ and are divisible, , and .
- (3)
- and .
- (1)
- For a first concrete example, let and . Then , and is the divisible hull of and .
- (2)
- Next let . Then , is torsion-free, and is the divisible hull of Δ, so where is the additive group of p-adic numbers.
- (3)
- For , , , , but , is the divisible hull of , so .
6. Resolutions
- (i)
- ([1], Proposition 7.38(i), p. 374) and commutes with products, i.e., .
- (ii)
- ([1], Proposition 7.38(ii), p. 374) If is a morphism in , then is injective, whenever is totally disconnected;
- (iii)
- ([1], Corollary 8.19, p. 419) if G is a compact group and with , then, with , is a topological isomorphism. The last equality is in fact a topological isomorphism obtained as composition of two others. The first one is the isomorphism from (i). The second one is , that can be obtained from the obvious equality , by letting for .
- (1)
- φ is continuous, surjective, and open, i.e., is a quotient morphism.
- (2)
- is algebraically and topologically isomorphic to , and Γ is a closed totally disconnected subgroup of . In particular, it does not contain any nonzero vector spaces.
- (3)
- is dense in , the identity component of G.
- (1)
- φ is surjective, continuous, and open.
- (2)
- . The projection maps Γ isomorphically onto , so . Furthermore, is a closed totally disconnected subgroup of .
- (3)
- , in particular ;
- (4)
- where carries the discrete topology, i.e., the subspace topology in .
- (5)
- is dense in Δ.
- (1)
- the map is surjective, continuous, and open;
- (2)
- is torsion-free and φ induces an isomorphism ;
- (3)
- If G is connected of finite dimension , then .
- (4)
- is dense in G.
- (a)
- For the solenoid, there is an isomorphism and , where , by Definition 3(iii). Since , we obtain the canonical resolution with and evidently .
- (b)∧
- For the solenoid from Example 1 (2) is the divisible hull of its delta subgroup . Moreover, (see Remark 5(c)). Theorem 15 gives the canonical resolution with as in (a) and dense in .Denote by the group equipped with the finer topology obtained by taking Δ as an open topological subgroup of . Then is a locally compact ring and is the adele ring of . Composing φ with the identity we obtain a continuous surjective homomorphism which is again open by the Open Mapping Theorem (as is σ-compact). Hence, is a quotient of .
7. Fat Delta through the Looking Glass of Quasi-Torsion Elements
7.1. Quasi-Torsion Elements
- 1
- If , then if and only if there exists a continuous homomorphism with ;
- 2
- is a subgroup of G containing every compact totally disconnected subgroup of G;
- 3
- If G is complete (in particular, locally compact), then coincides with the union of all compact, totally disconnected subgroups of G.
- (a)
- Items (1), (3) and (4) follow from Proposition 9 and reinforce Corollary 3(1) by showing that td is a functorial subgroup in thelargercategory .
- (b)
- In (2) “compact” cannot be replaced by “locally compact” (take , and f the canonical quotient map, then , while ).
- (c)
- Item (4) reinforces Theorem 10(3) showing that it remains valid in the largercategory .
7.2. The Subgroup of Compact Groups and Minimality
- (a)
- minimalif every continuous isomorphism onto a Hausdorff topological group H is open.
- (b)
- totally minimalif G satisfies the (full) Open Mapping Theorem, i.e., every continuous homomorphism onto a Hausdorff topological group H is open.
7.3. Sylow Subgroups of for
- (1)
- G is totally disconnected;
- (2)
- , i.e., is compact;
- (3)
- is compact for every prime p;
- (4)
- is compact for some prime p;
- (5)
- is closed in G for some prime p (equivalently, for all primes p);
- (6)
- the topology induced from G on coincides with the topology induced by the product topology of .
- (1)
- is torsion;
- (2)
- is topologically essential;
- (3)
- G contains copies of the p-adic integers for no prime p;
- (4)
- and for every continuous surjective homomorphism we have , where each is a (bounded) compact p-group;
- (5)
- and there exists a homomorphism as in (3);
- (6)
- algebraically, where each is a (bounded) compact p-group;
- (7)
- A isstrongly non-divisible, i.e., all non-trivial quotients of A are non-divisible;
- (8)
- every proper subgroup of A is contained in some maximal subgroup of A;
- (9)
- A admits a surjective homomorphism for no prime p;
- (10)
- and , where each is a bounded p-group, for every ;
- (11)
- and there exists as in (10).
- (1)
- G is an exotic torus if and only if (i.e., has no entries ∞).
- (2)
- It follows from (1) that there are many pairwise non-isomorphic connected one-dimensional exotic tori G; they all have , according to Corollary 5. Nevertheless, for these exotic tori G the subgroups remain pairwise non isomorphic (since, similarly to Theorem 12, if , then for every pair of compact abelian groups ).
- (3)
- According to Theorem 13, if G is an exotic torus, then is dense in G if and only if is infinite (see ([32], Proposition 2.5) for a more general result in the case of connected exotic tori of arbitrary dimension). According to Theorem 21, in this case, is the smallest dense topologically essential subgroups of G.
- (4)
- The second assertion in (3) is related to the following more general fact proved in ([33], Theorem 5.1) justifying the interest in dense socles: a connected compact abelian group G contains a smallest dense topologically essential (i.e., smallest dense minimal) subgroup of G if and only if G is an exotic torus with dense .
8. Final Comments and Open Problems
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hofmann, K.H.; Morris, S.A. The Structure of Compact Groups, a Primer for the Student—A Handbook for the Expert, 4th ed.; De Gruyter: Berlin, Germany, 2020. [Google Scholar]
- Lewis, W.; Loth, P.; Mader, A. Free subgroups with torsion quotients and profinite subgroups with torus quotients. Rend. Sem. Mat. Padova 2020, 144, 177–195. [Google Scholar] [CrossRef]
- Dikranjan, D.; Prodanov, I.; Stoyanov, L. Topological Groups: Dualities and Minimal Group Topologies; Pure and Applied Mathematics; Marcel Dekker Inc.: New York, NY, USA; Basel, Switzerland, 1989; Volume 130. [Google Scholar]
- Stojanov, L. Weak periodicity and minimality of topological groups. Annu. Univ. Sofia Fac. Math. Méc. 1979, 73, 155–167. [Google Scholar]
- Banaschewski, B. Minimal topological algebras. Math. Ann. 1974, 211, 107–114. [Google Scholar]
- Dikranjan, D. On a class of finite-dimensional compact abelian groups. In Topology, Theory and Applications (Eger, 1983), Colloquia Mathematica Societatis János Bolyai; North-Holland Publishing Company: Amsterdam, The Netherlands, 1985; Volume 41, pp. 215–231. [Google Scholar]
- Dikranjan, D. Recent advances in minimal topological groups. Topol. Appl. 1998, 85, 53–91. [Google Scholar] [CrossRef] [Green Version]
- Dikranjan, D.; Megrelishvili, M. Minimality Conditions in Topological Groups; Recent Progress in General Topology. III; Atlantis Press: Paris, France, 2014; pp. 229–327. [Google Scholar]
- Doïtchinov, D. Produits des groupes topologiques minimaux. Bull. Sci. Math. 1972, 97, 59–64. [Google Scholar]
- Eberhard, V.; Schwanengel, U. (Q/Z)ω est un groupe topologique minimal. Rev. Roum. Math. Pures Appl. 1982, 27, 957–964. [Google Scholar]
- Prodanov, I. Precompact minimal group topologies and p–adic numbers. Annu. Univ. Sofia Fac. Math. Méc. 1971, 66, 249–266. [Google Scholar]
- Prodanov, I. Minimal topologies on countable abelian groups. Annu. Univ. Sofia Fac. Math. Méc. 1975, 70, 107–118. [Google Scholar]
- Prodanov, I. Some minimal group topologies are precompact. Math. Ann. 1977, 227, 117–125. [Google Scholar] [CrossRef] [Green Version]
- Prodanov, I.; Stoyanov, L. Every minimal abelian group is precompact. C. R. Acad. Bulg. Sci. 1984, 37, 23–26. [Google Scholar]
- Stephenson, R.M., Jr. Minimal topological groups. Math. Ann. 1971, 192, 193–195. [Google Scholar] [CrossRef]
- Dikranjan, D.; Lewis, W.; Loth, P.; Mader, A. Fat Delta 2: Functorial subgroups of topological abelian groups. Topol. Proc. 2022; submitted. [Google Scholar]
- Fuchs, L. Abelian Groups; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Moskowitz, M. Homological algebra in locally compact abelian groups. Trans. Am. Math. Soc. 1967, 127, 182–212. [Google Scholar] [CrossRef]
- Mader, A. Almost Completely Decomposable Groups (Algebra, Logic and Applications); Gordon and Breach Science Publishers: Amsterdam, The Netherlands, 2000; Volume 13. [Google Scholar]
- Reid, J. A note on torsion–free abelian groups of infinite rank. Proc. Am. Math. Soc. 1962, 13, 222–225. [Google Scholar] [CrossRef]
- Jacoby, C.; Loth, P. Abelian Groups: Structures and Classifications; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Lewis, W.; Loth, P.; Mader, A. The main decomposition of finite–dimensional protori. J. Group Theory 2021, 24, 109–127. [Google Scholar] [CrossRef]
- Hewitt, E.; Ross, K.A. Abstract Harmonic Analysis; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1963; Volume I. [Google Scholar]
- Stroppel, M. Locally Compact Groups; European Mathematical Society: Zürich, Switzerland, 2006. [Google Scholar]
- Chigogidze, A.; Hofmann, K.H.; Martin, J.R. Compact Groups and Fixed Point Sets. Trans. Am. Math. Soc. 1997, 349, 4537–4554. [Google Scholar] [CrossRef]
- Ribes, L.; Zalesskii, P. Profinite Groups, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Dikranjan, D.; Stoyanov, L. A–classes of minimal abelian groups. Annu. Univ. Sofia Fac. Math. Méc. 1976, 71 Pt 2, 53–62. [Google Scholar]
- Dikranjan, D.; Prodanov, I. Totally minimal groups. Annu. Univ. Sofia Fac. Math. Méc. 1974, 69, 5–11. [Google Scholar]
- Außenhofer, L.; Dikranjan, D.; Bruno, A.G. Topological Groups and the Pontryagin–van Kampen Duality. An Introduction; De Gruyter Studies in Mathematics; Walter de Gruyter GmbH: Berlin, Germany; Boston, MA, USA, 2022; Volume 83. [Google Scholar]
- Grant, D.L. Arbitrary powers of the roots of unity are minimal Hausdorff topological groups. Topol. Proc. 1979, 4, 103–108. [Google Scholar]
- Armacost, D.L. The Structure of Locally Compact Abelian Groups; Monographs and Textbooks in Pure and Applied Mathematics; Marcel Dekker, Inc.: New York, NY, USA, 1981; Volume 68. [Google Scholar]
- Dikranjan, D.; Prodanov, I. A class of compact abelian groups. Annu. Univ. Sofia Fac. Math. Méc. 1975, 70, 191–206. [Google Scholar]
- Comfort, W.; Dikranjan, D. On the poset of totally dense subgroups of compact groups. Topol. Proc. 1999, 24, 103–128. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dikranjan, D.; Lewis, W.; Loth, P.; Mader, A. A Distinguished Subgroup of Compact Abelian Groups. Axioms 2022, 11, 200. https://doi.org/10.3390/axioms11050200
Dikranjan D, Lewis W, Loth P, Mader A. A Distinguished Subgroup of Compact Abelian Groups. Axioms. 2022; 11(5):200. https://doi.org/10.3390/axioms11050200
Chicago/Turabian StyleDikranjan, Dikran, Wayne Lewis, Peter Loth, and Adolf Mader. 2022. "A Distinguished Subgroup of Compact Abelian Groups" Axioms 11, no. 5: 200. https://doi.org/10.3390/axioms11050200
APA StyleDikranjan, D., Lewis, W., Loth, P., & Mader, A. (2022). A Distinguished Subgroup of Compact Abelian Groups. Axioms, 11(5), 200. https://doi.org/10.3390/axioms11050200





