Continuous-Stage Runge–Kutta Approximation to Differential Problems
Abstract
:1. Introduction
2. Approximation of ODE-IVPs
2.1. Vector Formulation
2.2. Polynomial Approximation
3. Approximation of Special Second-Order ODE-IVPs
3.1. Vector Formulation
3.2. The Case of the General Second-Order Problem
3.3. Polynomial Approximation
3.4. Approximation of General kth-Order ODE-IVPs
4. Discretization
“As is well known, even many relatively simple integrals cannot be expressed in finite terms of elementary functions, and thus must be evaluated by numerical methods.”Dahlquist and Björk [41] p. 521
- Has order ;
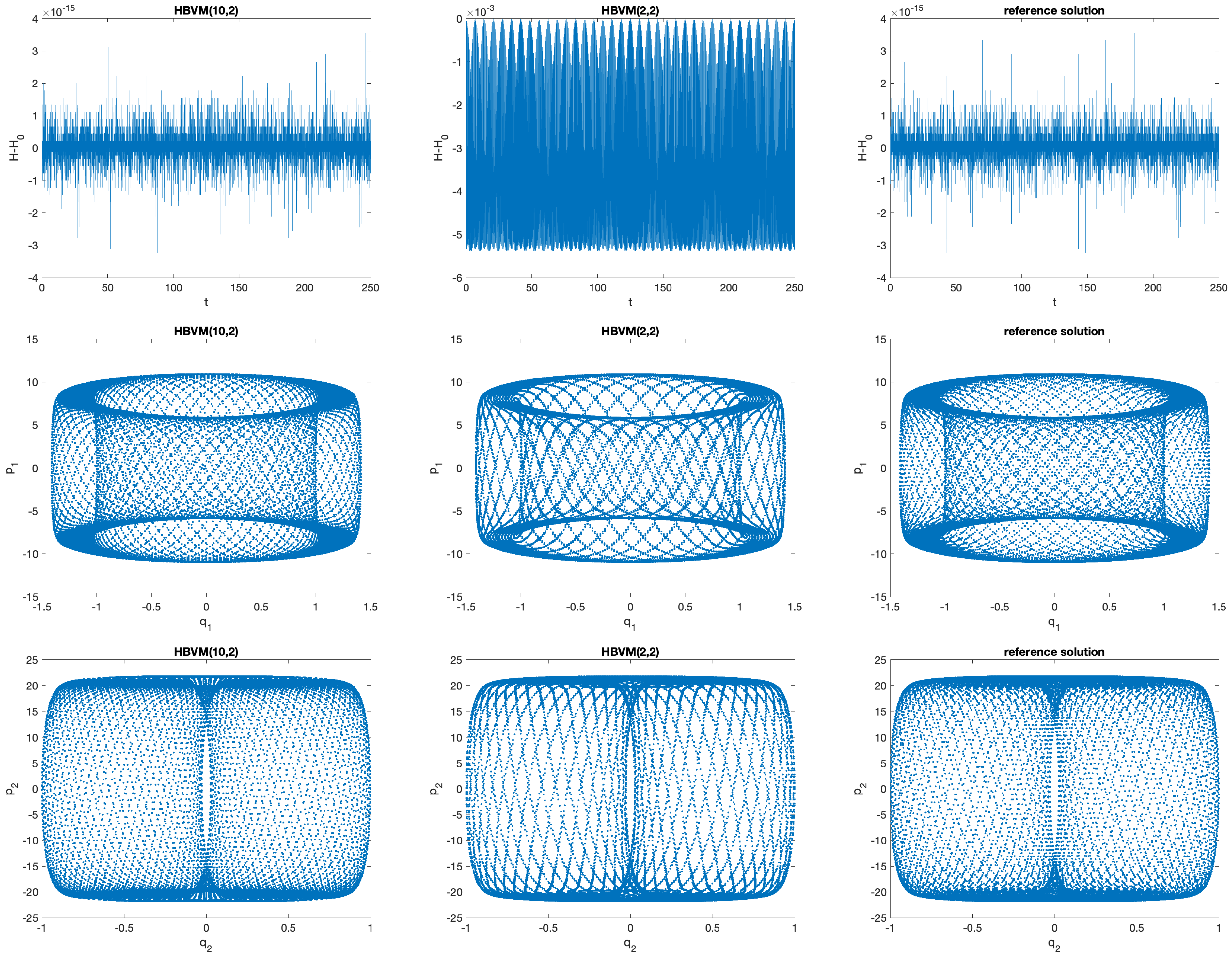
- Is energy-conserving, for all polynomial Hamiltonians of degree not larger that ;
- For general (and suitably regular Hamiltonians), the Hamiltonian error is . In this case, however, by using a value of k large enough so that the Hamiltonian error falls within the round-off error level, the method turns out to be practically energy-conserving.
- When HBVMs are used as spectral methods in time, i.e., choosing values of s and so that no further accuracy improvement can be obtained, for the considered finite-precision arithmetic and timestep h used [22,31,35], then there is no practical difference between the discrete methods and their continuous-stage counterparts.
Numerical Tests
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Butcher, J.C. An algebraic theory of integration methods. Math. Comp. 1972, 26, 79–106. [Google Scholar] [CrossRef]
- Butcher, J.C. The Numerical Analysis of Ordinary Differential Equations: Runge–Kutta and General Linear Methods; John Wiley & Sons: Chichester, UK, 1987. [Google Scholar]
- Butcher, J.C.; Wanner, G. Runge–Kutta methods: Some historical notes. Appl. Numer. Math. 1996, 22, 113–151. [Google Scholar] [CrossRef]
- Brugnano, L.; Iavernaro, F.; Trigiante, D. Hamiltonian Boundary Value Methods (Energy Preserving Discrete Line Integral Methods). JNAIAM J. Numer. Anal. Ind. Appl. Math. 2010, 5, 17–37. [Google Scholar]
- Brugnano, L.; Iavernaro, F.; Trigiante, D. A simple framework for the derivation and analysis of effective one-step methods for ODEs. Appl. Math. Comput. 2012, 218, 8475–8485. [Google Scholar] [CrossRef] [Green Version]
- Hairer, E. Energy-preserving variant of collocation methods. JNAIAM J. Numer. Anal. Ind. Appl. Math. 2010, 5, 73–84. [Google Scholar]
- Li, J.; Gao, Y. Energy-preserving trigonometrically fitted continuous stage Runge–Kutta-Nyström methods for oscillatory Hamiltonian systems. Numer. Algorithms 2019, 81, 1379–1401. [Google Scholar] [CrossRef]
- Miyatake, Y. An energy-preserving exponentially-fitted continuous stage Runge–Kutta method for Hamiltonian systems. BIT 2014, 54, 777–799. [Google Scholar] [CrossRef]
- Miyatake, Y.; Butcher, J.C. A characterization of energy preserving methods and the construction of parallel integrators for Hamiltonian systems. SIAM J. Numer. Anal. 2016, 54, 1993–2013. [Google Scholar] [CrossRef] [Green Version]
- Quispel, G.R.W.; McLaren, D.I. A new class of energy-preserving numerical integration methods. J. Phys. A Math. Theor. 2008, 41, 045206. [Google Scholar] [CrossRef]
- Tang, Q.; Chen, C.M. Continuous finite element methods for Hamiltonian systems. Appl. Math. Mech. 2007, 28, 1071–1080. [Google Scholar] [CrossRef]
- Tang, W. A note on continuous-stage Runge–Kutta methods. Appl. Math. Comput. 2018, 339, 231–241. [Google Scholar] [CrossRef] [Green Version]
- Tang, W.; Lang, G.; Luo, X. Construction of symplectic (partitioned) Runge–Kutta methods with continuous stage. Appl. Math. Comput. 2016, 286, 279–287. [Google Scholar] [CrossRef] [Green Version]
- Tang, W.; Sun, Y. Time finite element methods: A unified framework for numerical discretizations of ODEs. Appl. Math. Comput. 2012, 219, 2158–2179. [Google Scholar] [CrossRef]
- Tang, W.; Sun, Y. Construction of Runge–Kutta type methods for solving ordinary differential equations. Appl. Math. Comput. 2014, 234, 179–191. [Google Scholar] [CrossRef]
- Tang, W.; Zhang, J. Symmetric integrators based on continuous-stage Runge–Kutta-Nyström methods for reversible systems. Appl. Math. Comput. 2019, 361, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Xin, X.; Qin, W.; Ding, X. Continuous stage stochastic Runge–Kutta methods. Adv. Differ. Equ. 2021, 61, 1–22. [Google Scholar] [CrossRef]
- Wang, B.; Wu, X.; Fang, Y. A continuous-stage modified Leap-frog scheme for high-dimensional semi-linear Hamiltonian wave equations. Numer. Math. Theory Methods Appl. 2020, 13, 814–844. [Google Scholar] [CrossRef]
- Yamamoto, Y. On eigenvalues of a matrix arising in energy-preserving/dissipative continuous-stage Runge–Kutta methods. Spec. Matrices 2022, 10, 34–39. [Google Scholar] [CrossRef]
- Amodio, P.; Brugnano, L.; Iavernaro, F. Energy-conserving methods for Hamiltonian Boundary Value Problems and applications in astrodynamics. Adv. Comput. Math. 2015, 41, 881–905. [Google Scholar] [CrossRef] [Green Version]
- Amodio, P.; Brugnano, L.; Iavernaro, F. A note on the continuous-stage Runge–Kutta-(Nyström) formulation of Hamiltonian Boundary Value Methods (HBVMs). Appl. Math. Comput. 2019, 363, 124634. [Google Scholar] [CrossRef] [Green Version]
- Amodio, P.; Brugnano, L.; Iavernaro, F. Analysis of Spectral Hamiltonian Boundary Value Methods (SHBVMs) for the numerical solution of ODE problems. Numer. Algorithms 2020, 83, 1489–1508. [Google Scholar] [CrossRef] [Green Version]
- Amodio, P.; Brugnano, L.; Iavernaro, F. Arbitrarily high-order energy-conserving methods for Poisson problems. Numer. Algorithms 2022. [Google Scholar] [CrossRef]
- Barletti, L.; Brugnano, L.; Tang, Y.; Zhu, B. Spectrally accurate space-time solution of Manakov systems. J. Comput. Appl. Math. 2020, 377, 112918. [Google Scholar] [CrossRef]
- Brugnano, L.; Frasca-Caccia, G.; Iavernaro, F. Line Integral Solution of Hamiltonian PDEs. Mathematics 2019, 7, 275. [Google Scholar] [CrossRef] [Green Version]
- Brugnano, L.; Gurioli, G.; Iavernaro, F.; Weinmüller, E.B. Line integral solution of Hamiltonian systems with holonomic constraints. Appl. Numer. Math. 2018, 127, 56–77. [Google Scholar] [CrossRef] [Green Version]
- Brugnano, L.; Gurioli, G.; Sun, Y. Energy-conserving Hamiltonian Boundary Value Methods for the numerical solution of the Korteweg-de Vries equation. J. Comput. Appl. Math. 2019, 351, 117–135. [Google Scholar] [CrossRef] [Green Version]
- Brugnano, L.; Gurioli, G.; Zhang, C. Spectrally accurate energy-preserving methods for the numerical solution of the “Good” Boussinesq equation. Numer. Methods Partial. Differ. Equ. 2019, 35, 1343–1362. [Google Scholar] [CrossRef] [Green Version]
- Brugnano, L.; Iavernaro, F. Line Integral Methods for Conservative Problems; Chapman & Hall/CRC: Boca Raton, FL, USA, 2016; Available online: http://web.math.unifi.it/users/brugnano/LIMbook/ (accessed on 15 April 2022).
- Brugnano, L.; Iavernaro, F. Line Integral Solution of Differential Problems. Axioms 2018, 7, 36. [Google Scholar] [CrossRef] [Green Version]
- Brugnano, L.; Iavernaro, F.; Montijano, J.I.; Rández, L. Spectrally accurate space-time solution of Hamiltonian PDEs. Numer. Algorithms 2019, 81, 1183–1202. [Google Scholar] [CrossRef] [Green Version]
- Brugnano, L.; Iavernaro, F.; Trigiante, D. A note on the efficient implementation of Hamiltonian BVMs. J. Comput. Appl. Math. 2011, 236, 375–383. [Google Scholar] [CrossRef]
- Brugnano, L.; Iavernaro, F.; Trigiante, D. A two-step, fourth-order method with energy preserving properties. Comput. Phys. Commun. 2012, 183, 1860–1868. [Google Scholar] [CrossRef] [Green Version]
- Brugnano, L.; Iavernaro, F.; Zhang, R. Arbitrarily high-order energy-preserving methods for simulating the gyrocenter dynamics of charged particles. J. Comput. Appl. Math. 2020, 380, 112994. [Google Scholar] [CrossRef]
- Brugnano, L.; Montijano, J.I.; Rández, L. On the effectiveness of spectral methods for the numerical solution of multi-frequency highly-oscillatory Hamiltonian problems. Numer. Algorithms 2019, 81, 345–376. [Google Scholar] [CrossRef] [Green Version]
- Brugnano, L.; Montijano, J.I.; Rández, L. High-order energy-conserving Line Integral Methods for charged particle dynamics. J. Comput. Phys. 2019, 396, 209–227. [Google Scholar] [CrossRef] [Green Version]
- Brugnano, L.; Sun, Y. Multiple invariants conserving Runge–Kutta type methods for Hamiltonian problems. Numer. Algorithms 2014, 65, 611–632. [Google Scholar] [CrossRef] [Green Version]
- Tang, W.; Sun, Y.; Zhang, J. High order symplectic integrators based on continuous-stage Runge–Kutta-Nyström methods. Appl. Math. Comput. 2019, 361, 670–679. [Google Scholar] [CrossRef] [Green Version]
- Tang, W.; Zhang, J. Symplecticity-preserving continuous stage Runge–Kutta-Nyström methods. Appl. Math. Comput. 2018, 323, 204–219. [Google Scholar] [CrossRef] [Green Version]
- Hairer, E.; Wanner, G. Solving Ordinary Differential Equations II, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Dahlquist, G.; Björk, Å. Numerical Methods in Scientific Computing; SIAM: Philadelphia, PA, USA, 2008; Volume I. [Google Scholar]
- Blanes, S.; Casas, F. A Concise Introduction to Geometric Numerical Integration; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Hairer, E.; Lubich, C.; Wanner, G. Geometric Numerical Integration; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Leimkuhler, B.; Reich, S. Simulating Hamiltonian Dynamics; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Sanz-Serna, J.M.; Calvo, M.P. Numerical Hamiltonian Problems; Chapman & Hall: London, UK, 1994. [Google Scholar]
- Hairer, E.; Lubich, C. Long-term analysis of the Störmer-Verlet method for Hamiltonian systems with a solution-dependent high frequency. Numer. Math. 2016, 134, 119–138. [Google Scholar] [CrossRef]
- McLachlan, R.I. Tuning symplectic integrators is easy and worthwhile. Commun. Comput. Phys. 2022, 31, 987–996. [Google Scholar] [CrossRef]
- Sanz Serna, J.M. Symplectic Runge–Kutta schemes for adjoint equations, automatic differentiation, optimal control, and more. SIAM Rev. 2016, 58, 3–33. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Wu, X. A long-term numerical energy-preserving analysis of symmetric and/or symplectic extended RKN integrators for efficiently solving highly oscillatory Hamiltonian systems. Bit Numer. Math. 2021, 61, 977–1004. [Google Scholar] [CrossRef]
- Available online: https://www.mrsir.it/en/about-us/ (accessed on 15 April 2022).

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amodio, P.; Brugnano, L.; Iavernaro, F. Continuous-Stage Runge–Kutta Approximation to Differential Problems. Axioms 2022, 11, 192. https://doi.org/10.3390/axioms11050192
Amodio P, Brugnano L, Iavernaro F. Continuous-Stage Runge–Kutta Approximation to Differential Problems. Axioms. 2022; 11(5):192. https://doi.org/10.3390/axioms11050192
Chicago/Turabian StyleAmodio, Pierluigi, Luigi Brugnano, and Felice Iavernaro. 2022. "Continuous-Stage Runge–Kutta Approximation to Differential Problems" Axioms 11, no. 5: 192. https://doi.org/10.3390/axioms11050192
APA StyleAmodio, P., Brugnano, L., & Iavernaro, F. (2022). Continuous-Stage Runge–Kutta Approximation to Differential Problems. Axioms, 11(5), 192. https://doi.org/10.3390/axioms11050192







