Fractional Modelling and Optimal Control of COVID-19 Transmission in Portugal
Abstract
:1. Introduction
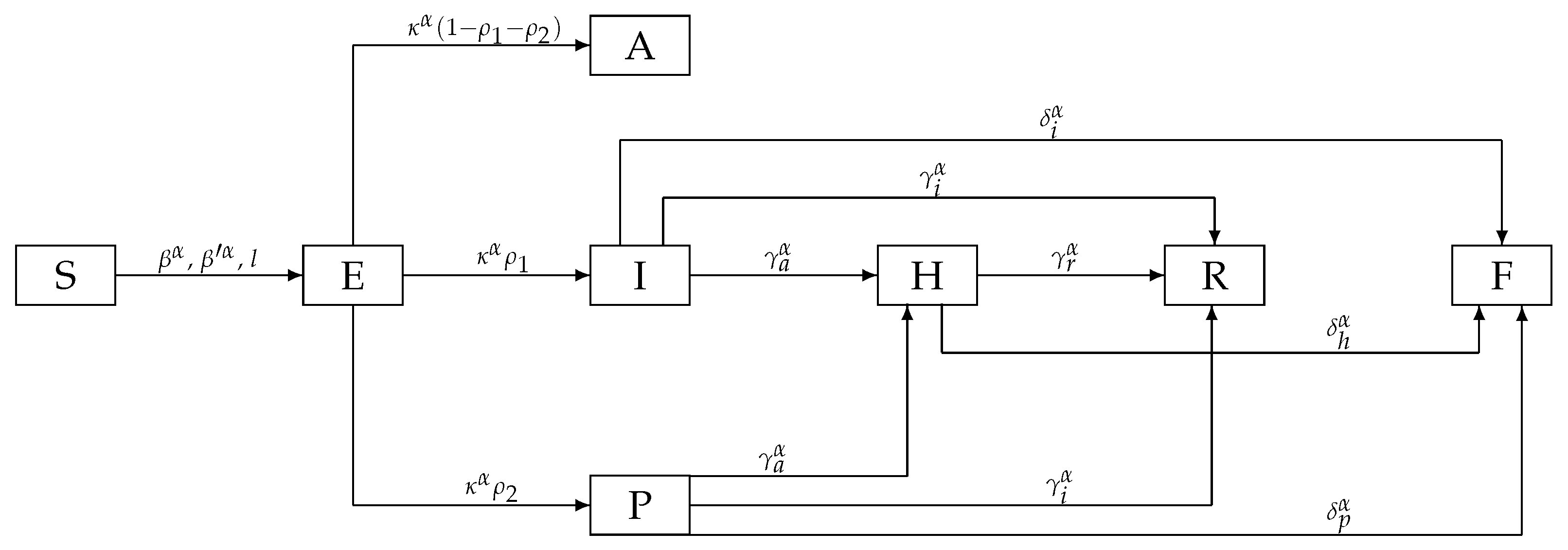
2. Fractional-Order COVID-19 Model
3. Main Results
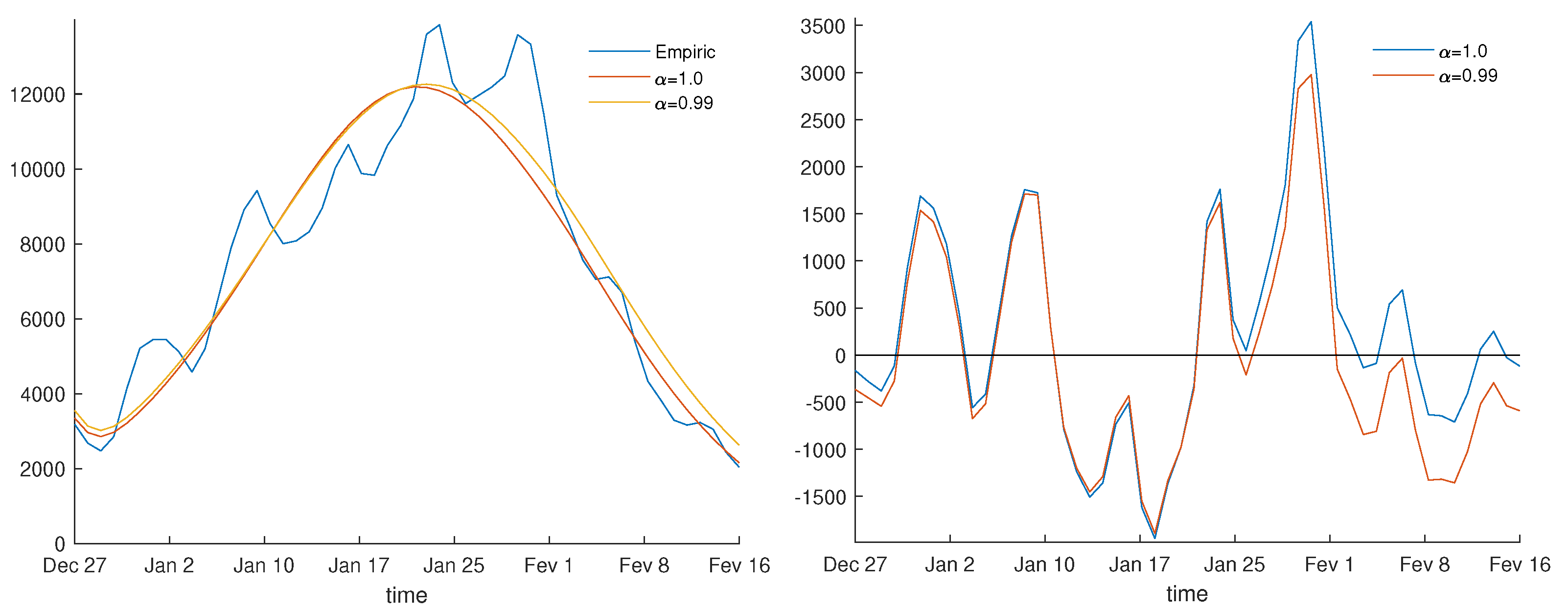
3.1. Parameter Estimation
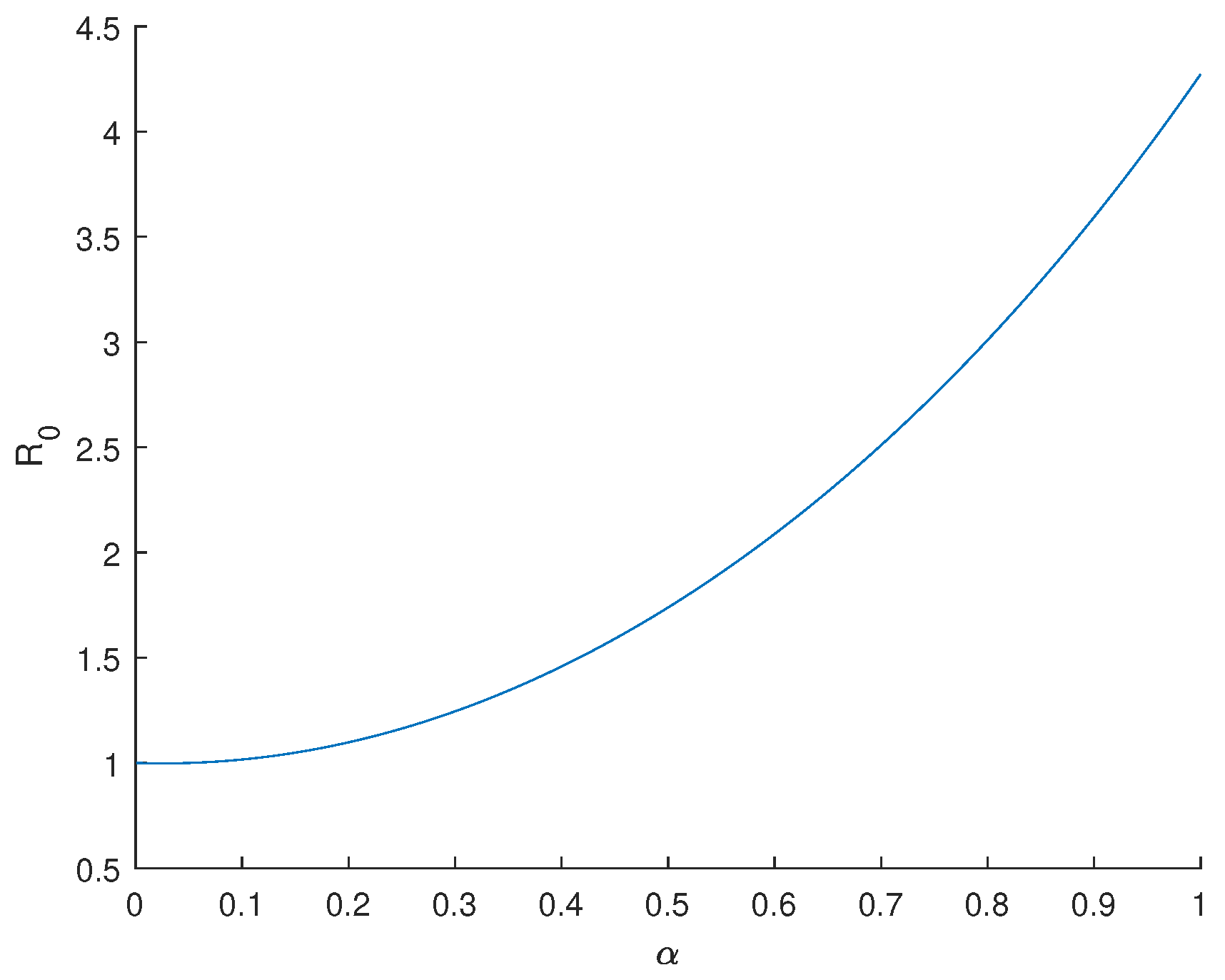
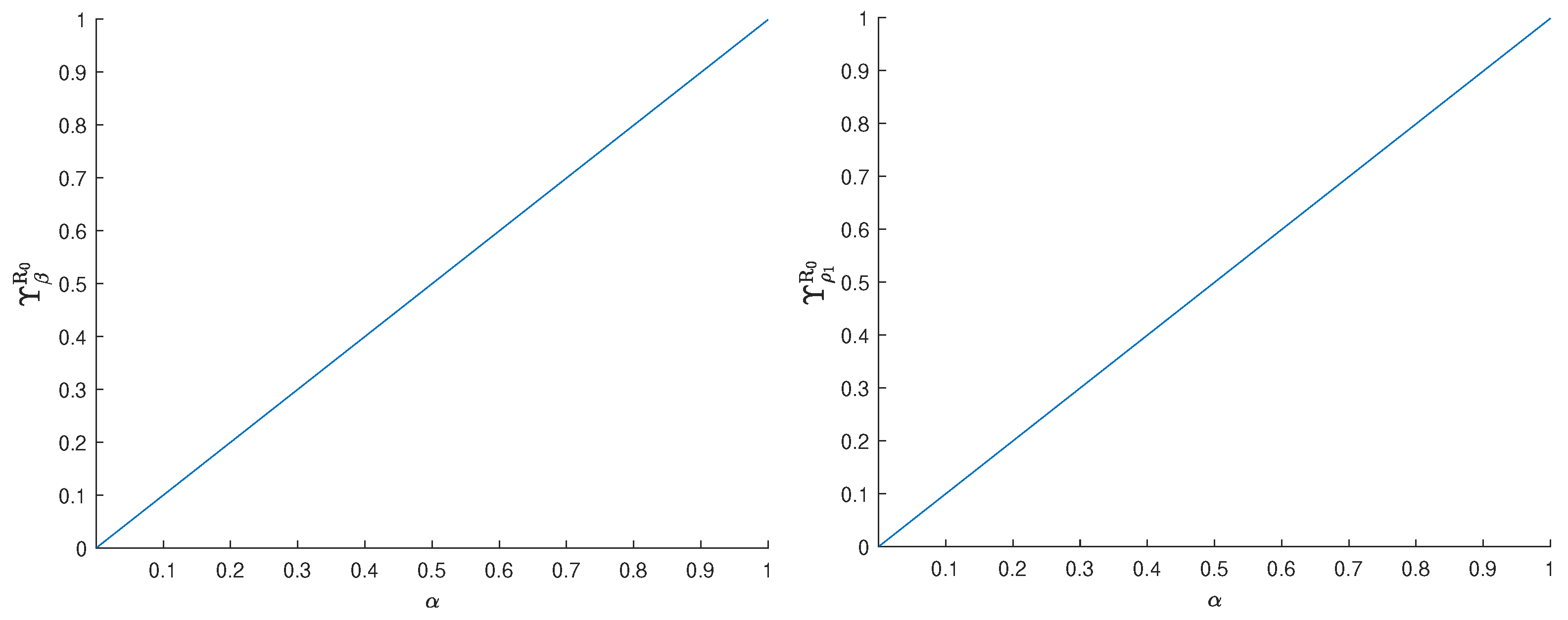
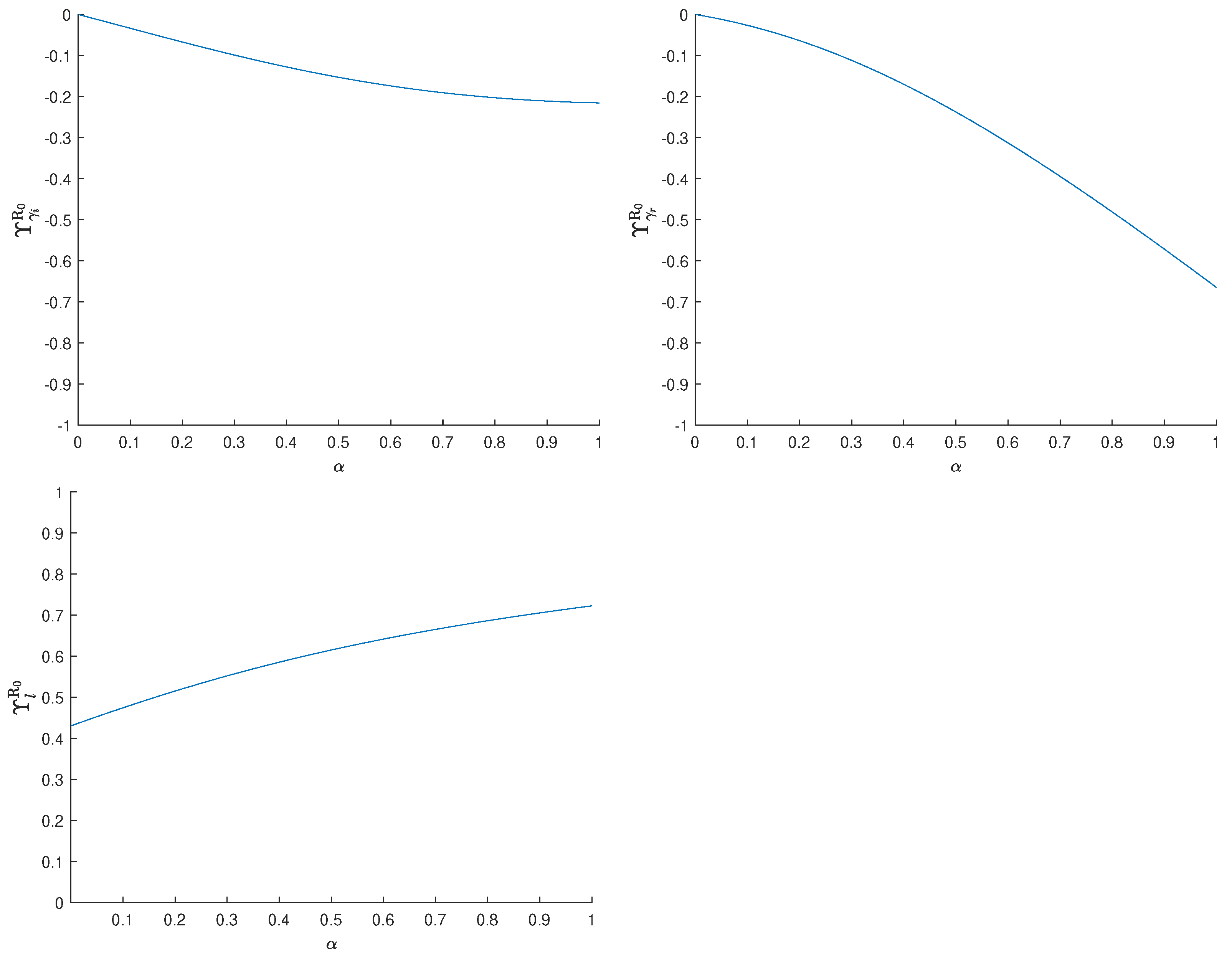
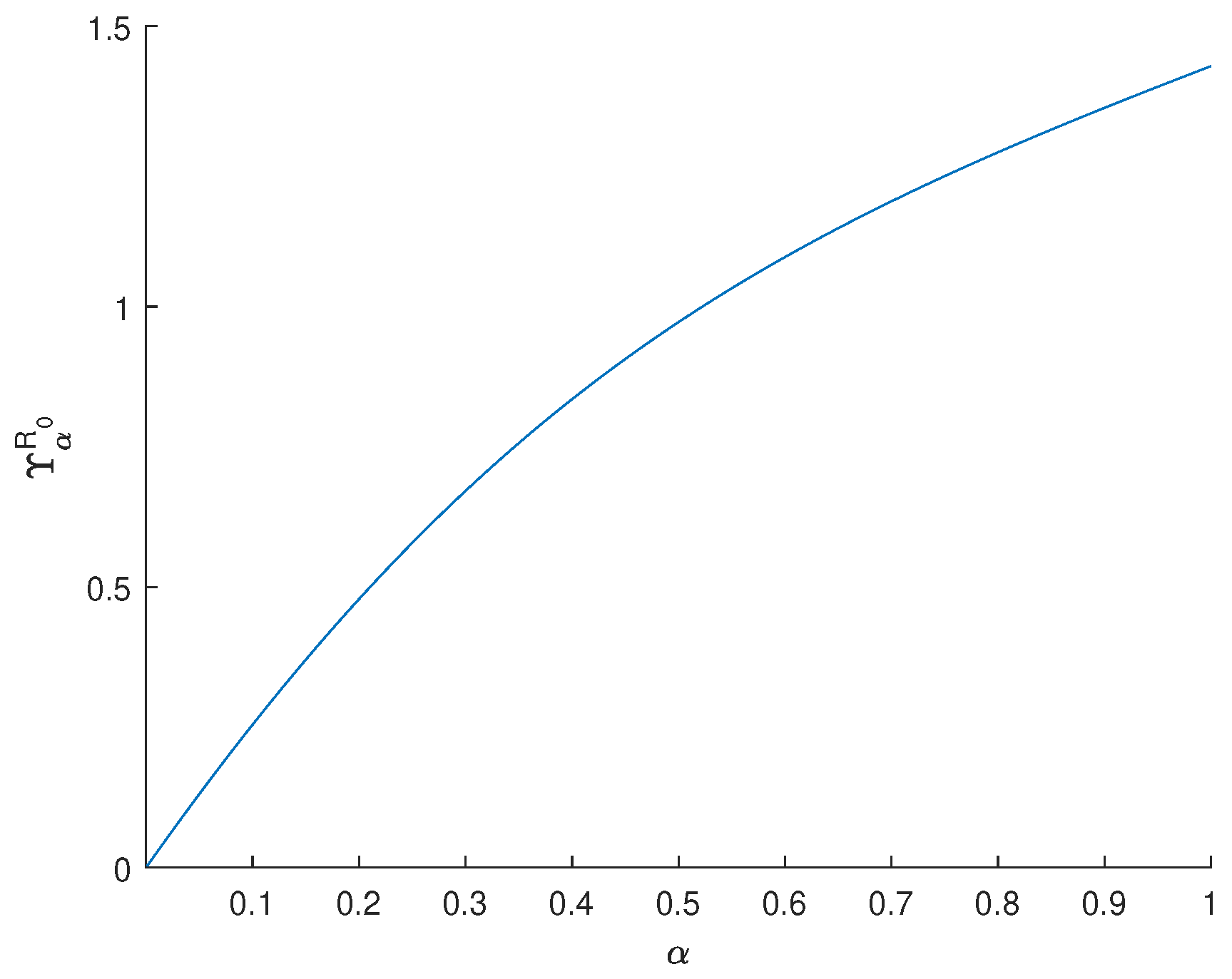
3.2. Sensitivity Analysis
3.3. Fractional Optimal Control of the Model
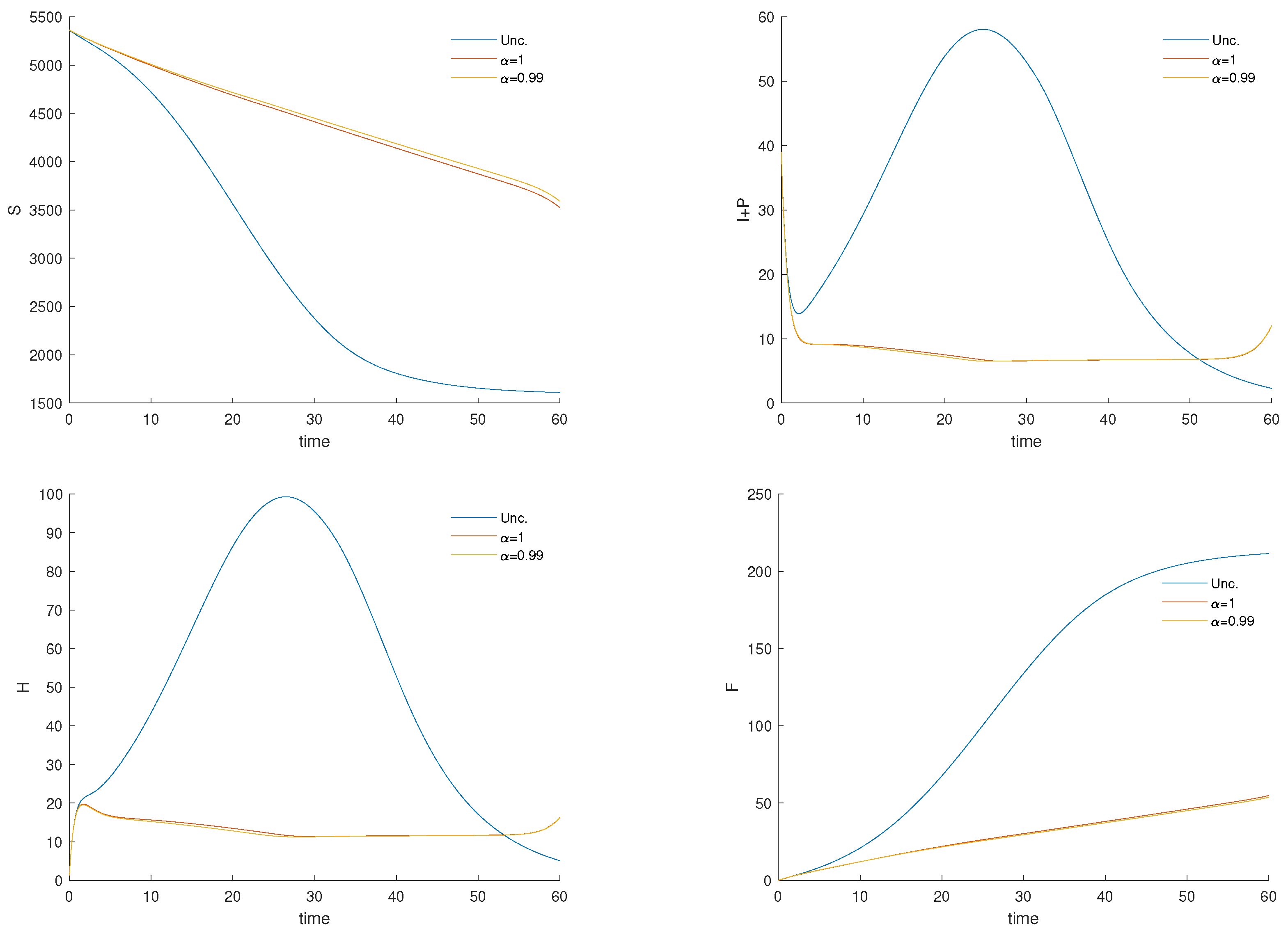
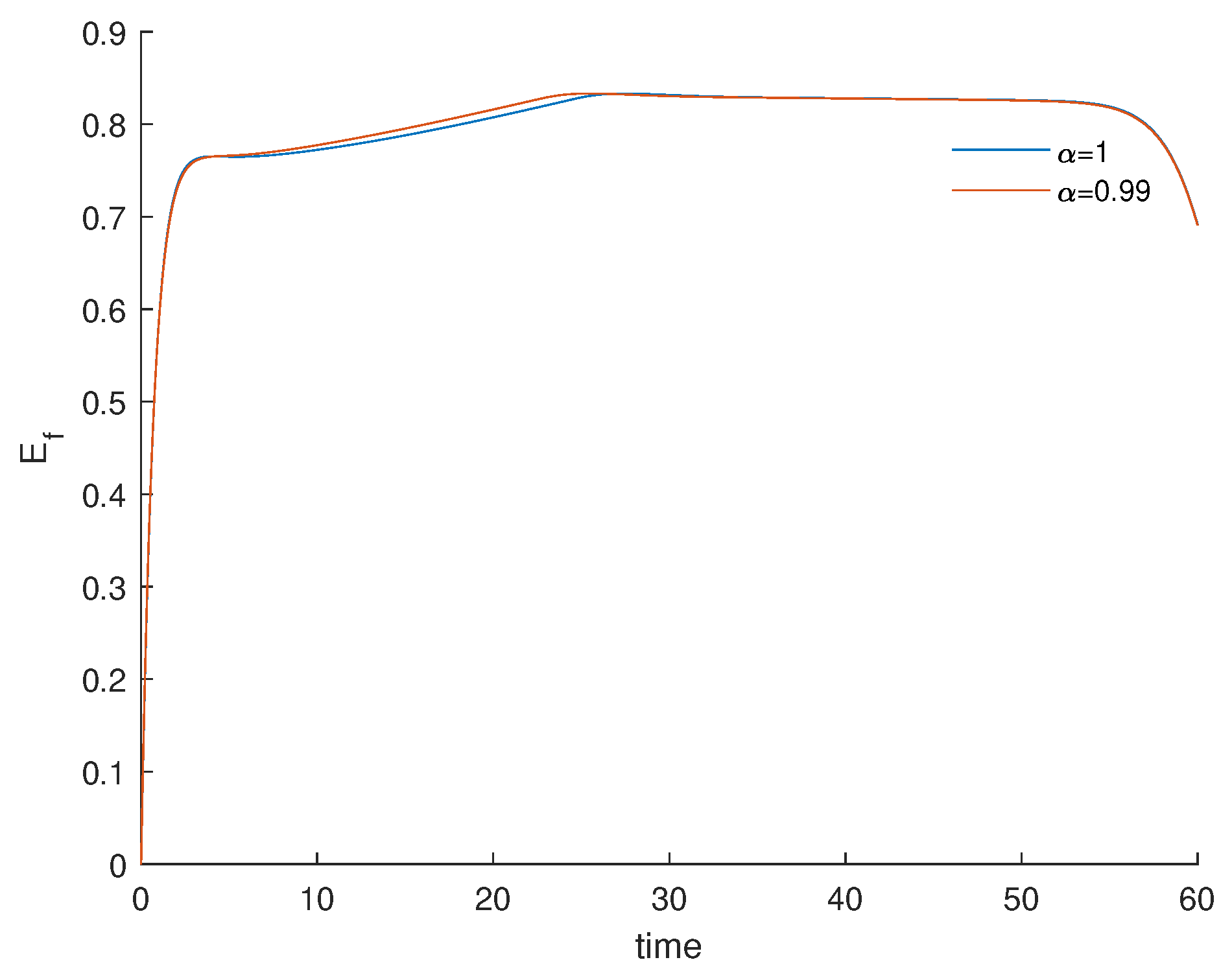
3.4. Numerical Results and Cost-Effectiveness of the Fractional Optimal Control Problem
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Health Organization. Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/interactive-timeline# (accessed on 7 July 2021).
- Agarwal, P.; Nieto, J.J.; Ruzhansky, M.; Torres, D.F.M. Analysis of Infectious Disease Problems (COVID-19) and Their Global Impact; Infosys Science Foundation Series in Mathematical Sciences; Springer: Singapore, 2021. [Google Scholar]
- Bracher, J.; Wolffram, D.; Deuschel, J.; Görgen, K.; Ketterer, J.L.; Ullrich, A.; Schienle, M. A pre-registered short-term forecasting study of COVID-19 in Germany and Poland during the second wave. Nat. Commun. 2021, 12, 5173. [Google Scholar] [CrossRef] [PubMed]
- Ghaffari, V.; Mobayen, S.; Din, S.U.; Bartoszewicz, A.; Jahromi, A.T. A Robust H∞ fault tolerant controller for uncertain systems described by linear fractional transformation model. IEEE Access 2021, 9, 104749–104760. [Google Scholar] [CrossRef]
- Jajarmi, A.; Baleanu, D.; Zarghami Vahid, K.; Mobayen, S. A general fractional formulation and tracking control for immunogenic tumor dynamics. Math. Meth. Appl. Sci. 2022, 45, 667–680. [Google Scholar] [CrossRef]
- Ndaïrou, F.; Area, I.; Nieto, J.J.; Silva, C.J.; Torres, D.F.M. Fractional model of COVID-19 applied to Galicia, Spain and Portugal. Chaos Solitons Fractals 2021, 144, 110652. [Google Scholar] [CrossRef] [PubMed]
- Bushnaq, S.; Saeed, T.; Torres, D.F.M.; Zeb, A. Control of COVID-19 dynamics through a fractional-order model. Alex. Eng. J. 2021, 60, 3587–3592. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations. In Mathematics in Science and Engineering; Academic Press, Inc.: San Diego, CA, USA, 1999; Volume 198. [Google Scholar]
- Ndaïrou, F.; Area, I.; Nieto, J.J.; Torres, D.F.M. Mathematical modeling of COVID-19 transmission dynamics with a case study of Wuhan. Chaos Solitons Fractals 2020, 135, 109846. [Google Scholar] [CrossRef] [PubMed]
- Ndaïrou, F.; Area, I.; Bader, G.; Nieto, J.J.; Torres, D.F.M. Corrigendum to ‘Mathematical Modeling of COVID-19 Transmission Dynamics with a Case Study of Wuhan’ [Chaos Solitons Fractals 135 (2020), 109846]. Chaos Solitons Fractals 2020, 141, 110311. [Google Scholar] [CrossRef] [PubMed]
- Almeida, R. Analysis of a fractional SEIR model with treatment. Appl. Math. Lett. 2018, 84, 56–62. [Google Scholar] [CrossRef]
- Carvalho, A.R.M.; Pinto, C.M.A. Immune response in HIV epidemics for distinct transmission rates and for saturated CTL response. Math. Model. Nat. Phenom. 2019, 14, 307. [Google Scholar] [CrossRef]
- DGS—COVID-19. Ponto de situação atual em Portugal. Available online: https://covid19.min-saude.pt/ponto-de-situacao-atual-em-portugal/ (accessed on 30 October 2021).
- Dados Relativos à Pandemia COVID-19 em Portugal. Available online: https://github.com/dssg-pt/covid19pt-data (accessed on 30 October 2021).
- Rosa, S.; Torres, D.F.M. Parameter estimation, sensitivity analysis and optimal control of a periodic epidemic model with application to HRSV in Florida. Stat. Optim. Inf. Comput. 2018, 6, 139–149. [Google Scholar] [CrossRef] [Green Version]
- Chitnis, N.; Hyman, J.M.; Cushing, J.M. Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bull. Math. Biol. 2008, 70, 1272–1296. [Google Scholar] [CrossRef]
- Rodrigues, H.S.; Monteiro, M.T.T.; Torres, D.F.M. Sensitivity analysis in a dengue epidemiological model. In Conference Papers in Science; Hindawi: London, UK, 2013; Volume 2013. [Google Scholar]
- Almeida, R.; Pooseh, S.; Torres, D.F.M. Computational Methods in the Fractional Calculus of Variations; Imperial College Press: London, UK, 2015. [Google Scholar]
- Diethelm, K.; Ford, N.J.; Freed, A.D.; Luchko, Y. Algorithms for the fractional calculus: A selection of numerical methods. Comput. Methods Appl. Mech. Eng. 2005, 194, 743–773. [Google Scholar] [CrossRef] [Green Version]
- Rosa, S.; Torres, D.F.M. Optimal control of a fractional order epidemic model with application to human respiratory syncytial virus infection. Chaos Solitons Fractals 2018, 117, 142–149. [Google Scholar] [CrossRef] [Green Version]
- Cave, E. COVID-19 super-spreaders: Definitional quandaries and implications. Asian Bioeth. Rev. 2020, 12, 235–242. [Google Scholar] [CrossRef] [PubMed]
- Lemos-Paião, A.P.; Silva, C.J.; Torres, D.F.M. A new compartmental epidemiological model for COVID-19 with a case study of Portugal. Ecol. Complex. 2020, 44, 100885. [Google Scholar] [CrossRef]
- Panja, P. Optimal Control Analysis of a Cholera Epidemic Model. Biophys. Rev. Lett. 2019, 14, 27–48. [Google Scholar] [CrossRef] [Green Version]
- van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Rodrigues, P.; Silva, C.J.; Torres, D.F.M. Cost-effectiveness analysis of optimal control measures for tuberculosis. Bull. Math. Biol. 2014, 76, 2627–2645. [Google Scholar] [CrossRef]
- Okosun, K.O.; Rachid, O.; Marcus, N. Optimal control strategies and cost-effectiveness analysis of a malaria model. BioSystems 2013, 111, 83–101. [Google Scholar] [CrossRef] [PubMed]
- Zine, H.; Boukhouima, A.; Lotfi, E.M.; Mahrouf, M.; Torres, D.F.M.; Yousfi, N. A stochastic time-delayed model for the effectiveness of Moroccan COVID-19 deconfinement strategy. Math. Model. Nat. Phenom. 2020, 15, 50. [Google Scholar] [CrossRef]
- Mahrouf, M.; Boukhouima, A.; Zine, H.; Lotfi, E.M.; Torres, D.F.M.; Yousfi, N. Modeling and forecasting of COVID-19 spreading by delayed stochastic differential equations. Axioms 2021, 10, 18. [Google Scholar] [CrossRef]
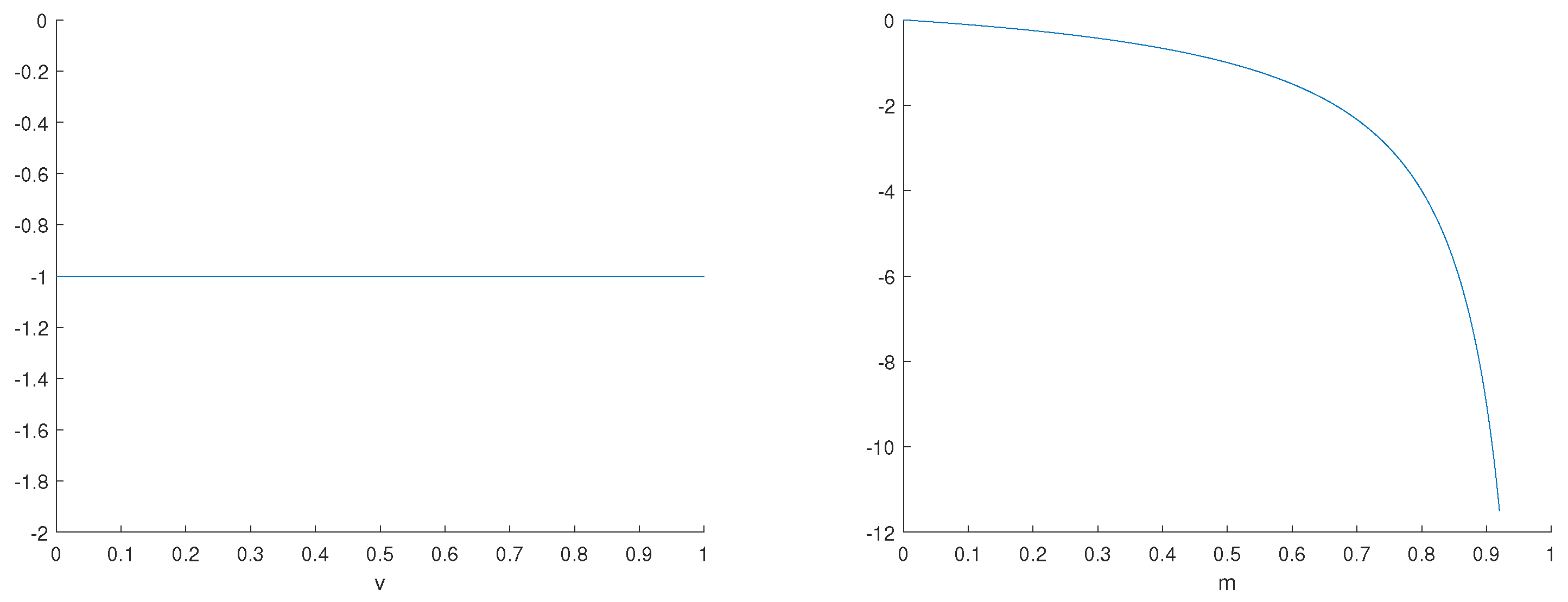
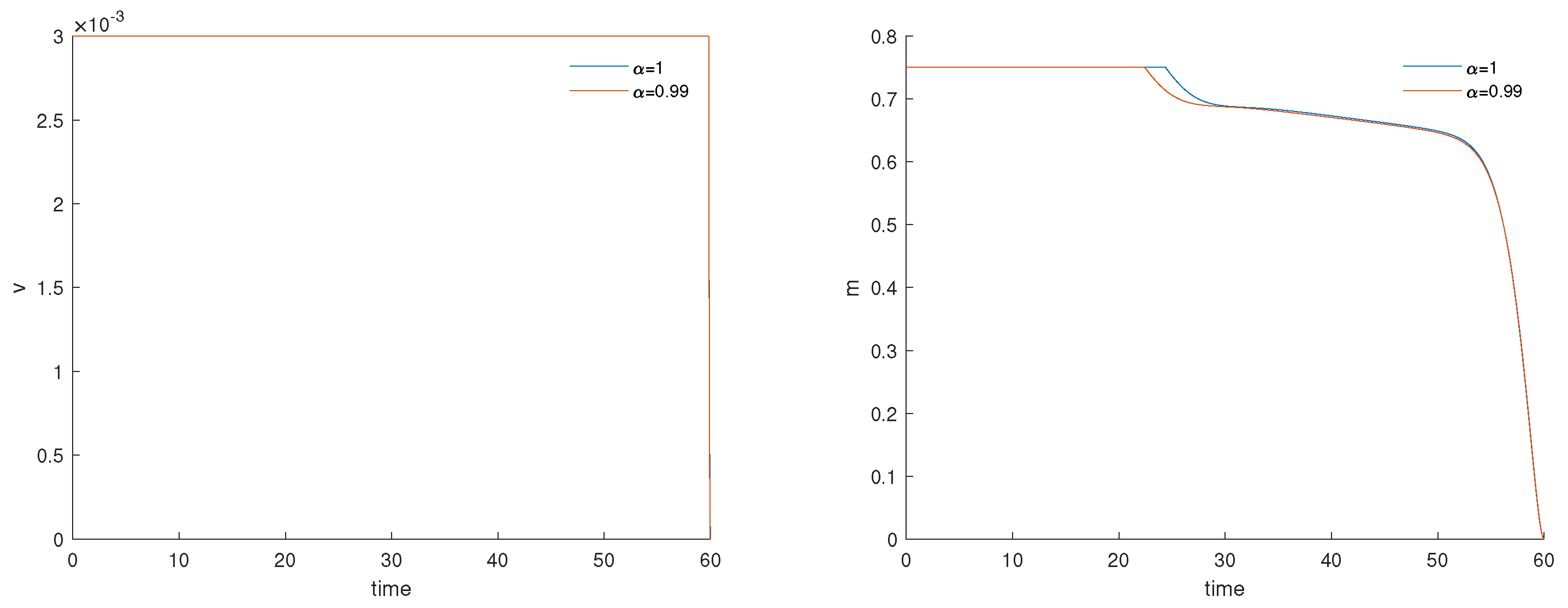
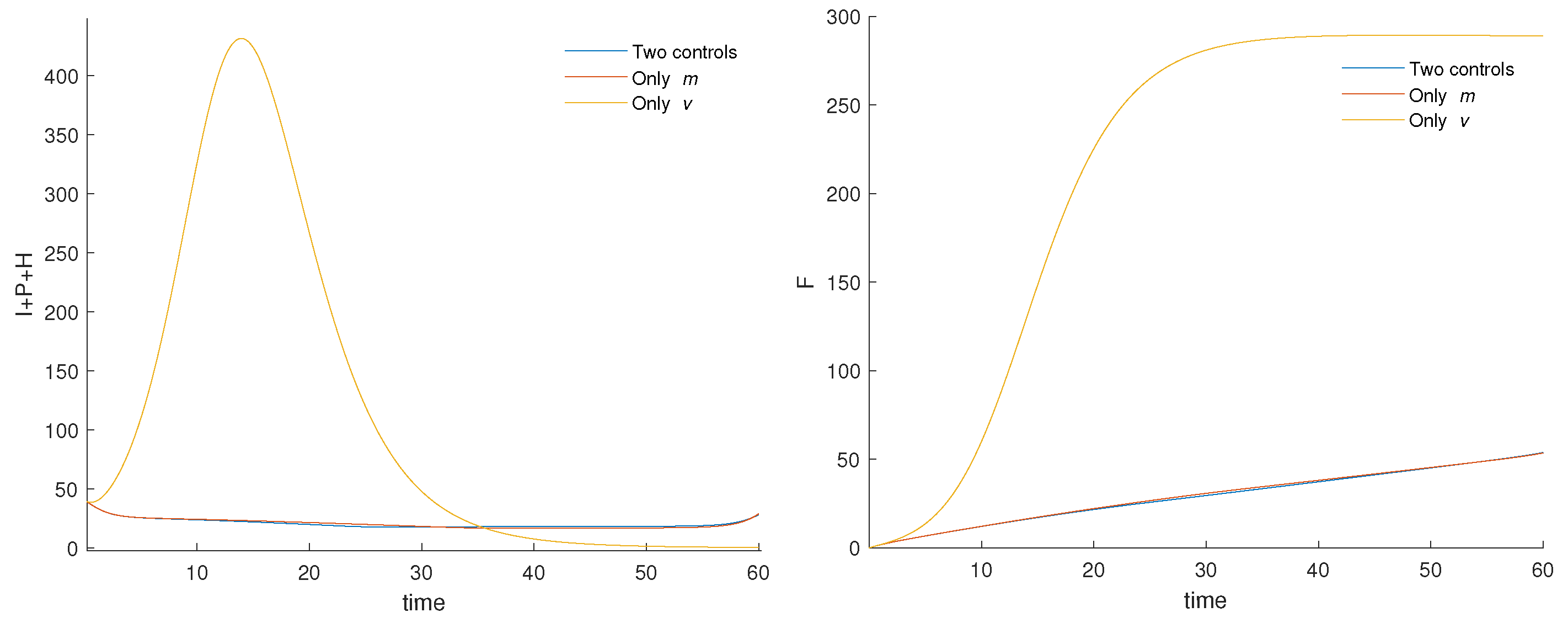
| Name | Description | Value |
|---|---|---|
| human-to-human transmission coefficient | 2.55 | |
| l | transmissibility of hospitalized patients | 1.56 |
| transmission coefficient of super-spreaders | 7.65 | |
| rate at which an individual leaves the exposed | 0.25 | |
| class to become infectious | ||
| proportion of progression from class E | 0.58 | |
| to symptomatic infectious class I | ||
| rate at which exposed ind. become super-spreaders | 0.001 | |
| rate at which symptomatic and super-spreaders | 0.94 | |
| become hospitalized | ||
| recovery rate without being hospitalized | 0.27 | |
| recovery rate of hospitalized patients | 0.5 | |
| disease induced death rate due to infected ind. | 1/23 | |
| disease induced death rate due to super-spreader ind. | 1/23 | |
| disease induced death rate due to hospitalized ind. | 1/23 |
| Derivative Order | s | Absolute Error | Relative Error (%) |
|---|---|---|---|
| 1.0 | 21.08 | 8595 | 14.13 |
| 0.99 | 19.87 | 8135 | 13.37 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosa, S.; Torres, D.F.M. Fractional Modelling and Optimal Control of COVID-19 Transmission in Portugal. Axioms 2022, 11, 170. https://doi.org/10.3390/axioms11040170
Rosa S, Torres DFM. Fractional Modelling and Optimal Control of COVID-19 Transmission in Portugal. Axioms. 2022; 11(4):170. https://doi.org/10.3390/axioms11040170
Chicago/Turabian StyleRosa, Silvério, and Delfim F. M. Torres. 2022. "Fractional Modelling and Optimal Control of COVID-19 Transmission in Portugal" Axioms 11, no. 4: 170. https://doi.org/10.3390/axioms11040170
APA StyleRosa, S., & Torres, D. F. M. (2022). Fractional Modelling and Optimal Control of COVID-19 Transmission in Portugal. Axioms, 11(4), 170. https://doi.org/10.3390/axioms11040170







