Two Open Problems on CA-Groupoids and Cancellativities of T2CA-Groupoids

Abstract

Cyclic associative groupoids (CA-groupoids) and Type-2 cyclic associative groupoids (T2CA-groupoids) are two types of non-associative groupoids which satisfy cyclic associative law and type-2 cyclic associative law, respectively. In this paper, we prove two theorems that weak cancellativity is cancellativity and right quasi-cancellativity is left quasi-cancellativity in a CA-groupoid, thus successfully solving two open problems. Moreover, the relationships among separativity, quasi-cancellativity and commutativity in a CA-groupoid are discussed. Finally, we study the various cancellativities of T2CA-groupoids such as power cancellativity, quasi-cancellativity and cancellativity. By determining the relationships between them, we can illuminate the structure of T2CA-groupoids.

1. Introduction

Semigroups are the simplest and most natural class of associative algebraic systems. In non-associative algebras, there are three studies of groupoids and commutative semigroups that are closely related. They are the Abel-Grassmann’s groupoid (AG-groupoid), CA-groupoid and T2CA-groupoid. The AG-groupoid was put forward by Kazim and Naseeruddin [1] in 1972. In an AG-groupoid, all its elements satisfy the left invertive law, which is $(x\ast y)\ast z=(z\ast y)\ast x$. In algebraic systems, the cyclic associative law has two different forms. The first is $x\ast (y\ast z)=z\ast (x\ast y)$, which the CA-groupoid satisfies; the second is $x\ast (y\ast z)=(z\ast x)\ast y$, which T2CA-groupoid satisfies. In order to distinguish the first, the second is called the type-2 cyclic associative law in [2].

Two different forms of cyclic associative laws are widely used in algebraic systems. As early as 1954, function equations satisfying the type-2 cyclic associative law were discussed by Hosszú in [3]. Continuous and strictly monotonic solutions of function equations satisfying the type-2 cyclic associative law were investigated in [4]. Schölzel and Tomaschek [5] characterized the power series solutions of function equations satisfying the type-2 cyclic associative law in the complex domain. A class of rings satisfying the cyclic associative law was studied in [6,7,8]. Behn et al. [9] studied flexible algebras satisfying the cyclic associative law. Moreover, a special groupoid named cyclic associative AG-groupoid (CA-AG-groupoid), which is both CA-groupoid and AG-groupoid, was introduced by Iqbal et al. in [10]. Other studies of the CA-AG-groupoid can be found in [11,12,13].

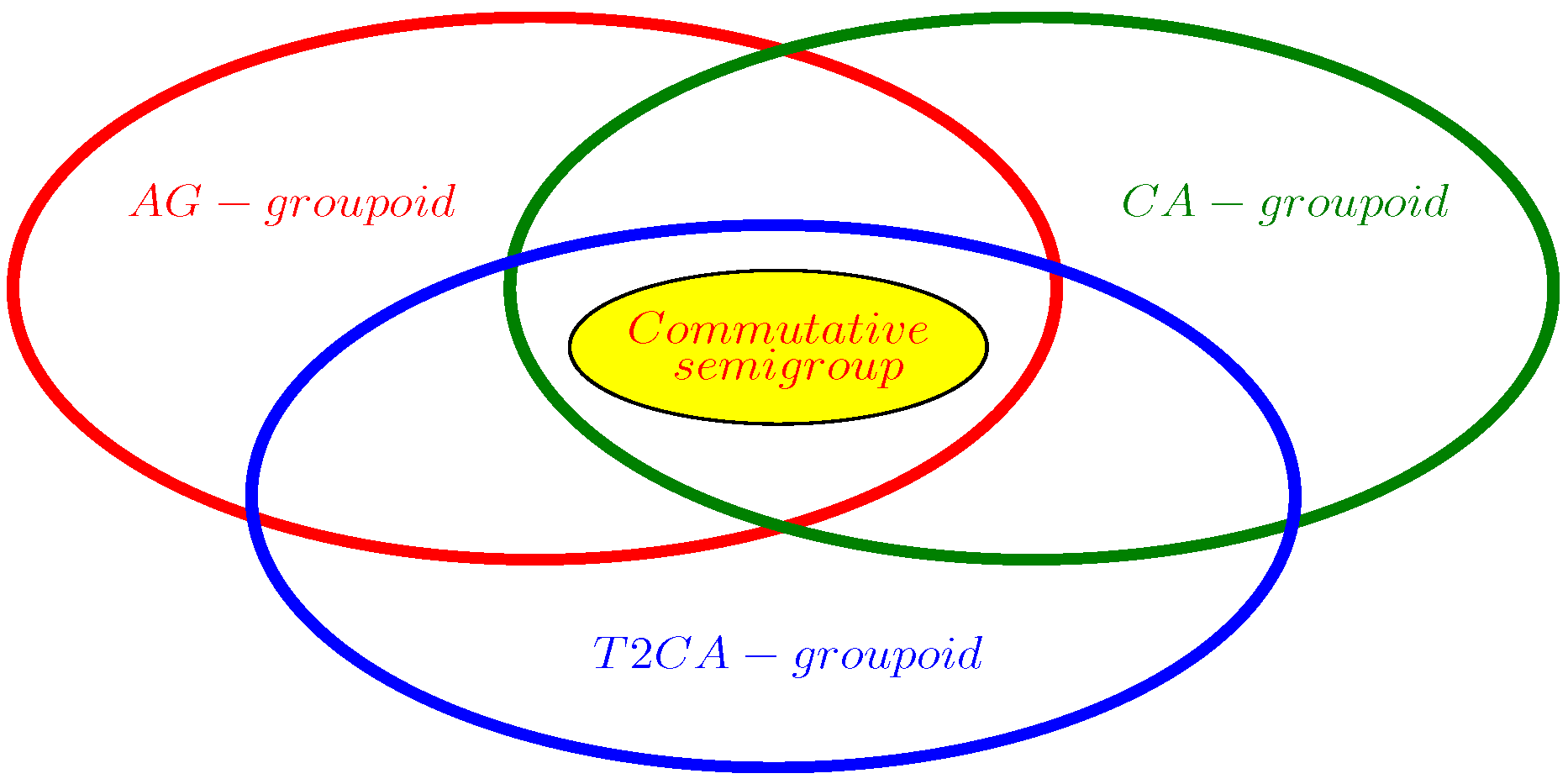
The three kinds of aforementioned non-associative groupoids extend the commutative semigroup from different perspectives and their relationships are shown in Figure 1.

In Figure 1, there are three large colored oval circles and a small yellow ellipse. The large oval circles of different colors represent different groupoids. The red oval circle represents the AG-groupoid, the green oval circle represents CA-groupoid; the blue oval circle represents the T2CA-groupoid; and the small yellow one at the intersection of the three large oval circles represents the commutative semigroup. From Figure 1, we can see that the commutative semigroup is indeed a special kind of groupoid which not only satisfies the left invertive law but also satisfies the cyclic associative law and the type-2 cyclic associative law.

Research on the various cancellativities of semigroups has always been an active research field (see [14,15,16,17,18,19,20,21,22,23,24]). By using the research method of cancellativities of semigroups, many important theoretical results about cancellativities have been obtained in different groupoids (see [2,25,26,27]). In [2,27], Xiaohong Zhang et al. studied the various cancellativities of groupoids satisfying the two kinds of cyclic associative laws described above. However, there are still two open problems that have not been solved in [27]. In [2], only cancellativity has been studied, while the weak cancellativity, quasi-cancellativity and separativity of T2CA-groupoids have not been studied. As a continuation of [2,27], we fully address two open problems. Furthermore, the cancellativities of T2CA-groupoids are studied in detail.

The rest of this paper is arranged as follows. In Section 2, some definitions and properties on the CA-groupoid and T2CA-groupoid are given. We study the relationships between the T2CA-groupoid and other groupoids in Section 3. The quasi-cancellativity and cancellativity of CA-groupoids are discussed in Section 4. We discuss the quasi-cancellativity and cancellativity of T2CA-groupoids and study the relationships between them in Section 5. Finally, Section 6 presents some conclusions and the direction of future efforts.

2. Preliminaries

This section introduces the basic concepts and related research results of the CA-groupoid and T2CA-groupoid.

In general, different groupoids are defined according to the properties of binary operation defined on groupoids. For example, the groupid is semigroup if the operation satisfies the associative law. If it satisfies the left invertive law, the groupid is AG-groupoid. If it satisfies the cyclic associative law, the groupid is CA-groupoid. The cyclic associative AG-groupoid, which is a subclass of AG-groupoid, satisfies both the left invertive law and the cyclic associative law (see [10]).

Proposition 1

([28]). If $(G,\ast )$ is a CA-groupoid, then for all $x_1,x_2,x_3,x_4\in G$, $(x_1\ast x_2)\ast (x_3\ast x_4)=(x_4\ast x_1)\ast (x_3\ast x_2)$.

Proposition 2

([28]). Every commutative CA-groupoid is a commutative semigroup.

Corollary 1

([27]). Right cancellativity and cancellativity in a CA-groupoid are equivalent.

Definition 1

([27]). A CA-groupoid $(G,\ast )$ has weak cancellativity if for all $x,a_1,a_2\in G$, $x\ast a_1=x\ast a_2$ and $a_1\ast x=a_2\ast x$ imply $a_1=a_2$.

Definition 2

([27]). A CA-groupoid $(G,\ast )$ has left separativity if for all $x_1,x_2\in G$, $x_1\ast x_1=x_1\ast x_2$ and $x_2\ast x_2=x_2\ast x_1$ imply $x_1=x_2$.

Definition 3

([27]). A CA-groupoid $(G,\ast )$ has right separativity if for all $x_1,x_2\in G$, $x_1\ast x_1=x_2\ast x_1$ and $x_2\ast x_2=x_1\ast x_2$ imply $x_1=x_2$.

A CA-groupoid has separativity if it has both left separativity and right separativity.

Corollary 2

([27]). Left separativity, right separativity and separativity in a CA-groupoid are equivalent.

Definition 4

([27]). A CA-groupoid $(G,\ast )$ has left quasi-cancellativity if for all $x_1,x_2\in G$, $x_1=x_1\ast x_2$ and $x_2\ast x_2=x_2\ast x_1$ imply $x_1=x_2$.

Definition 5

([27]). A CA-groupoid $(G,\ast )$ has right quasi-cancellativity if for all $x_1,x_2\in G$, $x_1=x_2\ast x_1$ and $x_2\ast x_2=x_1\ast x_2$ imply $x_1=x_2$.

A CA-groupoid has quasi-cancellativity if it has both left quasi-cancellativity and right quasi-cancellativity.

Proposition 3

([27]). In a CA-groupoid, cancellativity is separativity.

Corollary 3

([27]). A CA-groupoid with cancellativity is a commutative CA-groupoid.

Theorem 1

([27]). In a CA-groupoid, separativity is quasi-cancellativity.

Theorem 2

([27]). In a CA-groupoid, left quasi-cancellativity is right quasi-cancellativity.

Definition 6

([27]). A CA-groupoid $(G,\ast )$ is called a CA-3-band, if for all $x\in G$, $x^2\ast x=x\ast x^2=x$.

Theorem 3

([27]). Every CA-3-band has quasi-cancellativity.

A groupoid $(G,\ast )$ is called a T2CA-groupoid if it holds the type-2 cyclic associative law, that is, for all $x_1,x_2,x_3\in G,x_1\ast (x_2\ast x_3)=(x_3\ast x_1)\ast x_2.$

Proposition 4

([2]). If $(G,\ast )$ is a T2CA-groupoid, then for all $x_1,x_2,x_3,x_4\in G$, $(x_1\ast x_2)\ast (x_3\ast x_4)=(x_2\ast x_1)\ast (x_4\ast x_3)$.

Proposition 5

([2]). Every commutative T2CA-groupoid is a commutative semigroup.

3. The Relationships between T2CA-Groupoid and Other Groupoids

In this section, we further study the relationships between the T2CA-groupoid and other groupoids based on the research in [2].

In a T2CA-groupoid $(G,\ast )$, for all $x\in G$, $(x\ast x)\ast x=x\ast (x\ast x)$, the groupoid is called monoassociative. It is readily verified that every T2CA-groupoid is monoassociative. Because T2CA-groupoid is monoassociative, it also has the following result similar to the finite semigroup.

Theorem 4.

Let $(G,\ast )$ be a finite T2CA-groupoid. Then, $\exists a\in G,a^2=a$. That is, there exists an idempotent element in G.

Proof. 

Suppose that a T2CA-groupoid $(G,\ast )$ is finite. Then, for all $a\in G$, $n\in Z^{+},$ $a^n\in G$. Since G is finite, there exist $i,j\in Z^{+}$ such that $a^i=a^{i+j}$. According to the value of i and j, we will discuss this in three cases.

Case 1: if $j=i$, then $a^i=a^{2i}$, that is, $a^i=a^i\ast a^i$, $a^i$ is the idempotent element we are looking for.

Case 2: if $j>i$, then from $a^i=a^{i+j}$, we have

$a^j=a^i\ast a^{j-i}=a^{i+j}\ast a^{j-i}=a^{2j}=a^j\ast a^j$.

This means that $a^j$ is the idempotent element we are looking for.

Case 3: if $j<i$, then from $a^i=a^{i+j}$ we have

$a^i=a^{i+j}=a^i\ast a^j=a^{i+j}\ast a^j=a^{i+2j}$;

$a^i=a^{i+2j}=a^i\ast a^{2j}=a^{i+j}\ast a^{2j}=a^{i+3j}$;

$\dots \dots$

$a^i=a^{i+ij}$.

Since $i,j\in Z^{+},$ then $ij\ge i$. For $a^i=a^{i+ij}$, Case 3 becomes Case 1 when $ij=i,$ and Case 3 becomes Case 2 when $ij>i$. Therefore, we can find an idempotent element in G. □

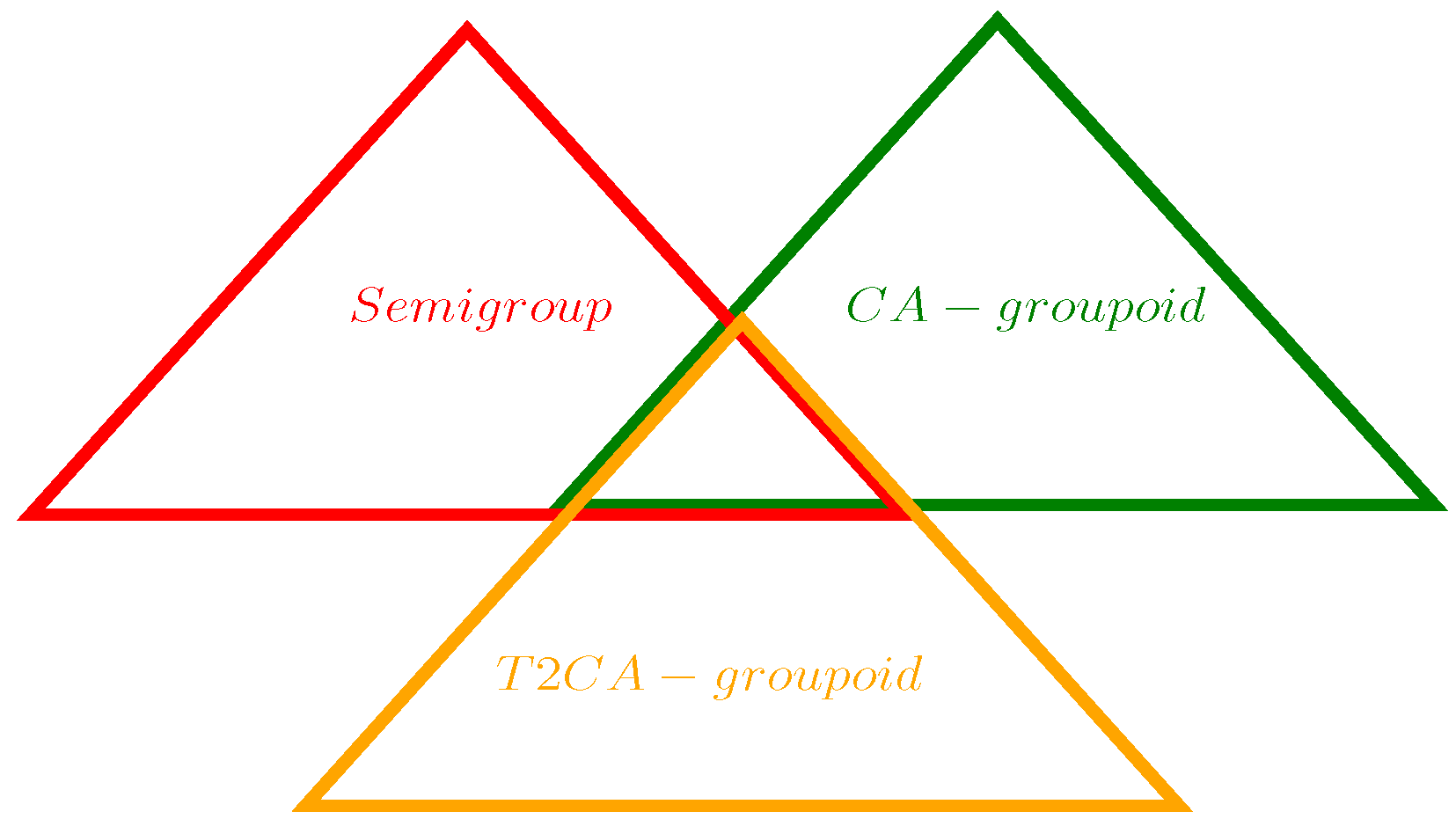
In [2], the commutative T2CA-groupoid is shown to be a commutative semigroup (see Proposition 5). We can easily prove the following three conclusions: the associative T2CA-groupoid is a CA-groupoid; the T2CA-groupoid that satisfies the cyclic associative law is a semigroup; and the associative CA-groupoid is a T2CA-groupoid. Therefore, the relationships between the T2CA-groupoid, CA-groupoid and semigroup are shown in Figure 2.

In Figure 2, there are three triangles of different colors. The red triangle represents the semigroup; the green triangle represents the CA-groupoid; and the orange triangle represents the T2CA-groupoid. We can see from Figure 2 that between the three algebraic structures—the semigroup, CA-groupoid and T2CA-groupoid—the intersection of any two is the proper subset of the third.

Example 1 shows that there is a T2CA-groupoid which is neither an AG-groupoid, nor a CA-groupoid, nor a semigroup.

Example 1.

Given $G=\{1,2,3,4,5,6,7,8,9\}$, we define the operation ∗ on G as shown in

Table 1. A T2CA-groupoid of Example 1.

*	1	2	3	4	5	6	7	8	9
1	1	1	1	1	1	1	1	1	1
2	1	1	1	1	1	1	1	1	1
3	1	1	1	2	1	1	2	1	2
4	1	1	1	1	1	1	1	1	1
5	1	1	1	1	1	2	2	1	2
6	1	1	5	1	1	4	5	1	4
7	1	1	2	2	1	4	2	2	4
8	1	1	2	1	1	1	2	1	2
9	1	1	5	1	1	4	5	2	4

. G is a T2CA-groupoid. However, $(6\ast 7)\ast 7\ne (7\ast 7)\ast 6$, $6\ast (6\ast 7)\ne 7\ast (6\ast 6)$ and $(6\ast 7)\ast 7\ne 6\ast (7\ast 7)$; thus, G is neither an AG-groupoid, nor a CA-groupoid, nor a semigroup.

Theorem 5.

Let $(G,\ast )$ be a T2CA-groupoid. Then, G is a CA-groupoid iff for all $x_1,x_2,x_3\in G$, $x_1\ast (x_2\ast x_3)=(x_2\ast x_3)\ast x_1$.

Proof. 

Suppose that $(G,\ast )$ is a T2CA-groupoid with the cyclic associative law. For all $x_1,x_2,x_3\in G,$ we have

$$\begin{array}{cc}\hfill x_1\ast (x_2\ast x_3)& =x_3\ast (x_1\ast x_2)\left(bythecyclicassociaivelaw\right)\hfill \\ \hfill & =(x_2\ast x_3)\ast x_1.(bythetype-2cyclicassociaivelaw)\hfill \end{array}$$

In contrast, if $(G,\ast )$ is a T2CA-groupoid and for all $x_1,x_2,x_3\in G,$ $x_1\ast (x_2\ast x_3)=(x_2\ast x_3)\ast x_1$, we have

$$\begin{array}{cc}\hfill x_1\ast (x_2\ast x_3)& =(x_2\ast x_3)\ast x_1(bytheidentity{x}_1\ast (x_2\ast x_3)=(x_2\ast x_3)\ast x_1)\hfill \\ \hfill & =x_3\ast (x_1\ast x_2).(bythetype-2cyclicassociaivelaw)\hfill \end{array}$$

Since the cyclic associative law holds, G is a CA-groupoid. □

Theorem 6.

Let $(G,\ast )$ be a T2CA-groupoid. Then, G is an AG-groupoid iff for all $x_1,x_2,x_3\in G$, $x_1\ast (x_2\ast x_3)=x_1\ast (x_3\ast x_2)$.

Proof. 

Suppose that $(G,\ast )$ is a T2CA-groupoid with the left invertive law. For all $x_1,x_2,x_3\in G,$ we have

$$\begin{array}{cc}\hfill x_1\ast (x_2\ast x_3)& =(x_3\ast x_1)\ast x_2(bythetype-2cyclicassociaivelaw)\hfill \\ \hfill & =(x_2\ast x_1)\ast x_3\left(accordingtotheleftinvertivelaw\right)\hfill \\ \hfill & =x_1\ast (x_3\ast x_2).(bythetype-2cyclicassociaivelaw)\hfill \end{array}$$

In contrast, if $(G,\ast )$ is a T2CA-groupoid and for all $x_1,x_2,x_3\in G,$ $x_1\ast (x_2\ast x_3)=x_1\ast (x_3\ast x_2)$, we have

$$\begin{array}{cc}\hfill (x_1\ast x_2)\ast x_3& =x_2\ast (x_3\ast x_1)(bythetype-2cyclicassociaivelaw)\hfill \\ \hfill & =x_2\ast (x_1\ast x_3)(bytheidentity{x}_1\ast (x_2\ast x_3)=x_1\ast (x_3\ast x_2))\hfill \\ \hfill & =(x_3\ast x_2)\ast x_1.(bythetype-2cyclicassociaivelaw)\hfill \end{array}$$

Since the left invertive law holds, G is an AG-groupoid. □

4. Quasi-Cancellativity and Cancellativity of CA-Groupoids

In this section, we prove two theorems that weak cancellativity is cancellativity and right quasi-cancellativity is left quasi-cancellativity in a CA-groupoid, thus successfully solving two open problems.

Zhirou Ma et al. [27] proved that cancellativity is weak cancellativity in a CA-groupoid and proposed an open problem: “Is weak cancellativity necessarily cancellativity in a CA-groupoid?” We tried to look for such an example by computer programming in finite weak cancellative CA-groupoids, which is not a cancellative CA-groupoid. However, it was not found. We therefore considered another possibility, namely that weak cancellativity is cancellativity in a CA-groupoid. Fortunately, this conjecture can be proven to be correct.

Theorem 7.

Weak cancellativity is cancellativity in a CA-groupoid.

Proof. 

Suppose that $(G,\ast )$ is a CA-groupoid with weak cancellativity. For all $x,a_1,a_2\in G,$ if $a_1\ast x=a_2\ast x$, then

$$\begin{array}{cc}\hfill x^2\ast (x\ast a_1)& =(x\ast x)\ast (x\ast a_1)\hfill \\ \hfill & =(a_1\ast x)\ast (x\ast x)\left(byProposition1\right)\hfill \\ \hfill & =(x\ast a_1)\ast (x\ast x)\left(byProposition1\right)\hfill \\ \hfill & =(x\ast a_1)\ast x^2.\hfill \end{array}$$

Similarly, we have $x^2\ast (x\ast a_2)=(x\ast a_2)\ast x^2,$ and

$$\begin{array}{cc}\hfill x^2\ast (x\ast a_1)& =(x\ast x)\ast (x\ast a_1)\hfill \\ \hfill & =(a_1\ast x)\ast (x\ast x)\hfill \\ \hfill & =(a_2\ast x)\ast (x\ast x)(by{a}_1\ast x=a_2\ast x)\hfill \\ \hfill & =(x\ast a_2)\ast (x\ast x)\left(byProposition1\right)\hfill \\ \hfill & =(x\ast a_2)\ast x^2.\hfill \end{array}$$

That is, $x^2\ast (x\ast a_1)=(x\ast a_1)\ast x^2=x^2\ast (x\ast a_2)=(x\ast a_2)\ast x^2$. With $x^2,(x\ast a_1)$, $(x\ast a_2)\in G$, by Definition 1, we can obtain $x\ast a_1=x\ast a_2$. From this and $a_1\ast x=a_2\ast x$, by Definition 1 again, $a_1=a_2$. Thus, $(G,\ast )$ has right cancellativity. According to Corollary 1, it follows that weak cancellativity is cancellativity in a CA-groupoid. □

Corollary 4.

Weak cancellativity and cancellativity are equivalent in a CA-groupoid.

Proof. 

This is a corollary to Theorem 7. □

In [27], left quasi-cancellativity in a CA-groupoid is proven to be right quasi-cancellativity. At the same time, another open problem was asked: “Is right quasi-cancellativity necessarily left quasi-cancellativity in a CA-groupoid?” After careful argumentation, we made clear the relationship between left quasi-cancellativity and right quasi-cancellativity in a CA-groupoid and answered this open problem.

Theorem 8.

Right quasi-cancellativity is left quasi-cancellativity in a CA-groupoid.

Proof. 

Suppose that $(G,\ast )$ is a CA-groupoid with right quasi-cancellativity. For all $x_1,x_2\in G,$ if $x_1=x_1\ast x_2$ and $x_2\ast x_2=x_2\ast x_1$, then

$$\begin{array}{cc}\hfill x_2\ast x_1& =x_2\ast (x_1\ast x_2)(by{x}_1=x_1\ast x_2)\hfill \\ \hfill & =x_2\ast (x_2\ast x_1)\left(bythecyclicassociaivelaw\right)\hfill \\ \hfill & =x_1\ast (x_2\ast x_2)\left(bythecyclicassociaivelaw\right)\hfill \\ \hfill & =(x_1\ast x_2)\ast (x_2\ast x_1),(by{x}_1=x_1\ast x_{2}and{x}_2\ast x_2=x_2\ast x_1)\hfill \end{array}$$

$$\begin{array}{cc}\hfill {(x_1\ast x_2)}^2=(x_1\ast x_2)\ast (x_1\ast x_2)& =(x_2\ast x_1)\ast (x_1\ast x_2).\left(byProposition1\right)\hfill \end{array}$$

From this and by Definition 5, we can obtain $x_1\ast x_2=x_2\ast x_1$. Therefore, based on the existing assumptions $x_1=x_1\ast x_2$ and $x_2\ast x_2=x_2\ast x_1$, we have $x_1=x_2\ast x_1$ and $x_2\ast x_2=x_1\ast x_2$. By Definition 5 again, we obtain that $x_1=x_2$. Thus, by Definition 4$(G,\ast )$ has left quasi-cancellativity. □

Corollary 5.

Left quasi-cancellativity, right quasi-cancellativity and quasi-cancellativity in a CA-groupoid are equivalent to each other.

Proof. 

This is the corollary of Theorems 2 and 8. □

Given that the relationships among separativity, quasi-cancellativity and commutativity in a CA-groupoid were not discussed in previous literature, we will now discuss their relationships.

Theorem 9.

A CA-groupoid with separativity is a commutative CA-groupoid.

Proof. 

We first proved that a CA-groupoid with right separativity is a commutative CA-groupoid. Suppose that $(G,\ast )$ is a CA-groupoid with right separativity. For all $x_1,x_2\in G,$ we have

$$\begin{array}{cc}\hfill (x_1\ast x_2)\ast (x_1\ast x_2)& =(x_2\ast x_1)\ast (x_1\ast x_2),\left(byProposition1\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill (x_2\ast x_1)\ast (x_2\ast x_1)& =(x_1\ast x_2)\ast (x_2\ast x_1).\left(byProposition1\right)\hfill \end{array}$$

From this and by Definition 3, we can obtain $x_1\ast x_2=x_2\ast x_1$. Therefore, $(G,\ast )$ is a commutative CA-groupoid. According to Corollary 2, it follows that a CA-groupoid with separativity is a commutative CA-groupoid. □

Obviously, Corollary 3 can be derived from Proposition 3 and Theorem 9.

Example 2 illustrates that a quasi-cancellative CA-groupoid is not always a commutative CA-groupoid.

Example 2.

Given $G=\{x_1,x_2,x_3,x_4\}$, we define the operation ∗ on G as shown in

Table 2. A quasi-cancellative CA-groupoid of Example 2.

*	${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{x}}_4$
$x_1$	$x_1$	$x_2$	$x_2$	$x_3$
$x_2$	$x_2$	$x_1$	$x_1$	$x_1$
$x_3$	$x_2$	$x_1$	$x_1$	$x_1$
$x_4$	$x_2$	$x_1$	$x_1$	$x_1$

. G is a quasi-cancellative CA-groupoid. However, $x_4\ast x_1\ne x_1\ast x_4$. G is not a commutative CA-groupoid.

Example 3 illustrates that a commutative CA-groupoid is not always a quasi-cancellative CA-groupoid.

Example 3.

Given $G=\{a,b,c,d\}$, we define the operation ∗ on G as shown in

Table 3. A commutative CA-groupoid of Example 3.

*	a	b	c	d
a	a	a	a	a
b	a	a	b	b
c	a	b	c	d
d	a	b	d	c

. G is a commutative CA-groupoid. However, $a=a\ast b=b\ast b=b\ast a$ and $a\ne b$. G is not a quasi-cancellative CA-groupoid.

Example 4 illustrates that a commutative CA-groupoid with quasi-cancellativity is not always a separative CA-groupoid.

Example 4.

Given $G=\{1,2,3,4\}$, we define the operation ∗ on G as shown in

Table 4. A commutative CA-groupoid with quasi-cancellativity of Example 4.

*	1	2	3	4
1	1	1	3	3
2	1	2	3	4
3	3	3	1	1
4	3	4	1	1

. G is a commutative CA-groupoid with quasi-cancellativity. However, $3\ast 3=3\ast 4=4\ast 3=4\ast 4$ and $3\ne 4$. G is not a separative CA-groupoid.

From Theorems 1 and 9, as well as Examples 2–4, we have Figure 3.

Figure 3 shows the relationships among the quasi-cancellative CA-groupoid, separative CA-groupoid and commutative CA-groupoid. Here, A stands for separative CA-groupoid; B stands for commutative CA-groupoid with quasi-cancellativity, as shown in Example 4, rather than a separative CA-groupoid; C stands for quasi-cancellative CA-groupoid, as shown in Example 2, rather than the commutative CA-groupoid; and D stands for commutative CA-groupoid, as shown in Example 3, rather than quasi-cancellative CA-groupoid. A + B + C stands for quasi-cancellative CA-groupoid; and A + B + D stands for commutative CA-groupoid.

In [27], Zhirou Ma et al. proved that separativity is quasi-cancellativity in a CA-groupoid and every CA-3-band has quasi-cancellativity (see Theorems 1 and 3). The relationship between the CA-3-band and separativity is given in the following Theorem 10.

Theorem 10.

Let $(G,\ast )$ be a CA-3-band. Then:

(1)

G has separativity;

(2)

G is a commutative semigroup.

Proof. 

(1) Suppose that $(G,\ast )$ is a CA-3-band. We first prove that the CA-3-band has left separativity. For all $x_1,x_2\in G,$ we have $x_1^2\ast x_1=x_1\ast x_1^2=x_1$ and $x_2^2\ast x_2=x_2\ast x_2^2=x_2$. If $x_1\ast x_1=x_1\ast x_2$ and $x_2\ast x_2=x_2\ast x_1$, then

$$\begin{array}{cc}\hfill x_1& =x_1\ast x_1^2\hfill \\ \hfill & =x_1\ast (x_1\ast x_2)(by{x}_1\ast x_1=x_1\ast x_2)\hfill \\ \hfill & =x_2\ast (x_1\ast x_1)\left(bythecyclicassociaivelaw\right)\hfill \\ \hfill & =x_2\ast (x_1\ast x_2)(by{x}_1\ast x_1=x_1\ast x_2)\hfill \\ \hfill & =x_2\ast (x_2\ast x_1)\left(bythecyclicassociaivelaw\right)\hfill \\ \hfill & =x_2\ast (x_2\ast x_2)(by{x}_2\ast x_2=x_2\ast x_1)\hfill \\ \hfill & =x_2\ast x_2^2\hfill \\ \hfill & =x_2.\hfill \end{array}$$

Therefore, $(G,\ast )$ has left separativity. According to Corollary 2, it follows that $(G,\ast )$ has separativity.

(2) This is the corollary of Theorem 9 and Proposition 2. □

By the definition of the CA-3-band (see Definition 6), we know that a CA-groupoid needs two conditions $x^2\ast x=x$ and $x\ast x^2=x$ to become a CA-3-band. It can be seen from the following Proposition 6 that only one condition ($x^2\ast x=x$ or $x\ast x^2=x$) is required.

Proposition 6.

Let $(G,\ast )$ be a CA-groupoid. Then, for all $x\in G$, $x^2\ast x=x$ iff $x\ast x^2=x$.

Proof. 

Suppose that $(G,\ast )$ is a CA-groupoid. For all $x\in G,$$x^2\ast x=x$, we have

$$\begin{array}{cc}\hfill x\ast x^2& =(x^2\ast x)\ast x^2(by{x}^2\ast x=x)\hfill \\ \hfill & =(x^2\ast x)\ast (x\ast x)\hfill \\ \hfill & =(x\ast x^2)\ast (x\ast x)\left(byProposition1\right)\hfill \\ \hfill & =(x\ast x)\ast (x\ast x^2)\left(byProposition1\right)\hfill \\ \hfill & =x^2\ast (x\ast x^2)\hfill \\ \hfill & =x^2\ast (x^2\ast x)\left(bythecyclicassociaivelaw\right)\hfill \\ \hfill & =x^2\ast x(by{x}^2\ast x=x)\hfill \\ \hfill & =x.\hfill \end{array}$$

In contrast, if $(G,\ast )$ is a CA-groupoid and for all $x\in G,$$x\ast x^2=x$, we have

$$\begin{array}{cc}\hfill x^2\ast x& =x^2\ast (x\ast x^2)(byx\ast x^2=x)\hfill \\ \hfill & =(x\ast x)\ast (x\ast x^2)\hfill \\ \hfill & =(x^2\ast x)\ast (x\ast x)\left(byProposition1\right)\hfill \\ \hfill & =(x\ast x^2)\ast (x\ast x)\left(byProposition1\right)\hfill \\ \hfill & =x\ast x^2(byx\ast x^2=x)\hfill \\ \hfill & =x.\hfill \end{array}$$

□

5. Quasi-Cancellativity and Cancellativity of T2CA-Groupoids

In this section, we discuss the quasi-cancellativity and cancellativity of T2CA-groupoids and study the relationships between them.

Definition 7

([2]). A T2CA-groupoid $(G,\ast )$ is called a left cancellative T2CA-groupoid if for all $x,a_1,a_2\in G$, $x\ast a_1=x\ast a_2$ implies that $a_1=a_2$.

Definition 8

([2]). A T2CA-groupoid $(G,\ast )$ is called a right cancellative T2CA-groupoid if for all $x,a_1,a_2\in G$, $a_1\ast x=a_2\ast x$ implies that $a_1=a_2$.

A groupoid is called a cancellative T2CA-groupoid if it is both a left cancellative T2CA-groupoid and a right cancellative T2CA-groupoid.

Corollary 6

([2]). A left cancellative T2CA-groupoid, a right cancellative T2CA-groupoid and a cancellative T2CA-groupoid are equivalent to each other.

Definition 9.

A T2CA-groupoid $(G,\ast )$ is called a weak cancellative T2CA-groupoid if for all $x,a_1,a_2\in G$, $x\ast a_1=x\ast a_2$ and $a_1\ast x=a_2\ast x$ imply that $a_1=a_2$.

Example 5.

Given $G=\{x_1,x_2,x_3,x_4,x_5,x_6\}$, we define the operation ∗ on G as shown in

Table 5. A weak cancellative T2CA-groupoid of Example 5.

*	${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{x}}_4$	${\mathit{x}}_5$	${\mathit{x}}_6$
$x_1$	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$x_6$
$x_2$	$x_2$	$x_1$	$x_4$	$x_3$	$x_6$	$x_5$
$x_3$	$x_3$	$x_4$	$x_5$	$x_6$	$x_1$	$x_2$
$x_4$	$x_4$	$x_3$	$x_6$	$x_5$	$x_2$	$x_1$
$x_5$	$x_5$	$x_6$	$x_1$	$x_2$	$x_3$	$x_4$
$x_6$	$x_6$	$x_5$	$x_2$	$x_1$	$x_4$	$x_3$

. By Definition 9, G is a weak cancellative T2CA-groupoid.

Theorem 11.

A weak cancellative T2CA-groupoid is a cancellative T2CA-groupoid.

Proof. 

Suppose that $(G,\ast )$ is a weak cancellative T2CA-groupoid. For all $x,a_1,a_2\in G,$ if $a_1\ast x=a_2\ast x$, then

$$\begin{array}{cc}\hfill x^2\ast (x\ast a_1)& =(x\ast x)\ast (x\ast a_1)\hfill \\ \hfill & =(x\ast x)\ast (a_1\ast x)\left(byProposition4\right)\hfill \\ \hfill & =(x\ast x)\ast (a_2\ast x)(by{a}_2\ast x=a_1\ast x)\hfill \\ \hfill & =(x\ast x)\ast (x\ast a_2)\left(byProposition4\right)\hfill \\ \hfill & =x^2\ast (x\ast a_2),\hfill \end{array}$$

$$\begin{array}{cc}\hfill (x\ast a_1)\ast x^2& =(x\ast a_1)\ast (x\ast x)\hfill \\ \hfill & =(a_1\ast x)\ast (x\ast x)\left(byProposition4\right)\hfill \\ \hfill & =(a_2\ast x)\ast (x\ast x)(by{a}_2\ast x=a_1\ast x)\hfill \\ \hfill & =(x\ast a_2)\ast (x\ast x)\left(byProposition4\right)\hfill \\ \hfill & =(x\ast a_2)\ast x^2.\hfill \end{array}$$

That is, $x^2\ast (x\ast a_1)=x^2\ast (x\ast a_2)$ and $(x\ast a_1)\ast x^2=(x\ast a_2)\ast x^2$. Since $x^2,(x\ast a_1),(x\ast a_2)\in G$, by Definition 9, we can obtain $x\ast a_1=x\ast a_2$. From this and $a_1\ast x=a_2\ast x$, by Definition 9 again, $a_1=a_2$. Thus, by Definition 8 $(G,\ast )$ is a right cancellative T2CA-groupoid. By Corollary 6, we know that a weak cancellative T2CA-groupoid is a cancellative T2CA-groupoid. □

Corollary 7.

A weak cancellative T2CA-groupoid is equal to a cancellative T2CA-groupoid.

Proof. 

This is a corollary to Theorem 11. □

Corollary 8.

Every cancellative T2CA-groupoid is a commutative T2CA-groupoid.

Proof. 

Suppose that $(G,\ast )$ is a cancellative T2CA-groupoid. For all $x_1,x_2\in G,$ we have

$$\begin{array}{cc}\hfill (x_1\ast x_2)\ast (x_2\ast x_2)& =(x_2\ast x_1)\ast (x_2\ast x_2).\left(byProposition4\right)\hfill \end{array}$$

By cancellative law, we can obtain $x_1\ast x_2=x_2\ast x_1$. Therefore, G is a commutative T2CA-groupoid. □

Definition 10.

A T2CA-groupoid $(G,\ast )$ is called a power cancellative T2CA-groupoid for all $x_1,x_2\in G$, if $x_1\ast x_1=x_2\ast x_2$ implies $x_1=x_2$.

Corollary 9.

Every power cancellative T2CA-groupoid is a commutative T2CA-groupoid.

Proof. 

Suppose that $(G,\ast )$ is a power cancellative T2CA-groupoid. For all $x_1,x_2\in G,$ we have

$$\begin{array}{cc}\hfill (x_1\ast x_2)\ast (x_1\ast x_2)& =(x_2\ast x_1)\ast (x_2\ast x_1).\left(byProposition4\right)\hfill \end{array}$$

By Definition 10, we can obtain $x_1\ast x_2=x_2\ast x_1$. Therefore, G is a commutative T2CA-groupoid. □

Example 6 illustrates that a T2CA-groupoid can be both a power cancellative T2CA-groupoid and a cancellative T2CA-groupoid.

Example 6.

Since $G=\{1,2,3,4,5\}$, we define the operation ∗ on G as shown in

Table 6. A T2CA-groupoid with both power cancellativity and the cancellativity of Example 6.

*	1	2	3	4	5
1	1	2	3	4	5
2	2	3	5	1	4
3	3	5	4	2	1
4	4	1	2	5	3
5	5	4	1	3	2

. G is both a power cancellative T2CA-groupoid and a cancellative T2CA-groupoid.

Example 7 illustrates that a power cancellative T2CA-groupoid is not always a cancellative T2CA-groupoid.

Example 7.

Since $G=\{x_1,x_2,x_3,x_4,x_5\}$, we define the operation ∗ on G as shown in

Table 7. A power cancellative T2CA-groupoid of Example 7.

*	${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{x}}_4$	${\mathit{x}}_5$
$x_1$	$x_1$	$x_1$	$x_1$	$x_4$	$x_5$
$x_2$	$x_1$	$x_2$	$x_2$	$x_4$	$x_5$
$x_3$	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$
$x_4$	$x_4$	$x_4$	$x_4$	$x_5$	$x_1$
$x_5$	$x_5$	$x_5$	$x_5$	$x_1$	$x_4$

. G is a power cancellative T2CA-groupoid. However, $x_1\ast x_2=x_1\ast x_3$ and $x_2\ne x_3$; thus, G is not a cancellative T2CA-groupoid.

Example 8 illustrates that a cancellative T2CA-groupoid is not always a power cancellative T2CA-groupoid.

Example 8.

Given $G=\{1,2,3,4,5,6,7,8\}$, we define the operation ∗ on G as shown in

Table 8. A cancellative T2CA-groupoid of Example 8.

*	1	2	3	4	5	6	7	8
1	1	2	3	4	5	6	7	8
2	2	1	4	3	6	5	8	7
3	3	4	1	2	7	8	5	6
4	4	3	2	1	8	7	6	5
5	5	6	7	8	1	2	3	4
6	6	5	8	7	2	1	4	3
7	7	8	5	6	3	4	1	2
8	8	7	6	5	4	3	2	1

. G is a cancellative T2CA-groupoid. However, $2^2=3^2$ and $2\ne 3$; thus, G is not a power cancellative T2CA-groupoid.

Definition 11.

A T2CA-groupoid $(G,\ast )$ is called a left separative T2CA-groupoid for all $x_1,x_2\in G$ if $x_1\ast x_1=x_1\ast x_2$ and $x_2\ast x_2=x_2\ast x_1$ imply $x_1=x_2$.

Definition 12.

A T2CA-groupoid $(G,\ast )$ is called a right separative T2CA-groupoid for all $x_1,x_2\in G$ if $x_1\ast x_1=x_2\ast x_1$ and $x_2\ast x_2=x_1\ast x_2$ imply $x_1=x_2$.

A groupoid is called a separative T2CA-groupoid, if it is both a left separative T2CA-groupoid and a right separative T2CA-groupoid.

Definition 13.

A T2CA-groupoid $(G,\ast )$ is called a quasi-separative T2CA-groupoid for all $x_1,x_2\in G$ if $x_1\ast x_1=x_1\ast x_2=x_2\ast x_2$ implies $x_1=x_2$.

Theorem 12.

Let $(G,\ast )$ be a T2CA-groupoid. Then, in this case, the following four statements are equivalent:

(1) 

G is a left separative T2CA-groupoid;

(2) 

G is a separative T2CA-groupoid;

(3) 

G is a right separative T2CA-groupoid;

(4) 

G is a quasi-separative T2CA-groupoid.

Proof. 

(1)⇒(2). Suppose that $(G,\ast )$ is a left separative T2CA-groupoid. For all $x_1,x_2\in G,$ if $x_1\ast x_1=x_2\ast x_1$ and $x_2\ast x_2=x_1\ast x_2$, then

$$\begin{array}{cc}\hfill {(x_1\ast x_2)}^2& =(x_1\ast x_2)\ast (x_1\ast x_2)\hfill \\ \hfill & =(x_2\ast x_2)\ast (x_1\ast x_2)(by{x}_2\ast x_2=x_1\ast x_2)\hfill \\ \hfill & =(x_2\ast x_2)\ast (x_2\ast x_1)\left(byProposition4\right)\hfill \\ \hfill & =(x_1\ast x_2)\ast (x_2\ast x_1),(by{x}_2\ast x_2=x_1\ast x_2)\hfill \end{array}$$

$$\begin{array}{cc}\hfill {(x_2\ast x_1)}^2& =(x_2\ast x_1)\ast (x_2\ast x_1)\hfill \\ \hfill & =(x_1\ast x_1)\ast (x_2\ast x_1)(by{x}_1\ast x_1=x_2\ast x_1)\hfill \\ \hfill & =(x_1\ast x_1)\ast (x_1\ast x_2)\left(byProposition4\right)\hfill \\ \hfill & =(x_2\ast x_1)\ast (x_1\ast x_2).(by{x}_1\ast x_1=x_2\ast x_1)\hfill \end{array}$$

By Definition 11, we obtain that $x_1\ast x_2=x_2\ast x_1$. Therefore, based on the existing assumptions $x_1\ast x_1=x_2\ast x_1$ and $x_2\ast x_2=x_1\ast x_2$, we have $x_1\ast x_1=x_1\ast x_2$ and $x_2\ast x_2=x_2\ast x_1$. By Definition 11, we again have $x_1=x_2$. Thus, from Definition 12, $(G,\ast )$ is a right separative T2CA-groupoid. $(G,\ast )$ is both a left and right separative, so it is a separative T2CA-groupoid.

(2)⇒(3). Obviously.

(3)⇒(4). Suppose that $(G,\ast )$ is a right separative T2CA-groupoid. For all $x_1,x_2\in G,$ if $x_1\ast x_1=x_1\ast x_2=x_2\ast x_2$, then

$$\begin{array}{cc}\hfill {(x_1\ast x_2)}^2& =(x_1\ast x_2)\ast (x_1\ast x_2)\hfill \\ \hfill & =(x_1\ast x_2)\ast (x_2\ast x_2)(by{x}_2\ast x_2=x_1\ast x_2)\hfill \\ \hfill & =(x_2\ast x_1)\ast (x_2\ast x_2)\left(byProposition4\right)\hfill \\ \hfill & =(x_2\ast x_1)\ast (x_1\ast x_2),(by{x}_2\ast x_2=x_1\ast x_2)\hfill \end{array}$$

$$\begin{array}{cc}\hfill {(x_2\ast x_1)}^2& =(x_2\ast x_1)\ast (x_2\ast x_1)\hfill \\ \hfill & =(x_1\ast x_2)\ast (x_1\ast x_2)\left(byProposition4\right)\hfill \\ \hfill & =(x_1\ast x_1)\ast (x_1\ast x_2)(by{x}_1\ast x_1=x_1\ast x_2)\hfill \\ \hfill & =(x_1\ast x_1)\ast (x_2\ast x_1)\left(byProposition4\right)\hfill \\ \hfill & =(x_1\ast x_2)\ast (x_2\ast x_1).(by{x}_1\ast x_1=x_1\ast x_2)\hfill \end{array}$$

By Definition 12, we obtain that $x_1\ast x_2=x_2\ast x_1$. Therefore, based on the existing assumptions $x_1\ast x_1=x_1\ast x_2=x_2\ast x_2$, we have $x_1\ast x_1=x_2\ast x_1$ and $x_2\ast x_2=x_1\ast x_2$. By Definition 12 again, we have $x_1=x_2$. Thus, from Definition 13, $(G,\ast )$ is a quasi-separative T2CA-groupoid.

(4)⇒(1). Suppose that $(G,\ast )$ is a quasi-separative T2CA-groupoid. For all $x_1,x_2\in G,$ if $x_1\ast x_1=x_1\ast x_2$ and $x_2\ast x_2=x_2\ast x_1$, then

$$\begin{array}{cc}\hfill {(x_1\ast x_2)}^2& =(x_1\ast x_2)\ast (x_1\ast x_2)\hfill \\ \hfill & =(x_2\ast x_1)\ast (x_2\ast x_1)\left(byProposition4\right)\hfill \\ \hfill & ={(x_2\ast x_1)}^2,\hfill \end{array}$$

$$\begin{array}{cc}\hfill (x_1\ast x_2)\ast (x_2\ast x_1)& =(x_1\ast x_1)\ast (x_2\ast x_1)(by{x}_1\ast x_1=x_1\ast x_2)\hfill \\ \hfill & =(x_1\ast x_1)\ast (x_1\ast x_2)\left(byProposition4\right)\hfill \\ \hfill & =(x_1\ast x_2)\ast (x_1\ast x_2)(by{x}_1\ast x_1=x_1\ast x_2)\hfill \\ \hfill & ={(x_1\ast x_2)}^2.\hfill \end{array}$$

That is ${(x_1\ast x_2)}^2=(x_1\ast x_2)\ast (x_2\ast x_1)={(x_2\ast x_1)}^2$. By Definition 13, we obtain that $x_1\ast x_2=x_2\ast x_1$. Therefore, based on the existing assumptions $x_1\ast x_1=x_1\ast x_2$ and $x_2\ast x_2=x_2\ast x_1$, we have $x_1\ast x_1=x_1\ast x_2=x_2\ast x_2$. By Definition 13, we again have $x_1=x_2$. Thus, from Definition 11, $(G,\ast )$ is a left separative T2CA-groupoid. □

Theorem 13.

A cancellative T2CA-groupoid is a separative T2CA-groupoid.

Proof. 

Suppose that $(G,\ast )$ is a cancellative T2CA-groupoid. For all $x_1,x_2\in G,$ if $x_1\ast x_1=x_1\ast x_2$ and $x_2\ast x_2=x_2\ast x_1$, then from cancellative law, we have $x_1=x_2$. Thus, $(G,\ast )$ is a left separative T2CA-groupoid. By Theorem 12, we can obtain that $(G,\ast )$ is a separative T2CA-groupoid. □

Theorem 14.

A power cancellative T2CA-groupoid is a separative T2CA-groupoid.

Proof. 

Suppose that $(G,\ast )$ is a power cancellative T2CA-groupoid. For all $x_1,x_2\in G,$ if $x_1\ast x_1=x_1\ast x_2=x_2\ast x_2$, then from power cancellative law, we have $x_1=x_2$. Thus, $(G,\ast )$ is a quasi-separative T2CA-groupoid. By Theorem 12, we can determine that $(G,\ast )$ is a separative T2CA-groupoid. □

Example 9 illustrates that a separative T2CA-groupoid is neither a power cancellative T2CA-groupoid nor a cancellative T2CA-groupoid.

Example 9.

Since $G=\{a,b,c,d,e\}$, we define operation * on G as shown in

Table 9. A separative T2CA-groupoid of Example 9.

*	a	b	c	d	e
a	a	b	a	a	a
b	b	a	b	b	b
c	a	b	c	d	e
d	a	b	d	e	c
e	a	b	e	c	d

. G is a separative T2CA-groupoid. However, $a^2=b^2,$ $a\ne b$, and $a\ast c=a\ast d,$ $c\ne d$; thus, G is neither a power cancellative T2CA-groupoid nor a cancellative T2CA-groupoid.

Definition 14.

A T2CA-groupoid $(G,\ast )$ is called a left quasi-cancellative T2CA-groupoid for all $x_1,x_2\in G$ if $x_1=x_1\ast x_2$ and $x_2\ast x_2=x_2\ast x_1$ which imply that $x_1=x_2$.

Definition 15.

A T2CA-groupoid $(G,\ast )$ is called a right quasi-cancellative T2CA-groupoid for all $x_1,x_2\in G$ if $x_1=x_2\ast x_1$ and $x_2\ast x_2=x_1\ast x_2$ imply that $x_1=x_2$.

A groupoid is called a quasi-cancellative T2CA-groupoid if it is both a left quasi-cancellative T2CA-groupoid and a right quasi-cancellative T2CA-groupoid.

Theorem 15.

Let $(G,\ast )$ be a T2CA-groupoid. Then, in this case, the following three statements are equivalent:

(1) 

G is a left quasi-cancellative T2CA-groupoid;

(2) 

G is a quasi-cancellative T2CA-groupoid;

(3) 

G is a right quasi-cancellative T2CA-groupoid.

Proof. 

(1)⇒(2). Suppose that $(G,\ast )$ is a left quasi-cancellative T2CA-groupoid. For all $x_1,x_2\in G,$ if $x_1=x_2\ast x_1$ and $x_2\ast x_2=x_1\ast x_2$, then

$$\begin{array}{cc}\hfill x_1\ast x_2& =(x_2\ast x_1)\ast x_2(by{x}_1=x_2\ast x_1)\hfill \\ \hfill & =x_1\ast (x_2\ast x_2)(bythetype-2cyclicassociaivelaw)\hfill \\ \hfill & =(x_2\ast x_1)\ast (x_2\ast x_2)(by{x}_1=x_2\ast x_1)\hfill \\ \hfill & =(x_1\ast x_2)\ast (x_2\ast x_2)\left(byProposition4\right)\hfill \\ \hfill & =(x_1\ast x_2)\ast (x_1\ast x_2)(by{x}_2\ast x_2=x_1\ast x_2)\hfill \\ \hfill & =(x_2\ast x_1)\ast (x_2\ast x_1)\left(byProposition4\right)\hfill \\ \hfill & =x_1\ast x_1,(by{x}_1=x_2\ast x_1)\hfill \end{array}$$

$$\begin{array}{cc}\hfill x_2\ast x_1& =x_2\ast (x_2\ast x_1)(by{x}_1=x_2\ast x_1)\hfill \\ \hfill & =(x_1\ast x_2)\ast x_2(bythetype-2cyclicassociaivelaw)\hfill \\ \hfill & =(x_1\ast x_1)\ast x_2(by{x}_1\ast x_2=x_1\ast x_1)\hfill \\ \hfill & =x_1\ast (x_2\ast x_1)(bythetype-2cyclicassociaivelaw)\hfill \\ \hfill & =x_1\ast x_1(by{x}_1=x_2\ast x_1)\hfill \\ \hfill & =x_1\ast x_2.(by{x}_1\ast x_2=x_1\ast x_1)\hfill \end{array}$$

According to the above derivation, we can obtain $x_1\ast x_2=x_2\ast x_1$. Therefore, based on the existing assumptions $x_1=x_2\ast x_1$ and $x_2\ast x_2=x_1\ast x_2$, we have $x_1=x_1\ast x_2$ and $x_2\ast x_2=x_2\ast x_1$. By Definition 14, we obtain that $x_1=x_2$. Thus, from Definition 15, $(G,\ast )$ is a right quasi-cancellative T2CA-groupoid. $(G,\ast )$ has both left and right quasi-cancellativity, so it is a quasi-cancellative T2CA-groupoid.

(2)⇒(3). This is evident.

(3)⇒(1). Suppose $(G,\ast )$ is a right quasi-cancellative T2CA-groupoid. For all $x_1,x_2\in G,$ if $x_1=x_1\ast x_2$ and $x_2\ast x_2=x_2\ast x_1$, then

$$\begin{array}{cc}\hfill x_2\ast x_1& =x_2\ast (x_1\ast x_2)(by{x}_1=x_1\ast x_2)\hfill \\ \hfill & =(x_2\ast x_2)\ast x_1(bythetype-2cyclicassociaivelaw)\hfill \\ \hfill & =(x_2\ast x_2)\ast (x_1\ast x_2)(by{x}_1=x_1\ast x_2)\hfill \\ \hfill & =(x_2\ast x_2)\ast (x_2\ast x_1)\left(byProposition4\right)\hfill \\ \hfill & =(x_2\ast x_1)\ast (x_2\ast x_1)(by{x}_2\ast x_2=x_2\ast x_1)\hfill \\ \hfill & =(x_1\ast x_2)\ast (x_1\ast x_2)\left(byProposition4\right)\hfill \\ \hfill & =x_1\ast x_1,(by{x}_1=x_1\ast x_2)\hfill \end{array}$$

$$\begin{array}{cc}\hfill x_1\ast x_2& =(x_1\ast x_2)\ast x_2(by{x}_1=x_1\ast x_2)\hfill \\ \hfill & =x_2\ast (x_2\ast x_1)(bythetype-2cyclicassociaivelaw)\hfill \\ \hfill & =x_2\ast (x_1\ast x_1)(by{x}_1\ast x_1=x_2\ast x_1)\hfill \\ \hfill & =(x_1\ast x_2)\ast x_1(bythetype-2cyclicassociaivelaw)\hfill \\ \hfill & =x_1\ast x_1(by{x}_1=x_1\ast x_2)\hfill \\ \hfill & =x_2\ast x_1.(by{x}_1\ast x_1=x_2\ast x_1)\hfill \end{array}$$

According to the above derivation, we can determine that $x_1\ast x_2=x_2\ast x_1$. Therefore, based on the existing assumptions $x_1=x_1\ast x_2$ and $x_2\ast x_2=x_2\ast x_1$, we have $x_1=x_2\ast x_1$ and $x_2\ast x_2=x_1\ast x_2$. By Definition 15, we obtain that $x_1=x_2$. Thus, from Definition 14, $(G,\ast )$ is a left quasi-cancellative T2CA-groupoid. □

Theorem 16.

A separative T2CA-groupoid is a quasi-cancellative T2CA-groupoid.

Proof. 

First, we prove that a quasi-separative T2CA-groupoid is a right quasi-cancellative T2CA-groupoid. Suppose $(G,\ast )$ is a quasi-separative T2CA-groupoid. For all $x_1,x_2\in G,$ if $x_1=x_2\ast x_1$ and $x_2\ast x_2=x_1\ast x_2$, then

$$\begin{array}{cc}\hfill x_1\ast x_1& =(x_2\ast x_1)\ast x_1(by{x}_1=x_2\ast x_1)\hfill \\ \hfill & =x_1\ast (x_1\ast x_2)(bythetype-2cyclicassociaivelaw)\hfill \\ \hfill & =x_1\ast (x_2\ast x_2)(by{x}_1\ast x_2=x_2\ast x_2)\hfill \\ \hfill & =(x_2\ast x_1)\ast x_2(bythetype-2cyclicassociaivelaw)\hfill \\ \hfill & =x_1\ast x_2(by{x}_1=x_2\ast x_1)\hfill \\ \hfill & =x_2\ast x_2.(by{x}_1\ast x_2=x_2\ast x_2)\hfill \end{array}$$

We can obtain $x_1\ast x_1=x_1\ast x_2=x_2\ast x_2$. By Definition 13, we determine that $x_1=x_2$. Thus, a quasi-separative T2CA-groupoid is a right quasi-cancellative T2CA-groupoid. According to Theorem 12 and Theorem 15, it follows that a separative T2CA-groupoid is a quasi-cancellative T2CA-groupoid. □

Example 10 illustrates that a quasi-cancellative T2CA-groupoid is not always a separative T2CA-groupoid.

Example 10.

Since $G=\{1,2,3,4,5\}$, we define the operation ∗ on G as shown in

Table 10. A quasi-cancellative T2CA-groupoid of Example 10.

*	1	2	3	4	5
1	1	1	3	4	4
2	1	2	3	4	5
3	3	3	4	1	1
4	4	4	1	3	3
5	4	5	1	3	3

. G is a quasi-cancellative T2CA-groupoid. However, $4^2=4\ast 5=5\ast 4=5^2$ and $4\ne 5$. G is not a separative T2CA-groupoid.

Figure 4 shows the relationships between the separative T2CA-groupoid and quasi-cancellative T2CA-groupoid. There are four ellipses of different colors and sizes in the picture.

A stands for both the power cancellative T2CA-groupoid and cancellative T2CA-groupoid shown in Example 6; B stands for the power cancellative T2CA-groupoid shown in Example 7 rather than the cancellative T2CA-groupoid; C stands for the cancellative T2CA-groupoid shown in Example 8 rather than the power cancellative T2CA-groupoid; D stands for the separative T2CA-groupoid shown in Example 9, which is, however, neither a power cancellative T2CA-groupoid nor a cancellative T2CA-groupoid; and E stands for the quasi-cancellative T2CA-groupoid shown in Example 10 rather than the separative T2CA-groupoid. A + B, which is the red ellipse, stands for the power cancellative T2CA-groupoid; A + C, which is the blue ellipse, stands for the cancellative T2CA-groupoid; A + B + C + D, which is the green ellipse, stands for the separative T2CA-groupoid; and A + B + C + D + E, which is the largest orange ellipse, stands for the quasi-cancellative T2CA-groupoid.

Theorem 17.

Let $(G,\ast )$ be a separative T2CA-groupoid. Then, G is a commutative T2CA-groupoid if for all $x_1,x_2\in G$ there exists $a\in G$ such that $x_1\ast x_2=a^n,n\in Z^{+},n>1$.

Proof. 

Suppose that $(G,\ast )$ is a separative T2CA-groupoid, then by Theorem 12, $(G,\ast )$ is a quasi-separative T2CA-groupoid. For all $x_1,x_2\in G,$ if there exists $a\in G,$ such that $x_1\ast x_2=a^n,n\in Z^{+},n>1$. Since the T2CA-groupoid is monoassociative, we have $a^n=a\ast a^{n-1}=a^{n-1}\ast a$. We can determine that

$$\begin{array}{cc}\hfill (x_1\ast x_2)\ast (x_1\ast x_2)& =(x_2\ast x_1)\ast (x_2\ast x_1),\left(byProposition4\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill (x_1\ast x_2)\ast (x_1\ast x_2)& =(a\ast a^{n-1})\ast (x_1\ast x_2)(by{x}_1\ast x_2=a^n=a\ast a^{n-1})\hfill \\ \hfill & =(a^{n-1}\ast a)\ast (x_2\ast x_1)\left(byProposition4\right)\hfill \\ \hfill & =(x_1\ast x_2)\ast (x_2\ast x_1).(by{a}^{n-1}\ast a=a^n=x_1\ast x_2)\hfill \end{array}$$

That is $(x_1\ast x_2)\ast (x_1\ast x_2)=(x_1\ast x_2)\ast (x_2\ast x_1)=(x_2\ast x_1)\ast (x_2\ast x_1)$. By Definition 13, we have $x_1\ast x_2=x_2\ast x_1$. Thus, G is a commutative T2CA-groupoid. □

Example 11.

Given $G=\{1,2,3,4,5\}$, we define the operation ∗ on G as shown in

Table 11. A separative T2CA-groupoid of Example 11.

*	1	2	3	4	5
1	1	2	3	4	1
2	2	1	4	3	2
3	3	4	2	1	3
4	4	3	1	2	4
5	1	2	3	4	5

. G is a separative T2CA-groupoid. For any $x_1,x_2\in G$, without losing generality, let $x_1=4,x_2=2$, and we can obtain $x_1\ast x_2=4\ast 2=3=4^3$. Since $1=1^2,2=3^2,3=4^3,4=3^3,5=5^2$, the other cases can be verified. By Theorem 17, G is a commutative T2CA-groupoid.

Definition 16.

A T2CA-groupoid $(G,\ast )$ is called a T2CA-band if for all $x\in G$, $x\ast x=x$.

Corollary 10.

Every T2CA-band is a power cancellative T2CA-groupoid.

Proof. 

This is evident. □

Definition 17.

A T2CA-groupoid $(G,\ast )$ is called a T2CA-3-band if for all $x\in G$, $x^2\ast x=x$.

Theorem 18.

Let $(G,\ast )$ be a T2CA-3-band. Then:

(1) 

G is a commutative semigroup; and

(2) 

G is a separative T2CA-groupoid.

Proof. 

(1) Suppose that $(G,\ast )$ is a T2CA-3-band. For all $x_1,x_2\in G,$ we have $x_1^2\ast x_1=x_1$ and $x_2^2\ast x_2=x_2$. Then,

$$\begin{array}{cc}\hfill x_1\ast x_2& =x_1\ast (x_2^2\ast x_2)(by{x}_2=x_2^2\ast x_2)\hfill \\ \hfill & =(x_2\ast x_1)\ast x_2^2(bythetype-2cyclicassociaivelaw)\hfill \\ \hfill & =(x_2\ast x_1)\ast (x_2\ast x_2)\hfill \\ \hfill & =(x_1\ast x_2)\ast (x_2\ast x_2)\left(byProposition4\right)\hfill \\ \hfill & =(x_1\ast x_2)\ast x_2^2\hfill \\ \hfill & =x_2\ast (x_2^2\ast x_1)(bythetype-2cyclicassociaivelaw)\hfill \\ \hfill & =(x_2^2\ast x_2)\ast (x_2^2\ast x_1)(by{x}_2=x_2^2\ast x_2)\hfill \\ \hfill & =(x_2\ast x_2^2)\ast (x_1\ast x_2^2)\left(byProposition4\right)\hfill \\ \hfill & =(x_2^2\ast x_2)\ast (x_1\ast x_2^2)(bythetype-2cyclicassociaivelaw)\hfill \\ \hfill & =x_2\ast (x_1\ast x_2^2)(by{x}_2=x_2^2\ast x_2)\hfill \\ \hfill & =(x_2^2\ast x_2)\ast x_1(bythetype-2cyclicassociaivelaw)\hfill \\ \hfill & =x_2\ast x_1.\hfill \end{array}$$

Therefore, G is a commutative T2CA-groupoid. By Proposition 5, G is a commutative semigroup.

(2) Suppose that $(G,\ast )$ is a T2CA-3-band. We first prove that a T2CA-3-band is a quasi-separative T2CA-groupoid. For all $x_1,x_2\in G,$ we have $x_1^2\ast x_1=x_1$ and $x_2^2\ast x_2=x_2$. If $x_1\ast x_1=x_1\ast x_2=x_2\ast x_2$, then

$$\begin{array}{cc}\hfill x_1& =x_1^2\ast x_1\hfill \\ \hfill & =(x_2\ast x_2)\ast x_1(by{x}_1\ast x_1=x_2\ast x_2)\hfill \\ \hfill & =x_2\ast (x_1\ast x_2)(bythetype-2cyclicassociaivelaw)\hfill \\ \hfill & =x_2\ast (x_2\ast x_2)(by{x}_1\ast x_2=x_2\ast x_2)\hfill \\ \hfill & =(x_2\ast x_2)\ast x_2(bythetype-2cyclicassociaivelaw)\hfill \\ \hfill & =x_2^2\ast x_2\hfill \\ \hfill & =x_2.\hfill \end{array}$$

Therefore, $(G,\ast )$ is a quasi-separative T2CA-groupoid. According to Theorem 12, it follows that every T2CA-3-band is a separative T2CA-groupoid. □

6. Conclusions

Using the research methods of cancellativities in semigroups, we mainly investigated the properties of weak cancellativity, separativity and quasi-cancellativity on T2CA-groupoids. Some important results were obtained which can assist further study of the structure of T2CA-groupoids. We prove that the left quasi-cancellative T2CA-groupoid, right quasi-cancellative T2CA-groupoid and quasi-cancellative T2CA-groupoid are equivalent (see Theorem 15); that the left separative T2CA-groupoid, right separative T2CA-groupoid, quasi-separative T2CA-groupoid and separative T2CA-groupoid are equivalent (see Theorem 12); and that the weak cancellative T2CA-groupoid and cancellative T2CA-groupoid are equivalent (see Corollary 7). Figure 5 shows the main results on the T2CA-groupoid in this paper.

Furthermore, we successfully solve two open problems in [27]. We prove that weak cancellativity is cancellativity and right quasi-cancellativity is left quasi-cancellativity in a CA-groupoid (see Theorems 7 and 8). The relationships among separativity, quasi-cancellativity and commutativity in a CA-groupoid were discussed (see Figure 3), thus clarifying the structure of a CA-groupoid. Figure 6 shows the main results obtained for the CA-groupoid in this paper.

Finally, we investigate the relationships between the T2CA-groupoid and other groupoids (see Figure 2). The necessary and sufficient conditions for the T2CA-groupoid to be the CA-groupoid and the necessary and sufficient conditions for the T2CA-groupoid to be the AG-groupoid are given (see Theorems 5 and 6). In future research, we will investigate the relationships between the T2CA-groupoid and other groupoids and the related logic algebras (as can be seen in [29,30,31,32]).