On the Bias in Confirmatory Factor Analysis When Treating Discrete Variables as Ordinal Instead of Continuous
Abstract
:1. Introduction
2. Factor Analysis for Ordinal Items
2.1. Gaussian Copula Model for Ordinal Items
2.2. Factor Model for Pearson Correlations and Polychoric Correlations
3. Simulation Studies
3.1. Simulation Study 1
3.1.1. Method
3.1.2. Results
3.1.3. Summary
3.2. Simulation Study 2: Unequal Loadings
3.2.1. Method
3.2.2. Results
3.2.3. Summary
4. Analytical Findings
4.1. Case 1: Equal Loadings
4.2. Case 2: Unequal Loadings
4.3. Case 3: General CFA with Simplifying Linear Assumptions
5. Discussion and Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFA | confirmatory factor analysis |
| ML | maximum likelihood |
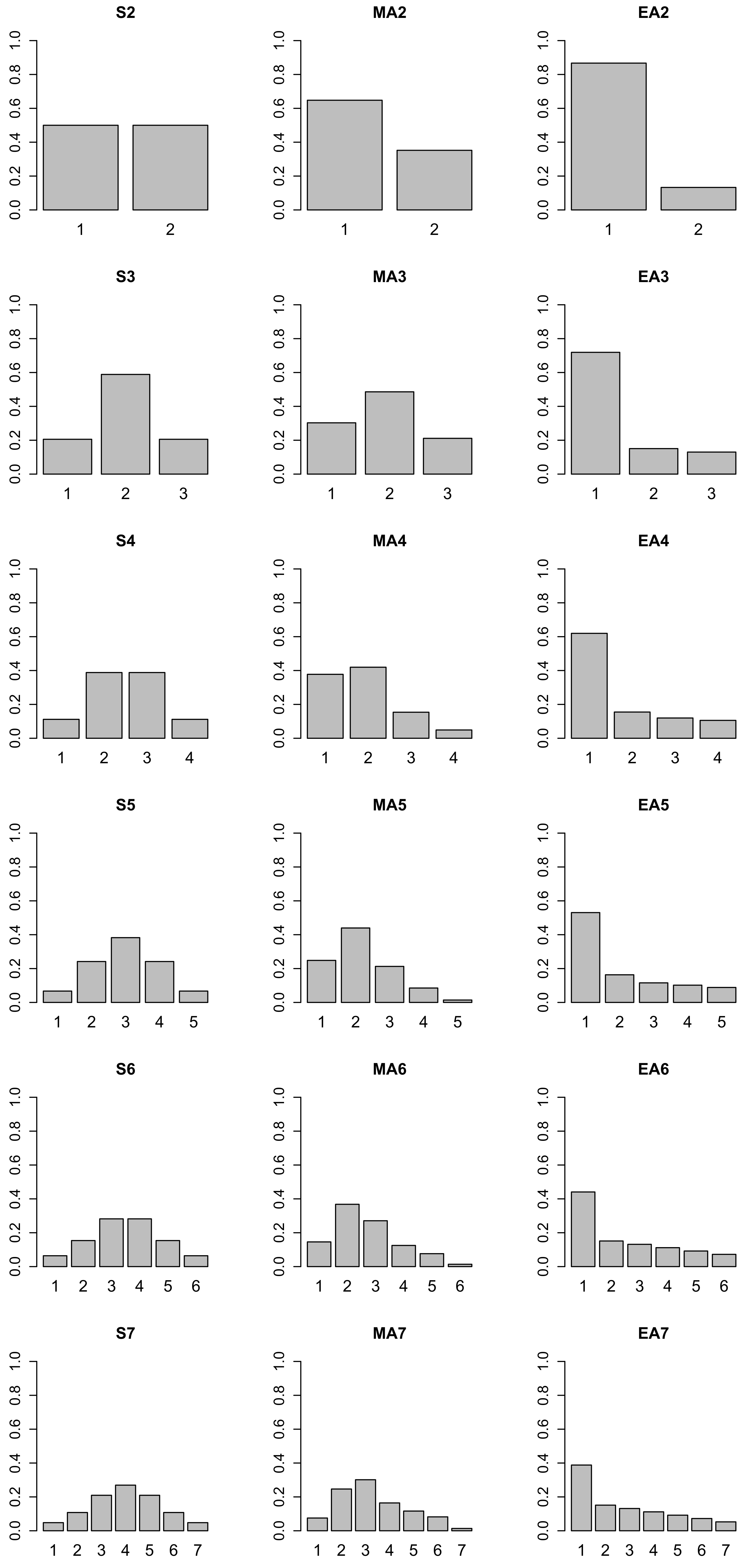
Appendix A. Data-Generating Parameters in the Simulation Studies
| Dist | Cat1 | Cat2 | Cat3 | Cat4 | Cat5 | Cat6 | Cat7 |
|---|---|---|---|---|---|---|---|
| S2 | 0.500 | 0.500 | |||||
| MA2 | 0.648 | 0.352 | |||||
| EA2 | 0.867 | 0.133 | |||||
| S3 | 0.206 | 0.589 | 0.206 | ||||
| MA3 | 0.303 | 0.486 | 0.211 | ||||
| EA3 | 0.719 | 0.151 | 0.130 | ||||
| S4 | 0.112 | 0.388 | 0.388 | 0.112 | |||
| MA4 | 0.378 | 0.420 | 0.154 | 0.049 | |||
| EA4 | 0.620 | 0.155 | 0.120 | 0.106 | |||
| S5 | 0.067 | 0.242 | 0.383 | 0.242 | 0.067 | ||
| MA5 | 0.248 | 0.440 | 0.213 | 0.085 | 0.014 | ||
| EA5 | 0.531 | 0.163 | 0.116 | 0.102 | 0.088 | ||
| S6 | 0.064 | 0.154 | 0.282 | 0.282 | 0.154 | 0.064 | |
| MA6 | 0.146 | 0.368 | 0.271 | 0.125 | 0.076 | 0.014 | |
| EA6 | 0.441 | 0.151 | 0.132 | 0.112 | 0.092 | 0.072 | |
| S7 | 0.048 | 0.108 | 0.210 | 0.269 | 0.210 | 0.108 | 0.048 |
| MA7 | 0.075 | 0.247 | 0.301 | 0.164 | 0.116 | 0.082 | 0.014 |
| EA7 | 0.388 | 0.151 | 0.132 | 0.112 | 0.092 | 0.072 | 0.053 |
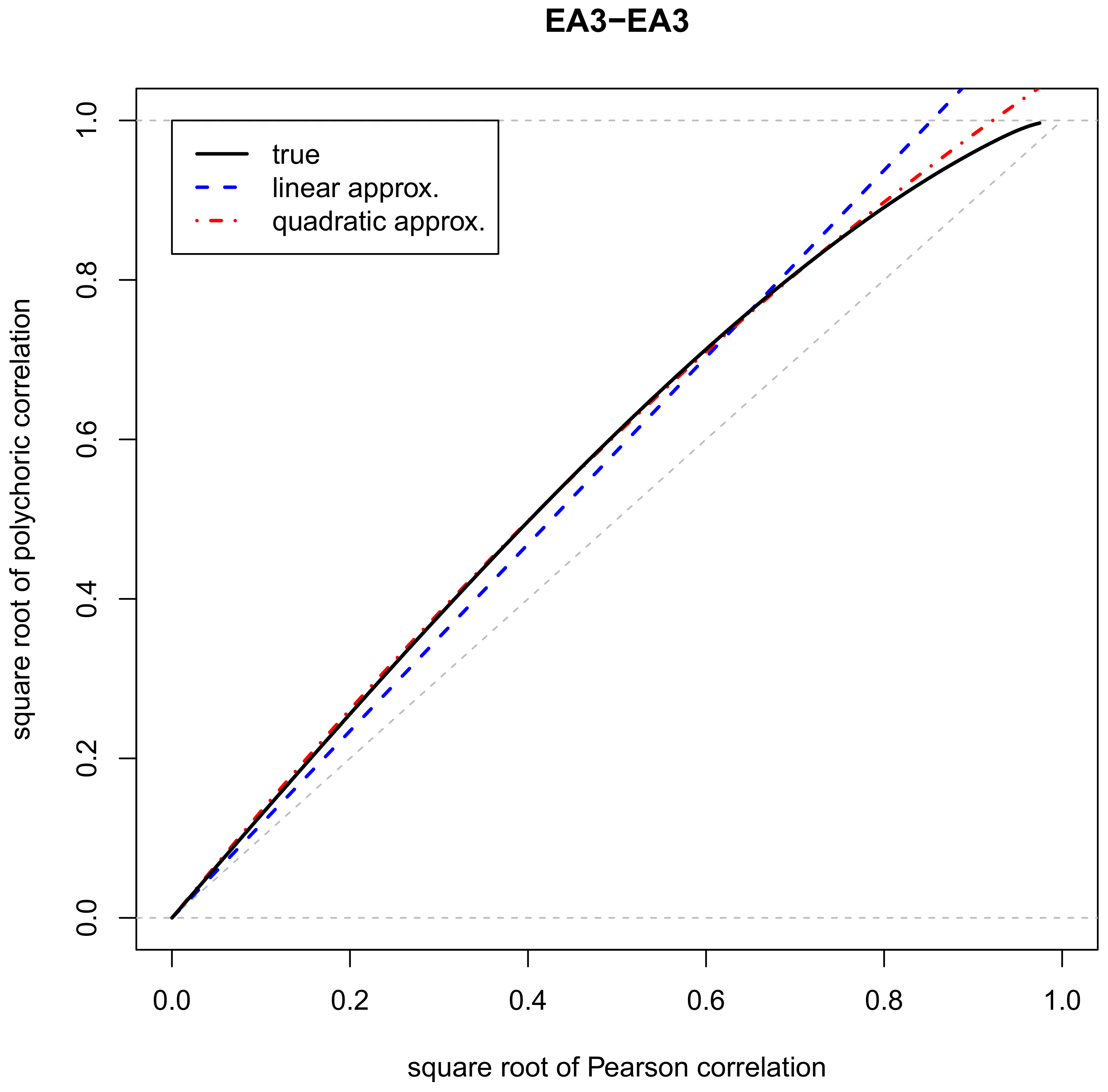
Appendix B. Approximation of the Relation of the Polychoric Correlation and the Pearson Correlation
| Dist1 | Dist2 | Error | ||
|---|---|---|---|---|
| S2 | S2 | 1.339 | 0.161 | 0.013 |
| MA2 | MA2 | 1.380 | 0.191 | 0.012 |
| EA2 | EA2 | 1.692 | 0.377 | 0.006 |
| S2 | MA2 | 1.347 | 0.144 | 0.011 |
| S2 | EA2 | 1.331 | −0.154 | 0.041 |
| MA2 | EA2 | 1.455 | 0.130 | 0.020 |
| S3 | S3 | 1.137 | 0.021 | 0.003 |
| MA3 | MA3 | 1.130 | 0.035 | 0.003 |
| EA3 | EA3 | 1.367 | 0.224 | 0.006 |
| S3 | MA3 | 1.130 | 0.021 | 0.002 |
| S3 | EA3 | 1.224 | 0.032 | 0.007 |
| MA3 | EA3 | 1.219 | 0.049 | 0.003 |
| S4 | S4 | 1.075 | 0.007 | 0.001 |
| MA4 | MA4 | 1.121 | 0.054 | 0.002 |
| EA4 | EA4 | 1.258 | 0.166 | 0.005 |
| S4 | MA4 | 1.092 | 0.009 | 0.001 |
| S4 | EA4 | 1.141 | 0.014 | 0.001 |
| MA4 | EA4 | 1.181 | 0.091 | 0.002 |
| S5 | S5 | 1.049 | 0.004 | 0.000 |
| MA5 | MA5 | 1.085 | 0.031 | 0.001 |
| EA5 | EA5 | 1.194 | 0.127 | 0.004 |
| S5 | MA5 | 1.063 | 0.004 | 0.000 |
| S5 | EA5 | 1.102 | 0.010 | 0.001 |
| MA5 | EA5 | 1.131 | 0.060 | 0.001 |
| S6 | S6 | 1.034 | 0.005 | 0.000 |
| MA6 | MA6 | 1.062 | 0.025 | 0.001 |
| EA6 | EA6 | 1.140 | 0.092 | 0.003 |
| S6 | MA6 | 1.045 | 0.004 | 0.000 |
| S6 | EA6 | 1.074 | 0.011 | 0.001 |
| MA6 | EA6 | 1.096 | 0.047 | 0.001 |
| S7 | S7 | 1.026 | 0.004 | 0.000 |
| MA7 | MA7 | 1.046 | 0.018 | 0.001 |
| EA7 | EA7 | 1.116 | 0.078 | 0.003 |
| S7 | MA7 | 1.034 | 0.004 | 0.000 |
| S7 | EA7 | 1.060 | 0.009 | 0.000 |
| MA7 | EA7 | 1.077 | 0.038 | 0.001 |
References
- Barendse, M.T.; Oort, F.J.; Timmerman, M.E. Using exploratory factor analysis to determine the dimensionality of discrete responses. Struct. Equ. Model. Multidiscip. J. 2015, 22, 87–101. [Google Scholar] [CrossRef]
- DiStefano, C. The impact of categorization with confirmatory factor analysis. Struct. Equ. Model. 2002, 9, 327–346. [Google Scholar] [CrossRef]
- Dolan, C.V. Factor analysis of variables with 2, 3, 5 and 7 response categories: A comparison of categorical variable estimators using simulated data. Br. J. Math. Stat. Psychol. 1994, 47, 309–326. [Google Scholar] [CrossRef]
- Li, C.H. The performance of ML, DWLS, and ULS estimation with robust corrections in structural equation models with ordinal variables. Psychol. Methods 2016, 21, 369–387. [Google Scholar] [CrossRef]
- Lei, P.W. Evaluating estimation methods for ordinal data in structural equation modeling. Qual. Quant. 2009, 43, 495–507. [Google Scholar] [CrossRef]
- Rhemtulla, M.; Brosseau-Liard, P.É.; Savalei, V. When can categorical variables be treated as continuous? A comparison of robust continuous and categorical SEM estimation methods under suboptimal conditions. Psychol. Methods 2012, 17, 354–373. [Google Scholar] [CrossRef] [Green Version]
- Sass, D.A.; Schmitt, T.A.; Marsh, H.W. Evaluating model fit with ordered categorical data within a measurement invariance framework: A comparison of estimators. Struct. Equ. Model. Multidiscip. J. 2014, 21, 167–180. [Google Scholar] [CrossRef]
- Robitzsch, A. Why ordinal variables can (almost) always be treated as continuous variables: Clarifying assumptions of robust continuous and ordinal factor analysis estimation methods. Front. Educ. 2020, 5, 589965. [Google Scholar] [CrossRef]
- Barbiero, A. Inducing a target association between ordinal variables by using a parametric copula family. Austrian J. Stat. 2020, 49, 9–18. [Google Scholar] [CrossRef] [Green Version]
- Demirtas, H. A method for multivariate ordinal data generation given marginal distributions and correlations. J. Stat. Comput. Simul. 2006, 76, 1017–1025. [Google Scholar] [CrossRef]
- Braeken, J.; Kuppens, P.; De Boeck, P.; Tuerlinckx, F. Contextualized personality questionnaires: A case for copulas in structural equation models for categorical data. Multivar. Behav. Res. 2013, 48, 845–870. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Muthén, B. A general structural equation model with dichotomous, ordered categorical, and continuous latent variable indicators. Psychometrika 1984, 49, 115–132. [Google Scholar] [CrossRef] [Green Version]
- Jorgensen, T.D.; Johnson, A.R. How to derive expected values of structural equation model parameters when treating discrete data as continuous. Struct. Equ. Model. Multidiscip. J. 2022. [Google Scholar] [CrossRef]
- Demirtas, H.; Hedeker, D. A practical way for computing approximate lower and upper correlation bounds. Am. Stat. 2011, 65, 104–109. [Google Scholar] [CrossRef]
- Lee, L.F. On the range of correlation coefficients of bivariate ordered discrete random variables. Econom. Theory 2001, 17, 247–256. [Google Scholar] [CrossRef] [Green Version]
- Olvera Astivia, O.L.; Kroc, E.; Zumbo, B.D. The role of item distributions on reliability estimation: The case of Cronbach’s coefficient alpha. Educ. Psychol. Meas. 2020, 80, 825–846. [Google Scholar] [CrossRef] [PubMed]
- Olsson, U. Maximum likelihood estimation of the polychoric correlation coefficient. Psychometrika 1979, 44, 443–460. [Google Scholar] [CrossRef]
- Van Ophem, H. A general method to estimate correlated discrete random variables. Econom. Theory 1999, 15, 228–237. [Google Scholar] [CrossRef]
- Barbiero, A.; Ferrari, P.A. An R package for the simulation of correlated discrete variables. Commun. Stat. Simul. Comput. 2017, 46, 5123–5140. [Google Scholar] [CrossRef]
- Ferrari, P.A.; Barbiero, A. Simulating ordinal data. Multivar. Behav. Res. 2012, 47, 566–589. [Google Scholar] [CrossRef] [PubMed]
- Mulaik, S.A. Foundations of Factor Analysis; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar] [CrossRef]
- Foldnes, N.; Grønneberg, S. The sensitivity of structural equation modeling with ordinal data to underlying non-normality and observed distributional forms. Psychol. Methods 2021. [Google Scholar] [CrossRef] [PubMed]
- Jöreskog, K.G.; Olsson, U.H.; Wallentin, F.Y. Multivariate Analysis with LISREL; Springer: Basel, Switzerland, 2016. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 11 January 2022).
- Rosseel, Y. Lavaan: An R package for structural equation modeling. J. Stat. Softw. 2012, 48, 1–36. [Google Scholar] [CrossRef] [Green Version]
- Steyer, R. Models of classical psychometric test theory as stochastic measurement models: Representation, uniqueness, meaningfulness, identifiability, and testability. Methodika 1989, 3, 25–60. Available online: https://bit.ly/3Js7N3S (accessed on 5 March 2022).
| True Loading = 0.3 | True Loading = 0.7 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Simulated cont | Simulated cat | Simulated cont | Simulated cat | |||||||||
| Estimation Methods | Estimation Methods | Estimation Methods | Estimation Methods | |||||||||
| Dist | cont | cont-adj | cat | cont | cont-adj | cat | cont | cont-adj | cat | cont | cont-adj | cat |
| S2 | 0.300 | 0.300 | 0.375 | 0.240 | 0.240 | 0.300 | 0.700 | 0.700 | 0.834 | 0.571 | 0.571 | 0.700 |
| S3 | 0.300 | 0.300 | 0.338 | 0.266 | 0.266 | 0.300 | 0.700 | 0.700 | 0.785 | 0.623 | 0.623 | 0.700 |
| S4 | 0.300 | 0.300 | 0.321 | 0.280 | 0.280 | 0.300 | 0.700 | 0.700 | 0.748 | 0.654 | 0.654 | 0.700 |
| S5 | 0.300 | 0.300 | 0.314 | 0.286 | 0.287 | 0.300 | 0.700 | 0.700 | 0.732 | 0.669 | 0.669 | 0.700 |
| S6 | 0.300 | 0.300 | 0.310 | 0.291 | 0.291 | 0.300 | 0.700 | 0.700 | 0.721 | 0.679 | 0.679 | 0.700 |
| S7 | 0.300 | 0.300 | 0.307 | 0.293 | 0.293 | 0.300 | 0.700 | 0.700 | 0.716 | 0.684 | 0.684 | 0.700 |
| MA2 | 0.300 | 0.300 | 0.383 | 0.234 | 0.234 | 0.300 | 0.700 | 0.700 | 0.839 | 0.564 | 0.564 | 0.700 |
| MA3 | 0.300 | 0.300 | 0.334 | 0.269 | 0.269 | 0.300 | 0.700 | 0.700 | 0.772 | 0.633 | 0.633 | 0.700 |
| MA4 | 0.300 | 0.301 | 0.330 | 0.273 | 0.273 | 0.300 | 0.700 | 0.698 | 0.756 | 0.646 | 0.645 | 0.700 |
| MA5 | 0.300 | 0.301 | 0.322 | 0.280 | 0.281 | 0.300 | 0.700 | 0.699 | 0.743 | 0.659 | 0.658 | 0.700 |
| MA6 | 0.300 | 0.302 | 0.316 | 0.285 | 0.287 | 0.300 | 0.700 | 0.701 | 0.731 | 0.670 | 0.672 | 0.700 |
| MA7 | 0.300 | 0.303 | 0.312 | 0.289 | 0.291 | 0.300 | 0.700 | 0.703 | 0.723 | 0.677 | 0.681 | 0.700 |
| EA2 | 0.300 | 0.300 | 0.447 | 0.195 | 0.195 | 0.300 | 0.700 | 0.700 | 0.873 | 0.511 | 0.511 | 0.700 |
| EA3 | 0.300 | 0.301 | 0.379 | 0.236 | 0.237 | 0.300 | 0.700 | 0.697 | 0.808 | 0.587 | 0.585 | 0.700 |
| EA4 | 0.300 | 0.302 | 0.356 | 0.252 | 0.254 | 0.300 | 0.700 | 0.699 | 0.780 | 0.617 | 0.618 | 0.700 |
| EA5 | 0.300 | 0.304 | 0.342 | 0.262 | 0.266 | 0.300 | 0.700 | 0.701 | 0.762 | 0.636 | 0.638 | 0.700 |
| EA6 | 0.300 | 0.304 | 0.331 | 0.272 | 0.275 | 0.300 | 0.700 | 0.702 | 0.747 | 0.652 | 0.654 | 0.700 |
| EA7 | 0.300 | 0.304 | 0.325 | 0.276 | 0.280 | 0.300 | 0.700 | 0.702 | 0.739 | 0.660 | 0.663 | 0.700 |
| True Factor Correlation = 0.3 | True Factor Correlation = 0.7 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Simulated cont | Simulated cat | Simulated cont | Simulated cat | |||||||||
| Estimation Methods | Estimation Methods | Estimation Methods | Estimation Methods | |||||||||
| Dist | cont | cont-adj | cat | cont | cont-adj | cat | cont | cont-adj | cat | cont | cont-adj | cat |
| True loading = 0.3 | ||||||||||||
| S2 | 0.300 | 0.300 | 0.301 | 0.300 | 0.300 | 0.300 | 0.700 | 0.700 | 0.701 | 0.700 | 0.700 | 0.700 |
| S3 | 0.300 | 0.300 | 0.300 | 0.300 | 0.300 | 0.300 | 0.700 | 0.700 | 0.700 | 0.700 | 0.700 | 0.700 |
| S4 | 0.300 | 0.300 | 0.300 | 0.300 | 0.300 | 0.300 | 0.700 | 0.700 | 0.700 | 0.700 | 0.700 | 0.700 |
| S5 | 0.300 | 0.300 | 0.300 | 0.300 | 0.300 | 0.300 | 0.700 | 0.700 | 0.700 | 0.700 | 0.700 | 0.700 |
| S6 | 0.300 | 0.300 | 0.300 | 0.300 | 0.300 | 0.300 | 0.700 | 0.700 | 0.700 | 0.700 | 0.700 | 0.700 |
| S7 | 0.300 | 0.300 | 0.300 | 0.300 | 0.300 | 0.300 | 0.700 | 0.700 | 0.700 | 0.700 | 0.700 | 0.700 |
| MA2 | 0.300 | 0.300 | 0.303 | 0.298 | 0.298 | 0.300 | 0.700 | 0.700 | 0.703 | 0.698 | 0.698 | 0.700 |
| MA3 | 0.300 | 0.300 | 0.300 | 0.300 | 0.300 | 0.300 | 0.700 | 0.700 | 0.700 | 0.700 | 0.700 | 0.700 |
| MA4 | 0.300 | 0.301 | 0.302 | 0.299 | 0.299 | 0.300 | 0.700 | 0.701 | 0.702 | 0.699 | 0.699 | 0.700 |
| MA5 | 0.300 | 0.301 | 0.301 | 0.299 | 0.300 | 0.300 | 0.700 | 0.701 | 0.701 | 0.699 | 0.700 | 0.700 |
| MA6 | 0.300 | 0.301 | 0.301 | 0.299 | 0.300 | 0.300 | 0.700 | 0.701 | 0.701 | 0.699 | 0.700 | 0.700 |
| MA7 | 0.300 | 0.300 | 0.300 | 0.300 | 0.300 | 0.300 | 0.700 | 0.700 | 0.700 | 0.700 | 0.700 | 0.700 |
| EA2 | 0.300 | 0.300 | 0.325 | 0.289 | 0.289 | 0.300 | 0.700 | 0.700 | 0.723 | 0.689 | 0.689 | 0.700 |
| EA3 | 0.300 | 0.301 | 0.309 | 0.294 | 0.295 | 0.300 | 0.700 | 0.701 | 0.709 | 0.694 | 0.695 | 0.700 |
| EA4 | 0.300 | 0.301 | 0.306 | 0.296 | 0.297 | 0.300 | 0.700 | 0.701 | 0.706 | 0.696 | 0.697 | 0.700 |
| EA5 | 0.300 | 0.301 | 0.304 | 0.297 | 0.298 | 0.300 | 0.700 | 0.701 | 0.704 | 0.697 | 0.698 | 0.700 |
| EA6 | 0.300 | 0.301 | 0.302 | 0.298 | 0.299 | 0.300 | 0.700 | 0.701 | 0.702 | 0.698 | 0.699 | 0.700 |
| EA7 | 0.300 | 0.301 | 0.302 | 0.298 | 0.299 | 0.300 | 0.700 | 0.701 | 0.702 | 0.698 | 0.699 | 0.700 |
| True loading = 0.7 | ||||||||||||
| S2 | 0.300 | 0.300 | 0.329 | 0.288 | 0.288 | 0.300 | 0.700 | 0.700 | 0.737 | 0.684 | 0.684 | 0.700 |
| S3 | 0.300 | 0.300 | 0.302 | 0.299 | 0.299 | 0.300 | 0.700 | 0.700 | 0.704 | 0.698 | 0.698 | 0.700 |
| S4 | 0.300 | 0.300 | 0.301 | 0.299 | 0.299 | 0.300 | 0.700 | 0.700 | 0.701 | 0.699 | 0.699 | 0.700 |
| S5 | 0.300 | 0.300 | 0.301 | 0.299 | 0.300 | 0.300 | 0.700 | 0.700 | 0.701 | 0.699 | 0.700 | 0.700 |
| S6 | 0.300 | 0.300 | 0.301 | 0.299 | 0.300 | 0.300 | 0.700 | 0.700 | 0.701 | 0.699 | 0.699 | 0.700 |
| S7 | 0.300 | 0.300 | 0.301 | 0.300 | 0.300 | 0.300 | 0.700 | 0.700 | 0.701 | 0.699 | 0.700 | 0.700 |
| MA2 | 0.300 | 0.300 | 0.337 | 0.283 | 0.283 | 0.300 | 0.700 | 0.700 | 0.744 | 0.679 | 0.679 | 0.700 |
| MA3 | 0.300 | 0.300 | 0.306 | 0.296 | 0.296 | 0.300 | 0.700 | 0.700 | 0.707 | 0.695 | 0.695 | 0.700 |
| MA4 | 0.300 | 0.303 | 0.310 | 0.292 | 0.294 | 0.300 | 0.700 | 0.702 | 0.710 | 0.691 | 0.694 | 0.700 |
| MA5 | 0.300 | 0.303 | 0.306 | 0.295 | 0.298 | 0.300 | 0.700 | 0.703 | 0.706 | 0.695 | 0.697 | 0.700 |
| MA6 | 0.300 | 0.303 | 0.305 | 0.296 | 0.299 | 0.300 | 0.700 | 0.703 | 0.705 | 0.696 | 0.699 | 0.700 |
| MA7 | 0.300 | 0.303 | 0.303 | 0.297 | 0.300 | 0.300 | 0.700 | 0.703 | 0.703 | 0.697 | 0.699 | 0.700 |
| EA2 | 0.300 | 0.300 | 0.403 | 0.246 | 0.246 | 0.300 | 0.700 | 0.700 | 0.788 | 0.642 | 0.642 | 0.700 |
| EA3 | 0.300 | 0.304 | 0.350 | 0.268 | 0.271 | 0.300 | 0.700 | 0.703 | 0.748 | 0.665 | 0.668 | 0.700 |
| EA4 | 0.300 | 0.305 | 0.334 | 0.275 | 0.279 | 0.300 | 0.700 | 0.704 | 0.734 | 0.673 | 0.677 | 0.700 |
| EA5 | 0.300 | 0.306 | 0.325 | 0.281 | 0.285 | 0.300 | 0.700 | 0.705 | 0.726 | 0.679 | 0.684 | 0.700 |
| EA6 | 0.300 | 0.305 | 0.317 | 0.286 | 0.290 | 0.300 | 0.700 | 0.705 | 0.718 | 0.684 | 0.689 | 0.700 |
| EA7 | 0.300 | 0.305 | 0.314 | 0.288 | 0.292 | 0.300 | 0.700 | 0.705 | 0.715 | 0.686 | 0.691 | 0.700 |
| Simulated cont, Estimated cat | Simulated cat, Estimated cont | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Parm True | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.3 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.3 |
| Dist | ||||||||||||
| S2 | 0.379 | 0.501 | 0.618 | 0.730 | 0.846 | 0.313 | 0.238 | 0.319 | 0.401 | 0.485 | 0.568 | 0.294 |
| S3 | 0.338 | 0.451 | 0.563 | 0.674 | 0.786 | 0.301 | 0.266 | 0.355 | 0.444 | 0.533 | 0.622 | 0.299 |
| S4 | 0.322 | 0.429 | 0.535 | 0.642 | 0.749 | 0.301 | 0.280 | 0.373 | 0.467 | 0.561 | 0.654 | 0.300 |
| S5 | 0.314 | 0.419 | 0.524 | 0.628 | 0.733 | 0.300 | 0.286 | 0.382 | 0.477 | 0.573 | 0.669 | 0.300 |
| S6 | 0.310 | 0.413 | 0.516 | 0.619 | 0.722 | 0.300 | 0.291 | 0.388 | 0.485 | 0.582 | 0.679 | 0.300 |
| S7 | 0.307 | 0.410 | 0.512 | 0.614 | 0.717 | 0.300 | 0.293 | 0.390 | 0.488 | 0.586 | 0.684 | 0.300 |
| MA2 | 0.388 | 0.510 | 0.626 | 0.738 | 0.853 | 0.318 | 0.232 | 0.312 | 0.394 | 0.478 | 0.560 | 0.290 |
| MA3 | 0.335 | 0.445 | 0.555 | 0.664 | 0.774 | 0.303 | 0.269 | 0.359 | 0.450 | 0.541 | 0.645 | 0.298 |
| MA4 | 0.331 | 0.439 | 0.546 | 0.652 | 0.758 | 0.306 | 0.272 | 0.364 | 0.457 | 0.551 | 0.658 | 0.294 |
| MA5 | 0.322 | 0.429 | 0.534 | 0.639 | 0.744 | 0.304 | 0.279 | 0.373 | 0.468 | 0.563 | 0.669 | 0.297 |
| MA6 | 0.316 | 0.421 | 0.525 | 0.628 | 0.732 | 0.303 | 0.284 | 0.380 | 0.476 | 0.573 | 0.677 | 0.297 |
| MA7 | 0.312 | 0.415 | 0.518 | 0.621 | 0.724 | 0.302 | 0.288 | 0.385 | 0.482 | 0.580 | 0.504 | 0.298 |
| EA2 | 0.454 | 0.575 | 0.686 | 0.789 | 0.893 | 0.367 | 0.191 | 0.263 | 0.341 | 0.423 | 0.582 | 0.262 |
| EA3 | 0.383 | 0.498 | 0.608 | 0.712 | 0.819 | 0.331 | 0.232 | 0.316 | 0.403 | 0.493 | 0.613 | 0.278 |
| EA4 | 0.359 | 0.470 | 0.578 | 0.682 | 0.787 | 0.321 | 0.249 | 0.337 | 0.428 | 0.521 | 0.633 | 0.283 |
| EA5 | 0.344 | 0.454 | 0.560 | 0.663 | 0.768 | 0.315 | 0.260 | 0.351 | 0.444 | 0.539 | 0.649 | 0.287 |
| EA6 | 0.332 | 0.440 | 0.545 | 0.648 | 0.752 | 0.310 | 0.270 | 0.363 | 0.457 | 0.554 | 0.658 | 0.291 |
| EA7 | 0.327 | 0.433 | 0.537 | 0.640 | 0.743 | 0.309 | 0.275 | 0.369 | 0.464 | 0.561 | 0.632 | 0.292 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Robitzsch, A. On the Bias in Confirmatory Factor Analysis When Treating Discrete Variables as Ordinal Instead of Continuous. Axioms 2022, 11, 162. https://doi.org/10.3390/axioms11040162
Robitzsch A. On the Bias in Confirmatory Factor Analysis When Treating Discrete Variables as Ordinal Instead of Continuous. Axioms. 2022; 11(4):162. https://doi.org/10.3390/axioms11040162
Chicago/Turabian StyleRobitzsch, Alexander. 2022. "On the Bias in Confirmatory Factor Analysis When Treating Discrete Variables as Ordinal Instead of Continuous" Axioms 11, no. 4: 162. https://doi.org/10.3390/axioms11040162
APA StyleRobitzsch, A. (2022). On the Bias in Confirmatory Factor Analysis When Treating Discrete Variables as Ordinal Instead of Continuous. Axioms, 11(4), 162. https://doi.org/10.3390/axioms11040162






