RainPredRNN: A New Approach for Precipitation Nowcasting with Weather Radar Echo Images Based on Deep Learning
Abstract
:1. Introduction
2. Data and Background
2.1. Background
2.1.1. Convolutional LSTM (ConvLSTM)
2.1.2. Spatiotemporal LSTM with Spatiotemporal Memory Flow (ST-LSTM)
2.1.3. Spatiotemporal LSTM with Memory Decoupling
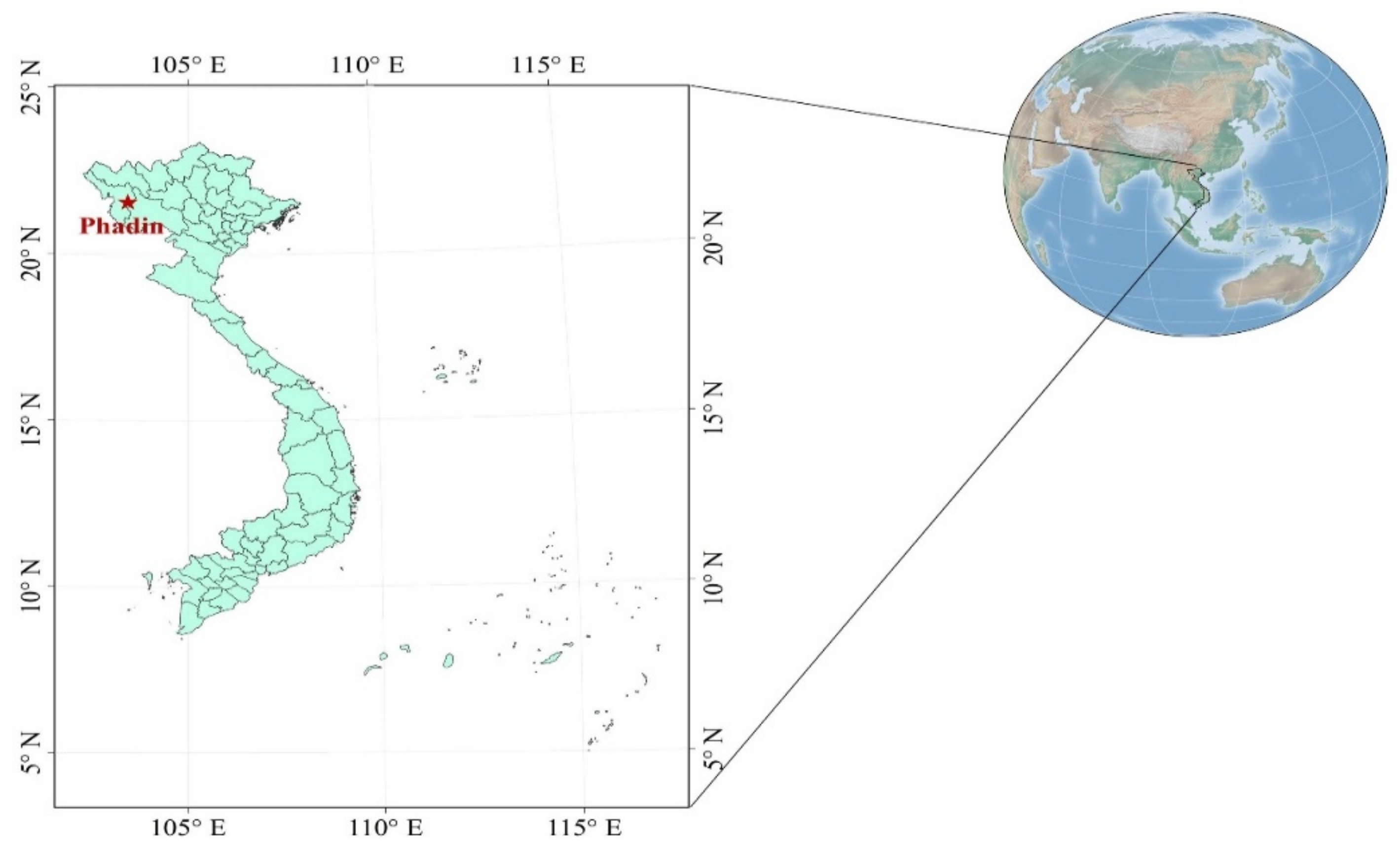
2.2. Study Area
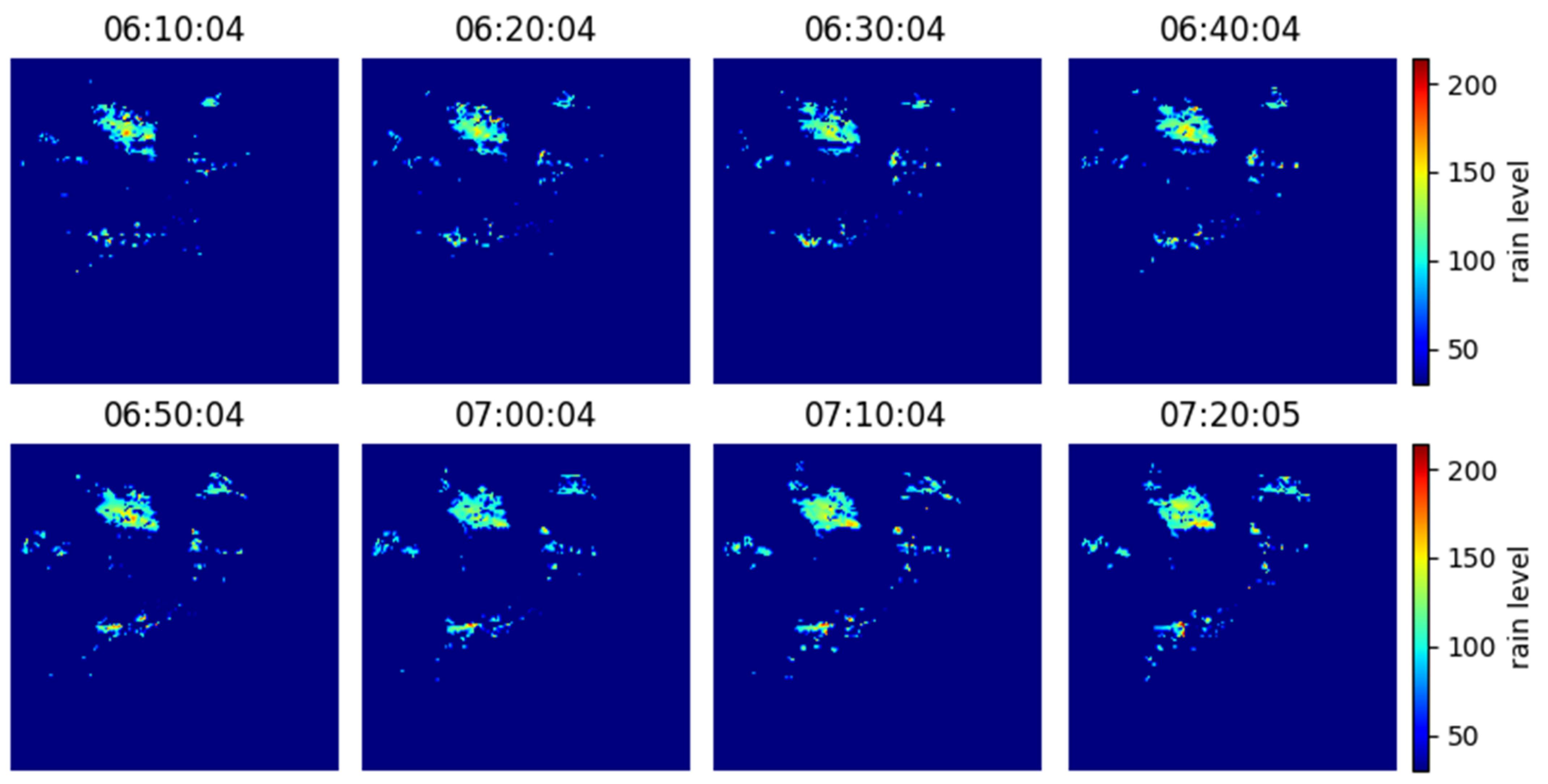
2.3. Data Preparation
- Training set: The weights and biases of the model will be trained and updated on the samples of the set until reaching convergence.
- Validation set: An unbiased evaluation will be calculated to see how fit the model is on the training set. This set helps to improve the model performance by fine-tuning the model,
- Testing set: This set informs us about the final accuracy of the model after completing the training phase.
2.4. Evaluation Criteria
3. Proposed RainPredRNN
3.1. Benefit of the Encoder–Decoder Path
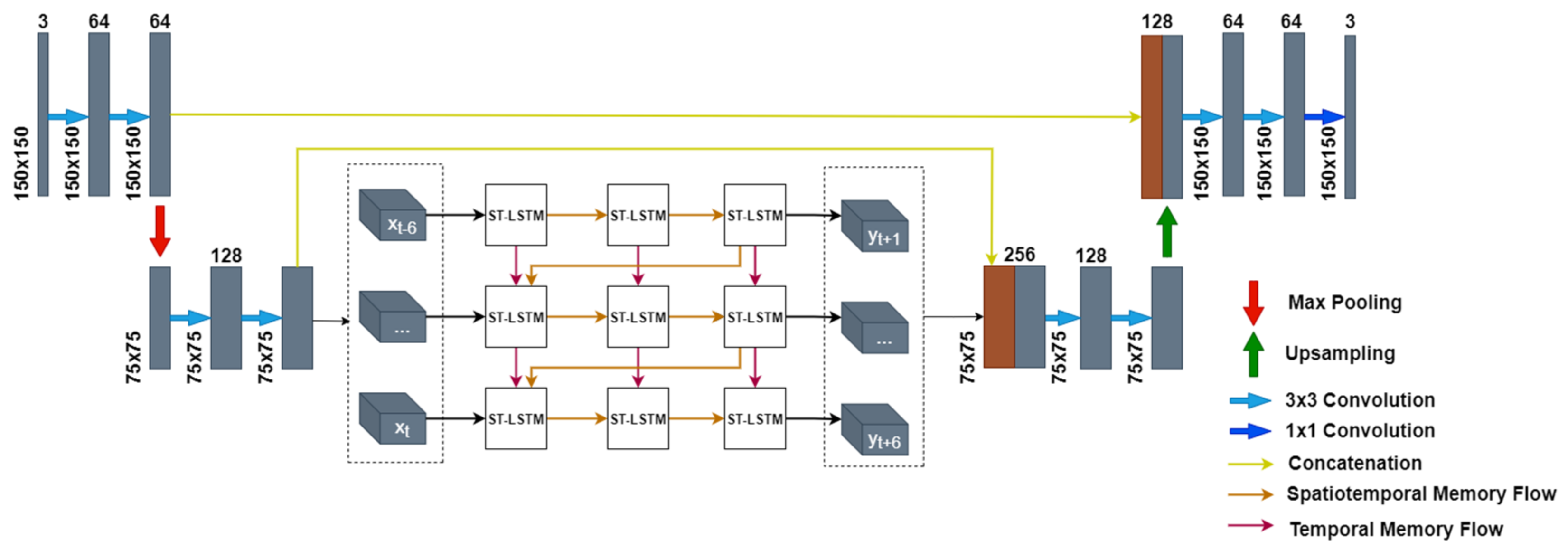
3.2. Unified RainPredRNN
3.3. Implementation
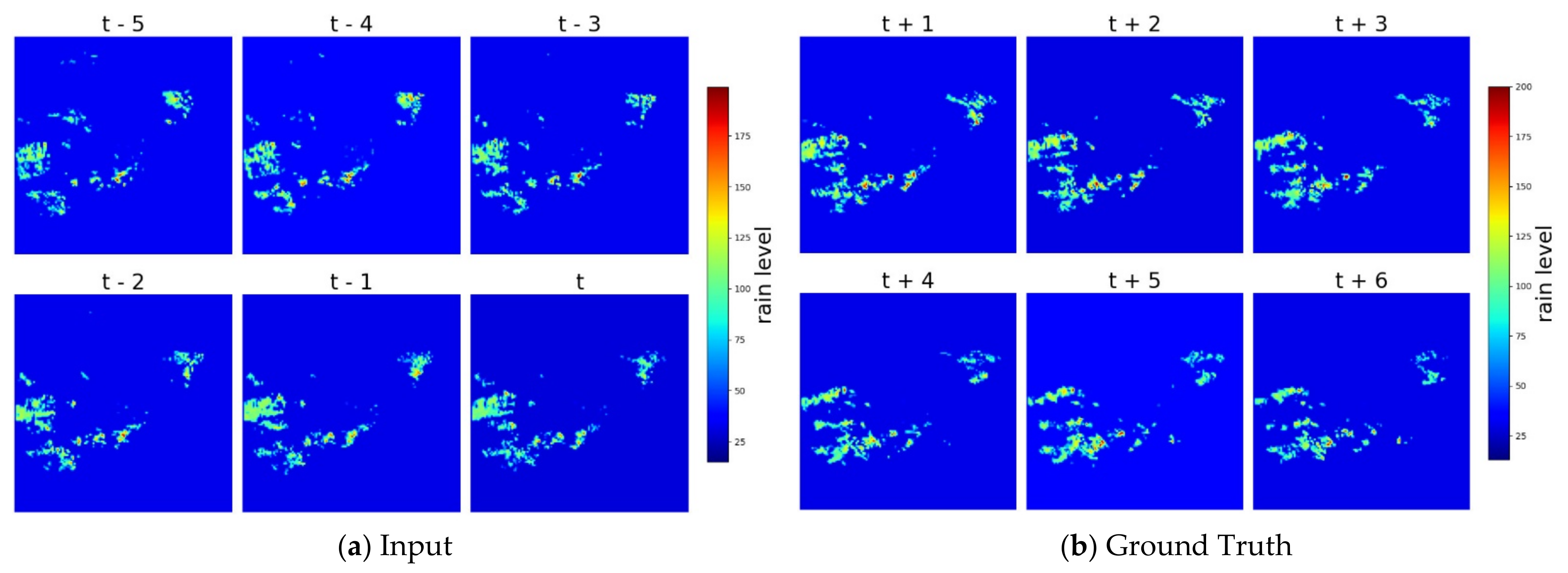
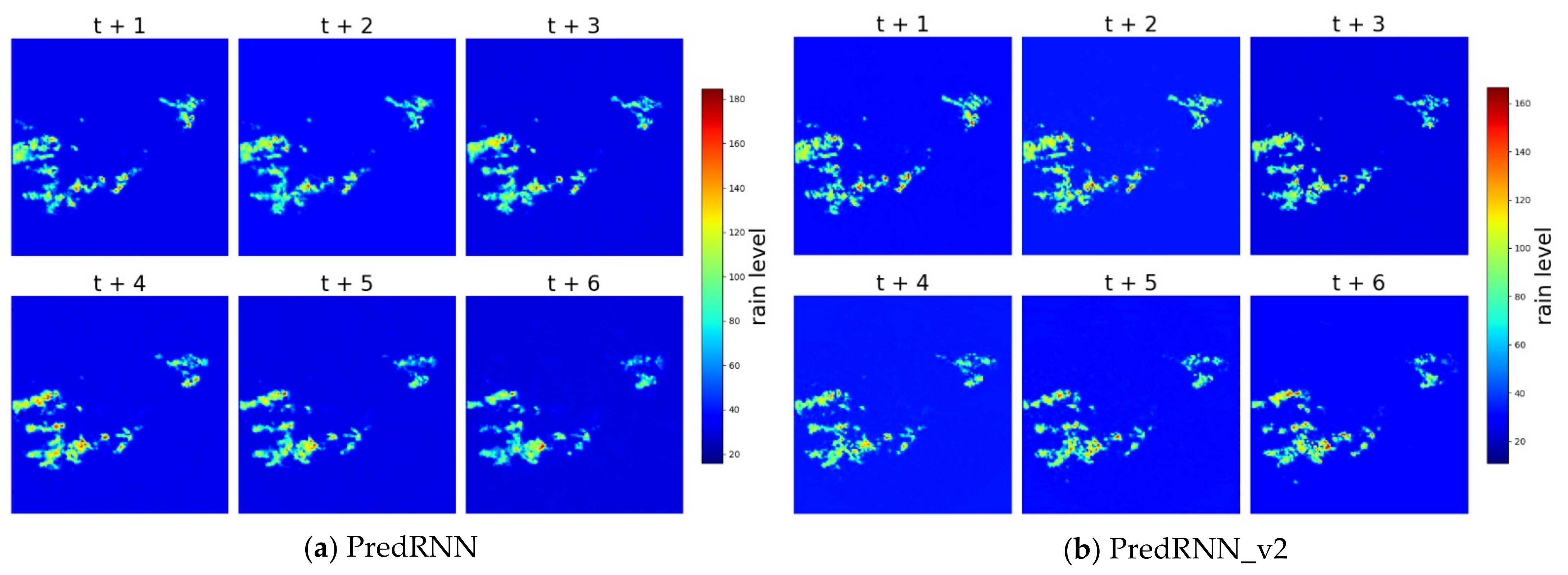
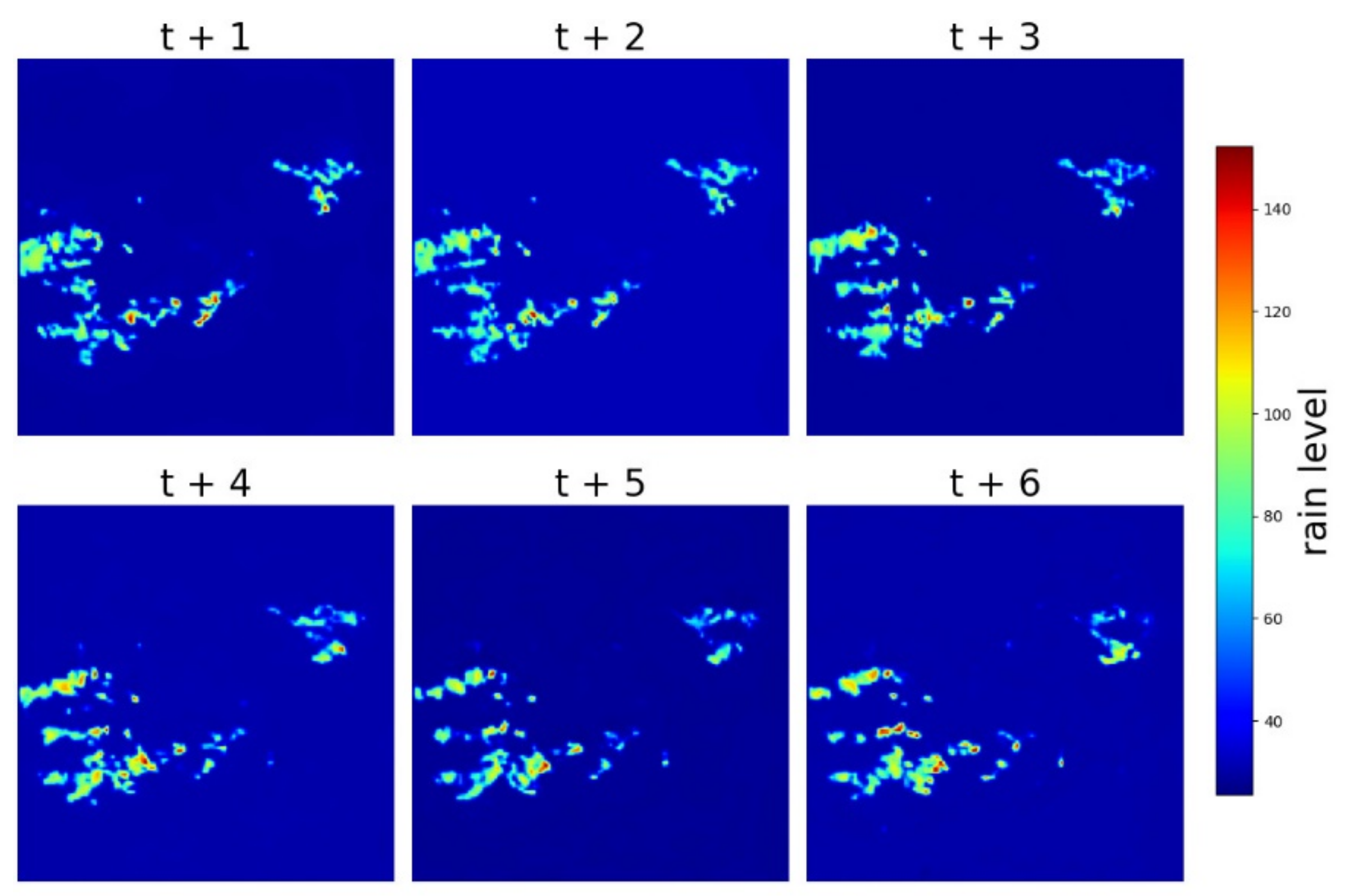
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
- Adam is the learning algorithm that is used in the training phase to seek the convergence point of the model. The parameters of the model are modified until the model converges.
- Convolutional LSTM is the general version of LSTM that is designed to tackle the problem of processing image inputs. By replacing the multiply operator with the convolution operator of spatial structure information, the model successfully encodes the spatial structure information of input.
- PredRNN combines the spatiotemporal LSTM (ST-LSTM) as the building block with the memory flow technique. The ST-LSTM introduces improvements to the memory cells, which contain the information of the flow (the memory flow technique) in both horizontal and vertical directions.
- PredRNN_v2 introduces the new component of the final loss function. This improvement trains the model more effectively and successfully, but the overall size of the model remains.
- RainPredRNN is the proposed model, which is a combination of the strength of the PredRNN_v2 model and the UNet model. The model borrows the contracting and expansive path of the UNet model for processing input to reduce the computational operators of the overall model. From that, the proposed model produces satisfactory results in a short time.
References
- Wapler, K.; de Coning, E.; Buzzi, M. Nowcasting. In Reference Module in Earth Systems and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar] [CrossRef]
- CRED. Natural Disasters; Centre for Research on the Epidemiology of Disasters (CRED): Brussels, Belgium, 2019; Available online: https://www.cred.be/sites/default/files/CREDNaturalDisaster2018.pdf (accessed on 10 October 2021).
- Keay, K.; Simmonds, I. Road accidents and rainfall in a large Australian city. Accid. Anal. Prev. 2006, 38, 445–454. [Google Scholar] [CrossRef]
- Chung, E.; Ohtani, O.; Warita, H.; Kuwahara, M.; Morita, H. Effect of rain on travel demand and traffic accidents. In Proceedings of the IEEE Intelligent Transportation Systems, Vienna, Austria, 16 September 2005; pp. 1080–1083. [Google Scholar]
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.-L. A Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef] [Green Version]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Sit, M.A.; Demiray, B.Z.; Xiang, Z.; Ewing, G.; Sermet, Y.; Demir, I. A Comprehensive Review of Deep Learning Applications in Hydrology and Water Resources. Water Sci. Technol. 2020, 82, 2635–2670. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Shi, X.; Wang, H.; Yeung, D.; Woo, W.; Wong, W. Deep Learning and the Weather Forecasting Problem: Precipitation Nowcasting. In Deep Learning for the Earth Sciences: A Comprehensive Approach to Remote Sensing, Climate Science, and Geosciences; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2021; pp. 218–239. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Zhao, Z.-Q.; Zheng, P.; Xu, S.-T.; Wu, X. Object Detection With Deep Learning: A Review. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3212–3232. [Google Scholar] [CrossRef] [Green Version]
- Le, X.H.; Lee, G.; Jung, K.; An, H.-U.; Lee, S.; Jung, Y. Application of Convolutional Neural Network for Spatiotemporal Bias Correction of Daily Satellite-Based Precipitation. Remote Sens. 2020, 12, 2731. [Google Scholar] [CrossRef]
- Ayzel, G.; Scheffer, T.; Heistermann, M. RainNet v1.0: A convolutional neural network for radar-based precipitation nowcasting. Geosci. Model Dev. 2020, 13, 2631–2644. [Google Scholar] [CrossRef]
- Khiali, L.; Ienco, D.; Teisseire, M. Object-oriented satellite image time series analysis using a graph-based representation. Ecol. Inform. 2018, 43, 52–64. [Google Scholar] [CrossRef] [Green Version]
- Fahim, S.R.; Sarker, Y.; Sarker, S.K.; Sheikh, R.I.; Das, S.K. Self attention convolutional neural network with time series imaging based feature extraction for transmission line fault detection and classification. Electr. Power Syst. Res. 2020, 187, 106437. [Google Scholar] [CrossRef]
- Li, X.; Kang, Y.; Li, F. Forecasting with time series imaging. Expert Syst. Appl. 2020, 160, 113680. [Google Scholar] [CrossRef]
- Ravuri, S.; Lenc, K.; Willson, M.; Kangin, D.; Lam, R.; Mirowski, P.; Fitzsimons, M.; Athanassiadou, M.; Kashem, S.; Madge, S.; et al. Skilful precipitation nowcasting using deep generative models of radar. Nature 2021, 597, 672–677. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Liu, Y.; Chen, C. MSDM v1.0: A machine learning model for precipitation nowcasting over eastern China using multisource data. Geosci. Model Dev. 2021, 14, 4019–4034. [Google Scholar] [CrossRef]
- Chen, L.; Cao, Y.; Ma, L.; Zhang, J. A Deep Learning-Based Methodology for Precipitation Nowcasting with Radar. Earth Space Sci. 2020, 7, e2019EA000812. [Google Scholar] [CrossRef] [Green Version]
- Agrawal, S.; Barrington, L.; Bromberg, C.; Burge, J.; Gazen, C.; Hickey, J. Machine Learning for Precipitation Nowcasting from Radar Images. arXiv 2019, arXiv:1912.12132. [Google Scholar]
- Fernández, J.G.; Mehrkanoon, S. Broad-UNet: Multi-scale feature learning for nowcasting tasks. Neural Netw. 2021, 144, 419–427. [Google Scholar] [CrossRef]
- Ionescu, V.-S.; Czibula, G.; Mihuleţ, E. DeePS at: A deep learning model for prediction of satellite images for nowcasting purposes. Procedia Comput. Sci. 2021, 192, 622–631. [Google Scholar] [CrossRef]
- Zhang, L.; Huang, Z.; Liu, W.; Guo, Z.; Zhang, Z. Weather radar echo prediction method based on convolution neural network and Long Short-Term memory networks for sustainable e-agriculture. J. Clean. Prod. 2021, 298, 126776. [Google Scholar] [CrossRef]
- Trebing, K.; Staǹczyk, T.; Mehrkanoon, S. SmaAt-UNet: Precipitation nowcasting using a small attention-UNet architecture. Pattern Recognit. Lett. 2021, 145, 178–186. [Google Scholar] [CrossRef]
- Le, X.H.; Ho, H.V.; Lee, G.; Jung, S. Application of Long Short-Term Memory (LSTM) Neural Network for Flood Forecasting. Water 2019, 11, 1387. [Google Scholar] [CrossRef] [Green Version]
- Le, X.H.; Nguyen, D.H.; Jung, S.; Yeon, M.; Lee, G. Comparison of Deep Learning Techniques for River Streamflow Forecasting. IEEE Access 2021, 9, 71805–71820. [Google Scholar] [CrossRef]
- Kreklow, J.; Tetzlaff, B.; Burkhard, B.; Kuhnt, G. Radar-Based Precipitation Climatology in Germany—Developments, Uncertainties and Potentials. Atmosphere 2020, 11, 217. [Google Scholar] [CrossRef] [Green Version]
- Otsuka, S.; Kotsuki, S.; Ohhigashi, M.; Miyoshi, T. GSMaP RIKEN Nowcast: Global Precipitation Nowcasting with Data Assimilation. J. Meteorol. Soc. Jpn. 2019, 97, 1099–1117. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Wu, H.; Zhang, J.; Gao, Z.; Wang, J.; Yu, P.; Long, M. PredRNN: A Recurrent Neural Network for Spatiotemporal Predictive Learning. arXiv 2021, arXiv:2103.09504. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
- Cho, K.; van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W.-C. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. arXiv 2015, arXiv:1506.04214. [Google Scholar]
- Wang, Y.; Long, M.; Wang, J.; Gao, Z.; Yu, P. PredRNN: Recurrent Neural Networks for Predictive Learning using Spatio-temporal LSTMs. In Advances in Neural Information Processing Systems; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Maaten, L.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Berrar, D. Cross-Validation. In Encyclopedia of Bioinformatics and Computational Biology; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process 2004, 13, 600–612. [Google Scholar] [CrossRef] [Green Version]
- Schaefer, J. The Critical Success Index as an Indicator of Warning Skill. Weather. Forecast. 1990, 5, 570–575. [Google Scholar] [CrossRef] [Green Version]
- Townsend, J. Theoretical analysis of an alphabetic confusion matrix. Percept. Psychophys. 1971, 9, 40–50. [Google Scholar] [CrossRef]

| Dataset | Quantity | Size |
|---|---|---|
| Training Set | 1947 | 150 × 150 |
| Validation Set | 242 | 150 × 150 |
| Testing Set | 242 | 150 × 150 |
| Ground Truth | |||
|---|---|---|---|
| Rain | No Rain | ||
| Predicted | Rain | TP | FP |
| No Rain | FN | TN | |
| Model | MAE | CSI | SSIM | Training Time (hour) | MACs(G) |
|---|---|---|---|---|---|
| PredRNN | 0.4535 | 0.9455 | 0.9397 | 15.1 | 101.469 |
| PredRNN_v2 | 0.4157 | 0.9420 | 0.9430 | 15.53 | 103.885 |
| RainPredRNN | 0.4301 | 0.9590 | 0.9412 | 4.46 | 54.705 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuyen, D.N.; Tuan, T.M.; Le, X.-H.; Tung, N.T.; Chau, T.K.; Van Hai, P.; Gerogiannis, V.C.; Son, L.H. RainPredRNN: A New Approach for Precipitation Nowcasting with Weather Radar Echo Images Based on Deep Learning. Axioms 2022, 11, 107. https://doi.org/10.3390/axioms11030107
Tuyen DN, Tuan TM, Le X-H, Tung NT, Chau TK, Van Hai P, Gerogiannis VC, Son LH. RainPredRNN: A New Approach for Precipitation Nowcasting with Weather Radar Echo Images Based on Deep Learning. Axioms. 2022; 11(3):107. https://doi.org/10.3390/axioms11030107
Chicago/Turabian StyleTuyen, Do Ngoc, Tran Manh Tuan, Xuan-Hien Le, Nguyen Thanh Tung, Tran Kim Chau, Pham Van Hai, Vassilis C. Gerogiannis, and Le Hoang Son. 2022. "RainPredRNN: A New Approach for Precipitation Nowcasting with Weather Radar Echo Images Based on Deep Learning" Axioms 11, no. 3: 107. https://doi.org/10.3390/axioms11030107
APA StyleTuyen, D. N., Tuan, T. M., Le, X.-H., Tung, N. T., Chau, T. K., Van Hai, P., Gerogiannis, V. C., & Son, L. H. (2022). RainPredRNN: A New Approach for Precipitation Nowcasting with Weather Radar Echo Images Based on Deep Learning. Axioms, 11(3), 107. https://doi.org/10.3390/axioms11030107








