Analytical and Numerical Simulations of a Delay Model: The Pantograph Delay Equation
Abstract
1. Introduction
2. Analytic Solution at ,
The Solution in Simplest Form
3. Convergence Analysis
4. Exact Solution at
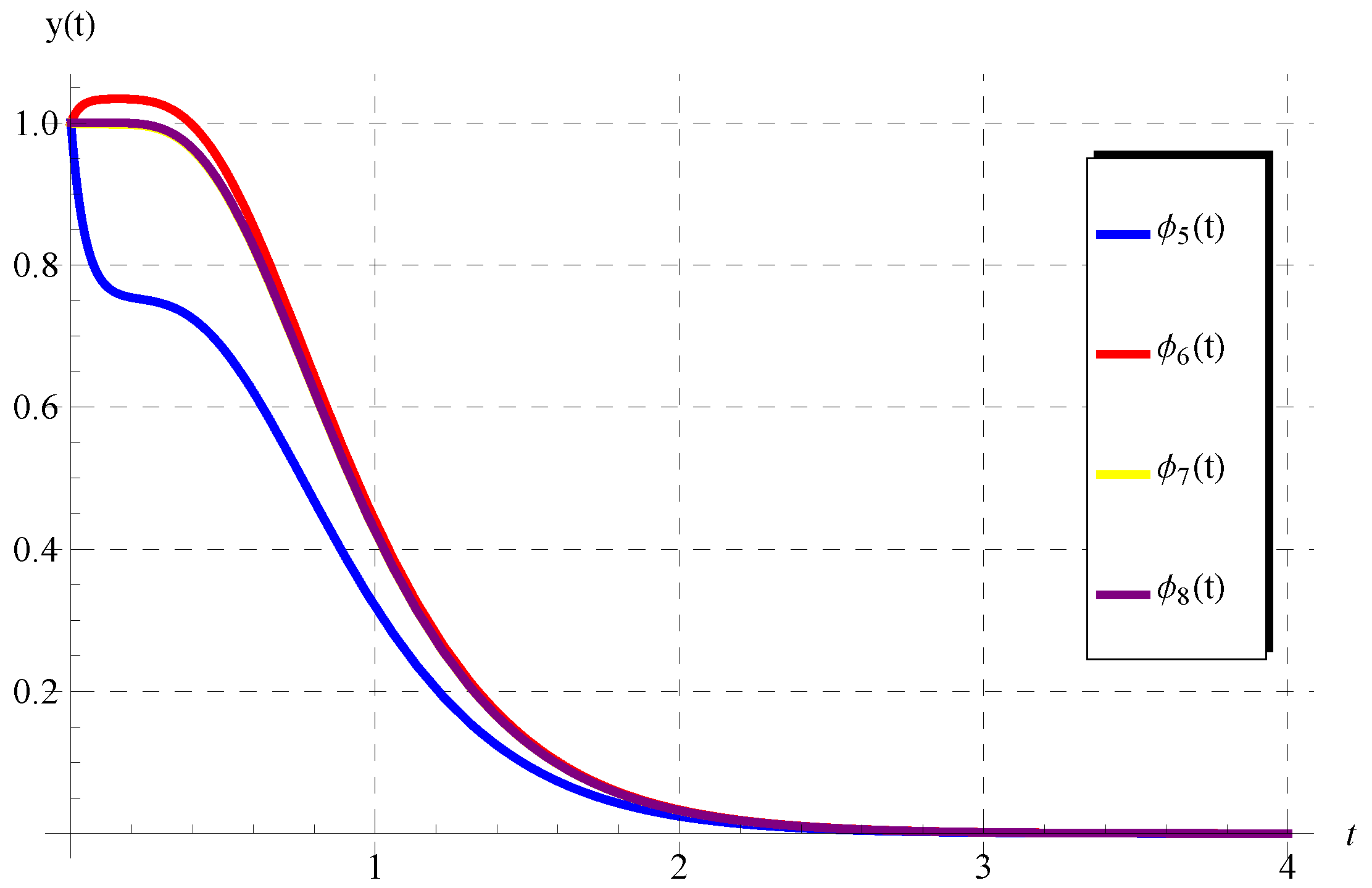
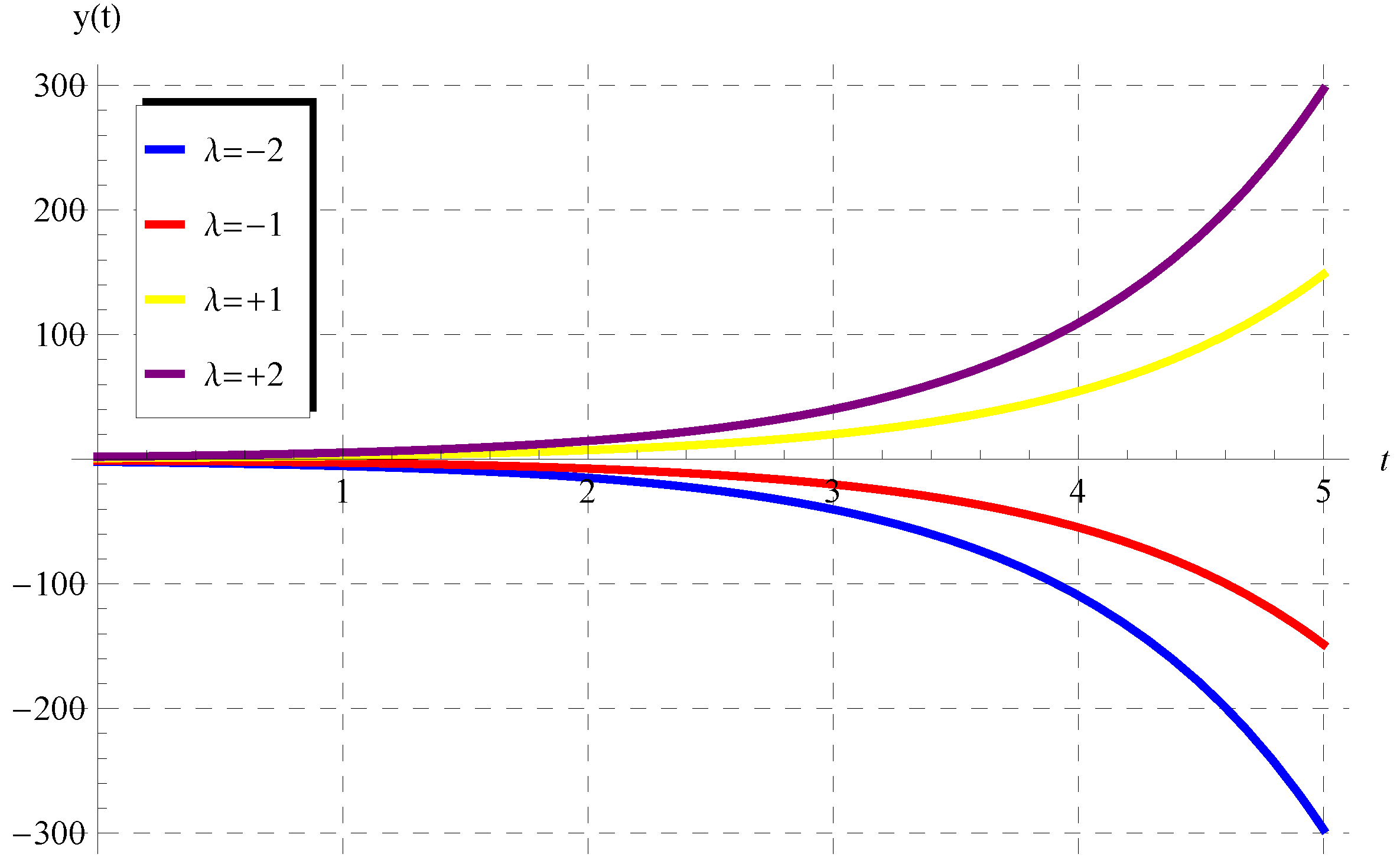
5. Results
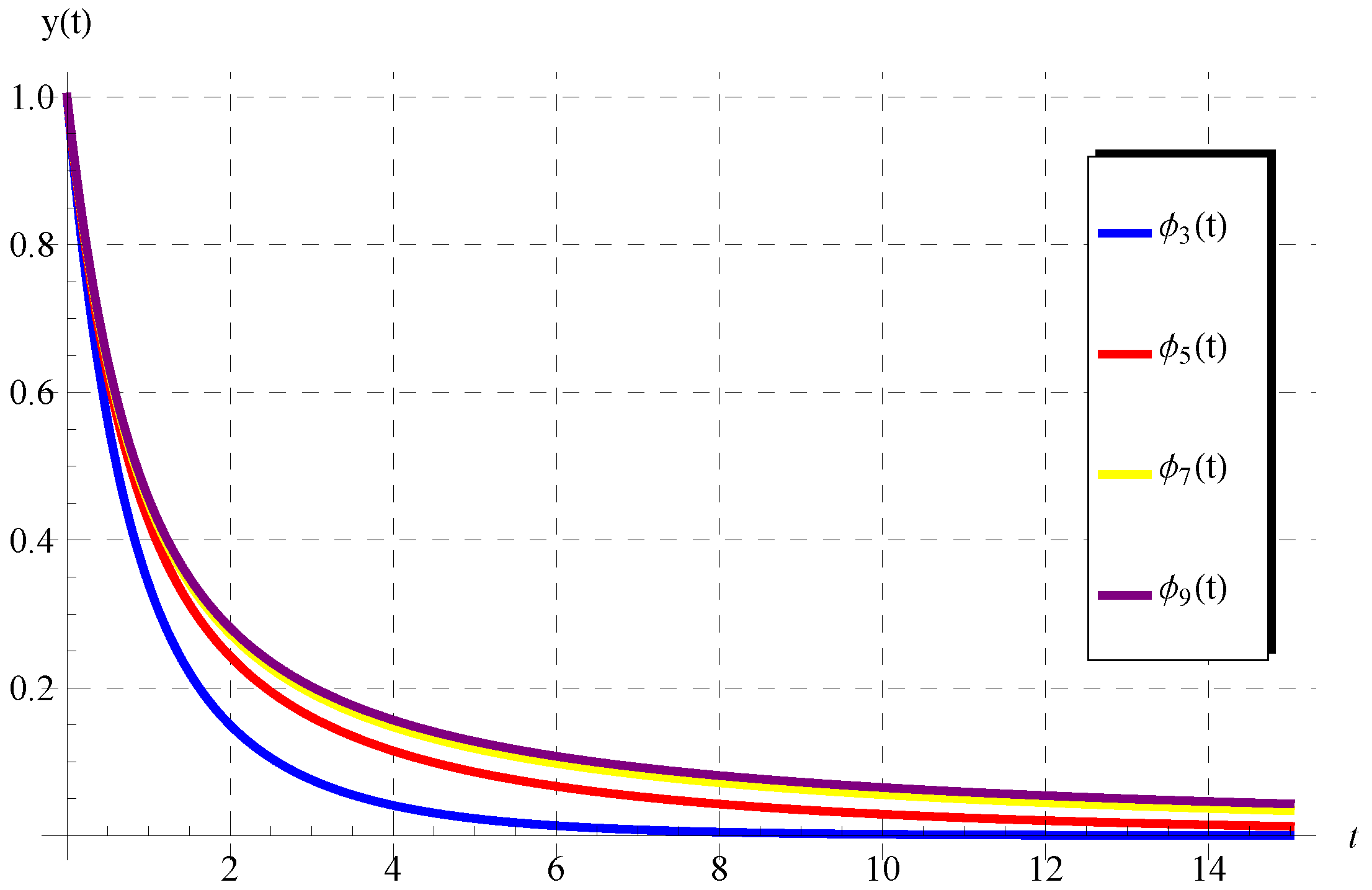
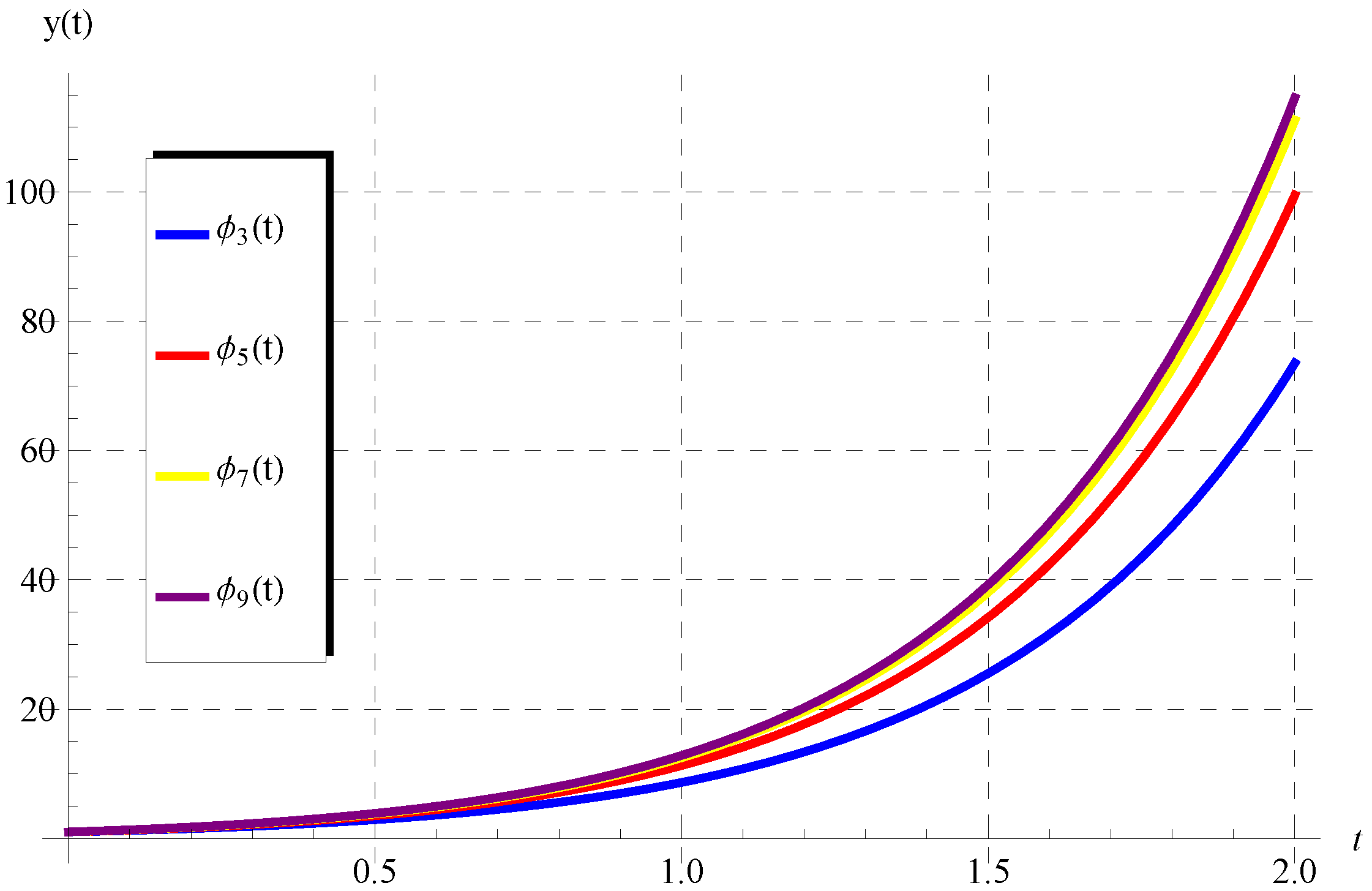
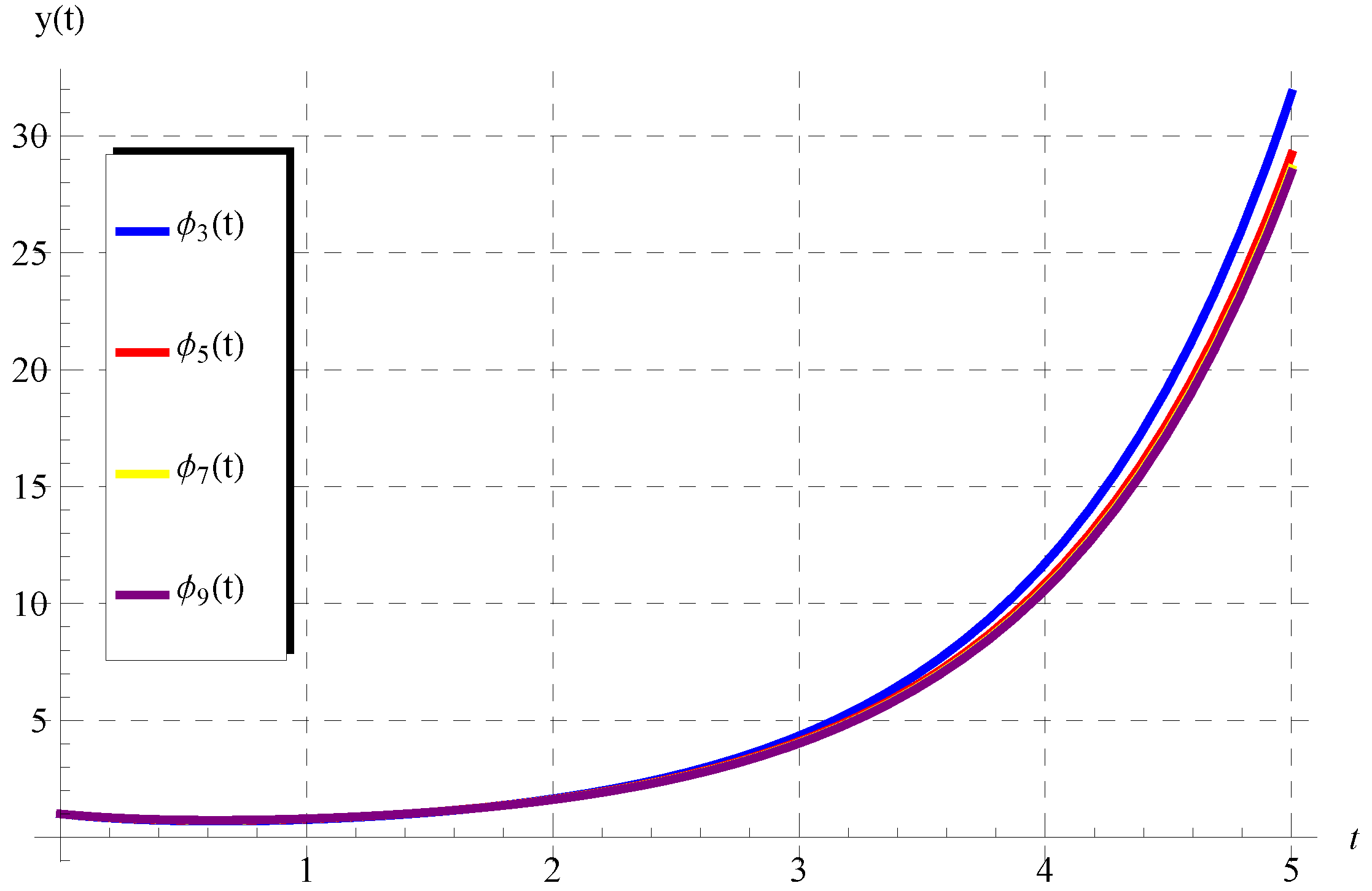
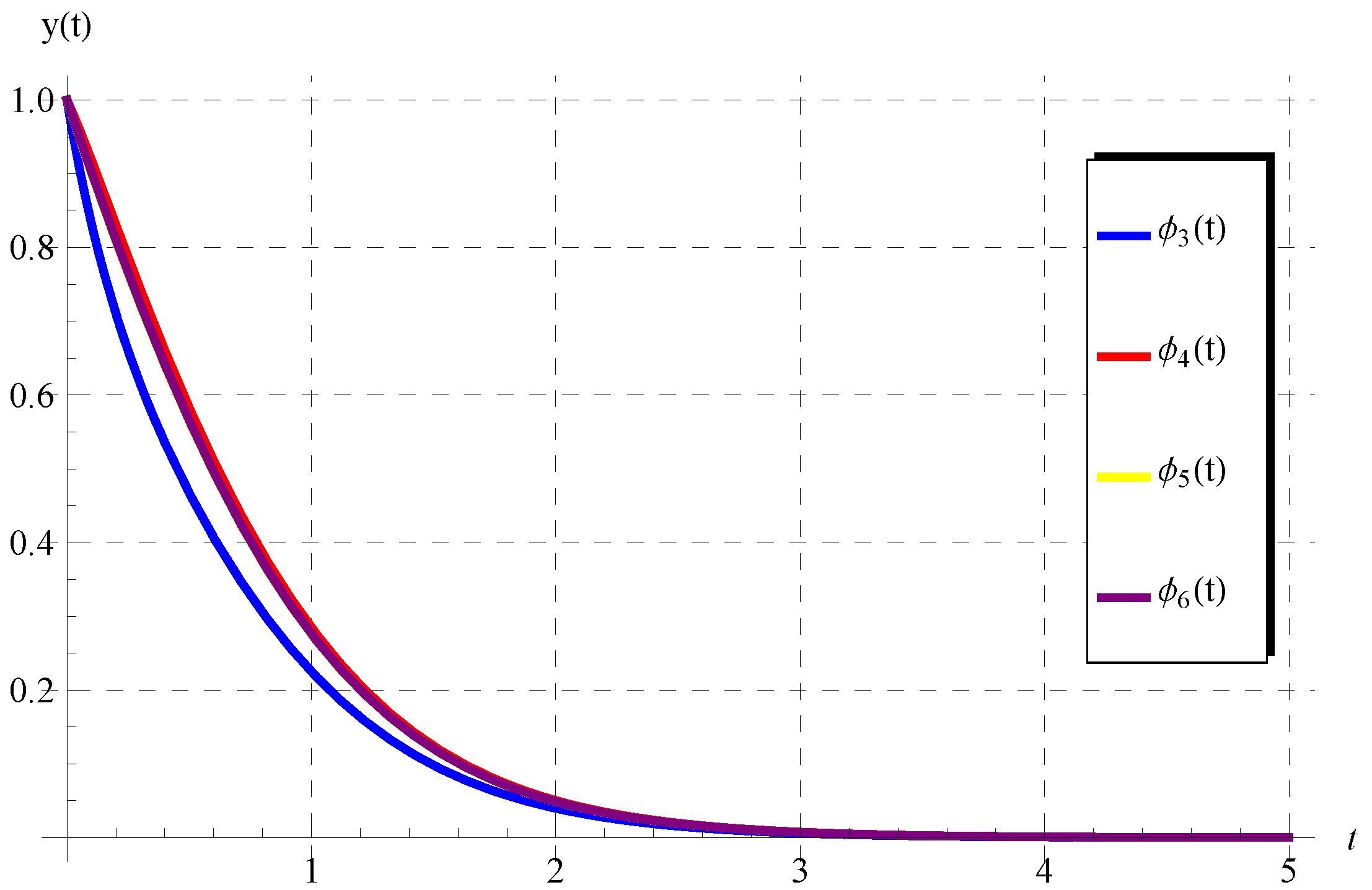
5.1. , ,
5.2. , ,
5.3. ,
5.4.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fox, L.; Mayers, D.F.; Ockendon, J.R.; Tayler, A.B. On a Functional Differential Equation. IMA J. Appl. Math. 1971, 8, 271–307. [Google Scholar] [CrossRef]
- Kato, T.; McLeod, J.B. The functional-differential equation y′(x) = ay(λx) + by(x). Bull. Am. Math. Soc. 1971, 77, 891–935. [Google Scholar]
- Derfel, G.; Iserles, A. The pantograph equation in the complex plane. J. Math. Anal. Appl. 1997, 213, 117–132. [Google Scholar] [CrossRef]
- Iserles, A. On the generalized pantograph functional differential equation. Eur. J. Appl. Math. 1993, 4, 1–38. [Google Scholar] [CrossRef]
- Marshall, J.; van-Brunt, B.; Wake, G. Natural boundaries for solutions to a certain class of functional differential equations. J. Math. Anal. Appl. 2002, 268, 157–170. [Google Scholar] [CrossRef][Green Version]
- Basse, B.; Baguley, B.; Marshall, E.; Joseph, W.; van Brunt, B.; Wake, G.; Wall, D. Modelling cell death in human tumour cell lines exposed to the anticancer drug paclitaxel. J. Math. Biol. 2004, 49, 329–357. [Google Scholar] [CrossRef]
- Hall, A.J.; Wake, G.C. A functional differential equation arising in the modelling of cell-growth. J. Aust. Math. Soc. Ser. B 1989, 30, 424–435. [Google Scholar] [CrossRef]
- Hall, A.J.; Wake, G.C. A functional differential equation determining steady size distributions for populations of cells growing exponentially. J. Aust. Math. Soc. Ser. B 1990, 31, 344–353. [Google Scholar] [CrossRef][Green Version]
- Gaver, D.P. An absorption probability problem. J. Math. Anal. Appl. 1964, 9, 384–393. [Google Scholar] [CrossRef][Green Version]
- Ambartsumian, V.A. On the fluctuation of the brightness of the milky way. Doklady Akad Nauk USSR 1994, 44, 223–226. [Google Scholar]
- Patade, J.; Bhalekar, S. On Analytical Solution of Ambartsumian Equation. Natl. Acad. Sci. Lett. 2017, 40, 291–293. [Google Scholar] [CrossRef]
- Alharbi, F.M.; Ebaid, A. New Analytic Solution for Ambartsumian Equation. J. Math. Syst. Sci. 2018, 8, 182–186. [Google Scholar] [CrossRef]
- Bakodah, H.O.; Ebaid, A. Exact solution of Ambartsumian delay differential equation and comparison with Daftardar-Gejji and Jafari approximate method. Mathematics 2018, 6, 331. [Google Scholar] [CrossRef]
- Khaled, S.M.; El-Zahar, E.R.; Ebaid, A. Solution of Ambartsumian delay differential equation with conformable derivative. Mathematics 2019, 7, 425. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D.; Rathore, S. Analysis of a fractional model of the Ambartsumian equation. Eur. Phys. J. Plus. 2018, 133, 133–259. [Google Scholar] [CrossRef]
- Kac, V.G.; Cheung, P. Quantum Calculus; Springer: New York, NY, USA, 2002. [Google Scholar]
- Ebaid, A.; Al-Jeaid, H.K. On the exact solution of the functional differential equation y′(t) = ay(t) + by(-t). Adv. Differ. Equ. Control Process. 2022, 26, 39–49. [Google Scholar] [CrossRef]
- Ruan, S. Delay Differential Equations In Single Species Dynamics. In Delay Differential Equations and Applications; NATO Science Series; Arino, O., Hbid, M., Dads, E.A., Eds.; Springer: Dordrecht, The Netherlands, 2006; Volume 205. [Google Scholar] [CrossRef]
- Yousef, F.; Alkam, O.; Saker, I. The dynamics of new motion styles in the time-dependent four-body problem: Weaving periodic solutions. Eur. Phys. J. Plus. 2020, 135, 742. [Google Scholar] [CrossRef]
- Folly-Gbetoula, M.; Nyirenda, D. A generalised two-dimensional system of higher order recursive sequences. J. Differ. Equ. Appl. 2020, 26, 244–260. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El-Zahar, E.R.; Ebaid, A. Analytical and Numerical Simulations of a Delay Model: The Pantograph Delay Equation. Axioms 2022, 11, 741. https://doi.org/10.3390/axioms11120741
El-Zahar ER, Ebaid A. Analytical and Numerical Simulations of a Delay Model: The Pantograph Delay Equation. Axioms. 2022; 11(12):741. https://doi.org/10.3390/axioms11120741
Chicago/Turabian StyleEl-Zahar, Essam Roshdy, and Abdelhalim Ebaid. 2022. "Analytical and Numerical Simulations of a Delay Model: The Pantograph Delay Equation" Axioms 11, no. 12: 741. https://doi.org/10.3390/axioms11120741
APA StyleEl-Zahar, E. R., & Ebaid, A. (2022). Analytical and Numerical Simulations of a Delay Model: The Pantograph Delay Equation. Axioms, 11(12), 741. https://doi.org/10.3390/axioms11120741






