Abstract
Tuberculosis (TB), caused by Mycobacterium tuberculosis is one of the treacherous infectious diseases of global concern. In this paper, we consider a deterministic model of TB infection with the public health education and hospital treatment impact. The effective reproductive number, that measures the potential spread of TB is presented by employing the next generation matrix approach. We investigate local and global stability of the TB-free equilibrium point, endemic equilibrium point, and sensitivity analysis. The analyses of the proposed model show that the model undergoes the phenomenon of backward bifurcation when the effective reproduction number is less than one, where two stable equilibria, namely, the DFE and an EEP coexist. Further, we compute the sensitivity of the impact of each parameter on the effective reproductive number of the model by employing a normalized sensitivity index formula. Numerical simulation of the proposed model was conducted using Maple 2016 and MatLab R2020b software and compared with the theoretical results for illustration purposes. The investigation results can be useful in providing information to policy makers and public health authorities in mitigating the spread of TB infection by public health education and hospital treatment.
Keywords:
tuberculosis infection; public health education; hospital treatment; effective reproduction number; stability analysis; bifurcation analysis; sensitivity analysis MSC:
97A30; 92B05
1. Introduction
Tuberculosis (TB) is one of the most hazardous infectious diseases that has become a significant widespread phenomenon, claiming more lives than any other contagious disease every day, according to [1]. Approximately 1/3 of the total population has a TB infection, resulting in millions of deaths and new cases annually (World Health Organization report). The report corroborates that TB is one of the top ten causes of mortality globally of both human and animal populations [2,3,4,5,6]. In 2020, for instance, 10 million individuals developed tuberculosis (TB), and more than 1.5 million died from it, including 214,000 HIV-positive persons (Human Immunodeficiency Virus) [7]. Typically, the signs may not be instantaneous when an individual contracts the disease. Thus, the individual remains asymptomatic for a long time or is latently infected for life [8]. Young adults may become infected by TB when they are most active [5]. Generally, TB-related deaths often happen in middle-income countries, for example, India, which leads the count, followed by Indonesia, China, the Philippines, Pakistan, Nigeria, Bangladesh, and South Africa. Such countries account for over of the entire TB trouble in the world. As a result, it is vital to implement techniques and methods that make it simple to understand how this disease spreads and predict its progression.
TB is a communicable disease caused by Mycobacterium tuberculosis affecting mostly the lungs [9,10]. However, it can also attack different organs including the brain, kidney, spine, central nervous system, or the lymphatic system [2,5,11,12,13]. It is important to note that the active lung TB disease typically begins with a cough, with sputum or blood on occasion, chest pains, fatigue, unexpected weight reduction, fever, and night sweats, which may last at least three or more weeks at a time. It has been reported by [14] that a pregnant woman who is infected may infect the foetus in some situations. Only individuals who have active TB can spread the disease. The latently infected individuals do not spread the bacteria [5,7]. Transmission starts with one individual, then onto the next, and relies upon the number of infected and expelled drops, the period of contaminated risk exposure, the virulence of the Mycobacterium tuberculosis, and the activity of environmental ventilation [7,10,15].
It was reported that behavioural change played a significant role in the transmission of infections [16,17,18]. Public health educational campaigns on TB disease plays a vital role in TB management and prevention [16,19], and can increase health literacy and awareness of TB among the population. The identification case rate and cure rate of TB patients can be improved by health education on TB disease, as it is an effective choice to minimize the spread of TB. As a result of the emergence of multi-resistance, treatment of TB is very challenging. Drug-resistant TB is a major public health concern across many developing countries, while treatment takes longer and needs more expensive drugs [5]. However, in many developing countries, the treatment of TB is not entirely free. Some TB patients cannot afford the full cost of treatment. As a result, some TB patients are treated at home to save money, as they can not afford to stay in the hospital. Some patients who were not cured choose to be discharged and continue their treatment at home [20].
Several mathematical models have been constructed to study the dynamical behaviour of TB infection. Abimbade et al. [21] formulated and analyzed an optimal control analysis of a TB transmission with incomplete treatment and exogenous re-infection, where they further divided the infected compartment into two groups, namely, uninformed and enlightened. Their findings revealed that both single controls and combinations of three controls have a positive influence on TB burden reduction. Recently, Ojo et al. [22] proposed a mathematical model for TB transmission with control. Their findings demonstrated that minimizing effective contact with infected people and increasing the rate of vaccinating susceptible persons with high vaccine efficacy will bring down the TB burden in a population. Xueyong et al. [16] formulated a TB model with healthy education and treatment. The qualitative analysis of their model exhibited the phenomenon of backward bifurcation, where the stable disease-free equilibrium co-exists with a stable endemic equilibrium, when the reproduction number is less than one. Huo and Zou [20] investigated a TB dynamics model with two types of treatment, namely, treatment at home and treatment in hospital. Their findings revealed that home treatment has a significant detrimental impact on tuberculosis spread. Okuonghae contributed significantly to TB epidemiology. They investigated the dynamics of TB and developed different models with comprehensive observations and results. Okuonghae and Egonmwan [23] presented a deterministic model that explores the impact of diagnosing and treating both latent and active TB infections on the disease’s infection dynamics in a population. Castillo and Song [6] studied a comprehensive review of the literature on TB dynamics. They compiled many dynamical models of TB and established a theoretical framework. Recently, Mustapha et al. [24] introduced a TB model with hospitalization and reinfection. A mathematical analysis of the equilibrium points, the basic reproduction number, and sensitivity analysis was discussed. However, the authors of [24] did not include public health education in their model. This factor continues to be one of the most important aspects in people’s lives. Public health services contributed to reducing the spread of TB infection.
Inspired by the above discussions, this paper seeks to fill a gap in the references cited, focusing on both public health education and hospital treatment. Infectious individuals in this model are divided into two classes: Infected individuals receiving treatment at home and infected individuals receiving treatment at the hospital. In this paper, we consider the impact of public health education and hospital treatment, comparing with the previous paper of [20]. The key differences are, in this paper, both the susceptible and infected compartment are divided into two classes, which are susceptible and educated susceptible, and infected individuals at home and in the hospital. The other parts of the paper are assembled as follows: Section 2 is devoted to the model formulation along with its fundamental properties. Section 3 deals with analysis of the existence of equilibria and how it relates to the effective reproduction number. Section 4, bifurcation analysis was conducted theoretically and supported with some numerical experiments to give a visualization of the results. Sensitivity analysis is presented in Section 5. Numerical results and discussions are given in Section 6. Finally, conclusions and future work are given in Section 7.
2. Materials and Methods
In this section, a TB model with the impact of public health education and hospital treatment was considered by stratifying total population into epidemiological classes represented as into six compartments, namely, susceptible individuals Educated Susceptible Exposed individuals Infectious individuals at home Infectious individuals receiving treatment at hospital and Recovered individuals so that:
2.1. Clinical Assumptions of the TB Model with Public Health Education and Hospital Treatment
The assumptions used in this model are as follows:
- There is a constant recruitment rate to the susceptible population, and natural cause of death affects individuals in all compartments, with an extra TB-induced death rate in the infected class.
- We assume that, at any moment, the educated susceptible group may act as ignorantly and enter the class of susceptible at a constant rate i.e., loss of temporary protection [16].
- We further assumed that some uncured TB patients wanted to be discharged and continue treatment at home at a rate [20].
- Both infected individuals at home and in the hospital experience the infections effect at the rate .
- The infected compartment is divided into two groups, namely, infected individuals who received treatment at home and infected individuals receiving treatment in hospital .
- The recovered individual may be again infected by an infectious individual [25].
In this model, it is assumed that the number of susceptible population is generated via recruitment of individuals into the population at a rate Susceptible individuals are educated at the rate and then transferred into the educated class. We further assume that education programs provide “temporary protection” at the per-capita rate [19,26]. We assume that both infected individuals at home and in the hospital experience the infections effect at the rate where
In (2), the parameter is the transmission rate, while is the modification parameter associated with reduced infectiousness of individuals in the hospital compared to individuals at home. Individuals who have received public health education have a high level of awareness. As a result, educated people are a low-risk population. Education reduces the risk of infection by a factor of The scenario indicates that the education is totally effective to prevent the infection, whereas models the case where the education program is totally ineffective [19,26]. The populations of susceptible and educated susceptible individuals are further decreased as a result of natural death rate Therefore, the rates of change of the populations of susceptible and educated susceptible individuals are given, respectively, by
The population of exposed individuals is generated via the infection of susceptible , educated susceptible and recovered , at the rate and and decreased as a result of disease symptoms at a rate and natural death at the rate and is taken as the reinfection rate so that
Similarly, the population of infected individuals at home is generated as result of disease symptoms at a rate the rate of TB patients who are not cured from the hospital at a rate and diminished due to progression to hospital at a rate , recovery by TB patients at home at a rate , natural death cause and TB-induced death at the rate , respectively. Thus,
In addition, the population of infected individuals receiving treatment at the hospital is increased as a result of the disease symptoms at a rate and hospital admittance of infected individuals receiving treatment at home at a rate and diminished due to their returning back home to at a rate natural death cause recovery by TB patients at hospital at a rate and TB induced death at the rate Therefore,
Finally, the population of recovered individuals is generated via recovery by both infected individuals treated at home and at hospital at a rate , respectively, and diminished as a result of natural death at a rate and progression to the exposed class at a rate
Therefore, based on the above description and assumptions, the model of TB with public health education and hospital treatment lead to following a system of non-linear differential equations; the schematic diagram Figure 1 below, and the parameters indicated in the diagram are explained in Table 1.
where
with the initial conditions given by Equation (5)
satisfies the equation
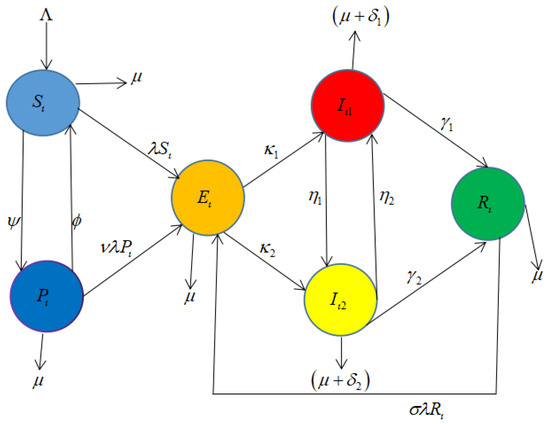
Figure 1.
The flow diagram of TB model with public health education and hospital treatment.

Table 1.
Interpretation of the Variables and Parameters of the TB Model with Public Education and hospital Treatment (23).
2.2. Basic Properties of the TB Model with Public Health Education and Hospital Treatment
The basic properties of the TB model (23) are explained in this subsection. In an invariant region, the model is proved to be positive and bounded. When studying the dynamical behaviour of an epidemiologically model, this analysis is crucial because it demonstrates whether the model is epidemiologically relevant and mathematically well-posed, that is, whether the model and its predictions are certain [27].
Positivity of Solutions
To established that the TB infection model system (23) is epidemiologically realistic, all the stated variables are positive all the time.
Theorem 1.
Let initial data be Thus, the solution of of the model system (23) is non-negative for all
2.3. Invariant Region
Theorem 2.
The solution of the TB model system (23) is enclosed in the region Φ subset , given by
for the initial conditions (5) in
Proof of Theorem 2
The change in the total population is given by
In the absence of TB infection, there is no death from TB transmission, (that is, = 0) [30], hence the rate of change of the total population size in Equation (8) is given as
The solution of Equation (9) is solved by using the same approach presented in [31,32], and is given by
where =
Using [33] we note that if <, asymptotically as in Equation (10) the total population size , which means that 0 Therefore, all the feasible solutions in the model converge in the region [34]. □
3. Existence of Equilibrium
3.1. Tuberculosis Free Equilibrium (TFE)
The state denoted as , is generally described as a state in which no disease exists in a given population. The infected population can be defined as a disease type. Using the first fourth equation of system model (23) with into consideration, we arrive at:
3.2. Calculation of Effective Reproduction Number For the System Model (23)
This section studies the effective reproduction number, which is a threshold parameter that controls the spread of a disease. To obtain the effective reproduction number, we apply the next generation approach described in [35]. The associated incidence matrix and the transition matrix of system model (23), are respectively obtained as:
where
Thus, the effective reproductive number of system model (23) is calculated from the spectral radius as:
The term effective reproduction number, represented by is defined as the expected number of secondary cases generated by a single infected individual during the period of infectiousness in a population of susceptible individuals where public health education and hospital treatment are incorporated [36].
3.3. Local Stability of TB Free Equilibrium
To prove the local stability of the TFE, the Jacobian of the proposed model system (23) is used. After that, the Jacobian is used to derive the characteristic equation, from which the eigenvalue result is obtained.
Theorem 3.
The TFE of the proposed model system (23) is locally asymptotically stable when
Proof of Theorem 3
To prove the system’s local stability, the Jacobian of the proposed model system (23) is investigated at TFE, which is then given by:
The characteristic equation of (16) is given by:
It can be seen from (17) that:
The result reveals that all the eigenvalues are negative given that all the parameters values are greater than zero. As a result, according to the principle of linearized stability [37], the TFE is asymptotically stable. □
3.4. Global Stability of the TB Free Equilibrium
This section investigates the global stability of the point of the model system (23). To investigate the global stability of the system model (23), we employ the techniques implemented by [38].
Here, the components and , where denotes the uninfected population and denotes the infected population.
The TB free equilibrium is defined by
The fixed point is a globally asymptotically stable equilibrium for the system model (23) provided that which is locally asymptotically stable, and the following two conditions must be satisfied:
is globally asymptotically stable (GAS),
If the system model (23) meets the given two criteria, then the following theorem holds.
Theorem 4.
The TB free equilibrium point of the system model (23) is globally asymptotically stable provided and the conditions and are satisfied.
Proof of Theorem 4
From system model (23) we can get and :
At Equation (20)
From the system (22) above, we see that is globally asymptotical stable. This can be verified from the solutions, namely,
As the solution which implies the global convergence of (22) in , and this satisfies condition .
Next, applying the second condition of the theorem
From we have = for
Therefore, = . where A is an matrix, is a column vector and is a column vector formed from the infectious compartments. We already know that
Now let compute A
The matrix A is a metzler matrix because all its off-diagonal elements are non-negative.
Thus, using one obtains the following
Since is not satisfied. This suggests that backward bifurcation may occur at when □
3.5. Endemic Equilibrium State
The stability of drives the disease’s short-term outbreaks. The stability at the endemic equilibrium points characterises its dynamics over a longer duration. We discovered that long-term behaviour has crucial epidemiological implications, such as whether an outbreak of a disease will lead to an endemic scenario or whether the infection will die out. We shall conduct an endemic analysis in this section. can now be determined by equating all of the model system in (23) to zero:
Theorem 5.
The endemic equilibrium state of the model system Equation (23) exists if the effective reproduction number
The proof of Theorem 5 is presented in Appendix A.
Theorem 6.
The TB model with public health education and hospital treatment (23) has:
- 1.
- One or more endemic equilibria when
- 2.
- A unique endemic equilibrium when
- 3.
- No endemic equilibrium otherwise.
4. Local Stability of Endemic Equilibrium
The local stability of endemic equilibrium of the model system can be investigated by employing the concept of center manifold presented in [6].
Theorem 7.
The TB model with public health education and hospital treatment (23) undergoes backward bifurcation with bistability of at
The proof of Theorem 7 is presented in Appendix B.
Figure 2 demonstrates a backward bifurcation diagram of force of infection against the effective reproduction number of the system model (23). We can see from the figure that as increases to one, the disease also increases and this occurs when At DFE and EEP coexists; this means that the disease cannot be eradicated from the population as a result of a high-level endemic. We can also discover that when the disease persists.

Figure 2.
The bifurcation diagram of force of infection against which illustrates a backward bifurcation for the system model (23).
5. Sensitivity Analysis
It is crucial to investigate how sensitive the TB model (23) is to changes in each of its parameters in order to identify control strategies that will assist in the lowering of the infection trajectory. In other words, conducting sensitivity analysis will assist in identifying what should be done or ignored in order to stop the spread of the TB transmission [29,39,40]. When a parameter changes, we can use sensitivity indices to calculate the relative change in a state variable. We employ the normalised forward sensitivity index of a variable to a parameter method provided in [41] in order to perform sensitivity analysis. The ratio of relative change in the variable to relative change in the parameter is known as the sensitivity index. The sensitivity index may also be defined using partial derivatives when the variable is a differentiable function of the parameter. Therefore, as stated in [41], the normalised forward sensitivity index of a threshold, , that is differentiable with respect to a parameter, , is defined as:
The sensitivity of to each of the 14 parameters presented in Table 2 is calculated using the effective reproduction number given below
where , and are given in Equation (14).

Table 2.
Sensitivity Indices of the Model Parameters in Relation to .
Sensitivity index implied the parameters values obtained in Table 2.
From Table 2, we can see that the parameters have both positive and negative effects on Positive values, such as as shown in Table 2 reveal that an increase in these parameters values increases which brings about the infection attacking the population. While the parameters have negative , that is, an increase in these parameters values decrease and as a result, the infection gradually fades from the population.
Figure 3 demonstrates the relationship between the effective reproduction number and Figure 3a, illustrates a linear relationship between and the awareness rate We observed from Figure 3a, that decreases with increasing the awareness rate of susceptible individuals. This means that susceptible individuals who are aware of the TB disease and understand how it is transmitted have a great positive impact on the spread of TB infection.

Figure 3.
The relationship between (a), (b), (c), and (d) and the effective reproduction number .
Figure 3b demonstrates a linear relationship between and the rate at which infected individuals progress from class to class. This indicates that decreases with the increasing the rate at which infected individuals at home undergo treatment at the hospital. This means that infected individuals treated at the hospital have a great positive impact on the spread of TB infection too.
6. Numerical Results and Discussions
The numerical simulation of the model system (23), is performed with the values of the parameters described in Table 3. We used ode45 solver in Matlab, which depends on the Runge-Kutta technique to stimulate model system (23) with the parameter values presented in Table 3, as well as the following initial conditions:

Table 3.
The Parameters and Baseline Values of the Model with Public Health Education and Hospital Treatment (23).
Figure 4 is a graphical representation of system model (23) showing the differences between susceptible and educated susceptible individuals. We can see from Figure 4 that, as time increases, the number of educated susceptible individuals’ health continues to increase until it reaches the carrying capacity, whereas, the number of susceptible individuals continues to decrease with time as more and more of them become infected.

Figure 4.
Simulations of system (23) showing the behaviour of susceptible and educated susceptible. Parameters used are
Figure 5 depicts the impact of the various values of awareness rate on the dynamics of In general, this figure reflects that when increases, the number of decreases rapidly. This demonstrates that public health education of susceptible individuals has the effect of limiting TB disease spread. As a result, public policymakers must focus on increasing the value of awareness rate in order to prevent and control TB infection in a population.
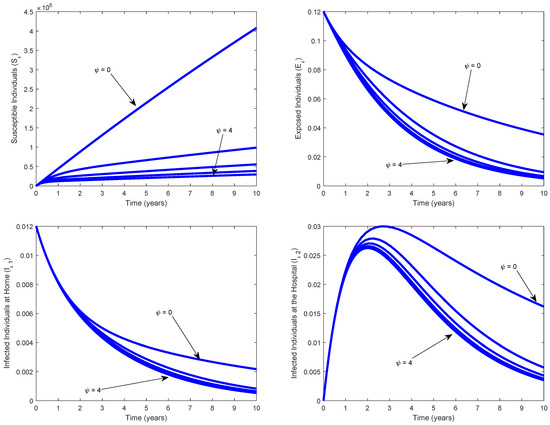
Figure 5.
Impact of awareness rate on varying Other parameters are given as
Figure 6 investigates the impact of varying the rate at which the educated susceptible lose the awareness . This figure demonstrates a worst-case scenario in which an increase in loss of awareness in the susceptible individual leads to an increase in the proportion of infectious individuals.
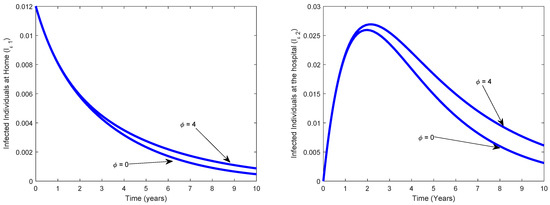
Figure 6.
Impact at which educated susceptible lose awareness on varying Other parameters are given as
Figure 7 investigates the effect of varying the reduction of infection by infected individuals receiving treatment at the hospital In this figure, is varied between 0 to 1. Of course, lowering the value of z, from 1 to 0, as expected, reduces the proportion of infected individuals, although at different rates.
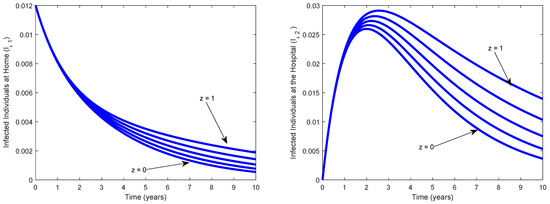
Figure 7.
Impact of reduction of infection rate as a result of on varying Other parameters are given as
Figure 8 illustrates the impact of varying the rate at which infected individuals at home go out for treatment in the hospital, between 0 and 1 on the individuals treated at home and infected individuals receiving treatment at the hospital, respectively. Obviously, as expected, an increase in the value of , from 0 to 1 greatly reduced the number of infected individuals both at home and at hospital. Epidemiologically, this shows that rate at which infected individuals at home go out for treatment in the hospital have a great impact on reducing the transmission of TB disease in the population.
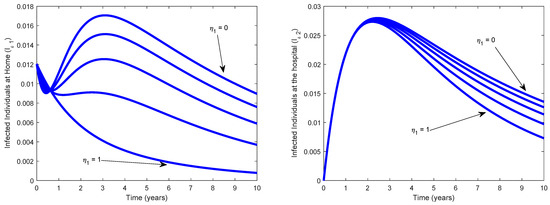
Figure 8.
Impact of progression rate from to on varying Other parameters are given as
7. Conclusions
This paper presented a new deterministic model of TB infection subject to the use of public health education and hospital treatment. To gain insight into its dynamic features, the model was rigorously analyzed. The analyses of the model, which contains six mutually-exclusive epidemiological partitions, show that the model undergoes the phenomenon of backward bifurcation when the effective reproduction number is less than one, where two stable equilibria, namely, the DFE and an EEP coexist when the corresponding effective reproductive number is less than one. This backward bifurcation phenomenon of this article is very vital, and this occurs only under education of susceptible individuals and treatment of TB-infected individuals in the hospital. This is mostly telling us that, even if the effective reproduction number is less than unity, while necessary, it is not sufficient for efficiently controlling the spread of a TB epidemic, which is against classical epidemiological theory. In this scenario, TB elimination will depend upon the initial sizes of the sub-populations of the model. The parameters are sensitive to the transmission dynamics of TB diseases, either negatively or positively . According to the numerical investigation, increasing the public health education on the class, and the progression rate from to have a significant great effect on reducing the prevalence of TB burden see Figure 5 and Figure 8. Given that public health education and hospital treatment can reduce the spread of TB infection, this programme should be continued and improved.
In light of the model study in this paper, some gaps in this paper need to be filled; these proposed gaps will allow for possible extension and improvement of the paper. The proposed model can be extended and improved in the future by:
- Considering a stochastic model approach. This will result in more realistic TB model dynamics.
- Since the spread of tuberculosis affects all age groups, it is crucial to consider the dynamics of the TB model by incorporating an age-structured model.
- Real data will also be considered because collecting data for TB patients is difficult in epidemiological models; as a result, we use data collected or estimated from literature sources. Once we have real-world data for TB patients, we can compare it to theoretical outcomes.
- Analyzing the dynamics of the TB model using a fractional order differential equation (FODE). It will be extremely interesting to use a FODE to examine the dynamics of TB model.
Author Contributions
Conceptualization, F.S. and F.A.A.; methodology, F.S. and F.A.A.; software, F.S.; validation, F.S. and F.A.A.; formal analysis, F.S.; data curation, F.S. and F.A.A.; writing—original draft preparation, F.S.; writing—review and editing, F.S.; visualization, F.A.A.; supervision, F.A.A.; project administration, F.A.A.; funding acquisition, F.A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Ministry of Higher Education (MoHE), Malaysia; Fundamental Research Grant Scheme (FRGS)—Grant code (FRGS/1/2021/STG06/USM/02/9) and Article Processing Charge (APC) Fund from Research Creativity and Management Office (RCMO), Universiti Sains Malaysia.
Data Availability Statement
All the data and models used and/or generated during the study contains in the submitted article.
Acknowledgments
We would like to acknowledge the funder from the Ministry of Higher Education (MoHE), Malaysia; Fundamental Research Grant Scheme (FRGS)—Grant code (FRGS/1/2021/STG06/ USM/02/9) and Article Processing Charge (APC) Fund from Research Creativity and Management Office (RCMO), Universiti Sains Malaysia. We would also like to thank the School of Mathematical Sciences, Universiti Sains Malaysia for research assistance and computing facilities.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Proof of Theorem 5
At the endemic state, the model system Equation (23) has an equilibrium point called TB endemic equilibrium point.
By setting the derivatives of the left hand side of Equation (23) to zero and solving simultaneously we have
Further
First, the nominator
and the denominator is After substituting the values of in Equation (A2), we obtain
where
where
Thus
⇒
⇒
where
Here, is the effective reproduction number given in (15).
Appendix B
Proof of Theorem 7
To apply the method in presented in Theorem 4.1 of [6], the following simplification and change of variables are made on the model system (23). Let
so that
Also, by utilizing the vector notation then, the model system (23) becomes = as follows
where
The Jacobian of the system (A17), evaluated at the (denoted by ), is given by
where are as in (13), from which it has been shown in (14) that the effective reproduction number, is given by
Consider the case when Suppose, further, that is chosen as a bifurcation parameter, since is often inconvenient to use directly as bifurcation parameter. Solving for gives when
The linearized system of the transformed model system (23) with chosen as a bifurcation parameter has a simple zero eigenvalue. We then calculate the right eigenvector W and the left eigenvector V which are associated with the zero eigenvalue of the Jacobian of (A19) at (denoted by ) chosen such that and with where
Then
i.e.,
Solving (A23), gives
Similarly, calculating the left eigenvector with gives
i.e.,
Solving (A26), gives
The local dynamics of model system (23) around TB free equilibrium are totally calculated by a and b represented as
Now, to determine the coefficients a and b described in Theorem 4.1 of Castillo Chavez and Song [6] as follow:
and
Hence, since and in this situation, it follows from Theorem 4.1 of Castillo Chavez and Song that the system model (23) or the transformed model (A17), will undergo a phenomenon of backward bifurcation when Therefore, establishing that TB endemic equilibrium is locally asymptotically stable if
References
- World Health Organization. Global Tuberculosis Report; WHO: Geneva, Switzerland, 2019; Volume 214. [Google Scholar]
- Ullah, S.; Khan, M.A.; Farooq, M.; Gul, T. Modeling and analysis of tuberculosis (TB) in Khyber Pakhtunkhwa, Pakistan. Math. Comput. Simul. 2019, 165, 181–199. [Google Scholar] [CrossRef]
- Sudre, P.; Ten Dam, G.; Kochi, A. Tuberculosis: A global overview of the situation today. Bull. World Health Organ. 1992, 70, 149. [Google Scholar] [PubMed]
- Dolin, P.J.; Raviglione, M.C.; Kochi, A. Global tuberculosis incidence and mortality during. Bull. World Health Organ. 1994, 72, 213. [Google Scholar] [PubMed]
- World Health Organization. Global Tuberculosis Report 2020; WHO: Geneva, Switzerland, 2020. [Google Scholar]
- Castillo-Chavez, C.; Song, B. Dynamical models of tuberculosis and their applications. Math. Biosci. Eng. 2004, 1, 361. [Google Scholar] [CrossRef]
- Kasereka Kabunga, S.; Doungmo Goufo, E.F.; Ho Tuong, V. Analysis and simulation of a mathematical model of tuberculosis transmission in Democratic Republic of the Congo. Adv. Differ. Equ. 2020, 2020, 642. [Google Scholar] [CrossRef]
- Adebiyi, A.O. Mathematical Modeling of the Population Dynamics of Tuberculosis. Master’s Thesis, University of the Western Cape, Cape Town, South Africa, 2016. [Google Scholar]
- Jaramillo, E. Tuberculosis and stigma: Predictors of prejudice against people with tuberculosis. J. Health Psychol. 1999, 4, 71–79. [Google Scholar] [CrossRef]
- Daniel, T.M.; Bates, J.H.; Downes, K.A. History of tuberculosis. In Tuberculosis: Pathogenesis, Protection, and Control; Wiley Online Library: Hoboken, NJ, USA, 1994; pp. 13–24. [Google Scholar]
- Khan, M.A.; Ahmad, M.; Ullah, S.; Farooq, M.; Gul, T. Modeling the transmission dynamics of tuberculosis in Khyber Pakhtunkhwa Pakistan. Adv. Mech. Eng. 2019, 11, 1687814019854835. [Google Scholar] [CrossRef]
- Khajanchi, S.; Das, D.K.; Kar, T.K. Dynamics of tuberculosis transmission with exogenous reinfections and endogenous reactivation. Phys. A Stat. Mech. Appl. 2018, 497, 52–71. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Zhang, X. Mathematical modeling of tuberculosis data of China. J. Theor. Biol. 2015, 365, 159–163. [Google Scholar] [CrossRef]
- Bar, B. Tuberculose et grossesse. Bull. Acad. Méd. 1922, 219. [Google Scholar]
- World Health Organization. WHO Consolidated Guidelines on Tuberculosis: Tuberculosis Preventive Treatment; WHO: Geneva, Switzerland, 2020. [Google Scholar]
- Zhou, X.; Shi, X.; Cheng, H. Modelling and stability analysis for a tuberculosis model with healthy education and treatment. Comput. Appl. 2015, 32, 245–260. [Google Scholar] [CrossRef]
- Xiang, H.; Song, N.N.; Huo, H.F. Modelling effects of public health educational campaigns on drinking dynamics. J. Biol. Dyn. 2016, 10, 164–178. [Google Scholar] [CrossRef] [PubMed]
- Del Valle, S.; Hethcote, H.; Hyman, J.M.; Castillo-Chavez, C. Effects of behavioural changes in a smallpox attack model. Math. Biosci. 2005, 195, 228–251. [Google Scholar] [CrossRef] [PubMed]
- Xiang, H.; Zou, M.X.; Huo, H.F. Modeling the effects of health education and early therapy on tuberculosis transmission dynamics. Int. J. Nonlinear Sci. Numer. 2019, 20, 243–255. [Google Scholar] [CrossRef]
- Huo, H.F.; Zou, M.X. Modelling effects of treatment at home on tuberculosis transmission dynamics. Appl. Math. Model. 2016, 40, 9474–9484. [Google Scholar] [CrossRef]
- Abimbade, S.F.; Olaniyi, S.; Ajala, O.A.; Ibrahim, M.O. Optimal control analysis of a tuberculosis model with exogenous reinfection and incomplete treatment. Optim. Control Appl. Methods 2020, 41, 2349–2368. [Google Scholar] [CrossRef]
- Ojo, M.M.; Peter, O.J.; Goufo, E.F.D.; Panigoro, H.S.; Oguntolu, F.A. Mathematical model for control of tuberculosis epidemiology. J. Appl. Math. Comput. 2022, 1–19. [Google Scholar] [CrossRef]
- Egonmwan, A.O.; Okuonghae, D. Analysis of a mathematical model for tuberculosis with diagnosis. J. Appl. Math Comput. 2019, 59, 129–162. [Google Scholar] [CrossRef]
- Mustapha, U.T.; Idris, B.; Musa, S.S.; Yusuf, A. Mathematical modeling and analysis of mycobacterium tuberculosis transmission in humans with hospitalization and reinfection. J. Appl. Math. Comput. Mech. 2022, 21, 55–66. [Google Scholar] [CrossRef]
- Kar, T.K.; Mondal, P.K. Global dynamics of a tuberculosis epidemic model and the influence of backward bifurcation. J. Math. Model. Algorithms 2012, 11, 433–459. [Google Scholar] [CrossRef]
- Okuonghae, D.; Omosigho, S.E. Analysis of a mathematical model for tuberculosis: What could be done to increase case detection. J. Theor. Biol. 2011, 269, 31–45. [Google Scholar] [CrossRef]
- Tang, H.; Li, M.; Yan, X.; Lu, Z.; Jia, Z. Modeling the dynamics of drug spreading in China. Int. J. Environ. Res. Public Health 2021, 18, 288. [Google Scholar] [CrossRef] [PubMed]
- Olaniyi, S.; Falowo, O.D.; Okosun, K.O.; Mukamuri, M.; Obabiyi, O.S.; Adepoju, O.A. Effect of saturated treatment on malaria spread with optimal intervention. Alex. Eng. J. in press. 2022. [CrossRef]
- Olaniyi, S.; Obabiyi, O.S.; Okosun, K.O.; Oladipo, A.T.; Adewale, S.O. Mathematical modelling and optimal cost-effective control of COVID-19 transmission dynamics. Eur. Phys. J. Plus. 2020, 135, 938. [Google Scholar] [CrossRef] [PubMed]
- Cooke, K.L.; Van Den Driessche, P. Analysis of an SEIRS epidemic model with two delays. J. Math. Biol. 1996, 35, 240–260. [Google Scholar] [CrossRef]
- Obasi, C.; Mbah, G.C.E. On the stability analysis of a mathematical model of Lassa fever disease dynamics. J. Nig. Soc. Math. Biol. 2019, 2, 135–144. [Google Scholar]
- Srivastava, A.; Srivastava, P.K. Nonlinear dynamics of a SIRI model incorporating the impact of information and saturated treatment with optimal control. Eur. Phys. J. Plus. 2022, 137, 1–25. [Google Scholar] [CrossRef]
- Rota, G.C.; Birkhoff, G. Ordinary Differential Equations; Blaisdell Publishing Company: Waltham, MA, USA, 1969. [Google Scholar]
- Hethcote, H.W. The mathematics of infectious diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Falowo, O.D.; Olaniyi, S.; Oladipo, A.T. Optimal control assessment of Rift Valley fever model with vaccination and environmental sanitation in the presence of treatment delay. Model. Earth Syst. Environ. 2022, 1–15. [Google Scholar] [CrossRef]
- Keeling, M.J.; Rohani, P. Temporally forced models. In Modeling Infectious Diseases in Humans and Animals; Princeton University Press: Princeton, NJ, USA, 2011; pp. 155–189. [Google Scholar]
- Castillo-Chavez, C.; Feng, Z.; Huang, W. On the computation of R0 and its role on. In Mathematical Approaches for Emerging and Reemerging Infectious Diseases: An Introduction; Springer: Berlin/Heidelberg, Germany, 2002; Volume 1, p. 229. [Google Scholar]
- Islam, M.S.; Ira, J.I.; Kabir, K.A.; Kamrujjaman, M. COVID-19 Epidemic compartments model and Bangladesh. Preprint 2020, 10. [Google Scholar] [CrossRef]
- Olaniyi, S. Dynamics of Zika virus model with nonlinear incidence and optimal control strategies. Appl. Math. Inf. Sci. 2018, 12, 969–982. [Google Scholar] [CrossRef]
- Chitnis, N.; Hyman, J.M.; Cushing, J.M. Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bull. Math. Biol. 2008, 70, 1272–1296. [Google Scholar] [CrossRef] [PubMed]
- Song, B.; Castillo-Chavez, C.; Aparicio, J.P. Tuberculosis models with fast and slow dynamics: The role of close and casual contacts. Math. Biosci. 2002, 180, 187–205. [Google Scholar] [CrossRef] [PubMed]
- Gomes, M.G.M.; Aguas, R.; Lopes, J.S.; Nunes, M.C.; Rebelo, C.; Rodrigues, P.; Struchiner, C.J. How host heterogeneity governs tuberculosis reinfection? Proc. R. Soc. B Biol. Sci. 2012, 279, 2473–2478. [Google Scholar] [CrossRef]
- Rodrigues, P.; Gomes, M.G.M.; Rebelo, C. Drug resistance in tuberculosis—A reinfection model. Theor. Popul. Biol. 2007, 71, 196–212. [Google Scholar] [CrossRef]
- Bowong, S.; Tewa, J.J. Global analysis of a dynamical model for transmission of tuberculosis with a general contact rate. Commun. Nonlinear. Sci. Numer. Simul. Commun Nonlinear Sci. 2010, 15, 3621–3631. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).