Mathematical Computations of Long-Term Settlement and Bearing Capacity of Soil Bases and Foundations near Vertical Excavation Pits
Abstract
1. Introduction
2. Materials and Methods
3. Results
4. Discussion
5. Conclusions
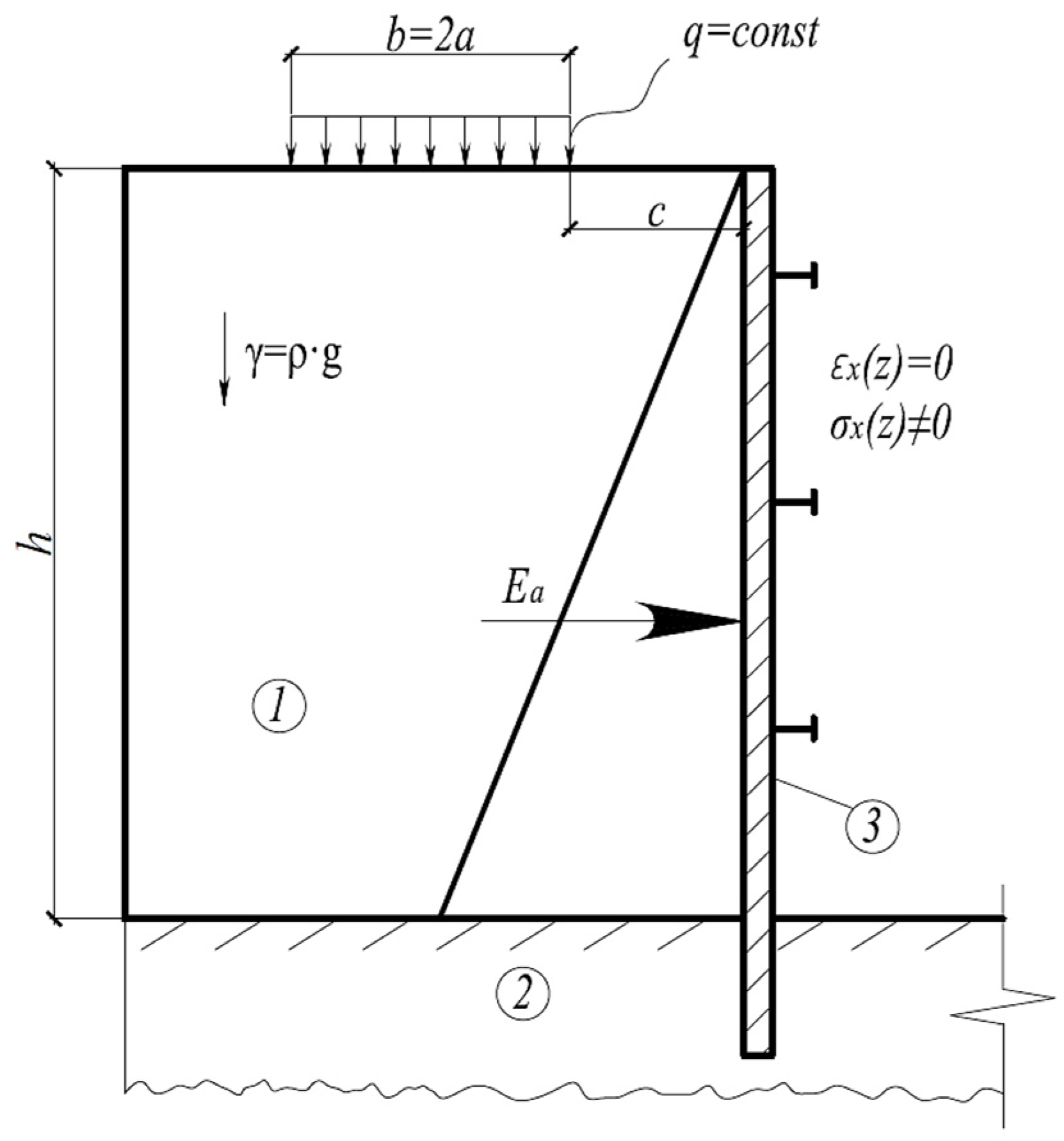
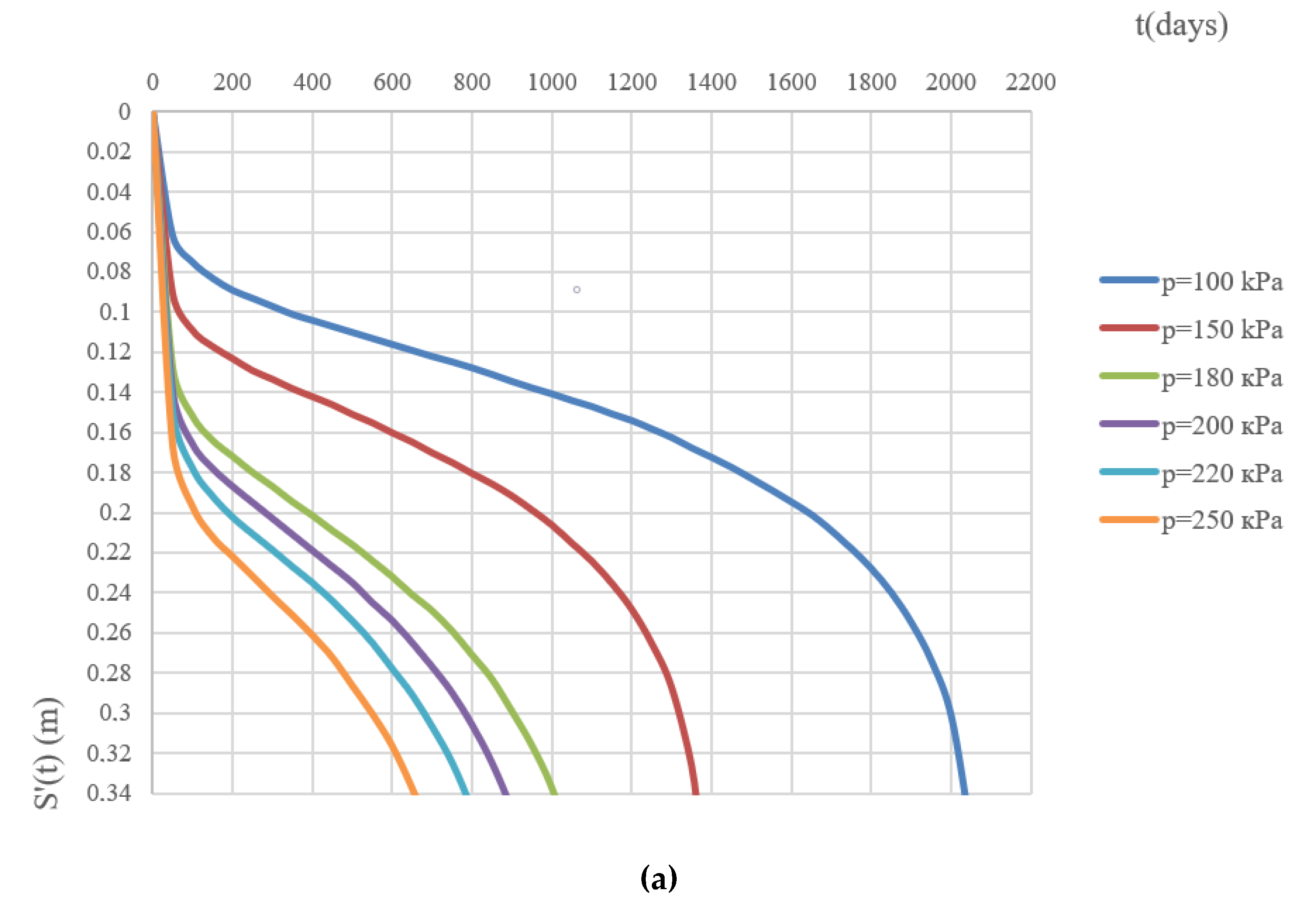
- The selected geomechanical soil base model (its geometric parameters and initial and boundary conditions), as well as the computational model of the soil ground (linear, nonlinear and rheological) and the type of physical equations used (Hooke’s system and Hencky’s system), have a significant impact on the type of settlement–load curve (S′(t)–t) and on the long-term stability of a soil basis.
- The authors’ analytical method for the quantitative evaluation of the settlement of soil bases and foundations in time was developed for adjacent built-up areas outside the enclosure of an excavation pit.
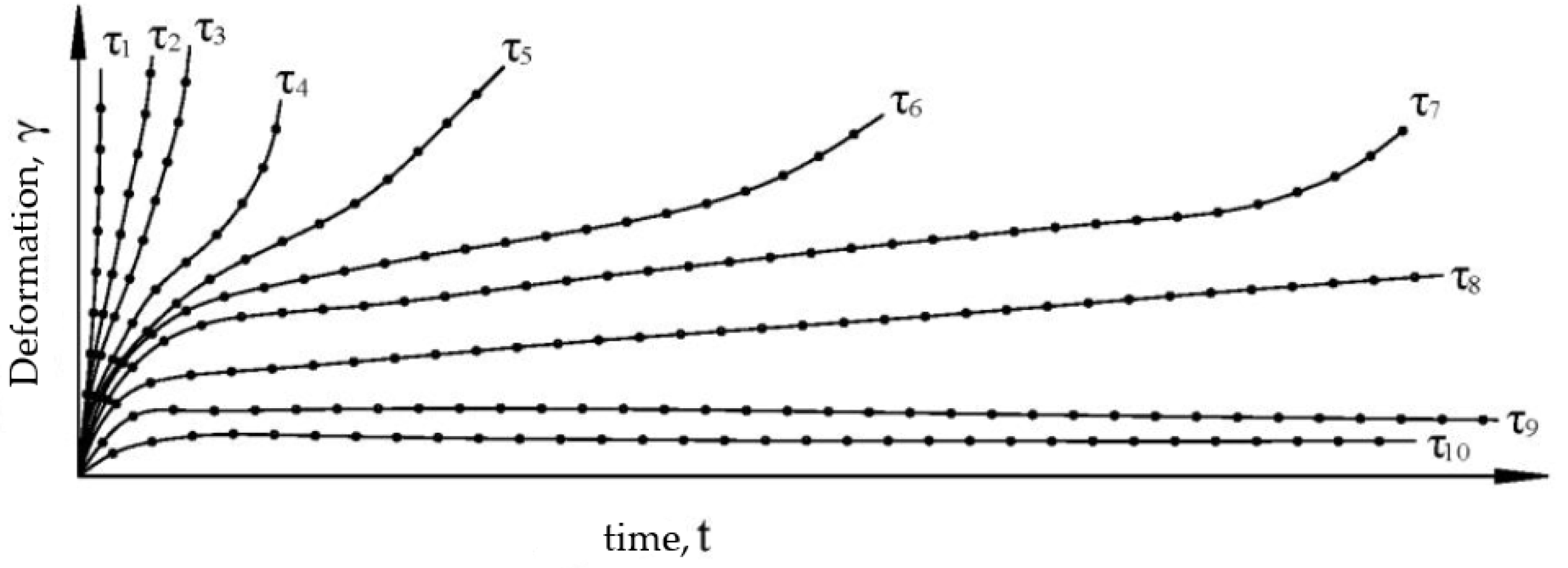
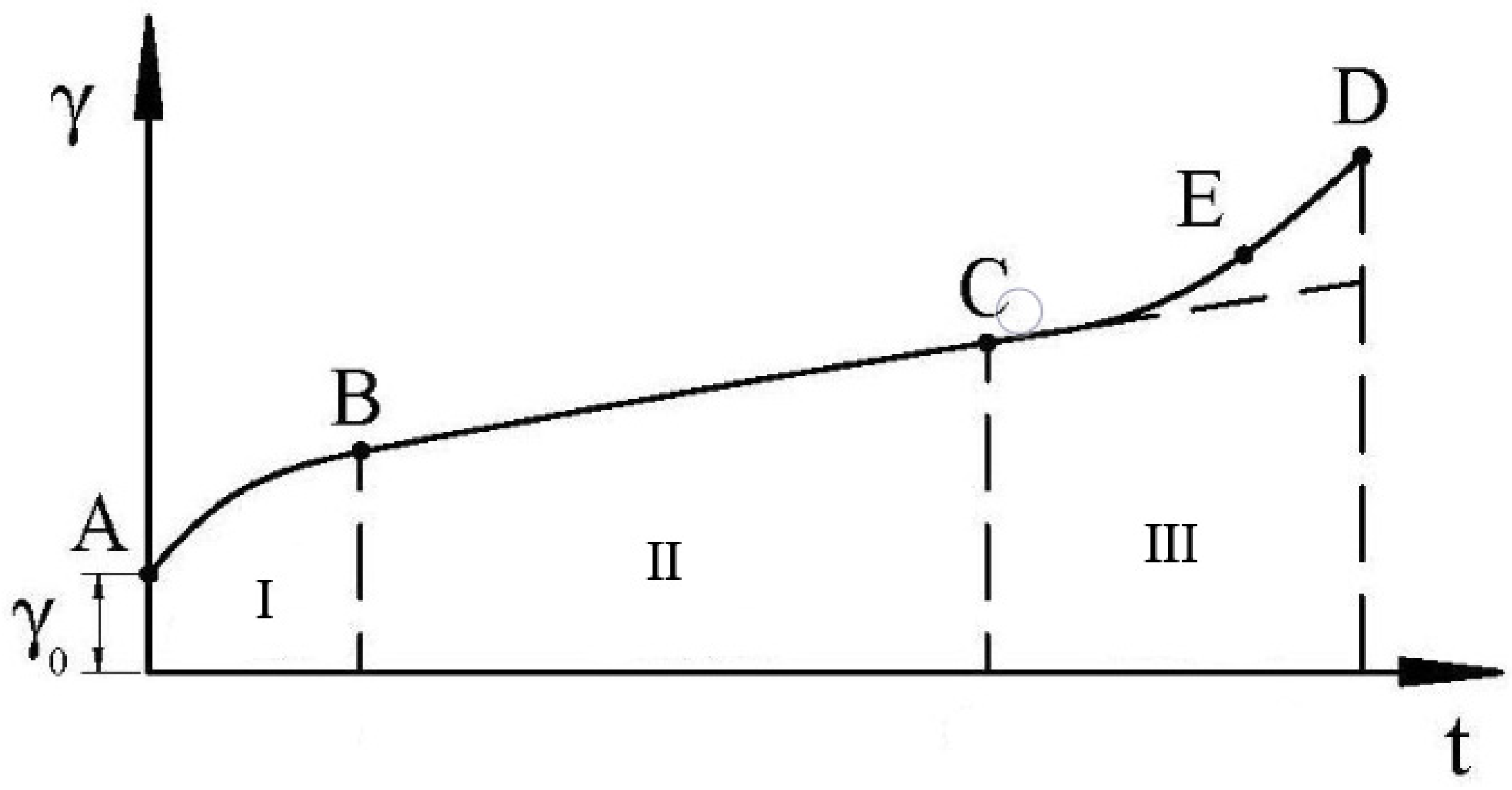
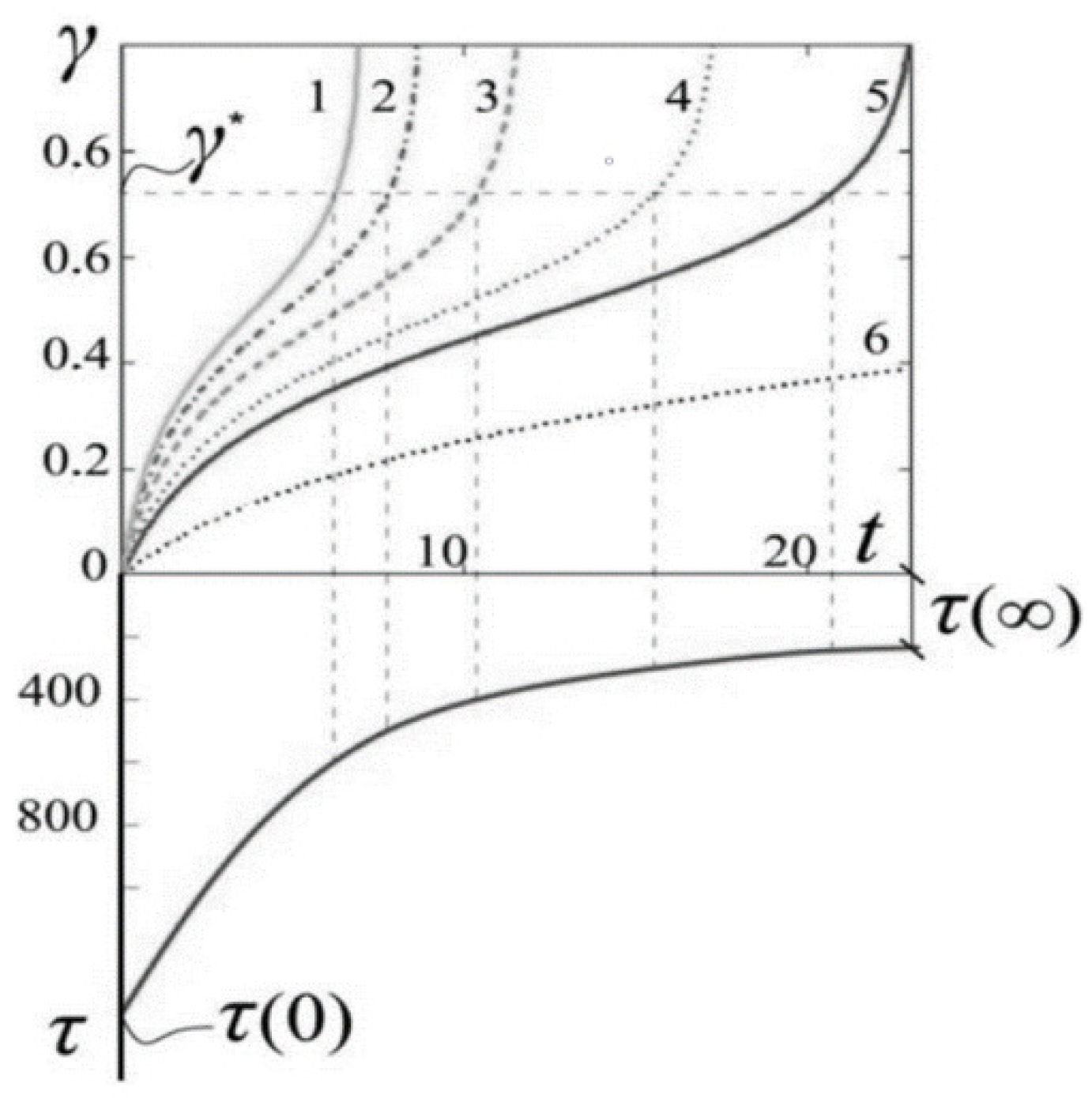
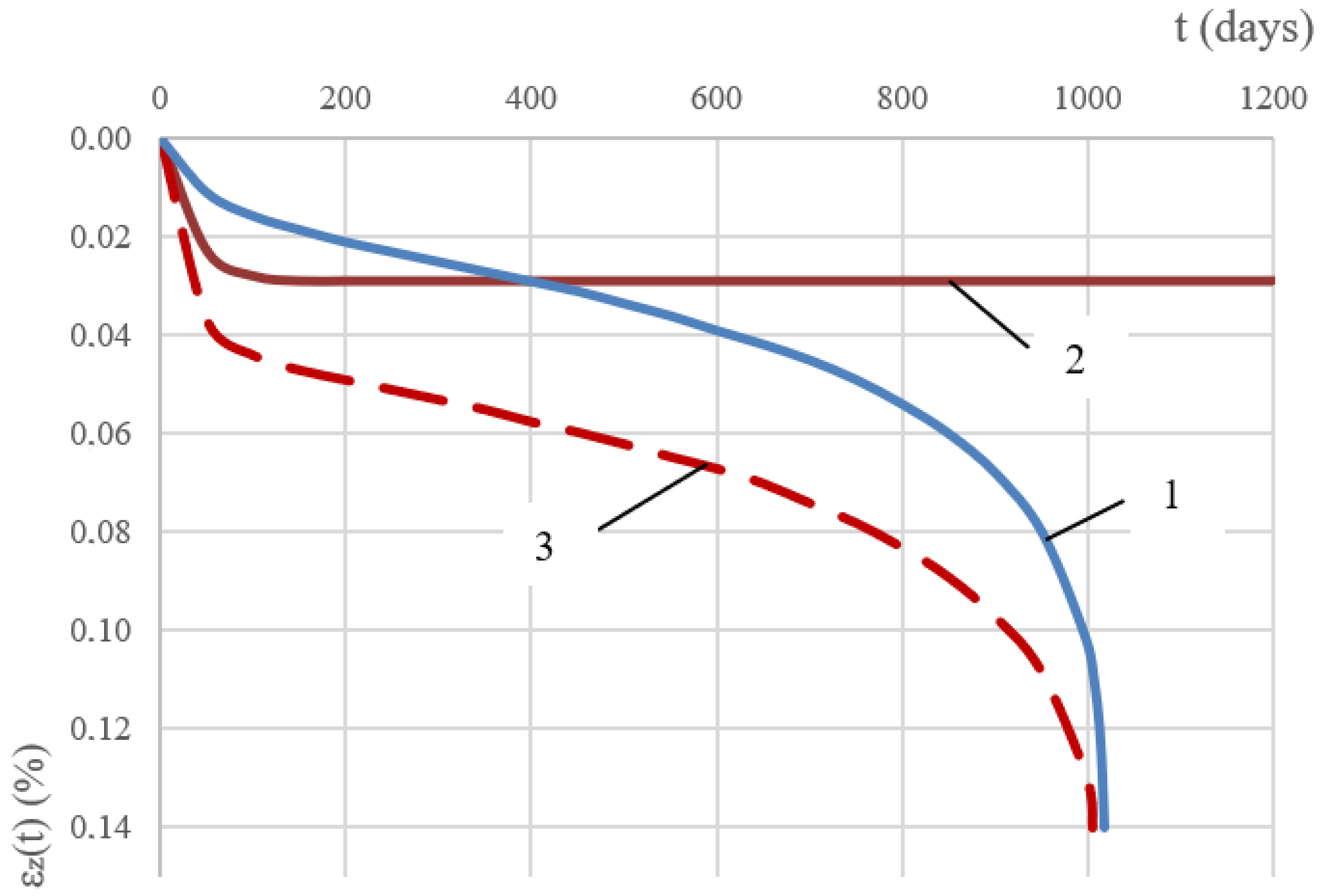
- The computational model used in this research along with the rheological model of A.Z. Ter-Martirosyan for shear and the volumetric soil deformation model of Kelvin–Voigt used as part of the physical equations derived by H. Hencky, allowed determining soil deformations ε(σ–ε, τ–γ), represented as the sum of volumetric and shear components of the deformations (εz = εz,ν + εz,γ). In this case, the deformation–time curve (εz(t)—t) had a double curvature.
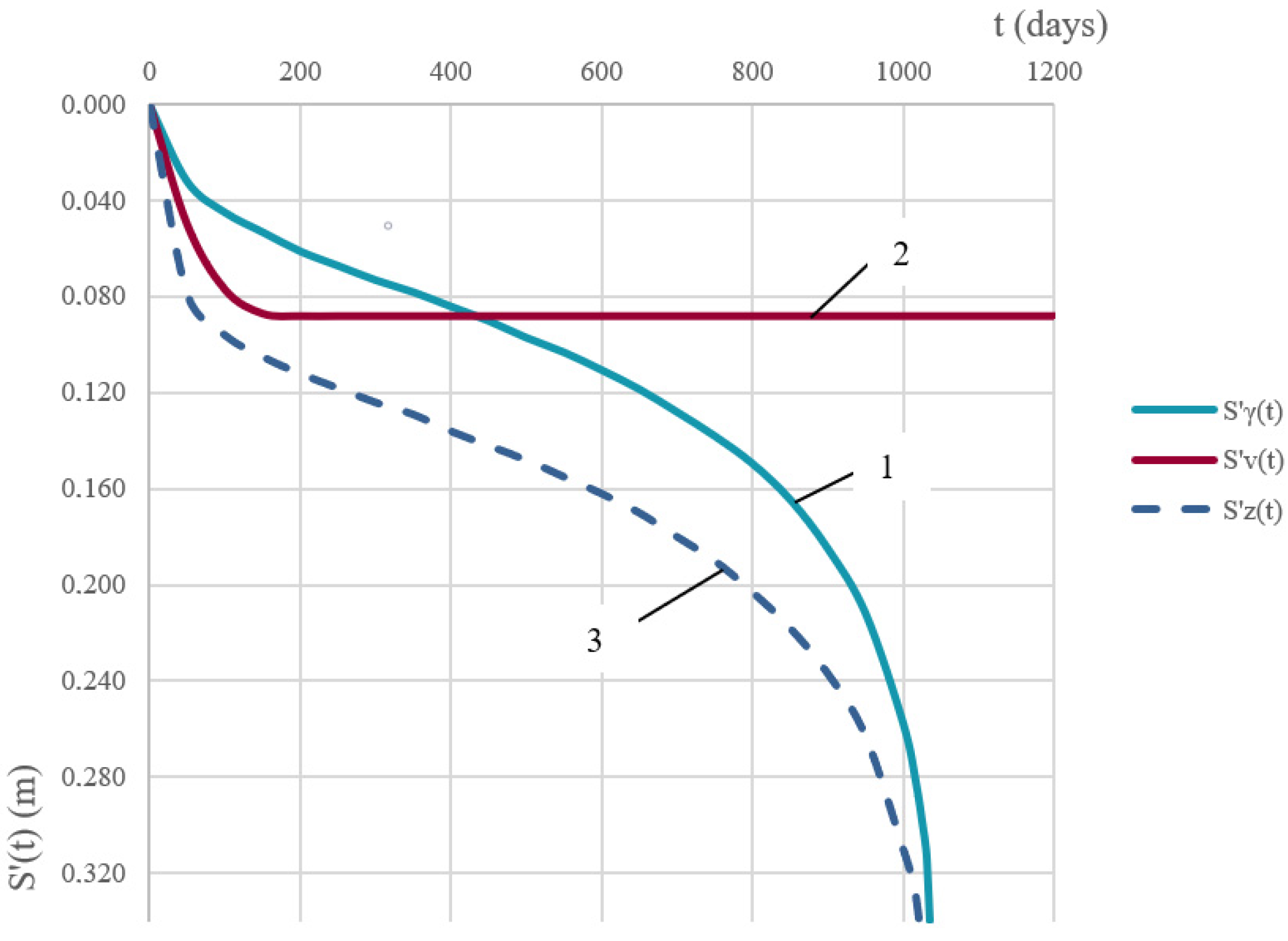
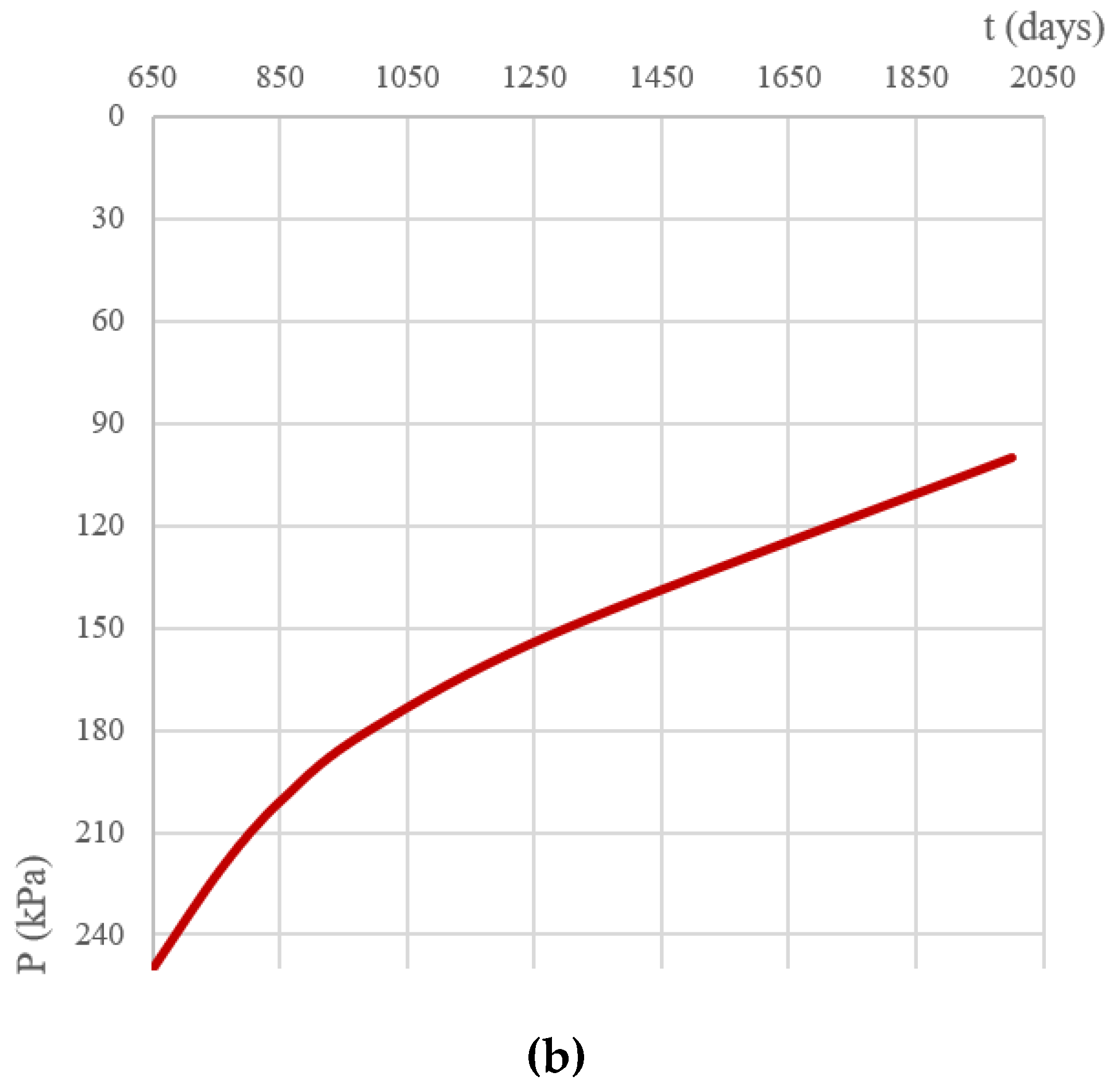
- The joint application of the models, developed by A.Z. Ter-Martirosyan and Kelvin–Voigt allows obtaining a graph describing the long-term bearing capacity of a soil base for various loads p = q = const.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ter-Martirosyan, A.Z. Interaction of Foundations of Buildings and Structures with a Water-Saturated Base When Taking into Account the Nonlinear and Rheological Properties of Soils. Ph.D. Thesis, National Research University Moscow State University of Civil Engineering, Moscow, Russia, 2016. Specialty 05.23.02—Soilbases and Foundations, Underground Structures (Vzaimodejstvie Fundamentov Zdanij i Sooruzhenij s Vodonasyshchennym Osnovaniem pri Uchete Nelinejnyh i Reologicheskih Svojstv Gruntov. Dissertaciya na Soiskanie Uchenoj Stepeni Doktora Tekhnicheskih Nauk. Special’nost’ 05.23.02—Osnovaniya i Fundamenty, Podzemnye Sooruzheniya) (In Russian). [Google Scholar]
- Vyalov, S.S. Rheological Basis of Soil Mechanics (Reologicheskie Osnovy Mekhaniki Gruntov); Vyshaya Shkola: Moscow, Russia, 1978. (In Russian) [Google Scholar]
- Hencky, H. Zur Theorie plastischer Deformationen und der hierdurch im Material hervorgerufenen Nachspannungen. Zammzeitschrift Angew. Math. Mech. 1924, 4, 323–334. [Google Scholar] [CrossRef]
- Gorbunov-Posadov, M.I.; Shekhter, O.Y.; Kofman, V.A. The Pressure of the Soil on the Deep Foundation and Free Deformation of the Pit (Davlenie Grunta na Zhestkij Zaglublennyj Fundament i Svobodnye Deformacii Kotlovina). In Works of the Research Institute of Foundation Bases and Foundations (Trudy NII Osnovanij i Fundamentov); Gostrojizdat: Moscow, Russia, 1954; Volume 24. (In Russian) [Google Scholar]
- Florin, V.A. Fundamentals of Soil Mechanics; Gosstroyizdat: Moscow, Russia, 1959; Volume I. (In Russian) [Google Scholar]
- Ter-Martirosyan, Z.G.; Ter-Martirosyan, A.Z. Soil Mechanics in High-Rise Building with a Developed Underground Part (Mekhanika Gruntov v Vysotnom Stroitel’stve s Razvitoj Podzemnoj Chast’yu); ASV Publisher: Moscow, Russia, 2020. (In Russian) [Google Scholar]
- Ter-Martirosyan, Z.G.; Pak, C.S. Consolidation and creep of a soil layer of limited width under the influence of local load (Konsolidaciya i polzuchest’ sloya grunta ogranichennoj shiriny pod dejstviem mestnoj nagruzki)). Soil Bases Found. Soil Mech. (Osn. Fundam. I Mekhanika Gruntov) 1998, 2, 2–6. (In Russian) [Google Scholar]
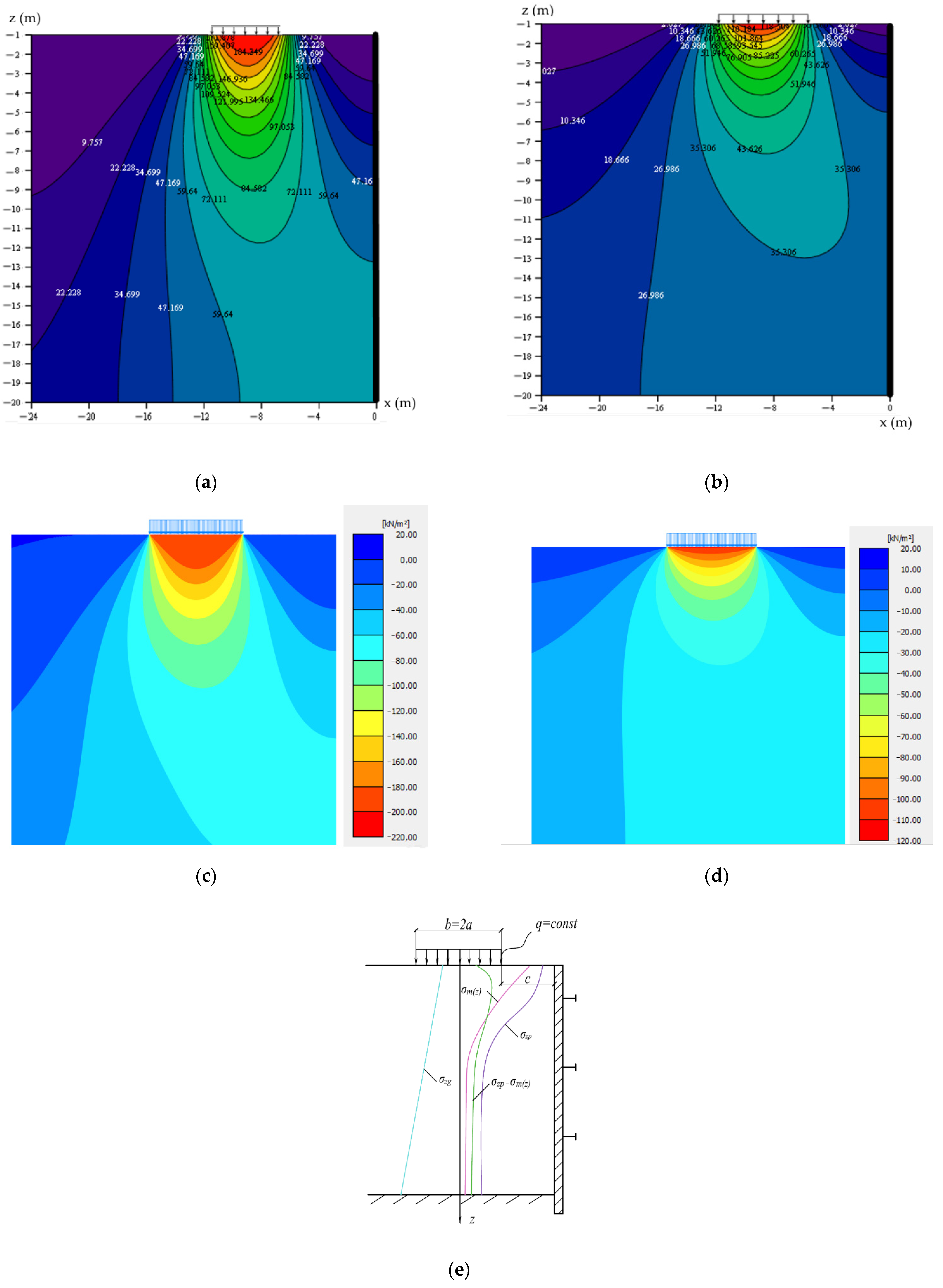
- Ter-Martirosyan, Z.G.; Luzin, I.N.; Vanina, Y.V.; Ter-Martirosyan, A.Z. Stress-strain state of the soil mass under the uniformly distributed load action adjacent to a vertical excavation. In IOP Conference Series Materials Science and Engineering, Proceedings of the International Scientific Conference “Construction and Architecture: Theory and Practice of Innovative Development” (CATPID 2020), Nalchik, Russia, 16–17 December 2020; IOP Publishing Ltd.: Bristol, UK, 2021; Volume 1083, p. 012015. [Google Scholar] [CrossRef]
- Korolev, K.V.; Karaulov, A.M. Analytical solution of the problem of the maximum pressure of the stamp on a weighty bulk base under heavy loads (Analiticheskoe reshenie zadachi o predel’nom davlenii na vesomoe sypuchee osnovanie pri bol’shih nagruzkah). In Topical Issues of Geotechnics in Solving Complex Problems of New Construction and Reconstruction: Sat. Tr. Sci.-Tech. Conf.; SPbGASU (Aktual’nye Voprosy Geotekhniki Pri Reshenii Slozhnyh Zadach Novogo Stroitel’stva i Rekonstrukcii: Sb. Tr. Nauch.-tekhn. Konf.; SPbGASU); Saint-Petersburg State University of Architecture and Civil Engineering: Saint Petersburg, Russia, 2010. (In Russian) [Google Scholar]
- Kudriavtcev, S.A.; Paramonov, V.N.; Kazharski, A.V.; Goncharova, E.D. Calculated evaluation of shoring of deep excavation in the restrained urban conditions. In Proceedings of the 15th Asian Regional Conference on Soil Mechanics and Geotechnical Engineering, Fukuoka, Japan, 9–13 November 2015; ARC New Innovations and Sustainability: Khabarovsk, Russia, 2015; Volume 15, pp. 2722–2725. [Google Scholar] [CrossRef]
- Mirsayapov, I.T.; Koroleva, I.V. The strength and deformability of clay soils under the regime spatial stress state in view of cracking. Grounds Found. Soil Mech. 2016, 1, 16–23. [Google Scholar]
- Brown, E.T.; Hoek, E. Trends in relationships between measured in situ stresses and depth. Int. J. Rock Mech. Min. Sci. 1978, 15, 211–215. [Google Scholar] [CrossRef]
- Khademian, Z.; Shahriar, K.; Nik, M.G. Developing an algorithm to estimate in situ stresses using a hybrid numerical method based on local stress measurement. Int. J. Rock Mech. Min. Sci. 2012, 55, 80–85. [Google Scholar] [CrossRef]
- Kuntsche, K. Deep excavations and slopes in urban areas. In Proceedings of the 14th European Conference on Soil Mechanics and Geotechnical Engineering, Spain, Madrid, 23–28 September 2007; Volume 1. [Google Scholar]
- Li, G.; Mizuta, Y.; Ishida, T.; Li, H.; Nakama, S.; Sato, T. Stress field determination from local stress measurements by numerical modeling. Int. J. Rock Mech. Min. Sci. 2009, 30, 111–123. [Google Scholar]
- Pei, Q.; Ding, X.; Liu, Y.; Lu, B.; Huang, S.; Fu, J. Optimized back analysis method for stress determination based on identification of local stress measurements and its application. Bull. Eng. Geol. Environ. 2019, 78, 375–396. [Google Scholar] [CrossRef]
- Terzaghi, K. The Shearing resistance of saturated soils and the angle between the plane of shear. In Proceedings of the 1st International Conference on Soil Mechanics and Foundation Engineering, Harvard, UK, 22–26 June 1936; Volume 1, pp. 54–56. [Google Scholar]
- Maslov, N.N. Long-Term Stability and Displacement Deformation of Retaining Walls (Dlitel’naya Ustojchivost’ i Deformaciya Smeshcheniya Podpornyh Stenok); Energiya: Moscow, Russia, 1968. (In Russian) [Google Scholar]
- Gol’dshtejn, M.N.; Turovskaya, A.Y.; Lapidus, L.S. Landslide Investigation (Issledovanie Opolznevogo Techeniya). In Geotechnical Issues (Voprosy Geotekhniki); Taylor: Moscow, Russia, 1932; Volume 5, pp. 3–23. (In Russian) [Google Scholar]
- Zareckij, Y.K. Long-Term Strength and Visco-Plasticity of Clay Soils (Dlitel’naya Prochnost’ i Vyazko-Plastichnost’ Glinistyh Gruntov). In Soil Bases, Foundations and Soil Mechanics (Osnovaniya, Fundamenty i Mekhanika Gruntov); Wiley: Moscow, Russia, 1995; Volume 2, pp. 2–6. (In Russian) [Google Scholar]
- Meschyan, S.R.; Badalyan, R.G. About One Important Regularity of Creep of Clay Soils during Shear (Ob Odnoj Vazhnoj Zakonomernosti Polzuchesti Glinistyh Gruntov Pri Sdvige). In Soil Bases, Foundations and Soil Mechanics (Osnovaniya, Fundamenty i Mekhanika Gruntov); Wiley: Moscow, Russia, 1976; Volume 1, pp. 21–23. (In Russian) [Google Scholar]
- Meschyan, S.R. Initial and Long-Term Strength of Clay Soils (Nachal’naya i Dlitel’naya Prochnost’ Glinistyh Gruntov); Nedra: Moscow, Russia, 1978. (In Russian) [Google Scholar]
- Ter-Stepanyan, G.I. Theory of Progressive Destruction in Ground and Rock Formations (Teoriya Progressiruyushchego Razrusheniya v Gruntovyh i Skal’nyh Porodah); Izdatelstvo AN ArmSSR: Yerevan, Armenia, 1975. (In Russian) [Google Scholar]
- Ter-Martirosyan, Z.G.; Cytovich, N.A. Secondary Consolidation of Clays (O Vtorichnoj Konsolidacii Glin). In Soil Bases, Foundations and Soil Mechanics (Osnovaniya, Fundamenty i Mekhanika Gruntov); Wiley: Moscow, Russia, 1965; Volume 5, pp. 12–15. (In Russian) [Google Scholar]
- Ter-Martirosyan, Z.G. Rheological Parameters of Soils and Calculation of the Foundations of Structures (Reologicheskie Parametry Gruntov i Raschet Osnovanij Sooruzhenij); Strojizdat: Moscow, Russia, 1990. (In Russian) [Google Scholar]
- Ter-Martirosyan, Z.G.; Ter-Martirosyan, A.Z.; Vanina, Y.V. Mathematical Analysis for the Evaluation of Settlement and Load-Bearing Capacity of a Soil Base Adjacent to an Excavation Pit. Axioms 2022, 11, 353. [Google Scholar] [CrossRef]
- Ter-Martirosyan, A.; Manukyan, A.; Ermoshina, L. Experience of determining the parameters of the elastoviscoplastic soil model. E3S Web Conf. 2021, 263, 02051. [Google Scholar] [CrossRef]
- Shukle, L. Rheological Problems of Soil Mechanics (Reologicheskie Problemy Mekhaniki Gruntov); Strojizdat: Moscow, Russia, 1976. (In Russian) [Google Scholar]
- Lu, T.; Liu, S.-Y.; Cai, G.-J.; Wu, K.; Xia, W.-J. Study on the disturbance and recompression settlement of soft soil induced by excavation pit excavation. Rock Soil Mech. 2021, 42, 565. [Google Scholar] [CrossRef]
- Idriss, I.M.; Dobry, R.; Singh, R.D. Non-linear behavior of soft clays during cyclic loading. J. Geotech. Eng. Div. 1978, 104, 1427–1447. [Google Scholar] [CrossRef]
- Wang, G.; Sitar, N. Numerical Analysis Of Piles In Elasto-Plastic Soils Under Axial Loading. In Proceedings of the 17th ASCE Engineering Mechanics Conference, Newark, DE, USA, 13–16 June 2004; pp. 1–7. [Google Scholar]
- Geuse, E.C.; Tan Tjong-Kie, W.A. The mechanical behaviors of clays. In Proceedings of the International Congress on Rheology, London, UK, 26–30 July 1954; pp. 247–259. [Google Scholar]
- Henkel, D.J. Investigation of two long-term failures in London clay slopes at Wood Green and Northolt. In Proceedings of the Fourth International Conference on Soil Mechanics and Foundation Engineering, London, UK, 12–24 August 1957; Volume 2, pp. 315–320. [Google Scholar]
- Higo, Y.A.; Oka, F.; Kodakat, T.; Kimoto, S. Three-Dimensional Elasto-Viscoplastic Strain Localization Analysis of Water-Satureted Clay. In Geo-Research Institute; GRI: Osaka, Japan, 2006; Volume 86, pp. 3205–3240. [Google Scholar]
- Rzhanicyn, A.R. Theory of Creep (Teoriya Polzuchesti); Strojizdat: Moscow, Russia, 1968. (In Russian) [Google Scholar]
- Arutyunyan, N.H.; Kolmakovskij, V.B. Theory of Creep of Inhomogeneous Bodies (Teoriya Polzuchesti Neodnorodnyh tel); Nauka: Moscow, Russia, 1983. (In Russian) [Google Scholar]
- Rabotnov, Y.N. Creep of Structural Elements (Polzuchest’ Elementov Konstrukcij); Nauka: Moscow, Russia, 1966. (In Russian) [Google Scholar]
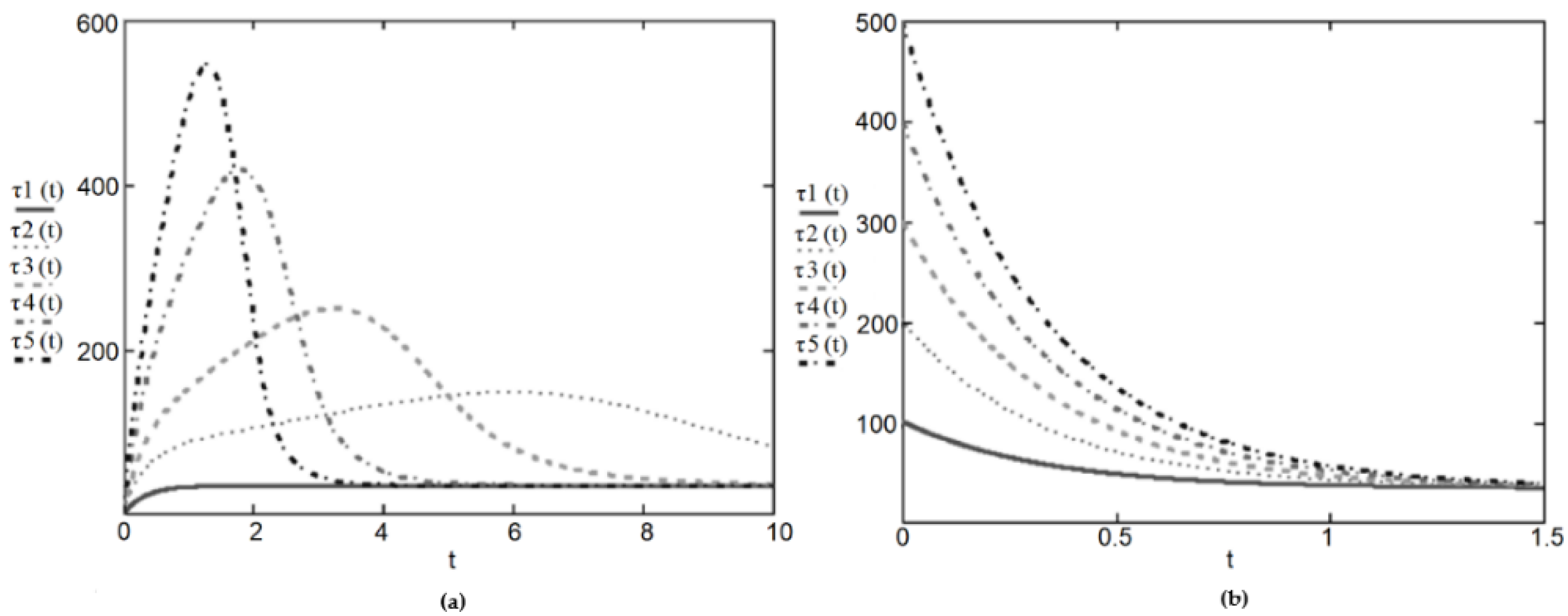
| ηγ, kPa Day | K, kPa | K/ηv, 1/Day | a | b | α | β |
|---|---|---|---|---|---|---|
| 1.157 × 105 | 3500 | 0.0043 | 1.2 | 60 | 171 | 40 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ter-Martirosyan, Z.G.; Ter-Martirosyan, A.Z.; Vanina, Y.V. Mathematical Computations of Long-Term Settlement and Bearing Capacity of Soil Bases and Foundations near Vertical Excavation Pits. Axioms 2022, 11, 679. https://doi.org/10.3390/axioms11120679
Ter-Martirosyan ZG, Ter-Martirosyan AZ, Vanina YV. Mathematical Computations of Long-Term Settlement and Bearing Capacity of Soil Bases and Foundations near Vertical Excavation Pits. Axioms. 2022; 11(12):679. https://doi.org/10.3390/axioms11120679
Chicago/Turabian StyleTer-Martirosyan, Zaven G., Armen Z. Ter-Martirosyan, and Yulia V. Vanina. 2022. "Mathematical Computations of Long-Term Settlement and Bearing Capacity of Soil Bases and Foundations near Vertical Excavation Pits" Axioms 11, no. 12: 679. https://doi.org/10.3390/axioms11120679
APA StyleTer-Martirosyan, Z. G., Ter-Martirosyan, A. Z., & Vanina, Y. V. (2022). Mathematical Computations of Long-Term Settlement and Bearing Capacity of Soil Bases and Foundations near Vertical Excavation Pits. Axioms, 11(12), 679. https://doi.org/10.3390/axioms11120679









