Text Data Analysis Using Generalized Linear Mixed Model and Bayesian Visualization
Abstract
1. Introduction
2. Research Background
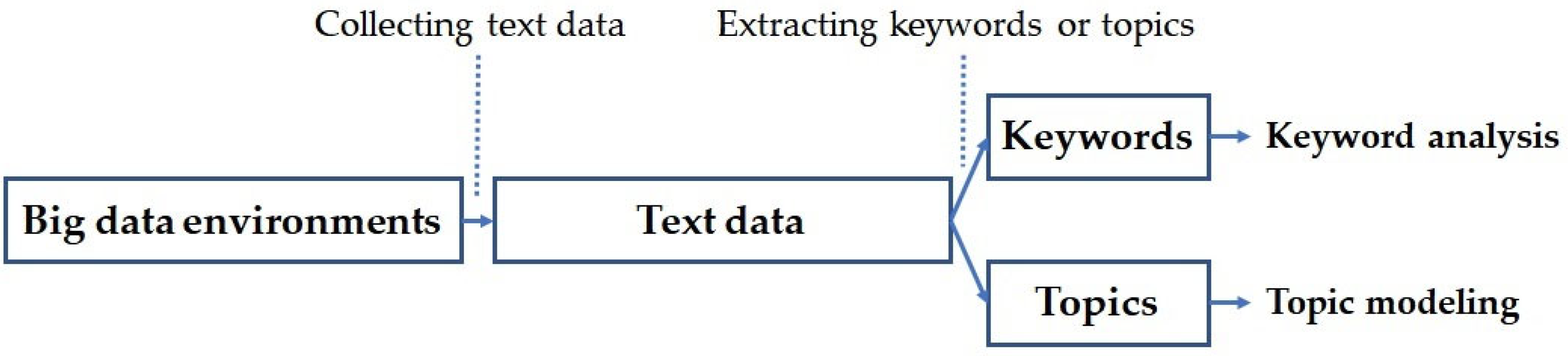
2.1. Text Data Analysis
2.2. Linear Model
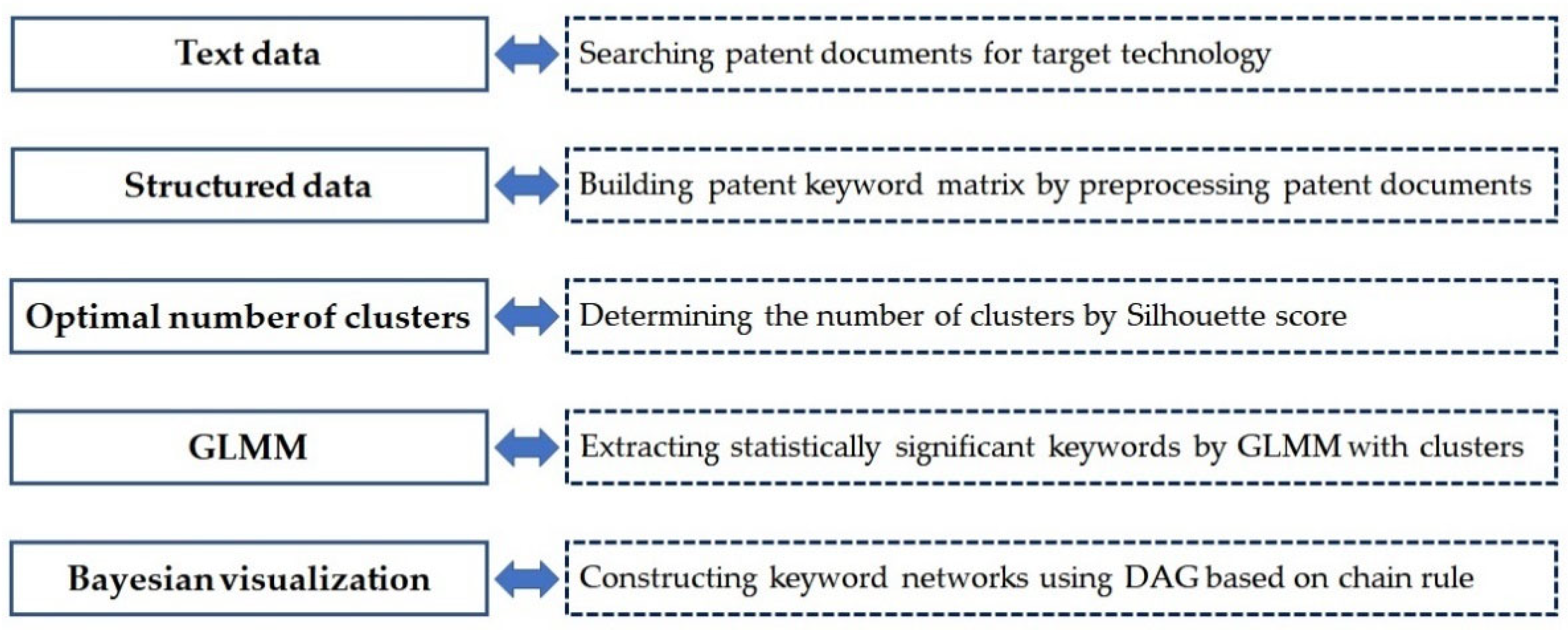
3. Proposed Methods
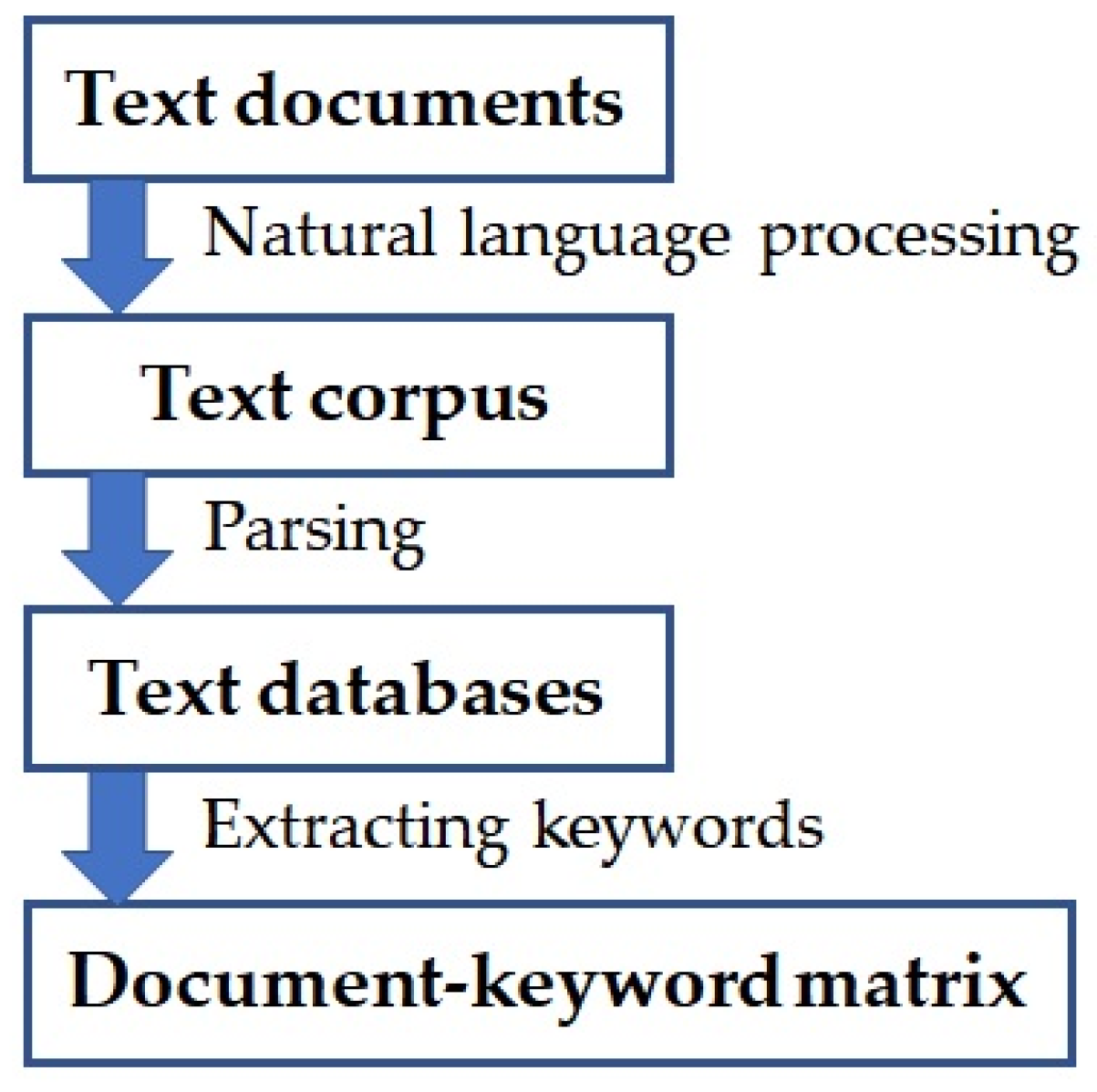
3.1. Preprocessing of Documents
3.2. Structure of Text Data
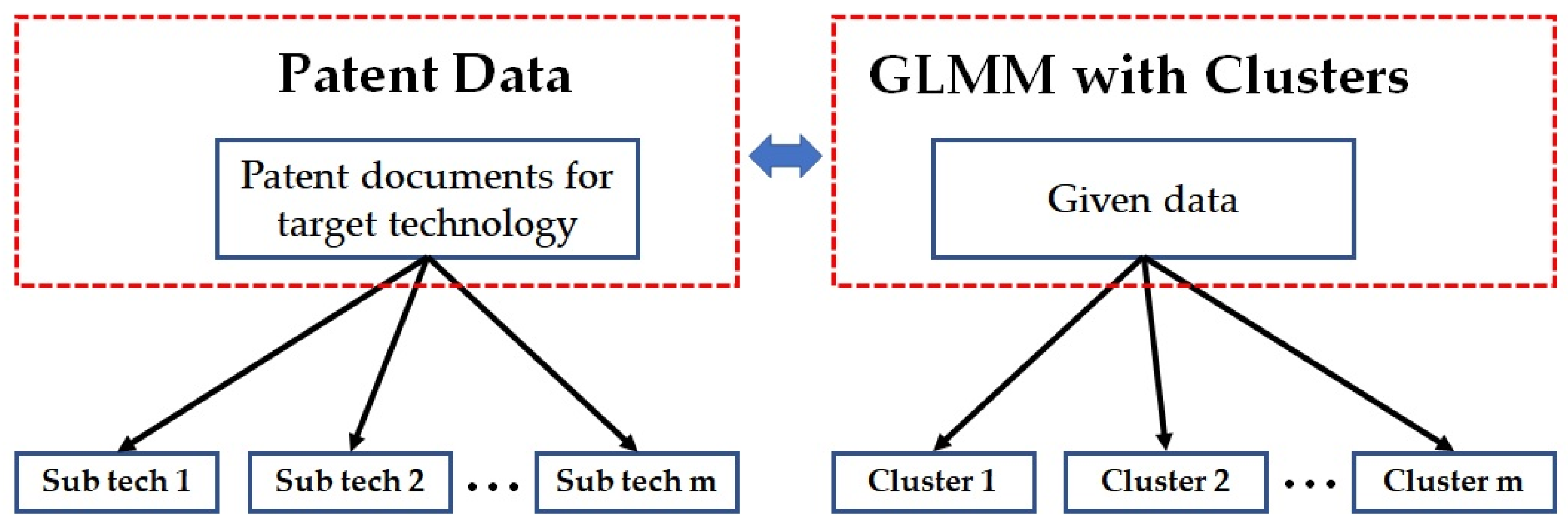
3.3. Clustering
3.4. Generalized Linear Mixed Model for Text Data Analysis
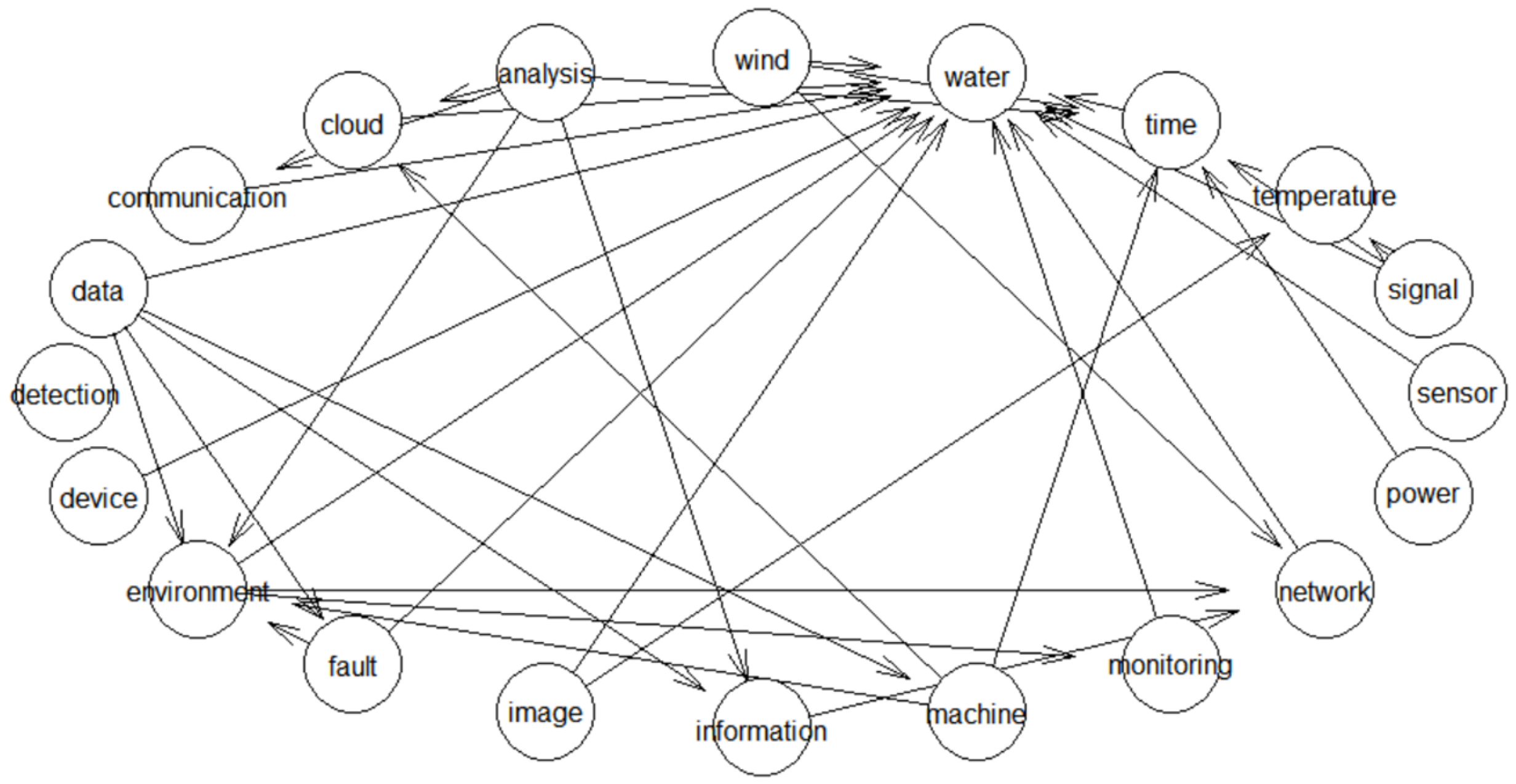
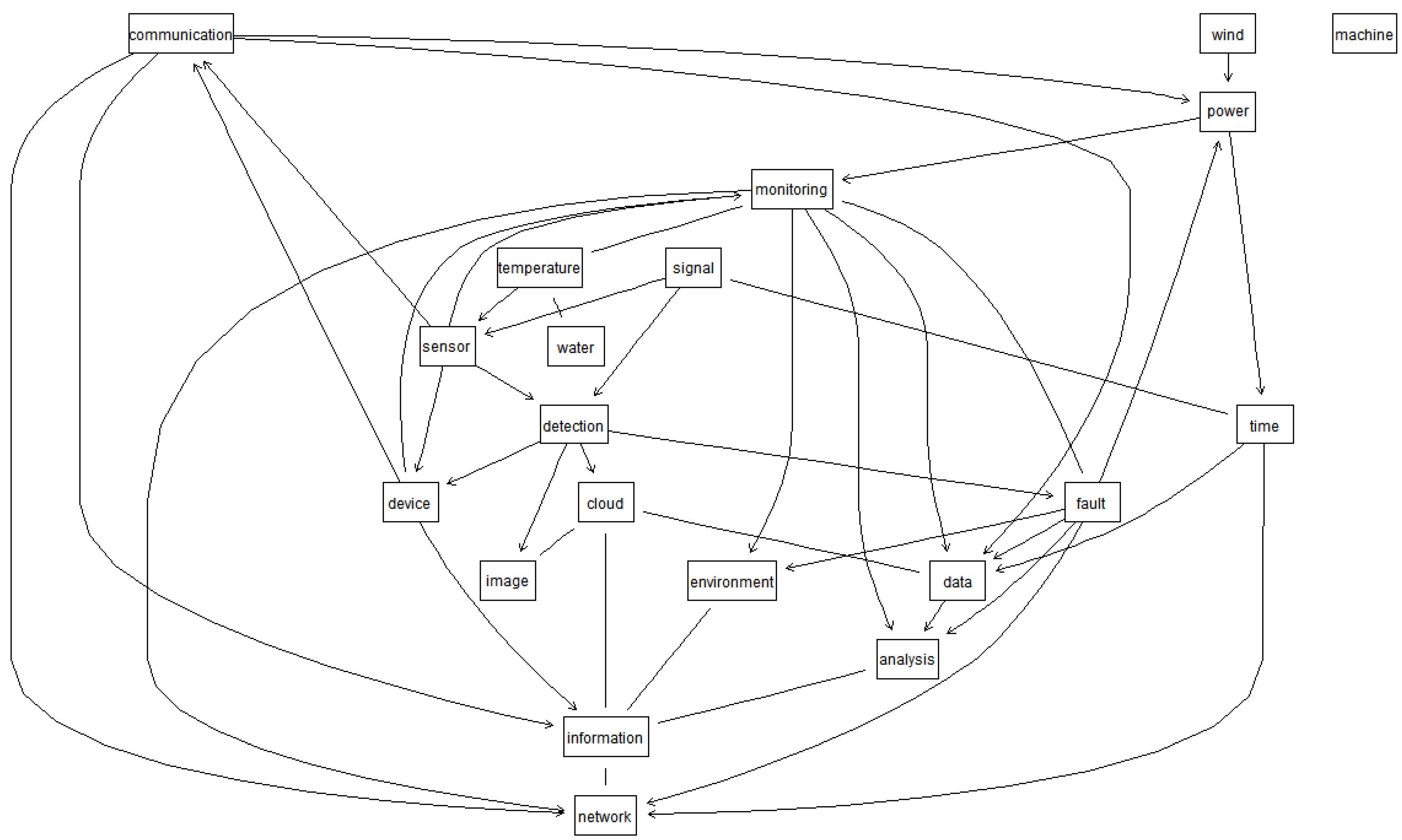
3.5. Bayesian Visualization
4. Experiments and Results
5. Discussion
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Choi, S.; Park, S.; Jun, S. Text Data Analysis using Bayesian Quantile Regression and Multidimensional Scaling. J. Korean Inst. Intell. Syst. 2021, 31, 177–183. [Google Scholar]
- Park, S.; Jun, S. Technological cognitive diagnosis model for patent keyword analysis. ICT Express 2020, 6, 57–61. [Google Scholar] [CrossRef]
- Park, S.; Jun, S. Patent Keyword Analysis of Disaster Artificial Intelligence Using Bayesian Network Modeling and Factor Analysis. Sustainability 2020, 12, 505. [Google Scholar] [CrossRef]
- Feinerer, I.; Hornik, K. Package ‘tm’ Version 0.7-8, Text Mining Package; CRAN of R Project, R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Jun, S.; Park, S.; Jang, D. Document Clustering Method Using Dimension Reduction and Support Vector Clustering to Overcome Sparseness. Expert Syst. Appl. 2014, 41, 3204–3212. [Google Scholar] [CrossRef]
- Uhm, D.; Jun, S. Zero-Inflated Patent Data Analysis Using Generating Synthetic Samples. Future Internet 2022, 14, 211. [Google Scholar] [CrossRef]
- Kim, J.M.; Jun, S. Zero-inflated Poisson and negative binomial regressions for technology analysis. Int. J. Softw. Eng. Its Appl. 2016, 10, 431–448. [Google Scholar] [CrossRef]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Kim, J.; Jun, S. Graphical Causal Inference and Copula Regression Model for Apple Keywords by Text Mining. Adv. Eng. Inform. 2015, 29, 918–929. [Google Scholar] [CrossRef]
- Park, S.; Jun, S. Patent Analysis Using Bayesian Data Analysis and Network Modeling. Appl. Sci. 2022, 12, 1423. [Google Scholar] [CrossRef]
- Stroup, W.W. Generalized Linear Mixed Models: Modern Concepts, Methods and Applications; CRC press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Berridge, D.M.; Crouchley, R. Multivariate Generalized Linear Mixed Models Using R; CRC press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Mizdrak, P. Clustering Profiles in Generalized Linear Mixed Models Settings Using Bayesian Nonparametric Statistics. Ph.D. Thesis, Carleton University, Ottawa, ON, Canada, 2018. [Google Scholar]
- Lee, J. A Study for Recent Development of Generalized Linear Mixed Model. Korean J. Appl. Stat. 2000, 13, 541–562. [Google Scholar]
- Broström, G.; Jin, J.; Holmberg, H. Package ‘glmmML’ Ver. 1.1.3, Generalized Linear Models with Clustering; CRAN of R Project, R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Di Corso, E.; Proto, S.; Vacchetti, B.; Bethaz, P.; Cerquitelli, T. Simplifying Text Mining Activities: Scalable and Self-Tuning Methodology for Topic Detection and Characterization. Appl. Sci. 2022, 12, 5125. [Google Scholar] [CrossRef]
- Allan, J.; Carbonell, J.G.; Doddington, G.; Yamron, J.; Yang, Y. Topic detection and tracking pilot study. In Proceedings of the DARPA Broadcast News Transcription and Understanding Workshop, Lansdowne, VA, USA, 8–11 February 1998; pp. 1–25. [Google Scholar]
- Nakov, P.; Popova, A.; Mateev, P. Weight functions impact on LSA performance. In Proceedings of the Euro Conference RANLP, online, 1–3 September 2021; pp. 1–7. [Google Scholar]
- Corso, E.D.; Proto, S.; Cerquitelli, T.; Chiusano, S. Towards automated visualisation of scientific literature. In Proceedings of the European Conference on Advances in Databases and Information Systems, Bled, Slovenia, 8–11 September 2019; pp. 28–36. [Google Scholar]
- Saxena, G.; Santurkar, S. An iterative MapReduce framework for sports-based tweet clustering. In Proceedings of the Sixth International Conference on Computer and Communication Technology, Allahabad, India, 25–27 September 2015; pp. 9–14. [Google Scholar]
- Bouaziz, A.; Pereira, C.C.; Pallez, C.D.; Precioso, F. Interactive generic learning method (IGLM): A new approach to interactive short text classification. In Proceedings of the 31st Annual ACM Symposium on Applied Computing, Pisa, Italy, 4–8 April 2016; pp. 847–852. [Google Scholar]
- Duchrow, T.; Shtatland, T.; Guettler, D.; Pivovarov, M.; Kramer, S.; Weissleder, R. Enhancing navigation in biomedical databases by community voting and database-driven text classification. BMC Bioinform. 2009, 10, 317. [Google Scholar] [CrossRef] [PubMed]
- Gross, O.; Doucet, A.; Toivonen, H. Language-independent multi-document text summarization with document-specific word associations. In Proceedings of the 31st Annual ACM Symposium on Applied Computing, Pisa, Italy, 4–8 April 2016; pp. 853–860. [Google Scholar]
- Hogg, R.V.; Tanis, E.A.; Zimmerman, D.L. Probability and Statistical Inference, 9th ed.; Pearson: Essex, UK, 2015. [Google Scholar]
- Bruce, P.; Bruce, A.; Gedeck, P. Practical Statistics for Data Scientists, 2nd ed.; O’Reilly Media: Sebastopol, CA, USA, 2020. [Google Scholar]
- Hogg, R.V.; Mckean, J.W.; Craig, A.T. Introduction to Mathematical Statistics, 8th ed.; Pearson: Essex, UK, 2020. [Google Scholar]
- Ross, S.M. Introduction to Probability and Statistics for Engineers and Scientists, 4th ed.; Elsevier: Seoul, Republic of Korea, 2012. [Google Scholar]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis, 3rd ed.; Chapman & Hall/CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Sun, Y.; Wang, Q. An adaptive group LASSO approach for domain selection in functional generalized linear models. J. Stat. Plan. Inference 2022, 219, 13–32. [Google Scholar] [CrossRef]
- Park, J.; Kang, S. Hierarchical Generalized Linear Models for Multiregional Clinical Trials. Stat. Biopharm. Res. 2022, 14, 358–367. [Google Scholar] [CrossRef]
- Adesina, O.; Agunbiade, D.; Oguntunde, P. Flexible Bayesian Dirichlet mixtures of generalized linear mixed models for count data. Sci. Afr. 2021, 13, e00963. [Google Scholar] [CrossRef]
- Hunt, D.; Nguyen, L.; Rodgers, M. Patent Searching Tools & Techniques; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Roper, A.T.; Cunningham, S.W.; Porter, A.L.; Mason, T.W.; Rossini, F.A.; Banks, J. Forecasting and Management of Technology; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- KIPRIS. Korea Intellectual Property Rights Information Service. Available online: www.kipris.or.kr (accessed on 1 July 2022).
- USPTO. The United States Patent and Trademark Office. Available online: http://www.uspto.gov (accessed on 1 July 2022).
- Batool, F.; Hennig, C. Clustering with the Average Silhouette Width. Comput. Stat. Data Anal. 2021, 158, 107190. [Google Scholar] [CrossRef]
- Lovmar, L.; Ahlford, A.; Jonsson, M.; Syvanen, A.C. Silhouette scores for assessment of SNP genotype clusters. BMC Genom. 2005, 6, 35. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Kamber, M.; Pei, J. Data Mining: Concepts and Techniques, 3rd ed.; Morgan Kaufmann: Waltham, MA, USA, 2012. [Google Scholar]
- Scutari, M.; Denis, J.B. Bayesian Networks with Examples in R, 2nd ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2021. [Google Scholar]
- Nagarajan, R.; Scutari, M.; Lebre, S. Bayesian Networks in R with Application and System Biology; Springer: London, UK, 2013. [Google Scholar]
| Patent Document | ||||
|---|---|---|---|---|
| Keyword | List |
|---|---|
| Total keywords | Abnormal, acoustic, air, alarm, analysis, artificial, audio, automatic, battery, big, camera, cloud, cluster, communication, computing, damage, data, database, deep, detection, device, digital, earth, earthquake, electric, energy, engine, engineering, environment, estimation, fault, feedback, fire, flow, fluid, forecast, fuzzy, gas, geological, grid, health, human, image, information, intelligence, interaction, interface, land, laser, learning, light, machine, magnetic, map, measurement, memory, mobile, monitoring, network, neural, normal, oil, optical, pattern, picture, power, pressure, probability, protocol, pulse, radar, radio, remote, risk, robot, rock, sampling, satellite, sea, security, sensor, signal, software, space, spatial, speed, stability, statistics, temperature, time, underground, vehicle, velocity, video, warning, water, weather, web, wind, wireless |
| Top 20 keywords | Data (117,091), analysis (39,875), information (28,972), time (27,115), signal (26,292), device (25,149), power (19,739), image (19,602), network (17,646), monitoring (16,454), fault (15,723), detection (13,475), sensor (11,862), temperature (11,208), environment (10,172), machine (9744), water (8807), wind (8311), cloud (8020), communication (7679) |
| Clustering | Number of Clusters | ||||||
|---|---|---|---|---|---|---|---|
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| Average Silhouette coefficient | 0.21 | 0.11 | 0.12 | 0.11 | 0.08 | 0.11 | 0.09 |
| Parameter and AIC | Significance Probability | |
|---|---|---|
| GLMM | GLM | |
| data | 0.0001 | 0.0036 |
| analysis | 0.0001 | 0.0086 |
| information | 0.0077 | 0.0034 |
| time | 0.6540 | 0.0862 |
| signal | 0.0001 | 0.0001 |
| device | 0.1250 | 0.0060 |
| power | 0.0448 | 0.0904 |
| image | 0.0009 | 0.0105 |
| network | 0.0001 | 0.1000 |
| monitoring | 0.0001 | 0.0001 |
| fault | 0.0001 | 0.0001 |
| detection | 0.0049 | 0.1004 |
| sensor | 0.0001 | 0.0001 |
| temperature | 0.0001 | 0.0001 |
| environment | 0.0194 | 0.4469 |
| machine | 0.1100 | 0.0135 |
| water | 0.9860 | 0.3872 |
| cloud | 0.6580 | 0.2273 |
| communication | 0.0582 | 0.0946 |
| AIC | 8603 | 85,487 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jun, S. Text Data Analysis Using Generalized Linear Mixed Model and Bayesian Visualization. Axioms 2022, 11, 674. https://doi.org/10.3390/axioms11120674
Jun S. Text Data Analysis Using Generalized Linear Mixed Model and Bayesian Visualization. Axioms. 2022; 11(12):674. https://doi.org/10.3390/axioms11120674
Chicago/Turabian StyleJun, Sunghae. 2022. "Text Data Analysis Using Generalized Linear Mixed Model and Bayesian Visualization" Axioms 11, no. 12: 674. https://doi.org/10.3390/axioms11120674
APA StyleJun, S. (2022). Text Data Analysis Using Generalized Linear Mixed Model and Bayesian Visualization. Axioms, 11(12), 674. https://doi.org/10.3390/axioms11120674






