Copula Dynamic Conditional Correlation and Functional Principal Component Analysis of COVID-19 Mortality in the United States
Abstract
1. Introduction
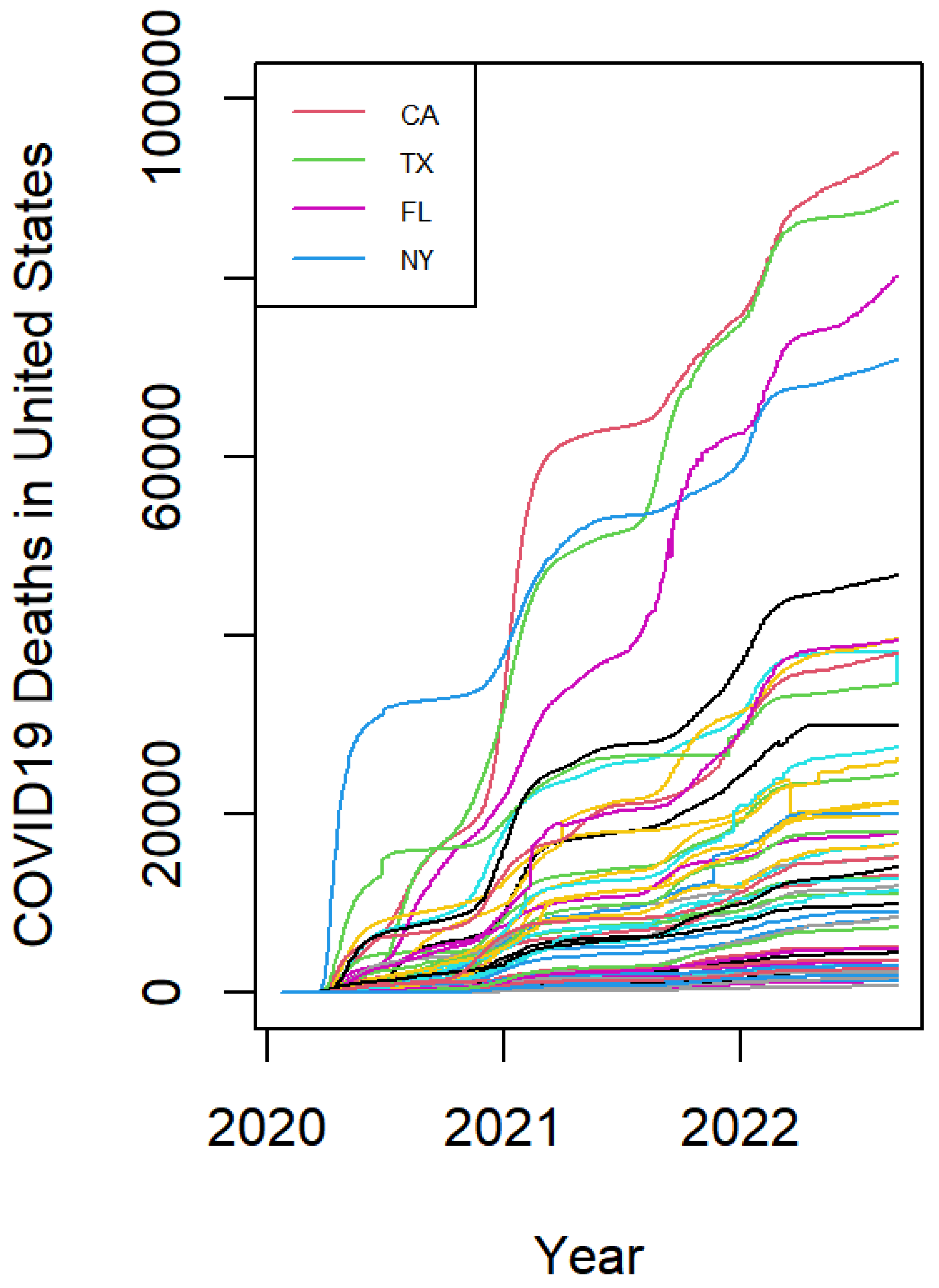
2. Data Description
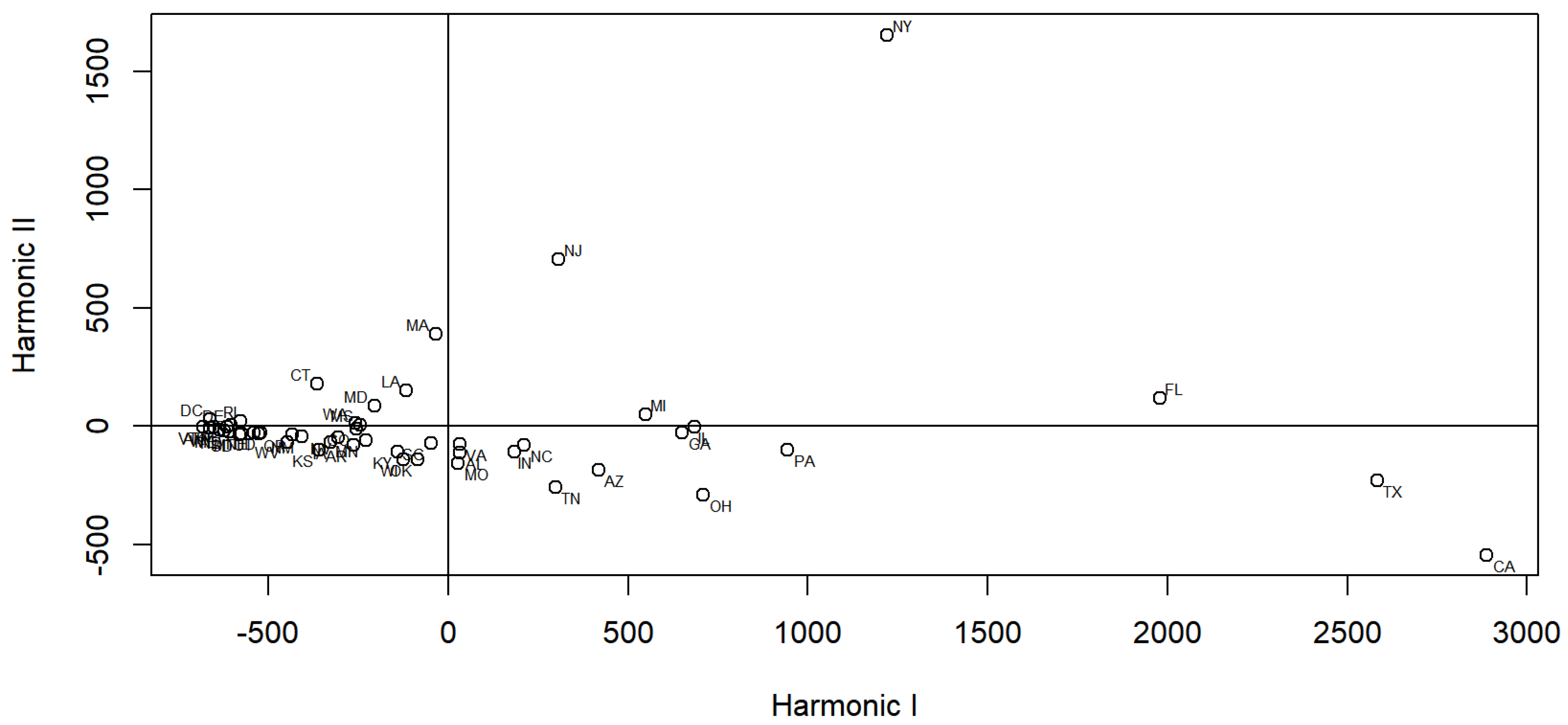
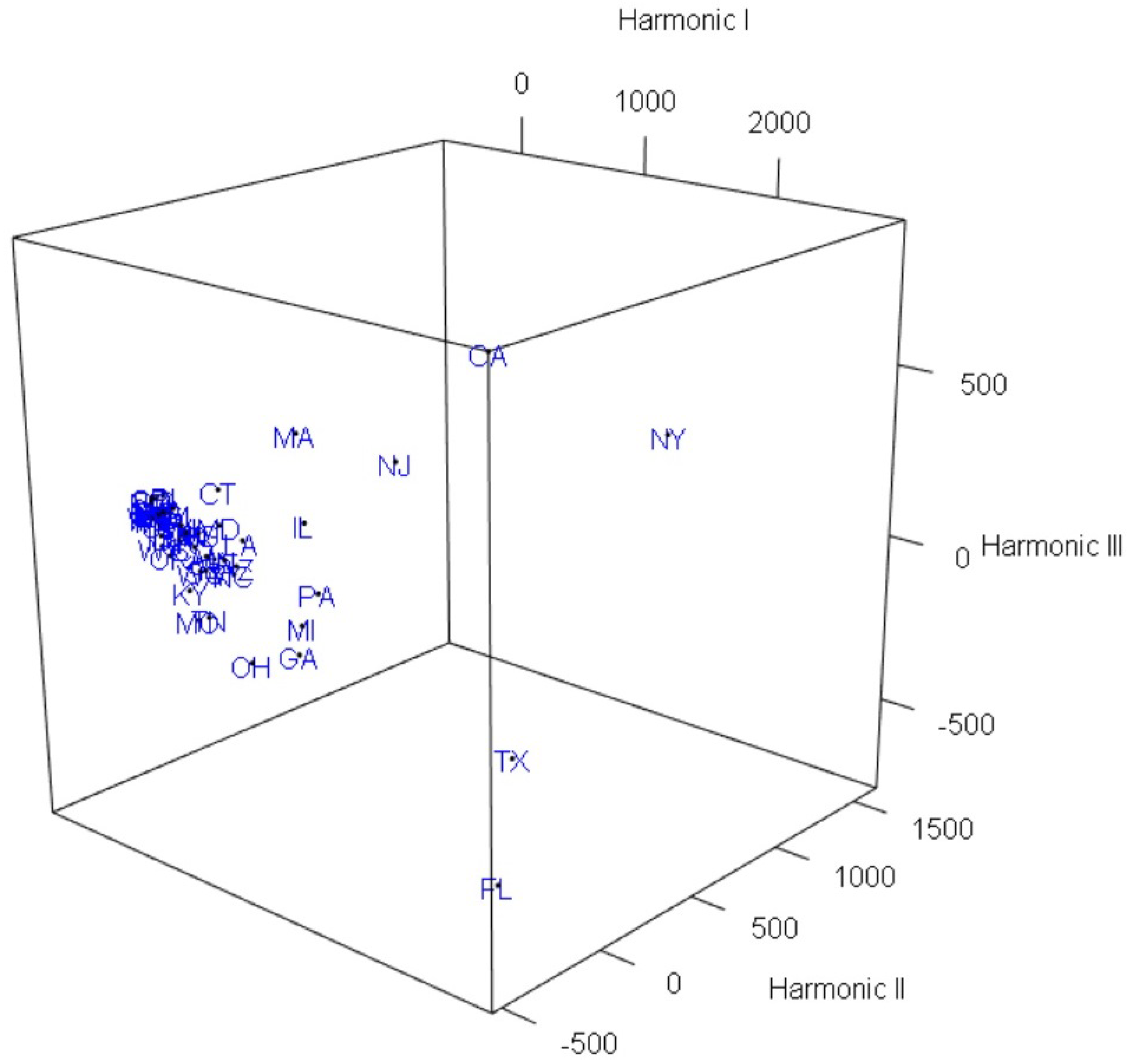
3. Graphical Visualization by FPCA
4. Copula Methods
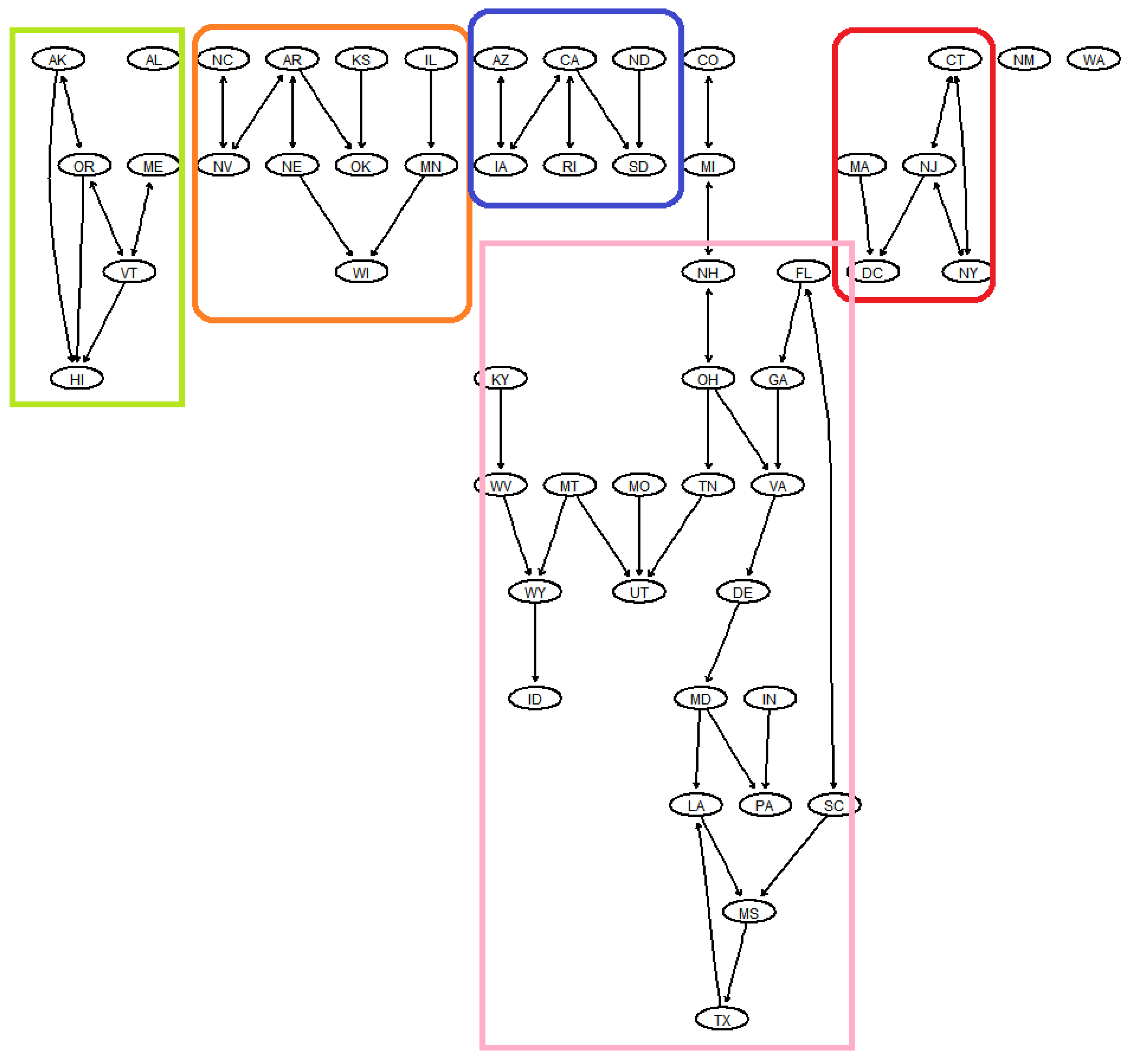
4.1. Graphical Visualization Using Copula
4.2. Gaussian Copula Marginal Regression
4.3. Copula Dynamic Conditional Correlation
5. Discussion
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ramsay, J.; Silverman, B. Functional Data Analysis, 2nd ed.; Springer: New York, NY, USA, 2005. [Google Scholar]
- Kokoszka, P.; Reimherr, M. Introduction to Functional Data Analysis, 1st ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2017. [Google Scholar]
- Joe, H. Multivariate Models and Multivariate Dependence Concepts; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas, 2nd ed.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Tang, C.; Wang, T.; Zhang, P. Functional Data Analysis: An Application to COVID-19 Data in the United States. arXiv 2020. [Google Scholar] [CrossRef]
- Lia, X.; Zhang, P.; Feng, Q. Exploring COVID-19 in mainland China during the lockdown of Wuhan via functional data analysis. Commun. Stat. Methods 2022, 29, 103–125. [Google Scholar]
- Oshinubi, K.; Ibrahim, F.; Rachdi, M.; Demongeot, J. Functional data analysis: Application to daily observation of COVID-19 prevalence in France. AIMS Math. 2022, 7, 5347–5385. [Google Scholar] [CrossRef]
- Acal, C.; Escabias, M.; Aguilera, A.M.; Valderrama, M.J. COVID-19 Data Imputation by Multiple Function-on-Function Principal Component Regression. Mathematics 2021, 9, 1237. [Google Scholar] [CrossRef]
- Cherubini, U.; Luciano, E.; Vecchiato, W. Copula Methods in Finance; John Wiley: Chichester, UK, 2004. [Google Scholar]
- Kim, J.-M. A Review of Copula Methods for Measuring Uncertainty in Finance and Economics. Quant. Bio-Sci. 2020, 39, 81–90. [Google Scholar]
- Sklar, A. Fonctions de repartition á n dimensions et leurs marges. Publ. Inst. Statist. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Masarotto, G.; Varin, C. Gaussian copula marginal regression. Electron. J. Stat. 2020, 6, 1517–1549. [Google Scholar] [CrossRef]
- Joe, H. Families of m-variate distributions with given margins and m(m−1)/2 bivariate dependence parameters. In Distributions with Fixed Marginals and Related Topics; Rüschendorf, L., Schweizer, B., Taylor, M.D., Eds.; Lecture Notes—Monograph Series; Institute of Mathematical Statistics: Tokyo, Japan, 1996; pp. 120–141. [Google Scholar] [CrossRef]
- Bedford, T.; Cooke, R.M. Vines—A new graphical model for dependent random variables. Ann. Stat. 2002, 30, 1031–1068. [Google Scholar] [CrossRef]
- Aas, K.; Berg, D. Models for construction of multivariate dependence: A comparison study. Eur. Financ. 2009, 15, 639–659. [Google Scholar] [CrossRef]
- Aas, K.; Czado, C.; Frigessi, A.; Bakken, H. Pair-copula constructions of multiple dependence. Insur. Math. Econ. 2009, 44, 182–198. [Google Scholar] [CrossRef]
- Brechmann, E.C.; Schepsmeier, U. Modeling Dependence with C- and D-Vine Copulas: The R Package CDVine. J. Stat. Softw. 2013, 52, 1–27. [Google Scholar] [CrossRef]
- Kraus, D.; Czado, C. D-vine copula based quantile regression. Comput. Stat. Data Anal. 2017, 110, 1–18. [Google Scholar] [CrossRef]
- D’Urso, P.; De Giovanni, L.; Vitale, V. A D-Vine Copula-Based Quantile Regression Model with Spatial Dependence for COVID-19 Infection Rate in Italy. Spat. Stat. 2022, 47, 100586. [Google Scholar] [CrossRef] [PubMed]
- Taamouti, A.; Doukali, M.; Bouezmarni, T. Copula-Based Estimation of Health Concentration Curves with an Application to COVID-19. Available online: https://ssrn.com/abstract=4064991 (accessed on 15 August 2022).
- Ansell, L.; Valle, L.D. A New Data Integration Framework for Covid-19 Social Media Information. arXiv 2021. [Google Scholar] [CrossRef]
- Kalisch, M.; Hauser, A.; Maathuis, M.H.; Mächler, M. An Overview of the pcalg Package for R; CRAN of R Project: Vienna, Austria, 2019; Available online: https://cran.microsoft.com/snapshot/2019-08-16/web/packages/pcalg/vignettes/vignette2018.pdf (accessed on 15 August 2022).
- Wang, J.-L.; Chiou, J.-M.; Muüller, H.-G. Functional Data Analysis. Annu. Rev. Stat. Appl. 2016, 3, 257–295. [Google Scholar] [CrossRef]
- Chen, K.; Zhang, X.; Petersen, A.; Muüller, H.-G. Quantifying Infinite-Dimensional Data: Functional Data Analysis in Action. Stat. Biosci. 2017, 9, 582–604. [Google Scholar] [CrossRef]
- Pearson, K.F.R.S. LIII. On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Ramsay, J.O.; Hooker, G.; Graves, S. Functional Data Analysis with R and MATLAB; Springer Science & Business Media: New York, NY, USA, 2009. [Google Scholar]
- Craven, P.; Wahba, G. Smoothing Noisy Data with Spline Functions. Estimating the Correct Degree of Smoothing by the Method of Generalized CrossValidation. Numer. Math. 1979, 31, 377–403. [Google Scholar] [CrossRef]
- Dissmann, J.F.; Brechmann, E.C.; Czado, C.; Kurowicka, D. Selecting and estimating regular vine copulae and application to financial returns. Comput. Stat. Data Anal. 2013, 59, 52–69. [Google Scholar] [CrossRef]
- Kim, J.-M.; Jung, H. Linear Time Varying Regression with Copula DCC-GARCH Model for Volatility. Econ. Lett. 2016, 145, 262–265. [Google Scholar] [CrossRef]
- Ghalanos, A. The Rmgarch Models: Background and Properties. (Version 1.3-0). 2019. Available online: https://cran.microsoft.com/snapshot/2020-05-24/web/packages/rmgarch/vignettes/The_rmgarch_models.pdf (accessed on 15 August 2022).
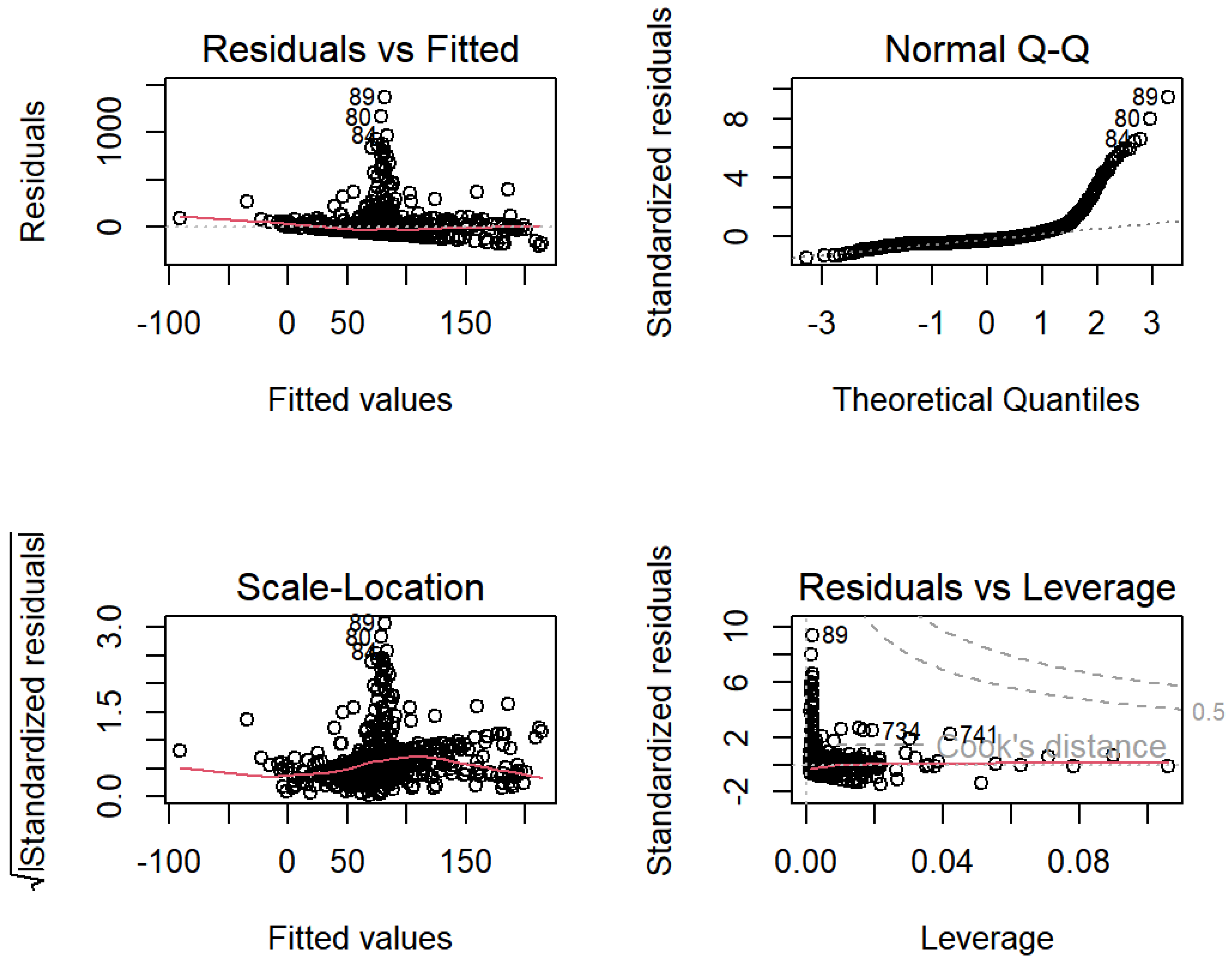

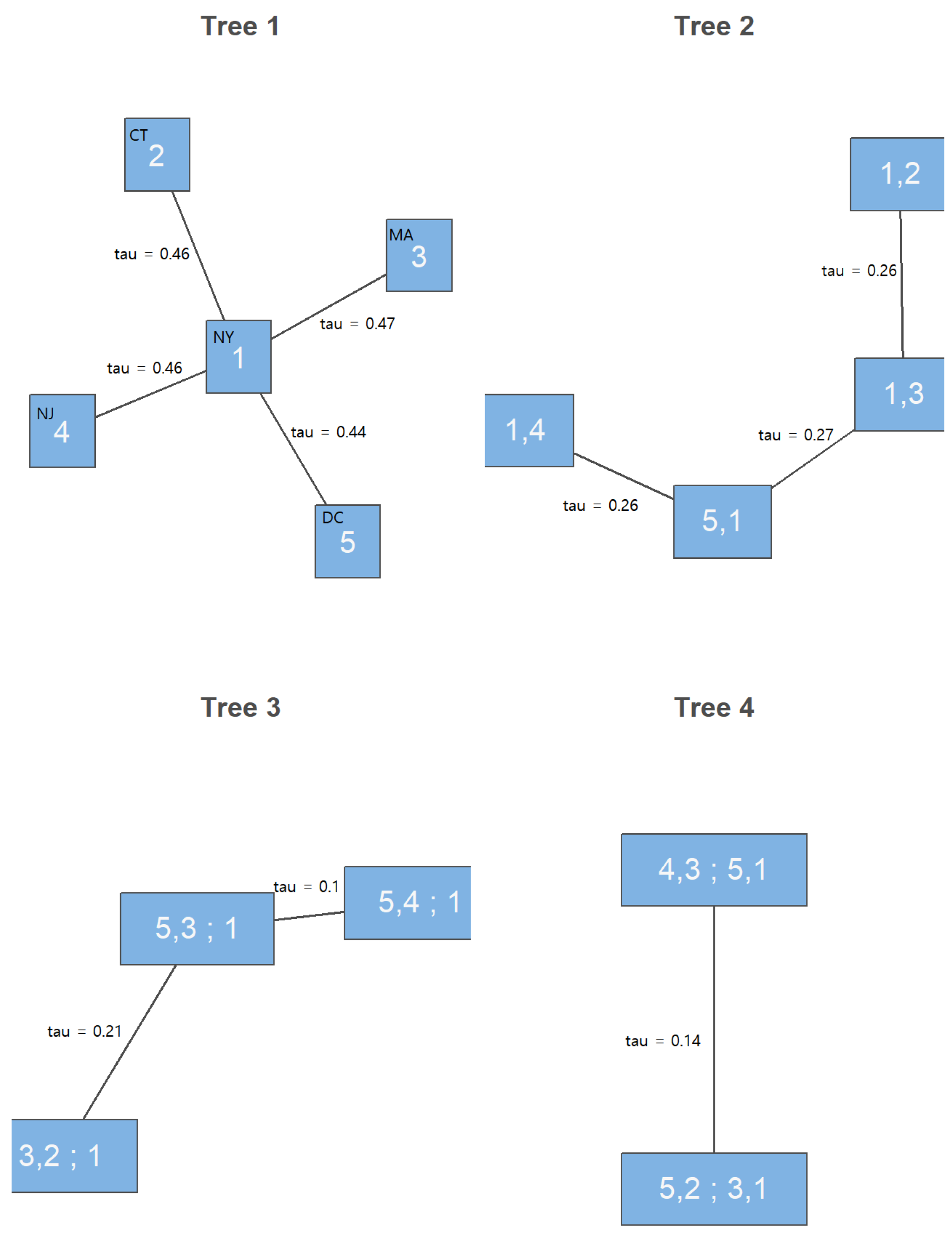

| AK | AL | AR | AZ | CA | CO | CT | DC | DE | FL | GA | HI | IA | ID | IL | IN | KS | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 1.3 | 21.2 | 12.5 | 31.3 | 98.6 | 13.8 | 11.6 | 1.5 | 3.2 | 84 | 41.7 | 1.7 | 10.4 | 5.4 | 40 | 25.7 | 9.4 |
| Median | 0 | 7 | 6 | 6 | 54 | 6 | 1 | 0 | 0 | 44 | 25 | 0 | 0 | 1 | 22 | 13 | 0 |
| SD | 5.2 | 39 | 19.5 | 58.1 | 142.2 | 25.3 | 23.3 | 2.9 | 7.6 | 152.2 | 92.8 | 4.1 | 29.1 | 9.6 | 53.1 | 58.7 | 27.4 |
| Kurtosis | 87 | 21.4 | 70.6 | 14.1 | 6 | 36.2 | 13.5 | 56.5 | 104.6 | 29.2 | 516.8 | 44.4 | 108 | 9.7 | 6.5 | 471.8 | 44.6 |
| Skewness | 8.5 | 3.9 | 5.8 | 3.3 | 2.4 | 4.8 | 3.2 | 5.4 | 7.9 | 4.7 | 19.7 | 5 | 8.1 | 2.8 | 2.3 | 18.6 | 5.5 |
| Minimum | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Maximum | 68 | 389 | 322 | 498 | 704 | 309 | 204 | 45 | 133 | 1552 | 2499 | 59 | 518 | 65 | 401 | 1546 | 371 |
| Total | 1281 | 20,160 | 11,923 | 29,852 | 93,924 | 13,148 | 11,034 | 1382 | 3042 | 80,027 | 39,772 | 1644 | 9940 | 5115 | 38,161 | 24,454 | 8958 |
| Count | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 |
| Population | 738,023 | 5,073,187 | 3,030,646 | 7,303,398 | 39,995,077 | 5,922,618 | 3,612,314 | 644,743 | 1,008,350 | 22,085,563 | 10,916,760 | 1,474,265 | 3,219,171 | 1,893,410 | 12,808,884 | 6,845,874 | 2,954,832 |
| Mortality Rate | 0.17% | 0.40% | 0.39% | 0.41% | 0.23% | 0.22% | 0.31% | 0.21% | 0.30% | 0.36% | 0.36% | 0.11% | 0.31% | 0.27% | 0.30% | 0.36% | 0.30% |
| KY | LA | MA | MD | ME | MI | MN | MO | MS | MT | NC | ND | NE | NH | NJ | NM | NV | |
| Mean | 17.5 | 18.8 | 22.1 | 15.9 | 2.6 | 39.9 | 13.4 | 21 | 13.4 | 3.7 | 27.6 | 2.3 | 4.7 | 2.8 | 36.3 | 8.9 | 12 |
| Median | 6 | 10 | 10 | 9 | 1 | 7 | 7 | 3 | 6 | 1 | 11 | 0 | 0 | 1 | 9 | 5 | 3 |
| SD | 33.7 | 27.3 | 37 | 29 | 6 | 71.9 | 18.8 | 104 | 20 | 6.9 | 56.4 | 6.5 | 15.6 | 5 | 108.6 | 10.7 | 21.6 |
| Kurtosis | 44.6 | 40.5 | 26.3 | 159.5 | 48.6 | 10.7 | 6.2 | 603.5 | 9.6 | 14.2 | 186.9 | 220.7 | 433.7 | 24.1 | 213 | 7.4 | 82.2 |
| Skewness | 5.4 | 4.6 | 3.9 | 10.1 | 5.6 | 2.9 | 2.3 | 22.3 | 2.6 | 3.3 | 10.5 | 11.6 | 17.8 | 3.9 | 12.7 | 2.1 | 6.4 |
| Minimum | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Maximum | 448 | 362 | 459 | 549 | 83 | 566 | 140 | 2881 | 177 | 55 | 1172 | 140 | 399 | 59 | 2037 | 99 | 365 |
| Total | 16,679 | 17,877 | 21,035 | 15,199 | 2512 | 38,038 | 12,806 | 19,993 | 12,794 | 3504 | 26,335 | 2232 | 4455 | 2662 | 34,567 | 8465 | 11,400 |
| Count | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 |
| Population | 4,539,130 | 4,682,633 | 7,126,375 | 6,257,958 | 1,369,159 | 10,116,069 | 5,787,008 | 6,188,111 | 2,960,075 | 1,103,187 | 10,620,168 | 800,394 | 1,988,536 | 1,389,741 | 9,388,414 | 2,129,190 | 3,185,426 |
| Mortality Rate | 0.37% | 0.38% | 0.30% | 0.24% | 0.18% | 0.38% | 0.22% | 0.32% | 0.43% | 0.32% | 0.25% | 0.28% | 0.22% | 0.19% | 0.37% | 0.40% | 0.36% |
| NY | OH | OK | OR | PA | RI | SC | SD | TN | TX | UT | VA | VT | WA | WI | WV | WY | |
| Mean | 74.4 | 41.4 | 17.5 | 8.8 | 49 | 3.8 | 18.8 | 3.1 | 28.8 | 92.9 | 5.2 | 22.5 | 0.7 | 14.7 | 15.8 | 7.7 | 2 |
| Median | 23 | 0 | 0 | 3 | 22 | 0 | 7 | 0 | 8 | 45 | 2 | 11 | 0 | 6 | 6 | 2 | 0 |
| SD | 149.7 | 125 | 66.9 | 14.1 | 69.9 | 12.1 | 30.5 | 8.4 | 90.6 | 103.5 | 7.6 | 38.4 | 1.5 | 24.1 | 25 | 14.5 | 7.7 |
| Kurtosis | 23.9 | 185.4 | 26 | 13.6 | 7.1 | 53.1 | 12.1 | 19.2 | 338.9 | 2.5 | 7.6 | 34.1 | 17.5 | 19.8 | 11 | 34.3 | 39.2 |
| Skewness | 4.4 | 10.9 | 4.9 | 3 | 2.3 | 6.6 | 3 | 4 | 15.6 | 1.4 | 2.3 | 4.9 | 3.3 | 3.5 | 2.9 | 4.6 | 5.7 |
| Minimum | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Maximum | 1460 | 2559 | 548 | 134 | 547 | 137 | 241 | 78 | 2174 | 798 | 65 | 404 | 16 | 256 | 206 | 170 | 81 |
| Total | 70,877 | 39,490 | 16,720 | 8415 | 46,716 | 3645 | 17,869 | 2993 | 27,487 | 88,578 | 4981 | 21,439 | 707 | 14,039 | 15,084 | 7291 | 1881 |
| Count | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 | 953 |
| Population | 20,365,879 | 11,852,036 | 4,000,953 | 4,318,492 | 13,062,764 | 1,106,341 | 5,217,037 | 901,165 | 7,023,788 | 29,945,493 | 3,373,162 | 8,757,467 | 646,545 | 7,901,429 | 5,935,064 | 1,781,860 | 579,495 |
| Mortality Rate | 0.35% | 0.33% | 0.42% | 0.19% | 0.36% | 0.33% | 0.34% | 0.33% | 0.39% | 0.30% | 0.15% | 0.24% | 0.11% | 0.18% | 0.25% | 0.41% | 0.32% |
| FPC1 | FPC2 | FPC3 | FPC4 | FPC5 | |
|---|---|---|---|---|---|
| PV | 0.8194 | 0.1125 | 0.0512 | 0.0117 | 0.0052 |
| CPV | 0.8194 | 0.9320 | 0.9831 | 0.9948 | 1.0000 |
| CA | TX | FL | NY | |
|---|---|---|---|---|
| Dickey–Fuller Statistic | −18.02 | −12.118 | −21.365 | −15.552 |
| p-value | 0.01 | 0.01 | 0.01 | 0.01 |
| Stationary | Yes | Yes | Yes | Yes |
| CA | Estimate | Std. Error | z value | p-Value | TX | Estimate | Std. Error | z Value | p-Value | FL | Estimate | Std. Error | z Value | p-Value | NY | Estimate | Std. Error | z Value | p-Value |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Intercept | 0.007 | 0.036 | 0.210 | 0.834 | Intercept | 0.334 | 0.077 | 4.355 | 0.000 | Intercept | −0.019 | 0.065 | −0.292 | 0.770 | Intercept | 0.030 | 0.055 | 0.542 | 0.588 |
| AK | 0.105 | 0.028 | 3.813 | 0.000 | AK | 0.053 | 0.021 | 2.505 | 0.012 | AK | 0.000 | 0.032 | 0.014 | 0.989 | AK | −0.032 | 0.024 | −1.359 | 0.174 |
| AL | −0.026 | 0.030 | −0.865 | 0.387 | AL | 0.024 | 0.023 | 1.031 | 0.303 | AL | 0.009 | 0.034 | 0.262 | 0.793 | AL | −0.036 | 0.026 | −1.424 | 0.154 |
| AR | −0.012 | 0.035 | −0.355 | 0.723 | AR | −0.067 | 0.029 | −2.338 | 0.019 | AR | −0.071 | 0.042 | −1.683 | 0.092 | AR | 0.169 | 0.032 | 5.316 | 0.000 |
| AZ | 0.054 | 0.032 | 1.686 | 0.092 | AZ | 0.022 | 0.025 | 0.866 | 0.386 | AZ | −0.075 | 0.037 | −2.013 | 0.044 | AZ | 0.041 | 0.028 | 1.452 | 0.146 |
| CO | −0.008 | 0.024 | −0.317 | 0.752 | CA | 0.273 | 0.025 | 11.032 | 0.000 | CA | 0.391 | 0.037 | 10.621 | 0.000 | CA | 0.063 | 0.029 | 2.161 | 0.031 |
| CT | −0.034 | 0.034 | −0.999 | 0.318 | CO | 0.176 | 0.019 | 9.321 | 0.000 | CO | 0.016 | 0.029 | 0.549 | 0.583 | CO | −0.023 | 0.022 | −1.041 | 0.298 |
| DC | 0.001 | 0.029 | 0.022 | 0.982 | CT | −0.004 | 0.025 | −0.158 | 0.874 | CT | 0.026 | 0.038 | 0.686 | 0.493 | CT | 0.011 | 0.028 | 0.377 | 0.706 |
| DE | 0.063 | 0.027 | 2.383 | 0.017 | DC | 0.050 | 0.022 | 2.265 | 0.024 | DC | 0.069 | 0.033 | 2.088 | 0.037 | DC | 0.069 | 0.025 | 2.764 | 0.006 |
| FL | 0.249 | 0.026 | 9.718 | 0.000 | DE | −0.017 | 0.020 | −0.879 | 0.380 | DE | −0.045 | 0.029 | −1.534 | 0.125 | DE | 0.043 | 0.022 | 1.951 | 0.051 |
| GA | 0.090 | 0.034 | 2.655 | 0.008 | FL | 0.092 | 0.022 | 4.260 | 0.000 | GA | −0.012 | 0.039 | −0.318 | 0.751 | FL | −0.047 | 0.024 | −1.939 | 0.053 |
| HI | −0.099 | 0.031 | −3.213 | 0.001 | GA | −0.067 | 0.026 | −2.566 | 0.010 | HI | 0.106 | 0.035 | 3.023 | 0.003 | GA | −0.095 | 0.029 | −3.271 | 0.001 |
| IA | 0.030 | 0.028 | 1.042 | 0.297 | HI | 0.051 | 0.024 | 2.174 | 0.030 | IA | 0.018 | 0.033 | 0.544 | 0.586 | HI | 0.062 | 0.026 | 2.353 | 0.019 |
| ID | 0.070 | 0.030 | 2.314 | 0.021 | IA | −0.050 | 0.022 | −2.290 | 0.022 | ID | −0.019 | 0.034 | −0.551 | 0.581 | IA | −0.004 | 0.024 | −0.184 | 0.854 |
| IL | −0.015 | 0.041 | −0.361 | 0.718 | ID | −0.049 | 0.023 | −2.156 | 0.031 | IL | 0.052 | 0.049 | 1.059 | 0.289 | ID | −0.026 | 0.026 | −1.014 | 0.310 |
| IN | 0.069 | 0.040 | 1.698 | 0.089 | IL | −0.022 | 0.033 | −0.679 | 0.497 | IN | 0.013 | 0.047 | 0.280 | 0.780 | IL | 0.011 | 0.036 | 0.303 | 0.762 |
| KS | 0.003 | 0.028 | 0.113 | 0.910 | IN | −0.006 | 0.032 | −0.199 | 0.842 | KS | 0.010 | 0.031 | 0.316 | 0.752 | IN | 0.094 | 0.035 | 2.653 | 0.008 |
| KY | −0.091 | 0.033 | −2.709 | 0.007 | KS | −0.018 | 0.020 | −0.881 | 0.378 | KY | 0.041 | 0.040 | 1.014 | 0.311 | KS | 0.019 | 0.023 | 0.831 | 0.406 |
| LA | −0.001 | 0.030 | −0.039 | 0.969 | KY | 0.020 | 0.027 | 0.752 | 0.452 | LA | 0.078 | 0.037 | 2.105 | 0.035 | KY | 0.052 | 0.030 | 1.746 | 0.081 |
| MA | 0.014 | 0.031 | 0.462 | 0.644 | LA | 0.000 | 0.025 | −0.014 | 0.989 | MA | −0.067 | 0.042 | −1.592 | 0.111 | LA | 0.038 | 0.028 | 1.352 | 0.176 |
| MD | 0.057 | 0.029 | 1.952 | 0.051 | MA | 0.074 | 0.029 | 2.574 | 0.010 | MD | 0.062 | 0.036 | 1.730 | 0.084 | MA | 0.116 | 0.032 | 3.596 | 0.000 |
| ME | −0.029 | 0.025 | −1.137 | 0.255 | MD | 0.046 | 0.024 | 1.914 | 0.056 | ME | −0.013 | 0.029 | −0.452 | 0.651 | MD | 0.015 | 0.027 | 0.549 | 0.583 |
| MI | 0.025 | 0.030 | 0.816 | 0.415 | ME | −0.028 | 0.020 | −1.417 | 0.157 | MI | 0.059 | 0.034 | 1.724 | 0.085 | ME | −0.050 | 0.022 | −2.285 | 0.022 |
| MN | −0.036 | 0.036 | −0.987 | 0.324 | MI | −0.026 | 0.023 | −1.139 | 0.255 | MN | 0.081 | 0.043 | 1.890 | 0.059 | MI | −0.017 | 0.025 | −0.666 | 0.506 |
| MO | −0.067 | 0.030 | −2.203 | 0.028 | MN | −0.085 | 0.029 | −2.958 | 0.003 | MO | 0.058 | 0.034 | 1.709 | 0.087 | MN | 0.040 | 0.032 | 1.232 | 0.218 |
| MS | 0.025 | 0.035 | 0.720 | 0.472 | MO | −0.010 | 0.023 | −0.432 | 0.666 | MS | −0.024 | 0.040 | −0.602 | 0.547 | MO | −0.005 | 0.026 | −0.188 | 0.851 |
| MT | −0.083 | 0.032 | −2.545 | 0.011 | MS | −0.012 | 0.027 | −0.440 | 0.660 | MT | 0.049 | 0.037 | 1.319 | 0.187 | MS | −0.024 | 0.030 | −0.811 | 0.417 |
| NC | −0.002 | 0.036 | −0.054 | 0.957 | MT | −0.003 | 0.025 | −0.111 | 0.911 | NC | 0.130 | 0.041 | 3.144 | 0.002 | MT | −0.086 | 0.028 | −3.065 | 0.002 |
| ND | −0.031 | 0.027 | −1.173 | 0.241 | NC | 0.011 | 0.028 | 0.394 | 0.694 | ND | −0.028 | 0.031 | −0.895 | 0.371 | NC | 0.042 | 0.031 | 1.342 | 0.180 |
| NE | 0.057 | 0.027 | 2.102 | 0.036 | ND | −0.005 | 0.021 | −0.225 | 0.822 | NE | −0.058 | 0.031 | −1.902 | 0.057 | ND | −0.032 | 0.023 | −1.355 | 0.175 |
| NH | 0.016 | 0.028 | 0.574 | 0.566 | NE | −0.018 | 0.021 | −0.890 | 0.374 | NH | −0.001 | 0.032 | −0.041 | 0.967 | NE | −0.023 | 0.023 | −1.015 | 0.310 |
| NJ | 0.041 | 0.030 | 1.363 | 0.173 | NH | −0.006 | 0.021 | −0.274 | 0.784 | NJ | 0.017 | 0.044 | 0.393 | 0.695 | NH | 0.009 | 0.024 | 0.366 | 0.714 |
| NM | 0.052 | 0.035 | 1.459 | 0.145 | NJ | 0.014 | 0.031 | 0.444 | 0.657 | NM | −0.059 | 0.044 | −1.355 | 0.175 | NJ | 0.061 | 0.035 | 1.770 | 0.077 |
| NV | 0.014 | 0.033 | 0.428 | 0.668 | NM | 0.045 | 0.030 | 1.520 | 0.128 | NV | −0.002 | 0.036 | −0.062 | 0.950 | NM | 0.130 | 0.033 | 3.962 | 0.000 |
| NY | 0.072 | 0.035 | 2.065 | 0.039 | NV | −0.036 | 0.024 | −1.511 | 0.131 | NY | −0.089 | 0.043 | −2.089 | 0.037 | NV | −0.034 | 0.027 | −1.275 | 0.202 |
| OH | −0.038 | 0.029 | −1.279 | 0.201 | NY | −0.038 | 0.029 | −1.305 | 0.192 | OH | 0.225 | 0.033 | 6.799 | 0.000 | OH | 0.001 | 0.025 | 0.057 | 0.954 |
| OK | 0.006 | 0.036 | 0.165 | 0.869 | OH | 0.077 | 0.023 | 3.435 | 0.001 | OK | −0.045 | 0.042 | −1.075 | 0.282 | OK | 0.014 | 0.031 | 0.455 | 0.649 |
| OR | −0.115 | 0.033 | −3.454 | 0.001 | OK | −0.055 | 0.028 | −1.996 | 0.046 | OR | 0.034 | 0.038 | 0.890 | 0.374 | OR | 0.025 | 0.028 | 0.882 | 0.378 |
| PA | −0.019 | 0.031 | −0.603 | 0.546 | OR | −0.016 | 0.025 | −0.650 | 0.515 | PA | −0.035 | 0.037 | −0.959 | 0.338 | PA | −0.079 | 0.027 | −2.913 | 0.004 |
| RI | 0.007 | 0.027 | 0.256 | 0.798 | PA | −0.021 | 0.025 | −0.872 | 0.383 | RI | −0.015 | 0.032 | −0.469 | 0.639 | RI | 0.027 | 0.024 | 1.131 | 0.258 |
| SC | 0.047 | 0.034 | 1.384 | 0.166 | RI | −0.015 | 0.021 | −0.715 | 0.475 | SC | 0.059 | 0.038 | 1.543 | 0.123 | SC | 0.005 | 0.029 | 0.184 | 0.854 |
| SD | −0.022 | 0.030 | −0.740 | 0.459 | SC | −0.031 | 0.026 | −1.221 | 0.222 | SD | 0.017 | 0.034 | 0.490 | 0.624 | SD | 0.007 | 0.025 | 0.260 | 0.795 |
| TN | −0.108 | 0.029 | −3.684 | 0.000 | SD | −0.043 | 0.022 | −1.922 | 0.055 | TN | −0.033 | 0.035 | −0.925 | 0.355 | TN | −0.005 | 0.026 | −0.194 | 0.846 |
| TX | 0.430 | 0.030 | 14.238 | 0.000 | TN | 0.016 | 0.023 | 0.667 | 0.505 | TX | 0.188 | 0.046 | 4.107 | 0.000 | TX | −0.053 | 0.036 | −1.494 | 0.135 |
| UT | −0.023 | 0.032 | −0.726 | 0.468 | UT | −0.011 | 0.024 | −0.463 | 0.644 | UT | −0.018 | 0.036 | −0.504 | 0.615 | UT | 0.094 | 0.027 | 3.513 | 0.000 |
| VA | 0.038 | 0.029 | 1.284 | 0.199 | VA | 0.002 | 0.024 | 0.068 | 0.946 | VA | 0.045 | 0.035 | 1.292 | 0.196 | VA | 0.092 | 0.026 | 3.493 | 0.000 |
| VT | 0.071 | 0.027 | 2.691 | 0.007 | VT | 0.005 | 0.021 | 0.230 | 0.818 | VT | −0.042 | 0.031 | −1.342 | 0.179 | VT | −0.003 | 0.023 | −0.133 | 0.894 |
| WA | −0.028 | 0.027 | −1.051 | 0.293 | WA | 0.054 | 0.020 | 2.676 | 0.007 | WA | 0.047 | 0.030 | 1.554 | 0.120 | WA | 0.042 | 0.023 | 1.839 | 0.066 |
| WI | 0.201 | 0.027 | 7.466 | 0.000 | WI | 0.030 | 0.022 | 1.386 | 0.166 | WI | −0.003 | 0.033 | −0.105 | 0.917 | WI | 0.010 | 0.024 | 0.406 | 0.685 |
| WV | −0.005 | 0.031 | −0.165 | 0.869 | WV | −0.019 | 0.025 | −0.784 | 0.433 | WV | −0.062 | 0.037 | −1.697 | 0.090 | WV | 0.139 | 0.027 | 5.072 | 0.000 |
| WY | −0.031 | 0.035 | −0.877 | 0.381 | WY | 0.000 | 0.025 | 0.001 | 0.999 | WY | −0.030 | 0.038 | −0.795 | 0.427 | WY | 0.073 | 0.028 | 2.582 | 0.010 |
| sigma | 0.164 | 0.004 | 43.667 | 0.000 | sigma | 0.202 | 0.019 | 10.832 | 0.000 | sigma | 0.214 | 0.014 | 15.139 | 0.000 | sigma | 0.182 | 0.016 | 11.441 | 0.000 |
| 0.989 | 0.003 | 317.600 | 0.000 | 0.983 | 0.007 | 137.510 | 0.000 | 0.979 | 0.008 | 124.010 | 0.000 | ||||||||
| −0.806 | 0.018 | −45.970 | 0.000 | −0.875 | 0.016 | −53.210 | 0.000 | −0.807 | 0.023 | −34.950 | 0.000 |
| CA and TX | TX and FL | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CA | Estimate | Std. Error | z value | p-value | TX | Estimate | Std. Error | z value | p-value | TX | Estimate | Std. Error | z value | p-value | FL | Estimate | Std. Error | z value | p-value |
| 0.10 | 0.02 | 6.35 | 0.00 | 0.08 | 0.00 | 34.66 | 0.00 | 0.08 | 0.00 | 34.73 | 0.00 | 0.10 | 0.01 | 9.47 | 0.00 | ||||
| 1.00 | 0.00 | 816.06 | 0.00 | 1.00 | 0.01 | 157.53 | 0.00 | 1.00 | 0.01 | 157.68 | 0.00 | 1.00 | 0.02 | 55.00 | 0.00 | ||||
| −0.64 | 0.02 | −26.30 | 0.00 | −0.50 | 0.11 | −4.67 | 0.00 | −0.50 | 0.11 | −4.67 | 0.00 | −0.78 | 0.23 | −3.40 | 0.00 | ||||
| 0.00 | 0.00 | 1.04 | 0.30 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 1.00 | ||||
| 0.13 | 0.03 | 4.72 | 0.00 | 0.46 | 0.23 | 2.01 | 0.04 | 0.46 | 0.23 | 2.01 | 0.04 | 0.45 | 0.17 | 2.68 | 0.01 | ||||
| 0.83 | 0.03 | 28.65 | 0.00 | 0.52 | 0.15 | 3.58 | 0.00 | 0.52 | 0.15 | 3.58 | 0.00 | 0.47 | 0.12 | 3.88 | 0.00 | ||||
| 0.09 | 0.04 | 2.24 | 0.03 | 0.03 | 0.19 | 0.17 | 0.87 | 0.03 | 0.19 | 0.17 | 0.87 | 0.16 | 0.16 | 1.02 | 0.31 | ||||
| skew | 1.55 | 0.54 | 2.86 | 0.00 | skew | −0.05 | 0.08 | −0.66 | 0.51 | skew | −0.05 | 0.08 | −0.66 | 0.51 | skew | 0.20 | 0.43 | 0.47 | 0.64 |
| shape | 3.01 | 0.62 | 4.86 | 0.00 | shape | 1.24 | 0.17 | 7.32 | 0.00 | shape | 1.24 | 0.17 | 7.32 | 0.00 | shape | 1.24 | 0.26 | 4.82 | 0.00 |
| [Joint]dcca1 | 0.04 | 0.01 | 2.67 | 0.01 | Log−Likelihood | 2215.84 | AIC | −4.61 | [Joint]dcca1 | 0.02 | 0.02 | 0.87 | 0.38 | Log−Likelihood | 1549.04 | AIC | −3.21 | ||
| [Joint]dccb1 | 0.94 | 0.02 | 43.26 | 0.00 | N | 953 | BIC | −4.51 | [Joint]dccb1 | 0.96 | 0.06 | 16.16 | 0.00 | N | 953 | BIC | −3.11 | ||
| CA and FL | TX and NY | ||||||||||||||||||
| CA | Estimate | Std. Error | z value | p-value | FL | Estimate | Std. Error | z value | p-value | TX | Estimate | Std. Error | z value | p-value | NY | Estimate | Std. Error | z value | p-value |
| 0.10 | 0.02 | 6.35 | 0.00 | 0.10 | 0.01 | 9.47 | 0.00 | 0.08 | 0.00 | 34.69 | 0.00 | 0.12 | 0.00 | 679.52 | 0.00 | ||||
| 1.00 | 0.00 | 815.72 | 0.00 | 1.00 | 0.02 | 54.94 | 0.00 | 1.00 | 0.01 | 157.55 | 0.00 | 1.00 | 0.00 | 367.85 | 0.00 | ||||
| −0.64 | 0.02 | −26.34 | 0.00 | −0.78 | 0.23 | −3.40 | 0.00 | −0.50 | 0.11 | −4.67 | 0.00 | −0.73 | 0.08 | −9.13 | 0.00 | ||||
| 0.00 | 0.00 | 1.04 | 0.30 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 1.00 | ||||
| 0.13 | 0.03 | 4.73 | 0.00 | 0.45 | 0.17 | 2.68 | 0.01 | 0.46 | 0.23 | 2.01 | 0.04 | 0.35 | 0.14 | 2.48 | 0.01 | ||||
| 0.83 | 0.03 | 28.71 | 0.00 | 0.47 | 0.12 | 3.89 | 0.00 | 0.52 | 0.15 | 3.58 | 0.00 | 0.49 | 0.07 | 6.69 | 0.00 | ||||
| 0.09 | 0.04 | 2.24 | 0.03 | 0.16 | 0.16 | 1.02 | 0.31 | 0.03 | 0.19 | 0.17 | 0.87 | 0.32 | 0.17 | 1.94 | 0.05 | ||||
| skew | 1.55 | 0.54 | 2.86 | 0.00 | skew | 0.20 | 0.43 | 0.47 | 0.64 | skew | −0.05 | 0.08 | −0.66 | 0.51 | skew | −0.37 | 0.19 | −1.93 | 0.05 |
| shape | 3.01 | 0.62 | 4.86 | 0.00 | shape | 1.24 | 0.26 | 4.83 | 0.00 | shape | 1.24 | 0.17 | 7.32 | 0.00 | shape | 1.15 | 0.18 | 6.55 | 0.00 |
| [Joint]dcca1 | 0.01 | 0.00 | 3.00 | 0.00 | Log−Likelihood | 1293.03 | AIC | −2.67 | [Joint]dcca1 | 0.03 | 0.01 | 2.90 | 0.00 | Log−Likelihood | 1814.15 | AIC | −3.77 | ||
| [Joint]dccb1 | 0.99 | 0.00 | 253.89 | 0.00 | N | 953 | BIC | −2.57 | [Joint]dccb1 | 0.92 | 0.03 | 30.72 | 0.00 | N | 953 | BIC | −3.66 | ||
| CA and NY | FL and NY | ||||||||||||||||||
| CA | Estimate | Std. Error | z value | p-value | NY | Estimate | Std. Error | z value | p-value | FL | Estimate | Std. Error | z value | p-value | NY | Estimate | Std. Error | z value | p-value |
| 0.10 | 0.02 | 6.35 | 0.00 | 0.11 | 0.00 | 678.78 | 0.00 | 0.10 | 0.01 | 9.46 | 0.00 | 0.12 | 0.00 | 679.31 | 0.00 | ||||
| 1.00 | 0.00 | 816.34 | 0.00 | 1.00 | 0.00 | 366.63 | 0.00 | 1.00 | 0.02 | 54.91 | 0.00 | 1.00 | 0.00 | 367.74 | 0.00 | ||||
| −0.64 | 0.03 | −26.19 | 0.00 | −0.73 | 0.08 | −9.11 | 0.00 | −0.78 | 0.23 | −3.40 | 0.00 | −0.73 | 0.08 | −9.13 | 0.00 | ||||
| 0.00 | 0.00 | 1.04 | 0.30 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 1.00 | ||||
| 0.13 | 0.03 | 4.72 | 0.00 | 0.35 | 0.14 | 2.48 | 0.01 | 0.45 | 0.17 | 2.68 | 0.01 | 0.35 | 0.14 | 2.48 | 0.01 | ||||
| 0.83 | 0.03 | 28.67 | 0.00 | 0.49 | 0.07 | 6.69 | 0.00 | 0.47 | 0.12 | 3.88 | 0.00 | 0.49 | 0.07 | 6.69 | 0.00 | ||||
| 0.09 | 0.04 | 2.24 | 0.03 | 0.32 | 0.17 | 1.93 | 0.05 | 0.16 | 0.16 | 1.02 | 0.31 | 0.32 | 0.17 | 1.93 | 0.05 | ||||
| skew | 1.55 | 0.54 | 2.86 | 0.00 | skew | −0.37 | 0.19 | −1.93 | 0.05 | skew | 0.20 | 0.43 | 0.47 | 0.64 | skew | −0.37 | 0.19 | −1.93 | 0.05 |
| shape | 3.01 | 0.62 | 4.85 | 0.00 | shape | 1.15 | 0.18 | 6.55 | 0.00 | shape | 1.24 | 0.26 | 4.82 | 0.00 | shape | 1.15 | 0.18 | 6.55 | 0.00 |
| [Joint]dcca1 | 0.01 | 0.01 | 1.28 | 0.20 | Log−Likelihood | 1545.17 | AIC | −3.20 | [Joint]dcca1 | 0.01 | 0.01 | 1.30 | 0.19 | Log−Likelihood | 892.30 | AIC | −1.83 | ||
| [Joint]dccb1 | 0.96 | 0.04 | 24.01 | 0.00 | N | 953 | BIC | −3.10 | [Joint]dccb1 | 0.95 | 0.02 | 40.34 | 0.00 | N | 953 | BIC | −1.73 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.-M. Copula Dynamic Conditional Correlation and Functional Principal Component Analysis of COVID-19 Mortality in the United States. Axioms 2022, 11, 619. https://doi.org/10.3390/axioms11110619
Kim J-M. Copula Dynamic Conditional Correlation and Functional Principal Component Analysis of COVID-19 Mortality in the United States. Axioms. 2022; 11(11):619. https://doi.org/10.3390/axioms11110619
Chicago/Turabian StyleKim, Jong-Min. 2022. "Copula Dynamic Conditional Correlation and Functional Principal Component Analysis of COVID-19 Mortality in the United States" Axioms 11, no. 11: 619. https://doi.org/10.3390/axioms11110619
APA StyleKim, J.-M. (2022). Copula Dynamic Conditional Correlation and Functional Principal Component Analysis of COVID-19 Mortality in the United States. Axioms, 11(11), 619. https://doi.org/10.3390/axioms11110619






