Sketch-Based Retrieval Approach Using Artificial Intelligence Algorithms for Deep Vision Feature Extraction

Abstract

Since the onset of civilization, sketches have been used to portray our visual world, and they continue to do so in many different disciplines today. As in specific government agencies, establishing similarities between sketches is a crucial aspect of gathering forensic evidence in crimes, in addition to satisfying the user’s subjective requirements in searching and browsing for specific sorts of images (i.e., clip art images), especially with the proliferation of smartphones with touchscreens. With such a kind of search, quickly and effectively drawing and retrieving sketches from databases can occasionally be challenging, when using keywords or categories. Drawing some simple forms and searching for the image in that way could be simpler in some situations than attempting to put the vision into words, which is not always possible. Modern techniques, such as Content-Based Image Retrieval (CBIR), may offer a more useful solution. The key engine of such techniques that poses various challenges might be dealt with using effective visual feature representation. Object edge feature detectors are commonly used to extract features from different image sorts. However, they are inconvenient as they consume time due to their complexity in computation. In addition, they are complicated to implement with real-time responses. Therefore, assessing and identifying alternative solutions from the vast array of methods is essential. Scale Invariant Feature Transform (SIFT) is a typical solution that has been used by most prevalent research studies. Even for learning-based methods, SIFT is frequently used for comparison and assessment. However, SIFT has several downsides. Hence, this research is directed to the utilization of handcrafted-feature-based Oriented FAST and Rotated BRIEF (ORB) to capture visual features of sketched images to overcome SIFT limitations on small datasets. However, handcrafted-feature-based algorithms are generally unsuitable for large-scale sets of images. Efficient sketched image retrieval is achieved based on content and separation of the features of the black line drawings from the background into precisely-defined variables. Each variable is encoded as a distinct dimension in this disentangled representation. For representation of sketched images, this paper presents a Sketch-Based Image Retrieval (SBIR) system, which uses the information-maximizing GAN (InfoGAN) model. The establishment of such a retrieval system is based on features acquired by the unsupervised learning InfoGAN model to satisfy users’ expectations for large-scale datasets. The challenges with the matching and retrieval systems of such kinds of images develop when drawing clarity declines. Finally, the ORB-based matching system is introduced and compared to the SIFT-based system. Additionally, the InfoGAN-based system is compared with state-of-the-art solutions, including SIFT, ORB, and Convolutional Neural Network (CNN).

1. Introduction

Today, many applications including those for image retrieval and identification, are feature-based. Applications of this nature reflect the spirit of several sectors, including satellite, online browsing, and health care. With the popularity of touchscreen devices, searching by image might be used in addition to or as a replacement for the more popular language-based image searching. Search engine technology companies (i.e., Google and others) provide the community with free web-based diagramming programs called Google Drawings. In such types of programs, users can create and modify mind maps, idea maps, organization charts, flowcharts, and other sorts of diagrams and paintings, while working with other users in real time. This supplies the company and its users with a massive database of sketch drawings of different clarity degrees. Thus, sketch image search and retrieval can be performed on a vast number of web pages and huge databases. Retrieval according to sketch similarities also has a great role in many government agencies, as in finding forensic evidence in crimes.

However, matching and retrieval of this sort of images is an overwhelming problem. It involves the comparison of free color and semantic acquaintance hand drawings to determine their association based on the purpose of the users to address their demands. Besides, the degree of lucidity for these sorts of drawings presents a severe hurdle. In general, the efficacy of image retrieval is boosted by removing superfluous photos and/or downsizing images to have the most relevant images, especially with the huge growth of web images and databases [1]. The chosen method for similarity estimation and the suitable representation of the compared images play an essential role in handling all these problems. However, efficient and sufficient image feature representation is the key engine to the whole retrieval system for a swift matching process with high precision of retrieval results. Furthermore, image representation will affect not only the matching process, but also the computational retrieval speed, and it will cause an increase in the memory usage.

Similarity matching for image retrieval refers to the determination of the best correspondence points between distinctive shapes of an image and others, according to the spatial distance measure. This is achieved by comparing the feature details of a query image with those of other training images in the set. Therefore, the higher the attainment of accurate matches between images is, the more discriminative the image representation with a corresponding feature descriptor dimensionality. The efficient representation of an image dataset is crucial to decrease the frequency of false matches [2,3]. As a result, the feature extraction methods used to support image representation gain importance. Such methods differ in performance when the image content is refined [4]. Object edge feature detectors are typically used to extract features of images, but they take much time for processing. Thus, a deep evaluation of various extraction methods must be introduced to handle feature representation and match sketched images.

In general, feature representations are either local or global. Global features may be employed for large image databases to obtain duplicate images, since they reflect the complete image contour [5]. On the other hand, a local feature representation is a pattern or discernible structure seen in an image, such as a point, an edge, or a small image patch. Local feature representation techniques focus on a small number of crucial regions that vary within the same image and are unaffected by changes in perspective or illumination. Such features are crucial for many applications, including identifying human lesions. Therefore, how features are derived is a critical issue to consider.

Image-derived local features were given substantial relevance in segmentation [6] and characterization of change-invariant areas [7]. This ensures the significance of local feature extraction techniques in various applications. Several studies came to an end with the analysis of local feature validity. Image matching is burdened by the frequency of changes in perspective and/or lighting in visual situations [8].

The algorithms used for extracting features give either handcrafted or learning-based features. Handcrafted features extracted from visual data are categorized into global or local features. To achieve high matching speed and accuracy, the feature extraction algorithms face several challenges in identifying the most discriminating key feature points. For decades, SIFT [9], ORB [10], and other local feature extraction techniques have become essential. ORB is a binary descriptor proposed as an alternative for SIFT; however, it is not used widely. Generally, SIFT has been considered the benchmark for several methods, and up to now, its performance has also been comparable to those of other learning-based methods.

On the other hand, learned features are automatically extracted using Machine Learning (ML) algorithms. Deep Learning (DL), a subset of the larger family of ML, is the most popular learning technique used in large-scale applications. A family of deep neural networks called CNNs is the best for processing of visual images [11,12,13,14]. In a CNN, local features are basically gained from the feature maps obtained from the intermediate convolutional layers of the network. The activations produced by convolutional layers are used to produce the local features [15]. In contrast, global features are obtained from the maps created by the whole network. Hence, the global features are frequently provided as input to fully-connected layers.

To allow feature extraction from large-scale datasets, learning techniques are considered in this paper. However, the essence of the binary descriptor with handcraft features specifies the choice of the most suitable feature extraction. The concept is to simulate the operation of binary descriptors in comparing illumination changes of visual features within sketched images as logic zero/one or as a separate variable. Sketch lines should be separated from the white background to recognize the black lines and the quintessence of the drawn shape itself.

The disentangled representation presented in [16] was utilized as an unsupervised learning method, which divides each feature into precisely-specified variables and encodes each of those variables as a distinct dimension. The idea was to use both “high” and “low” dimension thinking to simulate the intuitive process of the human rapidly. Generative adversarial networks [17], or GANs, are generative modeling methods that use DL tools such as CNNs. Generative modeling is an ML activity that involves automatically finding and learning the regularities or patterns in incoming data to develop new instances that might have been properly deduced from the original datasets. InfoGAN [18] is a totally unsupervised information-theoretic version of the GAN that can learn disentangled representations. It optimizes the mutual information between a selected group of latent variables and the observation.

Thus, the performance evaluation of image matching and retrieval based on similarity with various feature extraction techniques is the main topic of this paper. The following items summarize the primary contributions of this paper:

• The study provides a performance comparison of sketched image matching using local descriptors produced by two distinct local feature extraction methods. Whether handcrafted or learning-based features were considered, the performance was assessed.
• The examination includes sketch matching with various levels of image quality (i.e., greater, and fewer degrees of lucidity).
• An influential notion is acquired from the comparison of the recommended methods based on handcrafted features.
• An image retrieval system based on InfoGAN is provided for retrieving sketches from large-scale datasets under different settings of sketch drawing quality. InfoGAN is trained for each dataset from scratch.
• Matching and retrieval performance, including the computational complexity, is assessed by applying time and space complexity measures in each experiment, and comparing with the state-of-the-art solutions and other existing retrieval systems.

The structure of this paper is divided into the following sections. The related work that describes feature extraction methods in recent research publications is covered in Section 2. The definition of the problem is shown in Section 3. In Section 4, the fundamental idea underlying the proposed InfoGAN model is shown. Additionally, the experimental protocol is used in the retrieval system experiments. The performance characterization and possible measurement metrics are presented in Section 5. A quick overview of the employed datasets is provided in Section 6. A brief description of the test scenarios is provided in Section 7. Next, an evaluation of the experimental tests is made clear in Section 8. Finally, the conclusion is provided in Section 9.

2. Literature Review

2.1. Overview of Feature Extraction Methods

Handcrafted features and learning-based features are both adopted for feature extraction. Both globally and locally specified image features are possible for each type. The mathematical concept underlying the various feature extraction methods is illustrated in this section.

2.1.1. Scale-Invariant Feature Transform (SIFT)

The SIFT descriptor was introduced by Lowe [9] as a brief invariant feature descriptor. It is frequently employed in features-based applications to identify and express local features. Over decades, SIFT has retained its place at the center despite the inclusion of additional extraction methods and new technologies.

SIFT descriptors are generated using the following steps:

• Important keypoint detection:

Scale–space extrema detection is used to identify these points as being scale- and orientation-invariant. The difference of Gaussian (DoG) function is used to calculate local extrema via scale–space extrema. The DoG function D (x, y, σ) is computed, involving the subtraction of neighboring scale levels of a Gaussian pyramid separated by a factor k. The subtracted Gaussian kernels at different scales are convolved with the input image I (x, y) as Equation (1) shows, where L (x, y, σ) is a scale–space representation at a given scale. Equation (2) is utilized to compute the scaled Gaussian kernel G (x, y, σ). Then, localization of these selected key potential points depends on their stability.

$$D\left(x,y,\sigma \right)=\left(G\left(x,y,k\sigma \right)-G\left(x,y,\sigma \right)\right)\star I\left(x,y\right)=L\left(x,y,k\sigma \right)-L\left(x,y,\sigma \right)$$

(1)

$$G\left(x,y,\sigma \right)=\frac{1}{2\pi {\sigma }^2}{e}^{\raisebox{1ex}{$-\left(x^2+y^2\right)$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\sigma }^2$$

(2)

b.

Orientation assignment for points of interest:

Depending on the local image gradient directions, one or more orientations are assigned to each keypoint position.

c.

Feature descriptor computation:

A feature vector is constructed with an appropriate size for the region surrounding each point. As a result, for each recognized keypoint, a SIFT descriptor is built using the local image content at the scale of features. A gradient orientation histogram for these points and their surrounding areas is used to construct the descriptor. Then, a search for the highest orientation value and others that account for about 80% of this value is performed. These orientations are considered as the primary orientations of the keypoints. Thus, for each detected point and region, SIFT generates a feature description that is invariant to both scale and orientation.

Nevertheless, with SIFT, little objects within images may produce a variety of features. Additionally, SIFT requires a lot of computations and sophisticated mathematics. Connecting points with sparse spatial features is also high dimensional [19,20,21]. This might be a hindrance for feature-based applications, since most applications require low feature descriptor dimensionality yet adequate and effective feature representation.

2.1.2. Oriented FAST and Rotated BRIEF (ORB)

Oriented FAST and rotated BRIEF (ORB) is a robust local feature detector proposed by Ethan Rublee [10]. ORB descriptors are estimated using Features Accelerated Segment Test (FAST) [22] and the enhanced Binary Robust Independent Elementary Features (BRIEF) [23] algorithms. To overcome the rotation variance of BRIEF and the noise sensitivity, Rublee created ORB as a quick binary descriptor.

The ORB descriptor is calculated through the employment of FAST to identify the keypoints of interest with effective orientation computation. The original FAST maintains the intensity threshold in the pixel circular center ring between its center and the adjacent pixels, where the Harris corner metric is used to order the top N FAST keypoints. The image scale pyramid is employed throughout time, and at each level of the pyramid, FAST features (filtered by Harris) are created. For corner orientation measurement, the intensity centroid method is used. The intensity centroid may be used to determine the direction, since it assumes that a corner intensity is offset from its center.

Equation (3) defines the moments of a patch, and Equation (4) may be used to calculate the centroid of the patch using these moments. Consequently, for creating a vector from the corner center O, Equation (5) makes it simple to determine the patch orientation where the quadrant-aware Arctan variant atan2 is used.

$${\mathrm{m}}_{pq}={\sum }_{x,y}{x}^p{y}^{q}I\left(x,y\right)$$

(3)

$$C=(\frac{m_{10}}{m_{00}},\frac{m_{01}}{m_{00}})$$

(4)

$${\theta =\mathrm{atan}2(m}_{01},m_{10})$$

(5)

As mentioned, ORB is based on BRIEF, which is a rotation variant algorithm. Thus, an enhancement is included in [10] for steering BRIEF based on keypoint orientation. For each feature set of n binary tests at location (x_i, y_i), the 2 × n matrix is defined as illustrated in Equation (6). Using the patch orientation θ and the associated rotation matrix $R_{\theta }$, a “steered” version $S_{\theta }$ of $S$ is built as indicated in Equation (7).

$$S=\left[\begin{array}{c}{x}_1,\dots \dots ..,x_n\\ y_1,\dots \dots ..,y_n\end{array}\right]$$

(6)

$$S_{\theta }=R_{\theta }S$$

(7)

Hence, Equation (8) provides the steered BRIEF operator.

$$g_{\mathrm{n}}(P,\theta ):=f_n\left(p\right)|(x_i,y_i)\in S_{\theta }$$

(8)

Angle discretization is performed using values from the lookup table for the pre-calculated BRIEF patterns. The suitable set of points S is employed with keypoint orientation to compute its descriptor. The most crucial property is that each bit characteristic in BRIEF has a wide range of values and a mean that is close to 0.5. It spreads out more as it is pointed in a keypoint direction. On the other hand, a feature with large variations is more discriminative, since it reacts differently to different inputs. BRIEF furthermore offers the advantageous quality of uncorrelated testing, which means that each test influences the outcome. To identify uncorrelated binary tests with a mean, ORB does a greedy search through all conceivable binary tests.

2.1.3. Information Maximizing GAN (InfoGAN)

Labeling a large amount of training data is difficult for the CBIR system to work on large-scale datasets. The supervised training for all target images limits the generalizability of the learned deep representations to new classes [24]. Thus, the insights are either to semi-supervised or unsupervised learning techniques. Unsupervised learning may be defined as the overall issue of obtaining a value from a massive amount of unlabeled data. Generative modeling is the primary driving force behind a sizeable portion of unsupervised learning research. The two most popular generating models are the Variational Auto-Encoder (VAE) and the GAN. The focus of this paper is on GAN and its variants.

GAN was introduced in 2014 [17] to address the problem of unsupervised learning. It is composed of a generator and discriminator deep neural network. The generator network uses random noise as an input and produces realistic images as an output. The discriminator accepts both fake and real images and attempts to determine if the input is real or false as a conventional neural network classifier. If the discriminator detects the false image that the generator creates during training, it is “penalized”. To “fool” the discriminator, the generator therefore learns to create fake images that are increasingly like the real ones.

Recently, GANs have shown some excellent and encouraging results in producing aesthetically realistic images. They are commonly used to synthesize new data, especially images. The power of artificial intelligence is not limited to only generating realistic images, it is extended to other applications such as image-to-image translation, high-quality image generation from low-quality images, image generation from text, and other applications [25]. Additionally, normal GANs do have a shortage as they provide no control over the types of images that are generated [26]. Besides, it is simple to build generative models with arbitrarily representations. This motivation stems from the idea that the ability to synthesize, or “create”, the observed data implies some level of understanding.

The purpose of representation learning, a prominent approach for unsupervised learning, is to use unlabeled data to develop a representation that exposes significant semantic features as readily decodable variables. One that explicitly captures the salient properties of a data instance is the disentangled representation. It is useful for relevant but unknown tasks such as problematic unsupervised learning, since the relevant downstream tasks are unknown at the training time. For tasks such as face and object identification that naturally need knowledge of the salient features of the input, a disentangled representation might be helpful. A competent generative model is expected to automatically pick up a disentangled representation of the information-maximizing GAN. It is known as InfoGAN.

InfoGAN is a modification to the GAN design that includes control variables that the architecture automatically learns and uses to govern the output image. These control variables, for instance, include style, thickness, and type for creating representations in problems of handwritten numbers or other applications. By maximizing the mutual information between a fixed small subset of the GAN noise variables and the observations, InfoGAN makes construction interpretable and meaningful representations simpler. InfoGAN provides additional information on top of random noise to the generator and makes it use the information, while creating false images to govern the sorts of images that are created. The additional information stream must be related to the desired features. A second network is added (commonly referred to as the auxiliary network) to replicate the additional information that was supplied to the generator. In this method, the auxiliary network cannot accurately recreate the additional information, forcing the generator to utilize it as if it does not exist, and the generator is “penalized” for doing so.

2.2. Recent Related Work

Sketches are uncolored, freehand drawings without a natural view. This makes it hard to retrieve matched sketches from images of different contents. The efficient and optimal capturing of image content with low-dimension feature vectors is crucial for the speed of matching between comparable images. As usual, object edge features and other detected features are frequently combined for feature extraction to perform matching and retrieval of sketches. In [27], the tensor-based image descriptor was presented to extract global features for edges in images. It is superior to the edge histogram descriptor. However, global extracted visual features might not work effectively when the target images have abundant background clutter. They might be used as additional features to improve the image retrieval accuracy, which is mostly based on local features [11].

The shape-to-image matching problem was addressed using the Angular Radial Partitioning (ARP) method in [28], where radial and angular partitioning are combined to enhance angular partitioning. The image is divided into M × N sectors, when the edges are found. This results in representing the entire image M × N sectors, where M is the number of partitioning angles and N is the number of radial partitions. However, the presented technique is vulnerable to affine transformations, making it difficult to match unperfectly-aligned, scaled, or rotated images. Additionally, it is hard to improve efficiency, speed, computational complexity, and performance of the retrieval system.

The Angular Radial Orientation Partition (AROP) technique, which employs global and local information in the matching process, was proposed in [29]. This technique depends on salient and global contour maps as two different types of contour maps that are extracted from images. The Berkeley detector is used to recover the contour maps, and Regional Contrast (RC) is used to extract the image salient areas from the dataset images. The AROP features are then specified using the retrieved candidate contour maps. In fact, by using orientation partitioning, the recently reported AROP feature extraction methodology enhances the ARP method. The AROP feature map has total dimensions of M × N × O. Thus, the AROP feature map represents each sector by several pixels under various orientation maps, while still being flexible enough for scaling and translation. The AROP technique is orientation-invariant. In addition, it has a high computational cost, which will be inconvenient as it slows the matching process.

In [30], the Edgel (edge pixel) index mechanism was introduced for pixel-to-pixel matching. It resolves the shape-to-image matching issue using the local feature matching technique. A mind finder is a real-time image retrieval system that matches pixels at the pixel level. Its objective was to deal comprehensively with the Sketched Based Image Retrieval (SBIR) problem. Oriented Chamfer Matching (OCM), a similarity metric for contour comparison, was used to construct distance maps. The Edgel index structure is created by converting these maps into hit maps, which are binary similarity maps. However, the high computational cost of this technique makes it problematic, when dealing with local affine changes. This is like the proposed idea of this paper, where ORB should be used as a binary descriptor when using handcrafted feature extraction methods. For using ORB, not only visual features within images are represented as binary descriptors, but low computational complexity is also gained. The spatial distance measurement for matching with this sort of descriptors may be simply carried with the Hamming distance via bitwise XOR or bit count. As a result, matching and retrieval of images with an efficient visual feature representation will be more quickly.

The bag-of-features approach was introduced in [31] to use local features to solve the shape-to-image matching conundrum. These local features are extracted using the SIFT descriptor and the Canny edge detector. Despite this, bag-of-feature techniques have been shown to perform better than traditional global descriptors at the expense of a high computational cost. Additionally, SIFT enforcement is not the ideal choice because of the sparse spatial distribution of its detected keypoints and the huge dimensions of its calculated descriptors [32].

TOP-SIFTs, a descriptor selection approach based on dictionary learning, was presented in [33] to eliminate redundant features. Dictionary learning, which works with sparse data, is reserved for a few excellent geographic distribution features. As a result, there will be two practical shortages. The first is with SIFT itself, which is complicated in terms of both mathematics and processing. The second issue is the selection strategy since the method demands that the whole descriptor computation be completed first before deploying the selectivity process. The combination of these two requirements has resulted in the introduction of additional computation enumeration. Thus, similarity matching in any feature-based application will take longer times. The idea of matching based on approximate forms was first proposed in [34], where the object is represented as a collection of recognized primitives. Each primitive has a description of its type and a few defining parameters. A quick-access method has been used, but it has only been tested on a tiny dataset. This could hardly be sustained, with the exponential growth of web images.

In [35], medical images were retrieved based on their content through a method for generating hash codes based on a feature selection process for the down-sampling of the extracted deep features. However, dependence on hash tables may lead to performance deterioration if many collisions are experienced. The more data there is, the more likely there will be a collision. Unfortunately, more calculations are added, increasing the complexity of the retrieval system. For example, as noted before, feature selection involves the computation of the feature vector before the selection is applied, leading to more additional computations.

In [36], a CBIR system was introduced using GAN to retrieve sketched images for the search of Merchant marks between documents. These marks are line drawings that are devoid of both texture and color. However, GANs lack a proper theoretical explanation and suffer from issues such as mode collapse, non-convergence, and instability during training [37]. To address these issues, researchers have proposed theoretically rigorous frameworks such as InfoGAN and others [38]. We will adopt InfoGAN in this paper for sketched image retrieval. In addition, the previously utilized sketched image datasets are completely different from that used in the proposed research work in this paper. We will work on datasets of different content and different clarity levels.

3. Problem Definition

Sketched image retrieval has a big role, especially with the popularity of touch screen devices and many online drawing programs. Furthermore, the newly introduced brand of search by images depends mainly on the subjectivity of users. This differs from one user to another, resulting in huge databases of choices and image sets. Moreover, it is beneficial to many government organizations for finding forensic evidence in crimes. However, with the wide range of usage and applications, matching or retrieval of similar sketched images is one of the most complicated problems to address. The challenge arises from being able to discern sketched shapes or objects from other frequent images. The lack of color features and high level of details hamper the recognition of contents within such sorts of images. In addition, the painter’s fantasy and the degree of lucidity of his drawings highly affect the precision of the matching process.

All the above factors boost the hitch of the similarity matching process, which is required to be rapid and precise. Two pivots drive this process; the first is the algorithm utilized in matching, while the second is the efficient visual representation of such images. Most feature-based applications require that the image content be efficiently and adequately captured in low-dimensional feature descriptors, especially with the huge growth of databases. Thus, the challenge is efficiently recognizing and representing sketched image contents for a large-scale database of different clarity degrees. This raises the difficulties and challenges behind the applied extraction method, whether it depends on handcrafted or learned features.

These methods are required to identify feature keypoints and descriptors, which have perfect localization or Probability Distribution (PD) to differentiate objects inside images. The number of keypoints must also be sufficient to correctly depict visual content, with the quality and kind of images having the greatest effect on the number of these points.

Furthermore, millions of people using devices with constrained processing and storage capacities will not be able to use high-dimensional vectors, as the complexity of the system is burdened by the enrichment of image content and database scale. Thus, there is a trade-off between the representation of such image content and quality and the retrieval system complexity.

Therefore, the ability of the extraction techniques serves as the fundamental driving force behind the entire process of enhancing performance accuracy to properly characterize image contents with strong spatial distribution points with low dimensions or adequate descriptors.

Thus, the presented study examines how drawings behave as black lines drawn over a transparent background that may be interpreted as either existing or not or as logic one or zero. The assessment study is made up of a number of test cases, each of which assesses the performance of matching for a sketched image type under different levels of free-hand drawing clarity. To verify the proposed concept, ORB is utilized as the binary local feature extraction algorithm to assess the similarity matching performance between sketched images. In addition, the SIFT is considered a benchmark for such kinds of methods. Despite being suggested as a substitute for SIFT, ORB has not been utilized widely in the literature. Hence, in this research, the performance of ORB is assessed practically over different-clarity sketch datasets compared to SIFT. The SIFT performance is not only compared to the corresponding methods based on handcrafted features and those based on learning-based features. We also look at how the spatial distribution of the extracted feature keypoints is affected by the sensitivity of both feature extraction methods and sketch image types. The primary flaw of these algorithms is how inconvenient they are for huge datasets. As a result, it is possible to use learning-based features, while using the same notions where shapes and objects drawn in sketches can be represented as separated variables.

The objective of this study is to evaluate the manual feature extraction methods and employ a novel retrieval system based on InfoGAN. InfoGAN is selected to build an image retrieval system, since it can achieve a disentangled representation that explicitly reflects the salient properties of a data instance. The discriminator model of the trained InfoGAN might be employed as a feature descriptor, once it has been trained. It offers full learning for visual features that were taken from the images used for training. According to the theory, the network picks up useful features from images based on shared knowledge. It seems that it provides an adequate and acceptable feature representation for images of different types. Thus, an InfoGAN-based image retrieval system for sketched images is proposed in this research work. Additionally, the retrieval performance evaluation for the proposed system will be conducted to gauge how effectively it can learn features to recognize objects in sketched images.

4. Proposed InfoGAN Architecture

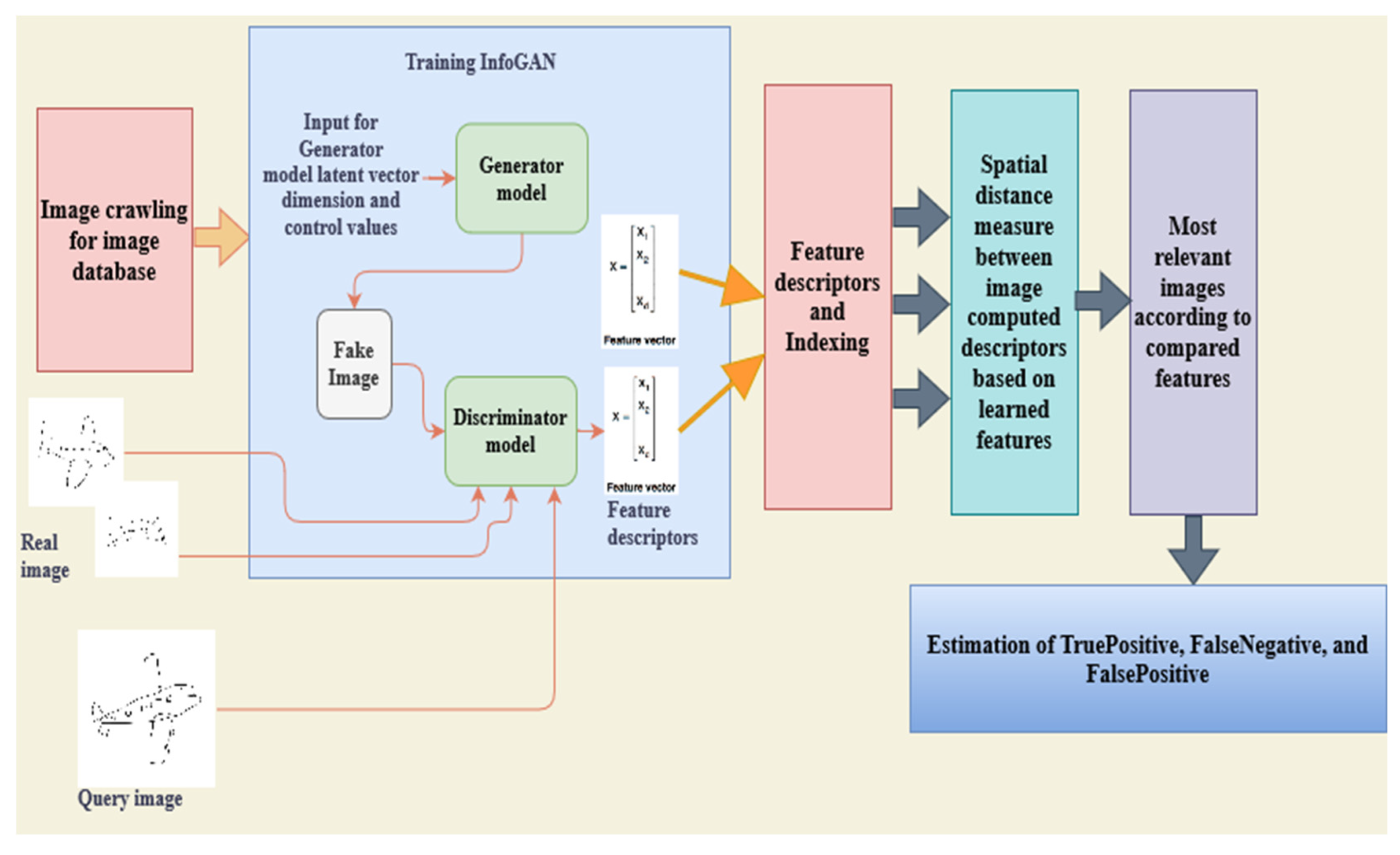
Here, image crawling is used to build the database, as Figure 1 illustrates. The proposed image retrieval system based on the created InfoGAN is tested twice by working on each image set, separately. Training, testing, and validation sets are separated for each dataset. The InfoGAN system is then trained by each crawled training set, and the InfoGAN-trained models are stored each time a dataset is used for training. Therefore, each dataset has a training image set used to train the InfoGAN models. By the way of random selection, the retrieval system chooses a group of query images from a different randomly-selected category, as shown in Figure 1. Hence, a set of reference query images is encoded by this model.

This raises a challenge for the proposed system, as learning all visually-confined features from all dataset images is required to accurately predict new unlearned query instances (i.e., split test set). Thus, the contents of each image are represented and well-learned as a set of significant features and vectors derived from images by the trained discriminator model of the InfoGAN model. In other words, the discriminator model learns deep and finely-detailed features from the training set for each dataset, individually. The output of the discriminator provides a feature descriptor of length 1,350465.

Then, all images are successfully indexed, and similarity matching is performed based on the spatial distance measured between the extracted features for each encoded query image and those taught by each trained model. The nearest matched neighbors in the feature space are calculated for each query-train combination using the distance metric (i.e., Euclidean distance). The most pertinent matched images are found using features extracted with the InfoGAN model. Finally, the number of true and false matches is estimated. Recall, 1-precision, and F-score metrics are computed using Equations (9)–(11) to evaluate the retrieval performance. Each query image is compared to each region in all training images.

5. Performance Evaluation Criteria

Similarity matching serves as the primary engine in many feature-based applications. It refers to the acquirement of the q best-matched points in an image to the previously extracted N points of interest in another image [4], depending on the spatial distance measured between descriptors that were extracted from images by the feature extraction technique. Two performance metrics, recall and 1-precision, are computed. They are frequently displayed as precision versus recall graphs (PR graphs), where each can have numerical values between 0 and 1 [39,40].

According to Equation (9), recall is a numerical metric that measures how many properly matched points are obtained compared to all points that have to be compared. It indicates the ratio of the model results of proper prediction for the positive class to its accurate foreseers of the negative class. As shown in Equation (10), precision is a numerical metric that counts the number of false matches compared to all matches. It refers to the ratio of the model results of proper prediction for the positive class to its results when forecasting the positive class, inaccurately. It is worth noting that results include the sum of multiple predictions of the model for each query image over different category datasets as shown in Equation (9)

$$\mathrm{Recall}=\frac{\mathrm{Number}\mathrm{of}\mathrm{correct}\mathrm{matching}}{\mathrm{Total}\mathrm{number}\mathrm{of}\mathrm{correspondence}}\mathrm{or}\frac{\mathrm{Sum}\mathrm{of}\_\mathrm{TruePositive}}{\mathrm{Sum}\_\mathrm{TruePositive}+\mathrm{Sum}\_\mathrm{FalseNegative}}$$

(9)

$$\mathrm{Precision}=\frac{\mathrm{Number}\mathrm{of}\mathrm{false}\mathrm{matching}}{\mathrm{Total}\mathrm{number}\mathrm{of}\mathrm{matches}}\mathrm{or}\frac{\mathrm{Sum}\mathrm{of}\_\mathrm{TruePositive}}{\mathrm{Sum}\_\mathrm{TruePositive}+\mathrm{Sum}\_\mathrm{FalsePositive}}$$

(10)

F-score is another performance metric for the accuracy of matching. As seen in Equation (11), combining the precision and recall metrics yields the F-score. It is the harmonic mean of the two metrics. It considers errors that are both false positive and false negative.

$$\mathrm{F}\text{-}\mathrm{score}=2\times \frac{\mathrm{Precision}\times \mathrm{Recall}}{\mathrm{Precision}+\mathrm{Recall}}$$

(11)

To evaluate how well the models extract features from images with strong spatial and discriminating traits and retrieve them, recall, 1-precision, and F-score are estimated for each sample. In addition, the time spent on visual feature extraction, indexing, and picture querying is included in the proposed evaluation. As the computational efficiency is considered, this improves the retrieval mechanism effectiveness [41].

6. Datasets

Two datasets with different categories are examined in this paper. The first is entitled ImageNet-Sketch [42]. It includes fifty images in each of the 1000 classes and has a total of 50,000 images. Figure 2 displays examples of different images within each category. Google image searches for “sketch of __”, where _ is the common class name, were used to create this dataset. Only “black and white” color schemes were used for the Google search. The initial Google search included 100 query images for each class, and the images were carefully cleaned by removing those that were extraneous or for classes that were similar but not the same. After manually cleaning of the dataset, there were fewer than 50 images for some classes. Thus, the dataset was gauged by flipping and rotating the images. Therefore, the extraction techniques and the suggested InfoGAN retrieval system are evaluated for both augmented sketched images. This increases the difficulty of similarity matching inside these sorts of data, since an effective representation of the image content is needed with an efficient matching algorithm. The clarity of paintings for sketches affects the image retrieval system performance. The quality of the query sketched images bridges the gap between the user’s subjective expectations and the retrieved results. A wide domain separates a crude sketch or freehand drawing from adequate retrieved results.

The second dataset, entitled TU Berlin [43], was used, as shown in Figure 3. This figure shows sample instances from the different categories of the dataset. There were over 20,000 low-quality drawings in the second dataset. They were uniformly dispersed over 250 different object categories. As a result of the image quality and the need to convey visual material in brief descriptors, the problem became more complex. The amount of retrieved features increases along with image quality. The advantage of the extraction technique employed is that it lessens this trade-off, while also narrowing the discrepancy between the intent of the user and the results delivered. This is the algorithm capability to efficiently convey important differentiating elements in a brief description. The fact that these sets were utilized for training the involved InfoGAN model must be noted. Additionally, a few images from each dataset for each category were chosen. It should be emphasized that the ImageNet-Sketch dataset exhibits high-quality sketches with a rich image content. Figure 2 displays examples of the sketched images from this set. The second set, termed Sketch, on the other hand, exhibits low-level hand drawings with fading details, as shown in Figure 3. Additionally, both datasets contain images of items with varying sizes and locations.

7. Experiments and Results

At first, this section outlines the overall method flow for the proposed test experiments and the related results. Second, it compromises several experimental scenarios for the performance assessment of sketched image matching and retrieval by either handcrafted or learning-based features. The proposed experiments matching and retrieval performance is based on the spatial distance extracted features. The InfoGAN and handcrafted features are also appropriate for two levels of freehand drawing clarities.

Time and space overhead and matching performance are two examples of how feature extraction methodologies have hindered system efficiency and complexity. The time complexity of any system is determined by how the execution time grows over the image dataset scale. Space complexity describes how much memory an algorithm uses as the input increases. Therefore, this section also assesses all provided test cases from the perspective of overloading the system. Additionally, the matching performance and system complexity for each case are evaluated. For matching performance evaluation, performance metrics are computed for each type of handcrafted features. In addition, performance metrics are computed for each instance of the learned features with the InfoGAN retrieval system. The performance of such a proposed InfoGAN system is compared to those of SIFT, ORB, state-of-the-art CNN networks, and other counterparts in [44] for complete insight.

7.1. Image Matching Based on Handcrafted Features

7.1.1. Test Cases Based on Handcrafted Features

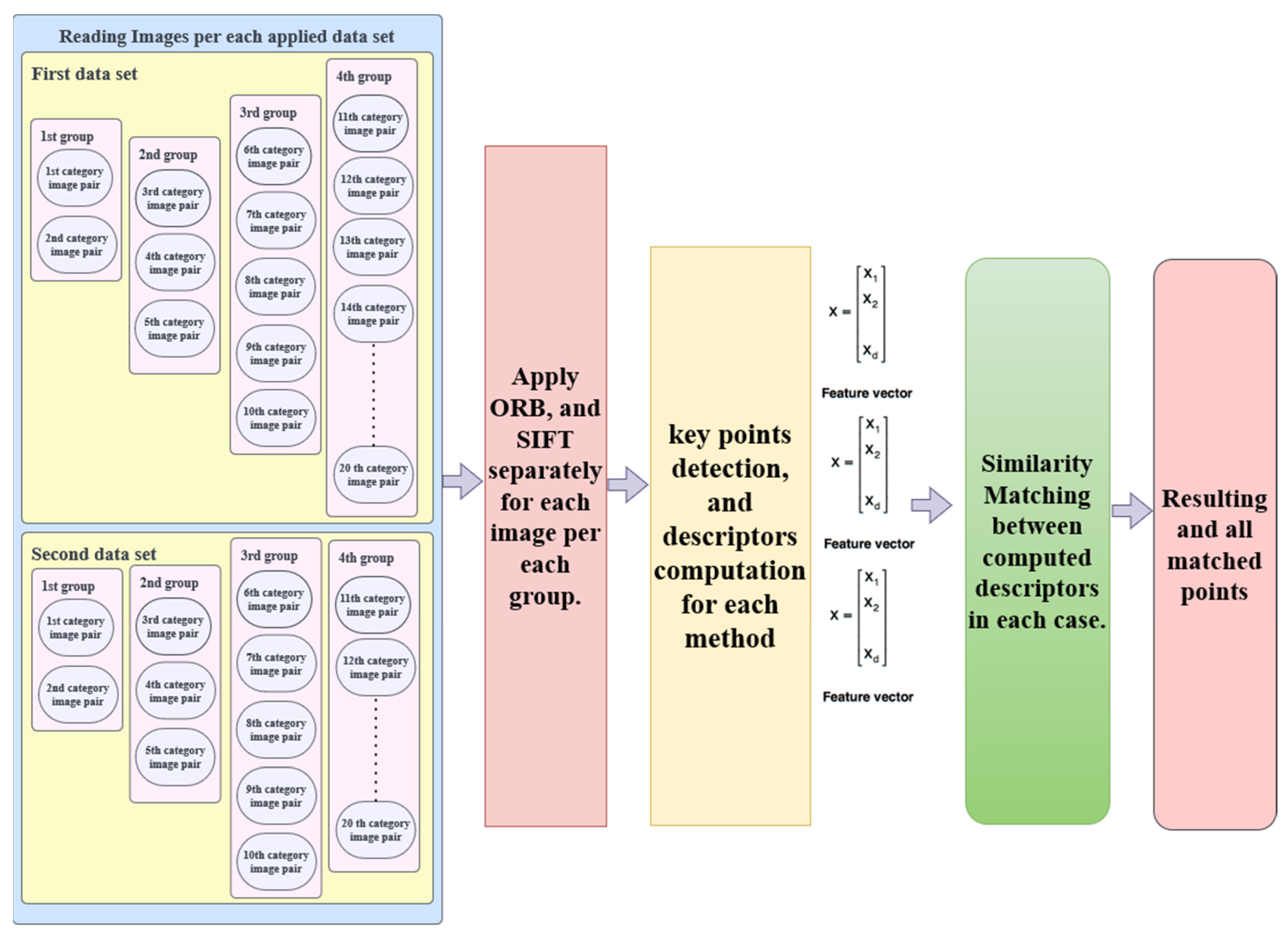
Each method based on handcrafted features is assessed twice on each dataset independently. Four small groups were created from each dataset; each was generated by random selection from different categories of the applied dataset. Each group was divided into several image pair subsets, each consisting of a reference query and training images chosen from the same category. The numbers of images selected per group are 8, 12, 20, and 40.

The first group is composed of 8 images in total forming four query–train image pairs, and each pair is of the same category. The second group consists of six query–train image pairs made up of 12 images, each of which belonging to the same category. In the same way, the third group has a total of 20 images composed of ten query–train pairs, each pair belonging to the same category. Finally, the fourth group has 20 query-train image pairs of 40 images in total; each is also in the same category.

As Figure 4 shows, per group (i.e., each image pair within the group), two local feature extraction methods were used independently for each image. Depending on the SIFT or ORB method, most keypoints of interest and their associated feature descriptors are found within each image. Therefore, the contents of the image are represented as a bundle of important features and vectors. The number of these extracted points for each approach and the descriptor dimensionality are determined. In each instance pair per group, similarity matching is performed using the spatial distance between these calculated descriptors. In other words, the computed query image descriptor is matched with its corresponding value for the training image (i.e., query–train pair).

The nearest matched neighbor in the feature space is therefore determined for each method, using a specific distance metric. The ORB assessment is performed using Hamming distance, while the SIFT assessment is performed using the Euclidean norm to perform spatial matching. The brute-force matcher (Bf-matcher) method [45,46] is used for similarity matching based on distance estimations, and only the closest matched points are returned. At the end, the numbers of true and false matches are checked; recall and 1-precision metrics are computed using Equations (9) and (10) to evaluate the matching performance. In Equation (9), the phrase “number of correspondences” refers to the total number of matching areas between the image pairs. The number of correspondences inside the suggested test instances is calculated using all visual features that were collected from the training image. Every feature keypoint (region) from the query image is compared with every feature from the training one.

Different similarity matching metrics, such as Hausdorff distance and/or Dice Similarity Coefficient (DSC), can be used. However, the authors of [47] stated that there is not much difference between using Hausdorff distance and Hamming distance. Thus, exploring such metrics could be one of the future works.

7.1.2. ImageNet-Sketch Dataset Test Cases

As mentioned in Section 7.1.1, four groups were chosen from the predefined ImageNet-Sketch dataset in Section 6. Each group was created from several image pairs. Figure 5 shows the six chosen image pairs per the second group, created by a random selection of image pairs from six different categories. In other words, several query-training images of the same object were chosen to make up an image pair per each created group, as Figure 4 illustrates. Then, for each sketched image inside each pair of each group, SIFT and ORB are independently applied. For SIFT or ORB, the number of detected keypoints and the descriptor dimension are calculated per image in the group. The descriptors of each image in the pair are spatially compared. All matching points are then found using the determined difference between these descriptors.

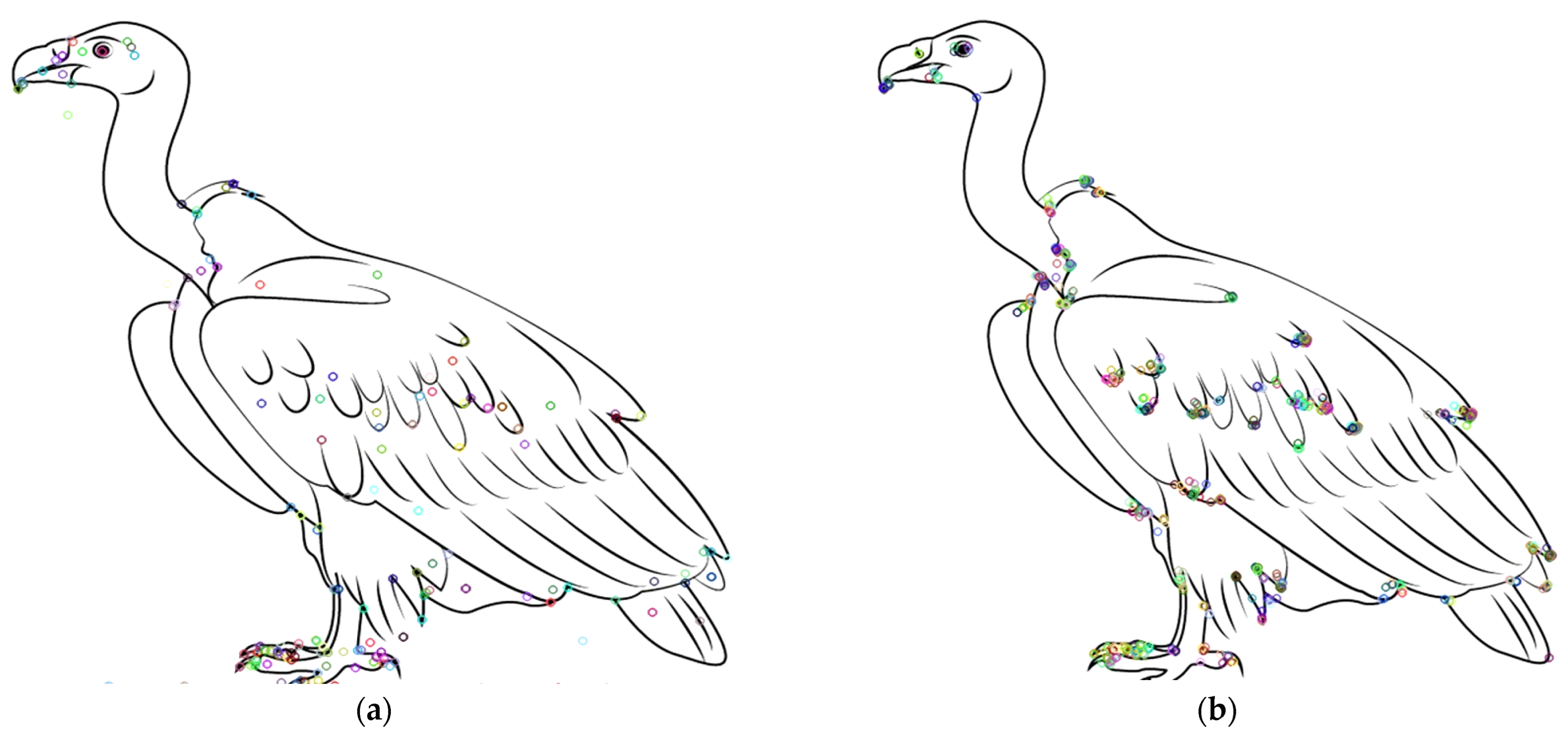
Figure 6 and Figure 7 display the significant points that SIFT, and ORB discovered from images of the second formed group. The figures demonstrate that SIFT performs poorly in object discrimination within sketched images. Figure 8a,b are used to infer this, as the extracted keypoints by SIFT and ORB from the images of this group are illustrated carefully. According to the extracted points’ spatial Probability Distribution (PD), ORB points are better than SIFT in representing the sketched-out drawn objects. Thus, ORB allows better feature extraction ability for well spatially-distributed feature points that discriminate the hawk countenance, i.e., eyes, beak, feather detours, legs, etc. The figures demonstrate how ORB outperforms SIFT in revealing visual clues that identify objects inside high-clarity sketches. This presumably impacts how well forms inside images are lined up.

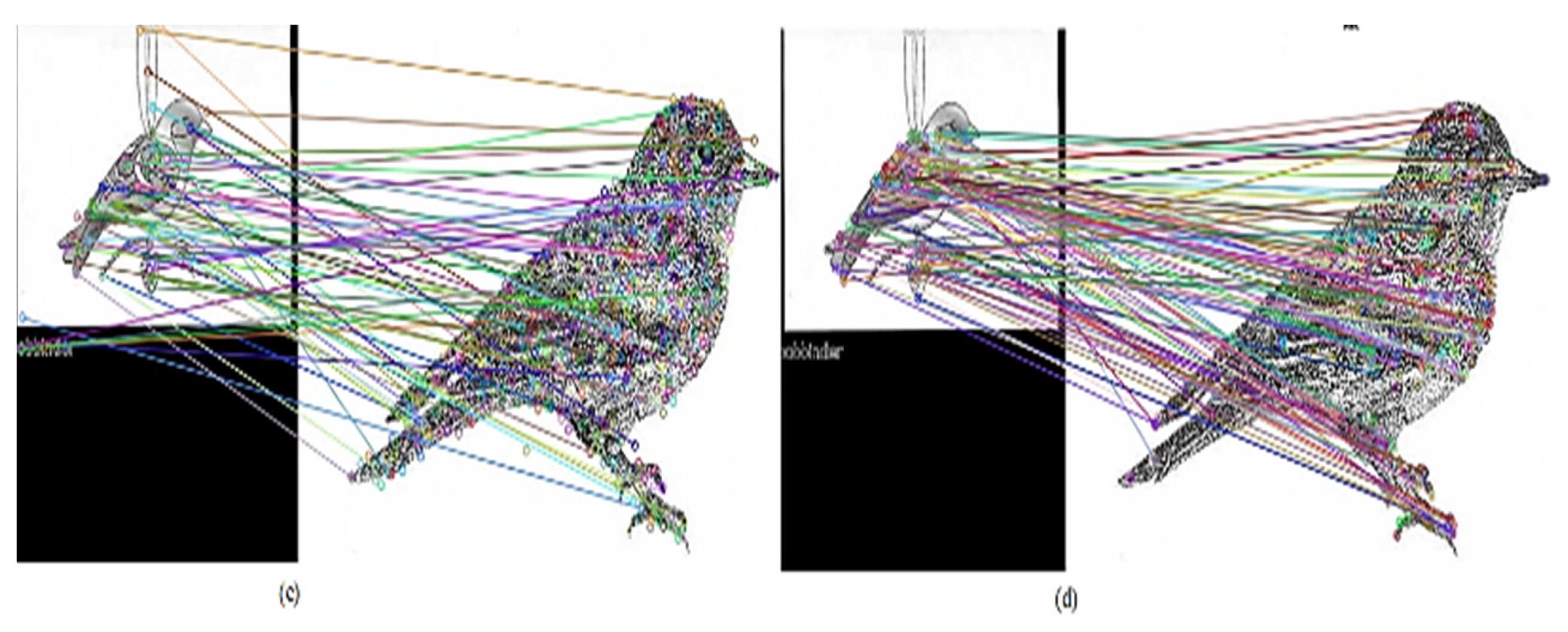
For the second created group, Figure 9a,c show the net matched points between the first two sketched query–train image pair computed descriptors using SIFT. In addition, Figure 10a,c,e illustrate the net matched points between some of the other query–train pairs, when SIFT is applied. For the ORB case, the net-matched points between the query and the first three train image pair descriptors are shown in Figure 9b,d. Similarly, Figure 10b,d,f show the matching between generated descriptors for the other pairs. The figures illustrate how well objects are matched within image pairs, reflecting the motive behind ORB usage compared to SIFT in object segregation within images. This might have been brought on by how many true/false matches there were for each image pair. As can be seen from the figures, ORB points correspond to objects inside pairs of sketch–train images. This is attributed to its ability to differentiate objects without redundant features, as seen in the SIFT case. In the SIFT example, many detected points are matched with undiscriminating redundant features, leading to high false matching. This is attributed to the sparse keypoint distribution of the SIFT.

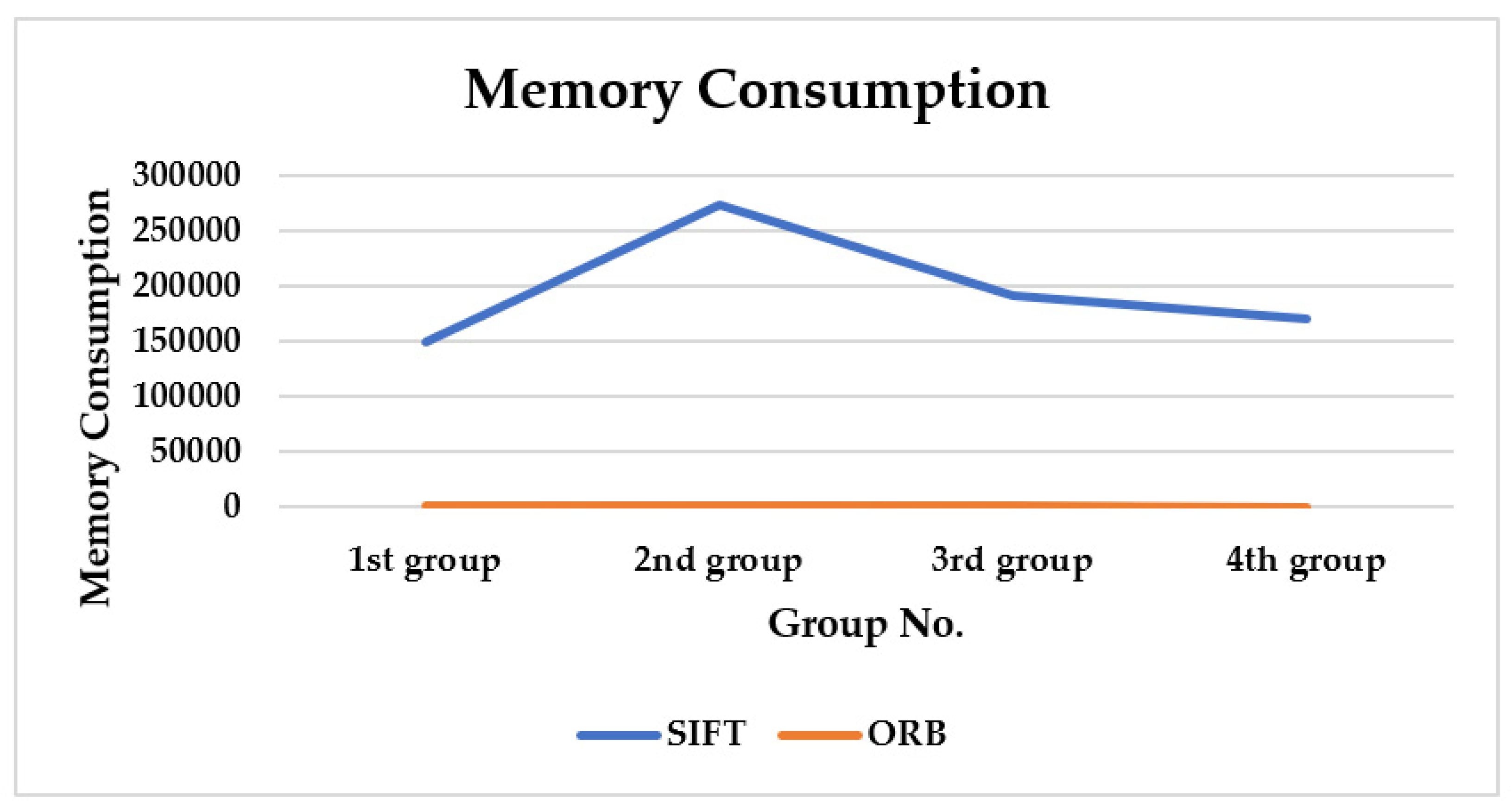
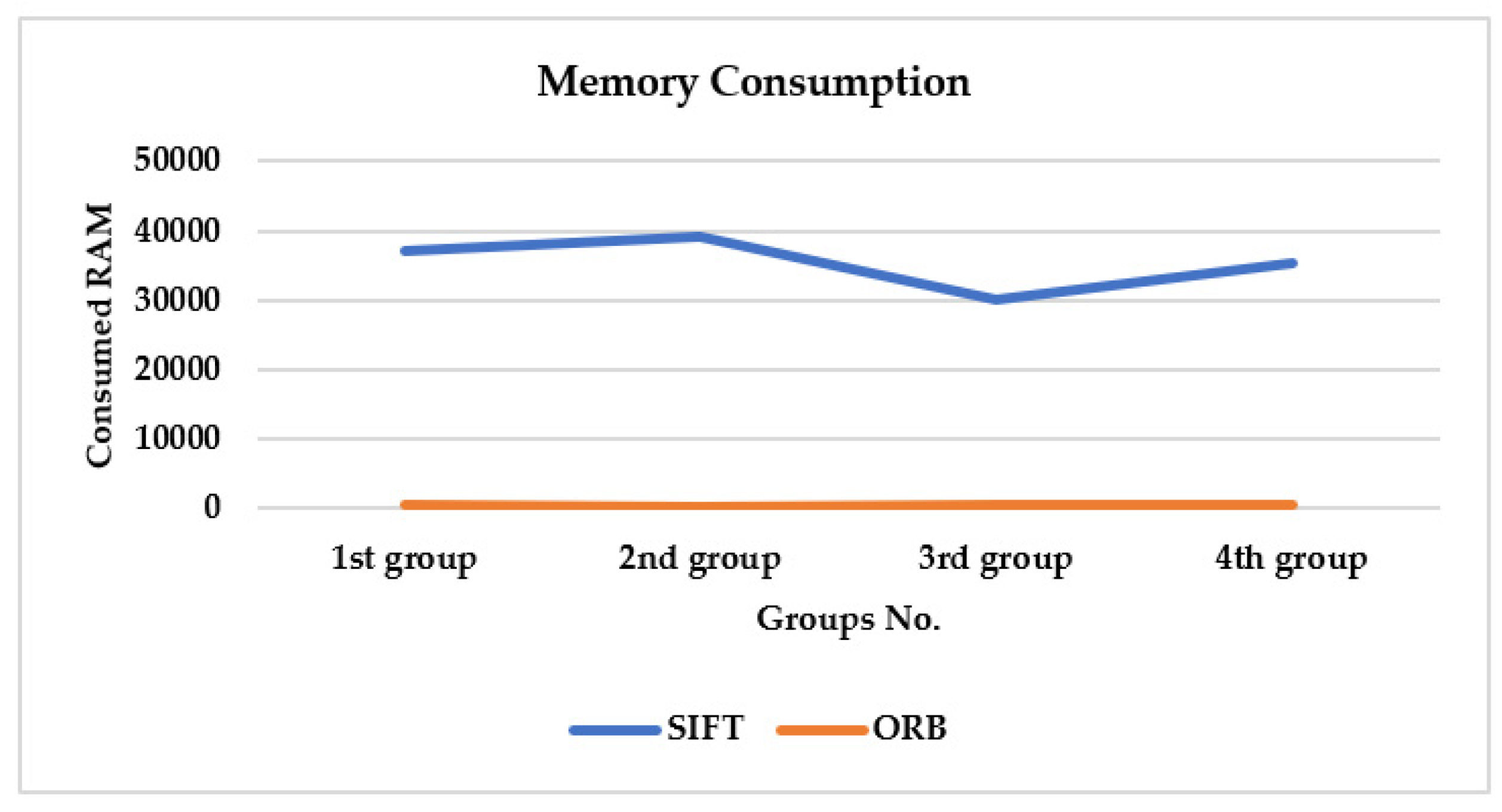
Memory Requirements: For both SIFT and ORB, the performance of the four groups is illustrated in

Table 1. Computed performance metrics for handcrafted features over the four groups of the ImageNet-Sketch dataset.

Method	Performance Metrics	Groups No.	Value
SIFT	Average memory consumed (MB)	1st	148,944
		2nd	273,568
		3rd	192,204.8
		4th	170,409.6
	Time consumed (s)	1st	15
		2nd	37.32
		3rd	20
		4th	55.43
	Average computed recall	1st	0.8
		2nd	0.883
		3rd	1.24
		4th	1.18
	Average computed 1-precision	1st	188.9233
		2nd	513.0511
		3rd	248.1415
		4th	252.0776
ORB	Average memory consumed (MB)	1st	493.75
		2nd	495.833
		3rd	493.15
		4th	482.05
	Time consumed (s)	1st	9.7
		2nd	33.27
		3rd	14.35
		4th	39.76988
	Average computed recall	1st	3.1595
		2nd	3.7458
		3rd	5.57384
		4th	2.5509
	Average computed 1-precision	1st	30.19503
		2nd	27.98405
		3rd	19.2868
		4th	12.53546

. For the randomly-selected image pairs within the four groups, the average required memory for SIFT is 785,127 MB, compared to 1964.783 MB for ORB, as illustrated in Figure 11. This indicates that the SIFT uses around 400 times more RAM than ORB.

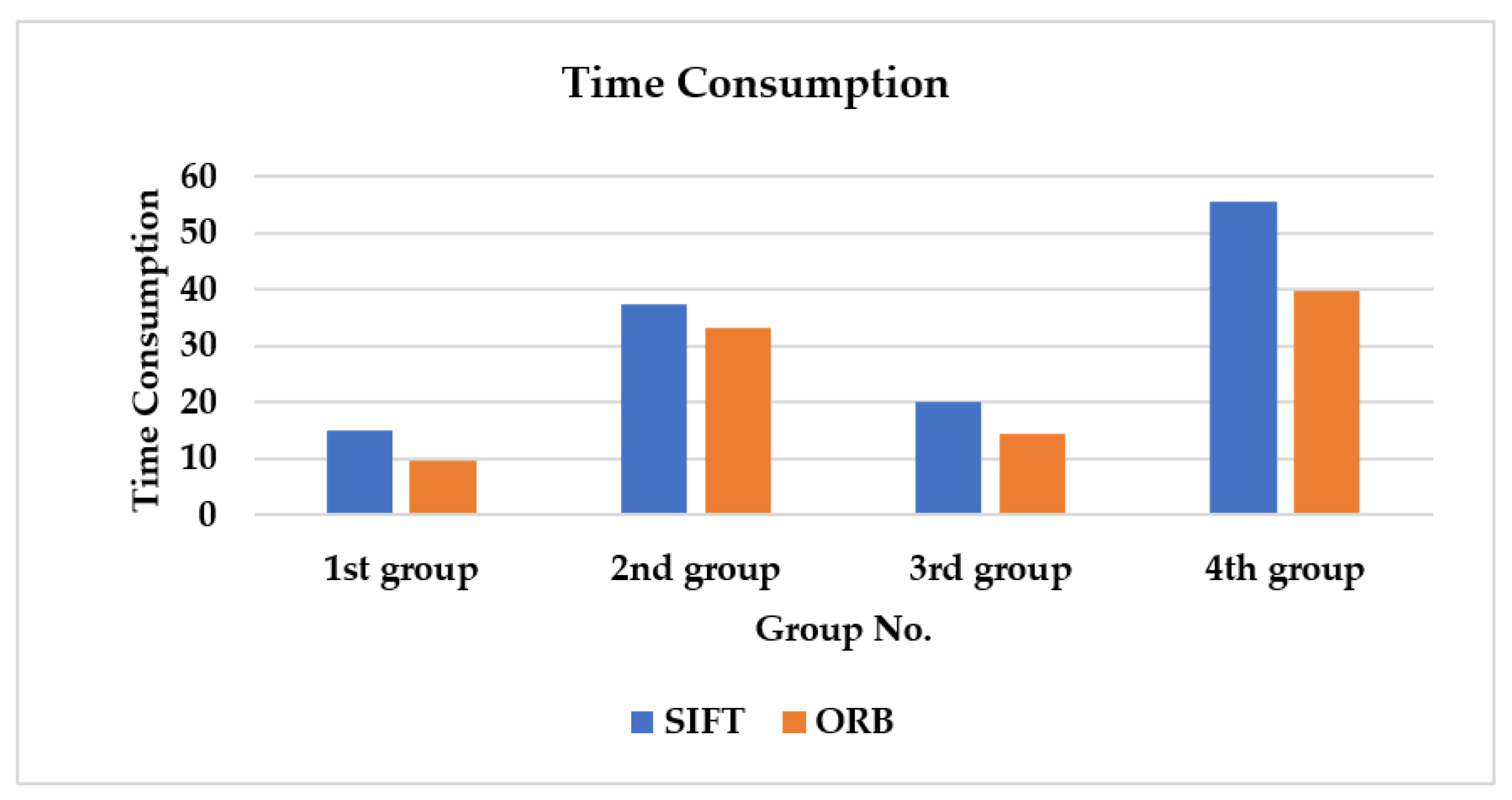
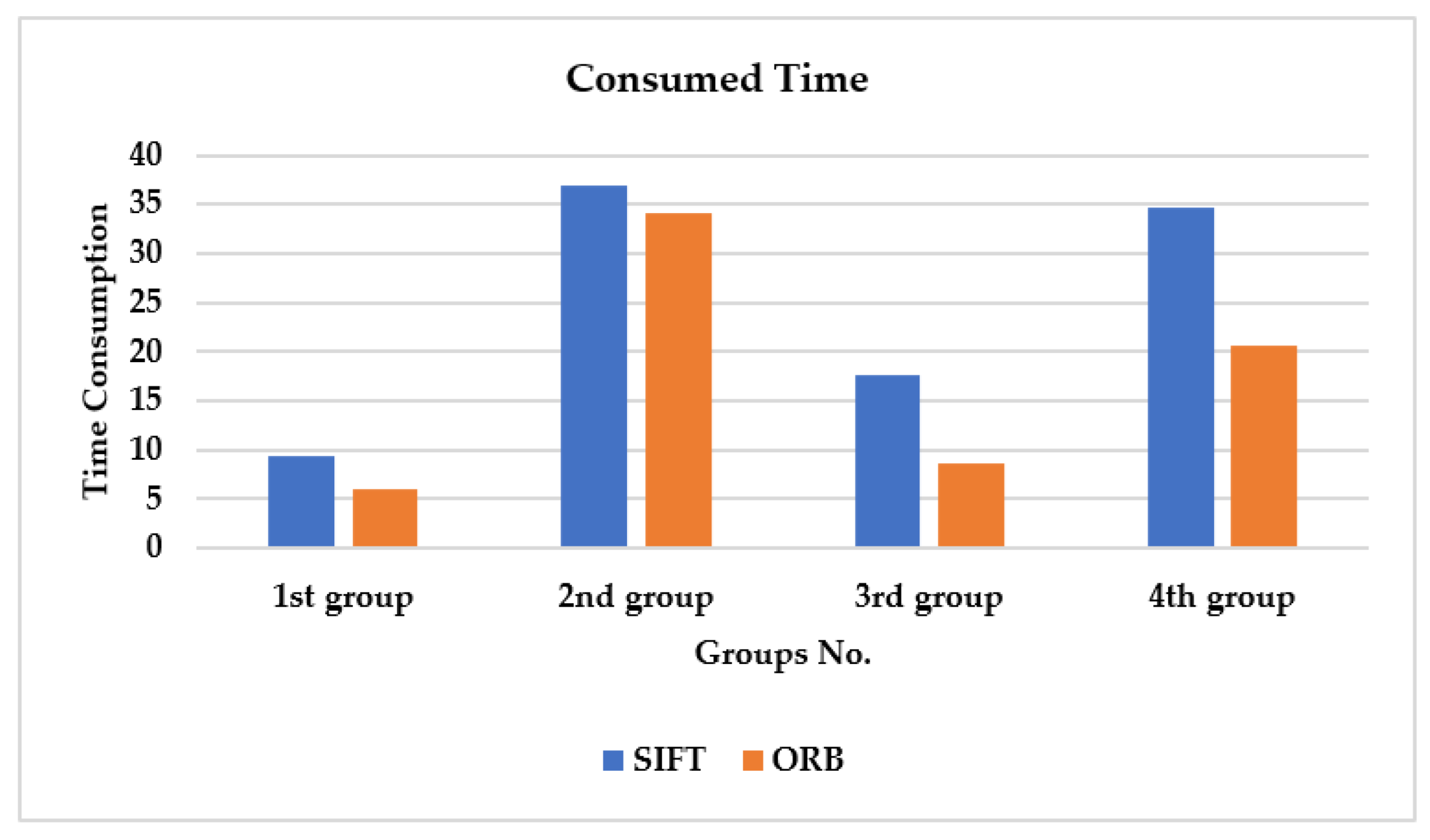
Time Consumption: The computation and matching time taken for SIFT descriptors is about 128 s, while for the ORB case it is 97 s. As can be seen in Figure 12, the time consumed by SIFT is much larger than that of ORB over all four groups. However, both still require a large time for groups two and four.

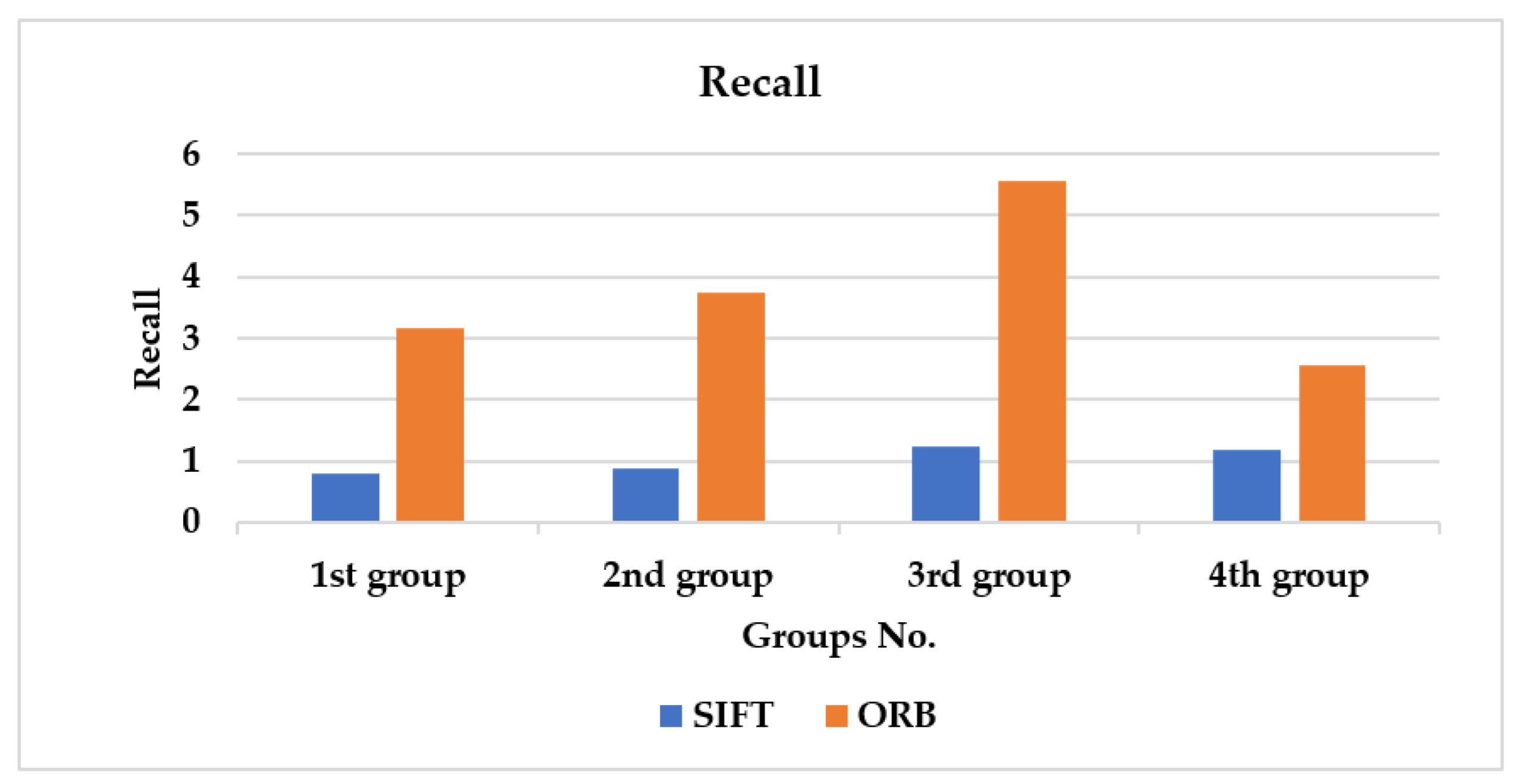
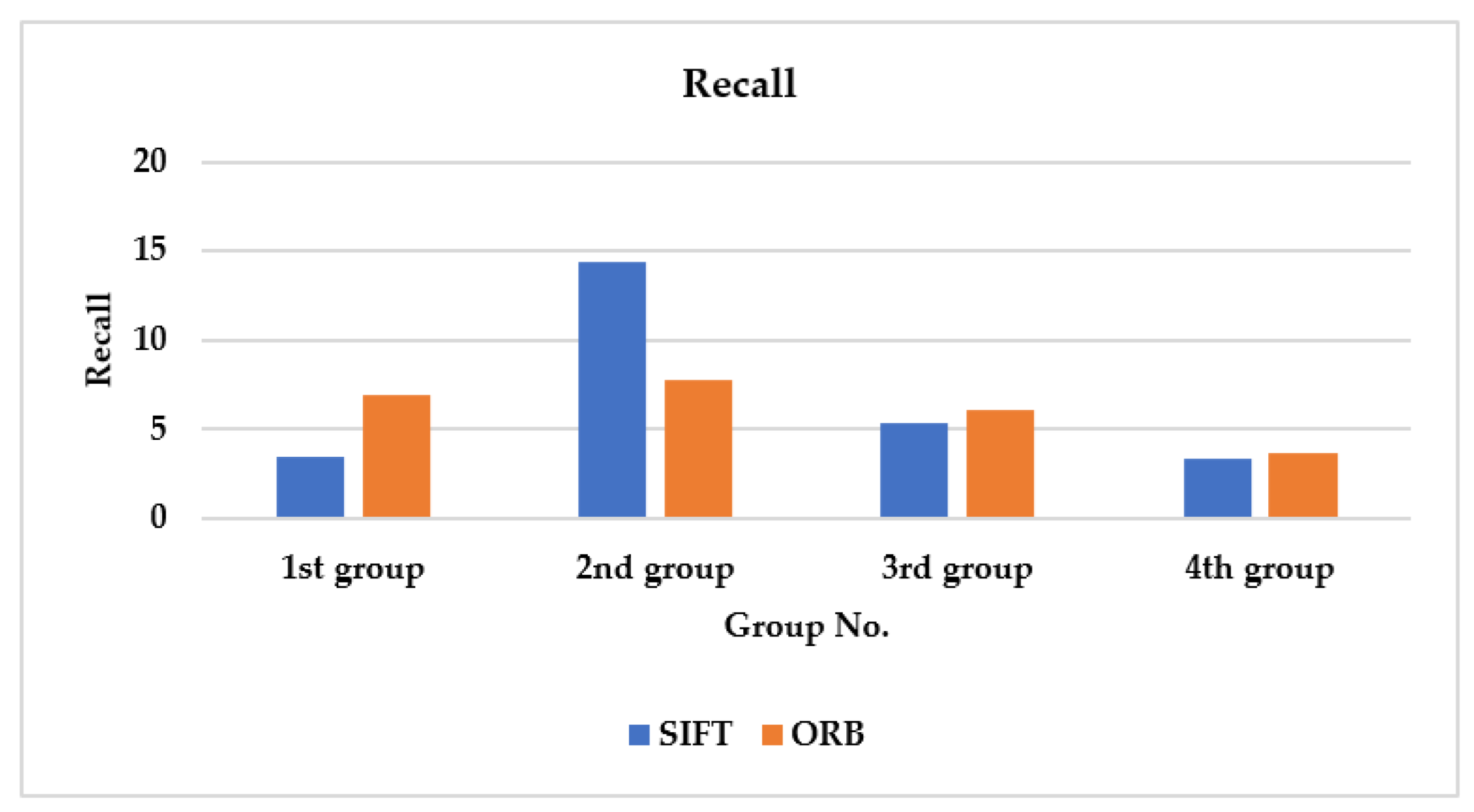
Recall: As shown in Table 1 and Figure 13, the recall value is computed over the four given groups. It is found that the average recall over the four groups in the SIFT case is 4.103, compared to 15.03004 for ORB. Thus, ORB surpasses SIFT by a factor of almost four, when correctly matching keypoints among high-clarity drawn images.

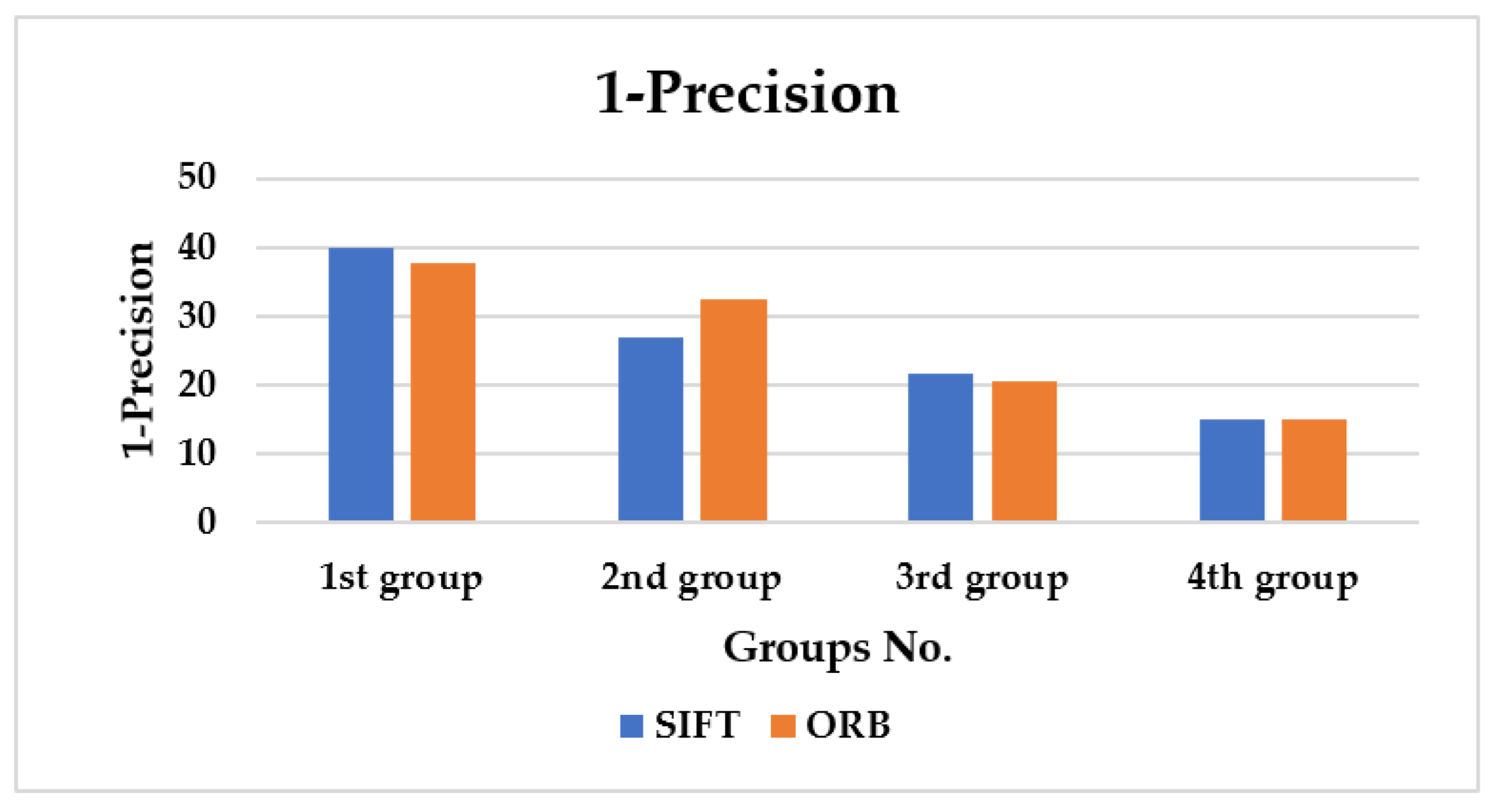
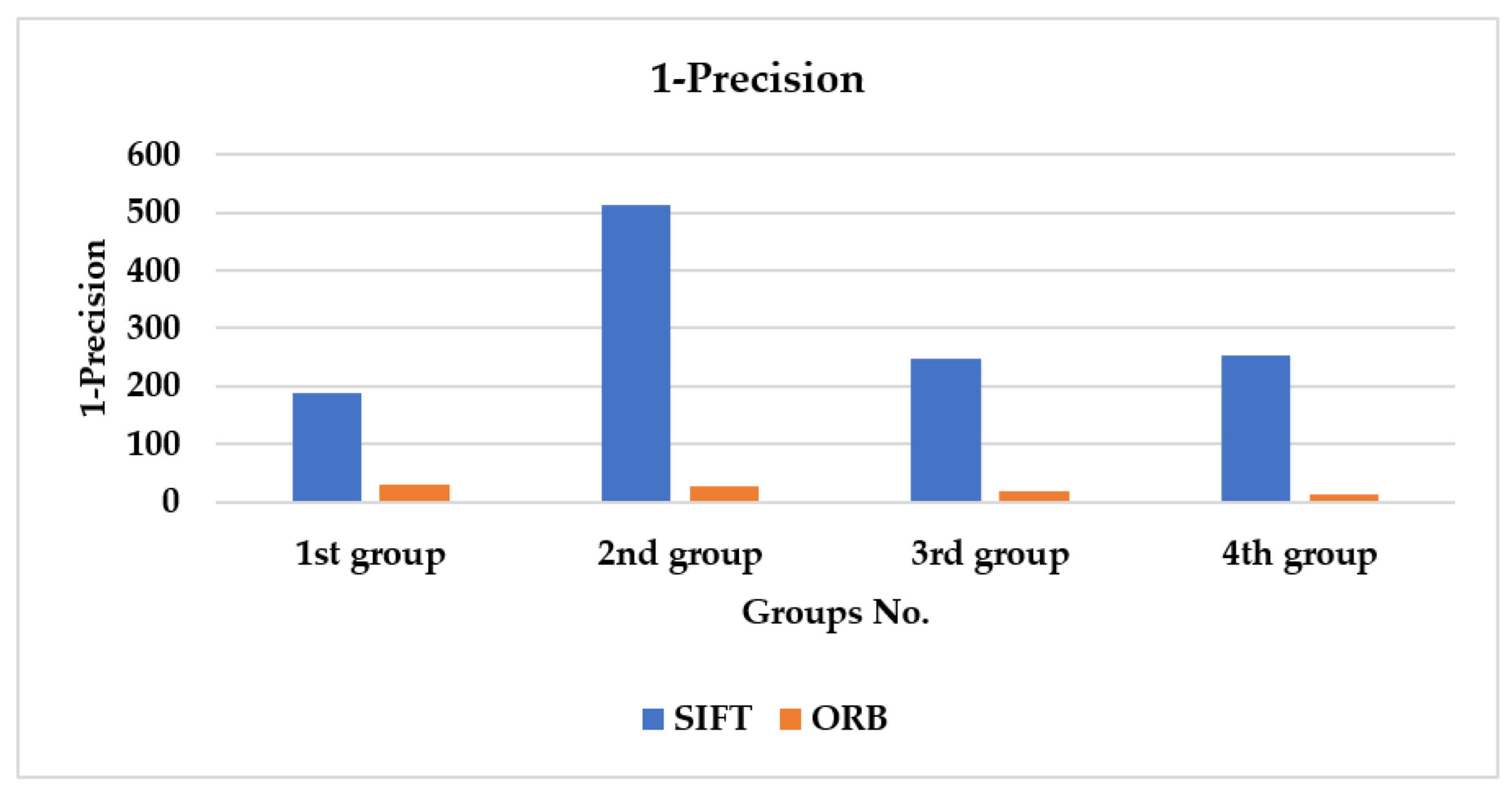
Precision: As shown in Figure 14, the 1-precision is computed for the given four groups. The SIFT seems to achieve a 1-precision of 1202.194, while ORB has 90.00134 on average. Once more, ORB is much better than SIFT.

7.1.3. Evaluation on TU Berlin Dataset

Following the same procedure declared in Section 7.1.1, four groups were created from the predefined TU Berlin dataset in Section 6. Each group is composed of several query–train image pairs chosen randomly from different categories. For illustration, in the second group, six pairs were chosen, and each pair was for the same object over the same category, as Figure 15 shows. The figure shows six different pairs; each pair belongs to the same category, or each image in the pair has the same object. Then, SIFT and ORB are separately applied on each sketched image pair of the second group and the remaining groups. For each case, computed descriptors from image pairs are spatially compared. Finally, the extracted points’ quantum and descriptor dimensions are calculated for each image in the pair per each group. All matched points are localized based on this calculated difference between the descriptors. It is important to note that dealing with this imagery can be challenging due to the lack of color and dazzling specifics. The difficulty increases with the TU Berlin dataset, since the images are human doodle drawings with poor semantic and visual traits and very low drawing precision.

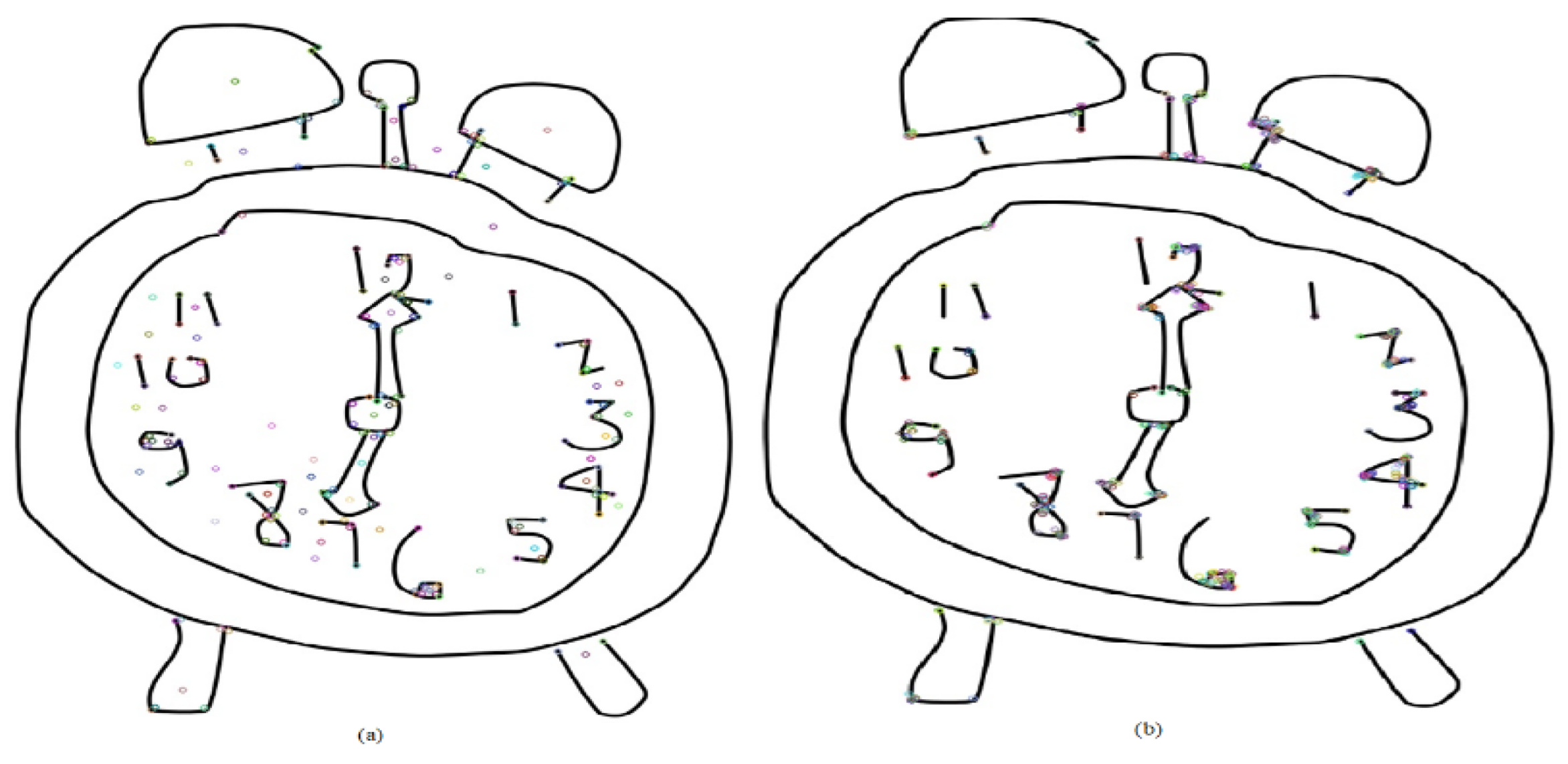
For the second chosen group, Figure 16 and Figure 17 demonstrate the detected keypoints from images using SIFT and ORB, respectively. In Figure 18a,b, we look closely at the keypoints detected by SIFT and ORB from the images of this group, respectively. The figures infer that ORB outperforms SIFT in describing the doodle-sketched drawn objects according to the extracted points’ spatial PD. The ORB achieves better extraction ability for well-spatially distributed feature points that discriminate the clock traits. The figures show that ORB outperforms SIFT in spotting visual clues that determine objects in low-clarity drawings.

For the second group with the SIFT case, the net matched points between the calculated descriptors of sketched query–train image pairs (i.e., the first three training images) are displayed in Figure 19a,c,e. Furthermore, Figure 20a,c,e illustrate the matched points for the other three training images in the SIFT case. Figure 19b,d,f, display the net matched points between the descriptors of the first three sketched query-train image pairs for the ORB example. In addition, Figure 20b,d,f, show the matched points for the next three training images in the ORB case. The figures show how ORB outperforms SIFT in segregation across images for object matching between both image pairs. The number of true and false matches for each image pair may have been the cause of this. The bulk of ORB points is related to items inside pairs of sketch–train images, as seen in the figures. This is attributed to the ability of ORB to distinguish objects without the need for redundant features, as compared to the case of SIFT. In the SIFT example, false matching results are attributed to the significant portion of the detected points being matched with undiscriminating redundant features due to the sparse keypoint distribution of SIFT. Thus, unlike ORB, SIFT performs poorly in object discrimination within doodle sketched images, as the figures indicate.

Memory Requirements: The performance metrics obtained for SIFT and ORB on the four groups are given in

Table 2. Computed performance metrics for methods based on handcrafted features over the four groups of the TU Berlin dataset.

Method	Performance Metrics	Groups No.	Value
SIFT	Average memory consumed (MB)	1st	37,008
		2nd	39,093.33
		3rd	29,971.2
		4th	35,276.8
	Time consumed (s)	1st	9.4
		2nd	37
		3rd	18
		4th	34.63
	Average computed recall	1st	3.41175
		2nd	14.43667
		3rd	5.353
		4th	3.30975
	Average computed 1-precision	1st	40
		2nd	27
		3rd	22
		4th	15
ORB	Average memory consumed (MB)	1st	497.875
		2nd	474.4167
		3rd	481.6
		4th	478.325
	Time consumed (s)	1st	6
		2nd	34.1
		3rd	8.65
		4th	20.7
	Average computed recall	1st	6.944
		2nd	7.73
		3rd	10.13
		4th	5.657
	Average computed 1-rrecision	1st	37.65
		2nd	32.6
		3rd	15.6
		4th	15

. Additionally, Figure 21 shows an illustrative curve for the space complexity on all four groups for a useful comparison to distinguish between the two cases. Compared to 1932.217 MB for ORB, the SIFT scenario requires a total of 141,349.3 MB of RAM for all query–train image pairs that were randomly chosen. The SIFT consumes around 74 times as much space complexity as ORB.

Time Consumption: The time complexity is shown in the illustrative curve in Figure 22, and results are given in Table 2 over all four groups. The computation and matching time of SIFT descriptors is about 100 s, compared to 67 s for the ORB case. Accordingly, SIFT is almost twice as complicated in terms of time as ORB.

Recall:Figure 23 demonstrates the computed recall based on correct and false matching outcomes and recorded results in Table 2. The SIFT case has a total average recall of 26.5 over the four groups, compared to 30.5 for the ORB scenario. Consequently, when it came to successfully matched keypoints among low-clarity drawn images, ORB outperforms SIFT by a factor of approximately 1.2.

Precision: According to Figure 24 and results in Table 2, it can be discovered that SIFT obtains, on average, 104 for the calculated 1-precision, whereas ORB only obtains 100.85.

7.2. Image Retrieval Based on InfoGAN

The learned-features-based approaches usually outperform the handcrafted-features-based approaches in some applications. However, their performance is still compared to those based on handcrafted features. Therefore, SIFT similarity matching could be used as a benchmark for the methods based on learned features, and ORB could be used as the binary extraction benchmark. Referring to the strategy used in ORB as a binary descriptor, it is possible to distinguish black edge drawings and lines of a sketched image on white background, as the process is mainly based on pixel intensity comparison. This simulates how “high” and “low” levels may be expressed, where “high” denotes existence and “low” denotes nonexistence. In other words, it is possible to isolate black lines of drawings within a sketched image from its background as a separate value. This important notion drives the need to utilize a disentangled representation, as each feature is divided into precisely specified variables, and each variable is encoded as a distinct dimension. Thus, the InfoGAN was chosen for disentangled representation of images, and image descriptors were generated through the discriminator after training and learning features for large-scale datasets.

7.2.1. InfoGAN Retrieval System Evaluation over ImageNet-Sketch Dataset

Using the image retrieval procedure highlighted in Section 4, the InfoGAN model was trained with the predefined ImageNet-Sketched dataset in Section 6. A batch of query images (i.e., eleven images) were chosen randomly from the first dataset of various categories. Then, through the declared outlines, a spatial distance measure was established between encoded features from each query image and the trained model based on the training images. Finally, the most relevant images were retrieved according to the performed spatial comparison. A sample of the matched query-retrieved images is shown in Figure 25. The figure includes a group of relevant and irrelevant images to the query image. It should be emphasized that this kind of image retrieval is quite difficult. As was already indicated, the drawings were made by hand, and they are devoid of colors or supporting evidence. Thus, for each query image, TruePositive, FalseNegative, and FalsePositive scenarios may be encountered after the retrieval process. Hence, recall, precision, and F-score can be computed to assess the accuracy of the suggested retrieval system and its time complexity.

Time Complexity: The outcome is obtained with the introduced InfoGAN, which was trained from scratch compared to the methods based on handcrafted features. It takes about 1087s to train all three InfoGAN models (i.e., generator, discriminator, and auxiliary models). It requires 0.4 s for image indexing and 7.8 s for searching by each query image of the eleven images. Compared with the methods based on handcrafted features, the InfoGAN system training takes 1055 s (i.e., feature learning) over the entire ImagNet-Sketched dataset of images, while it takes 128 s to generate and match feature descriptors using SIFT from the predefined groups of only 80 images. Additionally, for the ORB case, it takes 97s to compute and match the generated descriptors over the same selected images from the same dataset. Consequently, the use of SIFT to extract features across the entire dataset requires 300,000 s, and in the ORB case, 27,500 s are needed.

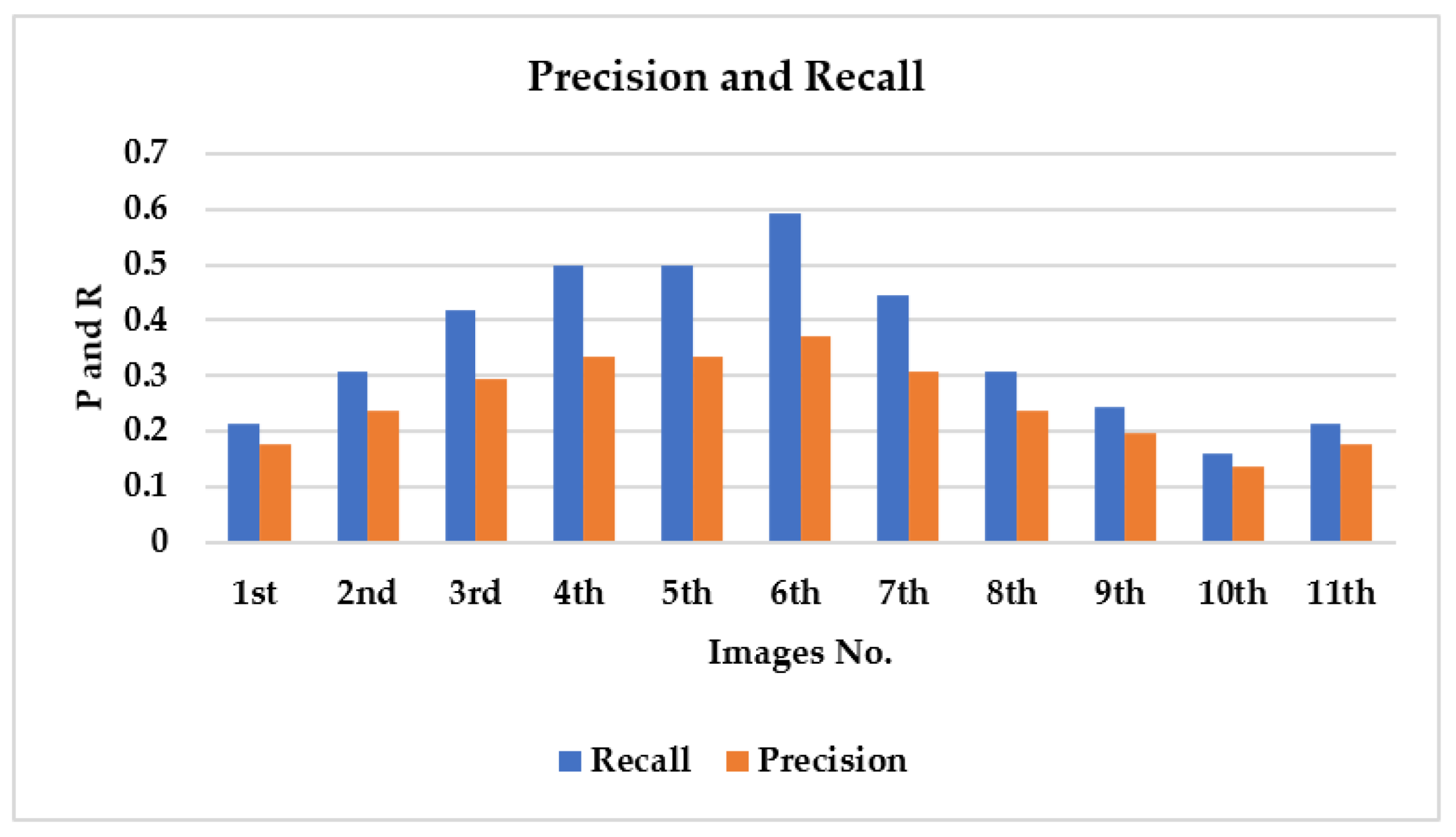
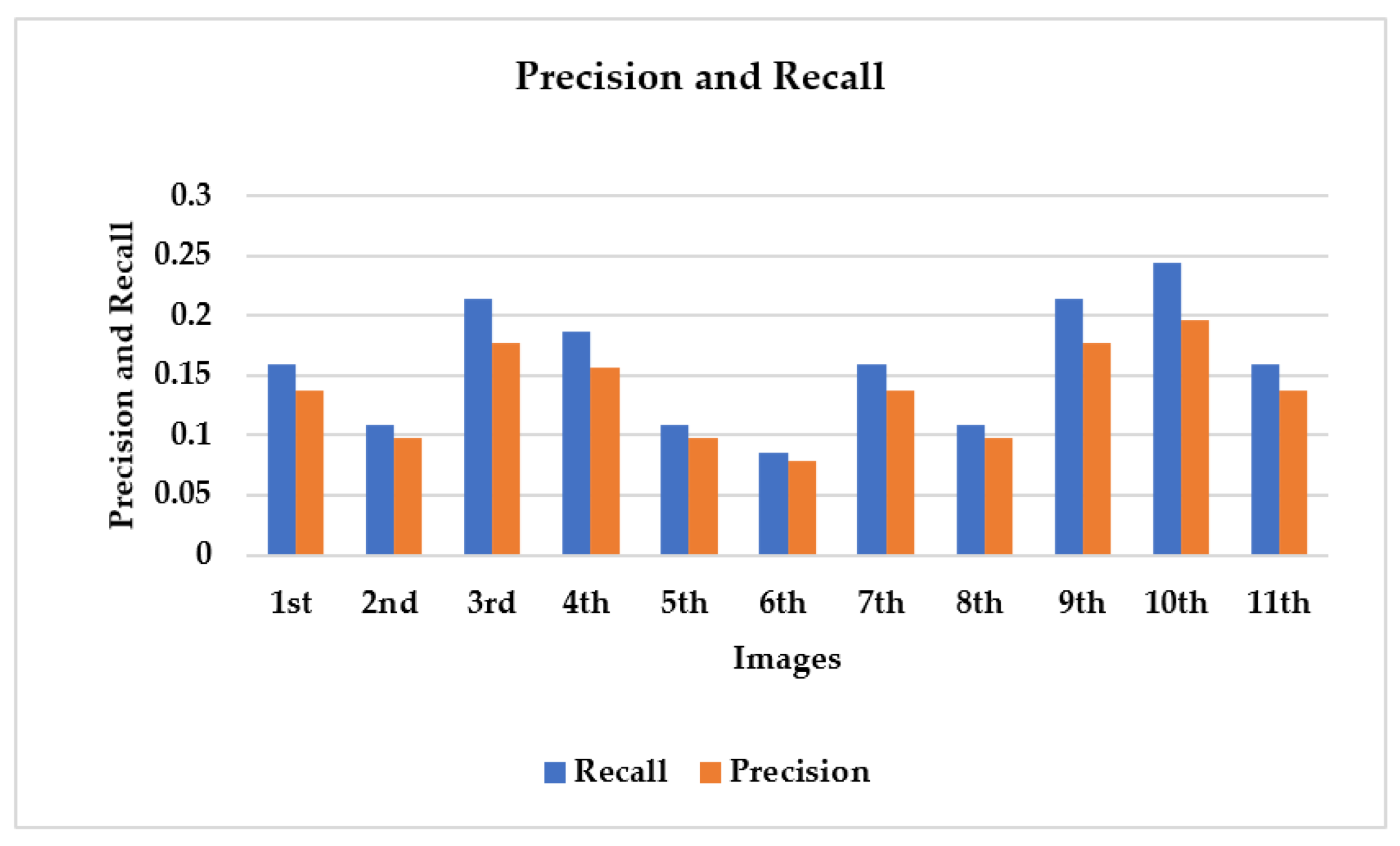
Recall/Precision: The computed metric values acquired by the suggested InfoGAN retrieval system are displayed in Figure 26. It shows the computed recall/precision for the retrieved images versus each of the eleven query images. The proposed system achieves average recall and precision values of about 0.35471 and 0.25435, respectively.

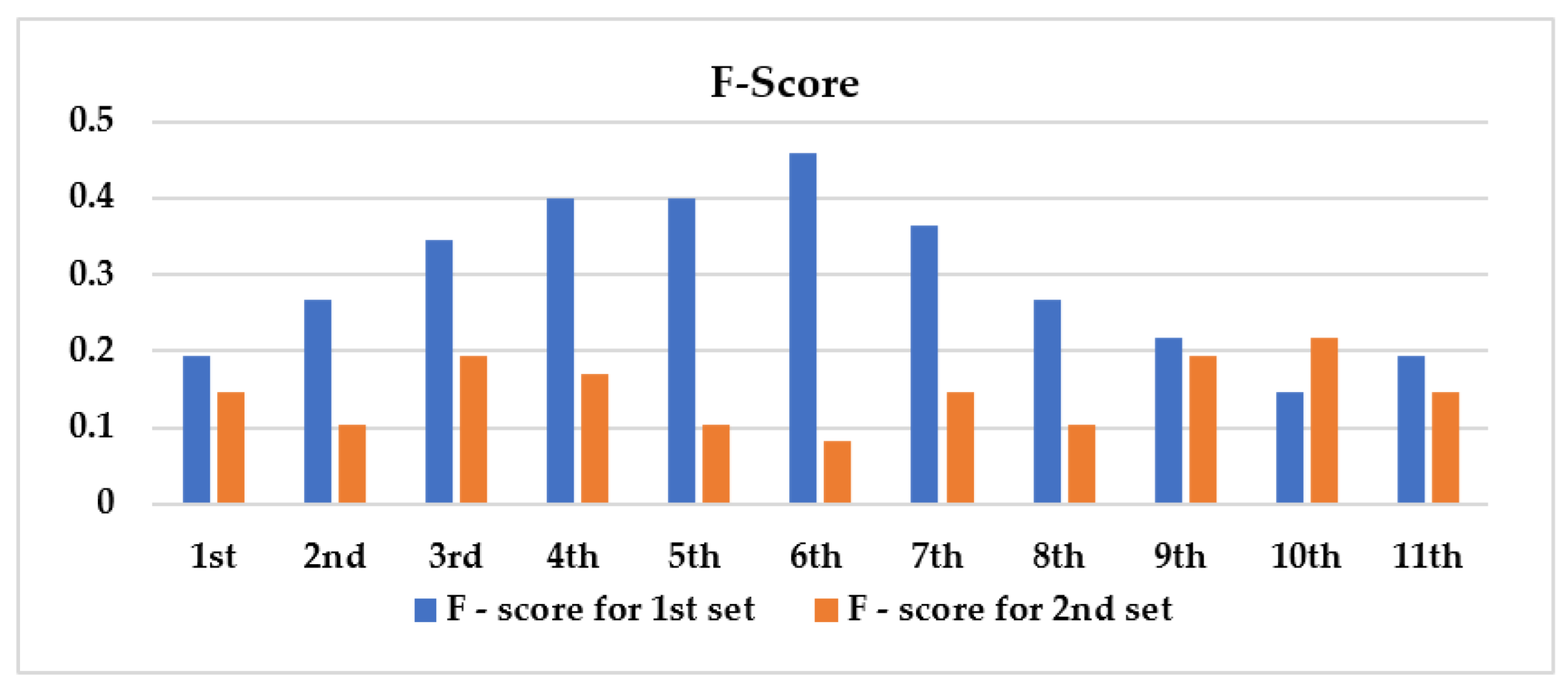
F-score: The computed F-score value for each applied query image throughout the model for both ImageNet-Sketch and TU Berlin datasets is displayed in a straightforward manner to illustrate the findings. For the ImageNet-Sketch dataset, the proposed model achieves, on average, a 0.29559 F-score value over all the retrieved images compared to each of the eleven query images.

7.2.2. For TU Berlin Dataset

The InfoGAN model was trained with the TU Berlin dataset defined in Section 6 using the image retrieval method indicated in Section 4. Eleven images were randomly selected from this dataset of various categories to serve as a mixture of query images. Then, based on the trained model, a spatial distance measure was constructed between the encoded features from each query image and the learned model through the stated outlines. Finally, the completed spatial comparison was used to obtain the most pertinent images. Figure 27 displays a selection of the matched query-retrieved images. It is important to keep in mind that this dataset shows a greater difficulty of matching, because the images are scribbled or scratched, making retrieval more difficult. This is clear in the sample retrieved images shown in Figure 27. However, the model retrieves most of the hassling objects from the one in the query image. Most retrieved images have a rounded shape analogous to the rounded shape of the alarm clock in the query image. Finally, after the retrieval process, the retrieval system TruePositive, FalseNegative, and FalsePositive counts are obtained for each query image for performance evaluation.

Time Complexity: For the TU Berlin dataset, it takes around 1035 s to train all three InfoGAN models (i.e., generator, discriminator, and auxiliary models). The indexing of the images takes 0.43 s, and each of the eleven images takes 8.56 s to be searched. Compared to methods with handcrafted features, SIFT requires 100 s, and ORB requires about 67 s to extract features from the 80 selected images. Thus, over the entire dataset, SIFT takes an extremely long time of 116,667 s, and ORB takes 6667 s. In contrast, the retrieval process with InfoGAN takes only 1025 s (i.e., feature learning).

Recall/Precision:Figure 28 displays the computed metric values for this dataset. The proposed system achieves average recall and precision values of about 1.587896 and 1.352941, respectively.

F-score: As shown in Figure 29, for the TU Berlin dataset, the proposed InfoGAN-based retrieval system reveals on average of 0.146 for F-score value. It must be noted that the computed F-score is averaged over the retrieval results for the eleven selected query images.

It is worth noting that the F-score is often used to evaluate information retrieval systems, such as search engines. Higher F-scores are often better. The F-score is between 0 and 1, with 1 denoting a model that accurately assigns each observation to the proper class and 0 denoting a model that cannot assign any observation to the correct class. The introduced InfoGAN system achieves a higher F-score in ImageNet-Sketched dataset retrieval than that for the TU Berlin dataset retrieval. This is mainly attributed to the quality of images drawn in both datasets that influences the extraction method, and consequently, the similarity matching. It should be mentioned that training and retrieval were performed on a gaming device that meets the following requirements: 4 GB GPU, 1650 and 256 GB SSD, and the models were run using the TensorFlow framework with a batch size of 64.

7.2.3. InfoGAN versus CNN Models

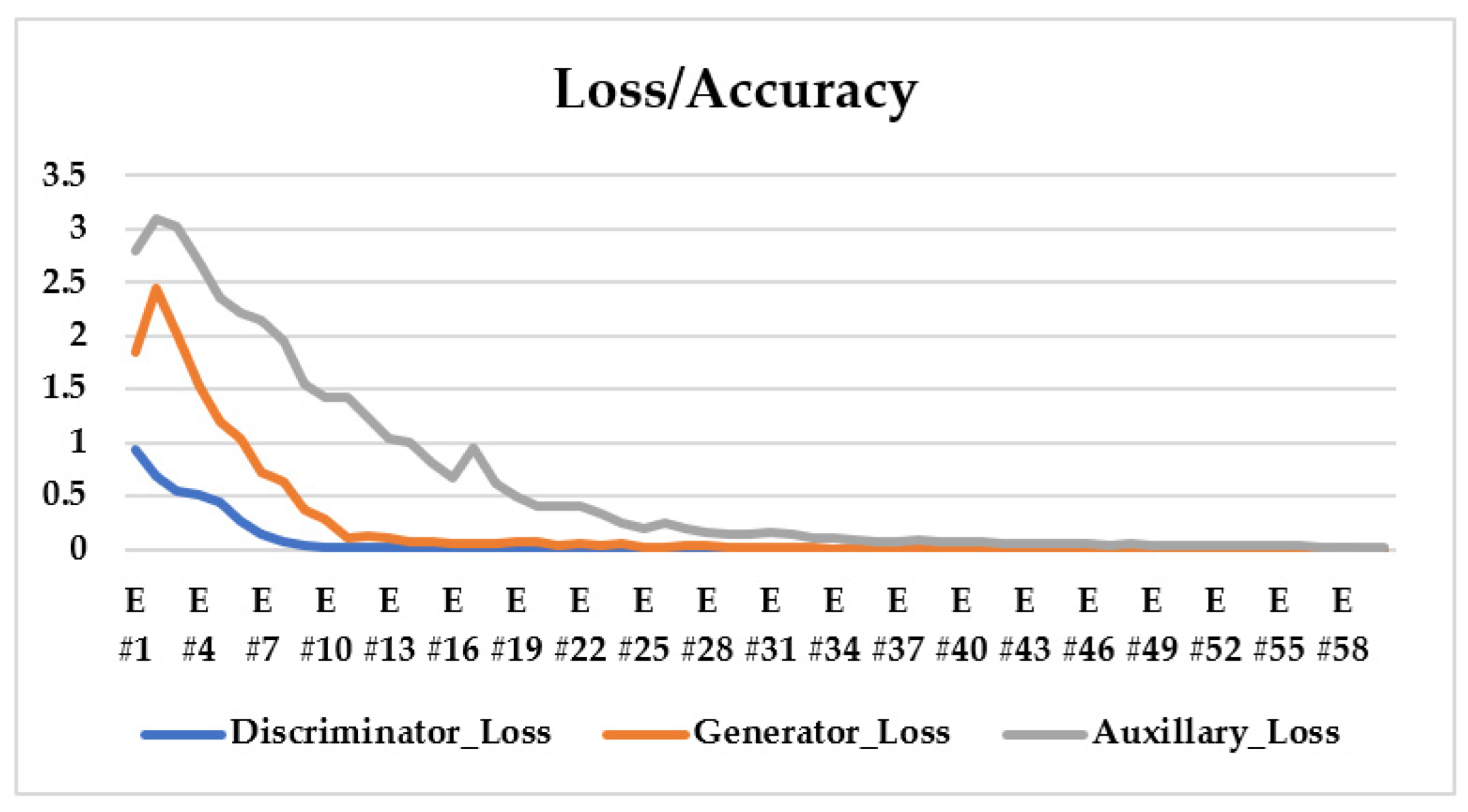
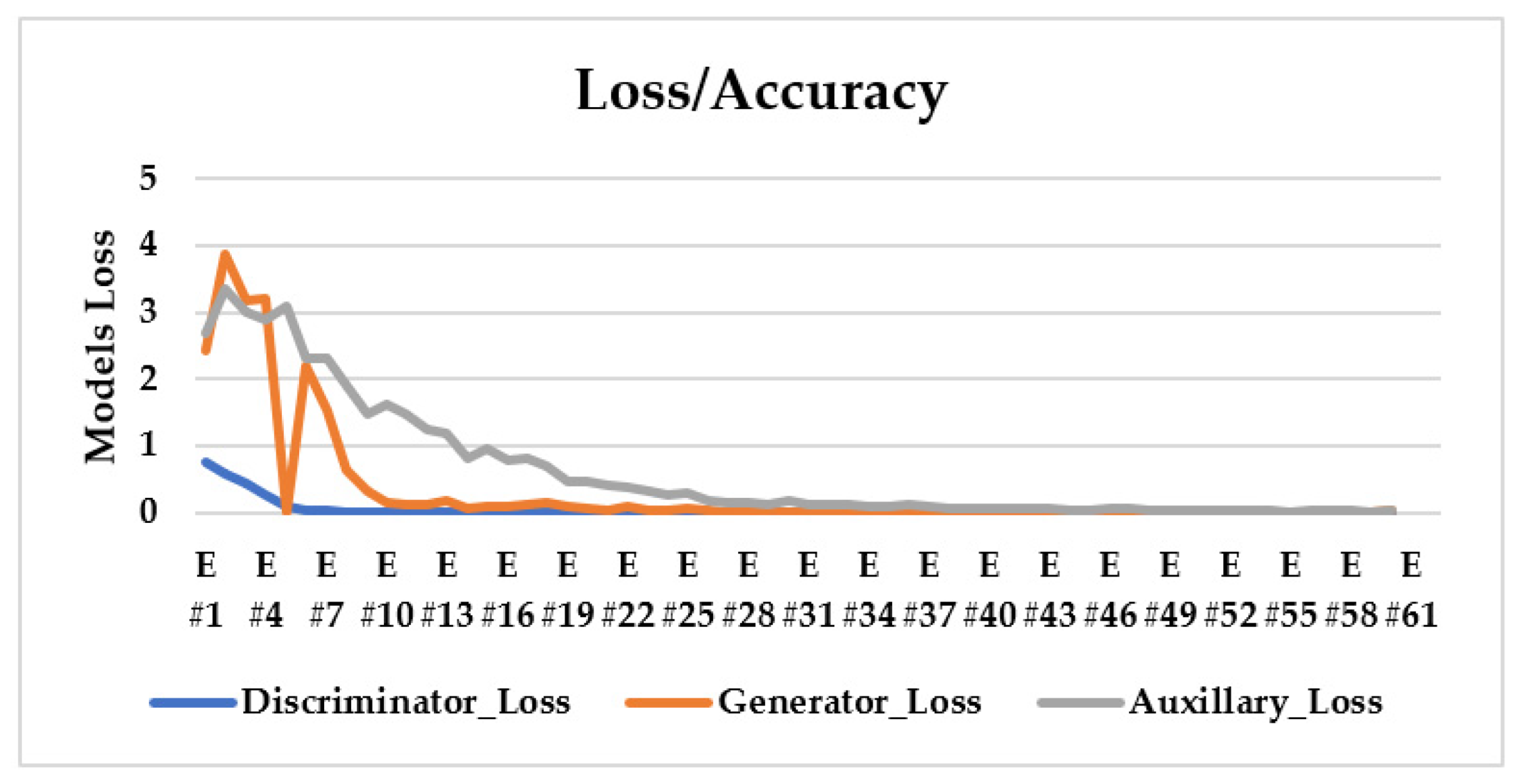
An important ML tool for assessing model learning performance across time or experience is the learning curve, which can be used to spot training-related learning issues. Loss over time is the most well-known illustration of a learning curve. The loss (or cost) curves quantify the accuracy of the trained model or “how poorly the suggested model is doing”. The loss curves demonstrate how well the model is learning, since they represent how well the model fits the training set of data. Thus, for learning performance evaluation of the proposed InfoGAN model, the trained learning curve was generated as one of such curves. It was produced from InfoGAN system training by ImageNet-Sketch and TU Berlin datasets, as seen in Figure 30 and Figure 31. As the figures show, the proposed model fits well with the training sets of the two datasets. In addition, it reveals an improvement in performance, as the model has been well-learned during training. This may have been induced by the loss decrease shown across the figures. Although there were brief ups and downs in the early epochs, the loss eventually went down, indicating that the model has been improved.

The authors of [44] presented a retrieval method based on GAN for a dataset of various shoe images. It was published for E-commerce platforms to obtain the best comparable images for shoe products. In [44], the authors presented a performance comparison of their proposed system with various CNN networks. According to their comparison, MobileNetV2 had an acceptable performance with low size (MB) and inference time (s). Thus, MobileNetV2 was chosen as a state-of-the-art solution, and it was trained by the ImageNet-Sketch dataset, one of the examined sketched image datasets with the highest degree of clarity of drawings. It was trained from scratch by such a dataset and compared to our proposed retrieval system. Figure 32 shows the retrieved images based on features learned through MobileNet training. According to the results, the inconvenience of CNN models in retrieving such kinds of images is assured. Additionally, it takes 1583.5 s for training, indexing, and searching, while our proposed retrieval system based on InfoGAN required 1095 s over the same dataset. Figure 33 shows the training/validation loss curve generated by training MobileNet by the ImageNet-Sketch dataset. The curve shows that the network did not fit well with the data, as there is a big difference between the training and validation losses. In addition, the figure demonstrates that the training loss is smaller than the validation loss. This indicates that the model suffers from underfitting, which happens when it cannot accurately model the training data and produce significant errors.

Moreover, the VGG19 was chosen according to [44] and trained by the same dataset. Indeed, the same results were concluded for the VGG19 with completely black retrieved images. In addition, it consumes about 4355.8 s for training and searching for all images in the dataset. This is about four times greater than that of the proposed InfoGAN-based retrieval system.

8. Discussion

In several test cases, two datasets were used to evaluate the matching and retrieval performance of methods based on handcrafted features (i.e., SIFT and ORB) and the proposed InfoGAN retrieval system. According to the findings,

Table 3. Complexity and matching performance comparison between the included systems.

Dataset	Metric	SIFT	ORB	InfoGAN
ImageNet-Sketched	Time complexity	− SIFT takes twice as long as ORB to extract and match visual feature descriptions. − SIFT needs 128 s to generate and match feature descriptors among the included four groups of just 80 images. − Therefore, it would take 300,000 s for SIFT to extract features from the entire dataset. − As a result, SIFT takes 285 times longer than InfoGAN to extract features.	− The calculation and matching of derived descriptors over the same chosen images from the same dataset takes 97 s for the ORB instance. − To extract and match feature descriptors over the full dataset, ORB requires 27,500 s. − Consequently, ORB needs around 26 times as much time to extract features as InfoGAN.	− All three InfoGAN models must be trained in roughly 1087 s − According to learned features, InfoGAN needs 0.4 s to index images and 7.8 s to search through by each of the eleven images as the query image. − InfoGAN system takes 1055 s for training to learn features over the entire dataset.
	Space complexity	− Over the predefined groups, SIFT was revealed to be around 400 times more complicated than ORB in terms of memory consumed by the generated descriptors.	− ORB had less computational complexity compared to its SIFT alternative.	− Complexity re quired to train its discriminator model.
	Image matching	− Each category is matched, separately.	− Each category is matched, separately.	− According to the learning ability of discriminator model for features, matching is generalized, making the prediction for new instances generalized as well.
	Time complexity	− SIFT takes twice as long as ORB to extract and match visual feature descriptions. − It takes 100 s to extract features from just 80 selected images. Thus, over the entire dataset, SIFT takes an extremely long time of 116,667 s. − Thus, compared to InfoGAN, SIFT takes 113 times longer than InfoGAN to extract features.	− ORB requires about 67 s to extract features from just 80 selected images. − Over the entire dataset, ORB takes 6667 s. − Compared to InfoGAN, ORB needs about 7 times longer than InfoGAN to extract features.	− All three InfoGAN models require about 1035 s to be trained. − It takes 0.43 s to index the images, and 8.56 s to search through each of the eleven query images. − In contrast, the retrieval process for InfoGAN takes only 1025 s (i.e., feature learning).
	Space complexity	− SIFT requires around 74 times more compared to ORB over the specified groups.	− Less complex compared to SIFT.	− The complexity is attributed to the training of the discriminator model.
	Image matching	− Each category is matched, separately.	− Each category is matched, separately.	− According to the learning ability of the discriminator model for features, matching is generalized, making the prediction of new instances generalized as well.

illustrates all used performance metrics for SIFT, ORB, and InfoGAN system.

For the ImageNet-Sketched dataset, the test scenarios involved led to the following conclusions:

○

Considering the results mentioned in Section 7.1.2.:

−

At first, the efficiency of the feature detectors used by such extraction methods makes it clear that they can support real-time applications. Hence, in terms of time complexity through the comparison of SIFT with ORB, SIFT takes almost twice as long to compute and match visual feature descriptors. Thus, according to the outcomes, ORB-based detection is more suitable for real-time applications.

−

Likewise, according to the comparison of the computed 1-precision shown in Figure 14, SIFT achieves a high degree of false-matched keypoints compared to the ORB instance.

○

Compared to InfoGAN results stated in Section 7.2.1.:

−

SIFT is around 285 times more complex than the InfoGAN system, while ORB is 26 times more complex.

The test scenarios used for the TU Berlin dataset resulted in the following findings:

○

According to the outcomes stated in Section 7.1.3.:

−

SIFT is almost twice that of ORB in terms of time complexity. Therefore, based on the findings, the suitability of ORB-based detection is emphasized for real-time applications.

−

As seen by the comparison of the 1-precision in Figure 24, SIFT leads to a significant proportion of incorrectly matched keypoints as compared to the ORB instance. It is important to note that the SIFT and ORB examples were quite similar on the TU Berlin dataset, when comparing the matching performance. Nevertheless, ORB barely outperforms SIFT. However, the space and time complexity settled the previously noted choice between the SIFT- and ORB-based methods.

○

Compared to InfoGAN results in Section 7.2.2.:

−

SIFT is around 113 times more complex than the InfoGAN system, while ORB is 7 times more complex.

A crucial point must be made considering the results of the relevant test scenarios for either ImageNet-Sketched or TU Berlin datasets. As Figure 12 and Figure 22 show, even with SIFT or ORB, the execution times are not constant with the growth of the number of images. This is mainly attributed to the content of images and the ability of the applied method to represent and visualize features. This affirms the concept behind the evaluation presented in this research for feature extraction methods for efficient image representation, as mentioned before. Furthermore, difficulties of this nature are quite rare for handcrafted feature extraction. Additionally, the large scale of feature dimensions and storage created a substantial number of undesirable redundant features.

It is important to remember that any retrieval system must search for images generically based on their extracted features, regardless of the user’s familiarity with the categories deposited in the dataset. This promotes the InfoGAN system and motivates its usage against methods based on handcrafted features. In the deployment of methods based on handcrafted features, it was intended to select images randomly but from the same category. Each group has several image pairs, and each pair is drawn from the same category; this lacks the generality concept, while in the retrieval system based on InfoGAN, query images (i.e., unknown new instances or predictions) were retrieved based on knowledge of the similarity obtained with the trained InfoGAN models.

Moreover, to reveal the value of this research, the performance of the provided InfoGAN retrieval system is compared to that in [44]. Unfortunately, the proposed retrieval system faces the following significant challenges in comparison to [44]:

Regarding image type and number of dataset categories: In [44], real shoe images of only eight categories of the dataset were used to train the retrieval system, making it simpler for the network to learn features. In such types of images, the probability that the network will recognize, predict, and retrieve objects (i.e., images) increases as the amount of color and information in images is increased. Our suggested retrieval system, in comparison, is trained to utilize datasets of different contents of sketched images from a wide range of categories. As was already noted, the datasets used were multicategory datasets of objects, birds, and animals.

Furthermore, the challenges for our system are increased, when the degree of painting lucidity is changed, since the images are colorless and are probably based on the artist’s imagination. Thus, two standard datasets of high and low levels of painting clarity were used to train and present results of the proposed DL network. The first dataset is composed of 1000 different categories, while the second is composed of 250 different categories.

In terms of performance metrics: In [44], only the inference time and precision metrics were included for evaluating the retrieval system, while for evaluating our proposed system, precision, recall, F-score, training loss curves, and space complexity were provided. In addition, the training, indexing, and searching times were included in each dataset, individually. This bolstered the outcomes and accuracy of the retrieval system results.

9. Conclusions

With the advances in technology, several image retrieval systems have been introduced. Some of these systems are based on real images. Therefore, a large number of algorithms have also been introduced to handle retrieval based on image similarity as in SIFT- and ORB-based cases. However, one of the problems in image retrieval is sketched image retrieval, where such sorts of images are free-hand, uncolored, and devoid of a natural perspective drawings. Therefore, the main purpose of this paper was to evaluate two of the most famous feature extraction algorithms that can be used in image retrieval and matching. In addition, this paper presented an InfoGAN model for sketched-image-retrieval enhancement. Based on our experiments whether for a low or high degree of drawing quality, ORB is more successful in differentiating freehand sketched drawings compared to SIFT. According to the beneficial assimilated clue from the outcomes of the assessment of methods based on handcrafted features, and to solve the retrieval problem on large-scale datasets, the InfoGAN image retrieval system was introduced. It works well in disentangled representation. The proposed InfoGAN model was compared to the CNN, and one of the recent algorithms found in the literature. The results show that the proposed system based on InfoGAN model outperforms other algorithms in terms of accuracy, time, and space complexity.

One of the extensions for the work in this paper is to use different distance metrics such as Hausdorff distance and/or DSC, where the one used in this paper was Euclidian distance for SIFT and InfoGAN cases. Hamming distance was used for the ORB case. In addition, different artificial intelligence techniques could be examined and different datasets could be used.