1. Introduction
Fitting a probability distribution to real data and synthesizing information from it is a challenging task for statisticians/researchers. Data generated from day-to-day work environments are more complex in nature nowadays, and consequently several lifetime models have been proposed and studied in the literature to analyze these data. The well-known exponential distribution is one of the basic continuous models used to examine continuous data. However, Bakouch et al. [
1] developed the binomial exponential II (BiExII) distribution, an extended variant of the ordinary exponential distribution, to provide additional flexibility. The BiExII model is constructed as a distribution of a random sum of independent exponential (Ex) random variables when the sample size has a zero-truncated binomial (Bi) distribution. The cumulative distribution function (CDF) of the BiExII model can be written as
where
is the shape parameter and
is the scale parameter. The probability density function (PDF) corresponding to Equation (
1) can be expressed as
As we observe from Equation (
1), the Ex distribution is a particular case for
, whereas for
, the gamma model with shape parameter 2 and scale parameter
is a special case. Thus, Equation (
2) can be written as
where
. Habibi and Asgharzadeh [
2] presented a power binomial exponential distribution by applying the power transformation on BiExII random variable. The hazard rate function of the proposed distribution portrays the decreasing, increasing, decreasing-increasing-decreasing and unimodal shapes. Al-babtain et al. [
3] developed a new extension of the BiExII model using the Marshall–Olkin (MO-G) family of distributions. They have also discussed a simple type Copula-based construction to derive the bivariate- and multivariate-type distributions. Recently, Zhang et al. [
4] first reviewed the two-parameter Poisson binomial-exponential 2 (PBE2) distribution, then they proposed a new integer-valued auto-regressive (INAR) model with PBE2 innovations.
Sometimes reliability/survival experiments yield data which are discrete in nature either due to limitations of measuring instruments or its inherent characteristic. For example, in reliability engineering, the number of successful cycle prior to the failure when device work in cycle, the number of times a device is switched on/off; in survival analysis, the survival times for those suffering from the diseases such as lung cancer or period from remission to relapse may be recorded as number of days/weeks, number of deaths/daily cases due to COVID-19 pandemic observed over a specified duration, etc. Moreover, in many practical problems, the count phenomenon occurs as, for example, the number of occurrences of earthquakes in a calendar year, the number of absences, the number of accidents, the number of kinds of species in ecology, the number of insurance claims, and so on. Therefore, it is reasonable to model such situations by a suitable discrete distribution.
Discretization of continuous models can be done by utilizing various techniques. The most widely used approach is the survival discretization method. One of the important virtues of this methodology is that the developed discrete distribution retains the same functional form of the survival function as that of its continuous counterpart. Due to this feature many reliability characteristics of the distribution remain unchanged. According to this method, for a given continuous random variable (RV)
Y with survival function (SF)
, the RV
(largest integer less than or equal to
Y) will have the probability mass function
Many authors have used Equation (
4) for generating the discrete analogue of the continuous distributions, for instance, discrete Rayleigh distribution (Roy [
5]), discrete Burr and Pareto distributions (Krishna and Pundir [
6]), discrete gamma distribution (Chakraborty and Chakravarty [
7]), discrete modified Weibull distribution (Almalki and Nadarajah [
8]), discrete generalized exponential and exponentiated discrete Weibull distributions (Nekoukhou and Bidram [
9,
10]), discrete extended Weibull distribution (Jia et al. [
11]), geometric-zero truncated Poisson distribution (Akdogan et al. [
12]), Poisson quasi-Lindley regression model and Poisson–Bilal distribution (Altun [
13,
14]), discrete Burr–Hatke distribution (El-Morshedy et al. [
15]), discrete inverted Nadarajah–Haghighi distributions (Singh et al. [
16]), discrete Teissier distribution (Singh et al. [
17]), and related references cited therein.
In view of the existing literature, we found that several discrete distributions have been introduced over the past few decades. Yet there is much scope left to introduce new plausible discrete distributions that can adequately capture the diversity of real data. This phenomenon motivates us to provide a flexible discrete model for fitting a wide spectrum of discrete real-world data sets. Therefore, in this paper, we have proposed the discrete analogue of the BiExII model, in the so-called discrete BiExII (DBiExII) distribution using survival discretization method. An important motivation of the proposed study is that the BiExII distribution has manageable and closed-form expressions for various important distributional properties, including probability mass function, cumulative distribution function, moments, etc. Furthermore, discrete data generated from many practical studies, such as mortality experiments, industrial experiments, etc., show constant or increasing failure rates, so the proposed distribution is useful for modelling monotonically increasing failure rate data. Other motivations for developing the BiExII distribution include its ability to analyze not only equi-, over-, and under-dispersed real data, but also a positively skewed, or leptokurtic data set. A final motivation for the new distribution is that the proposed distribution is capable of modelling count data as we will see later, and by this, it provides a well alternative to several discrete distributions for modelling discrete data in applications.
The rest of the article is organized as follows. In
Section 2, we have introduced the DBiExII model. Different distributional characteristics are discussed in
Section 3. In
Section 4, the model parameters are estimated by using maximum likelihood and Bayesian methods. Simulation study is presented in
Section 5. The two real data sets (COVID-19 and larvae Pyrausta) are analyzed to show the flexibility of the DBiExII distribution in
Section 6. Finally,
Section 7 provides some conclusions.
2. The DBiExII Distribution
Using the Equation (
4), the probability mass function (PMF) of the DBiExII distribution with positive parameters
and
, can be derived as
where
and
. The cumulative distribution function (CDF) corresponding to Equation (
5) can be expressed as
The behavior of the CDF of the DBiExII distribution can be described as
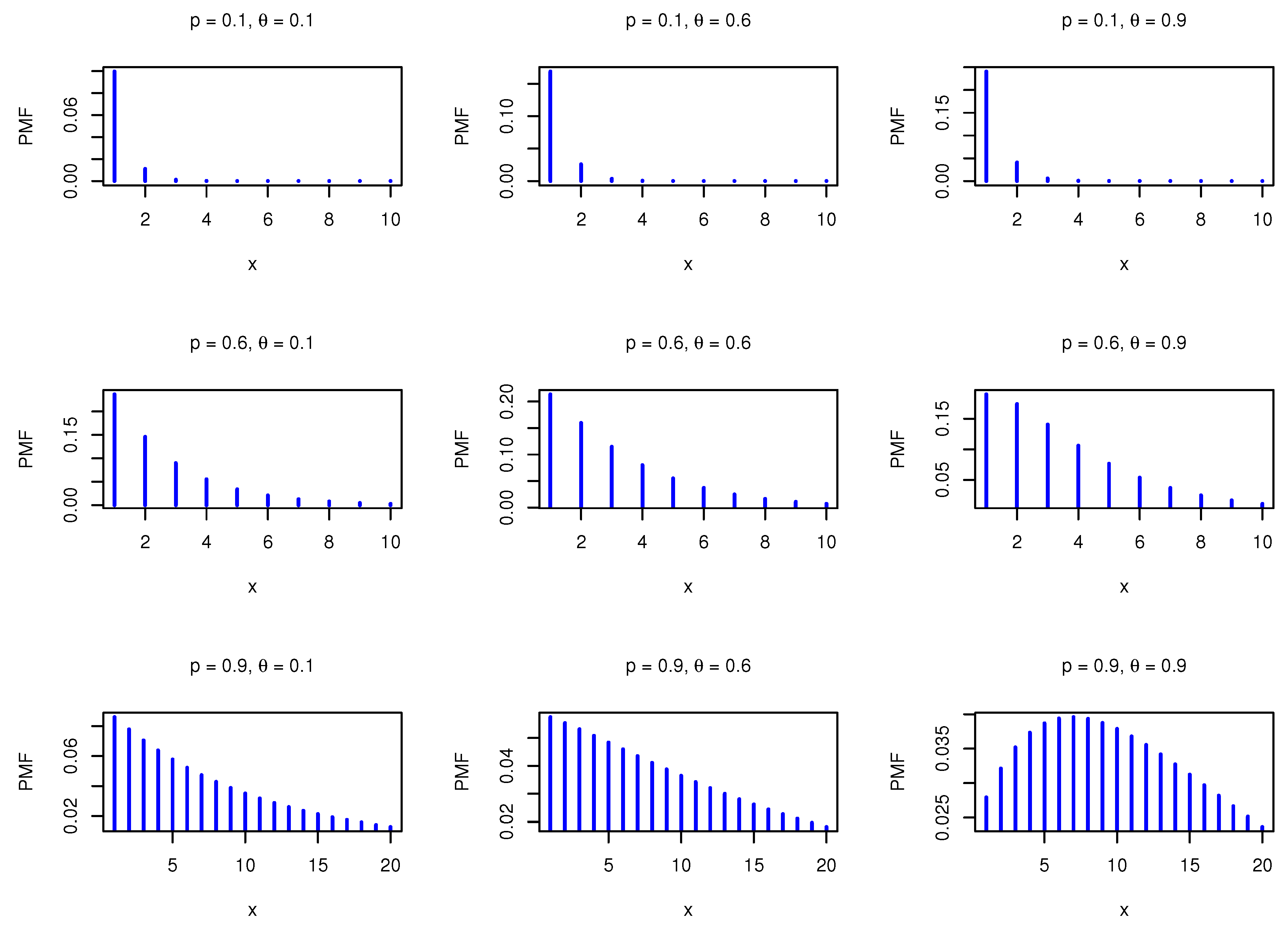
The behavior of the PMF is given by
The PMF in Equation (
5) is log-concave, where
is a decreasing function in
x for all values of the model parameters, and consequently the PMF is unimodal and right-skewed.
Figure 1 shows the PMF plots for different values of the parameters.
The PMF can take unimodal or decreasing-shaped. Assume
X has a DBiExII distribution with parameters
p and
. Then, the PMFs of
and
can be formulated, respectively, as
and
where
a is a positive integer number. The hazard rate function (HRF) of the DBiExII model can be expressed as
where
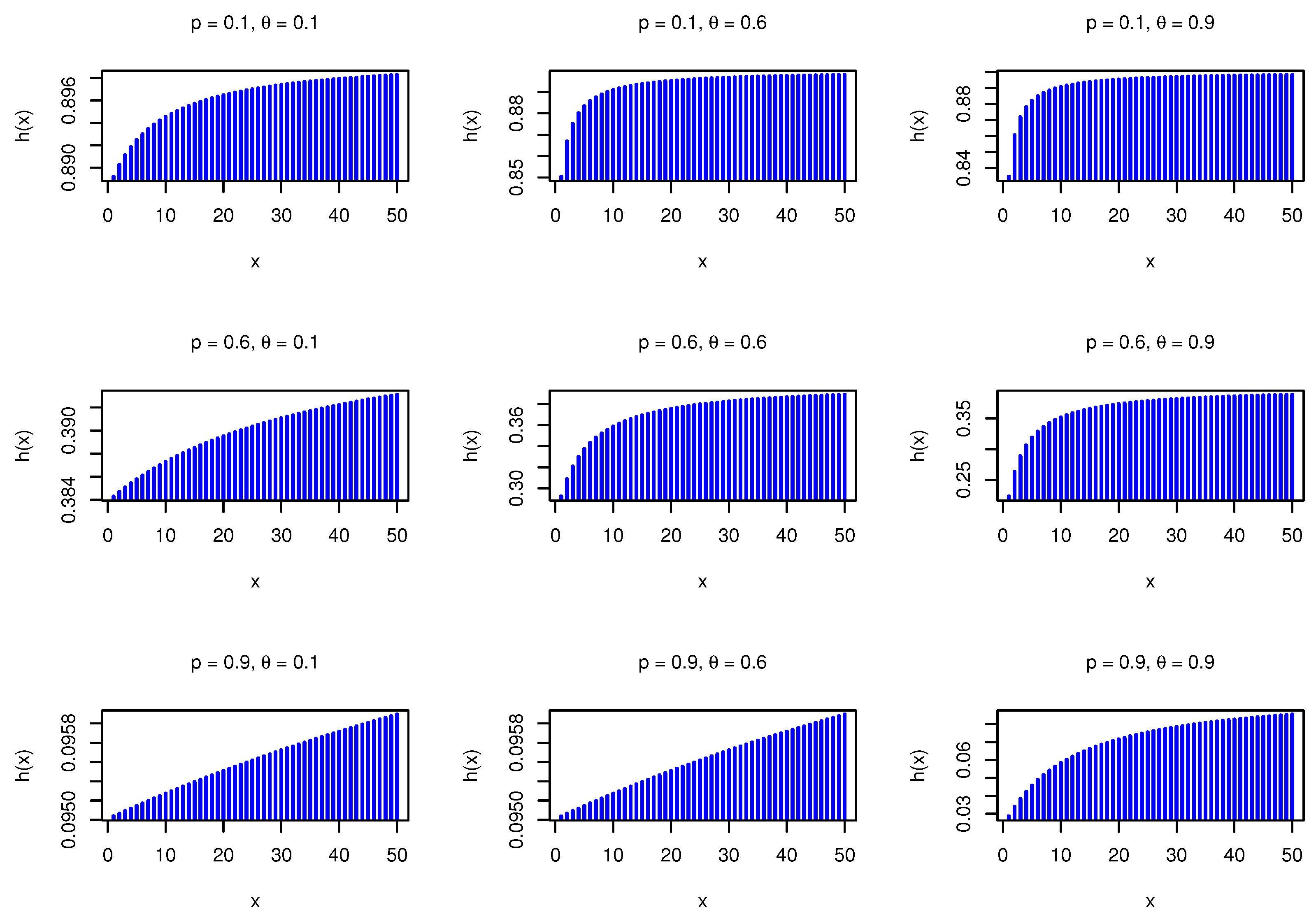
. The behavior of the HRF is given by
Based on the log-concavity properties, the DBiExII distribution has increasing failure rate. For more details around the log-concave function (Gupta and Balakrishnan [
18]).
Figure 2 shows the HRF plots for different values of the parameters.
It is observed that the HRF takes increasing shape. The second rate of failure (SRF) is given by
where
. The behavior of the SRF is given by
For more details about the difference between the HRF and SRF, we can refer to (Xie et al. [
19]).
7. Conclusions
The present article introduced a new two-parameter discrete model, called discrete binomial exponential II distribution. We have discussed several important properties of the proposed model. One of the key advantages of this newly developed model is that it can model a variety of data (over-, equi-, and under-dispersed, positively skewed, leptokurtic, and increasing failure time data). Two well-known estimation techniques, the method of maximum likelihood and Bayesian estimation, have been used to derive the point and interval estimators of the unknown parameters of the DBiExII distribution.
A detailed Monte Carlo simulation study has been performed to test the behaviour of different point and interval estimators with respect to sample size and parametric values. The results of this numerical study show that both estimation methods work satisfactorily, but Bayesian estimation under beta priors dominates the method of maximum likelihood in terms of estimation errors. In the end, the usefulness of the new distribution is illustrated by means of two real data sets to prove its versatility in practical applications. We, therefore, believe that the DBiExII distribution may be a better alternative to some popular existing discrete models and may be widely applicable for modelling real-life data sets in various fields. With regard to future work, the researchers may use the new model to propose a bi-variate distribution based on the shock model approach for modelling bi-variate data. In addition, a regression model and a first-order integer-valued auto-regressive process can be studied in detail.