Generalized Mathematical Model of Brinkman Fluid with Viscoelastic Properties: Case over a Sphere Embedded in Porous Media
Abstract
:1. Introduction
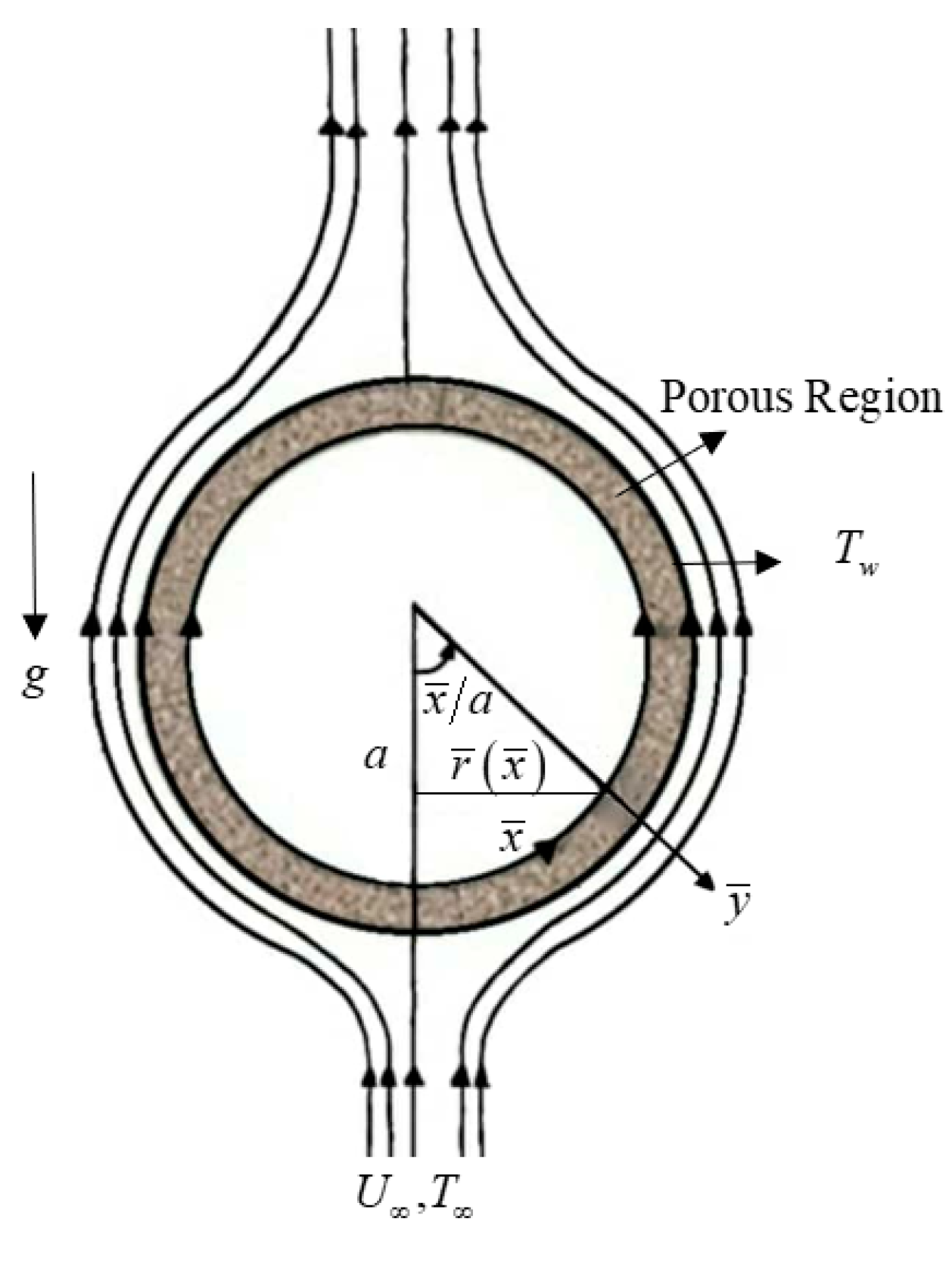
2. Model Formulation
3. Solution Procedures
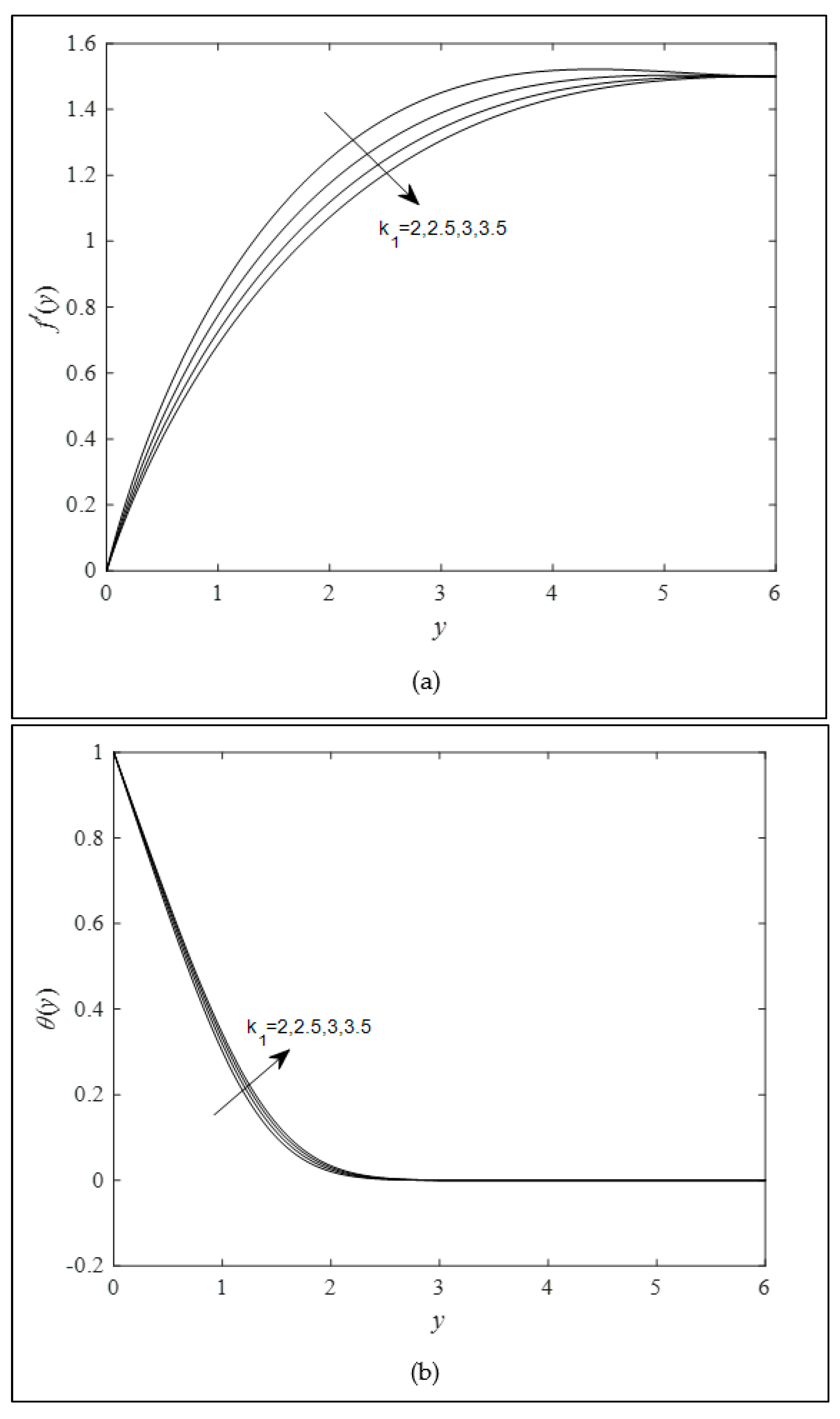
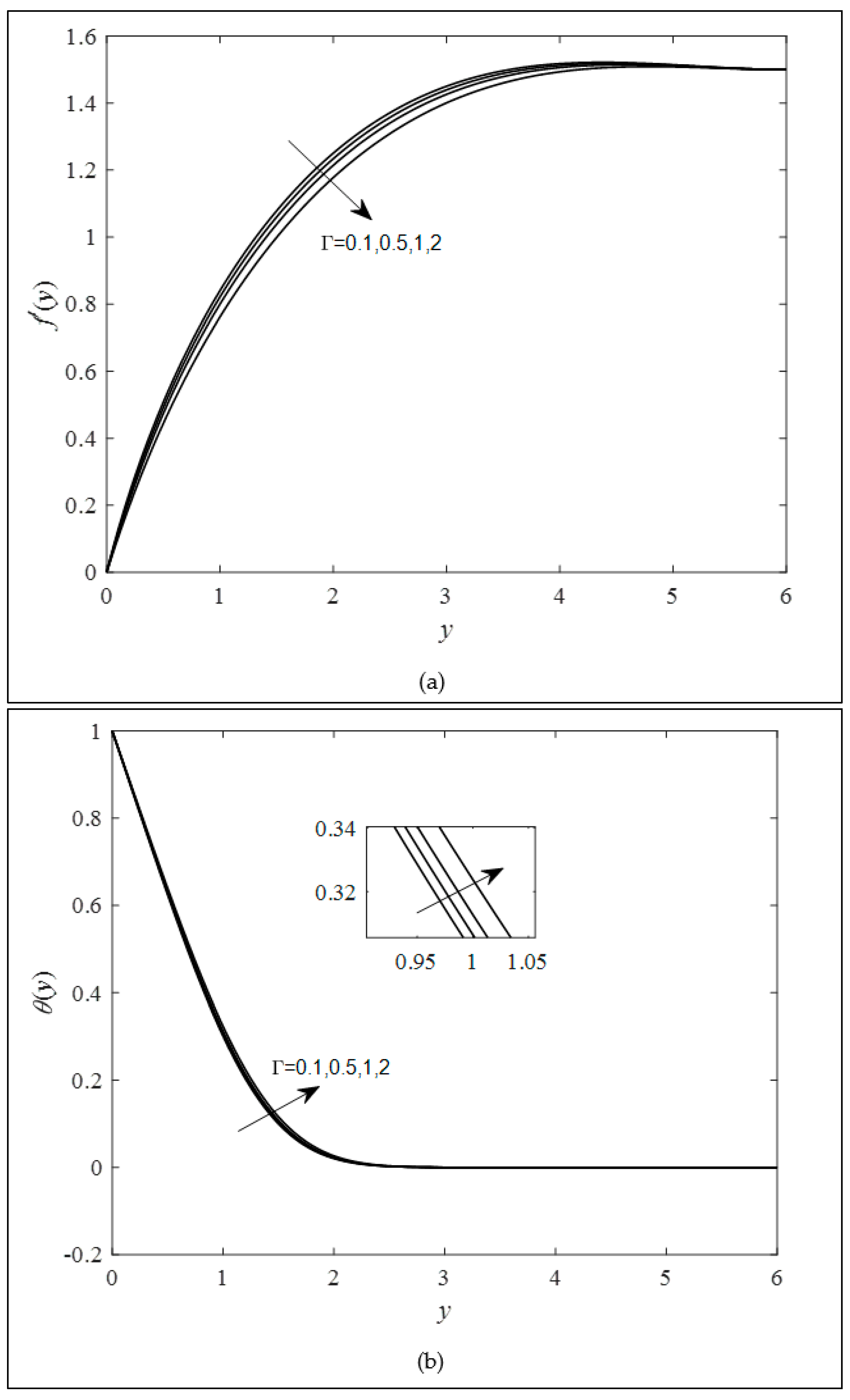
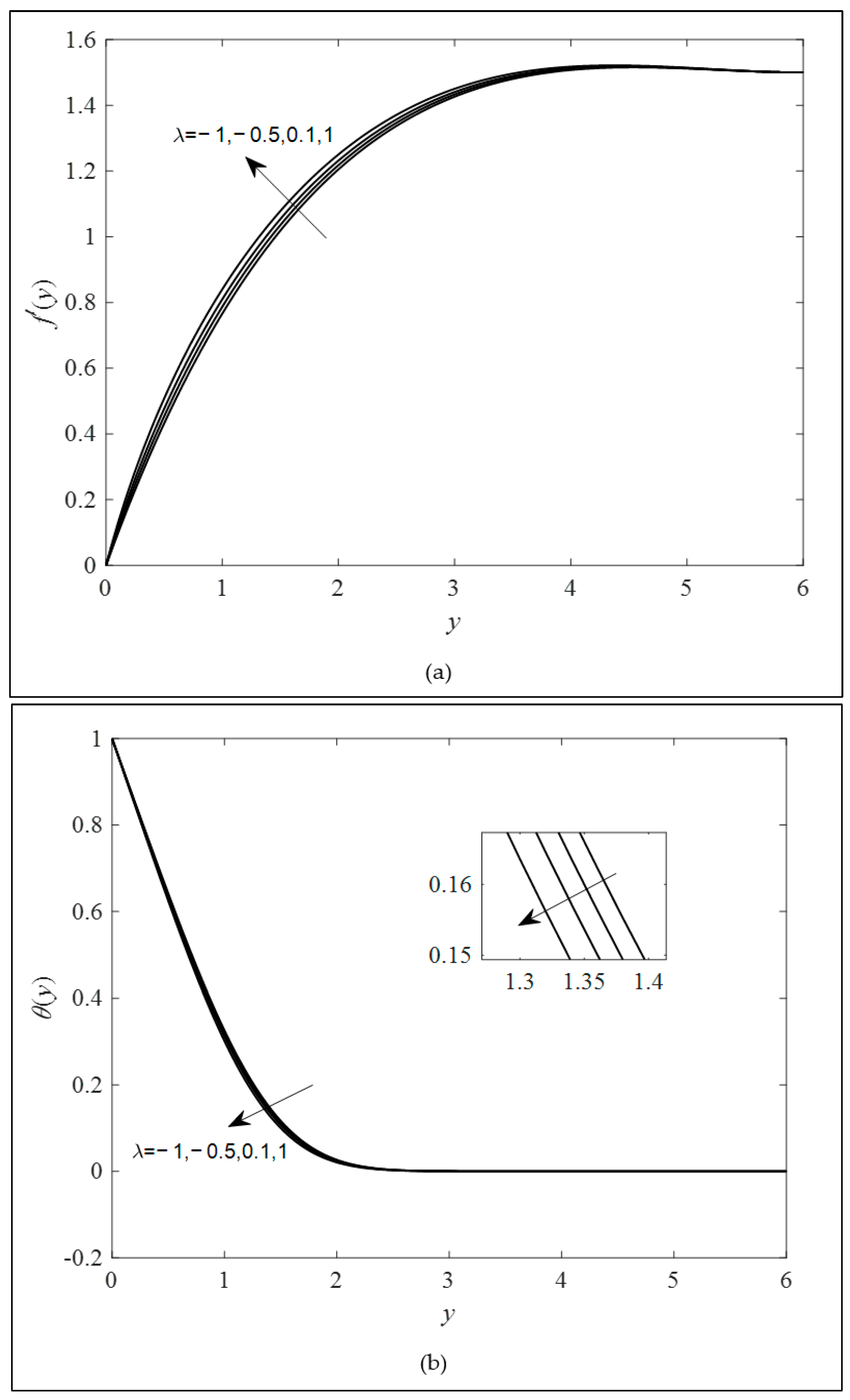
4. Results and Discussion
5. Conclusions
- Both the Brinkman and viscoelastic parameters reduced the velocity profile and increased the temperature profile.
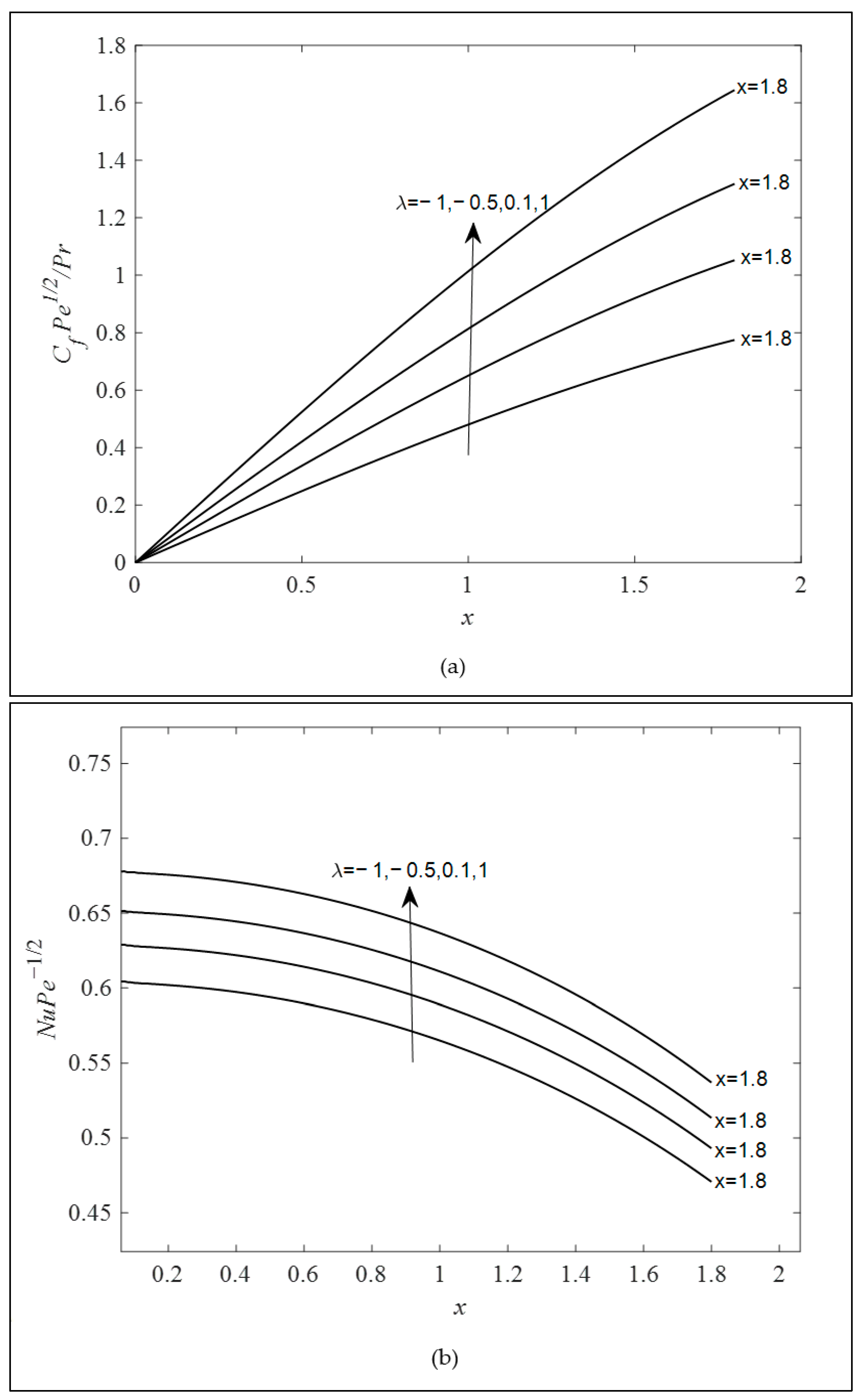
- A boost in the combined convection parameter can decrease the temperature and intensify the fluid velocity.
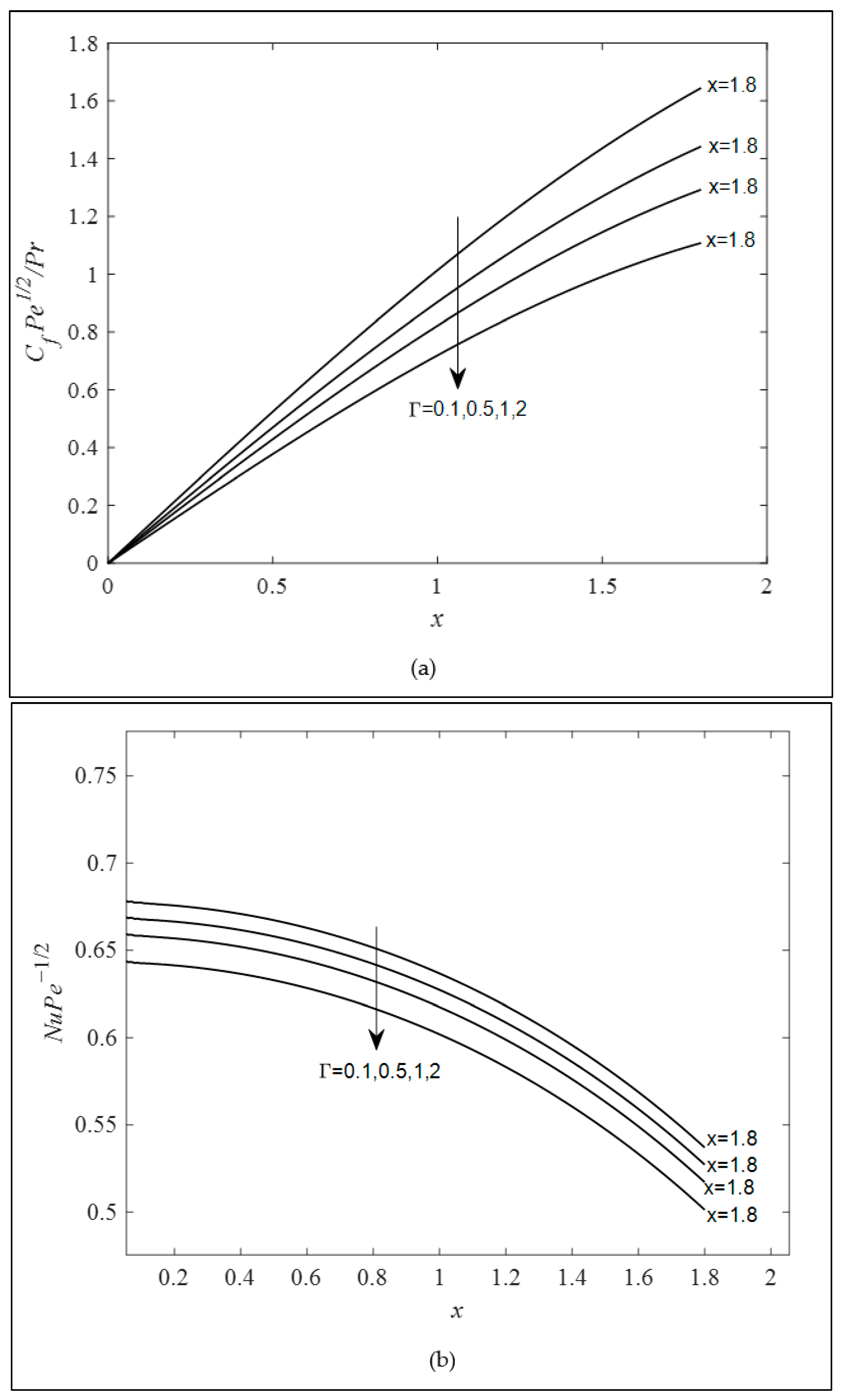
- Both the Brinkman and viscoelastic parameter reduced the Nusselt number (heat transfer rate) and skin friction coefficient, while the combined convection parameter behaved in an opposite manner. However, the variation in the Brinkman and combined convection parameter encounters the separation boundary layer after , whereas the increase in the viscoelastic parameter delayed the boundary layer separation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| radius of cylinder | local skin friction coefficient | ||
| free stream velocity | reduced Nusselt number | ||
| wall and ambient temperature | Greek Symbols | ||
| gravitational acceleration | dynamic viscosity | ||
| , | coordinate surface | porosity of porous medium | |
| , | velocity in , directions | fluid density | |
| permeability of porous medium | thermal expansion coefficient | ||
| viscoelastic parameter | effective thermal diffusivity of porous | ||
| fluid temperature | stream function | ||
| thermal conductivity | fluid temperature | ||
| external velocity | Brinkman parameter | ||
| modified Péclet number | kinematic viscosity | ||
| Darcy number | mixed convection parameter | ||
| Rayleigh number | |||
References
- Gorla, R.S.R.; El-Kabeir, S.M.M.; Rashad, A.M. Boundary-Layer Heat Transfer from a Stretching Circular Cylinder in a Nanofluid. J. Thermophys. Heat Transf. 2011, 25, 183–186. [Google Scholar] [CrossRef]
- Jain, S.; Bohra, S. Soret/Dufour Effects on Radiative Free Convection Flow and Mass Transfer over a Sphere with Velocity Slip and Thermal Jump. Walailak J. Sci. Technol. (WJST) 2018, 16, 701–721. [Google Scholar] [CrossRef]
- Kasim, A.R.M.; Admon, M.A.; Shafie, S. Free convection boundary layer flow of a viscoelastic fluid in the presence of heat generation, World Academy of Science. Eng. Technol. 2011, 5, 227–234. [Google Scholar]
- Kumari, P.; Nigam, M.; Kumar, S.; Kumar, V.; Raturi, S.; Pargaei, M.; Murthy, S.K.; Kumar, B.V.R. Magnetic field effect on non-darcy mixed convection from a horizontal plate in a nanofluid-saturated porous medium. J. Porous Media 2019, 22, 599–610. [Google Scholar] [CrossRef]
- Maghsoudi, P.; Shahriari, G.; Mirzaei, M.; Mirzaei, M. Natural convection of third-grade non-Newtonian fluid flow in a porous medium with heat source: Analytical solution. Eur. Phys. J. Plus 2018, 133, 502. [Google Scholar] [CrossRef]
- Mahat, R.; Rawi, N.A.; Kasim, A.R.M.; Shafie, S. Mixed Convection Flow of Viscoelastic Nanofluid Past a Horizontal Circular Cylinder with Viscous Dissipation. Sains Malays. 2018, 47, 1617–1623. [Google Scholar] [CrossRef]
- Mohamed, M.K.A.; Noar, N.A.Z.M.; Salleh, M.Z.; Ishak, A. Free convection boundary layer flow on a horizontal circular cylinder in a nanofluid with viscous dissipation. Sains Malays. 2016, 45, 289–296. [Google Scholar]
- Raju, B.H.S.; Nath, D.; Pati, S.; Baranyi, L. Analysis of mixed convective heat transfer from a sphere with an aligned magnetic field. Int. J. Heat Mass Transf. 2020, 162, 120342. [Google Scholar] [CrossRef]
- Khan, A.; Khan, D.; Khan, I.; Ali, F.; Karim, F.U.; Nisar, K.S. MHD Flow of Brinkman Type H₂O-Cu, Ag, TiO₂ and Al₂O₃ Nanofluids with Chemical Reaction and Heat Generation Effects in a Porous Medium. J. Magn. 2019, 24, 262–270. [Google Scholar] [CrossRef]
- Nazar, R.; Amin, N.; Filip, D.; Pop, I. The Brinkman model for the mixed convection boundary layer flow past a horizontal circular cylinder in a porous medium. Int. J. Heat Mass Transf. 2003, 46, 3167–3178. [Google Scholar] [CrossRef]
- Ali, F.; Khan, I.; Samiulhaq, N.; Shafie, S. A Note on New Exact Solutions for Some Unsteady Flows of Brinkman-Type Fluids over a Plane Wall. 2012, 67, 377–380. Z. Für Nat. A 2012, 67, 377–380. [Google Scholar] [CrossRef]
- Zakaria, M.N.; Hussanan, A.; Khan, I.; Shafie, S. The Effects of Radiation on Free Convection Flow with Ramped Wall Temperature in Brinkman Type Fluid. J. Teknol. 2013, 62, 1886. [Google Scholar] [CrossRef]
- Tham, L.; Nazar, R. Numerical solution of mixed convection flow about a sphere in a porous medium saturated by a nanofluid: Brinkman model. J. Scinece Technol. 2012, 35–46. [Google Scholar]
- Tham, L.; Nazar, R.; Pop, I. Mixed convection boundary layer flow past a horizontal circular cylinder embedded in a porous medium saturated by a nanofluid: Brinkman model. J. Porous Media 2013, 16, 445–457. [Google Scholar] [CrossRef]
- Khan, Z.A.; Haq, S.U.; Khan, T.S.; Khan, I.; Tlili, I. Unsteady MHD flow of a Brinkman type fluid between two side walls perpendicular to an infinite plate. Results Phys. 2018, 9, 1602–1608. [Google Scholar] [CrossRef]
- Shafie, S.; Saqib, M.; Khan, I.; Qushairi, A. Mixed Convection Flow of Brinkman Type Hybrid Nanofluid Based on Atangana-Baleanu Fractional Model. J. Phys. Conf. Ser. 2019, 1366, 012041. [Google Scholar] [CrossRef]
- Flilihi, E.; Sriti, M.; Achemlal, D.; El-Haroui, M. Semi-Analytical Prediction of Mixed Convection in Porous Medium Using Darcy-Brinkman Model. J. Eng. Appl. Sci. 2019, 14, 1122–1129. [Google Scholar] [CrossRef] [Green Version]
- Verma, A.K.; Bhattacharyya, K.; Rajput, S.; Mandal, M.S.; Chamkha, A.J.; Yadav, D. Buoyancy driven non-Newtonian Prandtl-Eyring nanofluid flow in Darcy-Forchheimer porous medium over inclined non-linear expanding sheet with double stratification. Waves Random Complex Media 2022, 1–33. [Google Scholar] [CrossRef]
- Gautam, A.K.; Verma, A.K.; Bhattacharyya, K.; Mukhopadhyay, S.; Chamkha, A.J. Impacts of activation energy and binary chemical reaction on MHD flow of Williamson nanofluid in Darcy–Forchheimer porous medium: A case of expanding sheet of variable thickness. Waves Random Complex Media 2021, 1–22. [Google Scholar] [CrossRef]
- Verma, A.K.; Gautam, A.K.; Bhattacharyya, K.; Pop, I. Entropy generation analysis of Falkner–Skan flow of Maxwell nanofluid in porous medium with temperature-dependent viscosity. Pramana 2021, 95, 69. [Google Scholar] [CrossRef]
- Chamkha, A.; Gorla, R.S.R.; Ghodeswar, K. Non-similar Solution for Natural Convective Boundary Layer Flow Over a Sphere Embedded in a Porous Medium Saturated with a Nanofluid. Transp. Porous Media 2010, 86, 13–22. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Al-Mudhaf, A.F.; Pop, I. Effect of heat generation or absorption on thermophoretic free convection boundary layer from a vertical flat plate embedded in a porous medium. Int. Commun. Heat Mass Transf. 2006, 33, 1096–1102. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Khaled, A.A. Hydromagnetic combined heat and mass transfer by natural convection from a permeable surface embedded in a fluid-saturated porous medium. Int. J. Numer. Methods Heat Fluid Flow 2000, 10, 455–477. [Google Scholar] [CrossRef]
- Anwar, I.; Amin, N.; Pop, I. Mixed convection boundary layer flow of a viscoelastic fluid over a horizontal circular cylinder. Int. J. Non-linear Mech. 2008, 43, 814–821. [Google Scholar] [CrossRef] [Green Version]
- Kasim, A.R.M.; Mohammad, N.F.; Aurangzaib; Shafie, S. Mixed convection flow of viscoelastic fluid over a sphere with constant heat flux. AIP Conf. Proc. 2013, 1522, 453–461. [Google Scholar] [CrossRef]
- Aziz, L.A.; Kasim, A.R.M.; Al-Sharifi, H.A.M.; Salleh, M.Z.; Mohammad, N.F.; Shafie, S.; Ali, A. Influence of aligned MHD on convective boundary layer flow of viscoelastic fluid. AIP Conf. Proc. 2017, 1842, 30005. [Google Scholar] [CrossRef] [Green Version]
- Aziz, L.A.; Kasim, A.R.M.; Salleh, M.Z. Development on mathematical model of convective boundary layer flow of viscoelastic fluid with microrotation effect under constant wall temperature thermal condition over a bluff body. ASM Sci. J. 2019, 12, 86–90. [Google Scholar]
- Mahat, R.; Afiqah, N.; Kasim, A.R.M.; Shafie, S. Heat generation effect on mixed convection flow of viscoelastic nanofluid: Convective boundary condition solution. J. Adv. Res. Micro Nano Eng. 2020, 16, 166–172. [Google Scholar]
- Mahat, R.; Shafie, S.; Januddi, F. Numerical Analysis of Mixed Convection Flow Past a Symmetric Cylinder with Viscous Dissipation in Viscoelastic Nanofluid. CFD Lett. 2021, 13, 12–28. [Google Scholar] [CrossRef]
- Jafar, A.B.; Shafie, S.; Ullah, I. Magnetohydrodynamic Boundary Layer Flow of a Viscoelastic Fluid Past a Nonlinear Stretching Sheet in the Presence of Viscous Dissipation Effect. Coatings 2019, 9, 490. [Google Scholar] [CrossRef] [Green Version]
- Kasim, A.; Jiann, L.; Rawi, N.; Ali, A.; Shafie, S. Mixed Convection Flow of Viscoelastic Fluid over a Sphere under Convective Boundary Condition Embedded in Porous Medium. Defect Diffus. Forum 2015, 362, 67–75. [Google Scholar] [CrossRef]
- Qiao, Y.; Wang, X.; Xu, H.; Qi, H. Numerical analysis for viscoelastic fluid flow with distributed/variable order time fractional Maxwell constitutive models. Appl. Math. Mech. 2021, 42, 1771–1786. [Google Scholar] [CrossRef]
- Gamachu, D.; Ibrahim, W. Mixed convection flow of viscoelastic Ag-Al2O3/water hybrid nanofluid past a rotating disk. Phys. Scr. 2021, 96, 125205. [Google Scholar] [CrossRef]
- Mahat, R.; Rawi, N.A.; Shafie, S.; Kasim, A.R.M. Mixed Convection Boundary Layer Flow of Viscoelastic Nanofluid Past a Horizontal Circular Cylinder with Convective Boundary Condition. Int. J. Mech. Eng. Robot. Res. 2019, 8, 87–91. [Google Scholar] [CrossRef]
- Vajravelu, K.; Prasad, K.V. Chapter 2. Principles of the Implicit Keller-box Method. In Keller-Box Method and Its Application; Walter de Gruyter GmbH & Co KG: Berlin, Germany, 2014. [Google Scholar] [CrossRef]
- Yirga, Y.; Shankar, B. MHD Flow and Heat Transfer of Nanofluids through a Porous Media Due to a Stretching Sheet with Viscous Dissipation and Chemical Reaction Effects. Int. J. Comput. Methods Eng. Sci. Mech. 2015, 16, 275–284. [Google Scholar] [CrossRef]
- Tham, L.; Nazar, R.; Pop, I. Mixed convection flow over a solid sphere embedded in a porous medium filled by a nanofluid containing gyrotactic microorganisms. Int. J. Heat Mass Transf. 2013, 62, 647–660. [Google Scholar] [CrossRef]
- Hill, A.A.; Rajagopal, K.R.; Vergori, L. On the stability and uniqueness of the flow of a fluid through a porous medium. Z. Für Angew. Math. Und Phys. 2016, 67, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Chamkha, A.J. Non-darcy fully developed mixed convection in a porous medium channel with heat generation/absorption and hydromagnetic effects. Numer. Heat Transfer, Part A Appl. 1997, 32, 653–675. [Google Scholar] [CrossRef]

| Dimensionless Parameters | Notations |
|---|---|
| Dynamic viscosity | |
| Permeability of porous medium | |
| Porosity of porous medium | |
| Viscoelasticity | |
| Fluid density | |
| Pressure | |
| Thermal expansion coefficient | |
| Fluid temperature | |
| Porous effective thermal diffusivity |
| Dimensionless Parameters | Notations | Definitions |
|---|---|---|
| Brinkman parameter | ||
| Darcy number | ||
| Mixed convection parameter | ||
| Rayleigh number | ||
| Viscoelastic parameter |
| Author | Model (Momentum) | Limiting Cases | |
|---|---|---|---|
| Current | 4.7555 | ||
| Nazar et al. [10] | - | 4.7234 | |
| Tham et al. [14] | 4.7555 |
| Nazar et al. [10] | Current | |
|---|---|---|
| 0.5 | 4.3999 | 4.3999 |
| 1 | 5.5923 | 5.5922 |
| 2 | 7.8768 | 7.8767 |
| 3 | 10.0613 | 10.0612 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanafiah, S.F.H.M.; Kasim, A.R.M.; Zokri, S.M. Generalized Mathematical Model of Brinkman Fluid with Viscoelastic Properties: Case over a Sphere Embedded in Porous Media. Axioms 2022, 11, 609. https://doi.org/10.3390/axioms11110609
Kanafiah SFHM, Kasim ARM, Zokri SM. Generalized Mathematical Model of Brinkman Fluid with Viscoelastic Properties: Case over a Sphere Embedded in Porous Media. Axioms. 2022; 11(11):609. https://doi.org/10.3390/axioms11110609
Chicago/Turabian StyleKanafiah, Siti Farah Haryatie Mohd, Abdul Rahman Mohd Kasim, and Syazwani Mohd Zokri. 2022. "Generalized Mathematical Model of Brinkman Fluid with Viscoelastic Properties: Case over a Sphere Embedded in Porous Media" Axioms 11, no. 11: 609. https://doi.org/10.3390/axioms11110609
APA StyleKanafiah, S. F. H. M., Kasim, A. R. M., & Zokri, S. M. (2022). Generalized Mathematical Model of Brinkman Fluid with Viscoelastic Properties: Case over a Sphere Embedded in Porous Media. Axioms, 11(11), 609. https://doi.org/10.3390/axioms11110609








