Generalized Mathematical Model of Brinkman Fluid with Viscoelastic Properties: Case over a Sphere Embedded in Porous Media

Abstract

The process of heat transfer that involves non-Newtonian fluids in porous regions has attracted considerable attention due to its practical application. A mathematical model is proposed for monitoring fluid flow properties and heat transmission in order to optimize the final output. Thus, this attempt aims to demonstrate the behavior of fluid flow in porous regions, using the Brinkman viscoelastic model for combined convective transport over a sphere embedded in porous medium. The governing partial differential equations (PDEs) of the proposed model are transformed into a set of less complex equations by applying the non-dimensional variables and non-similarity transformation, before they are numerically solved via the Keller-Box method (KBM) with the help of MATLAB software. In order to validate the model for the present issue, numerical values from current and earlier reports are compared in a particular case. The studied parameters such as combined convection, Brinkman and viscoelastic are analyzed to obtain the velocity and temperature distribution. Graphs are used to illustrate the variation in local skin friction and the Nusselt number. The results of this study showcase that when the viscoelastic and Brinkman parameters are enlarged, the fluid velocity drops and the temperature increases, while the combined convection parameter reacts in an opposite manner. Additionally, as the Brinkman and combined convection parameters are increased, the physical magnitudes of skin friction and Nusselt number are increased across the sphere. Of all the parameters reported in this study, the viscoelastic parameter could delay the separation of boundary layers, while the Brinkman and combined convection parameters show no effect on the flow separation. The results obtained can be used as a foundation for other complex boundary layer issues, particularly in the engineering field. The findings also can help researchers to gain a better understanding of heat transfer analysis and fluid flow properties.

1. Introduction

In science and engineering applications, fluid flow and convective heat transfer have received distinctive attention. Researchers have carried out extensive research on boundary layers to get insight in improving heat transfer conductivity and fluid characteristics. A fluid is defined as a substance that flows continuously due to shear stress and is generally categorized as a Newtonian or non-Newtonian fluid.

In recent decades, the combined convective flow of non-Newtonian fluids has attracted significant attention. The term “combined convective transport” refers to the interaction of pressure and buoyancy forces at different temperatures. Meanwhile, non-Newtonian fluids are fluids that defy Newton’s Law and cause variations in viscosity when shear stress is applied. Non-Newtonian fluids are widely used in a variety of applications, including oil reservoirs, wire coating, biological fluids, crystal growth, and geothermal energy extraction [1]. Many contributions have been made to the investigation of fluid flow properties, as highlighted in the following work [2,3,4,5,6,7,8].

According to Khan et al. [9], the Brinkman model is the classical model used in a porous medium that applies to a high-porosity incompressible surface. Nazar et al. [10] used the KBM to investigate the Brinkman model moving over a porous horizontal circular cylinder (HCC). They discovered that the Brinkman model’s results differed significantly from Darcy’s law model. Furthermore, they discovered that as the Darcy–Brinkman parameter increased, the heat transfers and sheer stress coefficient decreased. Ali et al. [11] determined the exact solutions of Brinkman fluid on an infinite rotating plate. Zakaria et al. [12], on the other hand, applied the Brinkman model in their investigation, which focused on the influence of radiative flow over unsteady free convection flow near a vertical surface. The wall temperature is thought to have a continuous temporally ramped profile. Both authors used the Laplace transformation technique to compute the solutions.

Tham and Nazar [13] solved another flow problem based on the Brinkman model. They investigated the combined mode of heat transfer of a nanofluid around a saturated porous sphere for assisting and opposing flow situations. In a similar scenario, Tham et al. [14] investigated the flow through an HCC. Both authors used the KBM for numerical solutions and discovered that the increase in combined convective transport affects the boundary layer separation and can suppress the separation in the range $0^{°}<x<{120}^{°}$ and $0^{°}<x<{180}^{°}$ for the sphere and HCC, respectively. Khan et al. [15] focused on the Brinkman flow of unsteady magnetohydrodynamics that passed over an infinite plate. They used the finite Fourier transform to obtain the numerical results. Shafie et al. [16] investigated the phenomena of fluid flow passing across an oscillating plate using the fractional Brinkman model. They used the Laplace transformation to solve the problems and discovered that increasing the Brinkman factor affected the fluid’s velocity. Furthermore, Flilihi et al. [17] investigated combined convection heat transfer under the Darcy–Brinkman model in a porous region. The authors discovered that a high Darcy number significantly increases the wideness of the thermal boundary layer. Recently, there have been several studies that have reported on the convective flow in porous medium [18,19,20,21,22,23].

Viscoelastic fluid is categorized as a non-Newtonian fluid with viscosity and elasticity properties. The modified viscoelastic model has been investigated by scholars due to its numerous applications in developing technology. Anwar et al. [24] explored the combined convective flow of a viscoelastic fluid over a HCC. They discovered that increasing the combined convection parameter slowed the separation of boundary layers within the range. Furthermore, Kasim et al. [25] extended the problem to a constant heat flux and concluded that the flow is influenced by both the Prandtl number and convective parameter. The effects of magnetohydrodynamics, which were aligned with the viscoelastic fluid heated by Newtonian heating around an HCC, were investigated by Aziz et al. [26]. In response to a similar issue raised in the following years, Aziz et al. [27] developed a viscoelastic fluid with microrotation characteristics. In addition, Mahat et al. [28] focused on the effect of generating heat on the convective flow of viscoelastic nanofluids. They discovered that strong heat generation increased both skin friction and heat transfer. Mahat et al. [29] recently published a study on the convection flow of viscoelastic nanofluids with the viscous dissipation effect under convective boundary conditions. The heat transfer rate had an impactful effect at the stagnation point due to the primary source of heat at the boundary layer. All the authors above have used the KBM to solve these problems. More research on viscoelastic fluids over various geometries has also been conducted [30,31,32,33,34].

Previous scholars have employed a variety of numerical methods to solve the boundary layer problem. In particular, there are two implicit finite difference techniques that have been widely used to solve the PDEs, the Crank–Nicolson method and KBM. However, according to Vajravelu and Prasad [35] and Yirga and Shankar [36], the KBM is one of the most powerful methods, it is easily adaptable to a new class of problems, provides more rapid net variation, easily obtains higher-order accuracy, is productive, and is well-suited to solve non-linear PDEs.

There are other models where the fluid flow across a porous surface with high porosity is not relevant in heat transfer enhancement. Therefore, this study aims to propose a new model for boundary layer flow that utilizes the basic Brinkman model with viscoelastic properties, namely the Brinkman-viscoelastic fluid by considering the combined convective flow that moves along a sphere. The proposed model, which is a hybrid of the Brinkman concept and viscoelastic knowledge, could improve the fluid’s properties and heat transfer performance. For instance, the performance of viscoelastic fluids for oil recovery was studied through the microfluidic device channel. The design of microfluidic devices allows the scholars to investigate the flow characteristics of viscoelastic fluids in porous media. Through the micro-channel, the different structures were designed to simulate the characteristics of porous medium. Inspired by the previous literature, the KBM is applied in solving the proposed model encoded in MATLAB software. Furthermore, the effect of relevant parameters, such as combined convective, viscoelastic, and Brinkman parameters on the fluid’s characteristics, is investigated.

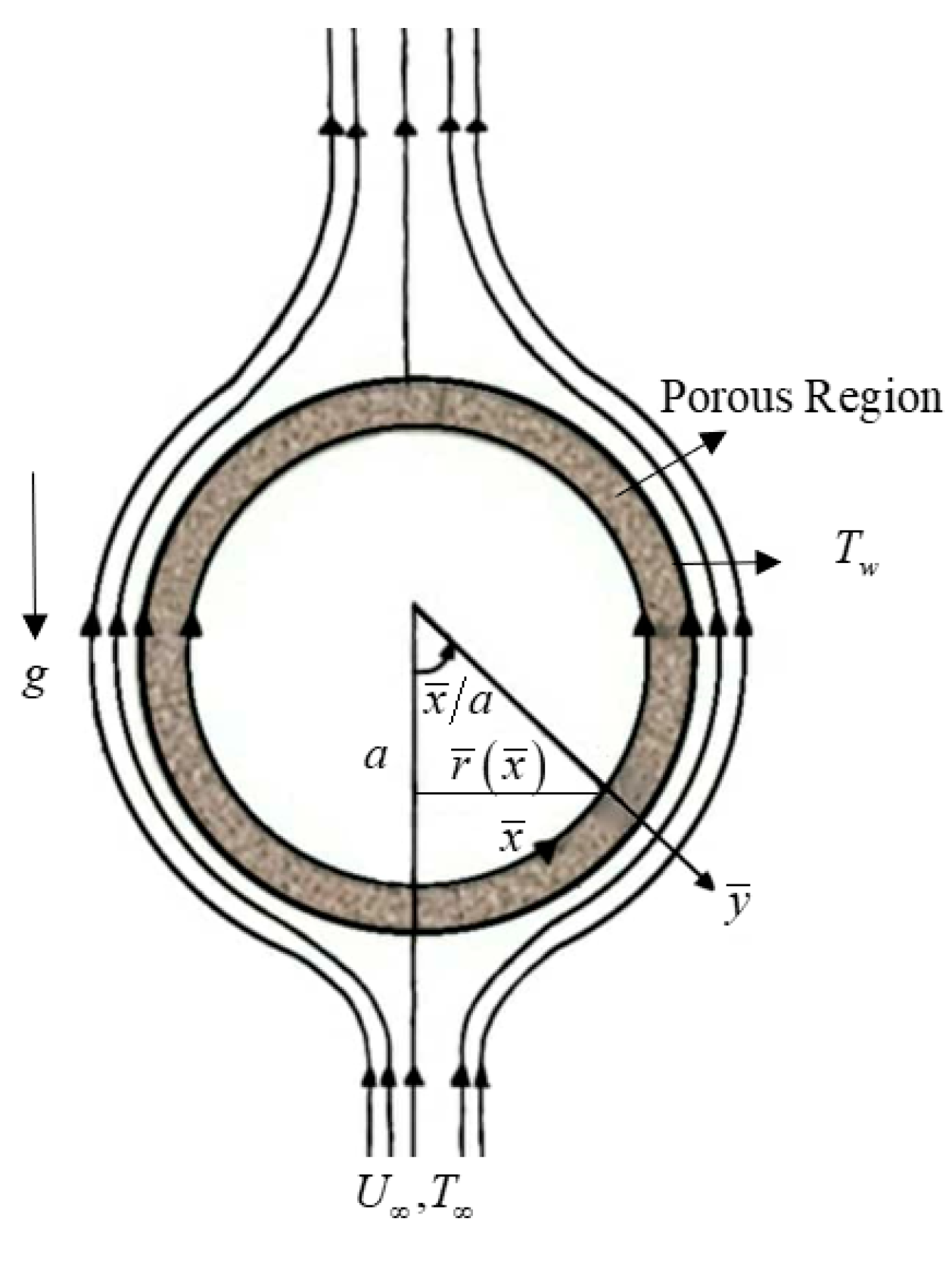
2. Model Formulation

A steady flow with combined convective transport over a porous sphere with radius $a$ is considered. According to Tham et al. [37], the exterior velocity is ${\overline{u}}_e\left(\overline{x}\right)=\left(3/2\right)U_{\infty }\sin \left(\overline{x}/a\right)$ by assuming that the uniform free stream velocity is $U_{\infty }$, which moves upwards across the sphere under gravitational acceleration, $g$. $T_{\infty }$ is the ambient temperature, $T_w$ is the constant surface temperature and the radial distance from the symmetrical axis is demarcated as $\overline{r}\left(\overline{x}\right)=a\sin \left(\overline{x}/a\right)$. The values of $\overline{x}$ are measured laterally to the sphere and $\overline{y}$ is perpendicular to the sphere’s surface.

The physical configuration is presented in Figure 1, where the sphere’s surface is subjected to a constant wall temperature boundary condition.

For this present problem, the continuity equation is introduced by Tham et al. [37], as in Equation (1). By employing the Brinkman model by Nazar et al. [10] to the Brinkman viscoelastic model, an additional viscoelastic term given by Aziz et al. [27] is incorporated into momentum Equation (2) to describe the viscosity and elasticity of the fluid. For the Brinkman model, it can be assumed that the flow is expected to be slow, so that the porous medium inertial effects can be ignored in the fluid [38,39]. Under the boundary layer assumptions, part of the governing equations of the proposed model can be written as

$$\frac{\partial \left(\overline{r}\overline{u}\right)}{\partial \overline{x}}+\frac{\partial \left(\overline{r}\overline{v}\right)}{\partial \overline{y}}=0,$$

(1)

$$\begin{array}{cc}\hfill \frac{\mu }{K} \overline{u}& =-\frac{dp}{d\overline{x}}+\frac{\mu }{\varphi } \frac{{\partial }^2\overline{u}}{\partial {\overline{y}}^2}+k_0\left[\overline{u}\frac{{\partial }^3\overline{u}}{\partial \overline{x}\partial {\overline{y}}^2}+\overline{v}\frac{{\partial }^3\overline{u}}{\partial {\overline{y}}^3}-\frac{\partial \overline{u}}{\partial \overline{y}}\frac{{\partial }^2\overline{u}}{\partial \overline{x}\partial \overline{y}}+\frac{\partial \overline{u}}{\partial \overline{x}}\frac{{\partial }^2\overline{u}}{\partial {\overline{y}}^2}\right] \hfill \\ \hfill & -\rho g \sin (\overline{x}/a),\hfill \end{array}$$

(2)

$$\overline{u}\frac{\partial T}{\partial \overline{x}}+\overline{v}\frac{\partial T}{\partial \overline{y}}={\alpha }_m \frac{{\partial }^{2}T}{\partial {\overline{y}}^2} ,$$

(3)

with respect to the boundary conditions

$$\begin{array}{l}\overline{v}=0,\hspace{1em}\overline{u}=0,\hspace{1em}T=T_w,\hspace{1em}\mathrm{at}\hspace{1em}\overline{y}=0,\\ \overline{u}\to {\overline{u}}_e(\overline{x}),\hspace{1em}\overline{v}\to 0,\hspace{1em}T\to T_{\infty }\hspace{1em}\mathrm{as}\hspace{1em}\overline{y}\to \infty .\end{array}$$

(4)

where $\rho ={\rho }_{\infty }\left[1-\beta \left(T-T_{\infty }\right)\right].$

The $\overline{x}$ and $\overline{y}$ are the components of velocity in the $\overline{u}$ and $\overline{v}$ direction.

The parameters that arise in Equations (1)–(3) are summarized in

Table 1. Parameters in model.

Dimensionless Parameters	Notations
Dynamic viscosity	$\mu$
Permeability of porous medium	$K$
Porosity of porous medium	$\varphi$
Viscoelasticity	$k_0$
Fluid density	$\rho$
Pressure	$p$
Thermal expansion coefficient	$\beta$
Fluid temperature	$T$
Porous effective thermal diffusivity	${\alpha }_m$

based on the work of Nazar et al. [10].

The PDEs in Equations (1)–(3) are transformed into dimensionless forms by using the non-dimensional variables adopted from the work of Tham et al. [37].

$$\begin{array}{l}x=\overline{x}/a,\hspace{1em}y=P{e}^{1/2} (\overline{y}/a),\hspace{1em}u=\overline{u}/U_{\infty },\hspace{1em}\\ v=P{e}^{1/2} (\overline{v}/U_{\infty }),u_e(\overline{x})={\overline{u}}_e(\overline{x})/U_{\infty },r=\overline{r}\left(\overline{x}\right)/a,\\ \theta =(T-T_{\infty })/(T_w-T_{\infty })\hspace{1em}\end{array}$$

(5)

It is noted that $Pe=U_{\infty }a/{\alpha }_m$ is a modified Péclet number for the case of the porous region.

By eliminating pressure, $p$ and applying the Boussinesq and boundary layer approximation [14], the formulation yields the following equations:

$$\frac{\partial }{\partial x}\left(ru\right)+\frac{\partial }{\partial y}\left(rv\right)=0,$$

(6)

$$\frac{\partial u}{\partial y}= \Gamma \frac{{\partial }^{3}u}{\partial y^3}+k_1\left[\begin{array}{l}u\frac{{\partial }^{4}u}{\partial x\partial y^3}+\frac{{\partial }^{3}u}{\partial x\partial y^2}\frac{\partial u}{\partial y}+v\frac{{\partial }^{4}u}{\partial y^4}+\frac{{\partial }^{3}u}{\partial y^3}\frac{\partial v}{\partial y}-\frac{\partial u}{\partial y}\frac{{\partial }^{3}u}{\partial x\partial y^2}\\ -\frac{{\partial }^{2}u}{\partial x\partial y}\frac{{\partial }^{2}u}{\partial y^2}+\frac{\partial u}{\partial x}\frac{{\partial }^{3}u}{\partial y^3}+\frac{{\partial }^{2}u}{\partial y^2}\frac{{\partial }^{2}u}{\partial x\partial y}\end{array}\right]+\lambda \frac{\partial \theta }{\partial y} \sin x,$$

(7)

$$u\frac{\partial \theta }{\partial x}+v\frac{\partial \theta }{\partial y}=\frac{{\partial }^2\theta }{\partial y^2}$$

(8)

and the boundary condition (4) becomes

$$\begin{array}{l}u=0,v=0,\hspace{1em}\theta =1 at \overline{y}=0,\\ u\to \left(3/2\right)\sin x,v\to 0,\theta \to 0 as \overline{y}\to \infty ,\end{array}$$

(9)

The dependent variables in (6)–(9) are reduced to a less complex form using non-similarity transformation by introducing the following variables from the work of Tham et al. [37]:

$$\psi =x rf(x,y),\theta =\theta (x,y),u=\left(\frac{1}{r}\right)\frac{\partial \psi }{\partial y},v=-\left(\frac{1}{r}\right)\frac{\partial \psi }{\partial x},$$

(10)

where $\psi$ and $\theta$ indicate the stream function and temperature of the fluid, respectively. As a result, Equation (6) is fully satisfied, and Equations (7)–(9) result in the following expressions:

$$\begin{array}{l}{f}^{\prime }-\mathsf{\Gamma }{f}^{‴} -k_1\left[2f^{\prime }{f}^{‴}-\left(1+x\frac{\cos x}{\sin x}\right)f{f}^{\left(iv\right)}-{\left(f^{″}\right)}^2\right]-\left(\left(3/2\right)+\lambda \theta \right) \frac{\sin x}{x}=\\ x{k}_1\left[f^{\prime }\frac{\partial f^{‴}}{\partial x}-\frac{\partial f}{\partial x}{f}^{\left(iv\right)}-f^{″}\frac{\partial f^{″}}{\partial x}+\frac{\partial f^{\prime }}{\partial x}{f}^{‴}\right]\end{array}$$

(11)

$${\theta }^{″}+\left(1+x\frac{\cos x}{\sin x}\right)f {\theta }^{\prime }=x \left(f^{\prime }\frac{\partial \theta }{\partial x}-\frac{\partial f}{\partial x} {\theta }^{\prime }\right).$$

(12)

The transformed boundary condition is obtained as

$$\begin{array}{l}f(0)=0,\hspace{1em}{f}^{\prime }(0)=0,\hspace{1em}\theta (0)=1,\hspace{1em}\mathrm{at}y=0,\\ f^{\prime }(\infty )\to \left(3/2\right)\frac{\sin x}{x},\hspace{1em}{f}^{″}(\infty )\to 0,\hspace{1em}\theta (\infty )\to 0\hspace{1em}\mathrm{as}y\to \infty .\end{array}$$

(13)

Equations (11)–(13) are reduced to the ordinary differential equations (the case at the lower stagnation point of the sphere ($x\approx 0$)) as follows:

$$f^{\prime }-\mathsf{\Gamma }{f}^{‴} -k_1\left[2f^{\prime }{f}^{‴}-2f{f}^{\left(iv\right)}-{\left(f^{″}\right)}^2\right]-\left(3/2\right)-\lambda \theta =0,$$

(14)

$${\theta }^{″}+2f {\theta }^{\prime }=0.$$

(15)

These are subjected to the following expressions:

$$\begin{array}{l}f(0)=0,\hspace{1em}{f}^{\prime }(0)=0,\hspace{1em}\theta (0)=1\hspace{1em}\\ f^{\prime }(\infty )\to 3/2,\hspace{1em}{f}^{″}(\infty )\to 0,\hspace{1em}\theta (\infty )\to 0\hspace{1em}\end{array}$$

(16)

Referring to Tham et al. [14], the local skin friction coefficient and Nusselt number are defined as

$$C_f=\frac{{\tau }_w}{\rho U_{\infty }{}^2},N{u}_x=\frac{a{q}_w}{k\left(T_w-T_{\infty }\right)}$$

(17)

Here, ${\tau }_w$ and $q_w$ are defined as the skin friction (wall shear stress) and heat flux from the surface, respectively, so that

$$\begin{array}{l}{\tau }_w=\mu {\left(\frac{\partial \overline{u}}{\partial \overline{y}}\right)}_{\overline{y}=0}+k_0{\left(\overline{u}\frac{{\partial }^2\overline{u}}{\partial \overline{x}\partial \overline{y}}+\overline{v}\frac{{\partial }^2\overline{u}}{\partial {\overline{y}}^2}+2\left(\frac{\partial \overline{u}}{\partial \overline{x}}\frac{\partial \overline{u}}{\partial \overline{y}}\right)\right)}_{\overline{y}=0}\\ q_w=-k{\left(\frac{\partial T}{\partial \overline{y}}\right)}_{\overline{y}=0}\end{array}$$

(18)

By substituting Equation (18) into Equation (17), the following skin friction and Nusselt number can be obtained:

$$C_f\left(P{e}^{1/2}/\mathrm{Pr}\right)=x\frac{{\partial }^{2}f}{\partial y^2},\hspace{1em}NuP{e}^{-1/2}=-\frac{\partial \theta }{\partial y}.$$

(19)

Referring to Nazar et al. [10], the dimensionless parameters in Equation (11) are declared, as shown in

Table 2. Definitions of dimensionless parameters.

Dimensionless Parameters	Notations	Definitions
Brinkman parameter	$\Gamma$	$\frac{Da}{\varphi }Pe$
Darcy number	$Da$	$\frac{K}{a^2}$
Mixed convection parameter	$\lambda$	$\frac{Ra}{Pe}$
Rayleigh number	$Ra$	$\frac{gK\beta \left(T_w-T_{\infty }\right)a}{{\alpha }_{m}v}$
Viscoelastic parameter	$k_1$	$\frac{k_{0}K{U}_{\infty }Pe}{\mu a^3}$

.

3. Solution Procedures

The KBM is applied to solve (11) to (13), as it proves to be unconditionally stable and quickly converges for highly non-linear flows. It is also one of the most used computational methods for solving any order of boundary layer flow equations [35,36]. This procedure consists of four steps with the help of MATLAB software, which are as follows:

Step 1: Convert the PDEs to a first-order system.

The new dependent variables are used to convert Equations (11)–(13) into a first order system, as follows:

$$\begin{array}{l}u-\mathsf{\Gamma }p -k_1\left[2up-\left(1+x\frac{\cos x}{\sin x}\right)f{p}^{\prime }-v^2\right]-\left(\left(3/2\right)+\lambda s\right) \frac{\sin x}{x}=\\ x{k}_1\left[u\frac{\partial p}{\partial x}-\frac{\partial f}{\partial x}{p}^{\prime }-v\frac{\partial v}{\partial x}+\frac{\partial u}{\partial x}p\right]\end{array}$$

(20)

$$t^{\prime }+\left(1+x\frac{\cos x}{\sin x}\right)ft=x \left(u\frac{\partial s}{\partial x}-\frac{\partial f}{\partial x} t\right)$$

(21)

$$\begin{array}{l}u(0)=0,\hspace{1em}f(0)=0,\hspace{1em}s(0)=1\\ u(\infty )\to \left(3/2\right)\frac{\sin x}{x},\hspace{1em}v(\infty )\to 0,\hspace{1em}s(\infty )\to 0.\end{array}$$

(22)

Step 2: Convert into finite difference form using central differences.

The central differences are used to transform the first-order system of Equations (20)–(22) into finite difference equations.

Step 3: Linearize the obtained equations in Step 2 using Newton’s method and take the equations in matrix–vector form.

The finite difference equations are linearized by implementing the Newton method using specific iterations. After some algebraic modifications, the system of equations is written in the form of block matrices.

Step 4: Solve the matrix using the block tridiagonal elimination technique.

The block matrices are solved by using the block tridiagonal elimination method, including the forward and backward sweep method in order to compute the significant parameters in this study.

The effects of the pertinent physical parameters are detailed and discussed. The boundary layer thickness of $y_{\infty }=6$ is chosen to ensure that the profiles asymptotically fulfil the boundary condition. The current findings are matched to the published works of Nazar et al. [10] and Tham et al. [14] in the absence of $k_1$ and the value of $\left(3/2\right)$ in (11) is set as a constant. The current model can be reduced to establish the model that is summarized in

Table 3. Comparative values of $C_{f}P{e}^{1/2}/Pr$ at $x=1$, $\Gamma =0.1$, $\lambda =1$ and $A=1$.

Author	Model (Momentum)	Limiting Cases	${\mathit{C}}_{\mathit{f}}\mathit{P}{\mathit{e}}^{1/2}/\mathit{P}\mathit{r}$
Current	$\begin{array}{l}{f}^{\prime }-\mathsf{\Gamma }{f}^{‴} -\left(A+\lambda \theta \right) \frac{\sin x}{x}-k_1\left[2f^{\prime }{f}^{‴}-2f{f}^{\left(iv\right)}-{\left(f^{″}\right)}^2\right]=\\ x{k}_1\left[f^{\prime }\frac{\partial f^{‴}}{\partial x}-\frac{\partial f}{\partial x}{f}^{\left(iv\right)}-f^{″}{\frac{\partial f^{″}}{\partial x}}^2+\frac{\partial f^{\prime }}{\partial x}{f}^{‴}\right]\end{array}$	$k_1=0$	4.7555
Nazar et al. [10]	$f^{\prime }-\mathsf{\Gamma }{f}^{‴} -\left(A+\lambda \theta \right) \frac{\sin x}{x}=0$	-	4.7234
Tham et al. [14]	$f^{\prime }-\mathsf{\Gamma }{f}^{‴} -\left(A+\left(\theta -Nr\phi \right)\lambda \right) \frac{\sin x}{x}=0$	$Nr=0$	4.7555

.

Table 4. Comparison of $f^{″}(0)$ at $\Gamma =0.1$, $k_1\to 0$ for various $\lambda$ (lower stagnation point).

$\mathit{\lambda }$	Nazar et al. [10]	Current
	${\mathit{f}}^{″}(0)$	${\mathit{f}}^{″}(0)$
0.5	4.3999	4.3999
1	5.5923	5.5922
2	7.8768	7.8767
3	10.0613	10.0612

also shows that the current results are in strong agreement with the existing output, indicating that the proposed model’s findings are acceptable.

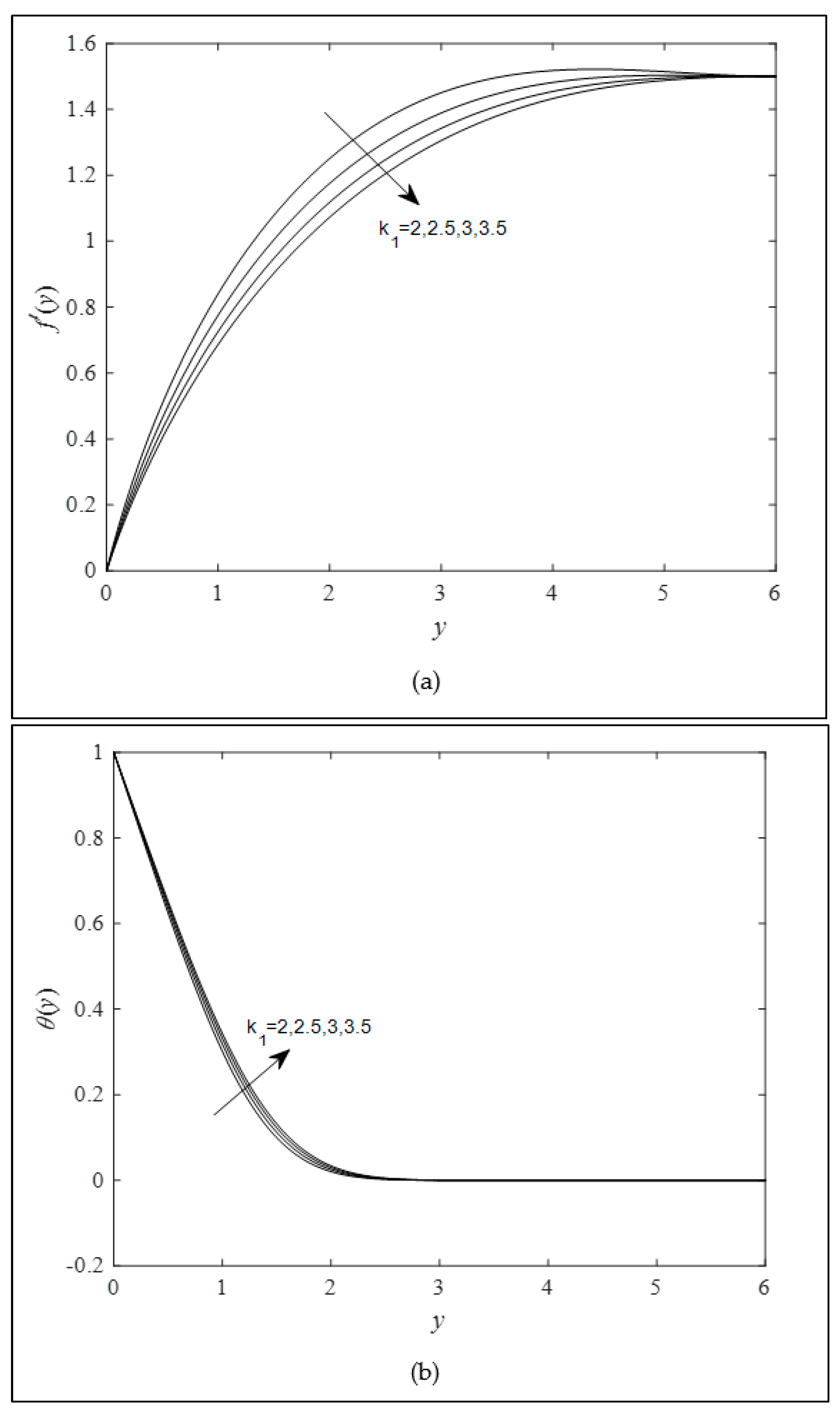
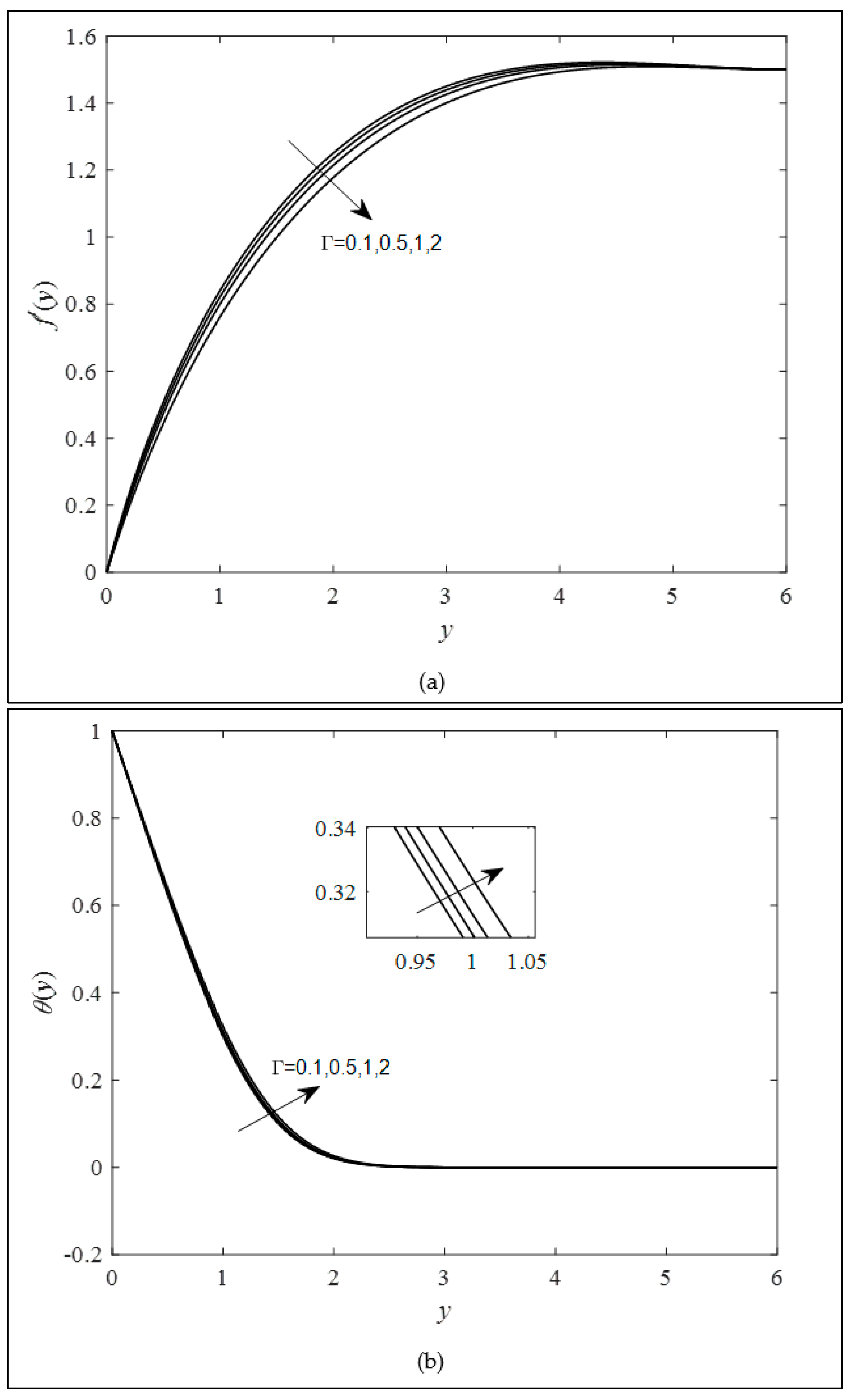
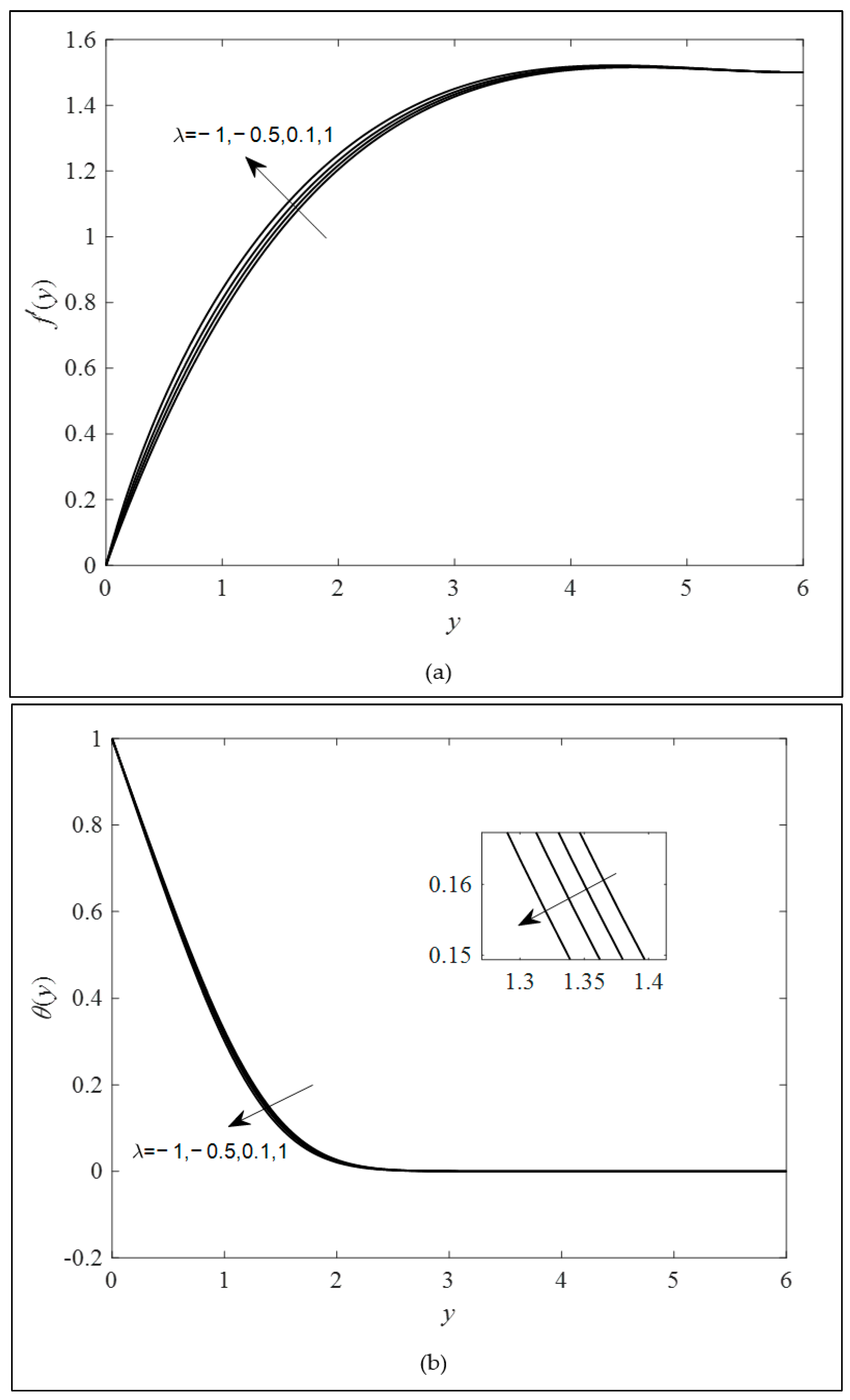
4. Results and Discussion

In this study, the viscoelastic fluid $k_1>0$ showcases the effect of viscoelastic properties. It is important to mention that $k_1\ge 2$ is chosen to ensure that the results meet the boundary condition asymptotically. The assisting and opposing flow, $\lambda >0$ and $\lambda <0$, are also considered, respectively. According to Tham et al. [14], in the presence of a solid matrix, the no-slip condition would be dominant at high Brinkman values. As a result, to characterize the Brinkman factor, $\Gamma >0$ is used. Figure 2, Figure 3 and Figure 4 depict the characteristics of $k_1$, $\Gamma$ and $\lambda$ against $f^{\prime }(y)$ and $\theta (y)$. In Figure 2a, the fluid velocity is reduced by the intensification of $k_1$. For example, when the value of $k_1$ is increased from 2 to 3.5, the velocity is decreased. This occurs due to the viscous and elastic properties of the fluid, which results in the delay of the velocity. Therefore, as shown in Figure 2b, it is likely that the incremental variations in $k_1$ cause the fluid temperature to rise. The increasing variation in $\Gamma$, which is similar to the drag force, reduces the fluid velocity, as depicted in Figure 3a. This is due to the increase in force caused by the existence of the solid matrix. Figure 3b reveals that the change in $\Gamma$ from 0.1 to 2 has a very small effect on the temperature field. This can be observed when $\Gamma$ increases, as the temperature distribution slightly improves. Figure 4a shows that the increasing combined convection parameter $\lambda$ has increased the velocity of the fluid due to the external flow of buoyancy forces caused by the pressure gradient. As shown in Figure 4b, the temperature profile tends to decrease as $\lambda$ increases. It is worth noting in this case that $\lambda$ is the buoyancy force that causes the increase in the convection cooling effect, which results in the temperature decrease.

The graphs of skin friction, $C_f\left(P{e}^{1/2}/\mathrm{Pr}\right)$ and Nusselt number (heat transfer) and $NuP{e}^{-1/2}$ versus various parameters are shown in Figure 5, Figure 6 and Figure 7. The increasing of $k_1$ and $\Gamma$ is noticed to decrease in $C_f\left(P{e}^{1/2}/\mathrm{Pr}\right)$, as shown in Figure 5a and Figure 6a. However, for the fixed value of $k_1$ and $\Gamma$, the skin friction is observed to increase along the sphere’s surface up to the separation point of $x$. This occurs due to the fluid’s viscosity and elasticity, which greatly influences the friction between the fluid molecules and the sphere’s surface. In Figure 7a, the variations in $\lambda$ have boosted the $C_f\left(P{e}^{1/2}/\mathrm{Pr}\right)$. The strength of buoyancy forces increases the fluid velocity, which improves local skin friction. As illustrated in Figure 5b and Figure 6b, $NuP{e}^{-1/2}$ decreases when $k_1$ and $\Gamma$ are increased. This result occurs due to the thickening of the thermal boundary layer. However, the opposite trend is observed in Figure 7b for $NuP{e}^{-1/2}$, where the graph shows that the Nusselt number improves as $\lambda$ increases, thereby decreasing the thermal boundary layer thickness. Based on this finding, Figure 5 shows that various values of $k_1$ delayed boundary layer separation within the range $0\le x\le 1.9$, since the viscoelastic properties are likely to decrease the fluid flow’s velocity. Meanwhile, it is concluded that various values of $\Gamma$ and $\lambda$ do not affect the separation of the flow.

5. Conclusions

The numerical analysis of the flow of Brinkman-viscoelastic fluid over a sphere in a porous region with the combined convective element have been discussed in this study. The models are reduced to a less complicated form of non-linear PDEs, before being fully solved using Matlab software. The conclusions drawn from the analysis are as follows:

• Both the Brinkman and viscoelastic parameters reduced the velocity profile and increased the temperature profile.
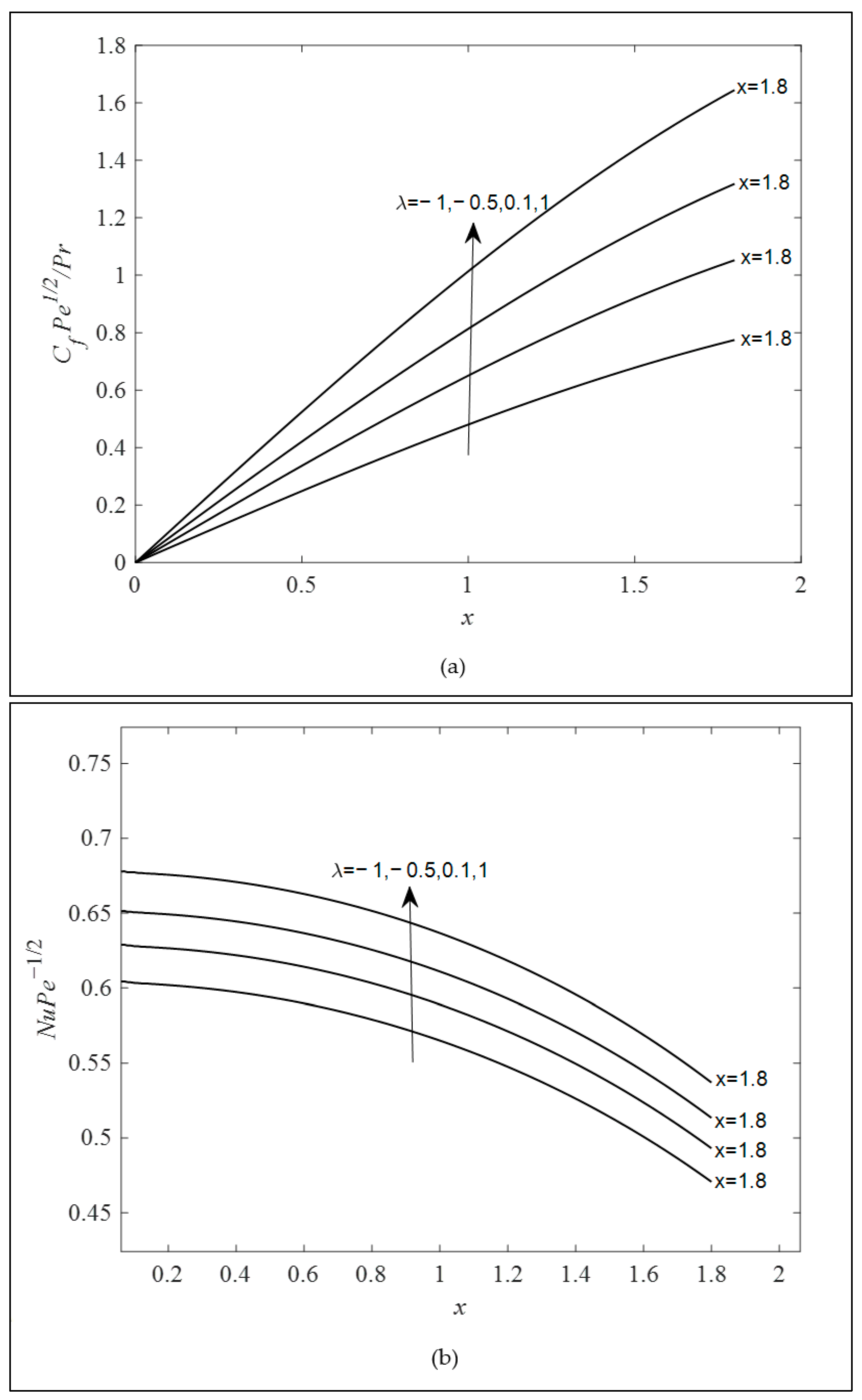
• A boost in the combined convection parameter can decrease the temperature and intensify the fluid velocity.
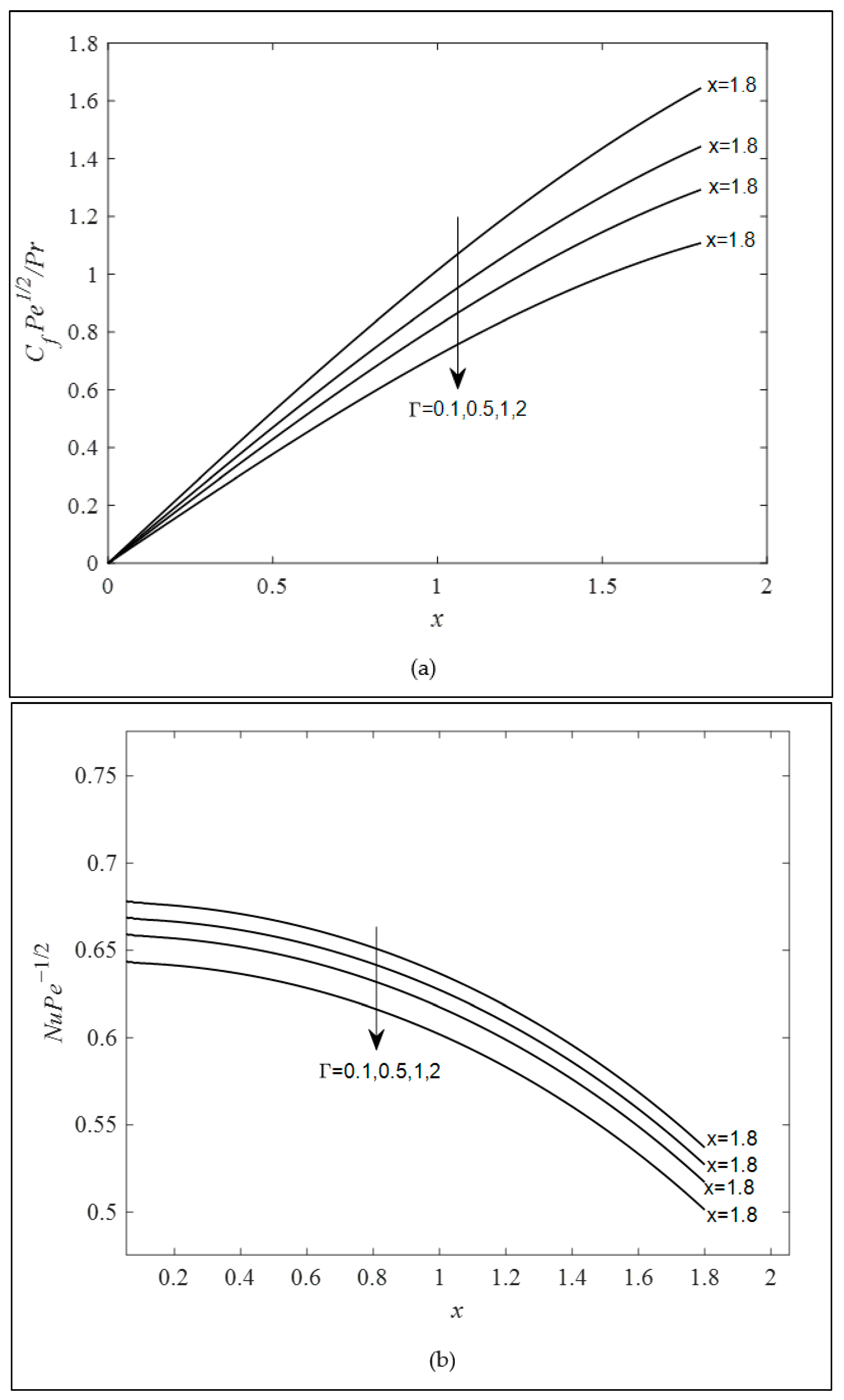
• Both the Brinkman and viscoelastic parameter reduced the Nusselt number (heat transfer rate) and skin friction coefficient, while the combined convection parameter behaved in an opposite manner. However, the variation in the Brinkman and combined convection parameter encounters the separation boundary layer after $x=1.8$, whereas the increase in the viscoelastic parameter delayed the boundary layer separation.

The current findings offer an inclusive theoretical analysis of fluid characteristics. This analysis allows engineers to validate their experimental work on the appropriate issue in fluid dynamics. Furthermore, this research only focuses on the convection of the Brinkman viscoelastic fluid model. For future research, this work could be improved by considering a nanofluid model, either the Tiwari and Das or Buongiorno models, due to their diverse applications in automotive radiator systems, glass fiber production and power plant cooling systems. Thus, further direction of this research may focus on convective boundary layer flow by considering the Brinkman-viscoelastic nanofluids model. In addition, the concept of fractional calculus can also be applied to solve the proposed problem and compared with the computational output.