On Symmetrized Stochastic Harmonically Convexity and Hermite–Hadamard Type Inequalities

Abstract

Throughout this study, the concept of symmetrized harmonically convex stochastic processes will be discussed in further detail. Some certain characterizations for symmetrized harmonically convex stochastic processes are discussed that use Hermite–Hadamard-type inequalities. A Hyers–Ulam-type stability result for harmonically convex stochastic processes is given as well.

1. Introduction

Nikodem [1] proposed the concept of convex stochastic processes in 1980. Skowroński [2] then extended the well-known characteristics of convex functions to convex stochastic processes. Kotrys [3] proved the Hermite–Hadamard inequality using convex stochastic processes in his study. A number of scholars have examined numerous integral inequalities in recent papers on convex stochastic processes. In [4], Agahi and Babakhani studied fractional inequalities related to the Hermite–Hadamard and Jensen types for convex stochastic processes. Kotrys [3] obtained the Hermite–Hadamard inequality for convex stochastic processes. In another study, Kotrys [5] discussed properties of strongly convex stochastic processes. Li and Hao [6] acquired the Hermite–Hadmard inequality for h-convex stochastic processes. Dragomir [7] defined symmetrized convex functions and highlighted their several features. Haq and Kotrys [8] introduced the concept of symmetrized convex stochastic processes and analyzed the Hermite–Hadmard-type inequalities in the perspective of the preceding papers. Additionally, Haq and Kotrys [8] addressed various ways of characterizing symmetrized convex stochastic processes. Okur et al. [9] extended a well-known work on harmonically convex functions to harmonically convex stochastic processes. In addition, the authors intended to find Hermite–Hadmard-type inequalities for harmonically convex stochastic processes. Following the prior studies on this topic, we introduce the concept of symmetrized harmonically convex stochastic processes and investigate the Hermite–Hadmard-type inequalities for symmetrized harmonically convex functions as well as their applications. In this study, we also describe a number of characterizations of harmonic symmetrized convex stochastic processes.

2. Preliminaries Section

Let ($\mathsf{\Lambda },\mathcal{F},\mathcal{P}$) be an arbitrary probability space. A function $\mathcal{H}:\mathsf{\Lambda }\to \mathit{R}$ is a random variable if it is $\mathcal{F}$-measurable. Let $\mathcal{I}\subset \mathit{R}$ be an interval. A function $\mathcal{H}:\mathcal{I}\times \mathsf{\Lambda }\to \mathit{R}$ is a stochastic process if the function $\mathcal{H}(\nu ,·)$ is a random variable for all $\nu \in \mathcal{I}$.

Definition 1

([8]). A stochastic process $\mathcal{H}:\mathcal{I}\times \mathsf{\Lambda }\to \mathit{R}$ is said to be continuous in probability in $\mathcal{I}$, if for all ${\nu }_0\in \mathcal{I}$

$$\mathcal{P}-\underset{\nu \to {\nu }_0}{lim}\mathcal{H}(\nu ,·)=\mathcal{H}({\nu }_0,·),$$

where $\mathcal{P}-lim$ denotes the limit in probability.

Definition 2

([8]). A stochastic process $\mathcal{H}:\mathcal{I}\times \mathsf{\Lambda }\to \mathit{R}$ is said to be mean-square continuous in $\mathcal{I}$, if for every ${\nu }_0\in \mathcal{I}$

$$\underset{\nu \to {\nu }_0}{lim}E\left[{\left(\mathcal{H}\left(\nu \right)-\mathcal{H}\left({\nu }_0\right)\right)}^2\right]=0,$$

where $E\left[\mathcal{H}\left(\nu \right)\right]$ denotes the expectated value of the random variable $\mathcal{H}(\nu ,·)$.

To be clear, it is important to note that mean-square continuity of $\mathcal{H}:\mathcal{I}\times \mathsf{\Lambda }\to \mathit{R}$ implies probability continuity but the converse does not hold true.

To refresh our memory, let us have a look at the mean-square integral.

Definition 3

([8]). For any normal sequence of partitions $\left[{\alpha }_1,{\alpha }_2\right]\subset \mathcal{I}$, a random variable $\mathcal{Y}:\mathsf{\Lambda }\to \mathit{R}$ is called the mean-square integral of the stochastic process $\mathcal{H}:\mathcal{I}\times \mathsf{\Lambda }\to \mathit{R}$ with $E\left[{\left(\mathcal{H}\left(\nu \right)\right)}^2\right]<\infty$, if the condition

$$\underset{n\to \infty }{lim}E\left[{\left(\sum _{k=1}^n\mathcal{H}\left(x_k\right)\left({\nu }_k-{\nu }_{k-1}\right)-\mathcal{Y}\right)}^2\right]=0$$

holds, where $x_k\in$$\left[{\nu }_{k-1},{\nu }_k\right]$, $k=1,2,3,\dots ,n$ and ${\alpha }_1={\nu }_0<{\nu }_1<{\nu }_2<\cdots <{\nu }_n={\alpha }_2$ is the partition of $\left[{\alpha }_1,{\alpha }_2\right]$. In this case, we can write

$${\int }_{{\alpha }_1}^{{\alpha }_2}\mathcal{H}(\nu ,·)d\nu =\mathcal{Y}(·)(a.e.).$$

Remark 1.

A stochastic process must have mean-square continuity in order for the mean-square integral to exist. The following inference follows directly from the concept of a mean-square integral. If for all $\nu \in \left[{\alpha }_1,{\alpha }_2\right]$ the inequality $\mathcal{H}(\nu ,·)\le \mathcal{Y}(\nu ,·)$ (a.e.) holds, then

$${\int }_{{\alpha }_1}^{{\alpha }_2}\mathcal{H}(\nu ,·)d\nu \le {\int }_{{\alpha }_1}^{{\alpha }_2}\mathcal{Y}(\nu ,·)d\nu (a.e.).$$

This shows that the mean-square integral satisfies the monotonocity property.

The monotonicity of mean-square integrals and the positivity of stochastic processes will be used extensively throughout this paper.

The proof of the following Lemma exists in [8].

Lemma 1

([8]). Let $\mathcal{H}:\mathcal{I}\times \mathsf{\Lambda }\to \mathit{R}$ be a mean-square continuous in $\mathcal{I}$ stochastic process, and let $\nu \in \left[{\alpha }_1,{\alpha }_2\right]\subset \mathcal{I}$. The following condition holds

$${\int }_{-{\alpha }_1+n}^{-{\alpha }_2+n}\mathcal{H}(\nu ,·)d\nu =-{\int }_{{\alpha }_1}^{{\alpha }_2}\mathcal{H}(-\nu +n,·)d\nu (a.e.)$$

(1)

for every $n\in \mathit{R}$.

We also need the following lemma to prove our results.

Lemma 2.

Let $\mathcal{H}:\mathcal{I}\times \mathsf{\Lambda }\to \mathit{R}$ be a mean-square continuous in $\mathcal{I}$ stochastic process, and let $\nu \in \left[{\alpha }_1,{\alpha }_2\right]\backslash \left\{0\right\}\subset \mathcal{I}$. The following condition holds

$${\int }_{\frac{{\alpha }_1}{-1+n{\alpha }_1}}^{\frac{{\alpha }_2}{-1+n{\alpha }_2}}\frac{\mathcal{H}\left(\nu ,·\right)}{{\nu }^2}d\nu =-{\int }_{{\alpha }_1}^{{\alpha }_2}\frac{\mathcal{H}\left(\frac{\nu }{-1+n\nu },·\right)}{{\nu }^2}d\nu (a.e.)$$

(2)

for every $n\in \mathit{R}$.

Proof. 

By making use of the change of $u=\frac{\nu }{-1+n\nu }$ for every $\nu \in \left[{\alpha }_1,{\alpha }_2\right]\backslash \left\{0\right\}$. We obtain $\frac{1}{u}=-\frac{1}{\nu }+n$ or every $\nu \in \left[{\alpha }_1,{\alpha }_2\right]\backslash \left\{0\right\}$.

Hence

$${\int }_{{\alpha }_1}^{{\alpha }_2}\frac{\mathcal{H}\left(\frac{\nu }{-1+n\nu },·\right)}{{\nu }^2}d\nu =-{\int }_{\frac{{\alpha }_1}{-1+n{\alpha }_1}}^{\frac{{\alpha }_2}{-1+n{\alpha }_2}}\frac{\mathcal{H}\left(u,·\right)}{u^2}du.$$

Thus, the result is achieved. □

We recall the definition of a convex stochastic process

Definition 4

([1]). A convex stochastic process. $\mathcal{H}:\mathcal{I}\times \mathsf{\Lambda }\to \mathit{R}$ is convex, if for all $\sigma \in \left[0,1\right]$ and ${\nu }_1$, ${\nu }_2\in \mathcal{I}$ the following inequality holds

$$\mathcal{H}\left(\sigma {\nu }_1+(1-\sigma ){\nu }_2,·\right)\le \sigma \mathcal{H}({\nu }_1,·)+(1-\sigma )\mathcal{H}({\nu }_2,·)({\alpha }_1.e.).$$

(3)

If the above inequality (3) holds for every ${\nu }_1$, ${\nu }_2\in \mathcal{I}$ and $\sigma =\frac{1}{2}$, then $\mathcal{H}$ is known as Jensen-convex or $\frac{1}{2}$-convex. A stochastic process $\mathcal{H}$ is said to be concave if ($-\mathcal{H}$) is convex.

Haq and Kotrys [8] defined the symmetrical form of a stochastic process as follows:

Definition 5.

A symmetrical form of a stochastic process $\mathcal{H}:\left[{\alpha }_1,{\alpha }_2\right]\times \mathsf{\Lambda }\to \mathit{R}$ denoted by $\mathcal{H}$ is defined as

$$\mathcal{H}\left(\nu ,·\right)=\frac{1}{2}\left[\mathcal{H}\left(\nu ,·\right)+\mathcal{H}\left({\alpha }_1+{\alpha }_2-\nu ,·\right)\right](\mathrm{a}.\mathrm{e}.).$$

The notion of a symmetrized convex stochastic process is given in the definition below:

Definition 6

([8]). A stochastic process $\mathcal{H}:\left[{\alpha }_1,{\alpha }_2\right]\times \mathsf{\Lambda }\to \mathit{R}$ is symmetrized convex (concave) on the interval $\left[{\alpha }_1,{\alpha }_2\right]$, if its symmetrical form $\mathcal{H}$ is convex (concave).

It is observed that every convex stochastic process is symmetrized convex, but there exists a stochastic process $\mathcal{H}$ which is not convex on $\left[{\alpha }_1,{\alpha }_2\right]$, whereas its symmetrical form is convex (see for instance [7]).

The well-known Hermite–Hadmard integral inequality for convex stochastic processes was proved by Kotrys in [3]:

Theorem 1

([3]). If $\mathcal{H}:\mathcal{I}\times \mathsf{\Lambda }\to \mathit{R}$ is Jensen-convex and mean square continuous in the interval $\mathcal{I}\times \mathsf{\Lambda }$, then for any ${\alpha }_1$, ${\alpha }_2\in \mathcal{I}$ with ${\alpha }_1<{\alpha }_2$ we have

$$\mathcal{H}\left(\frac{{\alpha }_1+{\alpha }_2}{2},·\right)\le \frac{1}{{\alpha }_2-{\alpha }_1}{\int }_{{\alpha }_1}^{{\alpha }_2}\mathcal{H}\left(\nu ,·\right)d\nu \le \frac{\mathcal{H}({\alpha }_1,·)+\mathcal{H}({\alpha }_2,·)}{2}(a.e.).$$

(4)

Haq and Kotrys [8] investigated with a counterpart of the Hermite–Hadmard inequality for symmetrized convex stochastic processes.

Theorem 2

([8]). If $\mathcal{H}:\mathcal{I}\times \mathsf{\Lambda }\to \mathit{R}$ is be a symmetrized convex and mean-square continuous stochastic process, then the inequality holds

$$\mathcal{H}\left(\frac{{\alpha }_1+{\alpha }_2}{2},·\right)\le \frac{1}{{\alpha }_2-{\alpha }_1}{\int }_{{\alpha }_1}^{{\alpha }_2}\mathcal{H}\left(\nu ,·\right)d\nu \le \frac{\mathcal{H}({\alpha }_1,·)+\mathcal{H}({\alpha }_2,·)}{2}(a.e.).$$

(5)

3. Hermite–Hadmard-Type Inequalities and Symmetrized Harmonic Convex Stochastic Process

It is our primary goal to discuss both the notion of the harmonic symmetrized form of stochastic processes and the inequalities of the Hermite–Hadmard-type that we will obtain as an application of the harmonic symmetrized stochastic processes. We also discuss the separation theorem for harmonically convex stochastic processes and the Hyers–Ulam stability of these stochastic processes as a result of the separation theorem. We construct Hyers–Ulam stability conditions for symmetrized harmonically convex stochastic processes by making use of this separation theorem.

Okur et al. [9] extended some results concerning harmonically convex functions to harmonically convex stochastic processes and obtained Hermite–Hadmard-type inequalities for harmonically convex stochastic processes.

Definition 7

([9]). Let $\mathcal{I}\subseteq \mathit{R}\backslash \left\{0\right\}$. A stochastic process $\mathcal{H}:\mathcal{I}\times \mathsf{\Lambda }\to \mathit{R}$ is said to be harmonically convex stochastic process, if

$$\mathcal{H}\left(\frac{{\nu }_1{\nu }_2}{\sigma {\nu }_1+(1-\sigma ){\nu }_2},·\right)\le \left(1-\sigma \right)\mathcal{H}({\nu }_1,·)+\sigma \mathcal{H}({\nu }_2,·)(a.e.)$$

for all ${\nu }_1$, ${\nu }_2\in \mathcal{I}$ and $\sigma \in \left[0,1\right]$. If the inequality above is reversed, then $\mathcal{H}$ is said to be harmonically concave.

The following result of the Hermite–Hadmard-type inequalities holds.

Theorem 3

([9]). Let $\mathcal{I}\subseteq \mathit{R}\backslash \left\{0\right\}$ and $\mathcal{H}:\mathcal{I}\times \mathsf{\Lambda }\to \mathit{R}$ be a harmonically convex stochastic process ${\alpha }_1$,${\alpha }_2\in \mathcal{I}$ with ${\alpha }_1<{\alpha }_2$. If $\mathcal{H}\in L\left(\left[{\alpha }_1,{\alpha }_2\right]\right)$, then the following inequalities hold

$$\mathcal{H}\left(\frac{2{\alpha }_1{\alpha }_2}{{\alpha }_1+{\alpha }_2},·\right)\le \frac{{\alpha }_1{\alpha }_2}{{\alpha }_2-{\alpha }_1}{\int }_{{\alpha }_1}^{{\alpha }_2}\frac{\mathcal{H}\left(\nu ,·\right)}{{\nu }^2}d\nu \le \frac{\mathcal{H}({\alpha }_1,·)+\mathcal{H}({\alpha }_2,·)}{2}(a.e.).$$

(6)

In what follows, we denote the symmetrical form of a harmonically convex stochastic process $\mathcal{H}:\left[{\alpha }_1,{\alpha }_2\right]\backslash \left\{0\right\}\times \mathsf{\Lambda }\to \mathit{R}$ by $\mathcal{H}$ and is defined as follows:

$$\mathcal{H}\left(\nu ,·\right)=\frac{1}{2}\left[\mathcal{H}\left(\nu ,·\right)+\mathcal{H}\left(\frac{{\alpha }_1{\alpha }_2\nu }{\left({\alpha }_1+{\alpha }_2\right)\nu -{\alpha }_1{\alpha }_2},·\right)\right](\mathrm{a}.\mathrm{e}.)$$

(7)

for all $\nu \in \left[{\alpha }_1,{\alpha }_2\right]\backslash \left\{0\right\}$.

Lemma 3.

If $\mathcal{H}:\left[{\alpha }_1,{\alpha }_2\right]\backslash \left\{0\right\}\times \mathsf{\Lambda }\to \mathit{R}$ is a harmonically convex stochastic process, then $\mathcal{H}:\left[{\alpha }_1,{\alpha }_2\right]\backslash \left\{0\right\}\times \mathsf{\Lambda }\to \mathit{R}$ is a harmonically convex stochastic process.

Proof. 

Let $\sigma \in \left[0,1\right]$ and ${\nu }_1$, ${\nu }_2\in \left[{\alpha }_1,{\alpha }_2\right]\backslash \left\{0\right\}$, then

$$\begin{array}{cc}\hfill & \mathcal{H}\left(\frac{{\nu }_1{\nu }_2}{\sigma {\nu }_2+\left(1-\sigma \right){\nu }_1},·\right)\hfill \\ \hfill & =\frac{1}{2}\left[\mathcal{H}\left(\frac{{\nu }_1{\nu }_2}{\sigma {\nu }_2+\left(1-\sigma \right){\nu }_1},·\right)+\mathcal{H}\left(\frac{1}{\frac{1}{{\alpha }_1}+\frac{1}{{\alpha }_2}-\sigma \frac{1}{{\nu }_1}-\left(1-\sigma \right)\frac{1}{{\nu }_2}},·\right)\right]\hfill \\ \hfill & =\frac{1}{2}\left[\mathcal{H}\left(\frac{{\nu }_1{\nu }_2}{\sigma {\nu }_2+\left(1-\sigma \right){\nu }_1},·\right)\right.\hfill \\ \hfill & \left.+\mathcal{H}\left(\frac{1}{\sigma \left(\frac{1}{{\alpha }_1}+\frac{1}{{\alpha }_2}-\frac{1}{{\nu }_1}\right)+\left(1-\sigma \right)\left(\frac{1}{{\alpha }_1}+\frac{1}{{\alpha }_2}-\frac{1}{{\nu }_2}\right)},·\right)\right]\hfill \\ \hfill & \le \frac{1}{2}\left[\sigma \mathcal{H}\left({\nu }_1,·\right)+\left(1-\sigma \right)\mathcal{H}\left({\nu }_2,·\right)\right.\hfill \\ \hfill & \left.+\sigma \mathcal{H}\left(\frac{{\alpha }_1{\alpha }_2{\nu }_1}{\left({\alpha }_1+{\alpha }_2\right){\nu }_1-{\alpha }_1{\alpha }_2},·\right)+\left(1-\sigma \right)\mathcal{H}\left(\frac{{\alpha }_1{\alpha }_2{\nu }_2}{\left({\alpha }_1+{\alpha }_2\right){\nu }_2-{\alpha }_1{\alpha }_2},·\right)\right]\hfill \\ \hfill & =\sigma \frac{1}{2}\left[\mathcal{H}\left({\nu }_1,·\right)+\mathcal{H}\left(\frac{{\alpha }_1{\alpha }_2{\nu }_1}{\left({\alpha }_1+{\alpha }_2\right){\nu }_1-{\alpha }_1{\alpha }_2},·\right)\right]\hfill \\ \hfill & +\left(1-\sigma \right)\frac{1}{2}\left[\mathcal{H}\left({\nu }_2,·\right)+\mathcal{H}\left(\frac{{\alpha }_1{\alpha }_2{\nu }_2}{\left({\alpha }_1+{\alpha }_2\right){\nu }_2-{\alpha }_1{\alpha }_2},·\right)\right]\hfill \\ \hfill & =\sigma \mathcal{H}\left({\nu }_1,·\right)+\left(1-\sigma \right)\mathcal{H}\left({\nu }_2,·\right)(\mathrm{a}.\mathrm{e}.).\hfill \end{array}$$

Thus, the result is established. □

The discussion presented above leads us to introduce the following definition of the symmetrized harmonically convex stochastic process.

Definition 8.

A stochastic process $\mathcal{H}:\left[{\alpha }_1,{\alpha }_2\right]\backslash \left\{0\right\}\times \mathsf{\Lambda }\to \mathit{R}$ is symmetrized harmonically convex (concave) on an interval $\left[{\alpha }_1,{\alpha }_2\right]\backslash \left\{0\right\}$, if its symmetrical form $\mathcal{H}$ is harmonically convex (concave) on $\left[{\alpha }_1,{\alpha }_2\right]\backslash \left\{0\right\}$.

We conclude, that every harmonically convex stochastic process is symmetrized harmonically convex. The following example illustrates that there are stochastic processes which are not harmonically convex, but their symmetrical form is harmonically convex.

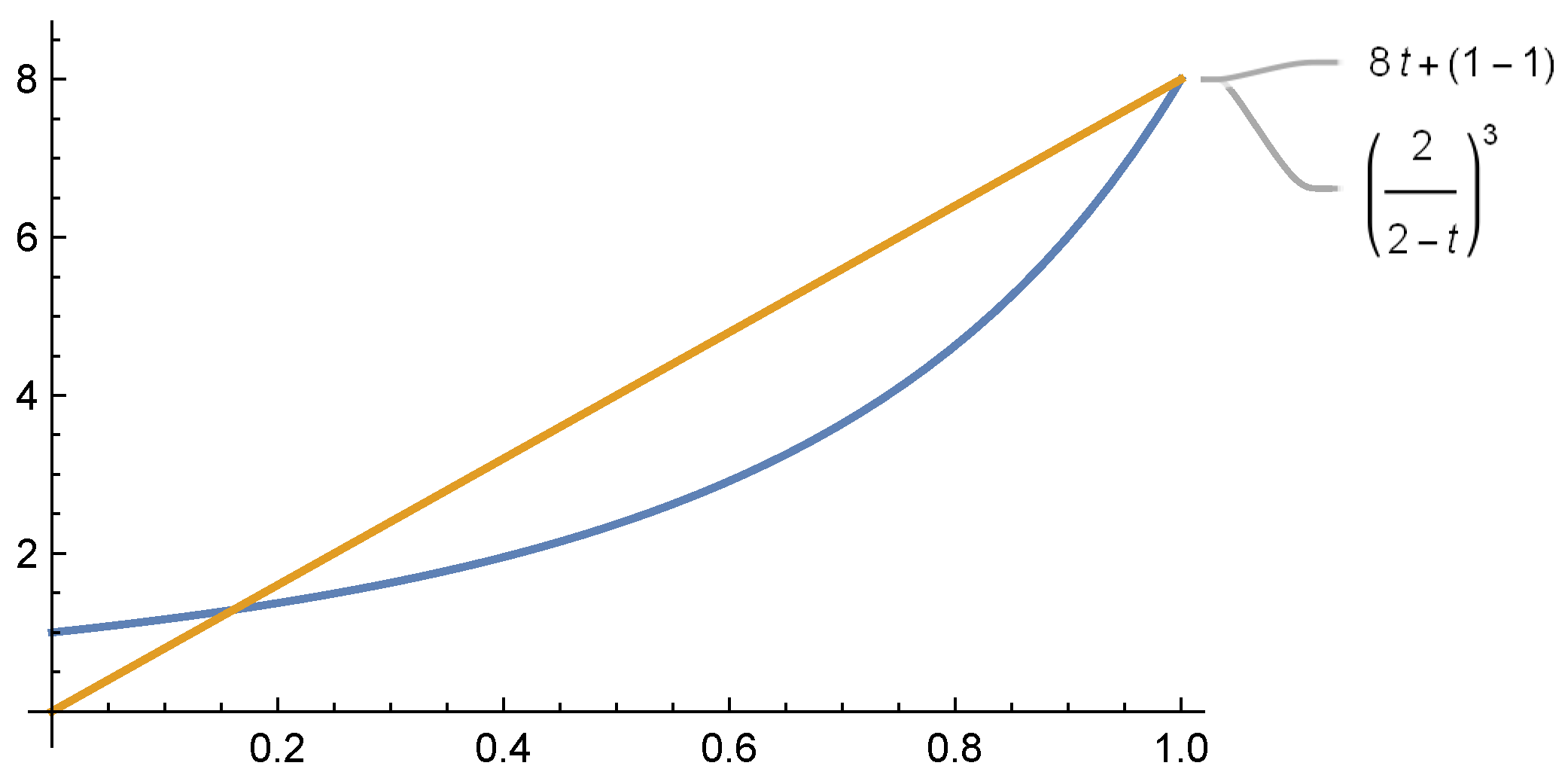
Example 1.

Let $\mathcal{H}:\left[1,2\right]\times \mathsf{\Lambda }\to \mathit{R}$ be defined as $\mathcal{H}\left(u,·\right)=u^3$, then $\mathcal{H}\left(u,·\right)$ is not harmonically convex on $\left[1,2\right]$, whereas its symmetrical form $\mathcal{H}:\left[{\alpha }_1,{\alpha }_2\right]\backslash \left\{0\right\}\times \mathsf{\Lambda }\to \mathit{R}$ given by

$$\begin{array}{ccc}\hfill \mathcal{H}\left(\nu ,·\right)& =\frac{1}{2}\left[\mathcal{H}\left(u,·\right)+\mathcal{H}\left(\frac{{\alpha }_1{\alpha }_{2}u}{\left({\alpha }_1+{\alpha }_2\right)u-{\alpha }_1{\alpha }_2},·\right)\right]\hfill & \hfill =\frac{9u^4\left(3u^2-6u+4\right)}{2{\left(3u-2\right)}^3}\end{array}$$

is harmonically convex as evident from the Figure 1 and Figure 2.

Theorem 4.

Let $\mathcal{H}:\left[{\alpha }_1,{\alpha }_2\right]\backslash \left\{0\right\}\times \mathsf{\Lambda }\to \mathit{R}$ be a symmetrized harmonically convex, mean-square continuous stochastic process. The following inequality holds

$$\mathcal{H}\left(\frac{2{\alpha }_1{\alpha }_2}{{\alpha }_1+{\alpha }_2},·\right)\le \frac{{\alpha }_1{\alpha }_2}{{\alpha }_2-{\alpha }_1}{\int }_{{\alpha }_1}^{{\alpha }_2}\frac{\mathcal{H}\left(\nu ,·\right)}{{\nu }^2}d\nu \le \frac{\mathcal{H}({\alpha }_1,·)+\mathcal{H}({\alpha }_2,·)}{2}(a.e.).$$

(8)

Proof. 

Since $\mathcal{H}$ is a symmetrized convex process, its symmetrical form is harmonically convex. By inequality (6), we obtain

$$\mathcal{H}\left(\frac{2{\alpha }_1{\alpha }_2}{{\alpha }_1+{\alpha }_2},·\right)\le \frac{{\alpha }_1{\alpha }_2}{{\alpha }_2-{\alpha }_1}{\int }_{{\alpha }_1}^{{\alpha }_2}\frac{\mathcal{H}\left(\nu ,·\right)}{{\nu }^2}d\nu \le \frac{\mathcal{H}({\alpha }_1,·)+\mathcal{H}({\alpha }_2,·)}{2}(\mathrm{a}.\mathrm{e}.).$$

(9)

By the harmonically symmetrical form of $\mathcal{H}$, we have

$$\begin{array}{cc}\hfill \mathcal{H}\left(\frac{2{\alpha }_1{\alpha }_2}{{\alpha }_1+{\alpha }_2},·\right)& =\frac{1}{2}\left[\mathcal{H}\left(\frac{2{\alpha }_1{\alpha }_2}{{\alpha }_1+{\alpha }_2},·\right)+\mathcal{H}\left(\frac{{\alpha }_1{\alpha }_2\left(\frac{2{\alpha }_1{\alpha }_2}{{\alpha }_1+{\alpha }_2}\right)}{\left({\alpha }_1+{\alpha }_2\right)\left(\frac{2{\alpha }_1{\alpha }_2}{{\alpha }_1+{\alpha }_2}\right)-{\alpha }_1{\alpha }_2},·\right)\right]\hfill \\ \hfill & =\mathcal{H}\left(\frac{2{\alpha }_1{\alpha }_2}{{\alpha }_1+{\alpha }_2},·\right)(\mathrm{a}.\mathrm{e}.)\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & \frac{\mathcal{H}({\alpha }_1,·)+\mathcal{H}({\alpha }_2,·)}{2}\hfill \\ \hfill & =\frac{\frac{1}{2}\left[\mathcal{H}\left({\alpha }_1,·\right)+\mathcal{H}\left(\frac{{\alpha }_1^2{\alpha }_2}{\left({\alpha }_1+{\alpha }_2\right){\alpha }_1-{\alpha }_1{\alpha }_2},·\right)\right]+\frac{1}{2}\left[\mathcal{H}\left({\alpha }_2,·\right)+\mathcal{H}\left(\frac{{\alpha }_1{\alpha }_2^2}{\left({\alpha }_1+{\alpha }_2\right){\alpha }_2-{\alpha }_1{\alpha }_2},·\right)\right]}{2}\hfill \\ \hfill & =\frac{\mathcal{H}\left({\alpha }_1,·\right)+\mathcal{H}\left({\alpha }_2,·\right)}{2}(\mathrm{a}.\mathrm{e}.).\hfill \end{array}$$

By Lemma 2 and the basic properties of the mean-square integral, we obtain

$${\int }_{{\alpha }_1}^{{\alpha }_2}\frac{\mathcal{H}\left(\frac{1}{\frac{1}{{\alpha }_1}+\frac{1}{{\alpha }_2}-\frac{1}{\nu }},·\right)}{{\nu }^2}d\nu ={\int }_{{\alpha }_1}^{{\alpha }_2}\frac{\mathcal{H}\left(\nu ,·\right)}{{\nu }^2}d\nu (\mathrm{a}.\mathrm{e}).$$

Thus, we obtain

$$\frac{{\alpha }_1{\alpha }_2}{{\alpha }_2-{\alpha }_1}{\int }_{{\alpha }_1}^{{\alpha }_2}\frac{\mathcal{H}\left(\nu ,·\right)}{{\nu }^2}d\nu =\frac{{\alpha }_1{\alpha }_2}{{\alpha }_2-{\alpha }_1}{\int }_{{\alpha }_1}^{{\alpha }_2}\frac{\mathcal{H}\left(\nu ,·\right)}{{\nu }^2}d\nu (\mathrm{a}.\mathrm{e}.).$$

The proof is thus accomplished. □

Similarly, as in the real function case, we can prove the following result.

Theorem 5.

Let $\mathcal{H}:\left[{\alpha }_1,{\alpha }_2\right]\backslash \left\{0\right\}\times \mathsf{\Lambda }\to \mathit{R}$ be a symmetrized harmonically convex stochastic process. Then, the inequality

$$\mathcal{H}\left(\frac{2{\alpha }_1{\alpha }_2}{{\alpha }_1+{\alpha }_2},·\right)\le \mathcal{H}\left(\nu ,·\right)\le \frac{\mathcal{H}({\alpha }_1,·)+\mathcal{H}({\alpha }_2,·)}{2}(a.e.)$$

(10)

hold ∀$\nu \in \left[{\alpha }_1,{\alpha }_2\right]\backslash \left\{0\right\}$.

Proof. 

Since $\mathcal{H}$ is harmonically convex, it is also Jensen harmonically convex. By this property, we have

$$\begin{array}{cc}\hfill \mathcal{H}\left(\frac{2{\alpha }_1{\alpha }_2}{{\alpha }_1+{\alpha }_2},·\right)& =\mathcal{H}\left(\frac{2{\alpha }_1{\alpha }_2}{{\alpha }_1+{\alpha }_2},·\right)\hfill \\ \hfill & =\mathcal{H}\left(\frac{1}{\frac{1}{2}\frac{1}{\nu }+\frac{1}{2}\left(\frac{1}{{\alpha }_1}+\frac{1}{{\alpha }_2}-\frac{1}{\nu }\right)},·\right)\hfill & \hfill \le \frac{\mathcal{H}\left(\nu ,·\right)+\mathcal{H}\left(\frac{1}{\frac{1}{{\alpha }_1}+\frac{1}{{\alpha }_2}-\frac{1}{\nu }},·\right)}{2}(\mathrm{a}.\mathrm{e}.).\end{array}$$

We also observe that

$$\begin{array}{ccc}\hfill & \frac{\mathcal{H}\left(\nu ,·\right)+\mathcal{H}\left(\frac{1}{\frac{1}{{\alpha }_1}+\frac{1}{{\alpha }_2}-\frac{1}{\nu }},·\right)}{2}\hfill & \hfill =\frac{\mathcal{H}\left(\nu ,·\right)+\mathcal{H}\left(\frac{1}{\frac{1}{{\alpha }_1}+\frac{1}{{\alpha }_2}-\frac{1}{\nu }},·\right)}{2}=\mathcal{H}\left(\nu ,·\right)(\mathrm{a}.\mathrm{e}.)\end{array}$$

holds; thus, it is proved the left-hand side of the inequality (10) is valid.

We can write any $\nu \in \left[{\alpha }_1,{\alpha }_2\right]\backslash \left\{0\right\}$ as follows

$$\nu =\frac{1}{\frac{{\alpha }_2\left(\nu -{\alpha }_1\right)}{\nu \left({\alpha }_2-{\alpha }_1\right)}\frac{1}{{\alpha }_2}+\frac{{\alpha }_1\left({\alpha }_2-{\alpha }_1\right)}{\left({\alpha }_2-{\alpha }_1\right)\nu }\frac{1}{{\alpha }_1}}.$$

By using the harmonic convexity of $\mathcal{H}$

$$\begin{array}{cc}\hfill \mathcal{H}\left(\nu ,·\right)& =\mathcal{H}\left(\frac{1}{\frac{{\alpha }_2\left(\nu -{\alpha }_1\right)}{\nu \left({\alpha }_2-{\alpha }_1\right)}\frac{1}{{\alpha }_2}+\frac{{\alpha }_1\left({\alpha }_2-{\alpha }_1\right)}{\left({\alpha }_2-{\alpha }_1\right)\nu }\frac{1}{{\alpha }_1}},·\right)\hfill \\ \hfill & \le \frac{{\alpha }_2\left(\nu -{\alpha }_1\right)}{\nu \left({\alpha }_2-{\alpha }_1\right)}\mathcal{H}\left({\alpha }_1,·\right)+\frac{{\alpha }_1\left({\alpha }_2-{\alpha }_1\right)}{\left({\alpha }_2-{\alpha }_1\right)\nu }\mathcal{H}\left({\alpha }_2,·\right)\hfill \\ \hfill & =\frac{{\alpha }_2\left(\nu -{\alpha }_1\right)}{\nu \left({\alpha }_2-{\alpha }_1\right)}\frac{\mathcal{H}\left({\alpha }_1,·\right)+\mathcal{H}\left({\alpha }_2,·\right)}{2}+\frac{{\alpha }_1\left({\alpha }_2-{\alpha }_1\right)}{\left({\alpha }_2-{\alpha }_1\right)\nu }\frac{\mathcal{H}\left({\alpha }_1,·\right)+\mathcal{H}\left({\alpha }_2,·\right)}{2}\hfill \\ \hfill & =\frac{\mathcal{H}\left({\alpha }_1,·\right)+\mathcal{H}\left({\alpha }_2,·\right)}{2}(\mathrm{a}.\mathrm{e}.).\hfill \end{array}$$

The theorem is thus accomplished. □

4. Hyers–Ulam Type Stability and Harmonic Convexity

González et al. [10] demonstrated a separation theorem for convex stochastic processes and subsequently analyzed their Hyers–Ulam stability. Using this separation concept, the Hyers–Ulam stability criterion for symmetrized harmonically convex processes can be derived. See [10] for the usual result of the Hyers–Ulam stability. Let us recall the following definition of a $\epsilon$-convex stochastic process.

Definition 9

([10]). Let ε be a positive constant. A stochastic process $\mathcal{H}:\mathcal{I}\times \mathsf{\Lambda }\to \mathit{R}$ is ε-convex if

$$\mathcal{H}\left(\sum _{i=1}^n{\sigma }_i{\nu }_i,·\right)\le \sum _{i=1}^n{\sigma }_i\mathcal{H}\left({\nu }_i,·\right)+\epsilon (a.e.)$$

for all $n\in \mathbb{N}$, ${\nu }_1,\dots ,{\nu }_n\in \mathcal{I}$ and ${\sigma }_1,\dots ,{\sigma }_n\ge 0$ with ${\sigma }_1+\cdots +{\sigma }_n=1$.

Haq and Kotrys [8] introduced the definition of $\epsilon$-symmetrized convex stochastic processes and showed a Hyers–Ulam-type stability result for $\epsilon$-symmetrized convex stochastic processes.

Definition 10

([8]). A stochastic process $\mathcal{H}:\left[{\alpha }_1,{\alpha }_2\right]\times \mathsf{\Lambda }\to \mathit{R}$ is ε-symmetrized convex if its symmetrical form is ε-convex.

For symmetrical stochastic processes, Haq and Kotrys [8] demonstrated Hyers–Ulam-type stability.

Theorem 6

([8]). Let $\mathcal{H}:\left[{\alpha }_1,{\alpha }_2\right]\times \mathsf{\Lambda }\to \mathit{R}$ be a ε-symmetrized convex stochastic process. Then,

(i) 

for the symmetrical form $\mathcal{H}$ of $\mathcal{H}$, we can find a convex stochastic process $\mathcal{W}:\left[{\alpha }_1,{\alpha }_2\right]\times \mathsf{\Lambda }\to \mathit{R}$ with

$$\left|\mathcal{H}\left(\nu ,·\right)-\mathcal{W}\left(\nu ,·\right)\right|\le \frac{\epsilon }{2}(a.e.)$$

∀$\nu \in \left[{\alpha }_1,{\alpha }_2\right]$ and

(ii) 

for every symmetrized convex stochastic process $\mathcal{W}:\left[{\alpha }_1,{\alpha }_2\right]\times \mathsf{\Lambda }\to \mathit{R}$ with

$$\mathcal{W}\left(\nu ,·\right)=\frac{\mathcal{W}\left(\nu ,·\right)+\mathcal{W}\left({\alpha }_1+{\alpha }_2-\nu ,·\right)}{2}(a.e.)$$

the inequality

$$\left|\left|\mathcal{H}\left(\nu ,·\right)-\mathcal{W}\left(\nu ,·\right)\right|-\left|\mathcal{H}\left({\alpha }_1+{\alpha }_2-\nu ,·\right)-\mathcal{W}\left({\alpha }_1+{\alpha }_2-\nu ,·\right)\right|\right|\le \epsilon (a.e.)$$

holds ∀$\nu \in \left[{\alpha }_1,{\alpha }_2\right]$.

The following variant of Jensen’s inequality for a convex stochastic process can be established in a similar way as proved in Dragomir [11].

Theorem 7

([11]). Let $\mathcal{I}\backslash \left\{0\right\}$ be an interval and $\mathcal{H}:\mathcal{I}\backslash \left\{0\right\}\times \mathsf{\Lambda }\to \mathit{R}$ be a harmonically convex stochastic process. Then, the Jensen-type inequality holds

$$\mathcal{H}\left(\frac{1}{{\sum }_{i=1}^n\frac{{\sigma }_i}{{\nu }_i}},·\right)\le \sum _{i=1}^n{\sigma }_i\mathcal{Y}\left({\nu }_i,·\right)(a.e.)$$

for all $n\in \mathbb{N}$, ${\nu }_1,\dots ,{\nu }_n\in \mathcal{I}\backslash \left\{0\right\}$ and ${\sigma }_1,\dots ,{\sigma }_n\ge 0$ with ${\sigma }_1+\cdots +{\sigma }_n=1$.

Now, we present the main result of this section. It gives a condition under which two given stochastic processes can be separated by a harmonically convex stochastic process.

Theorem 8.

Let $\mathcal{H}$, $\mathcal{Y}:\left(\mathcal{I}\backslash \left\{0\right\}\right)\times \mathsf{\Lambda }\to \mathit{R}$ be stochastic processes, there exists a harmonically convex stochastic process $\mathcal{W}:\left(\mathcal{I}\backslash \left\{0\right\}\right)\times \mathsf{\Lambda }\to \mathit{R}$ with

$$\mathcal{H}\left(\nu ,·\right)\le \mathcal{W}\left(\nu ,·\right)\le \mathcal{Y}\left(\nu ,·\right)(a.e.)$$

∀$\nu \in \mathcal{I}$ iff

$$\mathcal{H}\left(\frac{1}{{\sum }_{i=1}^n\frac{{\sigma }_i}{{\nu }_i}},·\right)\le \sum _{i=1}^n{\sigma }_i\mathcal{Y}\left({\nu }_i,·\right)(a.e.)$$

(11)

∀$n\in \mathbb{N}$, ${\nu }_1,\dots ,{\nu }_n\in \mathcal{I}\backslash \left\{0\right\}$ and ${\sigma }_1,\dots ,{\sigma }_n\ge 0$ with ${\sigma }_1+\cdots +{\sigma }_n=1$.

Proof. 

Let $\mathcal{H}$, $\mathcal{Y}:\left(\mathcal{I}\backslash \left\{0\right\}\right)\times \mathsf{\Lambda }\to \mathit{R}$ be the stochastic processes, then we can find a harmonically convex stochastic process $\mathcal{W}:\left(\mathcal{I}\backslash \left\{0\right\}\right)\times \mathsf{\Lambda }\to \mathit{R}$ such that

$$\mathcal{H}\left(\nu ,·\right)\le \mathcal{W}\left(\nu ,·\right)\le \mathcal{Y}\left(\nu ,·\right)(\mathrm{a}.\mathrm{e}.)$$

∀$\nu \in \mathcal{I}\backslash \left\{0\right\}$, then

$$\begin{array}{c}\hfill \mathcal{H}\left(\frac{1}{{\sum }_{i=1}^n\frac{{\sigma }_i}{{\nu }_i}},·\right)\le \mathcal{W}\left(\frac{1}{{\sum }_{i=1}^n\frac{{\sigma }_i}{{\nu }_i}},·\right)\le \sum _{i=1}^n{\sigma }_i\mathcal{W}\left({\nu }_i,·\right)\le \sum _{i=1}^n{\sigma }_i\mathcal{Y}\left({\nu }_i,·\right)(\mathrm{a}.\mathrm{e}.).\end{array}$$

(12)

Now, we prove the “if” part of the result, fix $\nu \in \mathcal{I}\backslash \left\{0\right\}$ and define the process $\mathcal{W}$ by

$$\begin{array}{c}\mathcal{W}\left(\nu ,·\right)=essinf\left\{\sum _{i=1}^n{\sigma }_i\mathcal{Y}\left({\nu }_i,·\right):n\in \mathbb{N},{\nu }_1,\dots ,{\nu }_n\in \mathcal{I},{\sigma }_1,\dots ,{\sigma }_n\in \left[0,1\right]\right.\hfill \\ \hfill \left.\mathrm{with}{\sigma }_1+\cdots +{\sigma }_n=1\mathrm{and}\frac{1}{\nu }=\frac{{\sigma }_1}{{\nu }_1}+\cdots +\frac{{\sigma }_n}{{\nu }_n}\right\}(\mathrm{a}.\mathrm{e}.).\end{array}$$

(13)

By (11) and the definition of essential infimum, we have

$$\mathcal{H}\left(\nu ,·\right)\le \mathcal{W}\left(\nu ,·\right)(\mathrm{a}.\mathrm{e}.),\nu \in \mathcal{I}\backslash \left\{0\right\}.$$

By the definition of $\mathcal{W}$ (taking $n=1$, ${\sigma }_1$$=1$ and ${\nu }_1=\nu$), we also obtain that

$$\mathcal{W}\left(\nu ,·\right)\le \mathcal{Y}\left(\nu ,·\right)(\mathrm{a}.\mathrm{e}.),\nu \in \mathcal{I}\backslash \left\{0\right\}.$$

To prove that $\mathcal{W}$ is harmonically convex, fix ${\nu }_1,{\nu }_2\in \mathcal{I}\backslash \left\{0\right\}$ and $\sigma \in \left[0,1\right]$. Take arbitrary $u_1,\cdots ,u_n\in \mathcal{I}\backslash \left\{0\right\}$, ${\mu }_1,\cdots ,{\mu }_n\in \left[0,1\right]$ and $v_1,\cdots ,v_m\in \mathcal{I}\backslash \left\{0\right\}$, ${\beta }_1,\cdots ,{\beta }_m\in \left[0,1\right]$ such that ${\mu }_1+\cdots +{\mu }_n=1$, ${\beta }_1+\cdots +{\beta }_m=1$ and $\frac{1}{{\nu }_1}$ $=\frac{{\mu }_1}{u_1}+\cdots +\frac{{\mu }_n}{u_n}$, $\frac{1}{{\nu }_2}=\frac{{\beta }_1}{v_1}+\cdots +\frac{{\beta }_m}{v_m}$. Since

$$\sum _{i=1}^n\sigma {\mu }_i+\sum _{j=1}^m\left(1-\sigma \right){\beta }_j=1,$$

thus the point $\frac{1}{\sigma \frac{1}{{\nu }_1}+\left(1-\sigma \right)\frac{1}{{\nu }_2}}$ is a harmonic mean of $u_1,\cdots ,u_n$, $v_1,\cdots ,v_m$ and

$$\frac{1}{\sigma \frac{1}{{\nu }_1}+\left(1-\sigma \right)\frac{1}{{\nu }_2}}=\frac{1}{\sigma {\sum }_{i=1}^n\frac{{\mu }_i}{u_i}+\left(1-\sigma \right){\sum }_{j=1}^m\frac{{\beta }_j}{v_j}}.$$

Hence by the definition of $\mathcal{W}$, we have

$$\begin{array}{c}\hfill \mathcal{W}\left(\frac{1}{\sigma \frac{1}{{\nu }_1}+\left(1-\sigma \right)\frac{1}{{\nu }_2}},·\right)\le \sigma \sum _{i=1}^n{\mu }_i\mathcal{Y}\left(u_i,·\right)+\left(1-\sigma \right)\sum _{j=1}^m{\beta }_j\mathcal{Y}\left(v_i,·\right)(\mathrm{a}.\mathrm{e}.).\end{array}$$

(14)

This inequality holds for every $n\in \mathbb{N}$, $u_1,\cdots ,u_n\in \mathcal{I}$, ${\mu }_1,\cdots ,{\mu }_n\in \left[0,1\right]$ such that ${\mu }_1+\cdots +{\mu }_n=1$ as well as for all $m\in \mathbb{N}$, $v_1,\cdots ,v_m\in \mathcal{I}$, ${\mu }_1,\cdots ,{\mu }_n\in \left[0,1\right]$ such that ${\mu }_1+\cdots +{\mu }_n=1,$${\beta }_1,\cdots ,{\beta }_m\in \left[0,1\right]$ such that ${\mu }_1+\cdots +{\mu }_n=1$, ${\beta }_1+\cdots +{\beta }_m=1$. Therefore, by taking the essential infimum using the the definition of essential infimumon, we obtain from (14) that

$$\mathcal{W}\left(\frac{1}{\sigma \frac{1}{{\nu }_1}+\left(1-\sigma \right)\frac{1}{{\nu }_2}},·\right)\le \sigma \mathcal{W}\left({\nu }_1,·\right)+\left(1-\sigma \right)\sigma \mathcal{W}\left({\nu }_2,·\right)(\mathrm{a}.\mathrm{e}.).$$

(15)

This shows that $\mathcal{W}$ is harmonically convex. □

As an immediate consequence of the above theorem, we obtain the following Hyers–Ulam-type stability results for harmonically convex stochastic processes. For the classical Hyers–Ulam theorem, see [12].

Firstly, we introduce an $\epsilon$-harmonically convex stochastic process and $\epsilon$-symmetrized harmonically convex stochastic processes and establish a Hyers–Ulam-type stability result for $\epsilon$-symmetrized harmonic stochastic processes.

Definition 11.

Let $\epsilon >0$. A stochastic process $\mathcal{H}:\left(\mathcal{I}\backslash \left\{0\right\}\right)\times \mathsf{\Lambda }\to \mathit{R}$ is ε-harmonically convex if

$$\mathcal{H}\left(\frac{1}{{\sum }_{i=1}^n\frac{{\sigma }_i}{{\nu }_i}},·\right)\le \sum _{i=1}^n{\sigma }_i\mathcal{H}\left({\nu }_i,·\right)+\epsilon (a.e.)$$

(16)

∀$n\in \mathbb{N}$, ${\nu }_1,\dots ,{\nu }_n\in \mathcal{I}\backslash \left\{0\right\}$ and ${\sigma }_1,\dots ,{\sigma }_n\ge 0$ with ${\sigma }_1+\cdots +{\sigma }_n=1$.

Corollary 1.

If a stochastic process $\mathcal{H}:\mathcal{I}\backslash \left\{0\right\}\times \mathsf{\Lambda }\to \mathit{R}$ is ε-harmonically convex, we can find a harmonically convex stochastic process $\mathcal{W}$ with

$$\left|\mathcal{H}\left(\nu ,·\right)-\mathcal{W}\left(\nu ,·\right)\right|\le \frac{\epsilon }{2}(a.e.)$$

(17)

∀$\nu \in \mathcal{I}\backslash \left\{0\right\}$.

Proof. 

Let $\mathcal{Y}\left(\nu ,·\right)=\mathcal{W}\left(\nu ,·\right)+\epsilon$, $\nu \in \mathcal{I}\backslash \left\{0\right\}$. According to (16), the processes $\mathcal{H}$ and $\mathcal{Y}$ satisfy (11). Therefore, by Theorem 8, there exists a convex process ${\mathcal{W}}_1:\mathcal{I}\backslash \left\{0\right\}\times \mathsf{\Lambda }\to \mathit{R}$, such that $\mathcal{H}\left(\nu ,·\right)\le {\mathcal{W}}_1\left(\nu ,·\right)\le \mathcal{H}\left(\nu ,·\right)+\epsilon$ (a.e.), for all $\nu \in \mathcal{I}\backslash \left\{0\right\}$. Putting $\mathcal{W}\left(\nu ,·\right)={\mathcal{W}}_1\left(\nu ,·\right)+\frac{\epsilon }{2}$, we obtain (17). □

Definition 12.

A stochastic process $\mathcal{H}:\left[{\alpha }_1,{\alpha }_2\right]\times \mathsf{\Lambda }\to \mathit{R}$ is ε-symmetrized harmonically convex if its symmetrical form is ε-harmonically convex.

Let us prove a Hyers–Ulam-type stability result for $\epsilon$-symmetrized stochastic processes.

Theorem 9. 

Let $\mathcal{H}:\left[{\alpha }_1,{\alpha }_2\right]\backslash \left\{0\right\}\times \mathsf{\Lambda }\to \mathit{R}$ be a ε-symmetrized harmonically convex stochastic process. Then,

(i) 

for symmetrical form $\mathcal{H}$ of $\mathcal{H}$ we can find a harmonically convex stochastic process $\mathcal{W}:\left[{\alpha }_1,{\alpha }_2\right]\backslash \left\{0\right\}\times \mathsf{\Lambda }\to \mathit{R}$ with

$$\left|\mathcal{H}\left(\nu ,·\right)-\mathcal{W}\left(\nu ,·\right)\right|\le \frac{\epsilon }{2}(a.e.)$$

(18)

∀$\nu \in \left[{\alpha }_1,{\alpha }_2\right]\backslash \left\{0\right\}$ and

(ii) 

for every symmetrized harmonically convex stochastic process $\mathcal{W}:\left[{\alpha }_1,{\alpha }_2\right]\backslash \left\{0\right\}\times \mathsf{\Lambda }\to \mathit{R}$ with

$$\mathcal{W}\left(\nu ,·\right)=\frac{\mathcal{W}\left(\nu ,·\right)+\mathcal{W}\left(\frac{1}{\frac{1}{{\alpha }_1}+\frac{1}{{\alpha }_2}-\frac{1}{\nu }},·\right)}{2}(a.e.)$$

∀$\nu \in \left[{\alpha }_1,{\alpha }_2\right]\backslash \left\{0\right\}$, the inequality

$$\left|\left|\mathcal{H}\left(\nu ,·\right)-\mathcal{W}\left(\nu ,·\right)\right|-\left|\mathcal{H}\left(\frac{1}{\frac{1}{{\alpha }_1}+\frac{1}{{\alpha }_2}-\frac{1}{\nu }},·\right)-\mathcal{W}\left(\frac{1}{\frac{1}{{\alpha }_1}+\frac{1}{{\alpha }_2}-\frac{1}{\nu }},·\right)\right|\right|\le \epsilon (a.e),$$

holds ∀$\nu \in \left[{\alpha }_1,{\alpha }_2\right]\backslash \left\{0\right\}$.

Proof. 

(i) The proof follows from Corollary 1.

(ii) $\mathcal{H}$ is harmonically convex following from Definition 8 and conditions on $\mathcal{H}$. By (i), there exists a harmonically convex stochastic process $\mathcal{W}$ that fulfills (18). Let $\mathcal{W}$$:\left[{\alpha }_1,{\alpha }_2\right]\backslash \left\{0\right\}\times \mathsf{\Lambda }\to \mathit{R}$ be defined by

$$\mathcal{W}\left(\nu ,·\right)=\frac{\mathcal{W}\left(\nu ,·\right)+\mathcal{W}\left(\frac{1}{\frac{1}{{\alpha }_1}+\frac{1}{{\alpha }_2}-\frac{1}{\nu }},·\right)}{2}(\mathrm{a}.\mathrm{e}.),$$

∀$\nu \in \left[{\alpha }_1,{\alpha }_2\right]\backslash \left\{0\right\}$. The stochastic process $\mathcal{W}$ is symmetrized harmonically convex evident from Definition 8. Using reverse triangle inequality and (18) gives us

$$\begin{array}{cc}\hfill \frac{\epsilon }{2}& \ge \left|\mathcal{H}\left(\nu ,·\right)-\mathcal{W}\left(\nu ,·\right)\right|\hfill \\ \hfill & =\left|\frac{\mathcal{H}\left(\nu ,·\right)+\mathcal{H}\left(\frac{1}{\frac{1}{{\alpha }_1}+\frac{1}{{\alpha }_2}-\frac{1}{\nu }},·\right)}{2}-\frac{\mathcal{W}\left(\nu ,·\right)+\mathcal{W}\left(\frac{1}{\frac{1}{{\alpha }_1}+\frac{1}{{\alpha }_2}-\frac{1}{\nu }},·\right)}{2}\right|\hfill \\ \hfill & =\left|\frac{\mathcal{H}\left(\nu ,·\right)-\mathcal{W}\left(\nu ,·\right)}{2}-\frac{\mathcal{W}\left(\frac{1}{\frac{1}{{\alpha }_1}+\frac{1}{{\alpha }_2}-\frac{1}{\nu }},·\right)-\mathcal{H}\left(\frac{1}{\frac{1}{{\alpha }_1}+\frac{1}{{\alpha }_2}-\frac{1}{\nu }},·\right)}{2}\right|\hfill \\ \hfill & \ge \frac{1}{2}\left|\left|\mathcal{H}\left(\nu ,·\right)-\mathcal{W}\left(\nu ,·\right)\right|-\left|\mathcal{W}\left(\frac{1}{\frac{1}{{\alpha }_1}+\frac{1}{{\alpha }_2}-\frac{1}{\nu }},·\right)-\mathcal{H}\left(\frac{1}{\frac{1}{{\alpha }_1}+\frac{1}{{\alpha }_2}-\frac{1}{\nu }},·\right)\right|\right|(\mathrm{a}.\mathrm{e}.).\hfill \end{array}$$

The theorem is thus accomplished. □

5. Conclusions

This study contains the discussion of the topic of symmetrized harmonically convex stochastic processes in detail. We used the Hermite–Hadmard-type inequalities to describe the distinctive nature or features of symmetrized harmonically convex stochastic processes. We also clearly showed the existence of a Hyers–Ulam-type stability result for harmonically convex stochastic processes. We expect that this study will be a motivation for researchers to explore this field of study using the generalization of the theory of convex functions.