Development of Integrated Linear Programming Fuzzy-Rough MCDM Model for Production Optimization
Abstract
:1. Introduction
2. Materials and Methods
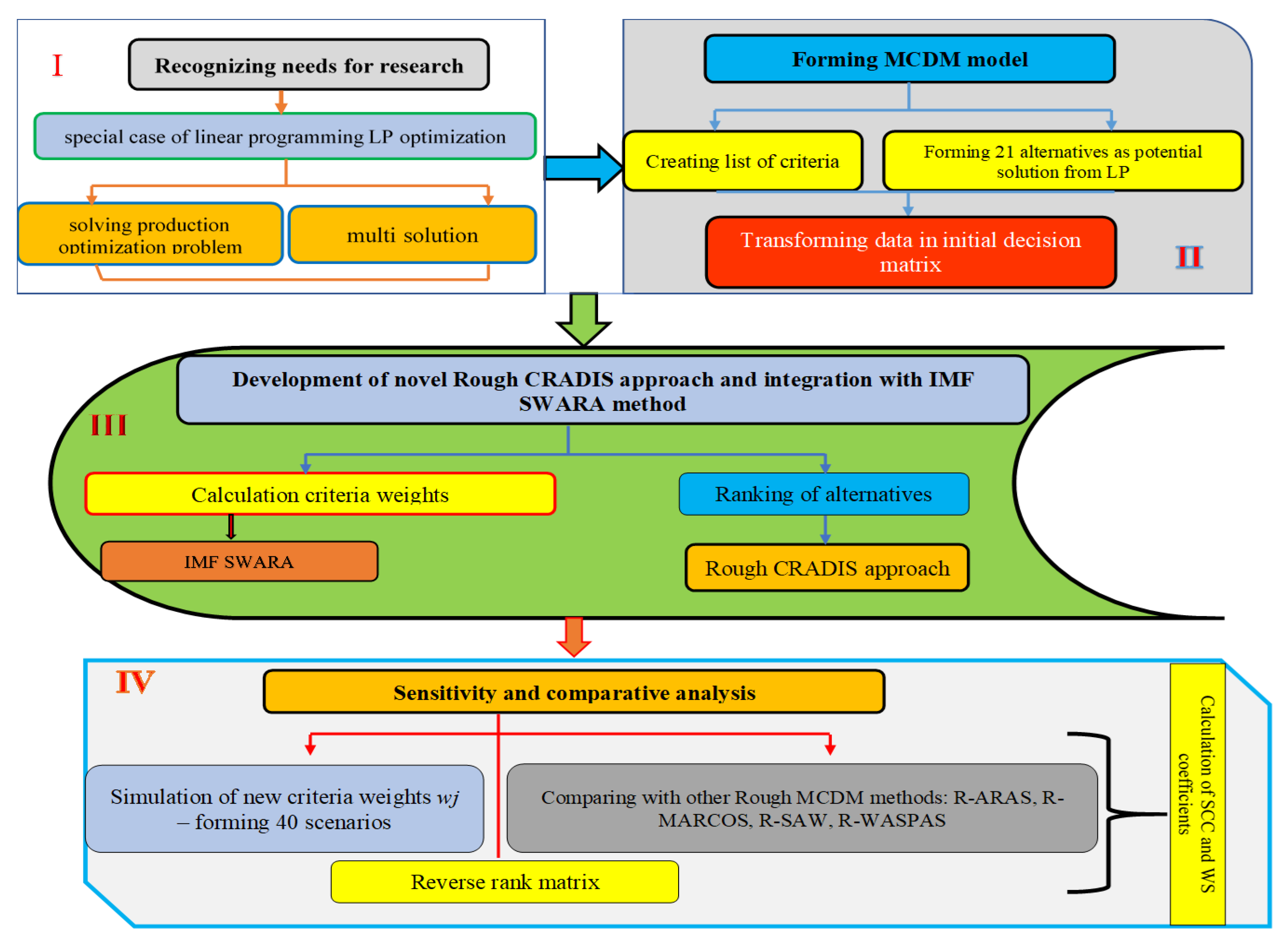
2.1. Methodology Steps
2.2. Linear Programming
2.3. IMF SWARA Method
2.4. Development of a Novel Rough CRADIS Approach
3. Integration of Linear Programming and a Fuzzy-Rough MCDM Model for Production Optimization
3.1. Special Case of Linear Programming Optimization
3.2. Formation of MCDM Model—Defining Criteria and Alternatives
3.3. Determining the Significance of Criteria Using the IMF SWARA Method
3.4. Determining the Optimal Solution Using the Rough CRADIS Approach
4. Verification of the Developed Model and Discussion
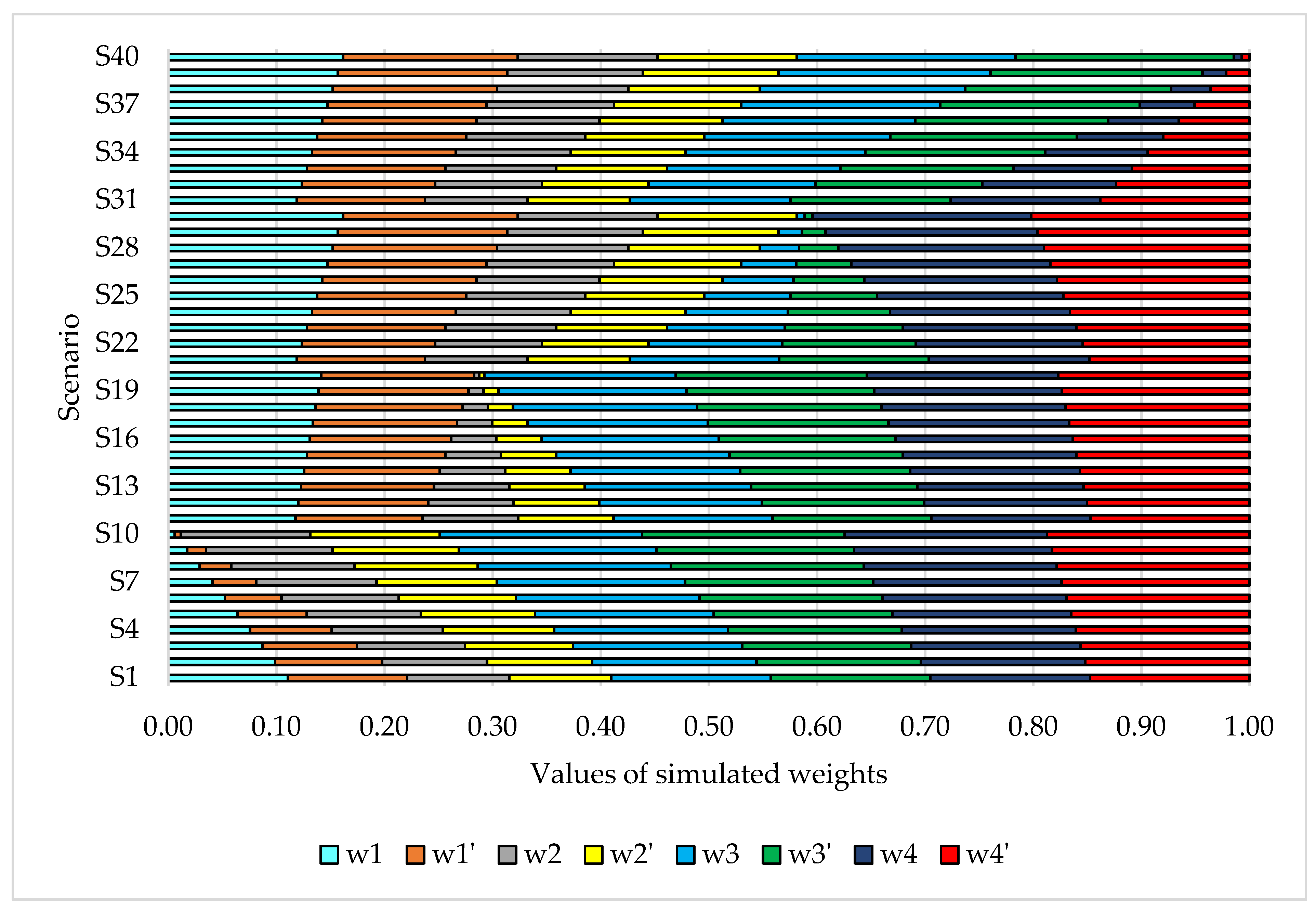
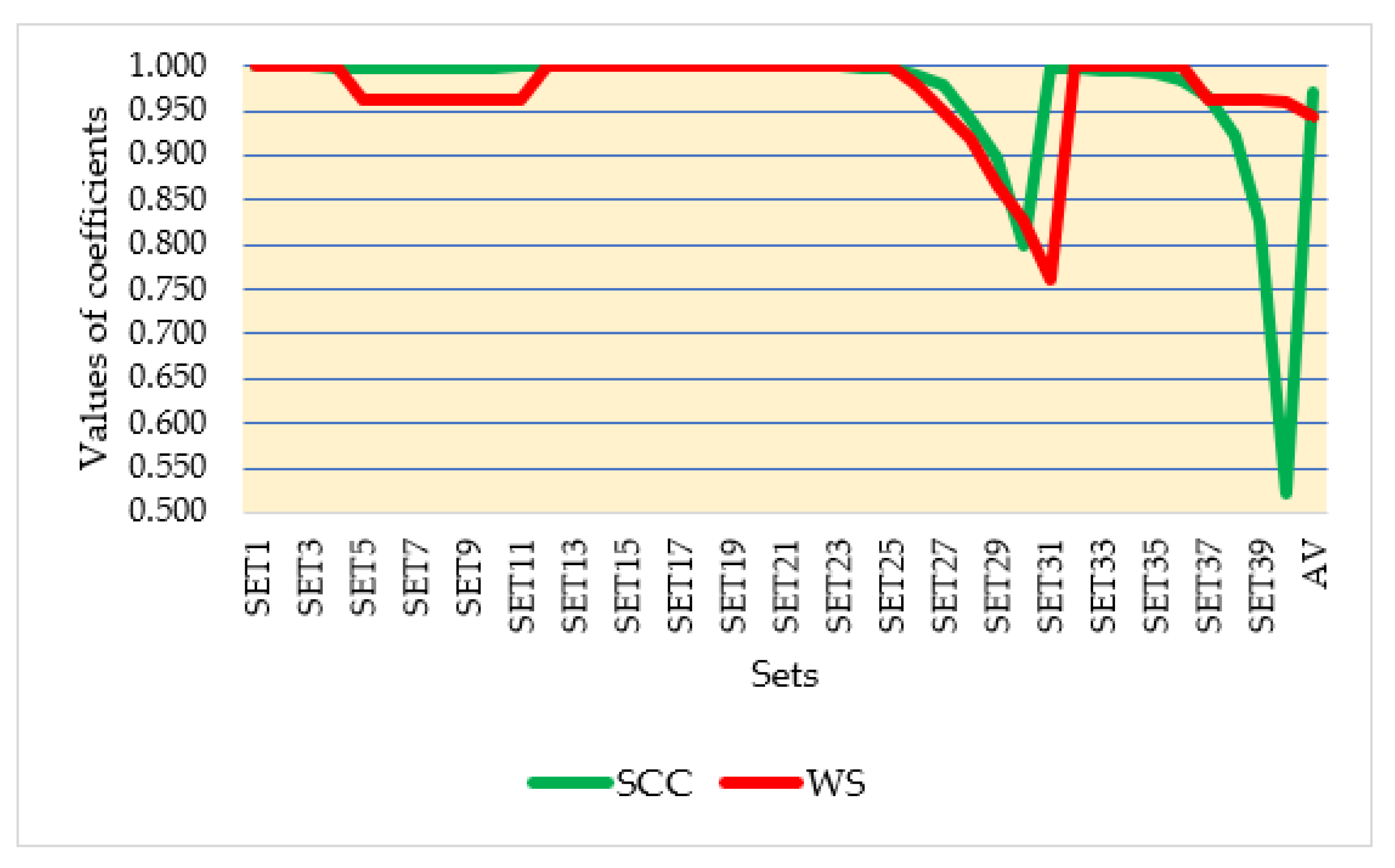
4.1. Sensitivity Analysis
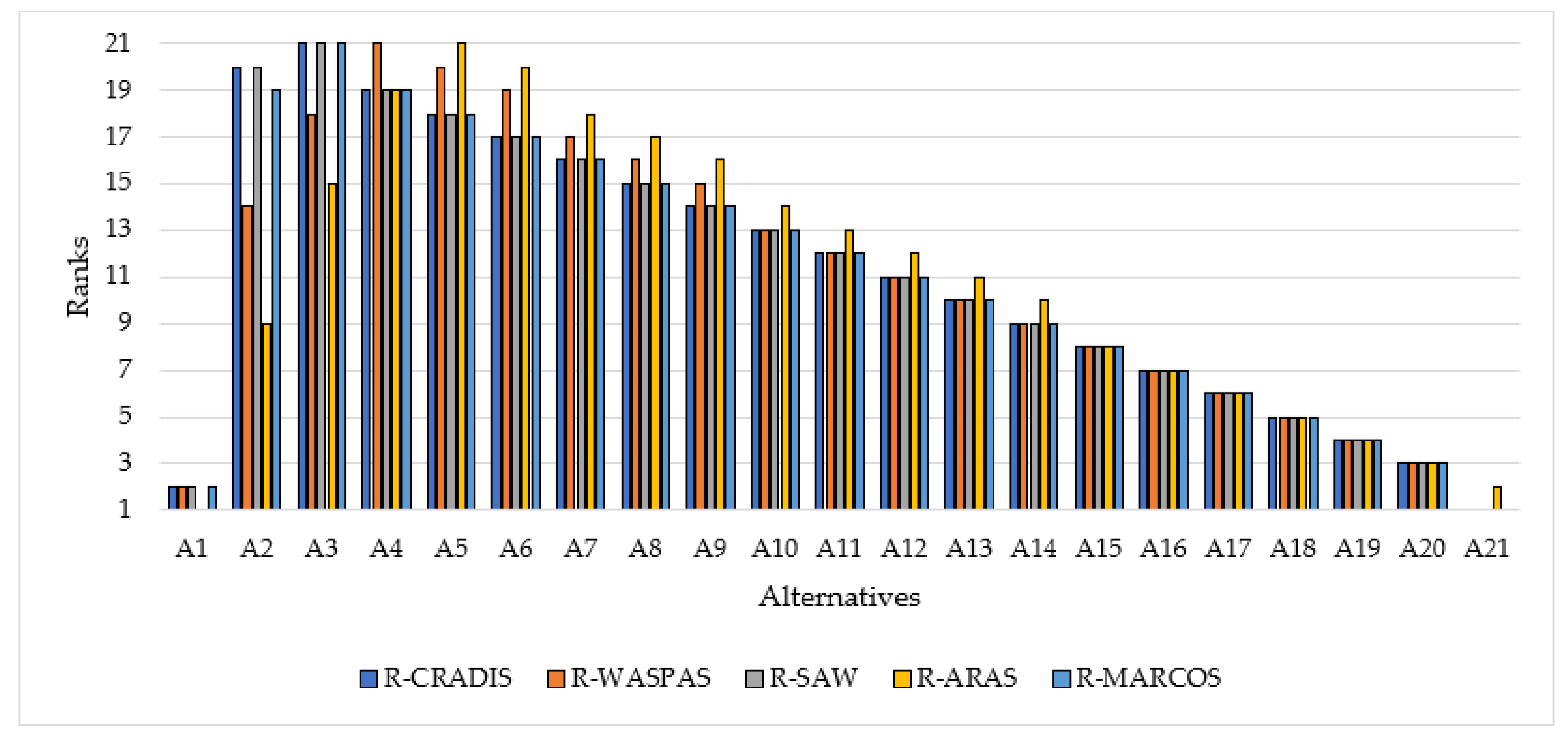
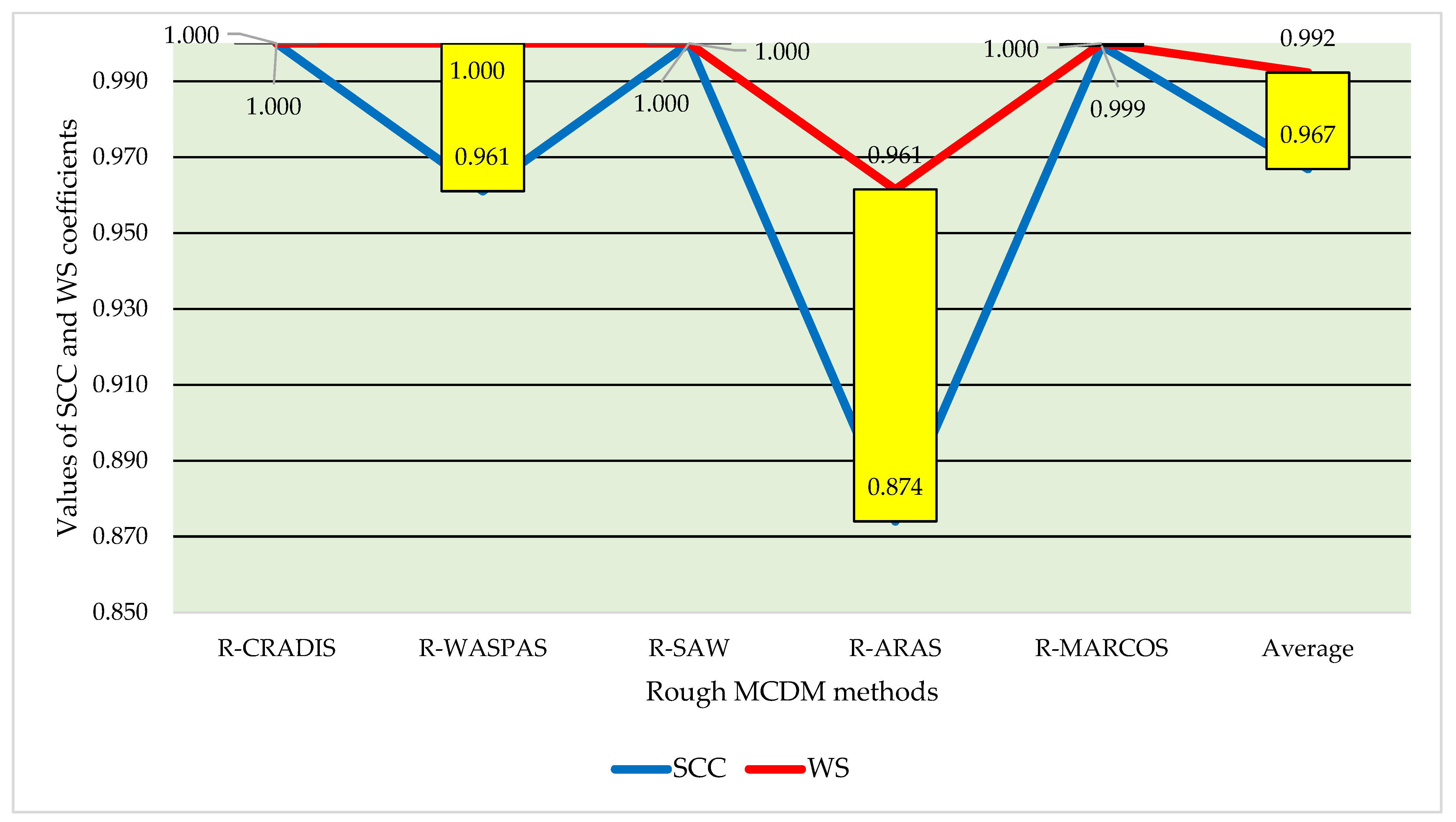
4.2. Comparative Analysis
4.3. Limitations and Managerial Implications
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bayá, G.; Canale, E.; Nesmachnow, S.; Robledo, F.; Sartor, P. Production Optimization in a Grain Facility through Mixed-Integer Linear Programming. Appl. Sci. 2022, 12, 8212. [Google Scholar] [CrossRef]
- Chandrawat, R.K.; Kumar, R.; Garg, B.P.; Dhiman, G.; Kumar, S. An analysis of modeling and optimization production cost through fuzzy linear programming problem with symmetric and right angle triangular fuzzy number. In Proceedings of the Sixth International Conference on Soft Computing for Problem Solving; Springer: Singapore, 2017; pp. 197–211. [Google Scholar]
- Pop, O.B.; Uifălean, D.C. The Impact of Innovation on the Management of Misapplication of Change in the Production System in the Automotive Industry. Econ. Innov. Econ. Res. J. 2022, 10, 199–210. [Google Scholar]
- Lazzerini, B.; Pistolesi, F. A linear programming-driven MCDM approach for multi-objective economic dispatch in smart grids. In Proceedings of the 2015 SAI Intelligent Systems Conference (IntelliSys), London, UK, 10–11 November 2015; pp. 475–484. [Google Scholar]
- Khalilzadeh, M.; Ghasemi, P.; Afrasiabi, A.; Shakeri, H. Hybrid fuzzy MCDM and FMEA integrating with linear programming approach for the health and safety executive risks: A case study. J. Model. Manag. 2021, 16, 1025–1053. [Google Scholar] [CrossRef]
- Malekpoor, H.; Chalvatzis, K.; Mishra, N.; Mehlawat, M.K.; Zafirakis, D.; Song, M. Integrated grey relational analysis and multi objective grey linear programming for sustainable electricity generation planning. Ann. Oper. Res. 2018, 269, 475–503. [Google Scholar] [CrossRef]
- Razak, N.H.; Hashim, H.; Yunus, N.A.; Klemeš, J. Integrated linear programming and analytical hierarchy process method for diesel/biodiesel/butanol in reducing diesel emissions. J. Clean. Prod. 2022, 337, 130297. [Google Scholar] [CrossRef]
- Cheng, S.; Chan, C.W.; Huang, G.H. An integrated multi-criteria decision analysis and inexact mixed integer linear programming approach for solid waste management. Eng. Appl. Artif. Intell. 2003, 16, 543–554. [Google Scholar] [CrossRef]
- Kannan, D.; Khodaverdi, R.; Olfat, L.; Jafarian, A.; Diabat, A. Integrated fuzzy multi criteria decision making method and multi-objective programming approach for supplier selection and order allocation in a green supply chain. J. Clean. Prod. 2013, 47, 355–367. [Google Scholar] [CrossRef]
- Sanayei, A.; Mousavi, S.F.; Abdi, M.R.; Mohaghar, A. An integrated group decision-making process for supplier selection and order allocation using multi-attribute utility theory and linear programming. J. Frankl. Inst. 2008, 345, 731–747. [Google Scholar] [CrossRef]
- Stojić, G.; Stević, Ž.; Antuchevičienė, J.; Pamučar, D.; Vasiljević, M. A novel rough WASPAS approach for supplier selection in a company manufacturing PVC carpentry products. Information 2018, 9, 121. [Google Scholar] [CrossRef]
- Durmić, E.; Stević, Ž.; Chatterjee, P.; Vasiljević, M.; Tomašević, M. Sustainable supplier selection using combined FUCOM–Rough SAW model. Rep. Mech. Eng. 2020, 1, 34–43. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Nunić, Z.; Stjepanović, Ž.; Prentkovskis, O. A novel rough range of value method (R-ROV) for selecting automatically guided vehicles (AGVs). Stud. Inform. Control 2018, 27, 385–394. [Google Scholar] [CrossRef]
- Vojinović, N.; Sremac, S.; Zlatanović, D. A Novel Integrated Fuzzy-Rough MCDM Model for Evaluation of Companies for Transport of Dangerous Goods. Complexity 2021, 2021, 1–16. [Google Scholar] [CrossRef]
- Kumar, S.; Maity, S.R.; Patnaik, L. Optimization of Wear Parameters for Duplex-TiAlN Coated MDC-K Tool Steel Using Fuzzy MCDM Techniques. Oper. Res. Eng. Sci. Theory Appl. 2022. [Google Scholar] [CrossRef]
- Sałabun, W.; Urbaniak, K. A new coefficient of rankings similarity in decision-making problems. In Proceedings of the International Conference on Computational Science, Amsterdam, The Netherlands, 3–5 June 2020; Springer: Cham, Switzerland, 2020; pp. 632–645. [Google Scholar]
- Vrtagić, S.; Softić, E.; Subotić, M.; Stević, Ž.; Dordevic, M.; Ponjavic, M. Ranking road sections based on MCDM model: New improved fuzzy SWARA (IMF SWARA). Axioms 2021, 10, 92. [Google Scholar] [CrossRef]
- Zolfani, S.H.; Görçün, Ö.F.; Küçükönder, H. Evaluating logistics villages in Turkey using hybrid improved fuzzy SWARA (IMF SWARA) and fuzzy MABAC techniques. Technol. Econ. Dev. Econ. 2021, 27, 1582–1612. [Google Scholar] [CrossRef]
- Puška, A.; Božanić, D.; Nedeljković, M.; Janošević, M. Green Supplier Selection in an Uncertain Environment in Agriculture Using a Hybrid MCDM Model: Z-Numbers–Fuzzy LMAW–Fuzzy CRADIS Model. Axioms 2022, 11, 427. [Google Scholar] [CrossRef]
- Puška, A.; Stević, Ž.; Pamučar, D. Evaluation and selection of healthcare waste incinerators using extended sustainability criteria and multi-criteria analysis methods. Environ. Dev. Sustain. 2022, 24, 11195–11225. [Google Scholar] [CrossRef]
- Puška, A.; Nedeljković, M.; Prodanović, R.; Vladisavljević, R.; Suzić, R. Market assessment of pear varieties in Serbia using fuzzy CRADIS and CRITIC methods. Agriculture 2022, 12, 139. [Google Scholar] [CrossRef]
- Božanić, D.; Milić, A.; Tešić, D.; Salabun, W.; Pamučar, D. D numbers–FUCOM–fuzzy RAFSI model for selecting the group of construction machines for enabling mobility. Facta Univ. Ser. Mech. Eng. 2021, 19, 447–471. [Google Scholar] [CrossRef]
- Mešić, A.; Miškić, S.; Stević, Ž.; Mastilo, Z. Hybrid MCDM solutions for evaluation of the logistics performance index of the Western Balkan countries. Econ.-Innov. Econ. Res. J. 2022, 10, 13–34. [Google Scholar] [CrossRef]
- Torkayesh, A.E.; Zolfani, S.H.; Kahvand, M.; Khazaelpour, P. Landfill location selection for healthcare waste of urban areas using hybrid BWM-grey MARCOS model based on GIS. Sustain. Cities Soc. 2021, 67, 102712. [Google Scholar] [CrossRef]
- Gergin, R.E.; Peker, İ.; Kısa, A.C.G. Supplier selection by integrated IFDEMATEL-IFTOPSIS Method: A case study of automotive supply industry. Decis. Mak. Appl. Manag. Eng. 2022, 5, 169–193. [Google Scholar] [CrossRef]


| Linguistic Variable | Abbreviation | TFN Scale | ||
|---|---|---|---|---|
| Absolutely less significant | ALS | 1 | 1 | 1 |
| Dominantly less significant | DLS | 1/2 | 2/3 | 1 |
| Much less significant | MLS | 2/5 | 1/2 | 2/3 |
| Really less significant | RLS | 1/3 | 2/5 | 1/2 |
| Less significant | LS | 2/7 | 1/3 | 2/5 |
| Moderately less significant | MDLS | 1/4 | 2/7 | 1/3 |
| Weakly less significant | WLS | 2/9 | 1/4 | 2/7 |
| Equally significant | ES | 0 | 0 | 0 |
| x1 | X2 | S1 | S2 | S3 | S4 | Const. |
|---|---|---|---|---|---|---|
| 0 | 0 | 1 | −3 | 3/2 | 0 | 750 |
| 0 | 1 | 0 | 2 | −2 | 0 | 1000 |
| 1 | 0 | 0 | 0 | 1 | 0 | 2500 |
| 0 | 0 | 0 | −2 | 2 | 1 | 2000 |
| 0 | 0 | 0 | −2000 | 0 | 0 | F − 6000000 |
| 0 | 0 | 2/3 | −2 | 1 | 0 | 500 |
| 0 | 1 | 0 | 2 | −2 | 0 | 1000 |
| 1 | 0 | 0 | 0 | 1 | 0 | 2500 |
| 0 | 0 | 0 | −2 | 2 | 1 | 2000 |
| 0 | 0 | 0 | −2000 | 0 | 0 | F − 6000000 |
| 0 | 0 | 2/3 | −2 | 1 | 0 | 500 |
| 0 | 1 | 4/3 | −2 | 0 | 0 | 2000 |
| 1 | 0 | −2/3 | 2 | 0 | 0 | 2000 |
| 0 | 0 | −4/3 | 2 | 0 | 1 | 1000 |
| 0 | 0 | 0 | −2000 | 0 | 0 | F − 6000000 |
| t | x1 | x2 | |
|---|---|---|---|
| A1 | 1 | 2500 | 1000 |
| A2 | 0.095 | 2475 | 1050 |
| A3 | 0.090 | 2450 | 1100 |
| A4 | 0.085 | 2425 | 1150 |
| A5 | 0.080 | 2400 | 1200 |
| A6 | 0.075 | 2375 | 1250 |
| A7 | 0.070 | 2350 | 1300 |
| A8 | 0.065 | 2325 | 1350 |
| A9 | 0.060 | 2300 | 1400 |
| A10 | 0.055 | 2275 | 1450 |
| A11 | 0.050 | 2250 | 1500 |
| A12 | 0.045 | 2225 | 1550 |
| A13 | 0.040 | 2200 | 1600 |
| A14 | 0.035 | 2175 | 1650 |
| A15 | 0.030 | 2150 | 1700 |
| A16 | 0.025 | 2125 | 1750 |
| A17 | 0.020 | 2100 | 1800 |
| A18 | 0.015 | 2075 | 1850 |
| A19 | 0.010 | 2050 | 1900 |
| A20 | 0.05 | 2025 | 1950 |
| A21 | 0 | 2000 | 2000 |
| C3 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.287 | 0.291 | 0.296 | |
| C4 | ES | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.287 | 0.291 | 0.296 |
| C1 | WLS | 1.222 | 1.250 | 1.286 | 0.778 | 0.800 | 0.818 | 0.223 | 0.233 | 0.242 |
| C2 | WLS | 1.222 | 1.250 | 1.286 | 0.605 | 0.640 | 0.669 | 0.173 | 0.186 | 0.198 |
| SUM | 3.383 | 3.440 | 3.488 | |||||||
| C1 | C2 | C3 | C4 | |||||
|---|---|---|---|---|---|---|---|---|
| A1 | 750.00 | 750.00 | 1 | 1 | 1 | 1 | 2000 | 2000 |
| A2 | 712.50 | 712.50 | 1 | 1 | 25 | 25 | 1950 | 1950 |
| A3 | 675.00 | 675.00 | 1 | 1 | 50 | 50 | 1900 | 1900 |
| A4 | 637.50 | 637.50 | 1 | 1 | 75 | 75 | 1850 | 1850 |
| A5 | 600.00 | 600.00 | 1 | 1 | 100 | 100 | 1800 | 1800 |
| A6 | 562.50 | 562.50 | 1 | 1 | 125 | 125 | 1750 | 1750 |
| A7 | 525.00 | 525.00 | 1 | 1 | 150 | 150 | 1700 | 1700 |
| A8 | 487.50 | 487.50 | 1 | 1 | 175 | 175 | 1650 | 1650 |
| A9 | 450.00 | 450.00 | 1 | 1 | 200 | 200 | 1600 | 1600 |
| A10 | 412.50 | 412.50 | 1 | 1 | 225 | 225 | 1550 | 1550 |
| A11 | 375.00 | 375.00 | 1 | 1 | 250 | 250 | 1500 | 1500 |
| A12 | 337.50 | 337.50 | 1 | 1 | 275 | 275 | 1450 | 1450 |
| A13 | 300.00 | 300.00 | 1 | 1 | 300 | 300 | 1400 | 1400 |
| A14 | 262.50 | 262.50 | 1 | 1 | 325 | 325 | 1350 | 1350 |
| A15 | 225.00 | 225.00 | 1 | 1 | 350 | 350 | 1300 | 1300 |
| A16 | 187.50 | 187.50 | 1 | 1 | 375 | 375 | 1250 | 1250 |
| A17 | 150.00 | 150.00 | 1 | 1 | 400 | 400 | 1200 | 1200 |
| A18 | 112.50 | 112.50 | 1 | 1 | 425 | 425 | 1150 | 1150 |
| A19 | 75.00 | 75.00 | 1 | 1 | 450 | 450 | 1100 | 1100 |
| A20 | 37.50 | 37.50 | 1 | 1 | 475 | 475 | 1050 | 1050 |
| A21 | 1.00 | 1.00 | 1 | 1 | 500 | 500 | 1000 | 1000 |
| Rank | ||||||||
|---|---|---|---|---|---|---|---|---|
| A1 | 0.9465 | 0.6685 | 0.6165 | 0.9985 | 0.6514 | 0.669542 | 0.660 | 1 |
| A2 | 1.3343 | 0.2807 | 0.4621 | 0.281146 | 0.372 | 3 | ||
| A3 | 1.3422 | 0.2729 | 0.4594 | 0.273271 | 0.366 | 7 | ||
| A4 | 1.3446 | 0.2704 | 0.4585 | 0.270808 | 0.365 | 11 | ||
| A5 | 1.3457 | 0.2693 | 0.4581 | 0.269709 | 0.364 | 14 | ||
| A6 | 1.3463 | 0.2688 | 0.4580 | 0.269167 | 0.364 | 17 | ||
| A7 | 1.3465 | 0.2685 | 0.4579 | 0.268913 | 0.363 | 19 | ||
| A8 | 1.3466 | 0.2684 | 0.4578 | 0.268834 | 0.363 | 21 | ||
| A9 | 1.3466 | 0.2685 | 0.4579 | 0.268876 | 0.363 | 20 | ||
| A10 | 1.3464 | 0.2686 | 0.4579 | 0.269011 | 0.363 | 18 | ||
| A11 | 1.3462 | 0.2688 | 0.4580 | 0.269222 | 0.364 | 16 | ||
| A12 | 1.3459 | 0.2691 | 0.4581 | 0.269506 | 0.364 | 15 | ||
| A13 | 1.3456 | 0.2695 | 0.4582 | 0.269862 | 0.364 | 13 | ||
| A14 | 1.3451 | 0.2699 | 0.4583 | 0.270297 | 0.364 | 12 | ||
| A15 | 1.3446 | 0.2704 | 0.4585 | 0.270829 | 0.365 | 10 | ||
| A16 | 1.3439 | 0.2711 | 0.4587 | 0.271487 | 0.365 | 9 | ||
| A17 | 1.3431 | 0.2719 | 0.4590 | 0.272337 | 0.366 | 8 | ||
| A18 | 1.3419 | 0.2731 | 0.4594 | 0.273524 | 0.366 | 6 | ||
| A19 | 1.3400 | 0.2751 | 0.4601 | 0.275485 | 0.368 | 5 | ||
| A20 | 1.3351 | 0.2800 | 0.4618 | 0.280383 | 0.371 | 4 | ||
| A21 | 1.0199 | 0.5951 | 0.6045 | 0.596012 | 0.600 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dordevic, M.; Tešić, R.; Todorović, S.; Jokić, M.; Das, D.K.; Stević, Ž.; Vrtagic, S. Development of Integrated Linear Programming Fuzzy-Rough MCDM Model for Production Optimization. Axioms 2022, 11, 510. https://doi.org/10.3390/axioms11100510
Dordevic M, Tešić R, Todorović S, Jokić M, Das DK, Stević Ž, Vrtagic S. Development of Integrated Linear Programming Fuzzy-Rough MCDM Model for Production Optimization. Axioms. 2022; 11(10):510. https://doi.org/10.3390/axioms11100510
Chicago/Turabian StyleDordevic, Milan, Rade Tešić, Srdjan Todorović, Miloš Jokić, Dillip Kumar Das, Željko Stević, and Sabahudin Vrtagic. 2022. "Development of Integrated Linear Programming Fuzzy-Rough MCDM Model for Production Optimization" Axioms 11, no. 10: 510. https://doi.org/10.3390/axioms11100510
APA StyleDordevic, M., Tešić, R., Todorović, S., Jokić, M., Das, D. K., Stević, Ž., & Vrtagic, S. (2022). Development of Integrated Linear Programming Fuzzy-Rough MCDM Model for Production Optimization. Axioms, 11(10), 510. https://doi.org/10.3390/axioms11100510








