A New Entropy Measurement for the Analysis of Uncertain Data in MCDA Problems Using Intuitionistic Fuzzy Sets and COPRAS Method
Abstract
:1. Introduction
2. Preliminaries
3. Entropy for Intuitionistic Fuzzy Set
- Minimality: , if A is crisp set;
- Maximality: if ;
- Resolution: , if A is less fuzzy than B,i.e., and for
- Symmetry: , where is the complement of A.
- Minimality: if S is a crisp set, i.e., or for all , then,Therefore,
- Maximality: for all , if for all , then,
- Resolution: in order to prove the fourth property, consider the function such thatwhere . The partial derivatives with respect to and are obtained asWe obtain that when and when , whereas when and when . Thus, f is increasing with respect to when and decreasing when . Moreover, f is decreasing with respect to when and increasing when .Now, by using this property of the function, we can conclude that , if A is less fuzzy than B, i.e., and for or and for .
- Symmetry: for the property, we have as . Thus, we have
4. Intuitionistic Fuzzy Multi-Criteria Decision-Making Based on COPRAS Approach
- Step 1:
- Establishment of intuitionistic fuzzy decision matrix.The initial move is relevant to the establishment of the intuitionistic fuzzy decision matrix. We determine the decision matrix , where are the alternatives concerning the criteria , such that and .
- Step 2:
- Judgment of the weights of criteria.Criteria weights symbolize a significant part of the clarification of MCDM issues. The weights can be obtained in different ways [75]. In a decision-making system, the experience concerning criteria weights is seldom entirely unknown or imperfectly known and somewhat known at specific times.
- For unknown criteria weights:If weights of criteria are entirely unknown, then we determine the weights by utilizing the following equation:where .
- For partially known criteria weights:Because of the increasing intricacy of decision-making issues, it may not frequently be reasonable for the decision-makers to describe their viewpoint as exact numbers. In case the criteria weights are imperfectly known for MCDM issues,
- Step 3:
- Calculate the weighted decision matrix :where .
- Step 4:
- Calculate the score function:where .
- Step 5:
- Determine the maximizing and minimizing index:andwhere, B is the set of benefit criteria and is the set of non-benefit criteria, for all .
- Step 6:
- Determine the relative significance value of each alternative:where .
- Step 7:
- Determine the priority order:where .
- Step 8:
- Ranking of the alternatives:The ranking of the alternatives is regulated in declining order based on the values of priority order. Thus, the highest final value has the highest rank.
5. Numerical Example
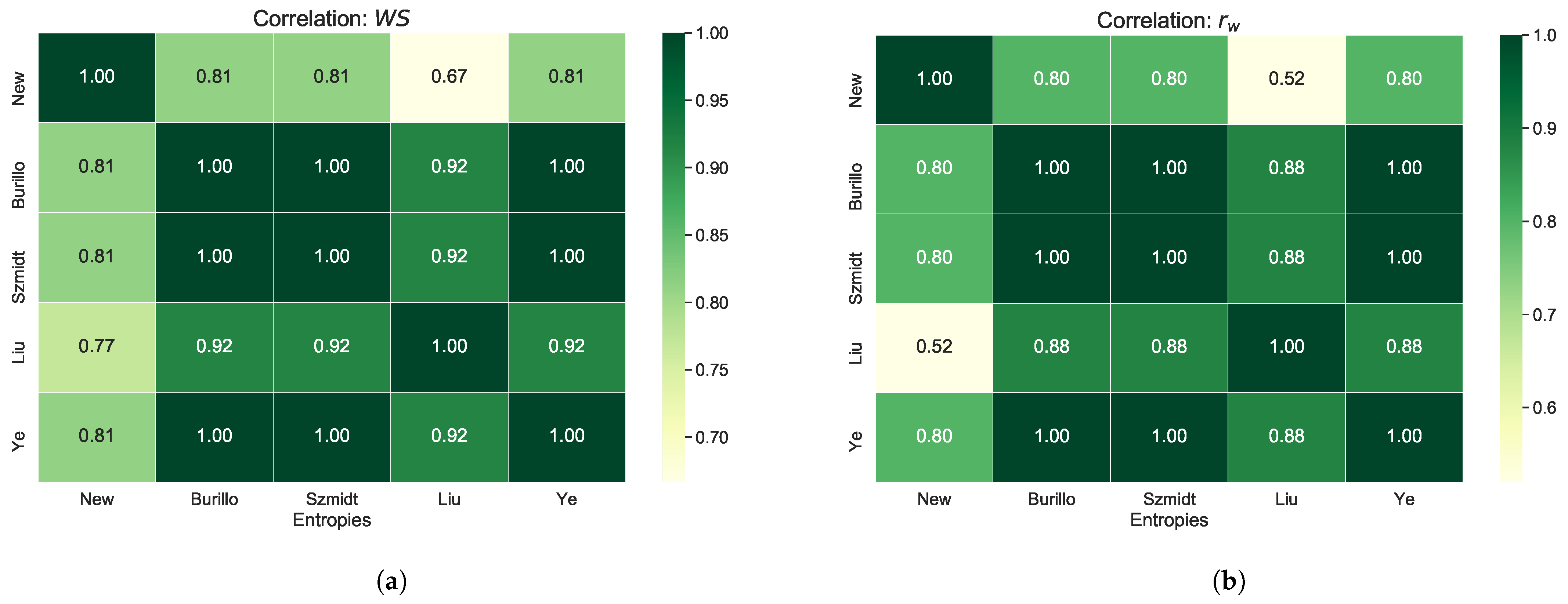
6. Comparative Analysis
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AHP | Analytic Hierarchy Process |
| ANP | Analytic Network Process |
| BWM | Best Worst Method |
| CODAS | COmbinative Distance-based ASsessment |
| CSTN | Color Super-Twisted Nematic |
| COMET | Characteristic Objects Method |
| COPRAS | COmplex PRoportional ASsessment |
| DEMATEL | Decision Making Trial and Evaluation Laboratory |
| DSS | Decision Support System |
| EDAS | Evaluation based on Distance from Average Solution |
| ELECTRE | ÉLimination et Choix Traduisant la REalité |
| FMEA | Failure Modes and Effects Analysis |
| HFS | Hesistant Fuzzy Sets |
| IFS | Intuitionistic Fuzzy Sets |
| MABAC | Multi-Attributive Border Approximation area Comparison |
| MADM | Multiple Attribute Decision Making |
| MARCOS | Measurement of Alternatives and Ranking according to COmpromise Solution |
| MCDA | Multi-criteria decision analysis |
| MOORA | Multi-Objective Optimization Method by Ratio Analysis |
| PFSs | Pythagorean fuzzy sets |
| PIPRECIA | PIvot Pairwise RElative Criteria Importance Assessment |
| PROMETHEE | Preference Ranking Organization METHod for Enrichment of Evaluations |
| PFSH-TOPSIS | Pythagorean fuzzy hybrid Order of Preference by Similarity to an Ideal Solution |
| PFH-ELECTRE I | Pythagorean fuzzy hybrid ELimination and Choice Translating REality I |
| SAF | Serbian Armed Forces |
| SAW | Simple Additive Weighing |
| SPOTIS | Stable Preference Ordering Towards Ideal Solution |
| SWARA | Stepwise Weight Assessment Ratio Analysis |
| TOPSIS | Technique for Order of Preference by Similarity to Ideal Solution |
| VIKOR | VIseKriterijumska Optimizacija I Kompromisno Resenje |
References
- Stević, Ž.; Karamaşa, Ç.; Demir, E.; Korucuk, S. Assessing sustainable production under circular economy context using a novel rough-fuzzy MCDM model: A case of the forestry industry in the Eastern Black Sea region. J. Enterp. Inf. Manag. 2021. [Google Scholar] [CrossRef]
- Kizielewicz, B.; Szyjewski, Z. Handling economic perspective in multicriteria model-renewable energy resources case study. Procedia Comput. Sci. 2020, 176, 3555–3562. [Google Scholar] [CrossRef]
- Shekhovtsov, A.; Kozlov, V.; Nosov, V.; Sałabun, W. Efficiency of Methods for Determining the Relevance of Criteria in Sustainable Transport Problems: A Comparative Case Study. Sustainability 2020, 12, 7915. [Google Scholar] [CrossRef]
- Kizielewicz, B.; Więckowski, J.; Shekhovtsov, A.; Wątróbski, J.; Depczyński, R.; Sałabun, W. Study towards the Time-Based MCDA Ranking Analysis—A Supplier Selection Case Study. Facta Univ. Ser. Mech. Eng. 2021, 19, 381–399. [Google Scholar] [CrossRef]
- Pamucar, D.S.; Savin, L.M. Multiple-criteria model for optimal off-road vehicle selection for passenger transportation: BWM-COPRAS model. Mil. Tech. Cour. 2020, 68, 28–64. [Google Scholar]
- La Scalia, G.; Aiello, G.; Rastellini, C.; Micale, R.; Cicalese, L. Multi-criteria decision making support system for pancreatic islet transplantation. Expert Syst. Appl. 2011, 38, 3091–3097. [Google Scholar] [CrossRef]
- Stević, Ž.; Pamučar, D.; Puška, A.; Chatterjee, P. Sustainable supplier selection in healthcare industries using a new MCDM method: Measurement of alternatives and ranking according to COmpromise solution (MARCOS). Comput. Ind. Eng. 2020, 140, 106231. [Google Scholar] [CrossRef]
- Muhammad, L.; Badi, I.; Haruna, A.A.; Mohammed, I. Selecting the Best Municipal Solid Waste Management Techniques in Nigeria Using Multi Criteria Decision Making Techniques. Rep. Mech. Eng. 2021, 2, 180–189. [Google Scholar] [CrossRef]
- Bączkiewicz, A.; Kizielewicz, B.; Shekhovtsov, A.; Yelmikheiev, M.; Kozlov, V.; Sałabun, W. Comparative Analysis of Solar Panels with Determination of Local Significance Levels of Criteria Using the MCDM Methods Resistant to the Rank Reversal Phenomenon. Energies 2021, 14, 5727. [Google Scholar] [CrossRef]
- Pamucar, D.; Iordache, M.; Deveci, M.; Schitea, D.; Iordache, I. A new hybrid fuzzy multi-criteria decision methodology model for prioritizing the alternatives of the hydrogen bus development: A case study from Romania. Int. J. Hydrogen Energy 2021, 46, 29616–29637. [Google Scholar] [CrossRef]
- Bączkiewicz, A.; Kizielewicz, B.; Shekhovtsov, A.; Wątróbski, J.; Sałabun, W. Methodical Aspects of MCDM Based E-Commerce Recommender System. J. Theor. Appl. Electron. Commer. Res. 2021, 16, 2192–2229. [Google Scholar] [CrossRef]
- Greis, M.; Schuff, H.; Kleiner, M.; Henze, N.; Schmidt, A. Input controls for entering uncertain data: Probability distribution sliders. Proc. ACM Hum. Comput. Interact. 2017, 1, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Sengupta, A.; Pal, T.K. On comparing interval numbers. Eur. J. Oper. Res. 2000, 127, 28–43. [Google Scholar] [CrossRef]
- Shekhovtsov, A.; Kizielewicz, B.; Sałabun, W. New Rank-Reversal Free Approach to Handle Interval Data in MCDA Problems. In Proceedings of the International Conference on Computational Science, Kraków, Poland, 16–18 June 2021; pp. 458–472. [Google Scholar]
- Zadeh, L. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Vesković, S.; Stević, Ž.; Karabašević, D.; Rajilić, S.; Milinković, S.; Stojić, G. A new integrated fuzzy approach to selecting the best solution for business balance of passenger rail operator: Fuzzy PIPRECIA-fuzzy EDAS model. Symmetry 2020, 12, 743. [Google Scholar] [CrossRef]
- Kizielewicz, B.; Bączkiewicz, A. Comparison of Fuzzy TOPSIS, Fuzzy VIKOR, Fuzzy WASPAS and Fuzzy MMOORA methods in the housing selection problem. Procedia Comput. Sci. 2021, 192, 4578–4591. [Google Scholar] [CrossRef]
- Yager, R.R.; Abbasov, A.M. Pythagorean membership grades, complex numbers, and decision making. Int. J. Intell. Syst. 2013, 28, 436–452. [Google Scholar] [CrossRef]
- Peng, X.; Yang, Y. Some results for Pythagorean fuzzy sets. Int. J. Intell. Syst. 2015, 30, 1133–1160. [Google Scholar] [CrossRef]
- Mete, S.; Serin, F.; Oz, N.E.; Gul, M. A decision-support system based on Pythagorean fuzzy VIKOR for occupational risk assessment of a natural gas pipeline construction. J. Nat. Gas Sci. Eng. 2019, 71, 102979. [Google Scholar] [CrossRef]
- Yucesan, M.; Gul, M. Hospital service quality evaluation: An integrated model based on Pythagorean fuzzy AHP and fuzzy TOPSIS. Soft Comput. 2020, 24, 3237–3255. [Google Scholar] [CrossRef]
- Akram, M.; Luqman, A.; Alcantud, J.C.R. Risk evaluation in failure modes and effects analysis: Hybrid TOPSIS and ELECTRE I solutions with Pythagorean fuzzy information. Neural Comput. Appl. 2021, 33, 5675–5703. [Google Scholar] [CrossRef]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Sałabun, W.; Karczmarczyk, A.; Wątróbski, J. Decision-making using the hesitant fuzzy sets COMET method: An empirical study of the electric city buses selection. In Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence (SSCI), Bangalore, India, 18–21 November 2018; pp. 1485–1492. [Google Scholar]
- Senvar, O.; Otay, I.; Bolturk, E. Hospital site selection via hesitant fuzzy TOPSIS. IFAC-PapersOnline 2016, 49, 1140–1145. [Google Scholar] [CrossRef]
- Faizi, S.; Sałabun, W.; Nawaz, S.; ur Rehman, A.; Wątróbski, J. Best-Worst method and Hamacher aggregation operations for intuitionistic 2-tuple linguistic sets. Expert Syst. Appl. 2021, 181, 115088. [Google Scholar] [CrossRef]
- Afful-Dadzie, E.; Oplatkova, Z.K.; Prieto, L.A.B. Comparative state-of-the-art survey of classical fuzzy set and intuitionistic fuzzy sets in multi-criteria decision making. Int. J. Fuzzy Syst. 2017, 19, 726–738. [Google Scholar] [CrossRef]
- Thakur, P.; Gandotra, N. Pythagorean fuzzy multi-criteria decision making and its application in fitting assembly. Mater. Today Proc. 2021, in press. [Google Scholar] [CrossRef]
- Kumar, R.; Gandotra, N. A novel pythagorean fuzzy entropy measure using MCDM application in preference of the advertising company with TOPSIS approach. Mater. Today Proc. 2021, in press. [Google Scholar] [CrossRef]
- Szmidt, E.; Kacprzyk, J. Distances between intuitionistic fuzzy sets. Fuzzy Sets Syst. 2000, 114, 505–518. [Google Scholar] [CrossRef]
- Turanli, N.; Çoker, D. Fuzzy connectedness in intuitionistic fuzzy topological spaces. Fuzzy Sets Syst. 2000, 116, 369–375. [Google Scholar] [CrossRef]
- Bustince, H. Construction of intuitionistic fuzzy relations with predetermined properties. Fuzzy Sets Syst. 2000, 109, 379–403. [Google Scholar] [CrossRef]
- Ciftcibasi, T.; Altunay, D. Two-sided (intuitionistic) fuzzy reasoning. IEEE Trans. Syst. Man Cybern. Part Syst. Hum. 1998, 28, 662–677. [Google Scholar] [CrossRef]
- Kumar, K.; Garg, H. Connection number of set pair analysis based TOPSIS method on intuitionistic fuzzy sets and their application to decision making. Appl. Intell. 2018, 48, 2112–2119. [Google Scholar] [CrossRef]
- Gerogiannis, V.C.; Fitsilis, P.; Kameas, A.D. Evaluation of project and portfolio Management Information Systems with the use of a hybrid IFS-TOPSIS method. Intell. Decis. Technol. 2013, 7, 91–105. [Google Scholar] [CrossRef] [Green Version]
- Feng, F.; Xu, Z.; Fujita, H.; Liang, M. Enhancing PROMETHEE method with intuitionistic fuzzy soft sets. Int. J. Intell. Syst. 2020, 35, 1071–1104. [Google Scholar] [CrossRef]
- Krishankumar, R.; Ravichandran, K.; Saeid, A.B. A new extension to PROMETHEE under intuitionistic fuzzy environment for solving supplier selection problem with linguistic preferences. Appl. Soft Comput. 2017, 60, 564–576. [Google Scholar]
- Krishankumar, R.; Premaladha, J.; Ravichandran, K.; Sekar, K.; Manikandan, R.; Gao, X. A novel extension to VIKOR method under intuitionistic fuzzy context for solving personnel selection problem. Soft Comput. 2020, 24, 1063–1081. [Google Scholar] [CrossRef]
- Çalı, S.; Balaman, Ş.Y. A novel outranking based multi criteria group decision making methodology integrating ELECTRE and VIKOR under intuitionistic fuzzy environment. Expert Syst. Appl. 2019, 119, 36–50. [Google Scholar] [CrossRef]
- Sadiq, R.; Tesfamariam, S. Environmental decision-making under uncertainty using intuitionistic fuzzy analytic hierarchy process (IF-AHP). Stoch. Environ. Res. Risk Assess. 2009, 23, 75–91. [Google Scholar] [CrossRef]
- Zhang, C.; Li, W.; Wang, L. AHP under the intuitionistic fuzzy environment. In Proceedings of the 2011 Eighth International Conference on Fuzzy Systems and Knowledge Discovery (FSKD), Shanghai, China, 26–28 July 2011; Volume 1, pp. 583–587. [Google Scholar]
- Rouyendegh, B.D. The intuitionistic fuzzy ELECTRE model. Int. J. Manag. Sci. Eng. Manag. 2018, 13, 139–145. [Google Scholar] [CrossRef]
- Wu, M.C.; Chen, T.Y. The ELECTRE multicriteria analysis approach based on Atanassov’s intuitionistic fuzzy sets. Expert Syst. Appl. 2011, 38, 12318–12327. [Google Scholar] [CrossRef]
- Xue, Y.X.; You, J.X.; Lai, X.D.; Liu, H.C. An interval-valued intuitionistic fuzzy MABAC approach for material selection with incomplete weight information. Appl. Soft Comput. 2016, 38, 703–713. [Google Scholar] [CrossRef]
- Karagoz, S.; Deveci, M.; Simic, V.; Aydin, N.; Bolukbas, U. A novel intuitionistic fuzzy MCDM-based CODAS approach for locating an authorized dismantling center: A case study of Istanbul. Waste Manag. Res. 2020, 38, 660–672. [Google Scholar] [CrossRef] [PubMed]
- Angeline, L.A.; Mystica, A.R.; Mary, S.F.J.; Merlin, M.M.M. A new integrated approach of combined FCM and CODAS method in interval valued intuitionistic fuzzy cognitive map for multi criteria decision making to evaluate and prioritize the branded mobile phones. Malaya J. Mat. (MJM) 2020, 8, 230–234. [Google Scholar]
- Mishra, A.R.; Rani, P.; Pandey, K.; Mardani, A.; Streimikis, J.; Streimikiene, D.; Alrasheedi, M. Novel multi-criteria intuitionistic fuzzy SWARA–COPRAS approach for sustainability evaluation of the bioenergy production process. Sustainability 2020, 12, 4155. [Google Scholar] [CrossRef]
- Thao, N.X. MOORA models based on new score function of interval-valued intuitionistic sets and apply to select materials for mushroom cultivation. Neural Comput. Appl. 2021, 17, 1–11. [Google Scholar] [CrossRef]
- Pérez-Domínguez, L.; Alvarado-Iniesta, A.; Rodríguez-Borbón, I.; Vergara-Villegas, O. Intuitionistic fuzzy MOORA for supplier selection. Dyna 2015, 82, 34–41. [Google Scholar] [CrossRef]
- Büyüközkan, G.; Güleryüz, S.; Karpak, B. A new combined IF-DEMATEL and IF-ANP approach for CRM partner evaluation. Int. J. Prod. Econ. 2017, 191, 194–206. [Google Scholar] [CrossRef]
- Shariati, S.; Abedi, M.; Saedi, A.; Yazdani-Chamzini, A.; Tamošaitienė, J.; Šaparauskas, J.; Stupak, S. Critical factors of the application of nanotechnology in construction industry by using ANP technique under fuzzy intuitionistic environment. J. Civ. Eng. Manag. 2017, 23, 914–925. [Google Scholar] [CrossRef] [Green Version]
- Nikjoo, A.V.; Saeedpoor, M. An intuitionistic fuzzy DEMATEL methodology for prioritising the components of SWOT matrix in the Iranian insurance industry. Int. J. Oper. Res. 2014, 20, 439–452. [Google Scholar] [CrossRef]
- Govindan, K.; Khodaverdi, R.; Vafadarnikjoo, A. Intuitionistic fuzzy based DEMATEL method for developing green practices and performances in a green supply chain. Expert Syst. Appl. 2015, 42, 7207–7220. [Google Scholar] [CrossRef]
- Amoozad Mahdiraji, H.; Zavadskas, E.; Arab, A.; Turskis, Z.; Sahebi, I. Formulation of Manufacturing Strategies Based on An Extended SWARA Method with Intuitionistic Fuzzy Numbers: An Automotive Industry Application. 2021. Available online: https://dora.dmu.ac.uk/bitstream/handle/2086/21082/SWARA%20IFS%2025-5-20%20Within.pdf?sequence=1&isAllowed=y (accessed on 4 April 2021).
- Hung, C.C.; Chen, L.H. A fuzzy TOPSIS decision making model with entropy weight under intuitionistic fuzzy environment. In Proceedings of the International Multiconference of Engineers and Computer Scientists, Hong Kong, China, 18–20 March 2009; Volume 1, pp. 13–16. [Google Scholar]
- Liu, X.; Qian, F.; Lin, L.; Zhang, K.; Zhu, L. Intuitionistic fuzzy entropy for group decision making of water engineering project delivery system selection. Entropy 2019, 21, 1101. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.Y.; Li, C.H. Determining objective weights with intuitionistic fuzzy entropy measures: A comparative analysis. Inf. Sci. 2010, 180, 4207–4222. [Google Scholar] [CrossRef]
- Sałabun, W.; Wątróbski, J.; Shekhovtsov, A. Are mcda methods benchmarkable? a comparative study of topsis, vikor, copras, and promethee ii methods. Symmetry 2020, 12, 1549. [Google Scholar] [CrossRef]
- Gandotra, N.; Bajaj, R.K.; Gupta, N. Sorting of decision making units in data envelopment analysis with intuitionistic fuzzy weighted entropy. In Advances in Computer Science, Engineering & Applications; Springer: Berlin/Heidelberg, Germany, 2012; pp. 567–576. [Google Scholar]
- XU, Z.S. Approaches to multiple attribute decision making with intuitionistic fuzzy preference information. Syst. Eng. Theory Pract. 2007, 27, 62–71. [Google Scholar] [CrossRef]
- Kumari, R.; Mishra, A.R. Multi-criteria COPRAS method based on parametric measures for intuitionistic fuzzy sets: Application of green supplier selection. Iran. J. Sci. Technol. Trans. Electr. Eng. 2020, 44, 1645–1662. [Google Scholar] [CrossRef]
- Kouchaksaraei, R.H.; Zolfani, S.H.; Golabchi, M. Glasshouse locating based on SWARA-COPRAS approach. Int. J. Strateg. Prop. Manag. 2015, 19, 111–122. [Google Scholar] [CrossRef]
- Banaitiene, N.; Banaitis, A.; Kaklauskas, A.; Zavadskas, E.K. Evaluating the life cycle of a building: A multivariant and multiple criteria approach. Omega 2008, 36, 429–441. [Google Scholar] [CrossRef]
- Ghorabaee, M.K.; Amiri, M.; Sadaghiani, J.S.; Goodarzi, G.H. Multiple criteria group decision-making for supplier selection based on COPRAS method with interval type-2 fuzzy sets. Int. J. Adv. Manuf. Technol. 2014, 75, 1115–1130. [Google Scholar] [CrossRef]
- Zagorskas, J.; Burinskienė, M.; Zavadskas, E.; Turskis, Z. Urbanistic assessment of city compactness on the basis of GIS applying the COPRAS method. Ekologija 2007, 53, 55–63. [Google Scholar]
- Zavadskas, E.K.; Kaklauskas, A.; Turskis, Z.; Tamošaitiene, J. Selection of the effective dwelling house walls by applying attributes values determined at intervals. J. Civ. Eng. Manag. 2008, 14, 85–93. [Google Scholar] [CrossRef] [Green Version]
- De Luca, A.; Termini, S. A definition of a nonprobabilistic entropy in the setting of fuzzy sets theory. Inf. Control 1972, 20, 301–312. [Google Scholar] [CrossRef] [Green Version]
- Hung, W.L.; Yang, M.S. Fuzzy entropy on intuitionistic fuzzy sets. Int. J. Intell. Syst. 2006, 21, 443–451. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Kaklauskas, A.; Sarka, V. The new method of multicriteria complex proportional assessment of projects. Technol. Econ. Dev. Econ. 1994, 1, 131–139. [Google Scholar]
- Zavadskas, E.K.; Kaklauskas, A.; Peldschus, F.; Turskis, Z. Multi-attribute assessment of road design solutions by using the COPRAS method. Balt. J. Road Bridge Eng. 2007, 2, 195–203. [Google Scholar]
- Kaklauskas, A.; Zavadskas, E.K.; Naimavicienė, J.; Krutinis, M.; Plakys, V.; Venskus, D. Model for a complex analysis of intelligent built environment. Autom. Constr. 2010, 19, 326–340. [Google Scholar] [CrossRef]
- Dhiman, H.S.; Deb, D. Fuzzy TOPSIS and fuzzy COPRAS based multi-criteria decision making for hybrid wind farms. Energy 2020, 202, 117755. [Google Scholar] [CrossRef]
- Ansari, Z.N.; Kant, R.; Shankar, R. Evaluation and ranking of solutions to mitigate sustainable remanufacturing supply chain risks: A hybrid fuzzy SWARA-fuzzy COPRAS framework approach. Int. J. Sustain. Eng. 2020, 13, 473–494. [Google Scholar] [CrossRef]
- Kizielewicz, B.; Więckowski, J.; Shekhovtsov, A.; Ziemba, E.; Wątróbski, J.; Sałabun, W. Input data preprocessing for the MCDM model: COPRAS method case study. In Proceedings of the AMCIS 2021 Proceedings, Online, 9–13 August 2021; p. 11. [Google Scholar]
- Kizielewicz, B.; Wątróbski, J.; Sałabun, W. Identification of relevant criteria set in the MCDA process—Wind farm location case study. Energies 2020, 13, 6548. [Google Scholar] [CrossRef]
- Burillo, P.; Bustince, H. Entropy on intuitionistic fuzzy sets and on interval-valued fuzzy sets. Fuzzy Sets Syst. 1996, 78, 305–316. [Google Scholar] [CrossRef]
- Szmidt, E.; Kacprzyk, J. Entropy for intuitionistic fuzzy sets. Fuzzy Sets Syst. 2001, 118, 467–477. [Google Scholar] [CrossRef]
- Liu, M.; Ren, H. A new intuitionistic fuzzy entropy and application in multi-attribute decision making. Information 2014, 5, 587–601. [Google Scholar] [CrossRef] [Green Version]
- Ye, J. Two effective measures of intuitionistic fuzzy entropy. Computing 2010, 87, 55–62. [Google Scholar] [CrossRef]
- Sałabun, W.; Urbaniak, K. A new coefficient of rankings similarity in decision-making problems. In Proceedings of the International Conference on Computational Science, Amsterdam, The Netherlands, 3–5 June 2020; pp. 632–645. [Google Scholar]

| Hospitals | |||||
|---|---|---|---|---|---|
| A | 0.41, 0.38 | 0.48, 0.57 | 0.36, 0.43 | 0.33, 0.37 | 0.28, 0.34 |
| B | 0.46, 0.37 | 0.48, 0.39 | 0.37, 0.41 | 0.35, 0.44 | 0.51, 0.39 |
| C | 0.36, 0.39 | 0.21, 0.37 | 0.41, 0.38 | 0.28, 0.34 | 0.32, 0.46 |
| D | 0.51, 0.39 | 0.37, 0.45 | 0.32, 0.46 | 0.37, 0.57 | 0.37, 0.45 |
| 0.7409 | 0.6374 | 0.7783 | 0.7979 | 0.7525 |
| A | 0.19028, 0.82374 | 0.26609, 0.85416 | 0.15334, 0.86528 | 0.13365, 0.85604 | 0.12452, 0.81342 |
| B | 0.21569, 0.81935 | 0.26609, 0.76794 | 0.15787, 0.85825 | 0.14220, 0.87954 | 0.23671, 0.83506 |
| C | 0.16562, 0.82804 | 0.11210, 0.75668 | 0.17623, 0.84714 | 0.11261, 0.84479 | 0.14306, 0.86187 |
| D | 0.24202, 0.82804 | 0.20110, 0.79938 | 0.13546, 0.87535 | 0.15084, 0.91587 | 0.16669, 0.85825 |
| g | Rank | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A | −0.64235 | −0.65879 | −0.72521 | −0.71494 | −0.64614 | −0.67123 | −0.68686 | −0.14581 | 100 | |
| B | −0.62482 | −0.51892 | −0.71167 | −0.75338 | −0.64130 | −0.65926 | −0.63615 | −0.15982 | 109.61 | |
| C | −0.65823 | −0.56000 | −0.68659 | −0.70100 | −0.72236 | −0.68906 | −0.63050 | −0.19243 | 131.97 | |
| D | −0.62708 | −0.59856 | −0.74789 | −0.81606 | −0.70881 | −0.69459 | −0.70731 | −0.15832 | 108.57 |
| Proposed Entropy | Burillo and Bustince [76] | Szmidt and Kacprzyk [77] | Liu and Ren [78] | Ye [79] | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Rank | Rank | Rank | Rank | Rank | ||||||
| A | 100 | IV | 100 | IV | 100 | IV | 105.77 | III | 100 | IV |
| B | 109.61 | II | 103.74 | III | 103.152 | III | 100 | IV | 103.23 | III |
| C | 131.97 | I | 129.67 | I | 128.631 | I | 126.03 | I | 129.43 | I |
| D | 108.57 | III | 105.25 | II | 104.78 | II | 120.17 | II | 104.61 | II |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thakur, P.; Kizielewicz, B.; Gandotra, N.; Shekhovtsov, A.; Saini, N.; Saeid, A.B.; Sałabun, W. A New Entropy Measurement for the Analysis of Uncertain Data in MCDA Problems Using Intuitionistic Fuzzy Sets and COPRAS Method. Axioms 2021, 10, 335. https://doi.org/10.3390/axioms10040335
Thakur P, Kizielewicz B, Gandotra N, Shekhovtsov A, Saini N, Saeid AB, Sałabun W. A New Entropy Measurement for the Analysis of Uncertain Data in MCDA Problems Using Intuitionistic Fuzzy Sets and COPRAS Method. Axioms. 2021; 10(4):335. https://doi.org/10.3390/axioms10040335
Chicago/Turabian StyleThakur, Parul, Bartłomiej Kizielewicz, Neeraj Gandotra, Andrii Shekhovtsov, Namita Saini, Arsham Borumand Saeid, and Wojciech Sałabun. 2021. "A New Entropy Measurement for the Analysis of Uncertain Data in MCDA Problems Using Intuitionistic Fuzzy Sets and COPRAS Method" Axioms 10, no. 4: 335. https://doi.org/10.3390/axioms10040335
APA StyleThakur, P., Kizielewicz, B., Gandotra, N., Shekhovtsov, A., Saini, N., Saeid, A. B., & Sałabun, W. (2021). A New Entropy Measurement for the Analysis of Uncertain Data in MCDA Problems Using Intuitionistic Fuzzy Sets and COPRAS Method. Axioms, 10(4), 335. https://doi.org/10.3390/axioms10040335







