Spatial Statistical Models: An Overview under the Bayesian Approach
Abstract
:1. Introduction
1.1. Aim
1.2. Outline
1.3. Spatial Modeling Overview
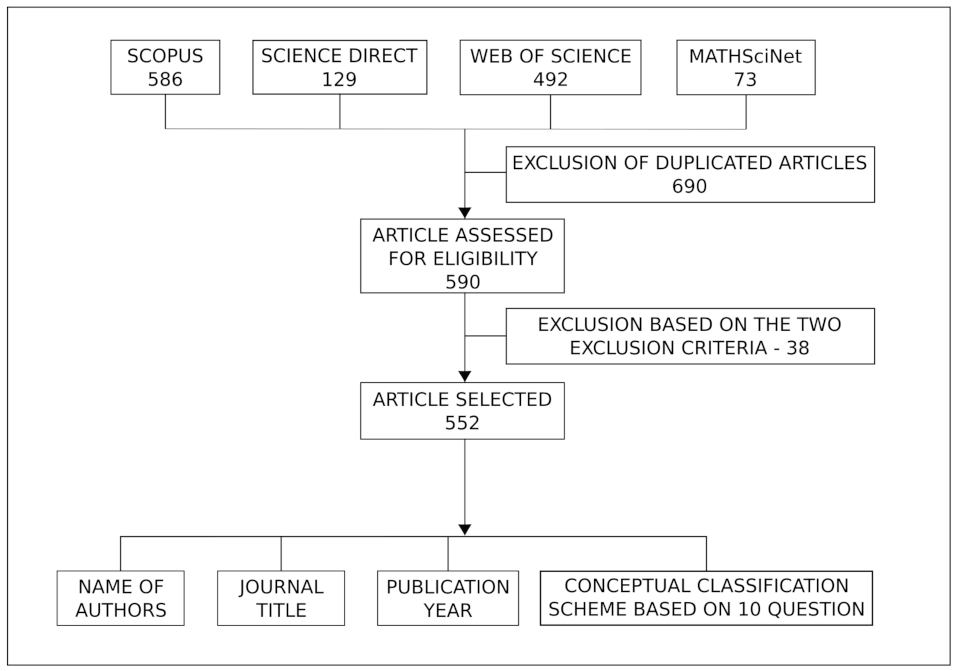
2. Research Methodology
- Search results that were written in English and articles published in peer-reviewed journals available online. We excluded books, dissertations/theses, conference proceedings, and reviews (or any other form that was not an article);
- Articles that specifically implemented Bayesian spatial models, excluding the ones that only mentioned Bayesian spatial models.
- Names of all authors;
- Publication year;
- Journal title;
- Response to the ten items of the conceptual classification scheme on Bayesian spatial models.
3. Conceptual Scheme for Spatial Models
3.1. Spatial Statistics Fields of Application
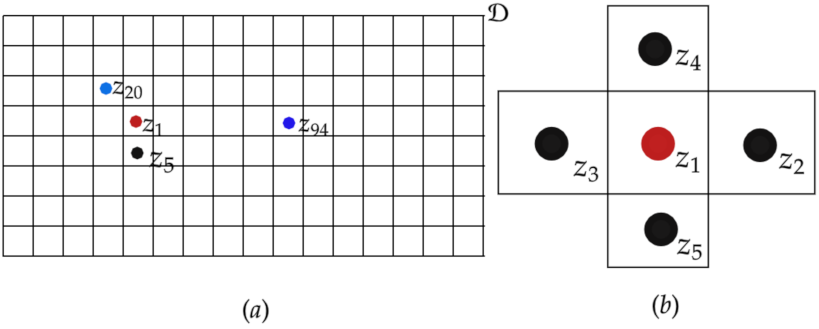
3.2. Spatial Domains
- Area or lattice data: This is a simple way to represent spatial data in the domain . In this type of spatial domain, is a random aggregated realization across an area s of distinct boundaries. For area data, the boundaries are irregular, such as administrative divisions, whereas for the lattice, the boundaries are a regular division of . For simplicity, it may be necessary to aggregate other types of spatial domain realizations to form area or lattice data. This process may sometimes be referred to as a discretization of ;
- Geostatistical or point-reference data: is a realization at a specific location s in a continuous spatial domain . Location s is considered to be a coordinate made up of longitudes and latitudes and sometimes includes altitudes. Location s could also be represented in Cartesian coordinates;
- Spatial point pattern: Realization represents the occurrence or nonoccurrence of an event at location s. In this case, the location itself is considered to be random. The random realization is a location indicator of the presence or absence of a phenomenon of interest in the domain . In agriculture, for example, the interest may be the distribution of a specific tree species, in which each realization is the presence or absence of the tree species in domain . In epidemiology, the realization may be the house address of a patient that has a particular disease [70,71].
3.3. Spatial Priors
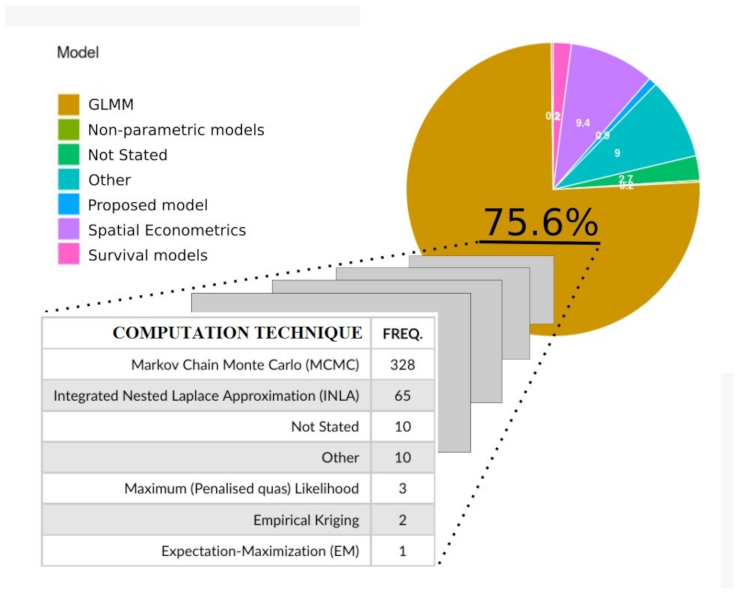
3.4. Computational Techniques
3.5. Simulation Study and Validation
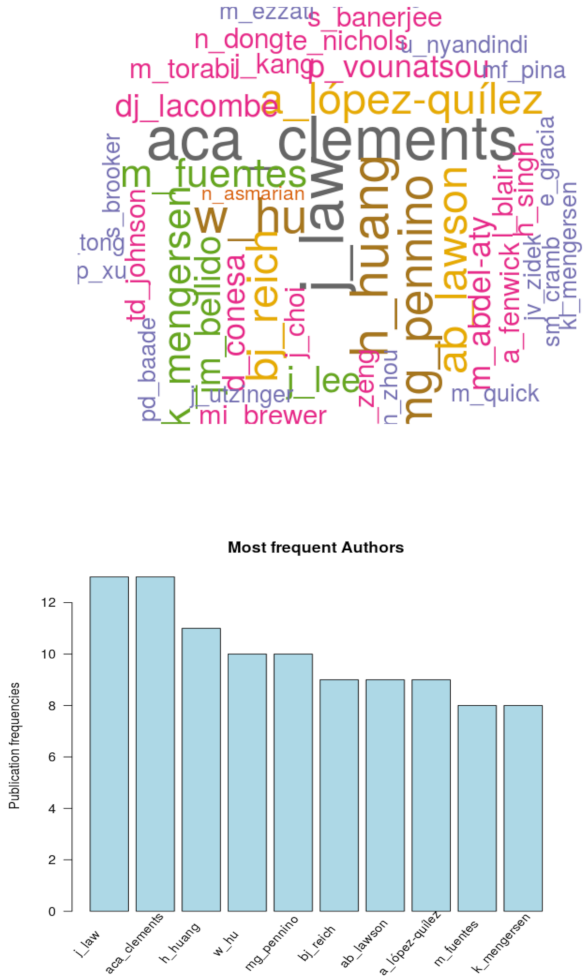
4. Analyses
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1
| QUESTION 1 | Is it only an application? |
| 1.1 | Yes |
| 1.2 | Both |
| 1.3 | No (only method) |
| QUESTION 2 | What is the field of application? |
| 2.1 | Medical science |
| 2.2 | Economics and humanities |
| 2.3 | Physical science and engineering |
| 2.4 | Agricultural and environmental science |
| 2.5 | Sports |
| QUESTION 3 | What spatial domain was employed? |
| 3.1 | Area or lattice |
| 3.2 | Geostatistical data |
| 3.3 | Spatial point patterns |
| 3.4 | Area and geostatistical data |
| QUESTION 4 | What type of spatial priors are used? |
| 4.1 | Conditional Autoregressive (CAR) |
| 4.2 | Besag–York–Mollié (BYM) |
| 4.3 | Leroux CAR |
| 4.4 | Gaussian Markov random field (other specifications) |
| 4.5 | Covariance function (Not GMRF) |
| 4.6 | Other (new methodology/proposed) |
| QUESTION 5 | What type of response variable is used? |
| 5.1 | Discrete (countable) |
| 5.2 | Continuous |
| 5.3 | Combined (mixed) |
| 5.4 | Ordinal |
| QUESTION 6 | What is the statistical model used? |
| 6.1 | Generalize linear (mixed) model (or hierarchical models) |
| 6.2 | Survival and longitudinal models |
| 6.3 | Nonparametric models (machine-learning models) |
| 6.4 | Spatial econometrics |
| 6.5 | Proposed |
| 6.6 | Not stated |
| 6.7 | Other |
| QUESTION 7 | How are model prior specified? |
| 7.1 | Vague prior (noninformative) |
| 7.2 | Used verbatim from the literature |
| 7.3 | Elicited from experts or from the problem |
| 7.4 | No explicit use or reference/not applicable |
| QUESTION 8 | What is the estimation method applied? |
| 8.1 | Markov Chain Monte Carlo (MCMC) |
| 8.2 | Integrated Nested Laplace Approximation (INLA) |
| 8.3 | Expectation–Maximization (EM) |
| 8.4 | Maximum (penalized quasi-) likelihood method |
| 8.5 | Not stated |
| 8.6 | Other |
| QUESTION 9 | Is the model validated through simulation? |
| 9.1 | Yes |
| 9.2 | No |
| QUESTION 10 | Is the application validated through data-driven procedures? |
| 10.1 | Cross-validation and data splitting (K-fold/holdout) |
| 10.2 | Leave-One-Out Cross-Validation (LOOCV) |
| 10.3 | Posterior predictive check |
| 10.4 | Other |
| 10.5 | None or not applicable |
Appendix A.2. Class of the Gaussian Markov Random Field
Appendix A.3. Class of Gaussian Non-Markov Random Field Models
Appendix A.4. Class of Non-Gaussian Random Fields Models
Appendix A.5. Statistical Models
Appendix A.6. Computation Technique
References
- Tao, W. Interdisciplinary urban GIS for smart cities: Advancements and opportunities. Geo-Spat. Inf. Sci. 2013, 16, 25–34. [Google Scholar] [CrossRef]
- Roche, S. Geographic information science II: Less space, more places in smart cities. Prog. Hum. Geogr. 2016, 40, 565–573. [Google Scholar] [CrossRef]
- Marjani, M.; Nasaruddin, F.; Gani, A.; Karim, A.; Hashem, I.A.T.; Siddiqa, A.; Yaqoob, I. Big IoT data analytics: Architecture, opportunities, and open research challenges. IEEE Access 2017, 5, 5247–5261. [Google Scholar]
- Razafimandimby, C.; Loscri, V.; Vegni, A.M.; Neri, A. A Bayesian and smart gateway based communication for noisy IoT scenario. In Proceedings of the 2017 International Conference on Computing, Networking and Communications (ICNC), Silicon Valley, CA, USA, 26–29 January 2017; pp. 481–485. [Google Scholar]
- Harquel, S.; Diard, J.; Raffin, E.; Passera, B.; Dall’Igna, G.; Marendaz, C.; David, O.; Chauvin, A. Automatized set-up procedure for transcranial magnetic stimulation protocols. Neuroimage 2017, 153, 307–318. [Google Scholar] [CrossRef] [Green Version]
- Meincke, J.; Hewitt, M.; Batsikadze, G.; Liebetanz, D. Automated TMS hotspot-hunting using a closed loop threshold-based algorithm. NeuroImage 2016, 124, 509–517. [Google Scholar] [CrossRef]
- Derado, G.; Bowman, F.D.; Zhang, L.; Initiative, A.D.N. Predicting brain activity using a Bayesian spatial model. Stat. Methods Med. Res. 2013, 22, 382–397. [Google Scholar] [CrossRef] [Green Version]
- Kang, J.; Johnson, T.D.; Nichols, T.E.; Wager, T.D. Meta analysis of functional neuroimaging data via Bayesian spatial point processes. J. Am. Stat. Assoc. 2011, 106, 124–134. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kang, S.Y.; Cramb, S.; White, N.; Ball, S.J.; Mengersen, K. Making the most of spatial information in health: A tutorial in Bayesian disease mapping for areal data. Geospat. Health 2016, 11, 190–198. [Google Scholar] [CrossRef] [Green Version]
- Fonseca, V.P.; Pennino, M.G.; de Nóbrega, M.F.; Oliveira, J.E.L.; de Figueiredo Mendes, L. Identifying fish diversity hot-spots in data-poor situations. Mar. Environ. Res. 2017, 129, 365–373. [Google Scholar] [CrossRef]
- Kennedy, M.C.; O’Hagan, A. Bayesian calibration of computer models. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2001, 63, 425–464. [Google Scholar] [CrossRef]
- Higdon, D.; Nakhleh, C.; Gattiker, J.; Williams, B. A Bayesian calibration approach to the thermal problem. Comput. Methods Appl. Mech. Eng. 2008, 197, 2431–2441. [Google Scholar] [CrossRef] [Green Version]
- Romanowski, A.; Grudzien, K.; Williams, R.A. Analysis and interpretation of hopper flow behaviour using electrical capacitance tomography. Part. Part. Syst. Charact. 2006, 23, 297–305. [Google Scholar] [CrossRef]
- Conti, S.; O’Hagan, A. Bayesian emulation of complex multi-output and dynamic computer models. J. Stat. Plan. Inference 2010, 140, 640–651. [Google Scholar] [CrossRef]
- Rappel, H.; Beex, L.A.; Noels, L.; Bordas, S. Identifying elastoplastic parameters with Bayes’ theorem considering output error, input error and model uncertainty. Probabilistic Eng. Mech. 2019, 55, 28–41. [Google Scholar] [CrossRef] [Green Version]
- Ozturk, D.; Kilic, F. Geostatistical approach for spatial interpolation of meteorological data. An. Acad. Bras. Ciências 2016, 88, 2121–2136. [Google Scholar] [CrossRef] [Green Version]
- Lindgren, F.; Rue, H.V.; Lindström, J. An explicit link between Gaussian fields and Gaussian Markov random fields: The stochastic partial differential equation approach. J. R. Stat. Soc. Ser. B Stat. Methodol. 2011, 73, 423–498. [Google Scholar] [CrossRef] [Green Version]
- Knorr-Held, L.; Raßer, G. Bayesian detection of clusters and discontinuities in disease maps. Biometrics 2000, 56, 13–21. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Corpas-Burgos, F.; Martinez-Beneito, M.A. An Autoregressive Disease Mapping Model for Spatio-Temporal Forecasting. Mathematics 2021, 9, 384. [Google Scholar] [CrossRef]
- Griffith, D.A.; Chun, Y. Gis and Spatial Statistics/Econometrics: An Overview; University of Texas at Dallas: Richardson, TX, USA, 2018. [Google Scholar]
- Hernandez-Lemus, E. Random fields in physics, biology and data science. Front. Phys. 2021. [Google Scholar] [CrossRef]
- Aswi, A.; Cramb, S.; Moraga, P.; Mengersen, K. Bayesian spatial and spatiotemporal approaches to modeling dengue fever: A systematic review. Epidemiol. Infect. 2019, 147, e33. [Google Scholar] [CrossRef] [Green Version]
- Duncan, E.W.; White, N.M.; Mengersen, K. Spatial smoothing in Bayesian models: A comparison of weights matrix specifications and their impact on inference. Int. J. Health Geogr. 2017, 16, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Wah, W.; Ahern, S.; Earnest, A. A systematic review of Bayesian spatial–temporal models on cancer incidence and mortality. Int. J. Public Health 2020, 65, 673–682. [Google Scholar] [CrossRef]
- Fisher, R.A. The Design of Experiments; Hafner Publishing Company: New York, NY, USA, 1935. [Google Scholar]
- Ibrahim, J.G.; Chen, M.H.; Gwon, Y.; Chen, F. The power prior: Theory and applications. Stat. Med. 2015, 34, 3724–3749. [Google Scholar] [CrossRef]
- Bachoc, F. Parametric Estimation of Covariance Function in Gaussian-Process Based Kriging Models. Application to Uncertainty Quantification for Computer Experiments. Ph.D. Thesis, Université Paris-Diderot-Paris VII, Paris, France, 2013. [Google Scholar]
- Hutton, B.; Salanti, G.; Caldwell, D.M.; Chaimani, A.; Schmid, C.H.; Cameron, C.; Ioannidis, J.P.; Straus, S.; Thorlund, K.; Jansen, J.P.; et al. The PRISMA extension statement for reporting of systematic reviews incorporating network meta-analyses of health care interventions: Checklist and explanations. Ann. Intern. Med. 2015, 162, 777–784. [Google Scholar] [CrossRef] [Green Version]
- Moher, D.; Liberati, A.; Tetzlaff, J.; Altman, D.G.; Altman, D.; Antes, G.; Atkins, D.; Barbour, V.; Barrowman, N.; Berlin, J.A.; et al. Preferred reporting items for systematic reviews and meta-analyses: The PRISMA statement (Chinese edition). J. Chin. Integr. Med. 2009, 7, 889–896. [Google Scholar] [CrossRef]
- Hsieh, H.F.; Shannon, S.E. Three approaches to qualitative content analysis. Qual. Health Res. 2005, 15, 1277–1288. [Google Scholar] [CrossRef]
- Lee, D.; Mitchell, R. Boundary detection in disease mapping studies. Biostatistics 2012, 13, 415–426. [Google Scholar] [CrossRef] [Green Version]
- Riley, S.; Eames, K.; Isham, V.; Mollison, D.; Trapman, P. Five challenges for spatial epidemic models. Epidemics 2015, 10, 68–71. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karimi, O.; Mohammadzadeh, M. Bayesian spatial regression models with closed skew normal correlated errors and missing observations. Stat. Pap. 2012, 53, 205–218. [Google Scholar] [CrossRef]
- Berliner, L.M. Spatial Statistical Methods. Int. Encycl. Soc. Behav. Sci. 2015, 23, 191–197. [Google Scholar]
- Isard, W. The general theory of location and space-economy. Q. J. Econ. 1949, 63, 476–506. [Google Scholar] [CrossRef]
- Sparks, P.J.; Sparks, C.S.; Campbell, J.J. An application of Bayesian spatial statistical methods to the study of racial and poverty segregation and infant mortality rates in the US. GeoJournal 2013, 78, 389–405. [Google Scholar] [CrossRef]
- Krige, D. Lognormal-de Wijsian Geostatistics for Ore Evaluation; South African Institute of Mining and Metallurgy: Johannesburg, South Africa, 1978. [Google Scholar]
- Gracia, E.; López-Quílez, A.; Marco, M.; Lladosa, S.; Lila, M. The Spatial Epidemiology of Intimate Partner Violence: Do Neighborhoods Matter? Am. J. Epidemiol. 2015, 182, 58–66. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luan, H.; Law, J.; Lysy, M. Diving into the consumer nutrition environment: A Bayesian spatial factor analysis of neighborhood restaurant environment. Spat. Spatio-Temporal Epidemiol. 2018, 24, 39–51. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Morris, R.S. Diseases, dilemmas, decisions—Converting epidemiological dilemmas into successful disease control decisions. Prev. Vet. Med. 2015, 122, 242–252. [Google Scholar] [CrossRef] [PubMed]
- Müller, I.; Betuela, I.; Hide, R. Regional patterns of birthweights in Papua New Guinea in relation to diet, environment and socio-economic factors. Ann. Hum. Biol. 2002, 29, 74–88. [Google Scholar] [CrossRef]
- Short, M.; Carlin, B.P.; Bushhouse, S. Using hierarchical spatial models for cancer control planning in Minnesota (United States). Cancer Causes Control CCC 2002, 13, 903–916. [Google Scholar] [CrossRef]
- Ward, M. Spatial Epidemiology: Where Have We come in 150 Years? In Geospatial Technologies and Homeland Security; The GeoJournal Library: Dordrecht, The Netherlands, 2008; Volume 94, pp. 257–282. [Google Scholar]
- Da Silva-Buttkus, P.; Marcelli, G.; Franks, S.; Stark, J.; Hardy, K. Inferring biological mechanisms from spatial analysis: Prediction of a local inhibitor in the ovary. Proc. Natl. Acad. Sci. USA 2009, 106, 456–461. [Google Scholar] [CrossRef] [Green Version]
- Arpòn, J.; Sakai, K.; Gaudin, V.; Andrey, P. Spatial modeling of biological patterns shows multiscale organization of Arabidopsis thaliana heterochromatin. Sci. Rep. 2021, 11, 1–17. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, M.; Xie, Y.; Xiao, G. Bayesian Modeling of Spatial Molecular Profiling Data via Gaussian Process. arXiv 2020, arXiv:2012.03326. [Google Scholar] [CrossRef]
- Adegboye, O.A.; Adekunle, A.I.; Pak, A.; Gayawan, E.; Leung, D.H.; Rojas, D.P.; Elfaki, F.; McBryde, E.S.; Eisen, D.P. Change in outbreak epicentre and its impact on the importation risks of COVID-19 progression: A modeling study. Travel Med. Infect. Dis. 2021, 40, 101988. [Google Scholar] [CrossRef] [PubMed]
- Saavedra, P.; Santana, A.; Bello, L.; Pacheco, J.M.; Sanjuán, E. A Bayesian spatiotemporal analysis of mortality rates in Spain: Application to the COVID-19 2020 outbreak. Popul. Health Metrics 2021, 19, 1–10. [Google Scholar] [CrossRef]
- Clements, A.C.; Lwambo, N.J.; Blair, L.; Nyandindi, U.; Kaatano, G.; Kinung’hi, S.; Webster, J.P.; Fenwick, A.; Brooker, S. Bayesian spatial analysis and disease mapping: Tools to enhance planning and implementation of a schistosomiasis control programme in Tanzania. Trop. Med. Int. Health 2006, 11, 490–503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huertas, I.; Oldehinkel, M.; van Oort, E.S.; Garcia-Solis, D.; Mir, P.; Beckmann, C.F.; Marquand, A.F. A Bayesian spatial model for neuroimaging data based on biologically informed basis functions. NeuroImage 2017, 161, 134–148. [Google Scholar] [CrossRef]
- Benassi, F.; Naccarato, A. Households in potential economic distress. A geographically weighted regression model for Italy, 2001–2011. Spat. Stat. 2017, 21, 362–376. [Google Scholar] [CrossRef]
- Simões, P.; Carvalho, M.; Aleixo, S.; Gomes, S.; Natário, I. A spatial econometric analysis of the calls to the portuguese national health line. Econometrics 2017, 5, 24. [Google Scholar] [CrossRef] [Green Version]
- Osama, A.; Sayed, T. A novel approach for identifying, diagnosing, and treating active transportation safety issues. Transp. Res. Rec. 2019, 2673, 813–823. [Google Scholar] [CrossRef]
- Law, J.; Quick, M.; Jadavji, A. A Bayesian spatial shared component model for identifying crime-general and crime-specific hotspots. Ann. GIS 2020, 26, 65–79. [Google Scholar] [CrossRef] [Green Version]
- Potter, J.E.; Schmertmann, C.P.; Assunção, R.M.; Cavenaghi, S.M. Mapping the timing, pace, and scale of the fertility transition in Brazil. Popul. Dev. Rev. 2010, 36, 283–307. [Google Scholar] [CrossRef] [Green Version]
- Gregory, A.; Lau, F.D.H.; Girolami, M.; Butler, L.J.; Elshafie, M.Z. The synthesis of data from instrumented structures and physics-based models via Gaussian processes. J. Comput. Phys. 2019, 392, 248–265. [Google Scholar] [CrossRef] [Green Version]
- Rappel, H.; Wu, L.; Noels, L.; Beex, L.A. A Bayesian framework to identify random parameter fields based on the copula theorem and Gaussian fields: Application to polycrystalline materials. J. Appl. Mech. 2019, 86, 121009. [Google Scholar] [CrossRef]
- Koutsourelakis, P.S. A multi-resolution, nonparametric, Bayesian framework for identification of spatially-varying model parameters. J. Comput. Phys. 2009, 228, 6184–6211. [Google Scholar] [CrossRef] [Green Version]
- Koutsourelakis, P.S. A novel Bayesian strategy for the identification of spatially varying material properties and model validation: An application to static elastography. Int. J. Numer. Methods Eng. 2012, 91, 249–268. [Google Scholar] [CrossRef] [Green Version]
- Sharkey, P.; Winter, H.C. A Bayesian spatial hierarchical model for extreme precipitation in Great Britain. Environmetrics 2019, 30, e2529. [Google Scholar] [CrossRef] [Green Version]
- Robinson, N.; Rampant, P.; Callinan, A.; Rab, M.; Fisher, P. Advances in precision agriculture in south-eastern Australia. II. Spatio-temporal prediction of crop yield using terrain derivatives and proximally sensed data. Crop Pasture Sci. 2009, 60, 859–869. [Google Scholar] [CrossRef]
- Yousefi, K.; Swartz, T.B. Advanced putting metrics in golf. J. Quant. Anal. Sport. 2013, 9, 239–248. [Google Scholar] [CrossRef] [Green Version]
- Woods, J. Two-dimensional discrete Markovian fields. IEEE Trans. Inf. Theory 1972, 18, 232–240. [Google Scholar] [CrossRef]
- Besag, J. Spatial interaction and the statistical analysis of lattice systems. J. R. Stat. Soc. Ser. B (Methodol. 1974, 36, 192–225. [Google Scholar] [CrossRef]
- El-Baz, A.; Farag, A.A. Image segmentation using GMRF models: Parameters estimation and applications. In Proceedings of the Proceedings 2003 International Conference on Image Processing (Cat. No. 03CH37429), Barcelona, Spain, 14–17 September 2003; Volume 2, pp. II–177. [Google Scholar] [CrossRef]
- Sidén, P.; Lindsten, F. Deep gaussian markov random fields. In Proceedings of the International Conference on Machine Learning PMLR, Virtual Event, 12–18 July 2020; pp. 8916–8926. [Google Scholar]
- Vemulapalli, R.; Tuzel, O.; Liu, M.Y. Deep gaussian conditional random field network: A model-based deep network for discriminative denoising. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4801–4809. [Google Scholar]
- Lee, J.; Bahri, Y.; Novak, R.; Schoenholz, S.S.; Pennington, J.; Sohl-Dickstein, J. Deep neural networks as gaussian processes. arXiv 2017, arXiv:1711.00165. [Google Scholar]
- Blangiardo, M.; Cameletti, M. Spatial and Spatiotemporal Bayesian Models with R-INLA; John Wiley and Sons, Ltd.: Hoboken, NJ, USA, 2015. [Google Scholar]
- Banerjee, S.; Carlin, B.; Gelfand, A. Hierarchical Modelling and Analysis of Spatial Data; Monographs on Statistics and Applied Probability; Chapman and Hall: New York, NY, USA, 2004. [Google Scholar]
- Cressie, N. Statistics for Spatial Data; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Munoz, F.; Pennino, M.G.; Conesa, D.; López-Quílez, A.; Bellido, J.M. Estimation and prediction of the spatial occurrence of fish species using Bayesian latent Gaussian models. Stoch. Environ. Res. Risk Assess. 2013, 27, 1171–1180. [Google Scholar] [CrossRef]
- Leininger, T.J.; Gelfand, A.E. Bayesian inference and model assessment for spatial point patterns using posterior predictive samples. Bayesian Anal. 2017, 12, 1–30. [Google Scholar] [CrossRef]
- Rue, H.v.; Tjelmeland, H.k. Fitting Gaussian Markov random fields to Gaussian fields. Scand. J. Statistics. Theory Appl. 2002, 29, 31–49. [Google Scholar] [CrossRef]
- Walker, M.; Curtis, A. Eliciting spatial statistics from geological experts using genetic algorithms. Geophys. J. Int. 2014, 198, 342–356. [Google Scholar] [CrossRef] [Green Version]
- Moala, F.A.; O’Hagan, A. Elicitation of multivariate prior distributions: A nonparametric Bayesian approach. J. Stat. Plan. Inference 2010, 140, 1635–1655. [Google Scholar] [CrossRef]
- Ordoñez, J.A.; Prates, M.O.; Matos, L.A.; Lachos, V.H. Objective Bayesian analysis for spatial Student-t regression models. arXiv 2020, arXiv:math.ST/2004.04341. [Google Scholar]
- Simpson, D.; Rue, H.v.; Riebler, A.; Martins, T.G.; Sø rbye, S.H. Penalising model component complexity: A principled, practical approach to constructing priors. Stat. Sci. A Rev. J. Inst. Math. Stat. 2017, 32, 1–28. [Google Scholar] [CrossRef]
- Rue, H.; Martino, S.; Chopin, N. Approximate Bayesian inference for latent Gaussian models by using integrated nested Laplace approximations. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2009, 71, 319–392. [Google Scholar] [CrossRef]
- Besag, J.; York, J.; Mollié, A. Bayesian image restoration, with two applications in spatial statistics. J. R. Stat. Soc. Ser. B (Methodol.) 1991, 43, 1–59. [Google Scholar] [CrossRef]
- Leroux, B.G.; Lei, X.; Breslow, N. Estimation of disease rates in small areas: A new mixed model for spatial dependence. In Statistical Models in Epidemiology, the Environment, and Clinical Trials; Springer: Berlin/Heidelberg, Germany, 2000; pp. 179–191. [Google Scholar]
- Lee, D.J.; Durbán, M. Smooth-CAR mixed models for spatial count data. Comput. Stat. Data Anal. 2009, 53, 2968–2979. [Google Scholar] [CrossRef] [Green Version]
- Dean, C.; Ugarte, M.; Militino, A. Detecting interaction between random region and fixed age effects in disease mapping. Biometrics 2001, 57, 197–202. [Google Scholar] [CrossRef] [PubMed]
- Green, P.J.; Richardson, S. Hidden Markov models and disease mapping. J. Am. Stat. Assoc. 2002, 97, 1055–1070. [Google Scholar] [CrossRef]
- Kozubowski, T.; Podgorski, K. A multivariate and asymmetric generalization of Laplace distribution. Comput. Stat. 2000, 15, 531–540. [Google Scholar] [CrossRef]
- Fonseca, T.C.O.; Ferreira, M.A.R.; Migon, H.S. Objective Bayesian analysis for the Student-t regression model [erratum to MR2521587]. Biometrika 2014, 101, 252. [Google Scholar] [CrossRef]
- Bradley, J.R.; Holan, S.H.; Wikle, C.K. Computationally efficient multivariate spatiotemporal models for high-dimensional count-valued data (with discussion). Bayesian Anal. 2018, 13, 253–310. [Google Scholar] [CrossRef]
- Gelfand, A.E.; Kottas, A.; MacEachern, S.N. Bayesian nonparametric spatial modeling with Dirichlet process mixing. J. Am. Stat. Assoc. 2005, 100, 1021–1035. [Google Scholar] [CrossRef]
- Obaromi, D. Spatial modeling of some conditional autoregressive priors in a disease mapping model: The Bayesian approach. Biomed. J. Sci. Tech. Res. 2019, 14. [Google Scholar]
- Egbon, O.A.; Somo-Aina, O.; Gayawan, E. Spatial Weighted Analysis of Malnutrition Among Children in Nigeria: A Bayesian Approach. Stat. Biosci. 2021, 13, 495–523. [Google Scholar] [CrossRef]
- Fontanella, L.; Ippoliti, L.; Sarra, A.; Valentini, P.; Palermi, S. Hierarchical generalised latent spatial quantile regression models with applications to indoor radon concentration. Stoch. Environ. Res. Risk Assess. 2015, 29, 357–367. [Google Scholar] [CrossRef]
- Nott, D.J.; Seah, M.; Al-Labadi, L.; Evans, M.; Ng, H.K.; Englert, B.G. Using prior expansions for prior-data conflict checking. Bayesian Anal. 2021, 16, 203–231. [Google Scholar] [CrossRef]
- Egidi, L.; Pauli, F.; Torelli, N. Avoiding prior–data conflict in regression models via mixture priors. Can. J. Stat. 2021. [Google Scholar] [CrossRef]
- Staubach, C.; Schmid, V.; Knorr-Held, L.; Ziller, M. A Bayesian model for spatial wildlife disease prevalence data. Prev. Vet. Med. 2002, 56, 75–87. [Google Scholar] [CrossRef] [Green Version]
- Teerapabolarn, K.; Jaioun, K. Approximation of binomial distribution by an improved poisson distribution. Int. J. Pure Appl. Math. 2014, 97, 491–495. [Google Scholar] [CrossRef]
- Burr, I.W. Some approximate relations between terms of the hypergeometric, binomial and Poisson distributions. Commun. Stat.-Theory Methods 1973, 1, 297–301. [Google Scholar]
- Alexander, N.; Moyeed, R.; Stander, J. Spatial modeling of individual-level parasite counts using the negative binomial distribution. Biostatistics 2000, 1, 453–463. [Google Scholar] [CrossRef] [PubMed]
- Krisztin, T.; Piribauer, P.; Wögerer, M. A spatial multinomial logit model for analysing urban expansion. Spat. Econ. Anal. 2021, 1–22. [Google Scholar] [CrossRef]
- Kwak, S.G.; Kim, J.H. Central limit theorem: The cornerstone of modern statistics. Korean J. Anesthesiol. 2017, 70, 144. [Google Scholar] [CrossRef]
- Aswi, A.; Cramb, S.; Duncan, E.; Hu, W.; White, G.; Mengersen, K. Bayesian spatial survival models for hospitalisation of Dengue: A case study of Wahidin hospital in Makassar, Indonesia. Int. J. Environ. Res. Public Health 2020, 17, 878. [Google Scholar] [CrossRef] [Green Version]
- Palacios, M.B.; Steel, M.F.J. Non-gaussian bayesian geostatistical modeling. J. Am. Stat. Assoc. 2006, 101, 604–618. [Google Scholar] [CrossRef]
- Kibria, B.G.; Sun, L.; Zidek, J.V.; Le, N.D. Bayesian spatial prediction of random space-time fields with application to mapping PM2. 5 exposure. J. Am. Stat. Assoc. 2002, 97, 112–124. [Google Scholar] [CrossRef]
- Fragoso, T.M.; Bertoli, W.; Louzada, F. Bayesian model averaging: A systematic review and conceptual classification. Int. Stat. Review. Rev. Int. De Stat. 2018, 86, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Sun, W.; Le, N.D.; Zidek, J.V.; Burnett, R. Assessment of a Bayesian multivariate interpolation approach for health impact studies. Environmetr. Off. J. Int. Environmetr. Soc. 1998, 9, 565–586. [Google Scholar] [CrossRef]
- Neill, D.; Moore, A.; Cooper, G. A Bayesian spatial scan statistic. Adv. Neural Inf. Process. Syst. 2005, 18, 1003–1010. [Google Scholar]
- Morris, T.P.; White, I.R.; Crowther, M.J. Using simulation studies to evaluate statistical methods. Stat. Med. 2019, 38, 2074–2102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gelman, A.; Meng, X.L.; Stern, H. Posterior predictive assessment of model fitness via realized discrepancies. Stat. Sin. 1996, 733–760. [Google Scholar]
- Akseer, N.; Bhatti, Z.; Mashal, T.; Soofi, S.; Moineddin, R.; Black, R.E.; Bhutta, Z.A. Geospatial inequalities and determinants of nutritional status among women and children in Afghanistan: An observational study. Lancet Glob. Health 2018, 6, e447–e459. [Google Scholar] [CrossRef]
- Gelfand, A.E.; Diggle, P.; Guttorp, P.; Fuentes, M. Handbook of Spatial Statistics; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Taniguchi, A.; Hagiwara, Y.; Taniguchi, T.; Inamura, T. Online spatial concept and lexical acquisition with simultaneous localization and mapping. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 811–818. [Google Scholar]
- Song, Y.; Nathoo, F.; Babul, A. A Potts-mixture spatiotemporal joint model for combined magnetoencephalography and electroencephalography data. Can. J. Stat. 2019, 47, 688–711. [Google Scholar] [CrossRef]
- Taschler, B.; Ge, T.; Bendfeldt, K.; Müller-Lenke, N.; Johnson, T.D.; Nichols, T.E. Spatial modeling of multiple sclerosis for disease subtype prediction. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin/Heidelberg, Germany, 2014; pp. 797–804. [Google Scholar]
- Hachicha, W.; Ghorbel, A. A survey of control-chart pattern-recognition literature (1991–2010) based on a new conceptual classification scheme. Comput. Ind. Eng. 2012, 63, 204–222. [Google Scholar] [CrossRef]
- Rue, H.v.; Held, L. Gaussian Markov Random Fields: Theory and Applications; Chapman and Hall/CRC: London, UK, 2005. [Google Scholar]
- Freni-Sterrantino, A.; Ventrucci, M.; Rue, H. A note on intrinsic conditional autoregressive models for disconnected graphs. Spat. Spatio-Temporal Epidemiol. 2018, 26, 25–34. [Google Scholar] [CrossRef] [Green Version]
- Lee, D. A comparison of conditional autoregressive models used in Bayesian disease mapping. Spat. Spatio-Temporal Epidemiol. 2011, 2, 79–89. [Google Scholar] [CrossRef]
- Cramb, S.; Duncan, E.; Baade, P.; Mengersen, K. Investigation of Bayesian Spatial Models; Cancer Council Queensland and Queensland University of Technology (QUT): Brisbane City, Australia, 2017. [Google Scholar]
- Lee, D.; Mitchell, R. Locally adaptive spatial smoothing using conditional auto-regressive models. J. R. Stat. Soc. Ser. C Appl. Stat. 2013, 62, 593–608. [Google Scholar] [CrossRef]
- Lee, D.; Rushworth, A.; Sahu, S.K. A Bayesian localized conditional autoregressive model for estimating the health effects of air pollution. Biometrics 2014, 70, 419–429. [Google Scholar] [CrossRef] [Green Version]
- Griffith, D.A. Selected challenges from spatial statistics for spatial econometricians. Comp. Econ. Res. 2012, 15, 71–85. [Google Scholar] [CrossRef]
- Sun, X.; He, Z.; Kabrick, J. Bayesian spatial prediction of the site index in the study of the Missouri Ozark Forest Ecosystem Project. Comput. Stat. Data Anal. 2008, 52, 3749–3764. [Google Scholar] [CrossRef] [Green Version]
- Karimi, O.; Mohammadzadeh, M. Bayesian spatial prediction for discrete closed skew Gaussian random field. Math. Geosci. 2011, 43, 565–582. [Google Scholar] [CrossRef]
- Rivaz, F. Optimal network design for Bayesian spatial prediction of multivariate non-Gaussian environmental data. J. Appl. Stat. 2016, 43, 1335–1348. [Google Scholar] [CrossRef]
- Lum, K.; Gelfand, A.E. Spatial quantile multiple regression using the asymmetric Laplace process. Bayesian Anal. 2012, 7, 235–258. [Google Scholar] [CrossRef]
- Hu, G.; Bradley, J. A Bayesian spatial-temporal model with latent multivariate log-gamma random effects with application to earthquake magnitudes. Stat 2018, 7, e179. [Google Scholar] [CrossRef]
- Yang, H.C.; Hu, G.; Chen, M.H. Bayesian Variable Selection for Pareto Regression Models with Latent Multivariate Log Gamma Process with Applications to Earthquake Magnitudes. Geosciences 2019, 9, 169. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schemmer, R.C.; Uribe-Opazo, M.A.; Galea, M.; Assumpção, R.A.B. Spatial variability of soybean yield through a reparameterized t-student model. Eng. Agrícola 2007, 37, 760–770. [Google Scholar] [CrossRef] [Green Version]
- Best, N.; Richardson, S.; Thomson, A. A comparison of Bayesian spatial models for disease mapping. Stat. Methods Med Res. 2005, 14, 35–59. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Wang, X.; Liang, F.; Yi, F.; Xie, Y.; Gazdar, A.; Xiao, G. A Bayesian hidden Potts mixture model for analyzing lung cancer pathology images. Biostatistics 2019, 20, 565–581. [Google Scholar] [CrossRef]
- Ferguson, T.S. A Bayesian analysis of some nonparametric problems. Ann. Stat. 1973, 1, 209–230. [Google Scholar] [CrossRef]
- Antoniak, C.E. Mixtures of Dirichlet processes with applications to Bayesian nonparametric problems. Ann. Stat. 1974, 2, 1152–1174. [Google Scholar] [CrossRef]
- MacEachern, S.N. Dependent Dirichlet Process; Technical Report; Ohio State University, Dept of Statistics: Columbus, OH, USA, 2000. [Google Scholar]
- Dey, D.K.; Ghosh, S.K.; Mallick, B.K. Generalized Linear Models: A Bayesian Perspective; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Fahrmeir, L.; Tutz, G. Multivariate Statistical Modelling Based on Generalized Linear Models; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Dasgupta, P.; Cramb, S.M.; Aitken, J.F.; Turrell, G.; Baade, P.D. Comparing multilevel and Bayesian spatial random effects survival models to assess geographical inequalities in colorectal cancer survival: A case study. Int. J. Health Geogr. 2014, 13, 36. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Onicescu, G.; Lawson, A.B. Bayesian cure-rate survival model with spatially structured censoring. Spat. Stat. 2018, 28, 352–364. [Google Scholar] [CrossRef] [PubMed]
- Jensen, C.D.; Lacombe, D.J.; McIntyre, S.G. A Bayesian spatial econometric analysis of the 2010 UK General Election. Pap. Reg. Sci. 2013, 92, 651–666. [Google Scholar] [CrossRef]
- LeSage, J.P. An Introduction to Spatial Econometrics; Chapman and Hall/CRC: London, UK, 2008. [Google Scholar]
- Neill, D.B.; Moore, A.W.; Cooper, G.F. A Bayesian spatial scan statistic. In Advances in Neural Information Processing Systems; MIT Press: Vancouver, BC, Canada, 2006; pp. 1003–1010. [Google Scholar]
- Pilz, J.; Kazianka, H.; Spöck, G. Some advances in Bayesian spatial prediction and sampling design. Spat. Stat. 2012, 1, 65–81. [Google Scholar] [CrossRef]
- Porto, E.D.; Revelli, F. Tax-limited reaction functions. J. Appl. Econom. 2013, 28, 823–839. [Google Scholar] [CrossRef] [Green Version]
- Yu, J.; De Jong, R.; Lee, L.f. Quasi-maximum likelihood estimators for spatial dynamic panel data with fixed effects when both n and T are large. J. Econom. 2008, 146, 118–134. [Google Scholar] [CrossRef] [Green Version]
- Su, L.; Yang, Z. QML estimation of dynamic panel data models with spatial errors. J. Econom. 2015, 185, 230–258. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B (Methodol.) 1977, 39, 1–22. [Google Scholar]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970. [Google Scholar] [CrossRef]
- Tierney, L.; Kadane, J.B. Accurate approximations for posterior moments and marginal densities. J. Am. Stat. Assoc. 1986, 81, 82–86. [Google Scholar] [CrossRef]
- Blangiardo, M.; Cameletti, M.; Baio, G.; Rue, H. Spatial and spatiotemporal models with R-INLA. Spat. Spatio-Temporal Epidemiol. 2013, 4, 33–49. [Google Scholar] [CrossRef] [PubMed] [Green Version]


| Spatial Smoothing | Gaussian Process | Non-Gaussian Process | ||||||
|---|---|---|---|---|---|---|---|---|
| Spatial Model | Article | Global | Local | GMRF | Non-GMRF | Parametric | Semiparametric | Nonparametric |
| CAR dissimilarity | Lee and Mitchell, 2012 [31] | ✔ | ✔ | ✔ | ||||
| Intrinsic CAR/BYM | Besag et al., 1991 [80] | ✔ | ✔ | ✔ | ||||
| Proper CAR | Besag, 1974 [64] | ✔ | ✔ | ✔ | ||||
| Leroux | Leroux et al., 2000 [81] | ✔ | ✔ | ✔ | ||||
| Geostatistical | Clements et al., 2006 [49] | ✔ | ✔ | ✔ | ||||
| Globalspline | Lee and Durbán (2009) [82] | ✔ | ✔ | ✔ | ||||
| Simpson CAR | Simpson et al. [78] | ✔ | ✔ | ✔ | ||||
| Dean’s CAR | Dean et al. [83] | ✔ | ✔ | ✔ | ||||
| SPDE | Lindgren, Rue and Lindström, 2011 [17] | ✔ | ✔ | ✔ | ||||
| Mixture Model | Green and Richardson [84] | ✔ | ✔ | ✔ | ||||
| Spatial Partition Model | Leonhard and Raßer [18] | ✔ | ✔ | ✔ | ||||
| Asymmetric Laplace | Kuzobowski and Pogorski [85] | ✔ | ✔ | ✔ | ||||
| Student-t | Fonseca [86] | ✔ | ✔ | ✔ | ||||
| Log-Gamma | Bradley et al. [87] | ✔ | ✔ | ✔ | ||||
| Dirichlet | Gelfand et al., 2005 [88] | ✔ | ✔ | ✔ | ||||
| GLMM | Nonparametric | Spatial Autoregressive | Proposed | Survival Models | Not Stated | Other | Total | |
|---|---|---|---|---|---|---|---|---|
| Conditional Autoregressive models (CARs) | 227 | 1 | 1 | 0 | 9 | 4 | 3 | 245 |
| Non-Gaussian Markov Random Field (non-GMRF) | 101 | 0 | 49 | 5 | 1 | 1 | 16 | 173 |
| Gaussian Markov Random Field (GMRF) | 19 | 0 | 0 | 0 | 0 | 0 | 3 | 22 |
| Stochastic Partial Differential Equations (SPDE) | 20 | 0 | 0 | 0 | 0 | 0 | 0 | 20 |
| Nonparametric | 4 | 0 | 0 | 0 | 0 | 1 | 2 | 7 |
| Not Stated | 30 | 0 | 2 | 0 | 0 | 9 | 4 | 45 |
| New Methodology | 17 | 0 | 0 | 0 | 0 | 0 | 23 | 40 |
| Total | 418 | 1 | 52 | 5 | 10 | 15 | 51 | 552 |
| Prior Specified | Freq. |
|---|---|
| Elicited from experts or from the problem | 168 |
| No explicit use or reference/not applicable | 101 |
| Used verbatim from the literature | 166 |
| Vague prior (noninformative) | 119 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Louzada, F.; Nascimento, D.C.d.; Egbon, O.A. Spatial Statistical Models: An Overview under the Bayesian Approach. Axioms 2021, 10, 307. https://doi.org/10.3390/axioms10040307
Louzada F, Nascimento DCd, Egbon OA. Spatial Statistical Models: An Overview under the Bayesian Approach. Axioms. 2021; 10(4):307. https://doi.org/10.3390/axioms10040307
Chicago/Turabian StyleLouzada, Francisco, Diego Carvalho do Nascimento, and Osafu Augustine Egbon. 2021. "Spatial Statistical Models: An Overview under the Bayesian Approach" Axioms 10, no. 4: 307. https://doi.org/10.3390/axioms10040307
APA StyleLouzada, F., Nascimento, D. C. d., & Egbon, O. A. (2021). Spatial Statistical Models: An Overview under the Bayesian Approach. Axioms, 10(4), 307. https://doi.org/10.3390/axioms10040307








