Multi-Asset Barrier Options Pricing by Collocation BEM (with Matlab® Code)
Abstract
:1. Introduction to the Differential Model Problem
- , for Basket options with weights ;
- for different kinds of Rainbow options,n-color better-of optiontwo-color worse-of optionoutperformance optionmin option
- , for spread option
2. Integral Representation Formula of the Solution for Options without Barriers
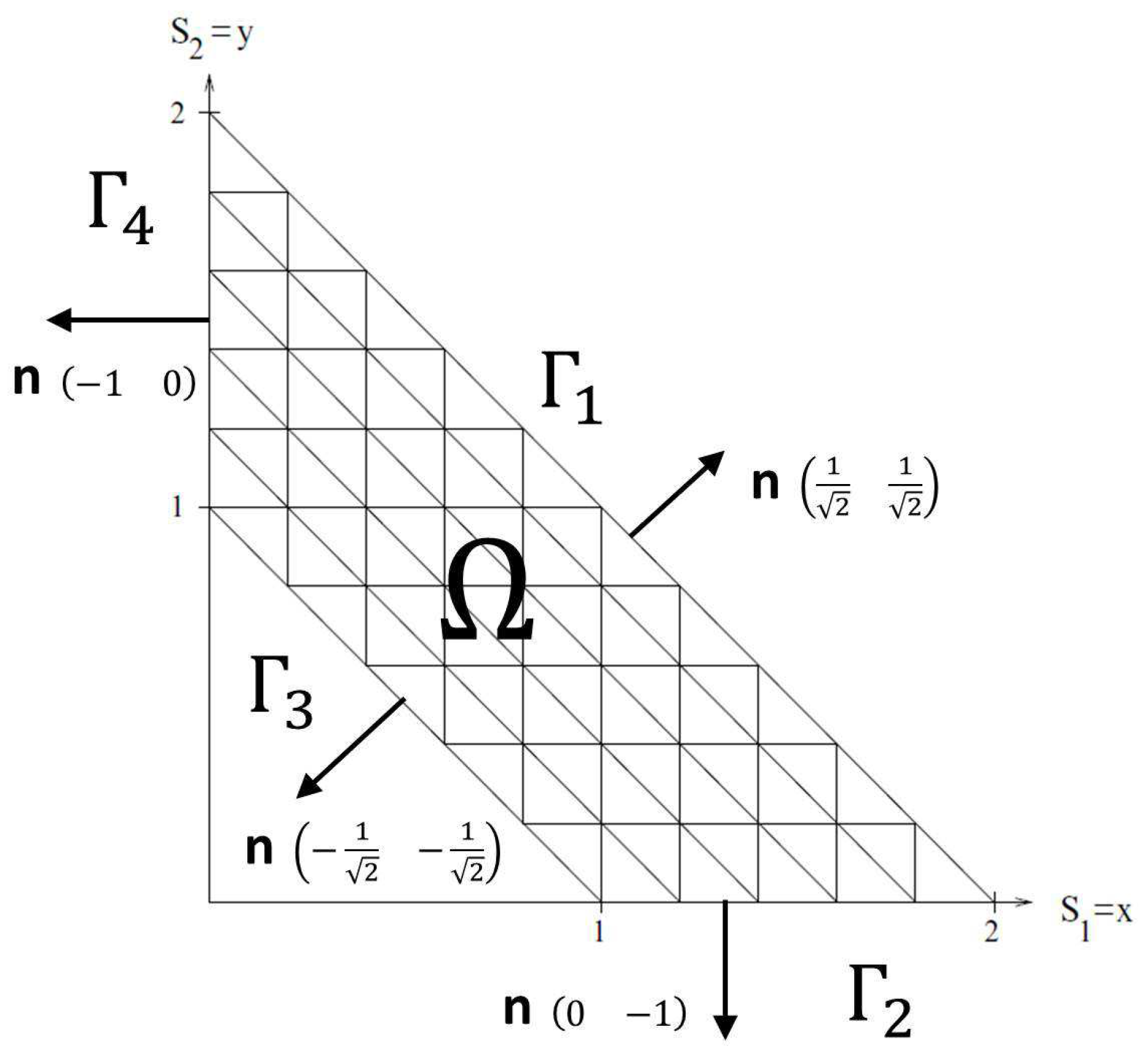
3. Integral Representation Formula of the Solution for Barrier Options
4. Boundary Integral Equation
5. Numerical Approximation by Collocation BEM
- piecewise constant functions in timedefined by the Heaviside functions on a uniform decomposition of the time interval :
- piecewise constant functions in space , defined on a decomposition on and on constituted by segments such that with if .
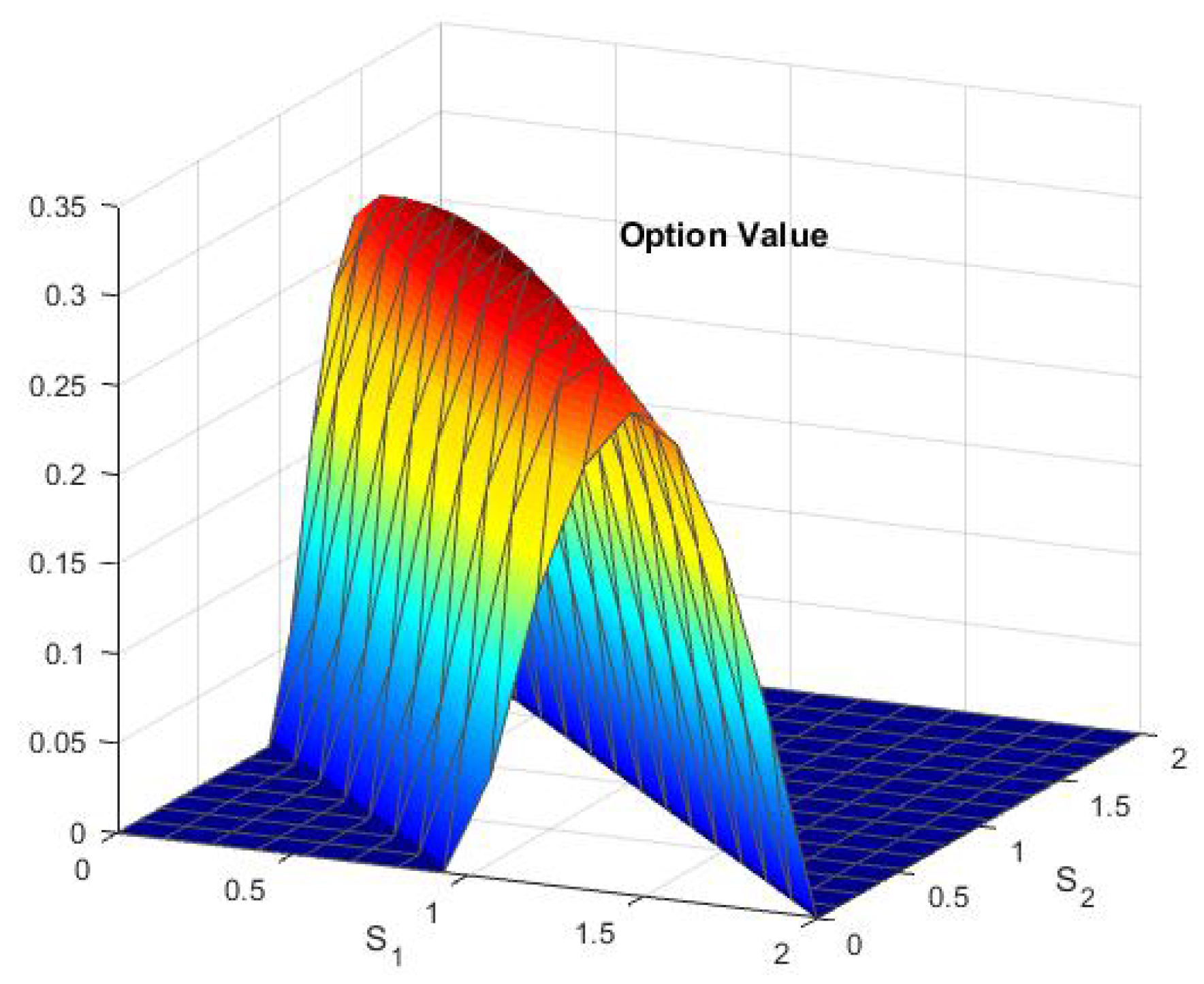
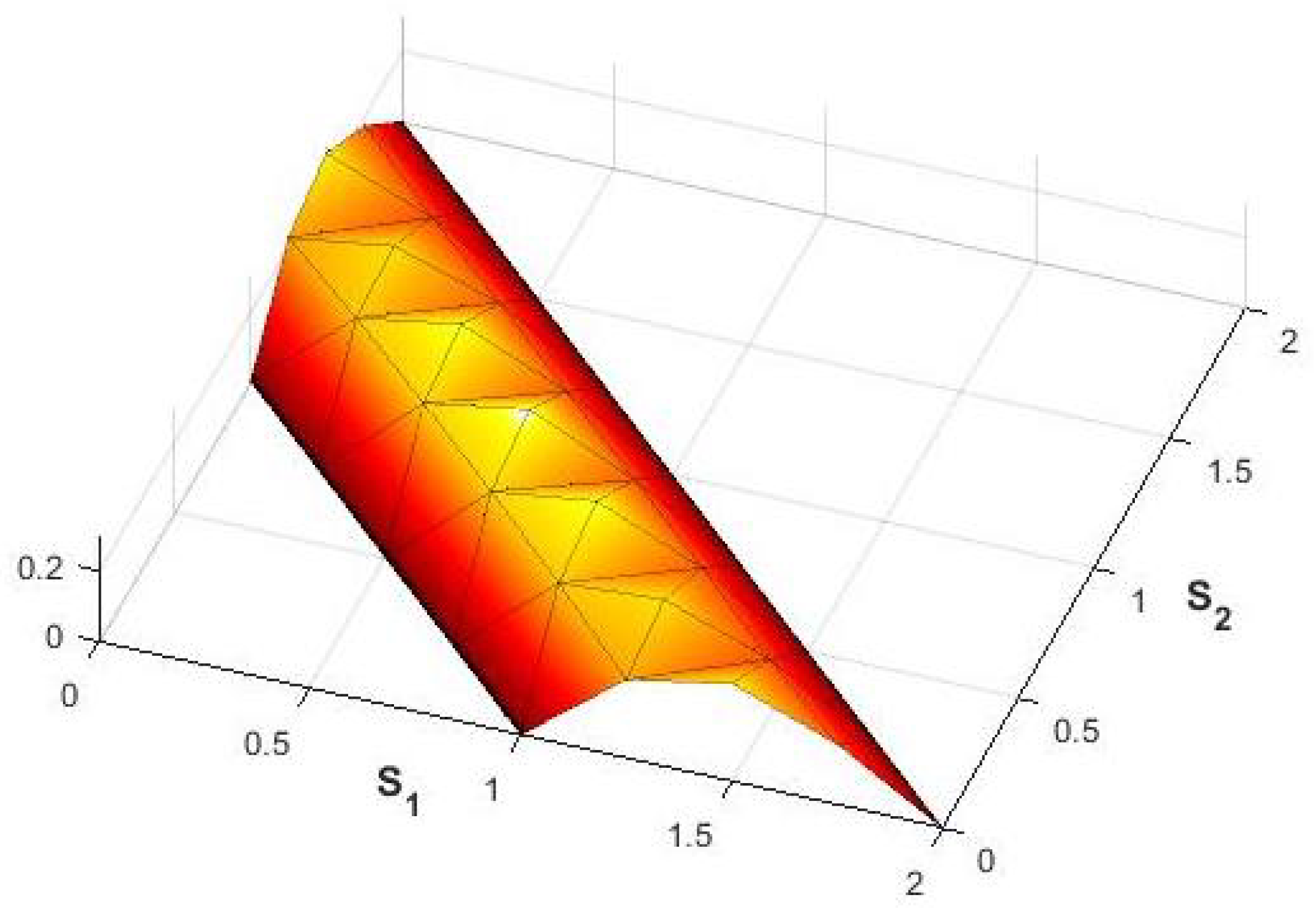
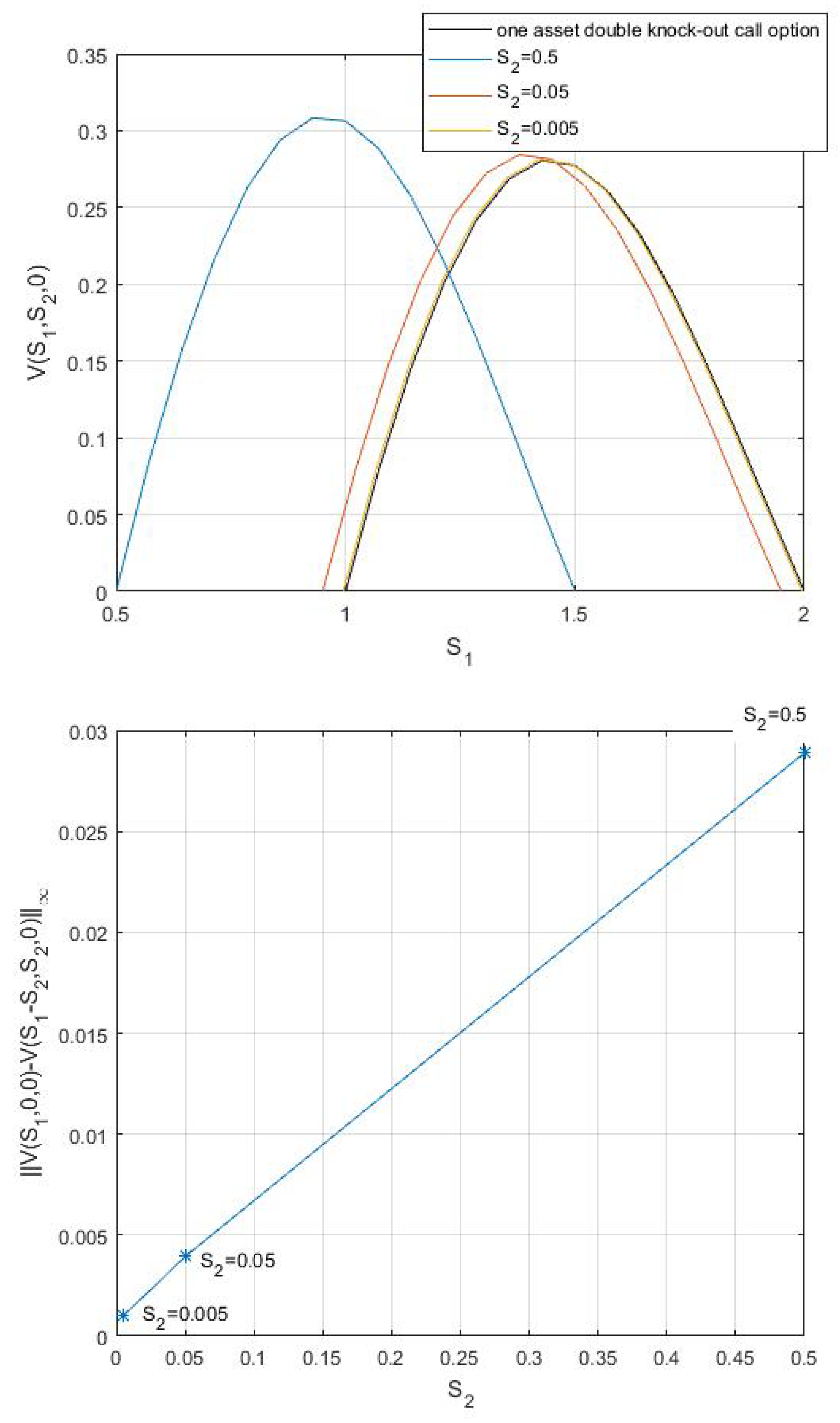
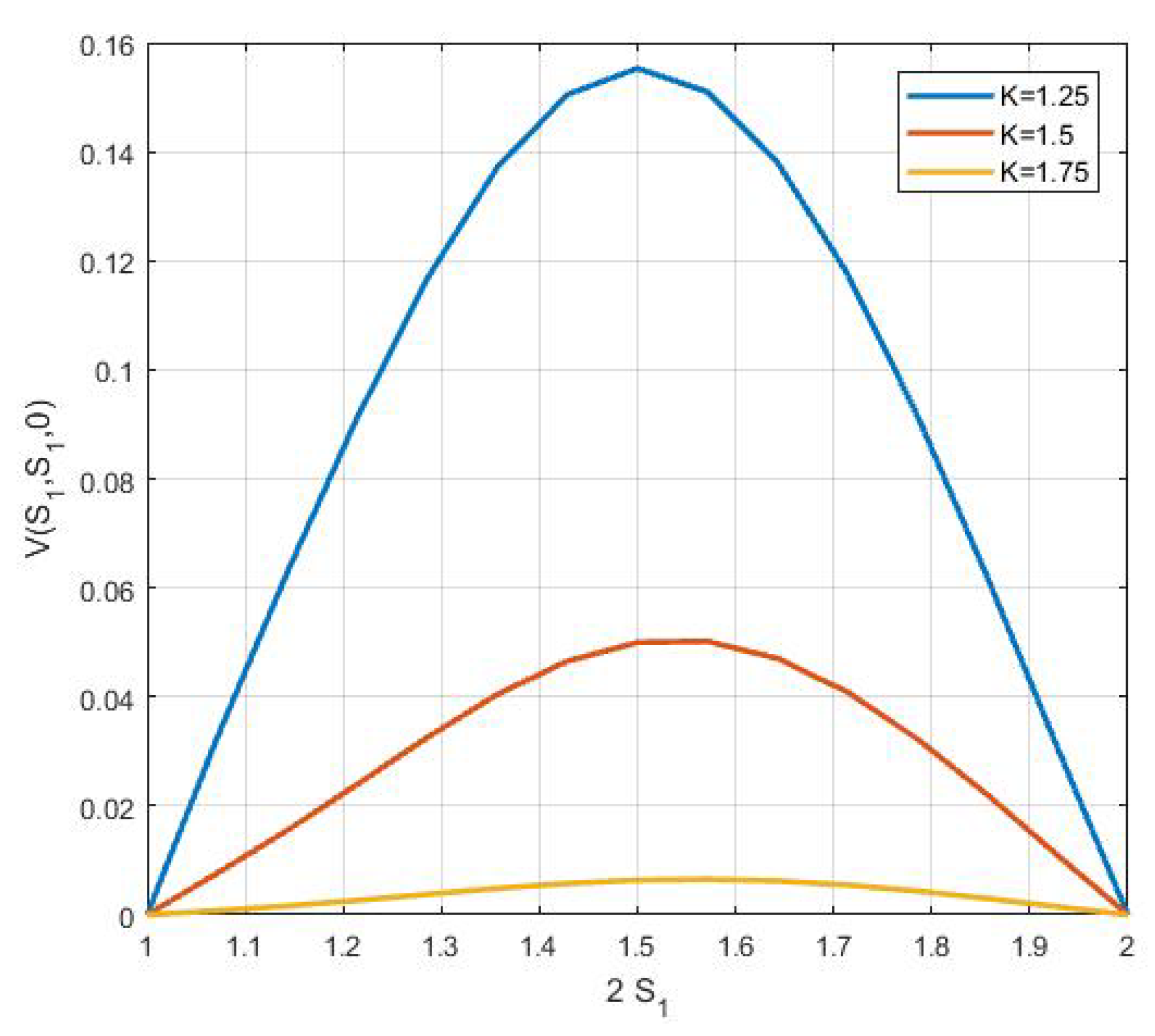
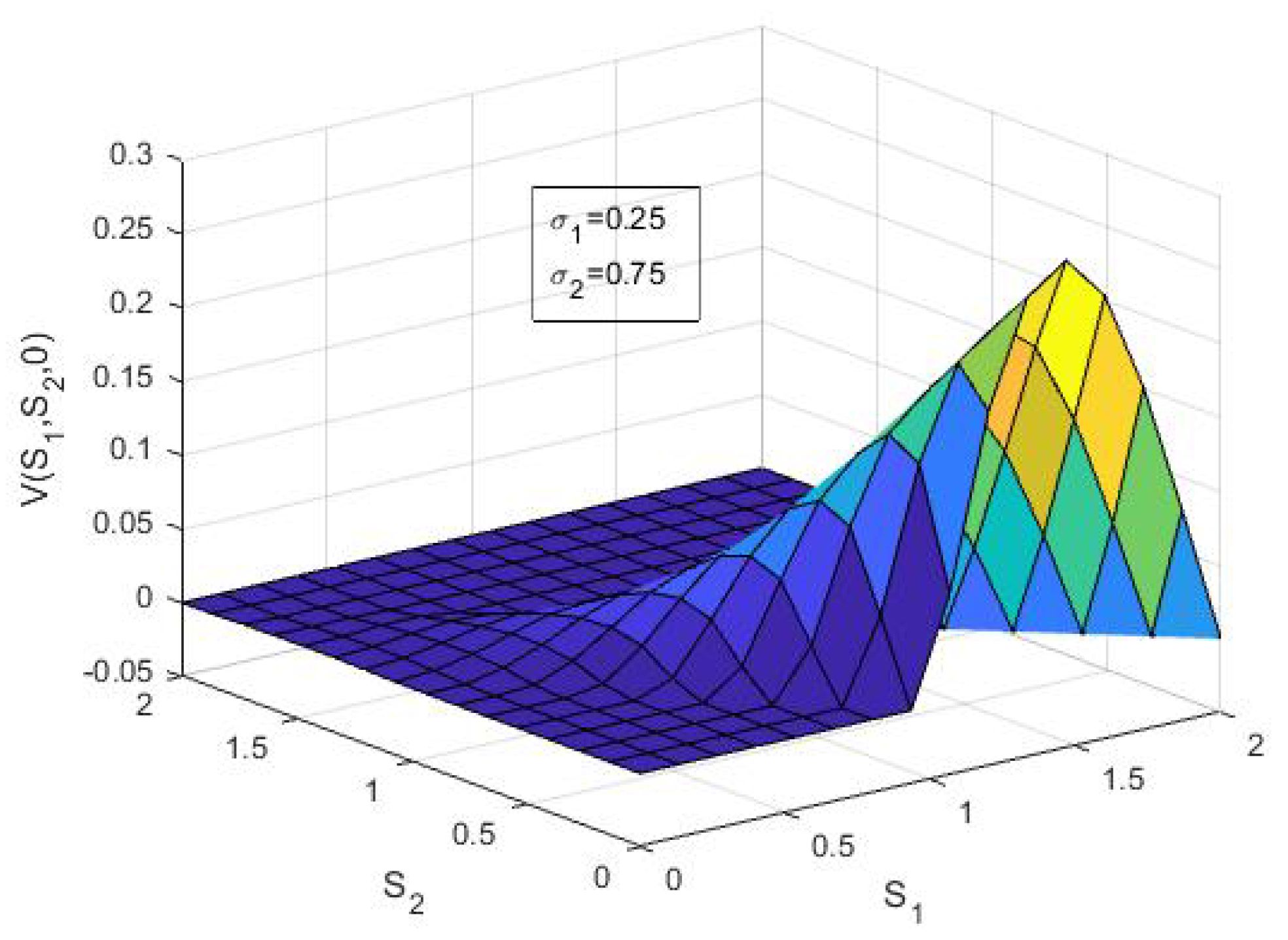
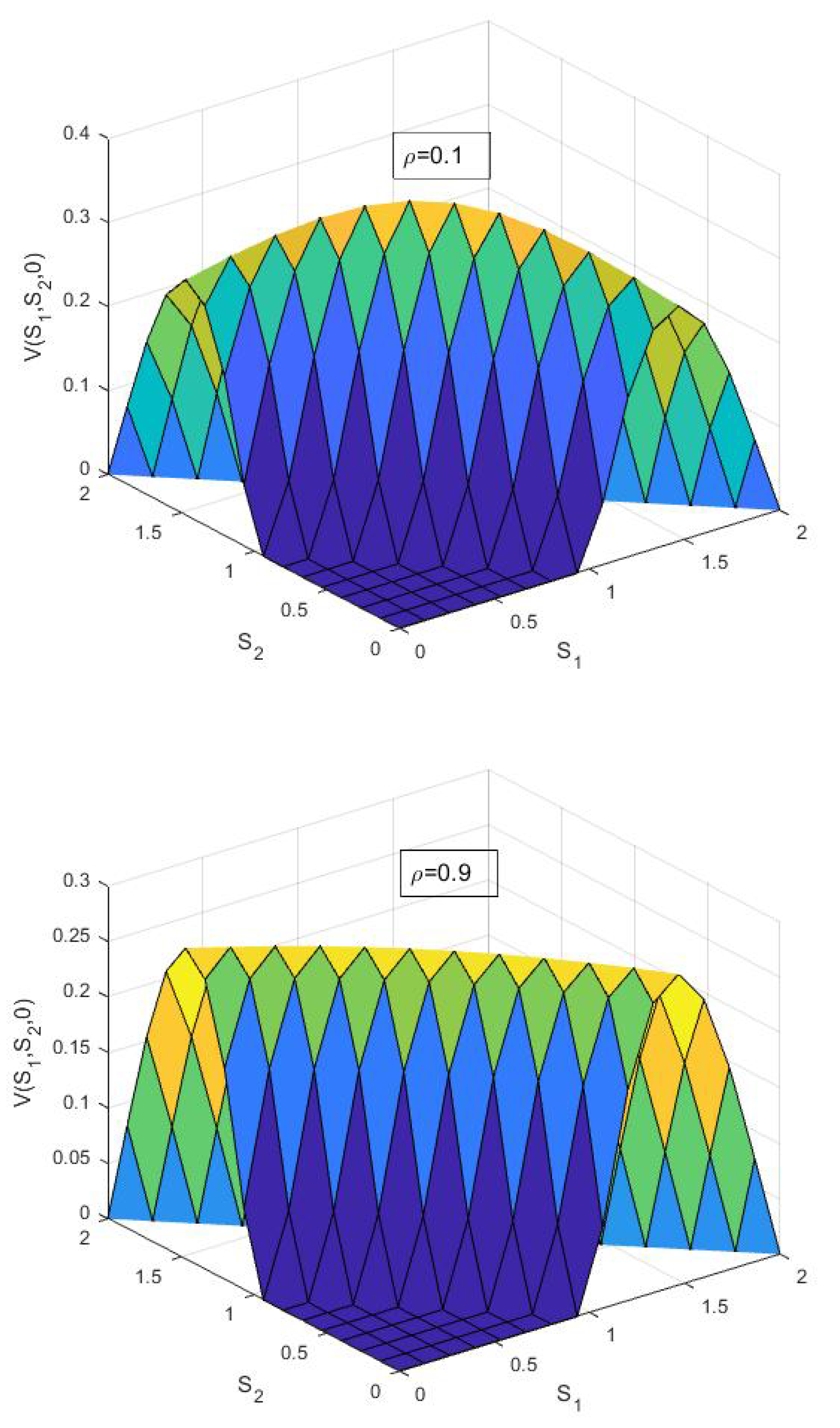
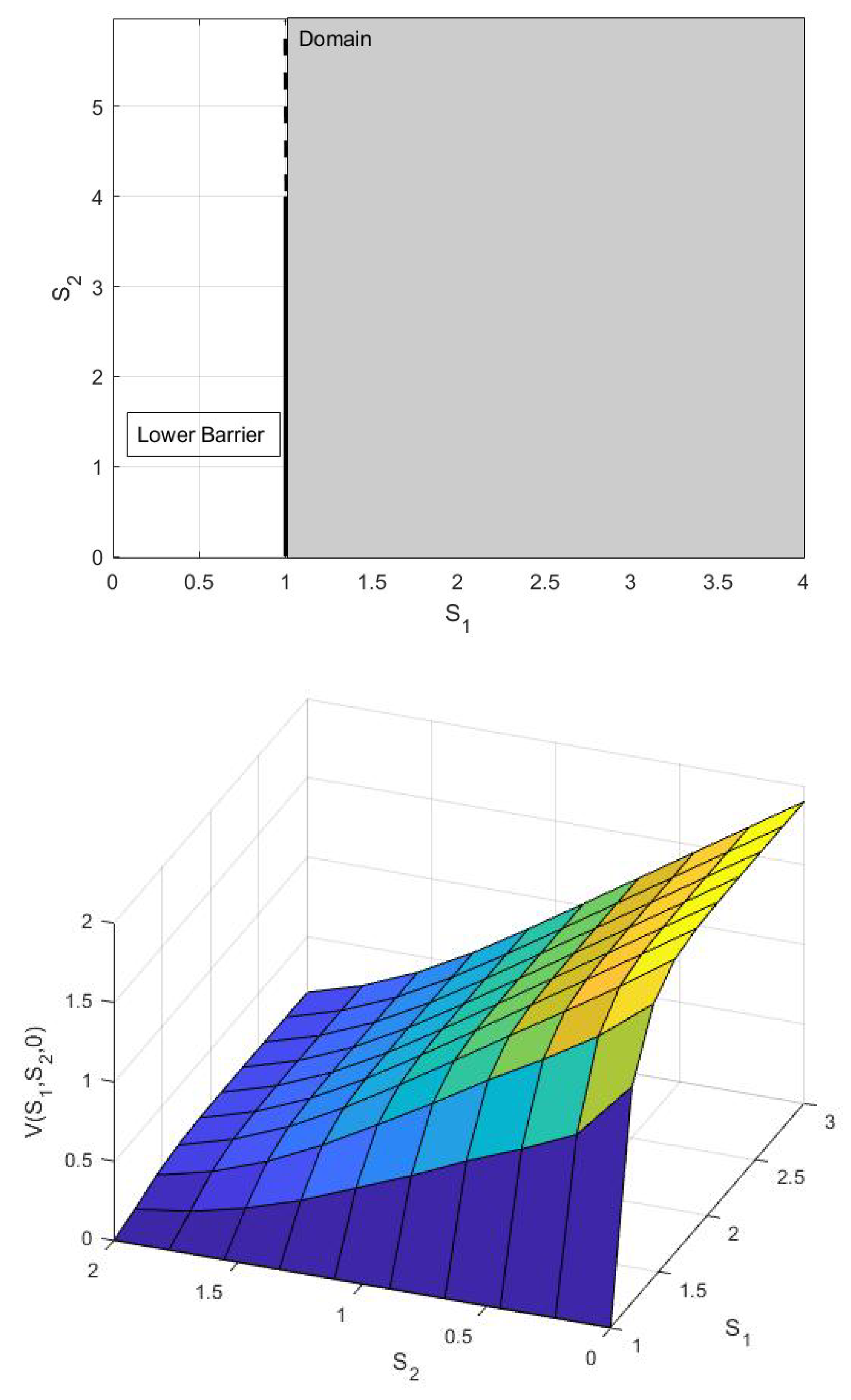
6. Numerical Results and Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Matlab® Code
- %Basket options
- %Code for the example with data taken from the book of R. Seydel
- close all
- clear
- clc
- %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
- global r sigma1 sigma2 rho
- %financial parameters
- B2=2; %50; %upper barrier
- B1=1; %0.1; %lower barrier
- T=1; %expiry
- r=0.05; %interest rate
- sigma1=0.25; %volatility of S1
- sigma2=0.25; %volatility of S2
- rho=0.7; %correlation
- K=1; %1.5; %strike price
- if K>=B2
- disp(’strike > upper barrier −> option value = 0’)
- return
- end
- %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
- %discretization in space
- tol=10^−12;
- epsi=10^−10;
- L1=B2∗sqrt(2); %length of Gamma1
- L3=B1∗sqrt(2); %length of Gamma3
- MS1=10; %n. of segments on Gamma1
- dS1=B2/MS1;
- MS3=ceil(B1/dS1); %n. of segments on Gamma1
- dS3=B1/MS3;
- L=[L1/MS1:L1 L3/MS3:L3]; %length of each segment
- B=[B2∗ones(1,MS1) B1∗ones(1,MS3)]; %belonged barrier
- x0=[B2:−dS1:dS1 0:dS3:B1−dS3]; %first abscissa of each segment
- x0(MS1+1)=epsi;
- x1=[B2−dS1:−dS1:0 dS3:dS3:B1]; %second abscissa of each segment
- x1(MS1)=epsi;
- y0=[0:dS1:B2−dS1 B1:−dS3:dS3]; %first ordinate of each segment
- y0(1)=epsi;
- y1=[dS1:dS1:B2 B1−dS3:−dS3:0]; %second ordinate of each segment
- y1(end)=epsi;
- xbar=[B2−dS1/2:−dS1:0 0+dS3/2:dS3:B1]; %abscissae midpoints
- ybar=[0+dS1/2:dS1:B2 B1−dS3/2:−dS3:0]; %ordinates midpoints
- %discretization in time
- Nt=10; %8;
- dt=T/Nt;
- t=0:dt:T;
- tbar=(t(1:end−1)+t(2:end))/2; %midpoints
- %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
- %Matrix entries
- disp(’Computation of the matrix entries’)
- M=zeros(MS1+MS3,MS1+MS3,Nt);
- %Matrix diagonal block
- for m=1:MS1+MS3
- for mbar=1:MS1+MS3
- M(mbar,m,1)=integral2(@(tau,l)…
- Solfond(xbar(mbar),ybar(mbar),tbar(1),l,B(m)−l,tau),…
- tbar(1)+epsi,t(2),x0(m),x1(m));%,’AbsTol’,tol,’RelTol’,tol);
- end
- end
- %Other matrix blocks of the first row
- for ell=2:Nt
- for m=1:MS1+MS3
- for mbar=1:MS1+MS3
- M(mbar,m,ell)=integral2(@(tau,l)…
- Solfond(xbar(mbar),ybar(mbar),tbar(1),l,B(m)−l,tau),…
- t(ell),t(ell+1),x0(m),x1(m));
- end
- end
- end
- %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
- %RHS
- disp(’Computation of the rhs entries’)
- MAX=max(B1,K);
- Smin=@(S1) MAX−S1;
- Smax=@(S1) B2−S1;
- for ell=1:Nt
- for mbar=1:MS1+MS3
- Beta(mbar,ell)=−integral2(@(S1,S2) (S1+S2−K).∗…
- Solfond(xbar(mbar),ybar(mbar),tbar(ell),S1,S2,T),…
- 0+epsi,MAX−epsi,Smin,Smax);
- Beta(mbar,ell)=Beta(mbar,ell)−…
- integral2(@(S1,S2) (S1+S2−K).∗…
- Solfond(xbar(mbar),ybar(mbar),tbar(ell),S1,S2,T),…
- MAX,B2−epsi,0+epsi,Smax);
- end
- end
- %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
- %Linear System resolution
- disp(’Linear System resolution’)
- Alpha(:,Nt)=M(:,:,1)\Beta(:,Nt);
- for ell=Nt−1:−1:1
- for j=2:Nt−ell+1
- Zeta(:,j−1)=M(:,:,j)∗Alpha(:,ell+j−1);
- end
- Alpha(:,ell)=M(:,:,1)\(Beta(:,ell)−sum(Zeta,2));
- end
- %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
- %Post processing at time t=0
- disp(’Post−processing: option value’)
- NXS1=25;
- NXS2=25;
- XS1=linspace(0,B2,NXS1);
- XS2=linspace(0,B2,NXS2);
- [X,Y]=meshgrid(XS1,XS2);
- Value=zeros(NXS2,NXS1);
- %Values of single asset double knock−out call on Gamma4
- for j=1:NXS2
- Value(j,1)=doubleOUT_call(XS2(j),K,B1,B2,T,r,sigma2^2);
- end
- %Values of single asset double knock−out call on Gamma2
- for i=1:NXS1
- Value(1,i)=doubleOUT_call(XS1(i),K,B1,B2,T,r,sigma1^2);
- end
- for i=2:NXS1
- for j=2:NXS2
- Value(j,i)=0;
- if(XS1(i)+XS2(j)>B1&&XS1(i)+XS2(j)<B2)
- Value(j,i)=integral2(@(S1,S2) (S1+S2−K).∗…
- Solfond(XS1(i),XS2(j),0,S1,S2,T),…
- 0+epsi,MAX−epsi,Smin,Smax);
- Value(j,i)=Value(j,i)+…
- integral2(@(S1,S2) (S1+S2−K).∗…
- Solfond(XS1(i),XS2(j),0,S1,S2,T),…
- MAX,B2,0+epsi,Smax);
- for ell=1:1:Nt
- for m=1:MS1+MS3
- SUM(m,ell)=Alpha(m,ell)∗integral2(@(tau,l)…
- Solfond(XS1(i),XS2(j),0,l,B(m)−l,tau),…
- t(ell),t(ell+1),x0(m),x1(m));
- end
- end
- Value(j,i)=Value(j,i)+sum(sum(SUM,1),2);
- end
- end
- end
- surf(X,Y,Value)
- xlabel(’S1’)
- ylabel(’S2’)
- %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
- function G=Solfond(SS1,SS2,tt,S1,S2,t)
- % fundamental solution
- global r sigma1 sigma2 rho
- alpha1=(log(SS1./S1)+(r−sigma1^2/2)∗(t−tt))./(sigma1∗sqrt(t−tt));
- alpha2=(log(SS2./S2)+(r−sigma2^2/2)∗(t−tt))./(sigma2∗sqrt(t−tt));
- G=exp(−r∗(t−tt))./(2∗pi∗(t−tt))/sqrt(1−rho^2)/(sigma1∗sigma2)./…
- (S1.∗S2).∗exp(−0.5∗(alpha1.^2+alpha2.^2−2∗alpha1.∗alpha2∗rho)/…
- (1−rho^2));
- end
- %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
- function c=doubleOUT_call(S,K,L,U,t,r,sigma2)
- % doubleOUT_call evaluates the call option with double out barrier
- % according to the formula in Section 3 in “The complete guide to
- % option pricing formulas” by E. G. Haug
- %
- % Inputs:
- % S: underlying asset value
- % K: strike price
- % L: lower barrier
- % U: upper barrier
- % t: time to maturity (0 not allowed!!!!!)
- % r: riskless interest rate
- % sigma2: variance of the assrt price
- % Output:
- % c: value of the option at S at time t
- %
- if S<=L || S>=U
- c=0;
- else
- N=5; % The sum whould be infinite, this is the approximation bound
- % Compute some parameters that do not change in the sum. it is therefore
- % convenient to compute them once for all
- sigma = sqrt(sigma2);
- m = (2∗r)/sigma2 + 1;
- A = (r+0.5∗sigma2)∗t;
- B = sigma∗sqrt(t);
- sum1=0;
- sum2=0;
- for ndx=−N:N
- % Define paramenters that change with ndx
- d1 = (log(S∗U^(2∗ndx)/(K∗L^(2∗ndx))) + A)./B;
- d2 = (log(S∗U^(2∗ndx−1)/(L^(2∗ndx))) + A)./B;
- d3 = (log((L^(2∗ndx+2))./(K∗S∗U^(2∗ndx))) + A)./B;
- d4 = (log((L^(2∗ndx+2))./(S∗U^(2∗ndx+1))) + A)./B;
- % Update the sums value
- sum1 = sum1 + (U/L)^(ndx∗m) ∗ (normcdf(d1)−normcdf(d2)) − …
- ((L^(ndx+1))./(S∗U^ndx)).^m .∗ (normcdf(d3)−normcdf(d4));
- sum2 = sum2 + (U/L)^(ndx∗(m−2)) .∗(normcdf(d1−B)−normcdf(d2−B))−…
- ((L^(ndx+1))./(U^ndx∗S)).^(m−2).∗(normcdf(d3−B)−normcdf(d4−B));
- end
- c = S .∗ sum1 − K∗exp(−r∗t) .∗ sum2;
- end
- end
References
- Black, F.; Scholes, M. The Pricing of Options and Corporate Liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef] [Green Version]
- Guardasoni, C. Semi-Analytical method for the pricing of barrier options in case of time-dependent parameters (with Matlab® codes). Commun. Appl. Ind. Math. 2018, 9, 42–67. [Google Scholar] [CrossRef] [Green Version]
- Guardasoni, C.; Sanfelici, S. Fast numerical pricing of barrier options under stochastic volatility and jumps. SIAM J. Appl. Math. 2016, 76, 27–57. [Google Scholar] [CrossRef]
- Aimi, A.; Diazzi, L.; Guardasoni, C. Efficient BEM-based algorithm for pricing floating strike Asian barrier options (with MATLAB® code). Axioms 2018, 7, 40. [Google Scholar] [CrossRef] [Green Version]
- Aimi, A.; Guardasoni, C. Collocation Boundary Element Method for the pricing of Geometric Asian Options. Eng. Anal. Bound. Elem. 2018, 92, 90–100. [Google Scholar] [CrossRef]
- Guillaume, T. On the multidimensional Black Scholes partial differential equation. Ann. Oper. Res. 2019, 281, 229–251. [Google Scholar] [CrossRef]
- Glasserman, P.; Staum, J. Conditioning on one-step survival for barrier options simulations. Oper. Res. 2001, 49, 923–937. [Google Scholar] [CrossRef] [Green Version]
- Cuomo, S.; Di Lorenzo, E.; Di Somma, V.; Toraldo, G. A sequential Monte Carlo approach for the pricing of barrier option under a stochastic volatility model. Electron. J. Appl. Stat. Anal. 2020, 13, 128–145. [Google Scholar]
- Giles, M.B. Multilevel Monte Carlo Path Simulation. Oper. Res. 2008, 56, 607–617. [Google Scholar] [CrossRef] [Green Version]
- Lars Kirkby, J.; Nguyen, D.; Nguyen, D. A general continuous time Markov chain approximation for multi-asset option pricing with systems of correlated diffusion. Appl. Math. Comput. 2020, 386, 125472. [Google Scholar]
- Leentvaar, C.; Oosterlee, C. Multi-asset option pricing using a parallel Fourier-based technique. J. Comput. Financ. 2008, 12, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Seydel, R.U. Tools for Computational Finance; Springer: Berlin, Germany, 2009. [Google Scholar]
- Friedman, A. Partial Differential Equations of Parabolic Type; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1964. [Google Scholar]
- Wilmott, P. Derivatives: The Theory and Practice of Financial Engineering; John Wiley: Hoboken, NJ, USA, 1998. [Google Scholar]
- Haug, E. The Complete Guide to Option Pricing Formulas; McGraw-Hill: New York, NY, USA, 2007. [Google Scholar]
- Ballestra, L.; Pacelli, G. A boundary element method to price time-dependent double barrier options. Appl. Math. Comput. 2011, 218, 4192–4210. [Google Scholar] [CrossRef]
- Carr, P.; Itkin, A.; Muravey, D. Semi-closed form prices of barrier options in the time-dependent CEV and CIR models. J. Deriv. 2020, 28, 26–50. [Google Scholar] [CrossRef]
- Escobar, M.; Ferrando, S. Barrier options in three dimensions. Int. J. Financ. Mark. Deriv. 2014, 3, 260–292. [Google Scholar] [CrossRef]
- Todorov, V.; Dimov, I. Monte Carlo methods for multidimensional integration for European option pricing. AIP Conf. Proc. 2016, 1773, 100009. [Google Scholar] [CrossRef]
- Aimi, A.; Diazzi, L.; Guardasoni, C. Numerical pricing of geometric asian options with barriers. Math. Methods Appl. Sci. 2018, 41, 7510–7529. [Google Scholar] [CrossRef]
- Kunimoto, N.; Ikeda, M. Pricing options with curved boundaries. Math. Financ. 1992, 2, 275–298. [Google Scholar] [CrossRef]
| K | T | r | |||||
|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.05 | 0.25 | 0.25 | 0.7 | 1 | 2 |
| SABO | FEM | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 | 4 | 8 | 16 | 25 | 50 | 100 | |||
| 2 | 0.304101 | 0.305635 | 0.305527 | 0.305501 | 0.293627 | 0.293663 | 0.293662 | ||
| 4 | 0.305242 | 0.306735 | 0.306631 | 0.306586 | 0.304109 | 0.304129 | 0.304134 | ||
| 8 | 0.304903 | 0.306424 | 0.306320 | 0.306274 | 0.305875 | 0.305891 | 0.305894 | ||
| 16 | 0.304916 | 0.306429 | 0.306329 | 0.306282 | 0.306171 | 0.306185 | 0.306188 | ||
| 0.306229 | 0.306243 | 0.306246 | |||||||
| CPU time SABO | CPU time FEM | ||||||||
| 2 | 4 | 8 | 16 | 25 | 50 | 100 | |||
| 2 | 2.1 | 5.8 | 8.6 | 1.1 | 7.2 | 1.4 | 3.4 | ||
| 4 | 5.1 | 7.8 | 1.2 | 2.1 | 4.3 | 8.3 | 1.5 | ||
| 8 | 9.2 | 1.5 | 2.5 | 4.5 | 8.1 | 1.3 | 2.2 | ||
| 16 | 2.1 | 4.1 | 6.8 | 1.3 | 3.0 | 3.6 | 4.8 | ||
| 6.4 | 6.7 | 7.1 | |||||||
| 5 | 10 | 20 | ||
|---|---|---|---|---|
| 5 | 0.89692 | 0.89731 | 0.89731 | |
| 10 | 0.89679 | 0.89719 | 0.89719 | |
| 20 | 0.89675 | 0.89715 | 0.89716 | |
| 40 | 0.89673 | 0.89714 | 0.89714 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aimi, A.; Guardasoni, C. Multi-Asset Barrier Options Pricing by Collocation BEM (with Matlab® Code). Axioms 2021, 10, 301. https://doi.org/10.3390/axioms10040301
Aimi A, Guardasoni C. Multi-Asset Barrier Options Pricing by Collocation BEM (with Matlab® Code). Axioms. 2021; 10(4):301. https://doi.org/10.3390/axioms10040301
Chicago/Turabian StyleAimi, Alessandra, and Chiara Guardasoni. 2021. "Multi-Asset Barrier Options Pricing by Collocation BEM (with Matlab® Code)" Axioms 10, no. 4: 301. https://doi.org/10.3390/axioms10040301
APA StyleAimi, A., & Guardasoni, C. (2021). Multi-Asset Barrier Options Pricing by Collocation BEM (with Matlab® Code). Axioms, 10(4), 301. https://doi.org/10.3390/axioms10040301






