Chaotic Dynamics by Some Quadratic Jerk Systems
Abstract
:1. Introduction
2. Hopf Bifurcation of a Five-Parameter Family of Quadratic Jerk Systems
- For , the origin is unstable. Moreover, it is a saddle-focus of the type (1,2) with 1D stable and 2D unstable manifolds [21].
- For , the origin is asymptotically stable. Moreover, it is a node-focus.
3. The Proposed Systems
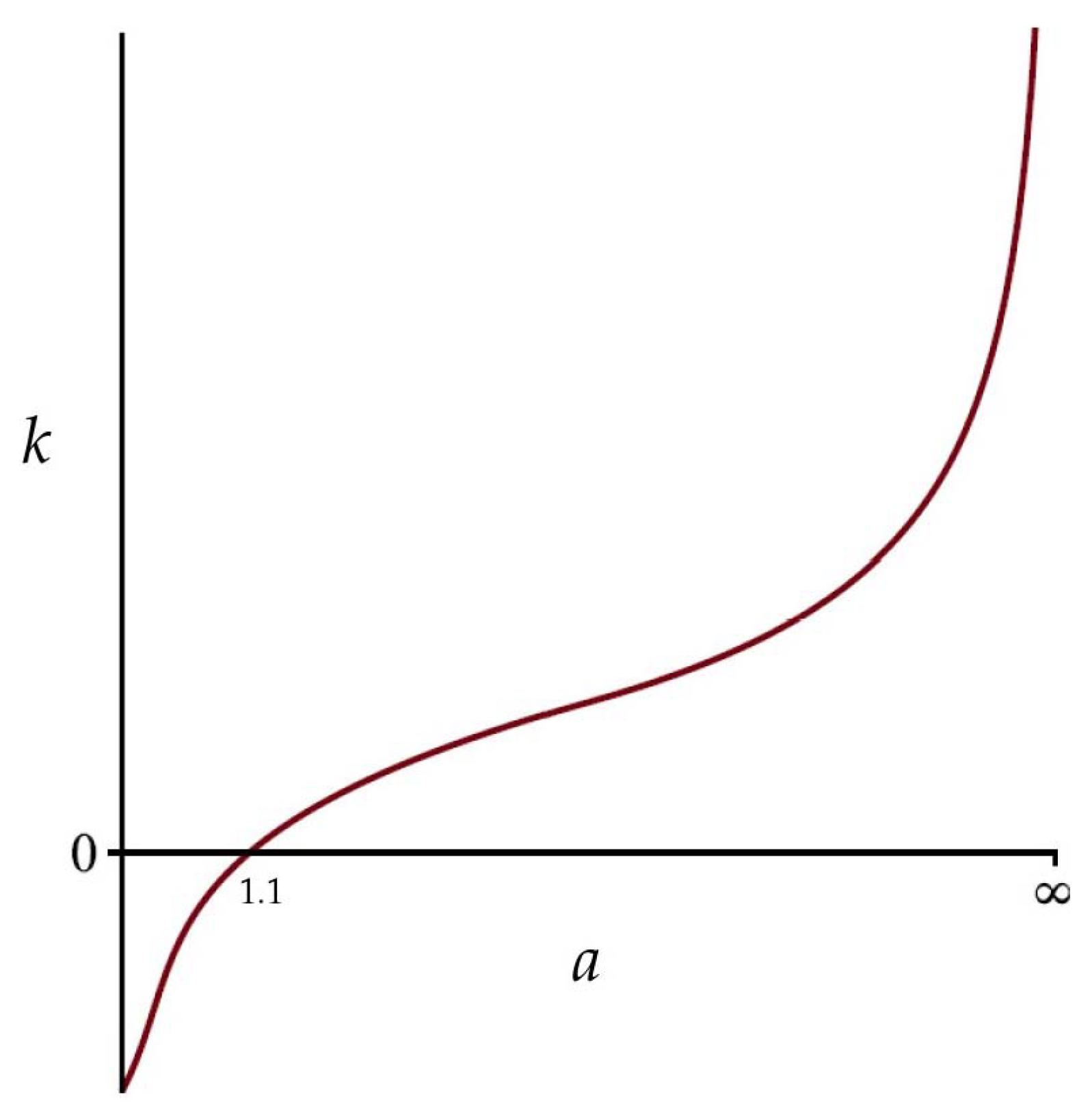
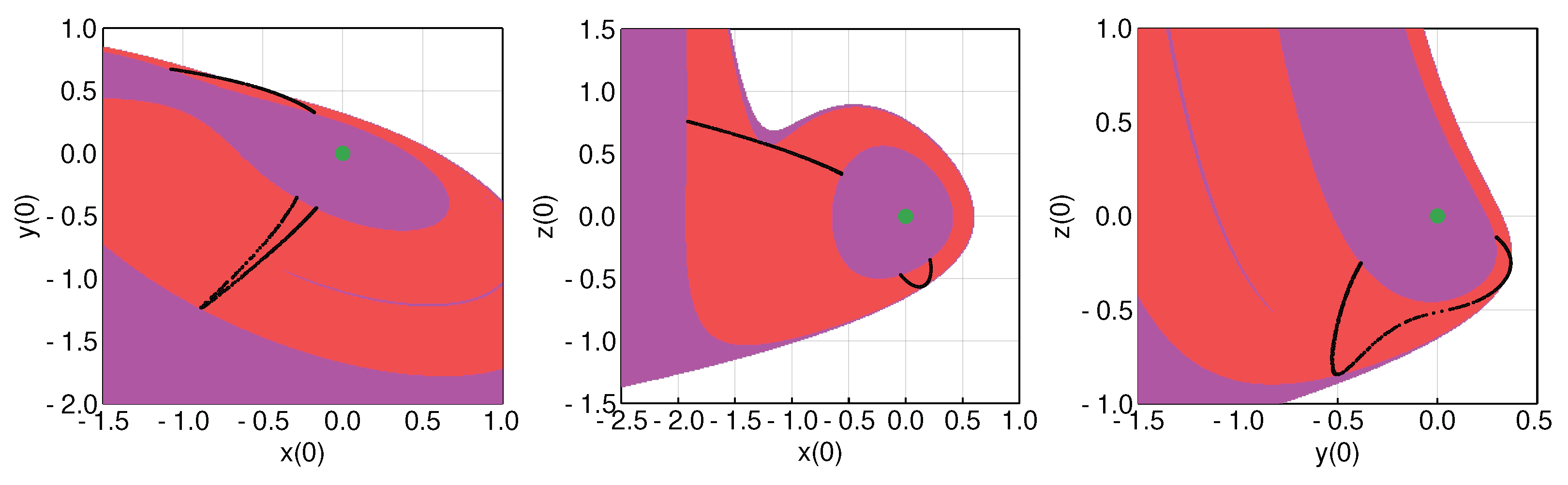
4. Nonchaotic Parameter Region
5. Hopf Bifurcation Analysis
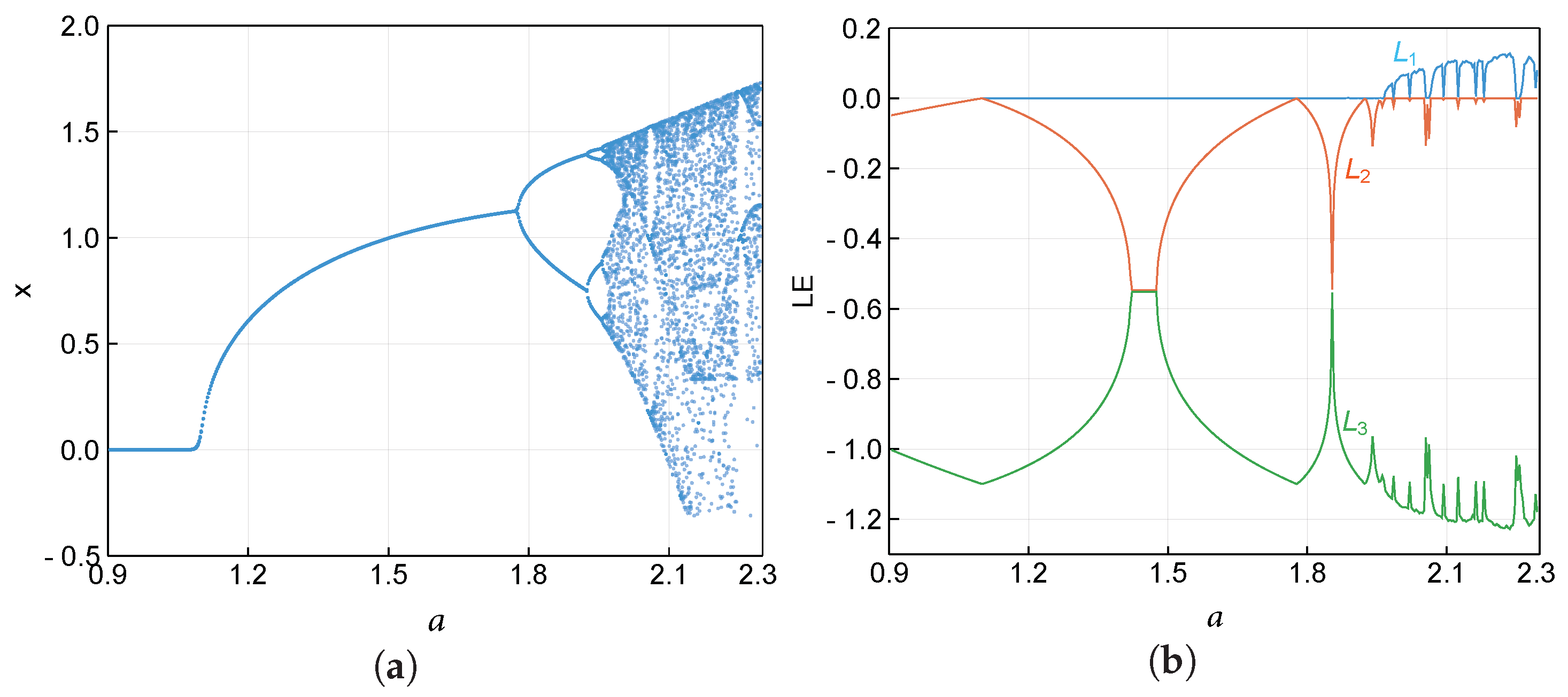
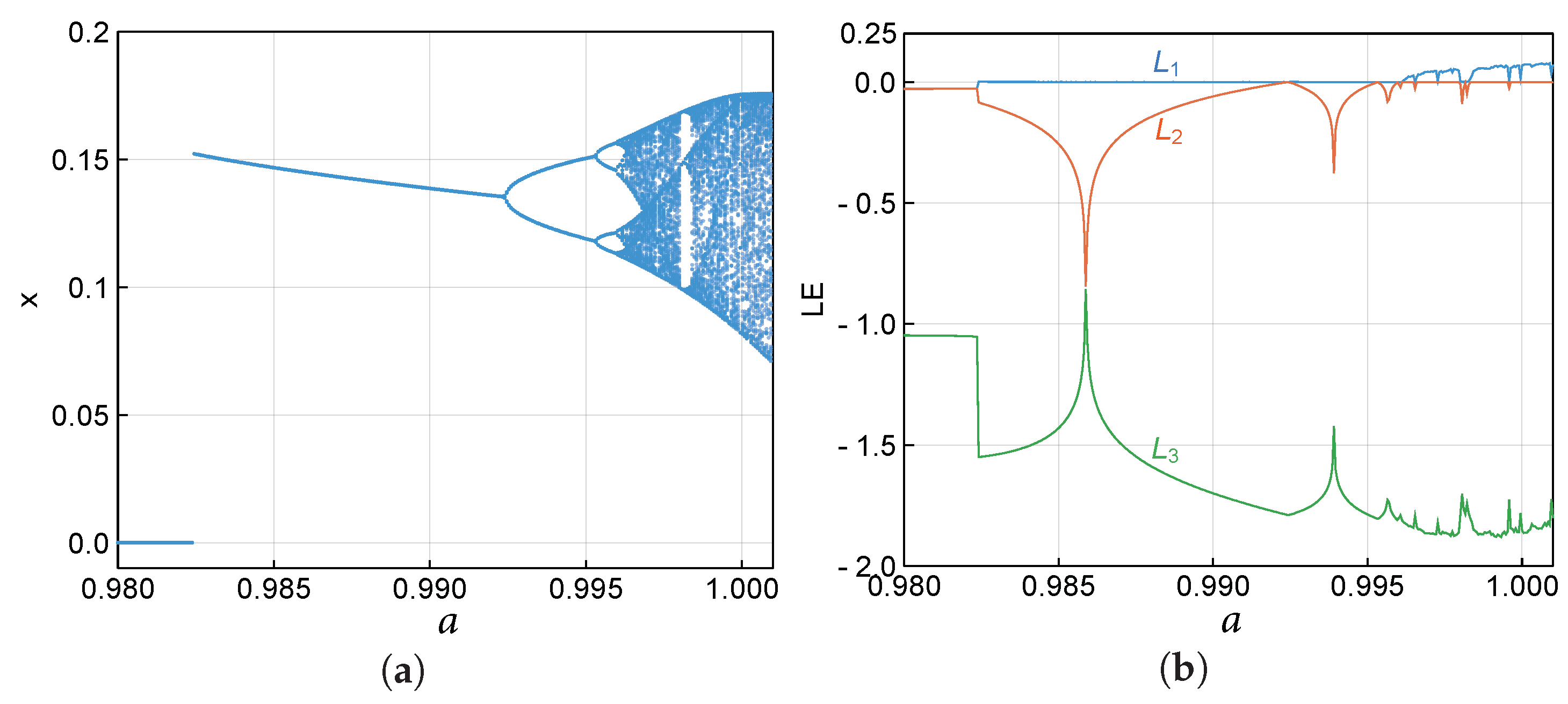
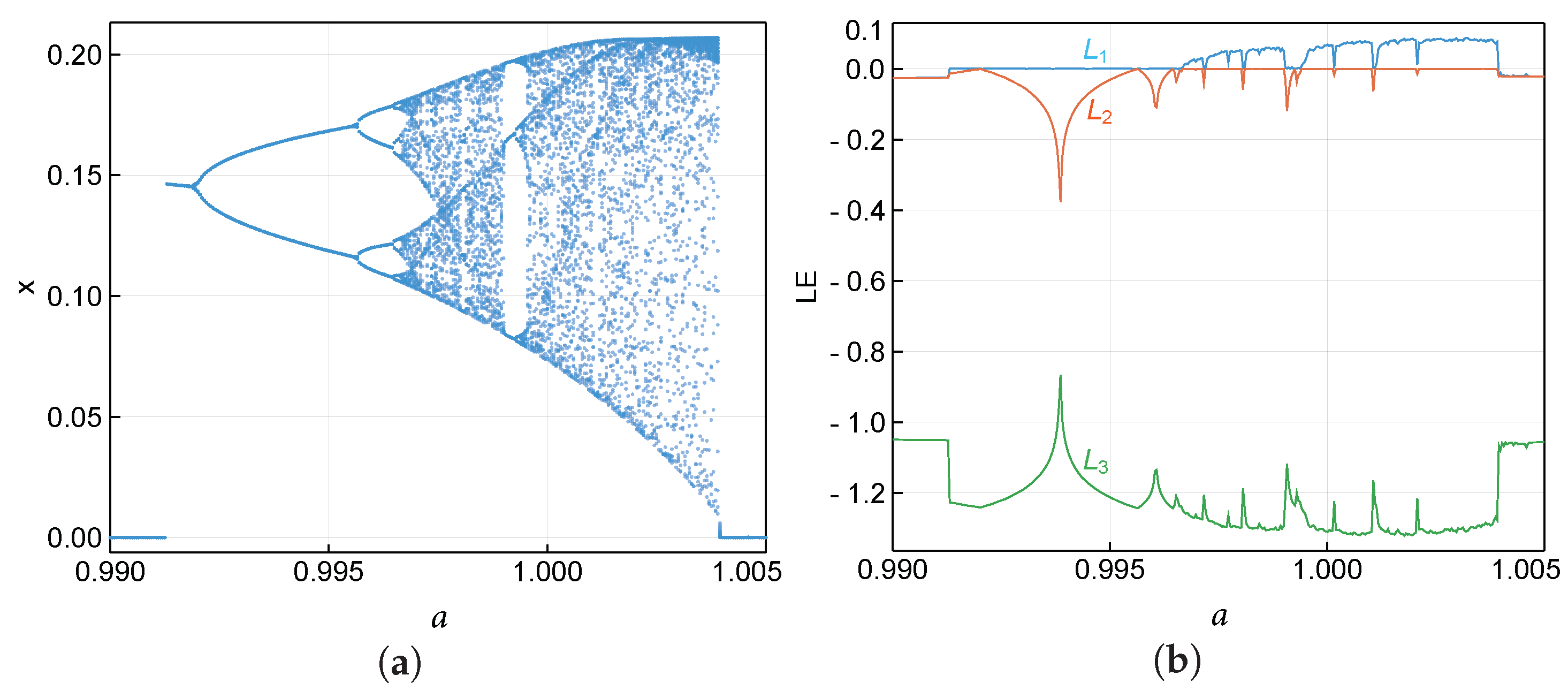
6. Route to a Self-Excited Chaotic Attractor
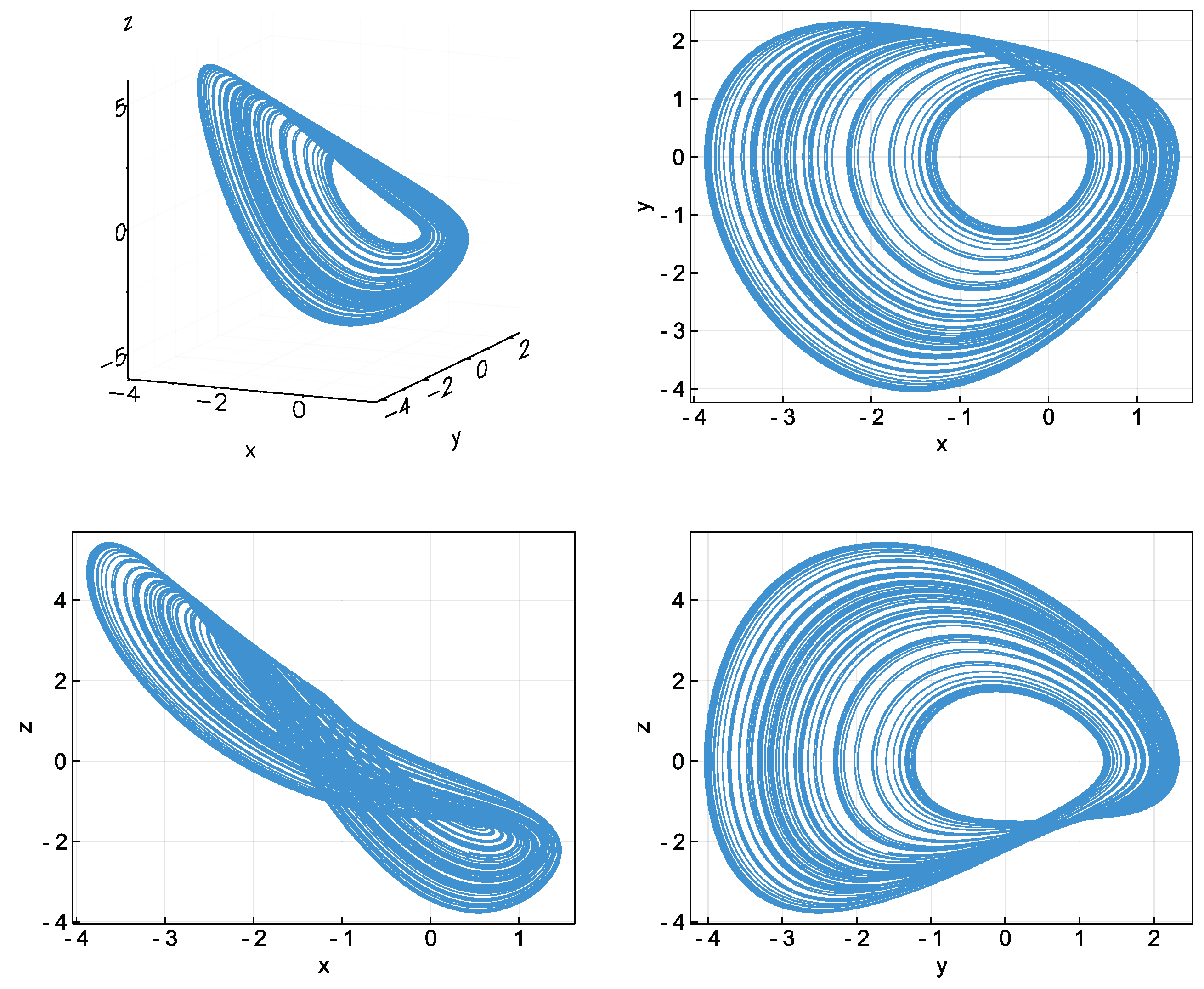
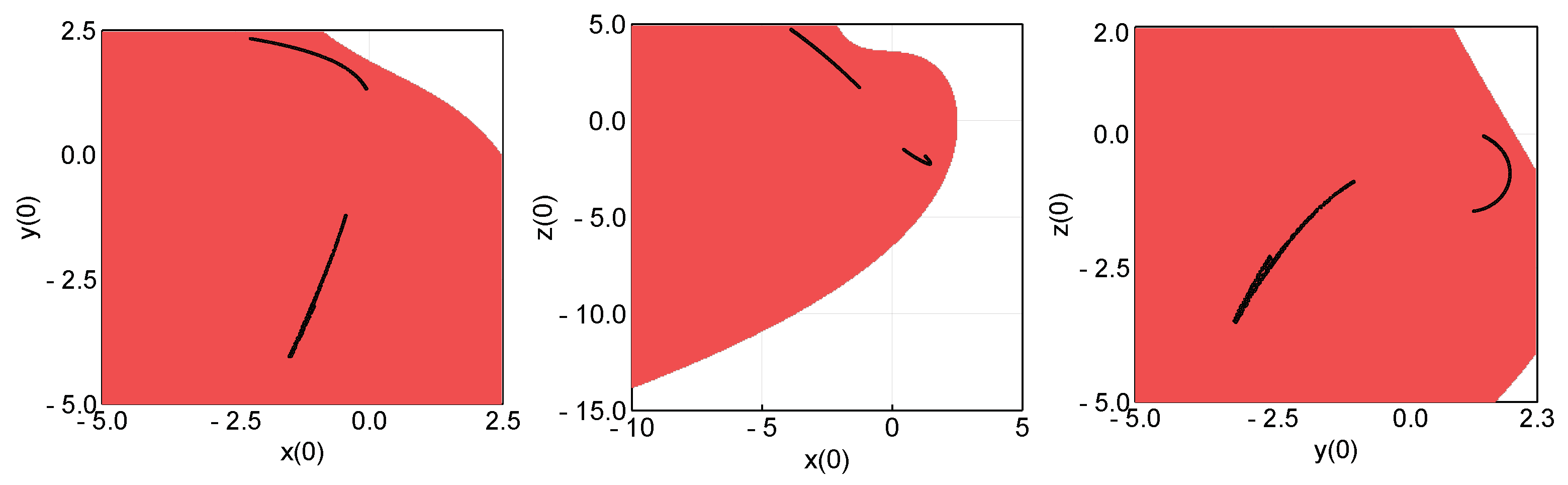
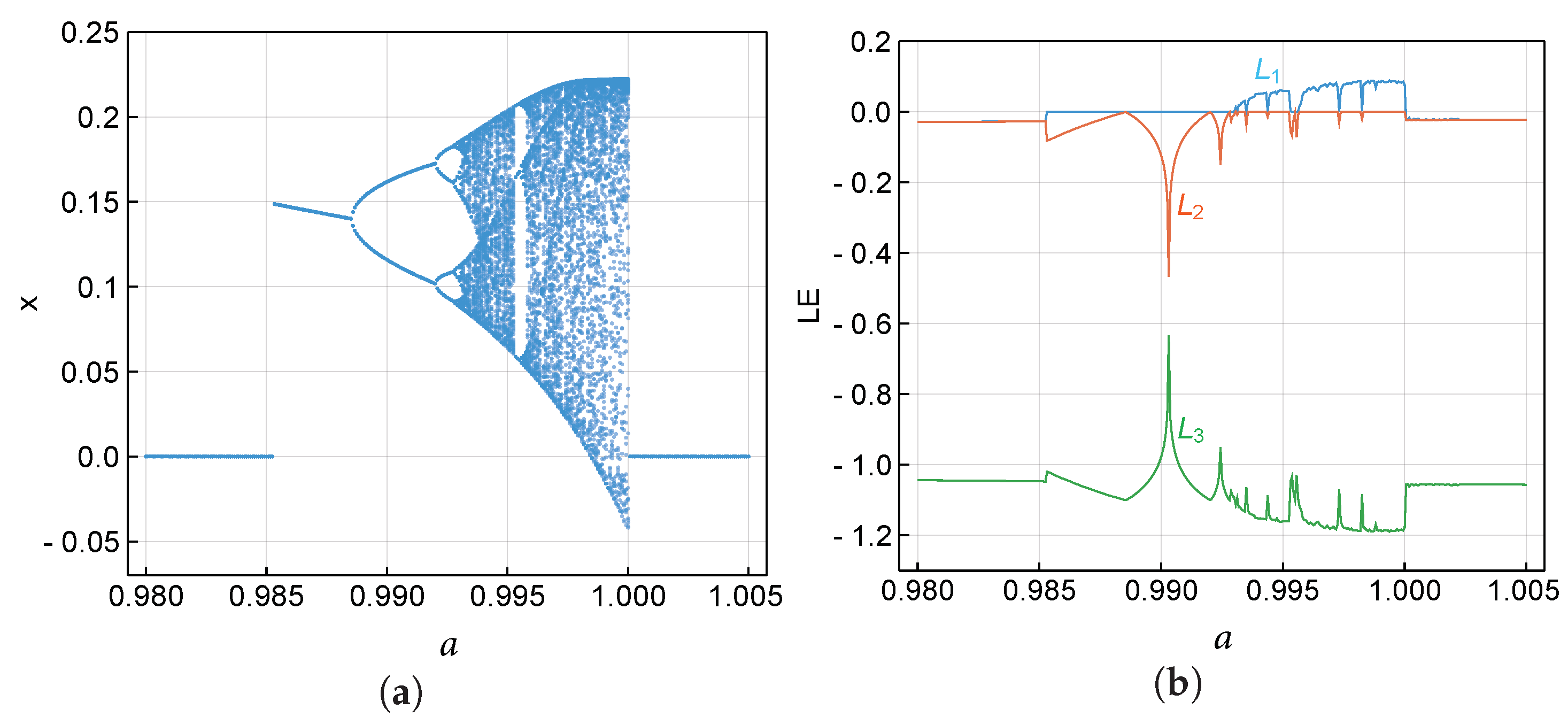
7. Route to a Hidden Chaotic Attractor
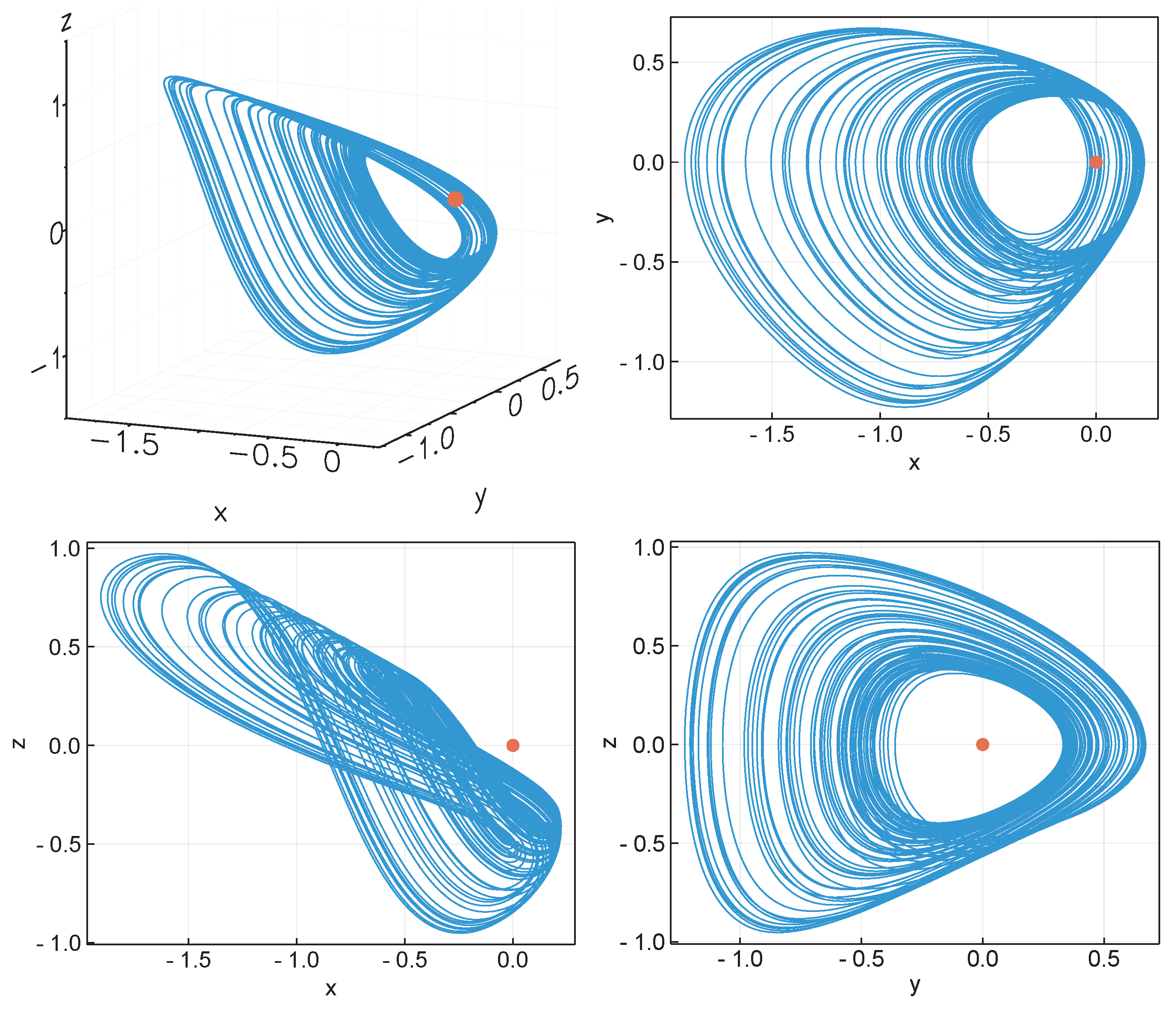
8. Hidden Chaotic Attractor
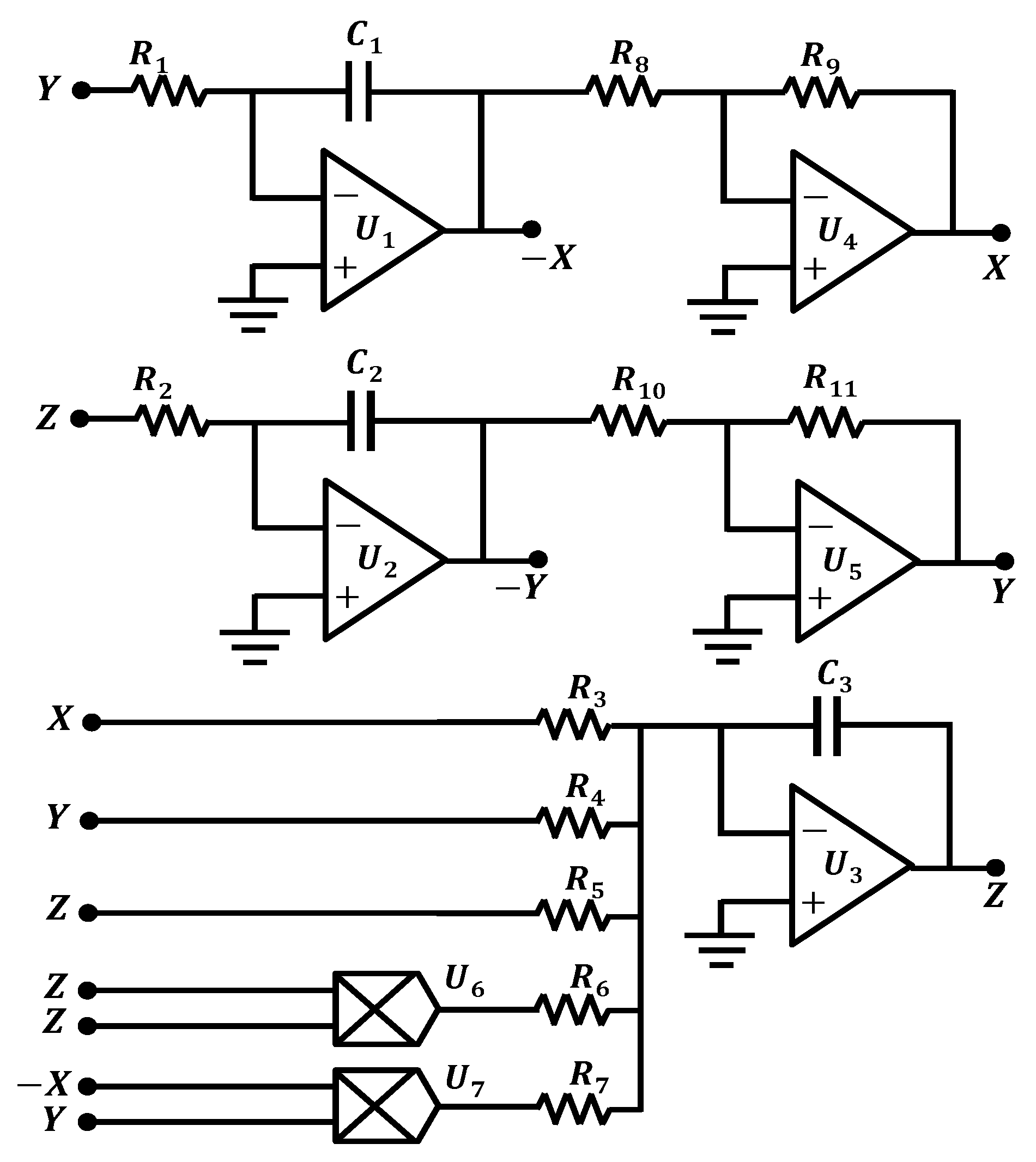
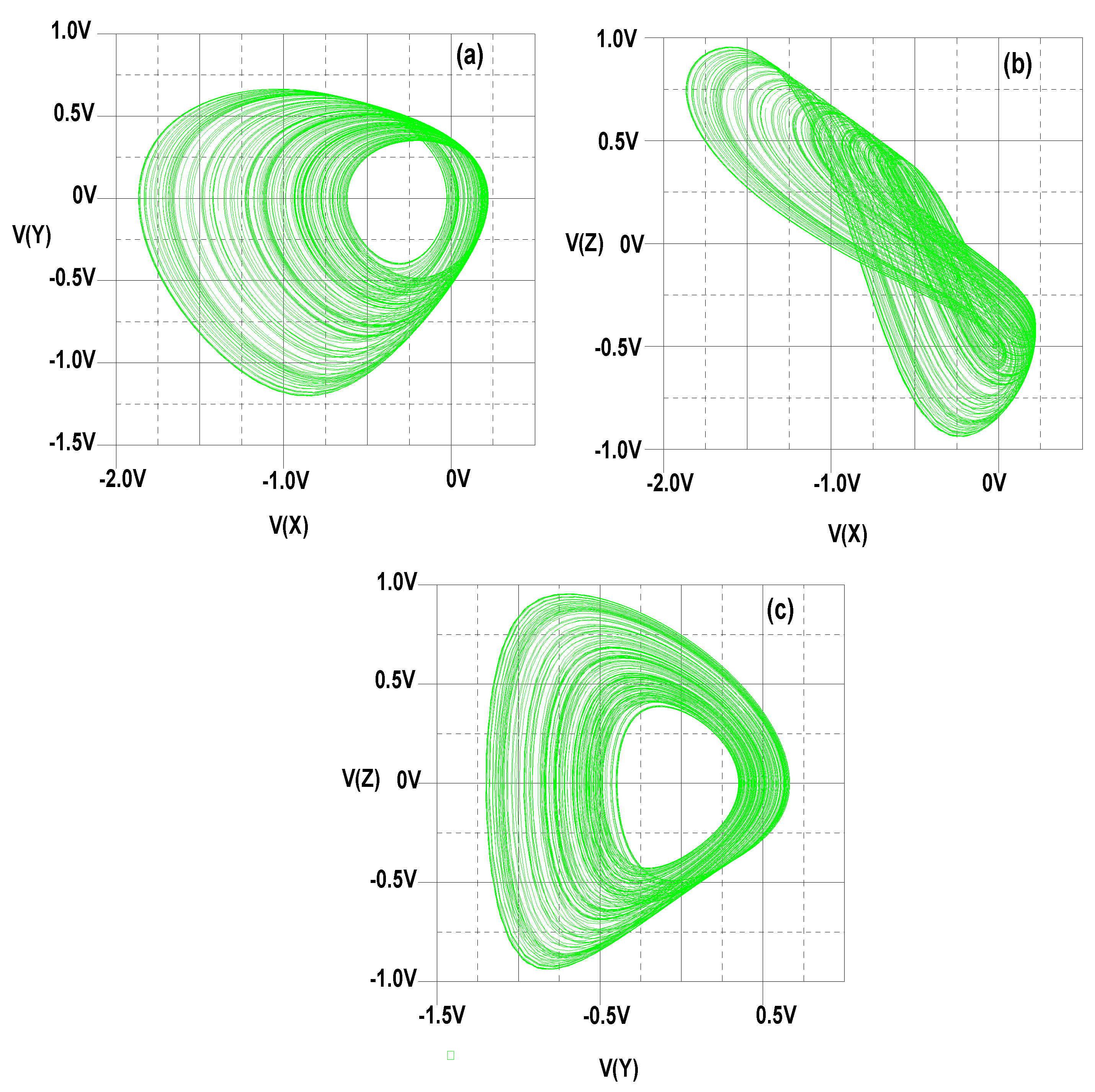
9. Circuit Realization
10. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Thompson, J.M.T.; Stewart, H.B. Nonlinear Dynamics and Chaos; Wiley: Chichester, UK, 2002. [Google Scholar]
- Wiggins, S. Introduction to Applied Nonlinear Dynamical Systems and Chaos; Springer: New York, NY, USA, 1990. [Google Scholar]
- Mangiarotti, S.; Peyre, M.; Zhang, Y.; Huc, M.; Roger, F.; Kerr, Y. Chaos theory applied to the outbreak of COVID-19: An ancillary approach to decision making in pandemic context. Epidemiol Infect. 2020, 148, 95. [Google Scholar] [CrossRef] [PubMed]
- Scheck, F. Mechanics: From Newton’s Laws to Deterministic Chaos; Springer: Berlin, Germany, 2012. [Google Scholar]
- Toker, D.; Sommer, F.T.; D’Esposito, M. A simple method for detecting chaos in nature. Commun. Biol. 2020, 3, 11. [Google Scholar] [CrossRef] [Green Version]
- Volos, C.K.; Kyprianidis, I.M.; Stouboulos, I.N. Experimental demonstration of a chaotic cryptographic scheme. WSEAS Trans. Circ. Syst. 2006, 5, 1654–1661. [Google Scholar]
- Zaher, A.A.; Abu-Rezq, A. On the design of chaos-based secure communication systems. Commun. Nonlinear Sci. Numer. Simulat. 2011, 16, 3721–3737. [Google Scholar] [CrossRef]
- Wei, Z.C.; Sprott, J.C.; Chen, H. Elementary quadratic chaotic flows with a single non-hyperbolic equilibrium. Phys. Lett. A 2015, 379, 2184–2187. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V. Hidden attractors in dynamical systems. From hidden oscillations in Hilbert-Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits. Int. J. Bifurc. Chaos 2013, 23, 1330002. [Google Scholar] [CrossRef] [Green Version]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef] [Green Version]
- Rössler, O.E. An equation for continuous chaos. Phys. Lett. A 1976, 57, 397–398. [Google Scholar] [CrossRef]
- Chua, L.O. The genesis of Chua’s circuit. AEÜ 1992, 46, 250–257. [Google Scholar]
- Silva, C.P. Shil’nikov’s theorem-a tutorial. IEEE Trans. Circuits Syst. I Reg. Pap. 1993, 40, 675–682. [Google Scholar] [CrossRef]
- Tchitnga, R.; Nguazon, T.; Fotso, P.H.L.; Gallas, J.A.C. Chaos in a single Op-Amp based jerk circuit. IEEE Trans. Circuits Syst. II Express Briefs 2016, 63, 239–243. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.R.; Ueda, T. Yet another chaotic attractor. Int. J. Bifurc. Chaos 1999, 9, 1465–1466. [Google Scholar] [CrossRef]
- Lü, J.H.; Chen, G.R. A new chaotic attractor coined. Int. J. Bifurc. Chaos 2002, 12, 659–661. [Google Scholar] [CrossRef]
- Sprott, J.C. Elegant Chaos: Algebraically Simple Chaotic Flows; World Scientific: Singapore, 2010. [Google Scholar]
- Kuznetsov, N.V.; Leonov, G.A.; Vagaitsev, V.I. Analytical-numerical method for attractor localization of generalized Chua’s system. IFAC Proc. 2010, 43, 29–33. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V.; Vagaitsev, V.I. Localization of hidden Chua’s attractors. Phys. Lett. A 2011, 375, 2230–2233. [Google Scholar] [CrossRef]
- Kuznetsov, N.V. Hidden attractors in fundamental problems and engineering models. A short survey. Lect. Notes Electr. Eng. 2016, 371, 13–25. [Google Scholar]
- Stankevich, N.V.; Kuznetsov, N.V.; Leonov, G.A.; Chua, L.O. Scenario of the birth of hidden attractors in the Chua circuit. Int. J. Bifurc. Chaos 2017, 27, 1730038. [Google Scholar] [CrossRef]
- Zhao, H.T.; Lin, Y.P.; Dai, Y.X. Hidden attractors and dynamics of a general autonomous van der Pol–Duffing oscillator. Int. J. Bifurc. Chaos 2014, 24, 1450080. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C.; Golpayegani, S.M.R.H. Elementary quadratic chaotic flows with no equilibria. Phys. Lett. A 2013, 377, 699–702. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C. Simple chaotic flows with a line equilibrium. Chaos Solitons Fractals 2013, 57, 79–84. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C.; Nazarimehr, F. Recent new examples of hidden attractors. Eur. Phys. J. Spec. Top. 2015, 224, 1469–1476. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C.; Molaie, M. A simple chaotic flow with a plane of equilibria. Int. J. Bifurcat. Chaos 2016, 26, 1650098. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C.; Pham, V.T.; Volos, C.; Li, C.B. Simple chaotic 3D flows with surfaces of equilibria. Nonlinear Dyn. 2016, 86, 1349–1358. [Google Scholar] [CrossRef]
- Sprott, J.C. Strange attractors with various equilibrium types. Eur. Phys. J. Spec. Top. 2015, 224, 1409–1419. [Google Scholar] [CrossRef]
- Bao, B.C.; Xu, L.; Wang, N.; Bao, H.; Xu, Q.; Chen, M. Third-order RLCM-four-elements-based chaotic circuit and its coexisting bubbles. AEÜ-Int. J. Electron. Commun. 2018, 94, 26–35. [Google Scholar] [CrossRef]
- Danca, M.F.; Kuznetsov, N. Hidden strange nonchaotic attractors. Mathematics 2021, 9, 652. [Google Scholar] [CrossRef]
- Jafari, M.A.; Mliki, E.; Akgul, A.; Pham, V.T.; Kingni, S.T.; Wang, X.; Jafari, S. Chameleon: The most hidden chaotic flow. Nonlinear Dyn. 2017, 88, 2303–2317. [Google Scholar] [CrossRef]
- Pham, V.T.; Vaidyanathan, S.; Volos, C.; Kapitaniak, T. (Eds.) Nonlinear Dynamical Systems with Self-Excited and Hidden Attractors; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Wang, N.; Zhang, G.S.; Kuznetsov, N.V.; Bao, H. Hidden attractors and multistability in a modified Chua’s circuit. Commun. Nonlinear Sci. Numer. Simul. 2021, 92, 105494. [Google Scholar] [CrossRef]
- Pham, V.T.; Volos, C.; Jafari, S.; Kapitaniak, T. Coexistence of hidden chaotic attractors in a novel no-equilibrium system. Nonlinear Dyn. 2017, 87, 2001–2010. [Google Scholar] [CrossRef]
- Shahzad, M.; Pham, V.T.; Ahmad, M.A.; Jafari, S.; Hadaeghi, F. Synchronization and circuit design of a chaotic system with coexisting hidden attractors. Eur. Phys. J. Spec. Top. 2015, 224, 1637–1652. [Google Scholar] [CrossRef]
- Tamba, V.K.; Pham, V.T.; Duy, V.H.; Jafari, S.; Alsaadi, F.E.; Alsaadi, F.E. Dynamic system with no equilibrium and its chaos anti-synchronization. Automatika 2018, 59, 35–42. [Google Scholar] [CrossRef]
- Tutueva, A.V.; Karimov, T.I.; Nepomuceno, E.G.; Butusov, D.N. Detection of hidden oscillations in systems without equilibrium. Int. J. Bifurc. Chaos 2021, 31, 2150043. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, X.P.; Zeng, Z.G. A simple no-equilibrium chaotic system with only one signum function for generating multidirectional variable hidden attractors and its hardware implementation. Chaos 2020, 30, 053129. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Wang, G.Y.; Shen, Y.R.; Yuan, F.; Yu, S.M. Hidden coexisting attractors in a chaotic system without equilibrium point. Int. J. Bifurc. Chaos 2018, 28, 1830033. [Google Scholar] [CrossRef]
- Bao, B.C.; Hu, F.W.; Chen, M.; Xu, Q.; Yu, Y.J. Self-excited and hidden attractors found simultaneously in a modified Chua’s circuit. Int. J. Bifurc. Chaos 2015, 25, 1550075. [Google Scholar] [CrossRef]
- Deng, Q.L.; Wang, C.H. Multi-scroll hidden attractors with two stable equilibrium points. Chaos 2019, 29, 093112. [Google Scholar] [CrossRef]
- Molaie, M.; Jafari, S.; Sprott, J.C.; Golpayegani, S.M.R.H. Simple chaotic flows with one stable equilibrium. Int. J. Bifurc. Chaos 2013, 23, 1350188. [Google Scholar] [CrossRef]
- Munmuangsaen, B.; Srisuchinwong, B. A hidden chaotic attractor in the classical Lorenz system. Chaos Solitons Fractals 2018, 107, 61–66. [Google Scholar] [CrossRef]
- Wang, X.; Pham, V.T.; Jafari, S.; Volos, C.; Munoz-Pacheco, J.M.; Tlelo-Cuautle, E. A new chaotic system with stable equilibrium: From theoretical model to circuit implementation. IEEE Access 2017, 5, 8851–8858. [Google Scholar] [CrossRef]
- Wei, Z.C.; Yang, Q.G. Dynamical analysis of a new autonomous 3-D chaotic system only with stable equilibria. Nonlin Anal. Real World Appl. 2011, 12, 106–118. [Google Scholar] [CrossRef]
- Wei, Z.C.; Wang, Z. Chaotic behavior and modified function projective synchronization of a simple system with one stable equilibrium. Kybernetika 2013, 49, 359–374. [Google Scholar]
- Barati, K.; Jafari, S.; Sprott, J.C.; Pham, V.T. Simple chaotic flows with a curve of equilibria. Int. J. Bifurc. Chaos 2016, 26, 1630034. [Google Scholar] [CrossRef]
- Gotthans, T.; Sprott, J.C.; Petrzela, J. Simple chaotic flow with circle and square equilibrium. Int. J. Bifurc. Chaos 2016, 26, 1650137. [Google Scholar] [CrossRef]
- Pham, V.T.; Volos, C.; Kapitaniak, T.; Jafari, S.; Wang, X. Dynamics and circuit of a chaotic system with a curve of equilibrium points. Int. J. Electron. 2018, 105, 385–397. [Google Scholar] [CrossRef]
- Pham, V.T.; Volos, C.; Jafari, S.; Wei, Z.C.; Wang, X. Constructing a novel no-equilibrium chaotic system. Int. J. Bifurc. Chaos 2014, 24, 1450073. [Google Scholar] [CrossRef]
- Pham, V.T.; Jafari, S.; Kapitaniak, T. Constructing a chaotic system with an infinite number of equilibrium points. Int. J. Bifurc. Chaos 2016, 26, 1650225. [Google Scholar] [CrossRef]
- Pham, V.T.; Jafari, S.; Kapitaniak, T.; Volos, C.; Kingni, S.T. Generating a chaotic system with one stable equilibrium. Int. J. Bifurc. Chaos 2017, 27, 1750053. [Google Scholar] [CrossRef]
- Joshi, M.; Ranjan, A. An autonomous simple chaotic jerk system with stable and unstable equilibria using reverse sine hyperbolic functions. Int. J. Bifurc. Chaos 2020, 30, 2050070. [Google Scholar] [CrossRef]
- Kingni, S.T.; Kuiate, G.F.; Tamba, V.K.; Pham, V.T.; Hoang, D.V. Self-excited and hidden attractors in an autonomous Josephson jerk oscillator: Analysis and its application to text encryption. J. Comput. Nonlinear Dynam. 2019, 14, 071004. [Google Scholar] [CrossRef]
- Li, C.B.; Sprott, J.C.; Joo-Chen Thio, W.; Gu, Z.Y. A simple memristive jerk system. IET Circuits Devices Syst. 2021, 15, 388–392. [Google Scholar] [CrossRef]
- Zhang, S.; Zeng, Y.C. A simple Jerk-like system without equilibrium: Asymmetric coexisting hidden attractors, bursting oscillation and double full Feigenbaum remerging trees. Chaos Solitons Fractals 2019, 120, 25–40. [Google Scholar] [CrossRef]
- Danca, M.F. Hidden chaotic attractors in fractional-order systems. Nonlinear Dyn. 2017, 89, 577–586. [Google Scholar] [CrossRef] [Green Version]
- Liu, T.M.; Ya, H.Z.; Banerjee, S.; Mou, J. A fractional-order chaotic system with hidden attractor and self-excited attractor and its DSP implementation. Chaos Solitons Fractals 2021, 145, 110791. [Google Scholar] [CrossRef]
- Li, C.B.; Sprott, J.C. Multistability in the Lorenz system: A broken butterfly. Int. J. Bifurcat. Chaos 2014, 24, 1450131. [Google Scholar] [CrossRef]
- Chudzik, A.; Perlikowski, P.; Stefanski, A.; Kapitaniak, T. Multistability and rare attractors in van der Pol-Duffing oscillator. Int. J. Bifurc. Chaos 2011, 21, 1907–1912. [Google Scholar] [CrossRef]
- He, S.B.; Natiq, H.; Mukherjee, S. Multistability and chaos in a noise-induced blood flow. Eur. Phys. J. Spec. Top. 2021, 230, 1525–1533. [Google Scholar] [CrossRef]
- Kapitaniak, T.; Leonov, G.A. Multistability: Uncovering hidden attractors. Eur. Phys. J. Spec. Top. 2015, 224, 1405–1408. [Google Scholar] [CrossRef] [Green Version]
- Tagne, R.L.M.; Kengne, J.; Nguomkam Negou, A. Multistability and chaotic dynamics of a simple Jerk system with a smoothly tuneable symmetry and nonlinearity. Int. J. Dyn. Control 2019, 7, 476–495. [Google Scholar] [CrossRef]
- Natiq, H.; Kamel Ariffin, M.R.; Asbullah, M.A.; Mahad, Z.; Najah, M. Enhancing chaos complexity of a plasma model through power input with desirable random features. Entropy 2021, 23, 48. [Google Scholar] [CrossRef] [PubMed]
- Lai, Q.; Norouzi, B.; Liu, F. Dynamic analysis, circuit realization, control design and image encryption application of an extended Lü system with coexisting attractors. Chaos Solitons Fractals 2018, 114, 230–245. [Google Scholar] [CrossRef]
- Peng, G.Y.; Min, F.H. Multistability analysis, circuit implementations and application in image encryption of a novel memristive chaotic circuit. Nonlinear Dyn. 2017, 90, 1607–1625. [Google Scholar] [CrossRef]
- Bao, J.H.; Liu, Y.J. Multistability and bifurcations in a 5D segmented disc dynamo with a curve of equilibria. Adv. Differ. Equ. 2019, 2019, 345. [Google Scholar] [CrossRef] [Green Version]
- Rajagopal, K.; Akgul, A.; Moroz, I.M.; Wei, Z.C.; Jafari, S.; Hussain, I. A simple chaotic system with topologically different attractors. IEEE Access 2019, 7, 89936–89947. [Google Scholar] [CrossRef]
- Singh, J.P.; Roy, B.K.; Kuznetsov, N.V. Multistability and hidden attractors in the dynamics of permanent magnet synchronous motor. Int. J. Bifurc. Chaos 2019, 29, 1950056. [Google Scholar] [CrossRef]
- Njitacke, Z.T.; Kengne, J.; Kamdjeu Kengne, L. Antimonotonicity, chaos and multiple coexisting attractors in a simple hybrid diode-based jerk circuit. Chaos Solitons Fractals 2017, 105, 77–91. [Google Scholar] [CrossRef]
- Zhang, Y.Z.; Liu, Z.; Wu, H.G.; Chen, S.Y.; Bao, B.C. Extreme multistability in memristive hyper-jerk system and stability mechanism analysis using dimensionality reduction model. Eur. Phys. J. Spec. Top. 2019, 228, 1995–2009. [Google Scholar] [CrossRef]
- Chen, H.; He, S.B.; Pano Azucena, A.D.; Yousefpour, A.; Jahanshahi, H.; López, M.A.; Alcaraz, R. A multistable chaotic jerk system with coexisting and hidden attractors: Dynamical and complexity analysis, FPGA-based realization, and chaos stabilization using a robust controller. Symmetry 2020, 12, 569. [Google Scholar] [CrossRef] [Green Version]
- Faghani, Z.; Nazarimehr, F.; Jafari, S.; Sprott, J.C. A new category of three-dimensional chaotic flows with identical eigenvalues. Int. J. Bifurc. Chaos 2020, 30, 2050026. [Google Scholar] [CrossRef]
- Rajagopal, K.; Kingni, S.T.; Kom, G.H.; Pham, V.T.; Karthikeyan, A.; Jafari, S. Self-excited and hidden attractors in a simple chaotic jerk system and in its time-delayed form: Analysis, electronic implementation, and synchronization. J. Korean Phys. Soc. 2020, 77, 145–152. [Google Scholar] [CrossRef]
- Sprott, J.C. A proposed standard for the publication of new chaotic systems. Int. J. Bifurc. Chaos 2011, 21, 2391–2394. [Google Scholar] [CrossRef] [Green Version]
- Sang, B. Hopf bifurcation formulae and applications to the Genesio-Tesi system. J. Nonlinear Funct. Anal. 2019, 2019, 34. [Google Scholar]
- Liu, W.M. Criterion of Hopf bifurcation without using eigenvalues. J. Math. Anal. Appl. 1994, 182, 250–256. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.L.; Liu, Y.R.; Chen, H.B. Hopf bifurcation for a class of three-dimensional nonlinear dynamic systems. Bull. Sci. Math. 2010, 134, 786–798. [Google Scholar] [CrossRef] [Green Version]
- Sang, B. The Hopf bifurcations in the permanent magnet synchronous motors. J. Nonlinear Model. Anal. 2021, 3, 179–191. [Google Scholar]
- Volos, C.K.; Kyprianidis, I.M.; Stouboulos, I.N. A chaotic path planning generator for autonomous mobile robots. Robot. Auton. Syst. 2012, 60, 651–656. [Google Scholar] [CrossRef]
- Chen, G.R.; Ueda, T. Chaos in Circuits and Systems; World Scientific: Singapore, 2002. [Google Scholar]
- Wang, N.; Zhang, G.S.; Bao, H. Bursting oscillations and coexisting attractors in a simple memristor-capacitor-based chaotic circuit. Nonlinear Dyn. 2019, 97, 1477–1494. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Sang, B.; Wang, N.; Ahmad, I. Chaotic Dynamics by Some Quadratic Jerk Systems. Axioms 2021, 10, 227. https://doi.org/10.3390/axioms10030227
Liu M, Sang B, Wang N, Ahmad I. Chaotic Dynamics by Some Quadratic Jerk Systems. Axioms. 2021; 10(3):227. https://doi.org/10.3390/axioms10030227
Chicago/Turabian StyleLiu, Mei, Bo Sang, Ning Wang, and Irfan Ahmad. 2021. "Chaotic Dynamics by Some Quadratic Jerk Systems" Axioms 10, no. 3: 227. https://doi.org/10.3390/axioms10030227
APA StyleLiu, M., Sang, B., Wang, N., & Ahmad, I. (2021). Chaotic Dynamics by Some Quadratic Jerk Systems. Axioms, 10(3), 227. https://doi.org/10.3390/axioms10030227






