Periodic Third-Order Problems with a Parameter

Abstract

This work concerns with the solvability of third-order periodic fully problems with a weighted parameter, where the nonlinearity must verify only a local monotone condition and no periodic, coercivity or super or sublinearity restrictions are assumed, as usual in the literature. The arguments are based on a new type of lower and upper solutions method, not necessarily well ordered. A Nagumo growth condition and Leray–Schauder’s topological degree theory are the existence tools. Only the existence of solution is studied here and it will remain open the discussion on the non-existence and the multiplicity of solutions. Last section contains a nonlinear third-order differential model for periodic catatonic phenomena, depending on biological and/or chemical parameters.

1. Introduction

In this paper we consider a third-order periodic problem composed by the differential equation

$$u^{‴}\left(t\right)+f\left(t,u\left(t\right),u^{\prime }\left(t\right),u^{″}\left(t\right)\right)=sg\left(t\right),t\in [0,1],$$

(1)

where $f:[0,1]\times {\mathbb{R}}^3\to \mathbb{R}$ and $g:[0,1]\to {\mathbb{R}}^{+}$ are continuous functions, $s\in \mathbb{R}$ a parameter, and the periodic boundary conditions

$$\begin{array}{ccc}\hfill u\left(0\right)& =& u\left(1\right),\hfill \\ \hfill u^{\prime }\left(0\right)& =& u^{\prime }\left(1\right),\hfill \\ \hfill u^{″}\left(0\right)& =& u^{″}\left(1\right).\hfill \end{array}$$

(2)

The so-called Ambrosetti–Prodi problem for an equation of the form

$$G\left(x\right)=s,$$

(3)

was introduced in [1], and the existence, non-existence or the multiplicity of solutions depend on the parameter. In short, it guarantees the existence of some number $s_0$ such that (3) has zero, at least one or at least two solutions if $s<s_0$, $s=s_0$ or $s>s_0,$ not necessarily by this order.

Since then, Ambrosetti–Prodi results have been obtained for different types of boundary value problems, such as with separated boundary conditions [2,3,4], Neuman’s type [5], three-point boundary conditions [6], among others.

The periodic case has been studied, in last decades, by in several authors, as, for example, [7,8,9,10,11,12,13,14,15,16,17]. However, third-order or higher-order periodic problems, with fully general nonlinearities, not necessarily periodic, are scarce in the literature (to the best of our knowledge, we mention [18,19].

Motivated by the above papers, we present in this work a first approach for third-order periodic fully differential equations, where the existence of periodic solutions depends on a weighted parameter, as in (1). The arguments are based on a new type of lower and upper solutions method, not necessarily well ordered, together with well-ordered adequate auxiliary functions, obtained from translation of lower and upper solutions. A Nagumo growth condition and Leray–Schauder’s topological degree theory, complete the existence tools to guarantee the solvability of our problem, for some values of the parameter $s.$ We underline that the nonlinearity must verify only a local monotone assumption and no periodic, coercivity or super and/or sublinearity conditions are assumed, as usual in the literature.

Remark that, it will remain open the issue of what are the sufficient conditions on the nonlinearity to have the non-existence and the multiplicity of solutions, depending on s.

Periodic problems have a huge variety of applications. Here we consider a reaction-diffusion linear system for the thyroid-pituitary interaction, which is translated by a nonlinear third-order differential equation. In this case the role of the parameter s is played by some coefficients with biological and chemical meaning, which ensuring the existence of periodic catatonia phenomena. Moreover, this application take advantage from the localization part of the main theorem, to show that the periodic solutions are not trivial.

This paper is organized as it follows: Section 2 contains the definitions and the a priori bounds for the second derivative, from Nagumo’s condition. In Section 3, we present the main result: an existence and localization theorem for the values of the parameter such that there are lower and upper solutions. Last section discuss the existence of periodic catatonic episodes based on some relations of certain coefficients, considered as parameters.

2. Definitions and a Priori Estimations

In higher-order periodic boundary value problems, the order between lower and upper solutions is an issue that should be avoided. The next definition suggests a method to overcome it, by translating, up and down, of upper and lower solutions, respectively, by perturbating them with the sup norm:

$${∥w∥}_{\infty }:=\underset{t\in \left[0,1\right]}{sup}\left|w\left(t\right)\right|.$$

Definition 1.

The function $\alpha \in {\mathcal{C}}^3[0,1]$ is a lower solution of problem (1) and (2) if:

(i) 

${\alpha }^{‴}\left(t\right)+f\left(t,{\alpha }_0\left(t\right),{\alpha }^{\prime }\left(t\right),{\alpha }^{″}\left(t\right)\right)\ge s$$g\left(t\right),$$t\in [0,1],$

where

$${\alpha }_0\left(t\right):=\alpha \left(t\right)-{∥\alpha ∥}_{\infty };$$

(4)

(ii) 

${\alpha }^{″}\left(0\right)\ge {\alpha }^{″}\left(1\right),$${\alpha }^{\prime }\left(0\right)={\alpha }^{\prime }\left(1\right).$

The function $\beta \in {\mathcal{C}}^3[0,1]$ is an upper solution of problem (1) and (2) if:

(iii) 

${\beta }^{‴}\left(t\right)+f\left(t,{\beta }_0\left(t\right),{\beta }^{\prime }\left(t\right),{\beta }^{″}\left(t\right)\right)\le s$$g\left(t\right),$$t\in [0,1],$

where

$${\beta }_0\left(t\right):=\beta \left(t\right)+{∥\beta ∥}_{\infty };$$

(5)

(iv) 

${\beta }^{″}\left(0\right)\le {\beta }^{″}\left(1\right),$${\beta }^{\prime }\left(0\right)={\beta }^{\prime }\left(1\right).$

We underline that although $\alpha$ and $\beta$ are not necessarily ordered, the auxiliary functions ${\alpha }_0$ and ${\beta }_0$ are well ordered, as

$${\alpha }_0\left(t\right)\le 0\le {\beta }_0\left(t\right),\mathrm{for}\mathrm{every}t\in [0,1].$$

The unique growth assumption required on the nonlinearity in (1) is given by a Nagumo-type condition:

Definition 2.

A continuous function $h:[0,1]\times {\mathbb{R}}^3\to \mathbb{R}$ verifies a Nagumo-type condition relatively to some continuous functions ${\gamma }_i,{\Gamma }_i,$$i=0,1,$ such that ${\gamma }_i\left(t\right)\le {\Gamma }_i\left(t\right),$ for every $t\in [0,1],$ in the set

$$S=\left\{(t,x_0,x_1,x_2)\in [0,1]\times {\mathbb{R}}^3:{\gamma }_i\left(t\right)\le x_i\le {\Gamma }_i\left(t\right),i=0,1\right\},$$

if there is a continuous function ${\psi }_S:[0,+\infty [\to [k,+\infty [$$(k>0)$ such that

$$\left|h(t,x_0,x_1,x_2)\right|\le {\psi }_S\left(\left|x_2\right|\right),\forall (t,x_0,x_1,x_2)\in S,$$

(6)

with

$${\int }_0^{+\infty }\frac{z}{{\psi }_S\left(z\right)}dz=+\infty .$$

(7)

Now we can have an a priori estimation for the second derivatives of possible solutions of (1), as it was proved in [20], Lemma 1.

Lemma 1.

Let $h:[0,1]\times {\mathbb{R}}^3\to \mathbb{R}$ be a continuous function verifying the Nagumo-type conditions (6) and (7) in $S.$ Then there is $r>0$ such that every solution $y\left(t\right)$ of (1) verifying

$${\gamma }_0\left(t\right)\le y\left(t\right)\le {\Gamma }_0\left(t\right),{\gamma }_1\left(t\right)\le y^{\prime }\left(t\right)\le {\Gamma }_1\left(t\right)$$

for every $t\in [0,1],$ satisfies

$$∥y^{″}∥<r.$$

Remark 1.

The radius r depends only on the parameter s and on the functions $h,{\psi }_s,{\gamma }_1$ and ${\Gamma }_1$ and it can be taken independent of s as long as it belongs to a bounded set.

3. Existence Result

For the values of the parameter s such that there are upper and lower solutions of (1) and (2), where the first derivatives are well ordered, we obtain the following result:

Theorem 1.

Let $f:[0,1]\times {\mathbb{R}}^3\to \mathbb{R}$ and $g:[0,1]\to {\mathbb{R}}^{+}$ be continuous functions. Assume that there are lower and upper solutions of problem (1) and (2), $\alpha \left(t\right)$ and $\beta \left(t\right),$ respectively, accordingly Definition 1, such that

$${\alpha }^{\prime }\left(t\right)\le {\beta }^{\prime }\left(t\right),fort\in [0,1],$$

and f verifies the Nagumo-type conditions (6) and (7) in

$$S_{*}=\left\{\begin{array}{c}(t,x_0,x_1,x_2)\in [0,1]\times {\mathbb{R}}^3:{\alpha }_0\left(t\right)\le x_0\le {\beta }_0\left(t\right),\\ {\alpha }^{\prime }\left(t\right)\le x_1\le {\beta }^{\prime }\left(t\right)\end{array}\right\}.$$

If

$$f(t,{\alpha }_0\left(t\right),x_1,x_2)\le f(t,x_0,x_1,x_2)\le f(t,{\beta }_0\left(t\right),x_1,x_2),$$

(8)

for fixed $(t,x_1,x_2)\in [0,1]\times {\mathbb{R}}^2$ and ${\alpha }_0\left(t\right)\le x_0\le {\beta }_0\left(t\right),$ then (1) and (2) has at least a solution $u\left(t\right)\in C^3\left(\left[0,1\right]\right)$ such that ${\alpha }_0\left(t\right)\le u\left(t\right)\le {\beta }_0\left(t\right)$, ${\alpha }^{\prime }\left(t\right)\le u^{\prime }\left(t\right)\le {\beta }^{\prime }\left(t\right),\forall t\in [0,1].$

Proof. 

For $\lambda \in \left[0,1\right]$ consider the homotopic and truncated auxiliary equation

$$\begin{array}{c}{u}^{‴}\left(t\right)+\lambda f\left(t,{\delta }_0\left(t,u\left(t\right)\right),{\delta }_1\left(t,u^{\prime }\left(t\right)\right),u^{″}\left(t\right)\right)\\ -u^{\prime }\left(t\right)+\lambda {\delta }_1\left(t,u^{\prime }\left(t\right)\right)=\lambda sg\left(t\right)\end{array}$$

(9)

where the continuos functions ${\delta }_0,{\delta }_1:\left[0,1\right]\times \mathbb{R}⟶\mathbb{R}$, are given by

$${\delta }_0(t,x)=\left\{\begin{array}{ccc}\hfill {\beta }_0\left(t\right)& \mathrm{if}& x>{\beta }_0\left(t\right)\hfill \\ \hfill x& \mathrm{if}& {\alpha }_0\left(t\right)\le x\le {\beta }_0\left(t\right)\hfill \\ \hfill {\alpha }_0\left(t\right)& \mathrm{if}& x<{\alpha }_0\left(t\right),\hfill \end{array}\right.$$

(10)

and

$${\delta }_1(t,y)=\left\{\begin{array}{ccc}\hfill {\beta }^{\prime }\left(t\right)& ,& y>{\beta }^{\prime }\left(t\right)\hfill \\ \hfill y& ,& {\alpha }^{\prime }\left(t\right)\le y\le {\beta }^{\prime }\left(t\right)\hfill \\ \hfill {\alpha }^{\prime }\left(t\right)& ,& y<{\alpha }^{\prime }\left(t\right),\hfill \end{array}\right.$$

(11)

with ${\alpha }_0$ and ${\beta }_0$ defined in (4) and (5), respectively, together with the boundary conditions

$$\begin{array}{c}u\left(0\right)=\lambda {\eta }_0\left(u\left(1\right)\right),\hfill \\ u^{\prime }\left(0\right)=u^{\prime }\left(1\right),\hfill \\ u^{″}\left(0\right)=u^{″}\left(1\right),\hfill \end{array}$$

(12)

where the function ${\eta }_0:\mathbb{R}⟼\mathbb{R},$ is defined by

$${\eta }_0\left(u\left(1\right)\right)=\left\{\begin{array}{ccc}{\beta }_0\left(1\right)& ,& u\left(1\right)>{\beta }_0\left(0\right)\\ u\left(1\right)& ,& {\alpha }_0\left(0\right)\le u\left(1\right)\le {\beta }_0\left(0\right)\\ {\alpha }_0\left(1\right)& ,& u\left(1\right)<{\alpha }_0\left(0\right).\end{array}\right.$$

(13)

Take $r_1>0$ such that, for $t\in [0,1]$,

$$\begin{array}{c}-r_1\le {\alpha }^{\prime }\left(t\right)\le {\beta }^{\prime }\left(t\right)\le r_1,\\ sg\left(t\right)-f\left(t,{\alpha }_0\left(t\right),{\alpha }^{\prime }\left(t\right),0\right)-r_1-{\alpha }^{\prime }\left(t\right)<0,\\ sg\left(t\right)-f\left(t,{\beta }_0\left(t\right),{\beta }^{\prime }\left(t\right),0\right)+r_1-{\beta }^{\prime }\left(t\right)>0.\end{array}$$

(14)

Step 1: Every solution of the problem (1) and (2) satisfies for every $t\in \left[0,1\right]$

$$\left|u^{\prime }\left(t\right)\right|<{\mathit{r}}_1,$$

independently of $\lambda \in \left[0,1\right]$.

Assume, by contradiction, that exist $t\in \left[0,1\right]$ such that $\left|u^{\prime }\left(t\right)\right|\ge r_1.$ Consider the case $u^{\prime }\left(t\right)\ge r_1$ and define

$$u^{\prime }\left(t_0\right):=\underset{t\in \left[0,1\right]}{max}{u}^{\prime }\left(t\right)\ge r_1>0.$$

(15)

If $t_0\in \left]0,1\right[$ and $\lambda \in \left]0,1\right[$, then $u^{″}\left(t_0\right)=0$ and $u^{‴}\left(t_0\right)\le 0$. By (10), (11) and (14), the following contradiction holds

$$\begin{array}{ccc}\hfill 0& \ge & u^{‴}\left(t_0\right)\hfill \\ & =& \lambda sg\left(t_0\right)-\lambda f\left(t_0,{\delta }_0\left(t_0,u\left(t_0\right)\right),{\delta }_1\left(t_0,u^{\prime }\left(t_0\right)\right),u^{″}\left(t_0\right)\right)\hfill \\ & & +u^{\prime }\left(t_0\right)-\lambda {\delta }_1\left(t_0,u^{\prime }\left(t_0\right)\right)\hfill \\ & \ge & \lambda \left[sg\left(t_0\right)-f\left(t_0,{\beta }_0\left(t_0\right),{\beta }^{{}^{\prime }}\left(t_0\right),0\right)+r_1-{\beta }^{{}^{\prime }}\left(t_0\right)\right]>0.\hfill \end{array}$$

If $\lambda =0$ the contradiction results from (15):

$$0\ge u^{‴}\left(t_0\right)=u^{\prime }\left(t_0\right)\ge r_1>0.$$

If $t_0=0$ then

$$u^{\prime }\left(0\right)=\underset{t\in \left[0,1\right]}{max}{u}^{\prime }\left(t\right).$$

By (12), $u^{\prime }\left(0\right)=u^{\prime }\left(1\right),$ then $u^{\prime }\left(1\right)$ is a maximum, too, and

$$0\ge u^{″}\left(0\right)=u^{″}\left(1\right)\ge 0,$$

therefore $u^{″}\left(0\right)=0$ and $u^{″}\left(0\right)\le 0$.

The case $t_0=1$ is analogous and so $u^{\prime }\left(t\right)<r_1$, for every $t\in \left[0,1\right].$

As the inequality $u^{\prime }\left(t\right)>-r_1$, for every $t\in \left[0,1\right]$, can be proved by the same arguments, then

$$\left|u^{\prime }\left(t\right)\right|<r_1,\forall t\in \left[0,1\right].$$

By integration in $\left[0,t\right]$, of previous inequality, using (12) and considering

$${\xi }_0=max\left\{{\beta }_0\left(0\right),-{\alpha }_0\left(0\right)\right\},$$

the following relations are obtained

$$\begin{array}{ccc}\hfill u\left(t\right)& <& u\left(0\right)+r_{1}t=\lambda {\eta }_0\left(u\left(1\right)\right)+r_{1}t\hfill \\ & \le & \lambda {\beta }_0\left(0\right)+r_1\le {\beta }_0\left(0\right)+r_1\hfill \\ & \le & {\xi }_0+r_1,\hfill \end{array}$$

(16)

and

$$u\left(t\right)>u\left(0\right)-r_{1}t\ge {\alpha }_0\left(0\right)-r_1\ge -{\xi }_0-r_1.$$

(17)

By (16) and (17), therefore $\left|u\left(t\right)\right|<r_0,\forall t\in \left[0,1\right]$, with $r_0={\xi }_0+r_1$.

Step 2: There exist $r>0$ such that every solution u of problem (9)–(12) satisfies

$$\left|u^{″}\left(t\right)\right|<r,\forall t\in \left[0,1\right],$$

independently of $\lambda \in \left[0,1\right]$.

For $r_0$ and $r_1$, given in the previous step, consider the set

$$E_r=\left\{\left(t,x,y,z\right)\in \left[0,1\right]\times {\mathbb{R}}^3:\left|x\right|<r_0,\left|y\right|<r_1\right\},$$

and the function $F_{\lambda }:E_r⟼\mathbb{R}$ given by

$$F_{\lambda }\left(t,x,y,z\right)=\lambda f\left(t,{\delta }_0\left(t,x\right),{\delta }_1\left(t,y\right),z\right)-y+\lambda {\delta }_1\left(t,u^{\prime }\left(t\right)\right)$$

As f satisfies the Nagumo-type conditions (6) and (7) in $S_{*}$, therefore $F_{\lambda }$ the same conditions in $E_r.$

In fact, by (11), (12) and $\lambda \in \left[0,1\right]$,

$$\begin{array}{ccc}\hfill \left|F_{\lambda }\left(t,x,y,z\right)\right|& \le & \left|f\left(t,{\delta }_0\left(t,x\right),{\delta }_1\left(t,y\right),z\right)\right|+y+\left|{\delta }_1\left(t,u^{\prime }\left(t\right)\right)\right|\hfill \\ & \le & {\psi }_{S_{*}}\left(\left|z\right|\right)+r_1+r_1={\psi }_{S_{*}}\left(\left|z\right|\right)+2r_1,\hfill \end{array}$$

Consider, $h_{E_r}\left(w\right):={\psi }_{S_{*}}\left(w\right)+2r_1$ ($w\ge 0)$. As ${\psi }_{S_{*}}:[0,+\infty [\to [k,+\infty [$ ($k>0)$ is a continuous function, then, by (7),

$$\begin{array}{ccc}\hfill \underset{0}{\overset{+\infty }{\int }}\frac{\tau }{h_{E_r}\left(\tau \right)}d\tau & =& \underset{0}{\overset{+\infty }{\int }}\frac{\tau }{{\psi }_{S_{*}}\left(\tau \right)+2r_1}d\tau =\underset{0}{\overset{+\infty }{\int }}\frac{\tau }{{\psi }_{S_{*}}\left(\tau \right)\left[1+\frac{2r_1}{{\psi }_{S_{*}}\left(\tau \right)}\right]}d\tau \hfill \\ & \ge & \frac{1}{1+\frac{2r_1}{k}}\underset{0}{\overset{+\infty }{\int }}\frac{\tau }{{\psi }_{S_{*}}\left(\tau \right)}d\tau =+\infty .\hfill \end{array}$$

Therefore, $F_{\lambda }$ satisfies the Nagumo condition in $E_r$ with $h_{S_{*}}$ replaced $h_{E_r}$, independently of $\lambda$.

Defining

$${\gamma }_i:=-r_i,{\Gamma }_i:=r_i,\mathrm{for}i=0,1,$$

the assumptions of (1) are satisfied with $S_{*}$ replaced be $E_r$.

So there exist $R>0$, depending only on $r_i$, $i=0,1$, and $h_{E_r}$, such that

$$\left|u^{″}\left(t\right)\right|<R,\forall t\in \left[0,1\right].$$

Step 3: For $\lambda =1$ the problem (9)–(12) has a solution $u_1$.

Consider the operators

$$\mathcal{L}:C^3\left(\left[0,1\right]\right)\subset C^2\left(\left[0,1\right]\right)⟼C\left(\left[0,1\right]\right)\times {\mathbb{R}}^3,$$

and, for $\lambda \in \left[0,1\right]$,

$${\Theta }_{\lambda }:C^3\left(\left[0,1\right]\right)\subset C^2\left(\left[0,1\right]\right)⟼C\left(\left[0,1\right]\right)\times {\mathbb{R}}^3,$$

Where

$$\mathcal{L}u=\left(u^{‴},u\left(0\right),u^{\prime }\left(0\right),u^{″}\left(0\right)\right)$$

and

$${\Theta }_{\lambda }u=\left(\begin{array}{c}-\lambda f\left(t,{\delta }_0\left(t,u\left(t\right)\right),{\delta }_1\left(t,u^{\prime }\left(t\right)\right),u^{″}\left(t\right)\right)+u^{\prime }\left(t\right)-\lambda {\delta }_1\left(t,u^{\prime }\left(t\right)\right)\\ +\lambda sg\left(t\right),\\ \lambda {\eta }_0\left(u\left(1\right)\right),u^{\prime }\left(1\right),u^{″}\left(1\right)\end{array}\right).$$

As $\mathcal{L}$ has a compact inverse it can be considered the completely continuous operator

$${\Psi }_{\lambda }:\left(C^2\left(\left[0,1\right]\right),\mathbb{R}\right)⟼\left(C^2\left(\left[0,1\right]\right),\mathbb{R}\right)$$

defined by

$${\Psi }_{\lambda }u=\left[{\mathcal{L}}^{-1}{\Theta }_{\lambda }\right]\left(u\right).$$

For r given by Step 2, consider the set

$$\Omega =\left\{u\in C^2\left(\left[0,1\right]\right):{∥u∥}_{\infty }<r_0,{∥u^{\prime }∥}_{\infty }<r_1,{∥u^{″}∥}_{\infty }<r\right\}$$

By Steps 1 and 2, for every u solution of (9)–(12), $u\notin \partial \Omega$, and so the degree $d\left({\Psi }_{\lambda },\Omega \right)$ is well defined for every $\lambda \in \left[0,1\right]$ and, by homotopy invariance,

$$d\left({\Psi }_0,\Omega \right)=d\left({\Psi }_1,\Omega \right).$$

As the equation $x={\Psi }_0\left(x\right)$ has only the trivial solution, by degree theory,

$$d\left({\Psi }_0,\Omega \right)=\pm 1.$$

Therefore, the equation $u=$${\Psi }_1\left(u\right)$ has at least one solution. As

$${\Psi }_1\left(u\right)=u,$$

is equivalent to

$${\Theta }_{1}u=\mathcal{L}u,$$

then

$$\begin{array}{c}{u}^{‴}\left(t\right)=sg\left(t\right)-f\left(t,{\delta }_0\left(t,u\left(t\right)\right),{\delta }_1\left(t,u^{\prime }\left(t\right)\right),u^{″}\left(t\right)\right)-{\delta }_1\left(t,u^{\prime }\left(t\right)\right)+u^{\prime }\left(t\right),\\ {\eta }_0\left(u\left(1\right)\right)=u\left(0\right)\\ u^{\prime }\left(1\right)=u^{\prime }\left(0\right)\\ u^{″}\left(1\right)=u^{″}\left(0\right).\end{array}$$

(18)

So, the problem (9)–(12), has least a solution $u_1$ in $\Omega$.

Step 4: $u_1$is a solution of (1) and (2).

This solution $u_1$ is a solution of (1) and (2) if it verifies,$\forall t\in \left[0,1\right]$

$$\begin{array}{ccc}\hfill {\alpha }^{\prime }\left(t\right)& \le & u_1^{\prime }\left(t\right)\le {\beta }^{\prime }\left(t\right),\hfill \end{array}$$

(19)

$$\begin{array}{ccc}\hfill {\alpha }_0\left(t\right)& \le & u_1\left(t\right)\le {\beta }_0\left(t\right),\hfill \\ \hfill {\alpha }_0\left(0\right)& \le & u_1\left(1\right)\le {\beta }_0\left(0\right).\hfill \end{array}$$

(20)

Suppose, by contradiction, that there is $t\in \left[0,1\right]$ such that

$${\alpha }^{\prime }\left(t\right)>u_1^{\prime }\left(t\right),$$

and define

$$\underset{t\in \left[0,1\right]}{min}\left[u_1^{\prime }\left(t\right)-{\alpha }^{\prime }\left(t\right)\right]:=u_1^{\prime }\left(t_1\right)-{\alpha }^{\prime }\left(t_1\right)<0.$$

If $t_1\in \left]0,1\right[$, then $u_1^{″}\left(t_1\right)-{\alpha }^{″}\left(t_1\right)=0$ and $u_1^{″}\left(t_1\right)-{\alpha }^{‴}\left(t_1\right)\ge 0$. Therefore, by (1), (10), (11) and (8), we obtain the following contradiction

$$\begin{array}{ccc}\hfill 0& \le & u_1^{‴}\left(t_1\right)-{\alpha }^{‴}\left(t_1\right)\hfill \\ & \le & f\left(t_1,{\delta }_0\left(t_1,u_1\left(t\right)\right),{\delta }_1\left(t_1,u_1^{\prime }\left(t_1\right)\right),u_1^{″}\left(t_1\right)\right)\hfill \\ & & +u_1^{\prime }\left(t_1\right)-{\alpha }^{\prime }\left(t_1\right)-f\left(t_1,{\alpha }_0\left(t_1\right),{\alpha }^{\prime }\left(t_1\right),{\alpha }^{″}\left(t_1\right)\right)\hfill \\ & \le & u_1^{\prime }\left(t\right)-{\alpha }^{\prime }\left(t\right)<0.\hfill \end{array}$$

If $t_1=0$ then

$$\underset{t\in \left[0,1\right]}{min}\left[u_1^{\prime }\left(t\right)-{\alpha }^{\prime }\left(t\right)\right]:=u_1^{\prime }\left(0\right)-{\alpha }^{\prime }\left(0\right)<0.$$

By (1)

$$0\le u_1^{″}\left(0\right)-{\alpha }^{″}\left(0\right)\le u_1^{″}\left(1\right)-{\alpha }^{″}\left(1\right)\le 0$$

and, therefore,

$$u_1^{″}\left(0\right)={\alpha }^{″}\left(0\right),u_1^{‴}\left(0\right)\ge {\alpha }^{‴}\left(0\right).$$

For the case where $t_1=1$ the proof is identical and so

$${\alpha }^{\prime }\left(t\right)\le u_1^{\prime }\left(t\right),\forall t\in \left[0,1\right].$$

(21)

Applying the same arguments, one can verify that

$$u_1^{\prime }\left(t\right)\le {\beta }^{\prime }\left(t\right),\forall t\in \left[0,1\right].$$

(22)

Integrating (21) in $\left[0,t\right]$, by (4) and (13)

$$\begin{array}{ccc}\hfill u_1\left(t\right)& \ge & u_1\left(0\right)+\alpha \left(t\right)-\alpha \left(0\right)\hfill \\ & \ge & {\alpha }_0\left(0\right)+\alpha \left(t\right)-\alpha \left(0\right)\hfill \\ & =& \alpha \left(t\right)\ge \alpha \left(t\right)-{∥\alpha ∥}_{\infty }={\alpha }_0\left(t\right).\hfill \end{array}$$

Analogously, Integrating (22), by (5) and (13)

$$\begin{array}{ccc}\hfill u_1\left(t\right)& \le & u_1\left(0\right)+\beta \left(t\right)-\beta \left(0\right)\hfill \\ & \le & {\beta }_0\left(0\right)+\beta \left(t\right)-\beta \left(0\right)\hfill \\ & =& \beta \left(t\right)\le \beta \left(t\right)+{∥\beta ∥}_{\infty }={\beta }_0\left(t\right),\hfill \end{array}$$

and, therefore,

$${\alpha }_0\left(t\right)\le u_1\left(t\right)\le {\beta }_0\left(t\right),\forall t\in \left[0,1\right].$$

□

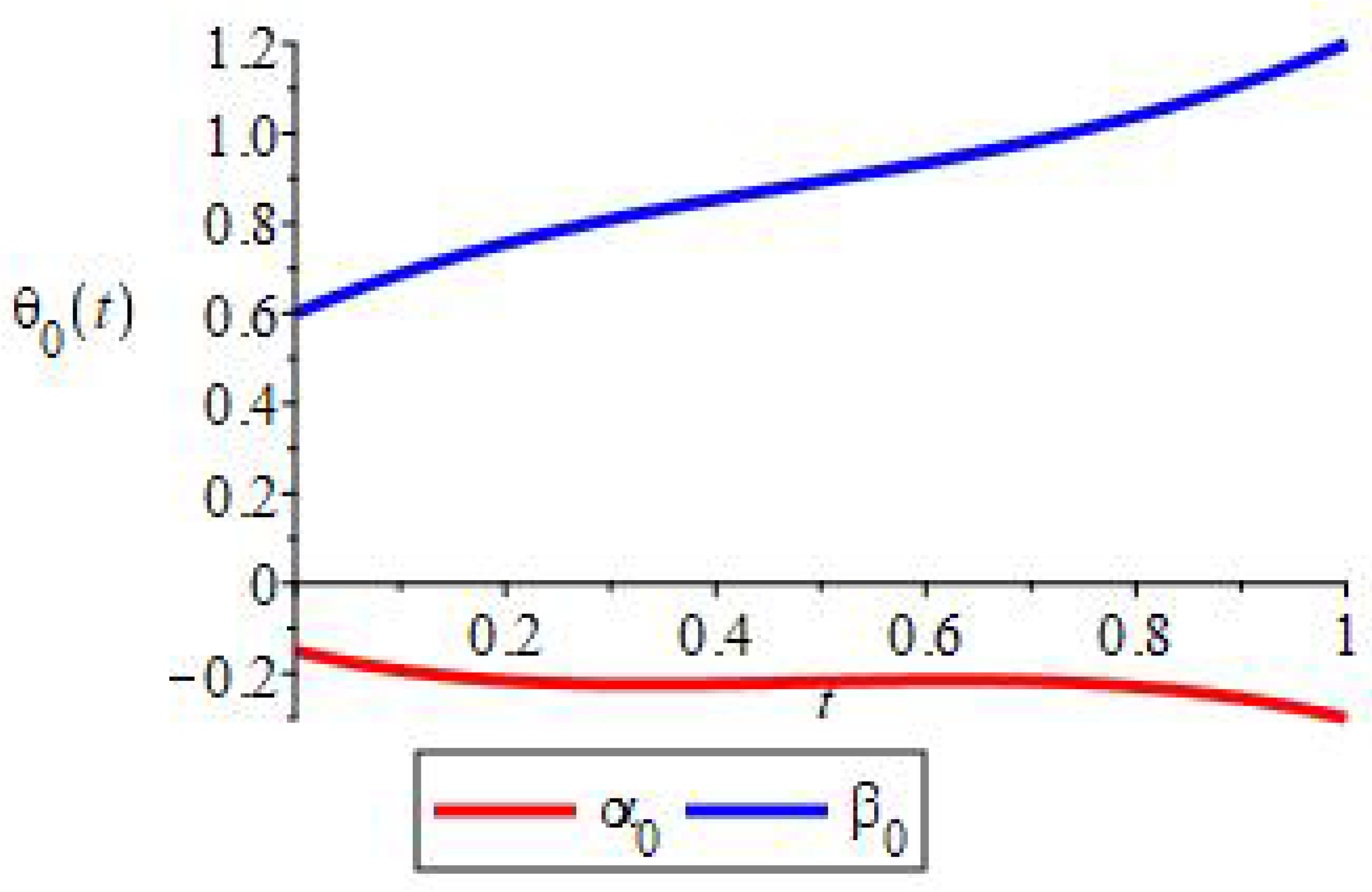
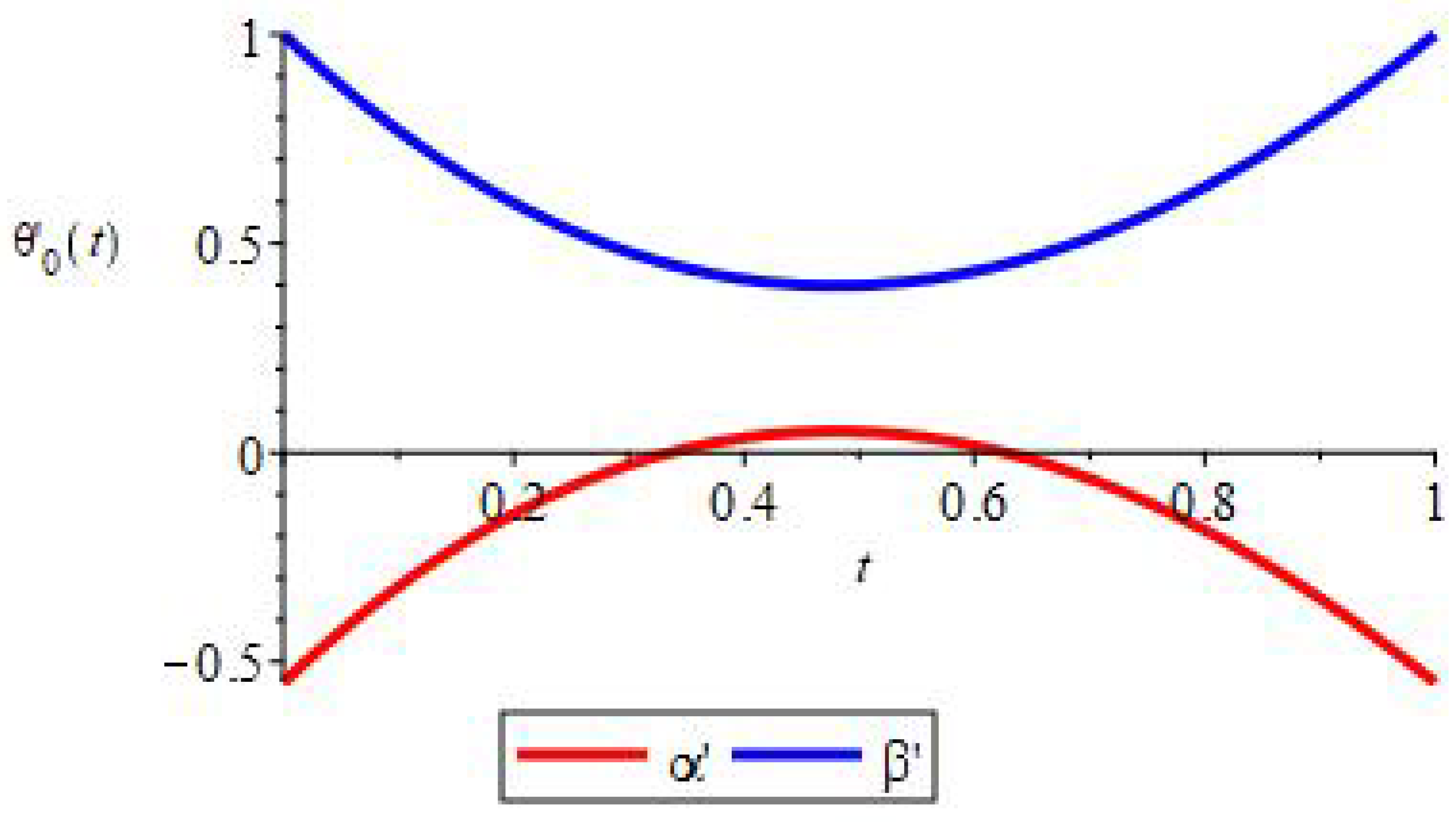
4. Periodic Catatonic Phenomena with a Parameter

In the literature there are several references studying reaction-diffusion phenomena of the thyroid-pituitary interaction. In short, the anterior lobe of the pituitary gland produces the hormone thyrotropin, under the influence of a thyroid releasing factor (TRF), a releasing hormone secreted by the hypothalamus. The thyrotropin induces the thyroid gland to generate an enzyme, that will produce thyroxine, when activated. The thyroxine has a negative feedback effect on the release of thyrotropin by the pituitary gland. The following diagram, Figure 1, outlines this type of interaction.

Figure 1. Thyroid-pituitary interaction.

In [21], the authors describe these interactions by the system

$$\left\{\begin{array}{c}{\displaystyle \frac{d\theta }{dt}}={\displaystyle \frac{k_{1}mP\left(t\right)}{1+mP\left(t\right)}}-b\theta \left(t\right)\\ {\displaystyle \frac{dP}{dt}}={\displaystyle \frac{c-k_{2}n\theta \left(t\right)}{1+n\theta \left(t\right)}}-gP\left(t\right)\end{array}\right.$$

where

P and $\theta$ represent the concentrations of thyrotropin and the thyroid hormone (thyroxine), respectively, at any time t;

c is the rate of production of thyrotropin in the absence of thyroid inhibition;

$k_1$ is a constant equal to the theoretical maximum production rate of the thyroid gland;

$k_2$ a constant assumed to be greater than c so that the production of thyrotropin may be zero for sufficiently large $\theta$;

m and n are the constants in the Langmuir adsorption equations;

b and g are the loss constants.

In [22,23] the authors introduce the concentration of activated enzyme, $E\left(t\right),$ considering the linearized system

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dP}{dt}}& =& \left\{\begin{array}{ccc}c-h\theta \left(t\right)-gP\left(t\right)& ,& \theta \left(t\right)\le \frac{c}{h},\\ & & \\ -gP\left(t\right)& ,& \theta \left(t\right)>\frac{c}{h},\end{array}\right.\hfill \\ \hfill {\displaystyle \frac{dE}{dt}}& =& mP\left(t\right)-kE\left(t\right)\hfill \\ \hfill {\displaystyle \frac{d\theta }{dt}}& =& aE\left(t\right)-b\theta \left(t\right)\hfill \end{array}$$

(23)

where

k represents the loss constants of activated enzyme;

a and h are constants expressing the sensitivities of the glands to stimulation or inhibition.

With the new variables

$$x\left(t\right)={\displaystyle \frac{g}{h}}P\left(t\right),y\left(t\right)={\displaystyle \frac{gk}{hm}}E\left(t\right),$$

and the constants

$$\begin{array}{ccc}\hfill C& =& {\displaystyle \frac{c}{h}},K={\displaystyle \frac{ahm}{bgk}},\hfill \\ \hfill T_1& =& {\displaystyle \frac{1}{g}},T_2={\displaystyle \frac{1}{k}},T_3={\displaystyle \frac{1}{b}},\hfill \end{array}$$

the system (23) becomes

$$\begin{array}{ccc}\hfill T_1{x}^{\prime }\left(t\right)+x\left(t\right)& =& C-\theta \left(t\right),\mathrm{if}\theta \left(t\right)\le C,\hfill \\ \hfill T_1{x}^{\prime }\left(t\right)+x\left(t\right)& =& 0,\mathrm{if}\theta \left(t\right)>C,\hfill \\ \hfill T_2{y}^{\prime }\left(t\right)+y\left(t\right)& =& x\left(t\right),\hfill \\ \hfill T_3{\theta }^{\prime }\left(t\right)+\theta \left(t\right)& =& Ky\left(t\right).\hfill \end{array}$$

(24)

Eliminating both variables x and y in (24) we obtain two third order linear differential equations:

$${\displaystyle \frac{d^3\theta }{d{t}^3}}+{\displaystyle \frac{a_2}{a_1}}{\displaystyle \frac{d^2\theta }{d{t}^2}}+{\displaystyle \frac{a_3}{a_1}}{\displaystyle \frac{d\theta }{dt}}+\frac{1+K}{a_1}\theta \left(t\right)={\displaystyle \frac{KC}{a_1}},\mathrm{if}\theta \left(t\right)\le C,$$

(25)

and

$${\displaystyle \frac{d^3\theta }{d{t}^3}}+{\displaystyle \frac{a_2}{a_1}}{\displaystyle \frac{d^2\theta }{d{t}^2}}+{\displaystyle \frac{a_3}{a_1}}{\displaystyle \frac{d\theta }{dt}}+\frac{K}{a_1}\theta \left(t\right)=0,\mathrm{if}\theta \left(t\right)>C,$$

with the constants

$$\begin{array}{ccc}\hfill a_1& =& T_1{T}_2{T}_3=\frac{k}{ahm}\hfill \\ \hfill a_2& =& T_1{T}_2+T_1{T}_3+T_2{T}_3=\frac{k\left(b+g\right)}{ahm}+\frac{1}{gb}\hfill \\ \hfill a_3& =& T_1+T_2+T_3=\frac{Kb+gb+gK}{gKb}.\hfill \end{array}$$

Relating to the initial parameters and our main result in the Equation (25), we have

$$f(t,\theta \left(t\right),{\theta }^{\prime }\left(t\right),{\theta }^{″}\left(t\right))=S_2{\theta }^{″}\left(t\right)+S_1{\theta }^{\prime }\left(t\right)+\frac{1+K}{a_1}\theta \left(t\right),$$

with

$$\begin{array}{ccc}\hfill S_2& :& ={\displaystyle \frac{a_2}{a_1}}=b+g+\frac{ahm}{kgb},\hfill \\ \hfill S_1& :& ={\displaystyle \frac{a_3}{a_1}}=\frac{\left(b+g\right)ahm}{{\left(kgb\right)}^2}+\frac{1}{k},\hfill \\ \hfill \frac{1+K}{a_1}& =& \frac{bgkahm+{\left(ahm\right)}^2}{bg{k}^2},\hfill \end{array}$$

the parameter

$$s:={\displaystyle \frac{KC}{a_1}}=\frac{a^2{m}^{2}hc}{bg{k}^2}$$

and $g\left(t\right)\equiv 1.$

If there are lower and upper solutions of the periodic problem composed by the nonlinear Equation (25) with the periodic boundary conditions

$${\theta }^{\left(i\right)}\left(0\right)={\theta }^{\left(i\right)}\left(1\right),i=0,1,2,$$

(26)

$\alpha \left(t\right)$ and $\beta \left(t\right),$ respectively, accordingly Definition 1, such that the assumptions of Theorem 1 hold, then there is a periodic solution of (25) and (26), if the parameters $a,m,h,c,b,g$ and k verify the relation

$$\begin{array}{c}{\beta }^{‴}\left(t\right)+S_2{\beta }^{″}\left(t\right)+S_1{\beta }^{\prime }\left(t\right)+\frac{1+K}{a_1}{\beta }_0\left(t\right)\le \frac{a^2{m}^{2}hc}{bg{k}^2}\\ \le {\alpha }^{‴}\left(t\right)+S_2{\alpha }^{″}\left(t\right)+S_1{\alpha }^{\prime }\left(t\right)+\frac{1+K}{a_1}{\alpha }_0\left(t\right).\end{array}$$

As a numeric example, we consider

$$\begin{array}{ccc}\hfill a& =& 1,b=-0.5,c=0.2,g=0.2,\hfill \\ \hfill h& =& 0.2,m=0.8,k=0.1.\hfill \end{array}$$

Related with these values the functions

$$\alpha \left(t\right)=0.1t^4-t^3+1.3t^2-0.55t$$

and

$$\beta \left(t\right)=-0.1t^4+t^3-1.3t^2+t$$

are, respectively, lower and upper solutions of (25), (26) with

$${\alpha }_0\left(t\right)=0.1t^4-t^3+1.3t^2-0.55t-0.15$$

and

$${\beta }_0\left(t\right)=-0.1t^4+t^3-1.3t^2+t+0.6.$$

Remark that all the hypothesis of Theorem 1 are satisfied and, therefore, there is a solution ${\theta }_0$ of (25), (26) for the parameter $s=-25.6,$ and, moreover, this solution ${\theta }_0$ verifies the following properties, for $t\in \left[0,1\right],$

$$\begin{array}{ccc}\hfill 0.1t^4-t^3+1.3t^2-0.55t-0.15& \le & {\theta }_0\left(t\right)\le -0.1t^4+t^3-1.3t^2+t+0.6,\hfill \\ \hfill 0.4t^3-3t^2+2.6t-0.55& \le & {\theta }_0^{\prime }\left(t\right)\le -0.4t^3+3t^2-2.6t+1.\hfill \end{array}$$

as it is illustrated in Figure 2 and Figure 3.

Figure 2. Variation of ${\theta }_0\left(t\right)$.

Figure 3. Variation of ${\theta }_0^{\prime }\left(t\right)$.

Remark that, from the variation of ${\theta }_0^{\prime }\left(t\right)$ this periodic solution ${\theta }_0\left(t\right)$ is not constant, that is, ${\theta }_0\left(t\right)$ is not a trivial periodic solution.