A Dynamic Model of Multiple Time-Delay Interactions between the Virus-Infected Cells and Body’s Immune System with Autoimmune Diseases
Abstract
1. Introduction
2. A Mathematical Model with Multiple Time-Delay Interactions between Infected-Virus and Immune Effector Cells
2.1. Immune Cell Model Formulation
- The effector cell has a constant growth rate, s, of effector cells [29].
- There is a constant rate f of the immune system attacking the body’s own healthy (effector) cells, resulting in an autoimmune disease. The constant f, in general, will be very small compared to c, so that when I is not too large, then the term f I2 will be negligible compared to cI.
- There will be a reduction in the number of effector cells due to their interaction with the virus-infected cells witha constant rate m [29].
2.2. Virus-Infected Cell Model Formulation
- 5.
- The virus-infected cell has a constant growth rate, a, ref. [29] with consideration of a constant factor of growth rate, g, and a time delay before the virus is to be infected.
- 6.
- There will be a constant elimination rate of the virus-infected cells by the healthy immune system (effector cells), b, by a time delay. In other word, b measures how efficiently the effector cells kill the virus-infected cells.
- 7.
- The number of virus-infected cells will decline by a constant parameter of the virus-infected cleanup of effector cells, p, ref. [29] with a time delay.
- 8.
- There will be a reduction in the number of virus-infected cells by a constant rate e that encounters of the two virus-infected cells per unit of time in competing with each other due to the limited number of host cells. The constant rate e here can be considered to be very small.
3. Model Analysis
4. Conclusions
Funding
Conflicts of Interest
References
- Thompson, E. The immune system. J. Am. Med. Assoc. JAMA 2015, 313, 16. [Google Scholar] [CrossRef]
- CRI Staff, How Does the Immune System Work? 30 April 2019. Available online: https://www.cancerresearch.org/blog/april-2019/how-does-the-immune-system-work-cancer?gclid=CjwKCAjwsNiIBhBdEiwAJK4khgG7w-9Ugv3HMGc1VWZbRuhFBOfIPMW2Qo3Dv1-VH1HGvmJruZjwxxoC3HYQAvD_BwE (accessed on 15 May 2021).
- Guide to Your Immune System. 2020. Available online: https://www.webmd.com/cold-and-flu/ss/slideshow-immune-system (accessed on 20 May 2021).
- Immune System, Cleveland Clinic. 2021. Available online: https://my.clevelandclinic.org/health/articles/21196-immune-system (accessed on 10 May 2021).
- Newman, T. How the Immune System Works. Medical News Today. 11 January 2018. Available online: https://www.medicalnewstoday.com/articles/320101 (accessed on 20 May 2021).
- How Does the Immune System Work? 2020. Available online: https://www.ncbi.nlm.nih.gov/books/NBK279364/ (accessed on 20 May 2021).
- Ng, J.; Stovezky, Y.R.; Brenner, D.J.; Formenti, S.C.; Shuryak, I. Development of a model to estimate the association between delay in cancer treatment and local tumor control and risk of metastates. JAMA Netw. Open 2021, 4, 1–10. [Google Scholar] [CrossRef]
- Talkington, A.; Durrett, R. Estimating tumor growth rates in vivo. Bull. Math. Biol. 2015, 77, 1934–1954. [Google Scholar] [CrossRef]
- Vaghi, C.; Rodallec, A.; Fanciullino, R.; Ciccolini, J.; Mochel, J.P.; Mastri, M. Population modeling of tumor growth curves and the reduced Gompertz model improve prediction of the age of experimental tumors. PLoS Comput. Biol. 2020, 16, e1007178. Available online: https://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1007178 (accessed on 25 April 2021). [CrossRef]
- Yin, D.J.; Moes, A.R.; van Hasselt, J.G.C.; Swen, J.J.; Guchelaar, H.-J. A Review of Mathematical Models for Tumor Dynamics and Treatment Resistance Evolution of Solid Tumors. CPT Pharmacomet. Syst. Pharmacol. 2019, 8, 720–737. [Google Scholar] [CrossRef] [PubMed]
- Bekiros, S.; Kouloumpou, D. SBDiEM: A new mathematical model of infectious-disease dynamics. Chaos Solitons Fractals 2020, 136, 109828. [Google Scholar] [CrossRef]
- Rothan, H.A.; Byrareddy, S.N. The epidemiology and pathogenesis of coronavirus disease (COVID-19) outbreak. J. Autoimmun. 2020, 2020, 102433. [Google Scholar] [CrossRef] [PubMed]
- Jackson, T.L.; Byrne, H.M. A mathematical model to study the effects of drug resistance and vasculature on the response of solid tumors to chemotherapy. Math. Biosci. 2000, 164, 17–38. [Google Scholar] [CrossRef]
- Meacham, C.E.; Morrison, S.J. Tumour heterogeneity and cancer cell plasticity. Nature 2013, 501, 328–337. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Bao, J.; Shaob, Y. Mathematical modeling of therapy-induced cancer drug resistance: Connecting cancer mechanisms to population survival rates. Sci. Rep. 2016, 6, 22498. [Google Scholar] [CrossRef]
- Taniguchi, K.; Okami, J.; Kodama, K.; Higashiyama, M.; Kato, K. Intratumor heterogeneity of epidermal growth factor receptor mutations in lung cancer and its correlation to the response to gefitinib. Cancer Sci. 2008, 99, 929–9354. [Google Scholar] [CrossRef] [PubMed]
- Al-Huniti, N.; Feng, Y.; Yu, J.; Lu, Z.; Nagase, M.; Zhou, D.; Sheng, J. Tumor growth dynamic modeling in oncology drug development and regulatory approval: Past, present, and future Opportunities. CPT Pharmacomet. Syst. Pharmacol. 2020, 9, 419–427. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.; Kang, Y.; Wang, W. A stochastic SIRS epidemic model with nonlinear incidence rate. Appl. Math. Comput. 2017, 305, 221–240. [Google Scholar] [CrossRef]
- Cai, Y.; Jiao, J.; Gui, Z.; Liu, Y.; Wang, W. Environmental variability in a stochastic epidemic model. Appl. Math. Comput. 2018, 329, 210–226. [Google Scholar] [CrossRef]
- Farajzadeh, M.; Doust, F.; Haghighifar, D.; Baleanu, D. The stability of gauss model having one-prey and two-predators. Abstr. Appl. Anal. 2012, 2012, 219640. [Google Scholar] [CrossRef]
- He, X.; Zheng, S. Protection zone in a diffusive predator-prey model with Beddington DeAngelis functional response. J. Math. Biol. 2016, 75, 239–257. [Google Scholar] [CrossRef]
- Huang, Y.; Shi, W.; Wei, C.; Zhang, S. A stochastic predator–prey model with Holling II increasing function in the predator. J. Biol. Dyn. 2021, 15, 1–18. [Google Scholar] [CrossRef]
- Jana, S.; Kar, T. Modeling and analysis of a prey-predator system with disease in the prey. Chaos Solitons Fractals 2013, 47, 42–53. [Google Scholar] [CrossRef]
- Kaur, G.; Ahmad, N. On study of immune response to tumor cells in prey-predator system. Int. Sch. Res. Not. 2014, 2014, 346597. [Google Scholar] [CrossRef]
- Bandyopadhyay, M.; Chattopadhyay, J. Ratio-dependent predator-prey model: Effect of environmental fluctuation and stability. Nonlinearity 2005, 18, 913–936. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, D.; Hayat, T.; Alsaedi, A. Dynamics of a stochastic predator–prey model with stage structure for predator and Holling type II functional response. J. Nonlinear Sci. 2018, 28, 1151–1187. [Google Scholar] [CrossRef]
- Bonate, P.L. Comprehensive overview of tumor growth modeling. In Proceedings of the 9th American Conference of Pharmacometrics (ACOP), San Diego, CA, USA, 7–11 October 2018. [Google Scholar]
- Singh, M.; Poonam, K. Qualitative analysis of a predator-prey model in the presence of additional food to predator and constant-yield predator harvesting. Univ. J. Appl. Math. Comput. 2019, 7, 20–34. [Google Scholar]
- Lestari, E.R.; Arifah, H. Dynamics of a mathematical model of cancer cells with chemotherapy. J. Phys. Conf. Ser. 2019, 1320, 1–8. [Google Scholar] [CrossRef]
- Li, S.; Wang, X. Analysis of a stochastic predator–prey model with disease in the predator and Beddington–Deangelis functional response. Adv. Differ. Equ. 2015, 2015, 224. [Google Scholar] [CrossRef]
- Liming, X.C.; Li, M.; Guo, B. Stability analysis of an HIV/AIDS epidemics model with treatment. J. Comput. Appl. 2009, 229, 313–323. [Google Scholar]
- Wahyuda, C.N.; Lestari, D. Local stability of AIDS epidemic model through treatment and vertical transmission with time delay. J. Phys. Conf. Ser. 2016, 693, 1–10. [Google Scholar]
- Alho, J.M. Forecasting life expectancy: A statistical look at model choice and use of auxiliary series. In Old and New Perspectives on Mortality Forecasting. Demographic Research Monographs; Bengtsson, T., Keilman, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Pham, H. Modeling U.S. mortality and risk-cost optimization on life expectancy. IEEE Trans. Reliab. 2011, 60, 125–133. [Google Scholar] [CrossRef]
- Derouich, M.; Boutayeb, A. An Avian influenzam mathematical model. Appl. Math. Sci. 2008, 2, 1749–1760. [Google Scholar]
- Mukhopadhyaya, B.; Bhattacharyya, R. Dynamics of a delay-diffusion prey-predator Model with disease in the prey. J. Appl. Math. Comput. 2005, 17, 361–377. [Google Scholar] [CrossRef]
- Aparico, J.P.; Chavez, C.C. Mathematical modelling of tuberculosis epidemics. Math. Biosci. Eng. 2009, 6, 209–237. [Google Scholar]
- Chavez, C.C.; Sony, B.J. Dynamical models of tuberculosis and their applications. Math. Biosci. Eng. 2004, 1, 361–404. [Google Scholar] [CrossRef]
- De Pillis, L.G.; Gu, W.; Fister, K.R.; Head, T.; Maples, K.; Murugan, A.; Neal, T.; Yoshida, K. Chemoterapy for tumors: An analysis of the dynamics and a study of quadratic and linear optimal control. Math. Biosci. 2006, 209, 292–315. [Google Scholar] [CrossRef]
- Kuznetsov, V.; Makalkin, I.; Taylor, M.; Perelson, A. Nonlinear dynamics of immunogenic tumors: Parameter estimation and global bifurcation analysis. Bull. Math. Biol. 1994, 56, 295–321. [Google Scholar] [CrossRef]
- Tsygvintsev, A.; Marino, S.; Kirschner, D.E. A Mathematical Model of Gene Therapy for The Treatment of Cancer. In Mathematical Models and Methods in Biomedicine; Springer: New York, NY, USA, 2012; pp. 357–373. [Google Scholar]
- Waziri, A.S.; Estomih, S.; Oluwole, D. Mathematical modelling of HIV/AIDS dynamic with treatment and vertical transmission. Appl. Math. 2012, 3, 77–89. [Google Scholar] [CrossRef]
- Wang, Y.; Kuang, C.; Ding, S.; Zhang, S. Stability and bifurcation of a stage-structured predator-prey model with both discete and distributed delays. Chaos Solitons Fractals 2013, 46, 19–27. [Google Scholar] [CrossRef]
- Kumar, S.; Chattopadh, S. A bioeconomic model of two equally dominated prey and one predator system. Mod. Appl. Sci. 2010, 4, 84–96. [Google Scholar] [CrossRef][Green Version]
- Liu, M. Dynamics of a stochastic regime-switching predator-prey model with modified Leslie–Gower Holling-type II schemes and prey harvesting. Nonlinear Dyn. 2019, 96, 417–442. [Google Scholar] [CrossRef]
- Liu, M.; Bai, C. Dynamics of a stochastic one-prey two-predator model with Lévy jumps. J. Comput. Appl. Math. 2016, 284, 308–321. [Google Scholar] [CrossRef]
- Liu, M.; Bai, C.; Deng, M.; Du, B. Analysis of stochastic two-prey one-predator model with Lévy jumps. Physica A 2016, 445, 176–188. [Google Scholar] [CrossRef]
- Tripathi, J.; Abbas, S.; Thakur, M. Local and global stability analysis of a two prey one predator model with help. Commun. Nonlinear Sci. 2014, 19, 3284–3297. [Google Scholar] [CrossRef]
- Pang, P.; Wang, M. Strategy and stationary pattern in a three-species predator–prey model. J. Differ. Equ. 2004, 200, 245–273. [Google Scholar] [CrossRef]
- Jiao, J.; Wang, R.; Chang, H.; Liu, X. Codimension bifurcation analysis of a modified Leslie–Gower predator-prey model with two delays. Int. J. Bifurcat. Chaos 2018, 28, 1850060. [Google Scholar] [CrossRef]
- Nie, L.; Peng, J.; Teng, Z.; Hu, L. Existence and stability of periodic solution of a Lotka–Volterra predator-prey model with state dependent impulsive effects. J. Comput. Appl. Math. 2009, 224, 544–555. [Google Scholar] [CrossRef]
- Tian, Y.; Sun, K.; Chen, L. Comment on existence and stability of periodic solution of a Lotka–Volterra predator–prey model with state dependent impulsive effects. J. Comput. Appl. Math. 2010, 234, 2916–2923. [Google Scholar] [CrossRef]
- Law, G.R. What do epidemiologists mean by ‘population mixing’? Pediatric Blood Cancer 2008, 51, 155–160. [Google Scholar] [CrossRef]
- Haque, M.; Zhen, J.; Ventrino, E. An eco-epidemiological predator-prey model with standard disease incidence. Math. Methods Appl. Sci. 2008, 35, 875–898. [Google Scholar]
- Jiang, D. Analysis of a predator-prey model with disease in the prey. Int. J. Biomath. 2013, 6, 1350012. [Google Scholar]
- Naji, R.K.; Mustafa, A.N. The dynamics of an eco-epidemiological model with nonlinear incidence rate. J. Appl. Math. 2012, 11, 853–862. [Google Scholar] [CrossRef]
- Pal, P.; Haque, M.; Mandal, P. Dynamics of a predator–prey model with disease in the predator. Math. Methods Appl. Sci. 2013, 37, 2429–2450. [Google Scholar] [CrossRef]
- Xiao, Y.; Chen, L. Modeling and analysis of a predator–prey model with disease in the prey. Math. Biosci. 2001, 171, 59–82. [Google Scholar] [CrossRef]
- Xu, R.; Zhang, S. Modelling and analysis of a delayed predator–prey model with disease in the predator. Appl. Math. Comput. 2013, 224, 372–386. [Google Scholar] [CrossRef]
- Battegay, M. 2019-novel Coronavirus (2019-nCoV): Estimating the case fatality rate—A word of caution. Swiss Med. Wkly. 2020, 150, 506. [Google Scholar] [CrossRef]
- Chin, W.H.; Chu, J.T.S.; Perara, M.R.A.; Hui, K.P.Y.; Yen, M.C.W.; Chan, M.; Paris, M.C.W.; Poon, L.L.M. Stability of SARS-CoV-2 in different environmental conditions. Lancet Mircobe 2020, 20, e145. [Google Scholar] [CrossRef]
- Kucharski, J. Early dynamics of transmission and control of COVID-19: A mathematical modelling study. Lancet Infect. Dis. 2020, 20, 553–558. [Google Scholar] [CrossRef]
- Pham, H. On estimating the number of deaths related to Covid-19. Mathematics 2000, 8, 655. [Google Scholar] [CrossRef]
- Pham, H. Estimating the COVID-19 death toll by considering the time-dependent effects of various pandemic restrictions. Mathematics 2020, 8, 1628. [Google Scholar] [CrossRef]
- Pham, H.; Pham, D.H. A novel generalized logistic dependent model to predict the presence of breast cancer based on biomarkers. Concurr. Comput. Pract. Exp. 2020, 32, 1. [Google Scholar] [CrossRef]
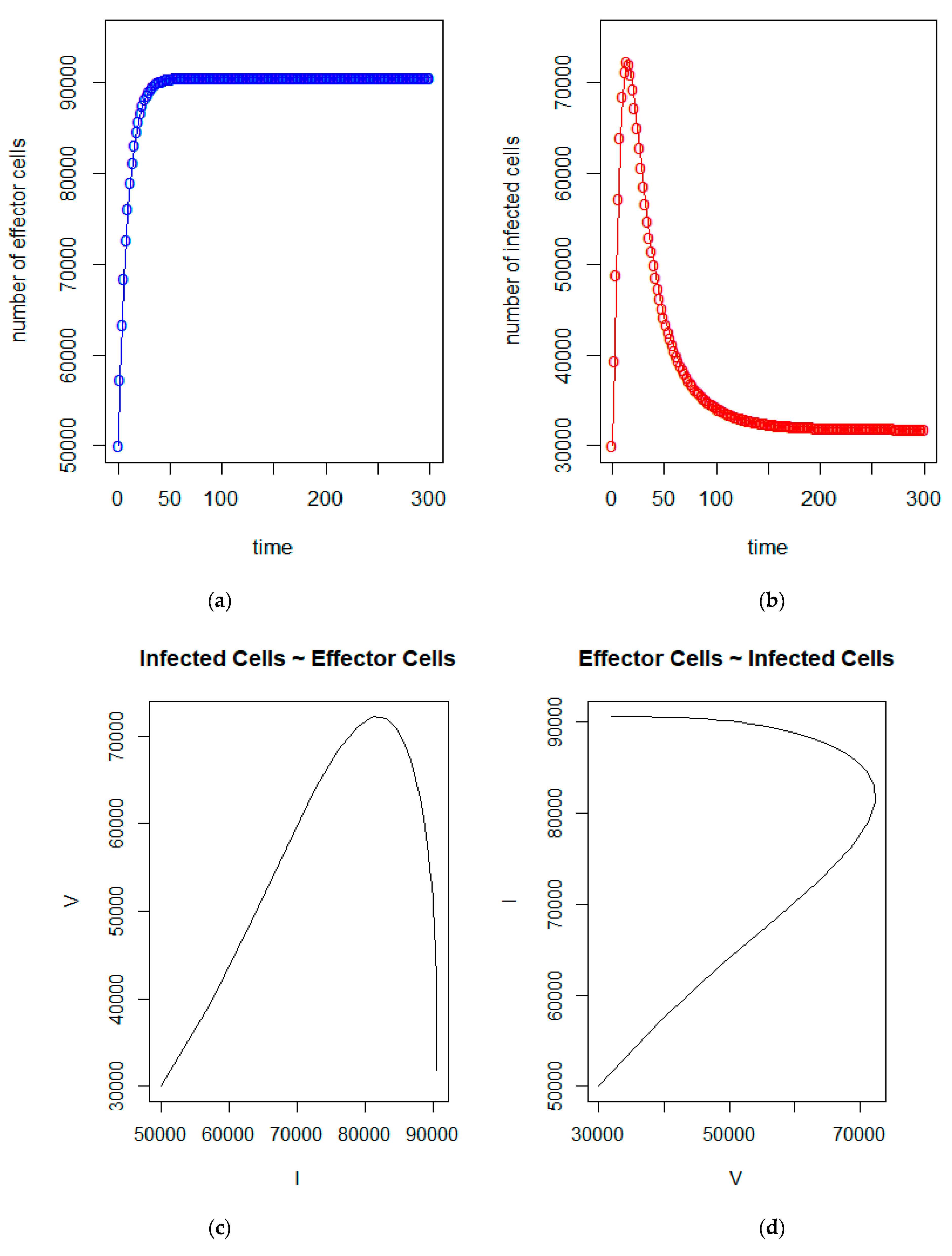
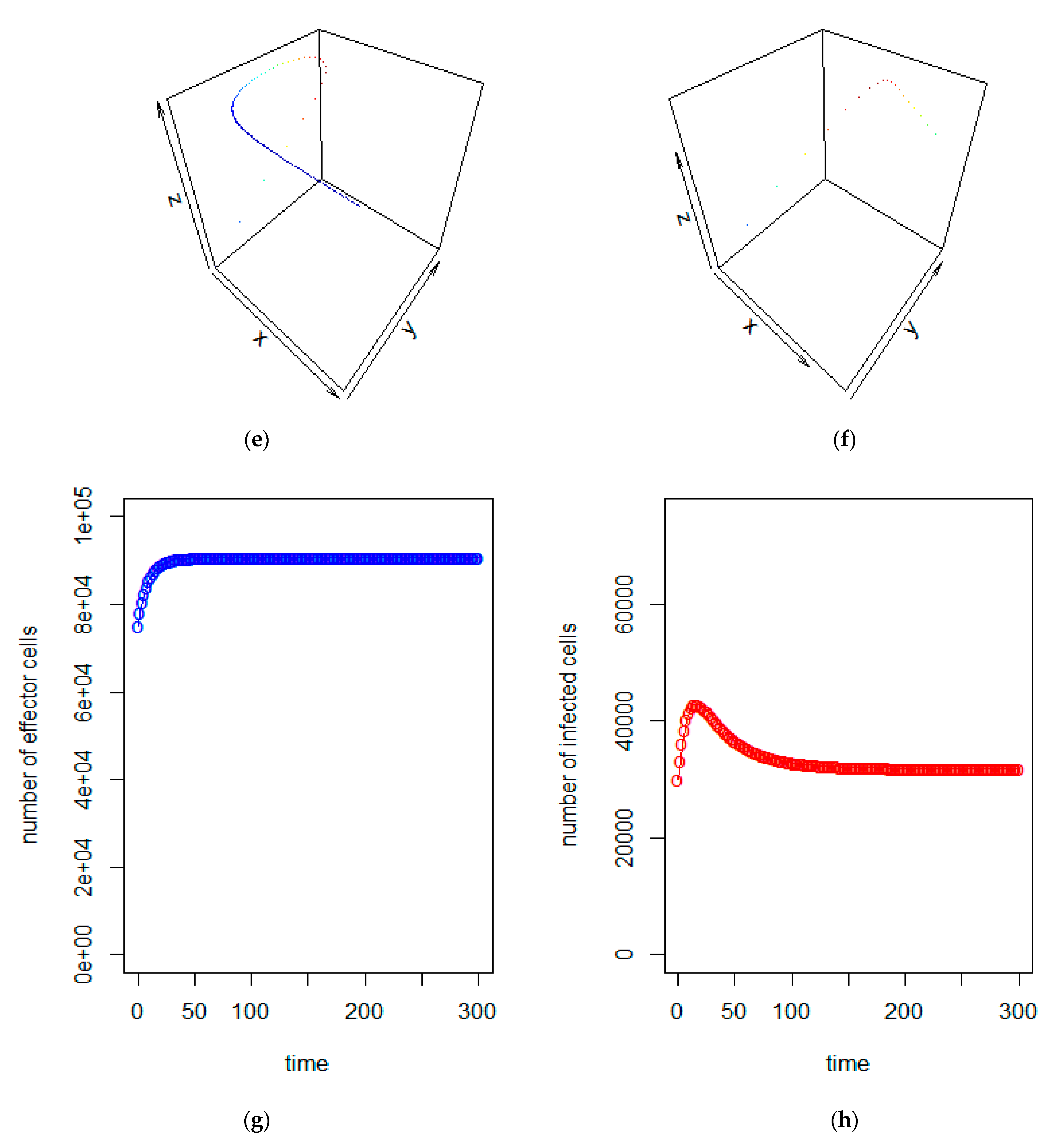
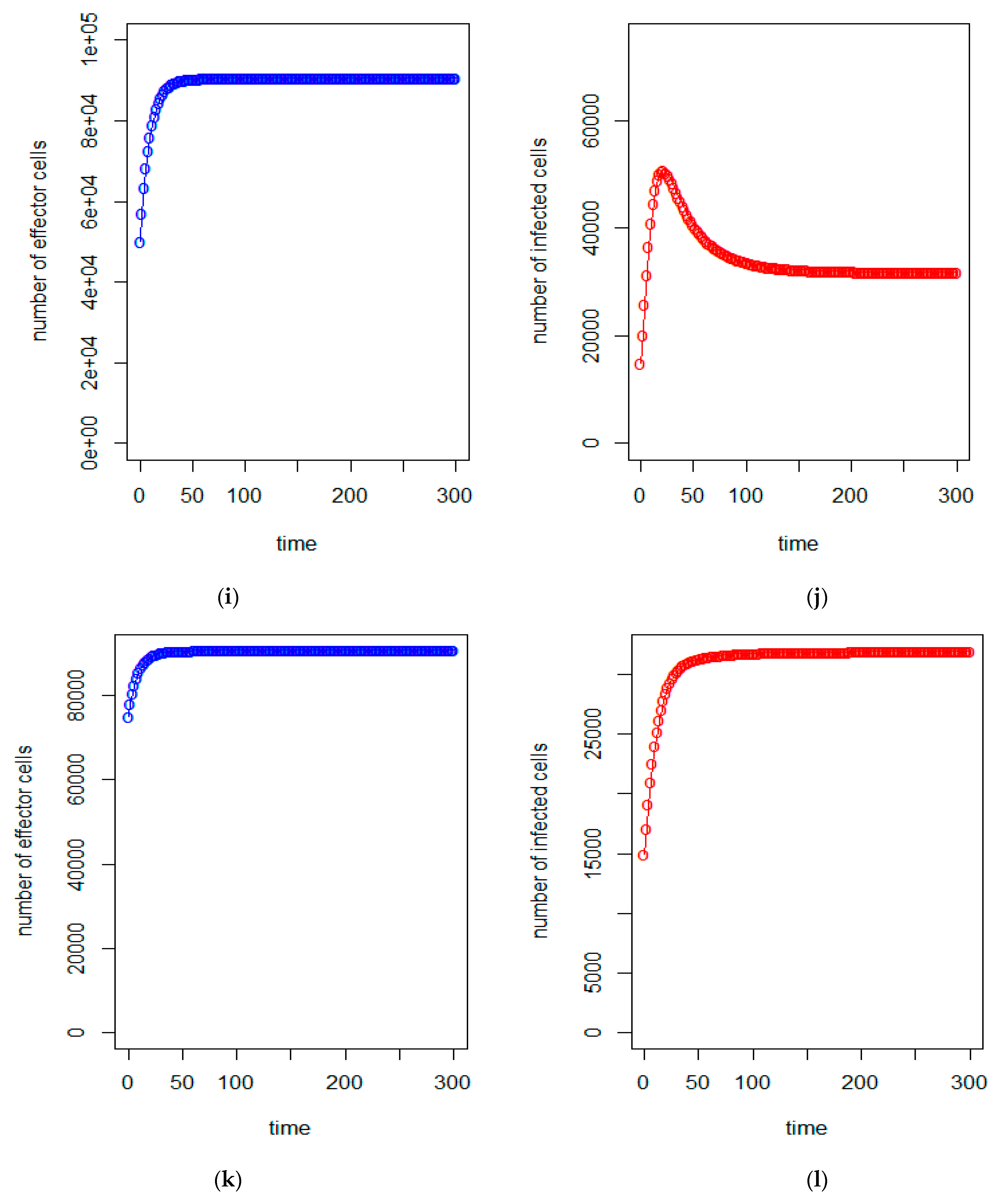
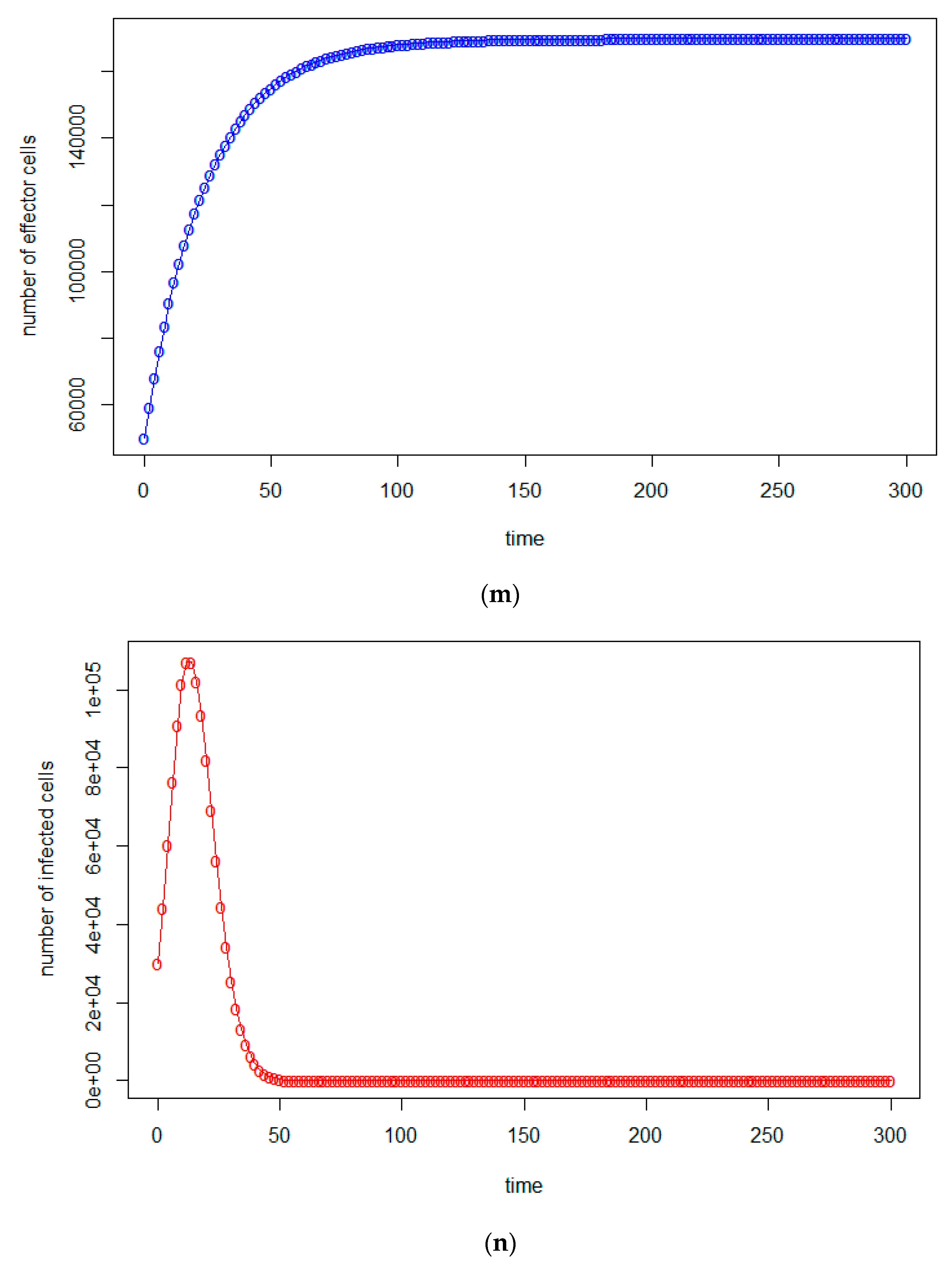
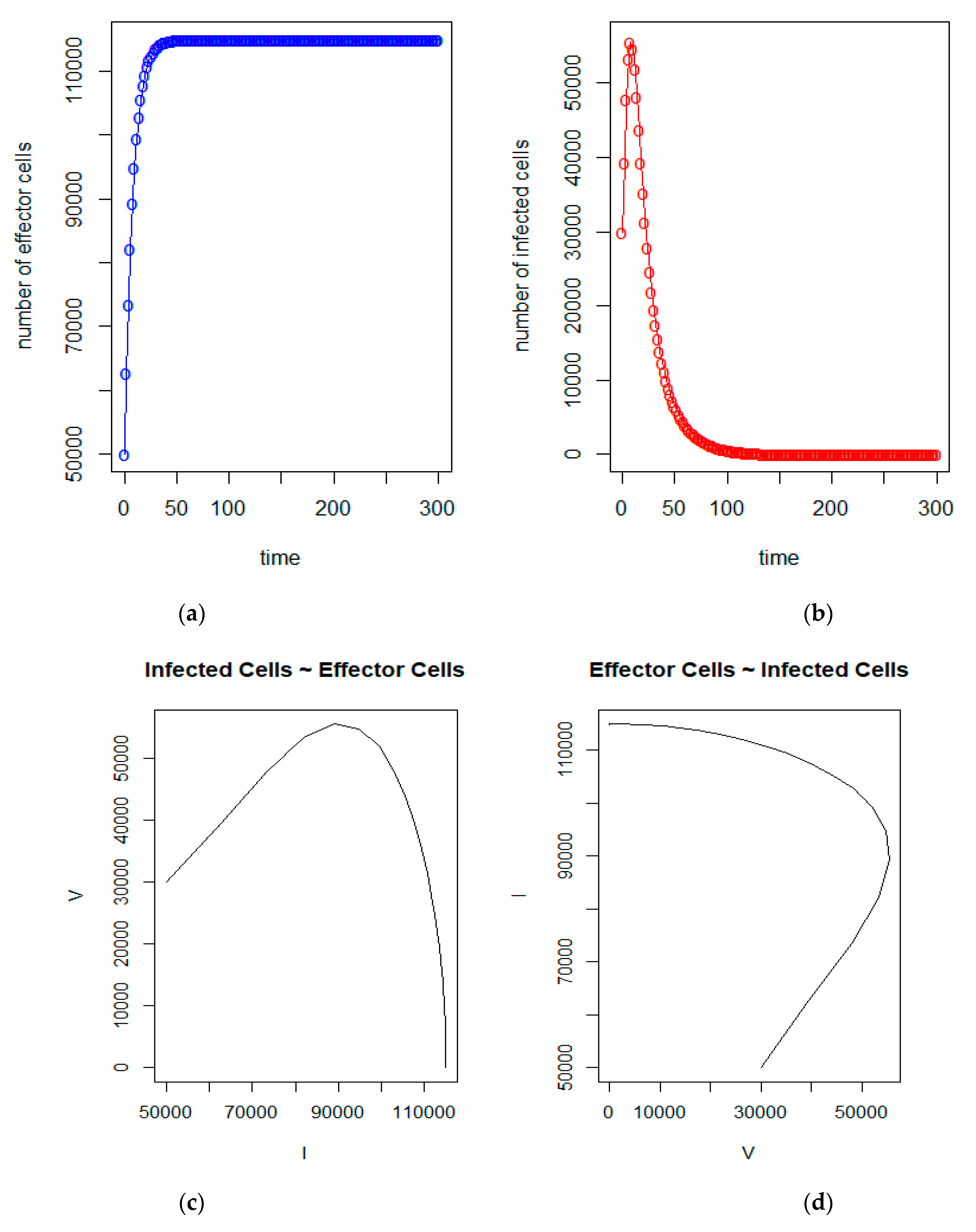


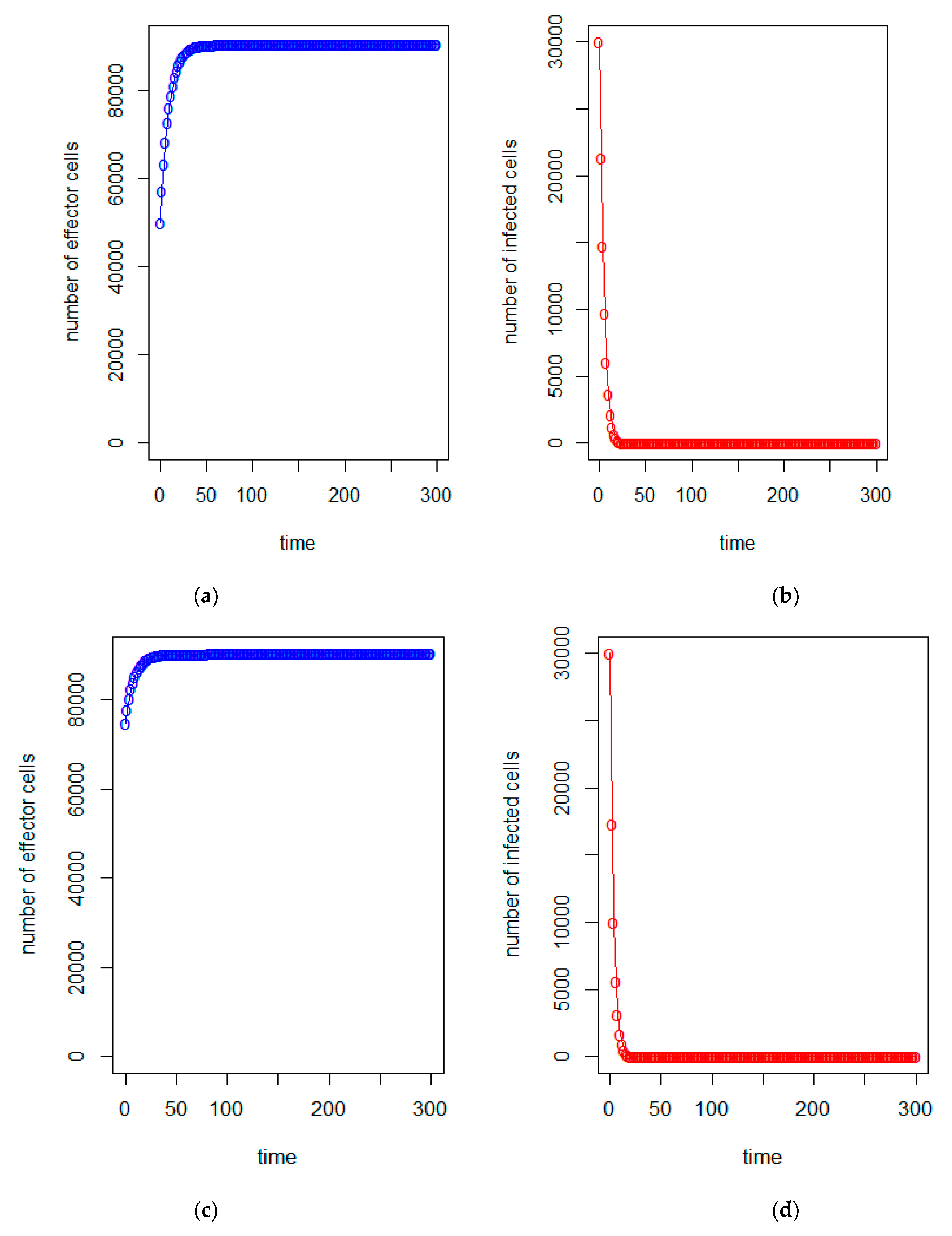
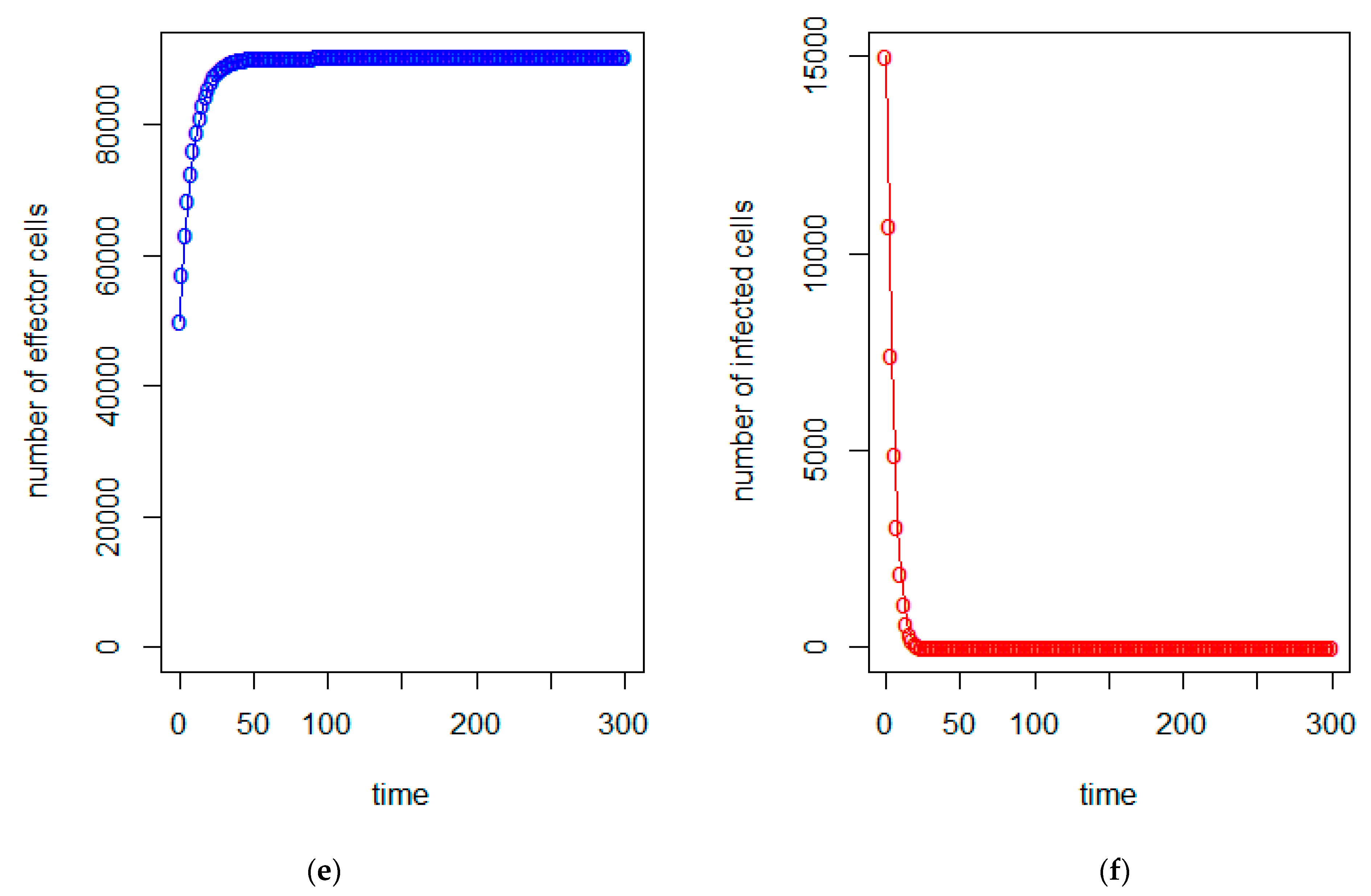
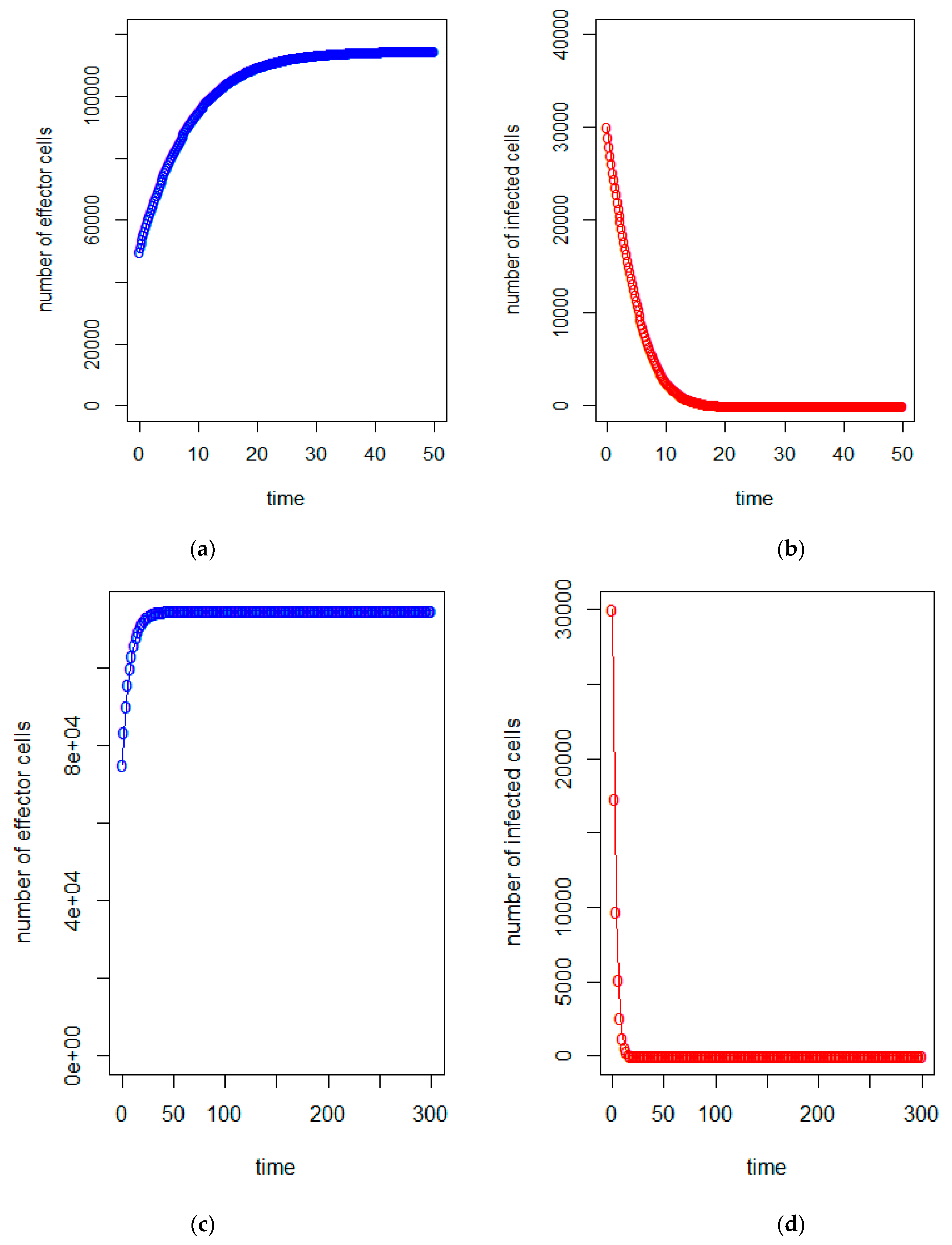
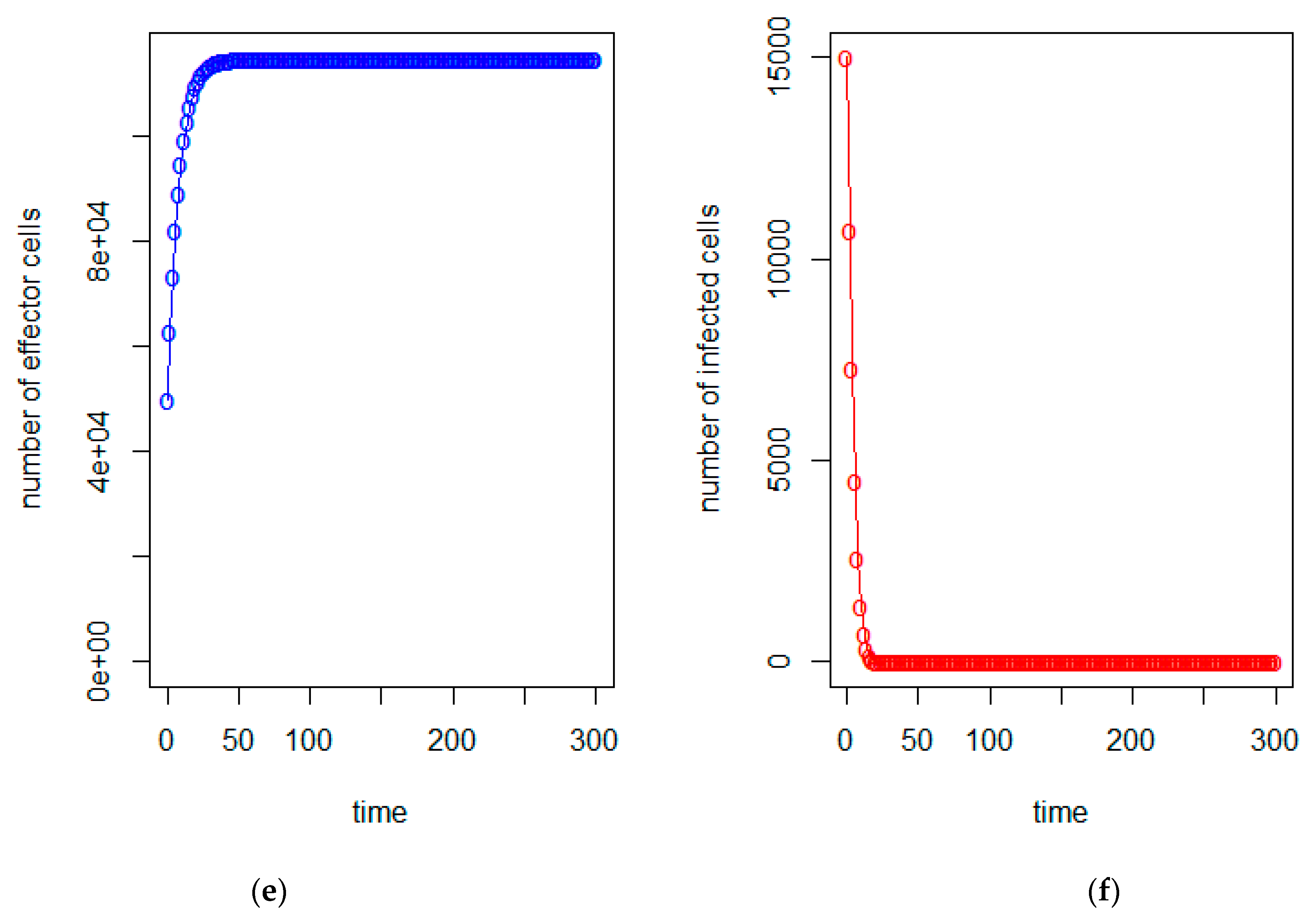
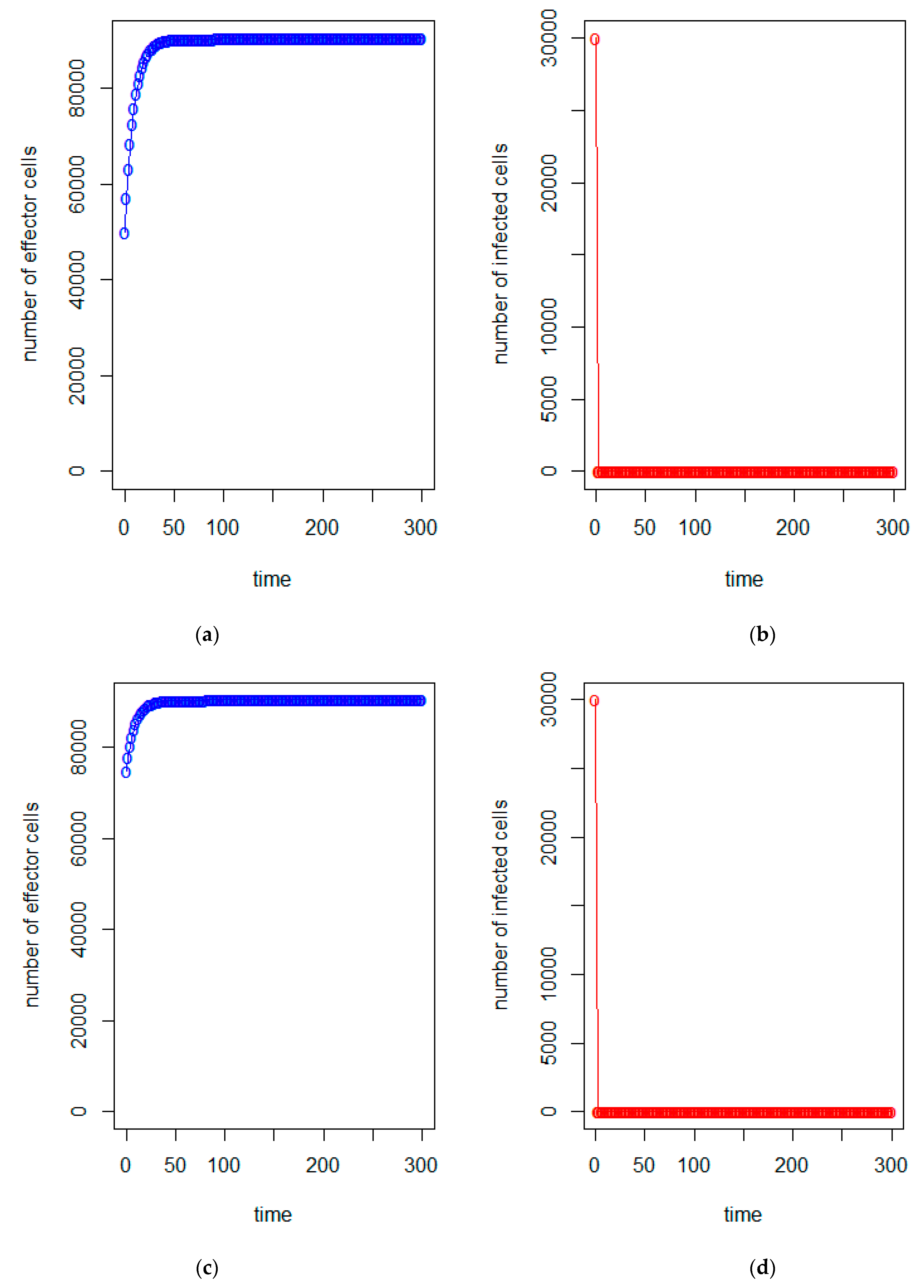
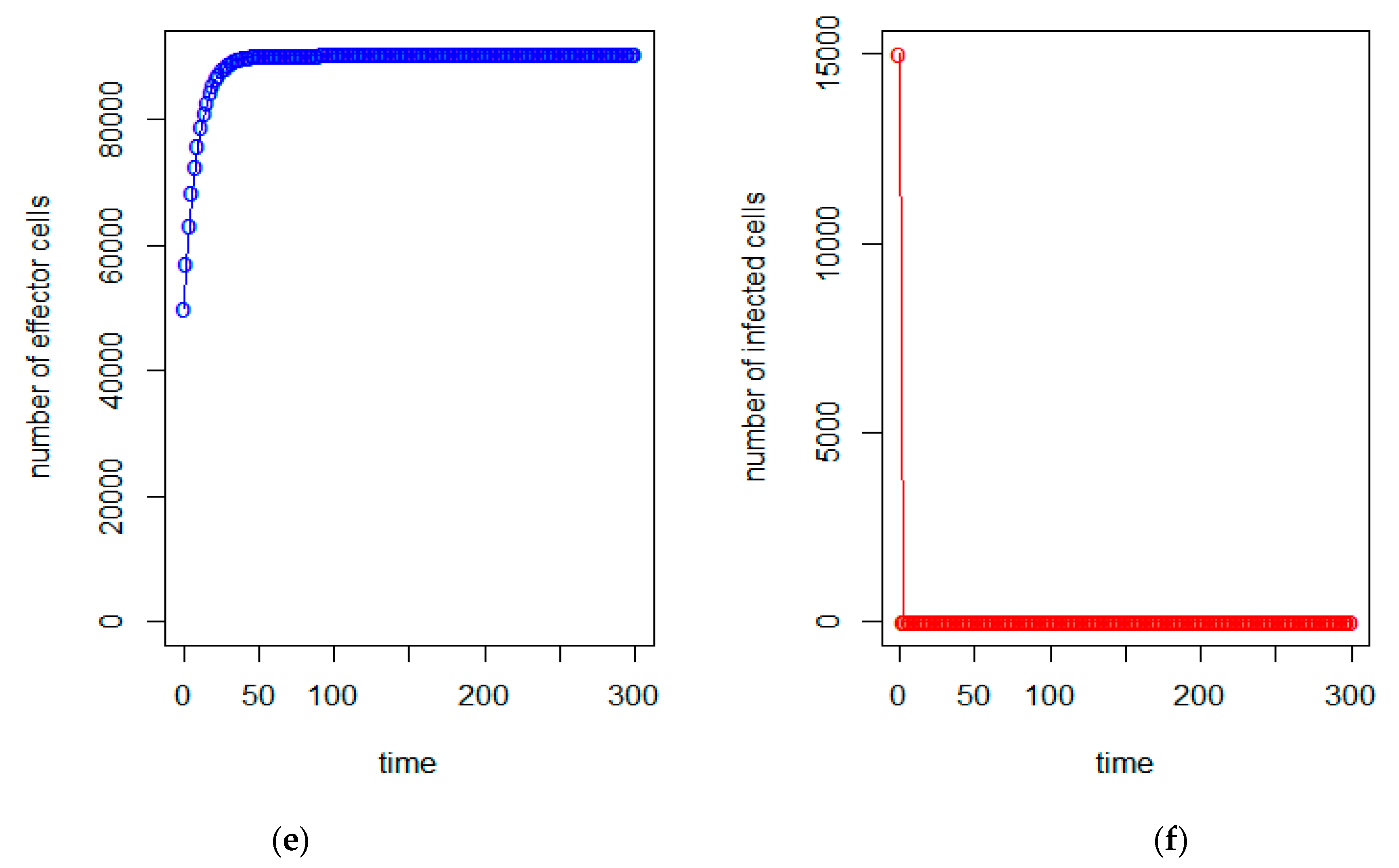

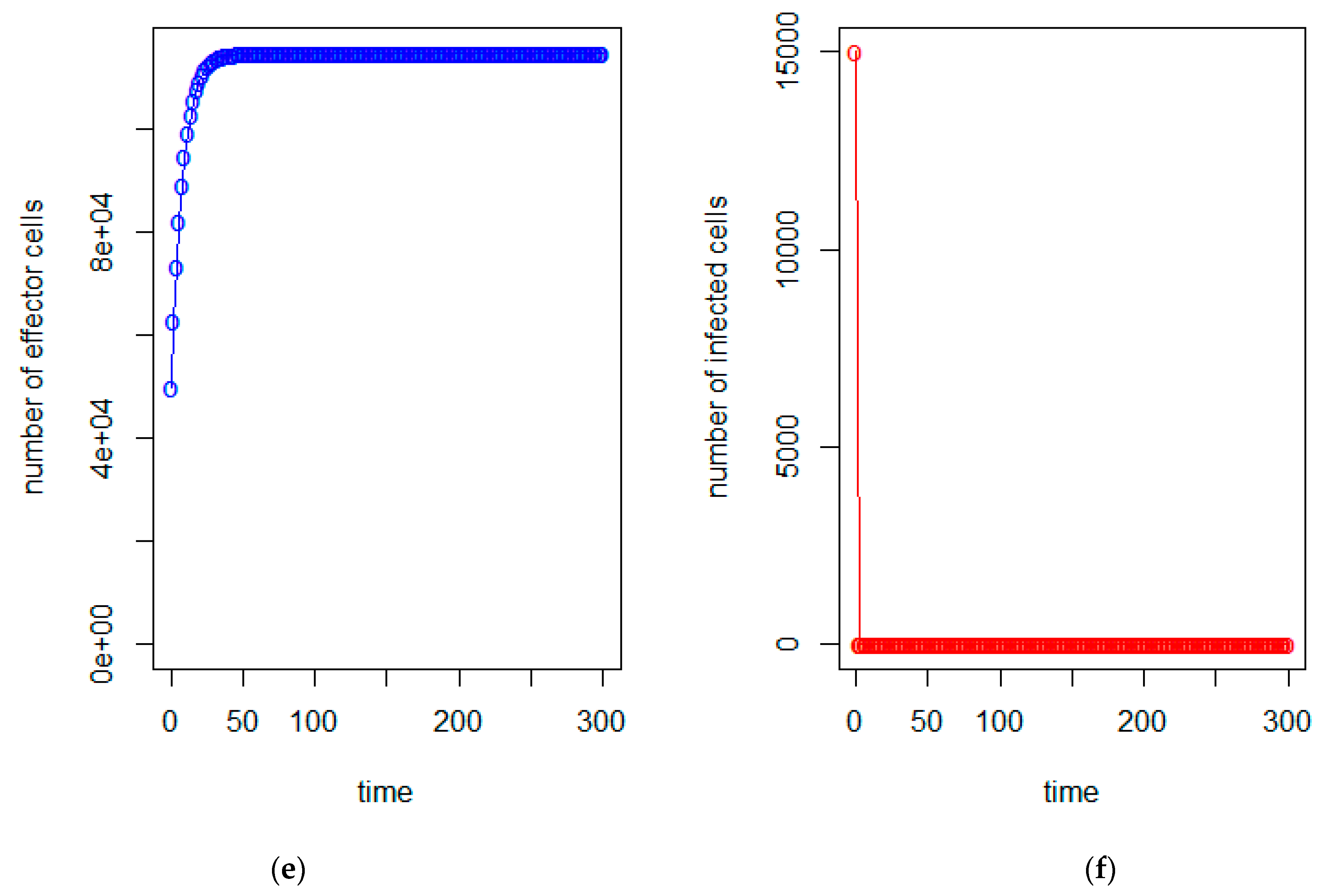
| a = 0.43/day | b = 43 × 10−7/cells/day | c = 4.12 × 10−2/day |
| d = 15 × 10−5/day | e = 4 × 10−8/day | f = 4 × 10−7/day |
| g = 3 × 10−6/day | h = 20.2 (cells) | k = 105/cells |
| m = 2 × 10−11 cells/day | p = 341 × 10−12/day | s = 7000 cells/day |
| a = 0.43/day | b = 4.3 × 10−4/(cells·day) | c = 4.12 × 10−2 0.0412/day |
| d = 15 × 10−5/day | e = 4 × 10−8/day | f = 0.0000004/day |
| g = 3 × 10−6/day | h = 20.2 (cells) | k = 105/cells |
| m = 2 × 10−11/day | p = 341 × 10−12/cell | s = 7000 cells/day |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, H. A Dynamic Model of Multiple Time-Delay Interactions between the Virus-Infected Cells and Body’s Immune System with Autoimmune Diseases. Axioms 2021, 10, 216. https://doi.org/10.3390/axioms10030216
Pham H. A Dynamic Model of Multiple Time-Delay Interactions between the Virus-Infected Cells and Body’s Immune System with Autoimmune Diseases. Axioms. 2021; 10(3):216. https://doi.org/10.3390/axioms10030216
Chicago/Turabian StylePham, Hoang. 2021. "A Dynamic Model of Multiple Time-Delay Interactions between the Virus-Infected Cells and Body’s Immune System with Autoimmune Diseases" Axioms 10, no. 3: 216. https://doi.org/10.3390/axioms10030216
APA StylePham, H. (2021). A Dynamic Model of Multiple Time-Delay Interactions between the Virus-Infected Cells and Body’s Immune System with Autoimmune Diseases. Axioms, 10(3), 216. https://doi.org/10.3390/axioms10030216





